A&A 426, 53-63 (2004)
DOI: 10.1051/0004-6361:20041205

Dwarf elliptical galaxies with kinematically decoupled cores

S. De Rijcke1,[*] - H. Dejonghe 1 - W. W. Zeilinger 2 - G. K. T. Hau 3


1 - Sterrenkundig Observatorium, Ghent University, Krijgslaan 281, S9, 9000 Gent, Belgium
2 - Institut für Astronomie, Universität Wien, Türkenschanzstraße 17, 1180 Wien, Austria
3 - ESO, Karl-Schwarzschild-Strasse 2, 85748 Garching bei München, Germany

Received 30 April 2004 / Accepted 7 July 2004

Abstract
We present, for the first time, photometric and kinematical evidence, obtained with FORS2 on the VLT, for the existence of kinematically decoupled cores (KDCs) in two dwarf elliptical galaxies; FS76 in the NGC 5044 group and FS373 in the NGC 3258 group. Both kinematically peculiar subcomponents rotate in the same sense as the main body of their host galaxy but betray their presence by a pronounced bump in the rotation velocity profiles at a radius of about 1''. The KDC in FS76 rotates at $10 \pm 3$ km s-1, with the host galaxy rotating at $15 \pm 6$ km s-1; the KDC in FS373 has a rotation velocity of $6 \pm 2$ km s-1 while the galaxy itself rotates at $20 \pm 5$ km s-1. FS373 has a very complex rotation velocity profile with the velocity changing sign at 1.5 $R_{\rm e}$. The velocity and velocity dispersion profiles of FS76 are asymmetric at larger radii. This could be caused by a past gravitational interaction with the giant elliptical NGC 5044, which is at a projected distance of 50 kpc. We argue that these decoupled cores are most likely not produced by mergers in a group or cluster environment because of the prohibitively large relative velocities. A plausible alternative is offered by flyby interactions between a dwarf elliptical or its disky progenitor and a massive galaxy. The tidal forces during an interaction at the relative velocities and impact parameters typical for a group environment exert a torque on the dwarf galaxy that, according to analytical estimates, transfers enough angular momentum to its stellar envelope to explain the observed peculiar kinematics.

Key words: galaxies: dwarf - galaxies: evolution - galaxies: kinematics and dynamics - galaxies: formation

1 Introduction

Dwarf elliptical galaxies (dEs) are small, low-luminosity galaxies with diffuse, exponentially declining surface-brightness profiles (Ferguson & Binggeli 1994). They are a gregarious species and are found abundantly in clusters and groups of galaxies (although they seem to avoid the very cluster center where the tidal forces exerted by the cluster potential are strong enough to disrupt them, Trujillo et al. 2002). According to one model for dE evolution, they are primordial objects. Supernova explosions heat the interstellar gas to temperatures exceeding the escape velocity, expelling gas from the galaxy (Dekel & Silk 1986; Mori & Yoshii 1999). This scenario explains the diffuse appearance of dEs with enhanced star formation at larger radii. They are expected to form a homogeneous class and to have properties that correlate tightly with mass. Alternatively, dEs could stem from late-type disk galaxies that entered the clusters and groups of galaxies about 5 Gyr ago (Conselice et al. 2001). N-body simulations show that high-speed gravitational interactions trigger bar-formation in any small disk galaxy orbiting in a cluster (Moore et al. 1996) or around a massive galaxy in a group environment (Mayer et al. 2001) and strip large amounts of stars, gas, and dark matter from it by tidal forces. Internal dynamical processes subsequently transform a disk galaxy into a dynamically hot spheriodal dE within a timespan of about 5 Gyr. Some dEs might still contain a memory of their former state. Examples are dEs with embedded stellar disks, bars, and spiral structure (Barazza et al. 2002; De Rijcke et al. 2003a; Graham et al. 2003) and with sizable amounts of warm gas, suggesting recent star formation in some dEs (De Rijcke et al. 2003b; Michielsen et al. 2004). Moreover, rotationally flattened dEs have been discovered (De Rijcke et al. 2001; Simien & Prugniel 2002). The harassment model also offers a natural explanation for the Butcher-Oemler effect (Butcher & Oemler 1978) and the morphology-density relation (Mayer et al. 2001).

  \begin{figure} \par\includegraphics[width=6.7cm,clip]{1205fig1.eps} \end{figure} Figure 1: 270 s I-band image of FS373, a dE2,N in the NGC 3258 group. North is up, east is left.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=6.7cm,clip]{1205fig2.eps} \end{figure} Figure 2: 300 s I-band image of FS76, a dE0,N in the NGC 5044 group. North is up, east is left.
Open with DEXTER

In this paper, we present photometric and kinematical evidence for the presence of kinematically decoupled cores (KDCs) in two dEs in a group environment: FS373 and FS76 (we use the galaxy identification numbers introduced by Ferguson & Sandage 1990). FS373 (Fig. 1) is a nucleated dwarf elliptical (dE2, N) in the NGC 3258 group at a distance of 41 Mpc (we use H0=70 km s-1 Mpc-1 throughout the paper). FS76 (Fig. 2) is a dE0 in the NGC 5044 group, at a distance of 36 Mpc.The pronounced bump in the rotation velocity profiles signals the presence of a dynamically peculiar component in corotation with the main body of these galaxies. Both in FS76 and FS373, the KDC dominates the kinematics out to a radius of  1.5''-2'', which is well outside the nucleus or the central density cusp. Hence, the KDC should not be associated with the nucleus in the center of the host dE. It is the first time that evidence is found for the existence of KDCs in dwarf elliptical galaxies.

Massive elliptical galaxies with KDCs both in corotation and in counterrotation with the host galaxy (e.g. Efstathiou et al. 1982; Cappellari et al. 2002) and ellipticals with peculiar central kinematics (Franx et al. 1991) have been known for a long time. Bender & Surma (1992) found KDCs in ellipticals to be more metalrich than the galaxies' main bodies. A merger of a giant and a dwarf galaxy was a plausible way of producing KDCs with the observed properties (Balcells & Quinn 1990). The KDC's angular momentum vector is set predominantly by the engulfed dwarf's angular momentum and need not be aligned with that of the giant galaxy. KDCs in S0s can equally well be explained by the merger of two unequal-mass spiral galaxies (Balcells & González 1998). KDCs thus provide strong evidence that mergers of (gasrich) progenitor galaxies played an important role in the past evolution of bright elliptical and lenticular galaxies, corroborating the hierarchical merging model for cosmological structure formation.

In Sect. 2, we discuss the details of the observations and the data-reduction process. The stellar kinematics, photometry, and measurements of the strength of the near-infrared Ca II triplet (quantified by the CaT index) of these objects are presented in Sect. 3, followed by a study of their internal dynamics in Sect. 4. The significance of these results in the light of the existing theories for dE evolution is discussed in Sect. 5. We summarize our conclusions in Sect. 6.

   
2 Observations and data reduction

Within the framework of an ESO Large Program, we collected Bessel VRI-band images and deep major and minor axis spectra with unprecedented spatial and spectral resolution of a sample of 15 dEs and dwarf lenticulars (dS0), both in group (NGC 5044, NGC 5898, and NGC 3258 groups) and cluster environments (Fornax cluster). The data were taken with the FORS2 imaging spectrograph mounted on the VLT. The images were bias-subtracted and flatfielded using skyflats taken during twilight of the same night as the science frames. The sky background was removed by fitting a tilted plane to regions of the images free of stars or other objects and subtracting it. The photometric zeropoints in each band were measured using photometric standard stars observed during the same night as the science frames. The images were corrected for airmass and interstellar extinction, using the Galactic extinction estimates from Schlegel et al. (1998).

The spectra, with typical exposure times of 5-8 h per position angle and a seeing in the range 0.3''-1.0'' FWHM, cover the wavelength region around the strong Ca II triplet absorption lines ($\sim $8600 Å). All standard data reduction procedures (bias-subtraction, flatfielding, cosmic removal, wavelength-calibration, sky-subtraction, flux-calibration) were carried out with ESO-MIDAS[*], IRAF[*], and our own software. Fitting the dispersion relation by a cubic spline, the lines of the arc spectra are rectified to an accuracy of 1-2 km s-1 FWHM. We extracted the stellar kinematical information by fitting a weighted mix of late G to late K giant stars, broadened with a parameterised line-of-sight velocity distribution (LOSVD) to the galaxy spectra. We approximated the LOSVD by a fourth-order Gauss-Hermite series (Gerhard 1993; van der Marel & Franx 1993) (the kinematics of the full sample will be presented in a forthcoming paper). The strong Ca II lines, which contain most of the kinematical information, are rather insensitive to the age and metallicity of an old stellar population (see Michielsen et al. 2003, and references therein), so template mismatch does not significantly affect the results. The spectra contain useful kinematical information out to 1.5-2 half-light radii ($R_{\rm e}$).

This is the first time a data set of dE kinematics is assembled on a par with what so far has been achieved for bright elliptical galaxies. Thanks to the excellent quality of the spectra, both in terms of instrumental resolution and of seeing, we are able to spatially resolve small-scale structures in the kinematic profiles.

   
3 Kinematics, line-strengths, and photometry

Before discussing our observations, we first focus on the environments of FS76 and FS373. Using ROSAT observations of the X-ray emitting gas in the NGC 5044 group, which is dominated by a single central giant elliptical, NGC 5044, David et al. (1994) derive a total gravitating mass of $M \approx 1.6 \times 10^{13}~h^{-1}_{50}~ M_\odot$ within a radius of 250  h-150 kpc, corresponding to $M/L_B \approx 130~h_{50}$ in solar units and a galaxy velocity dispersion $\sigma_{\rm gal}= 330$ km s-1. The mean systemic velocity of the NGC 5044 group is $v_{\rm sys}=2549$ km s-1, according to NED. The elongated NGC 3258 group is dominated by two giant ellipticals: NGC 3258 and NGC 3268. ASCA observations of the X-ray emitting gas in the NGC 3258 group by Pedersen et al. (1997) lead to a total mass estimate $M \approx 2.3 \times 10^{13}~h^{-1}_{50}~ M_\odot$ within a radius of 240  h-150 kpc, corresponding to $M/L_B \approx 240~h_{50}$ and a galaxy velocity dispersion $\sigma_{\rm gal} \approx 400$ km s-1. The mean recession velocity of the group is $v_{\rm sys}=2848$ km s-1, according to NED. The position of FS373 in the outskirts of the NGC 3258 group is indicated in Fig. 3. FS76 on the other hand has a position very close to the center of the group (in projection), at a projected distance of 50 kpc west of NGC 5044 (Fig. 4).

  \begin{figure} \par\includegraphics[width=8cm,clip]{1205fig3.eps} \end{figure} Figure 3: Position of FS373 (asterisk) inside the NGC 3258 group. Small dots indicate the positions of the 375 group members listed in NED. Large dots indicate the positions of galaxies brighter than MB = -20.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.6cm,clip]{1205fig4.eps} \end{figure} Figure 4: Position of FS76 (asterisk) inside the NGC 5044 group. Small dots indicate the positions of the 160 group members listed in NED. Large dots indicate the positions of galaxies brighter than MB = -20.
Open with DEXTER

3.1 Kinematics


  \begin{figure} \par\includegraphics[width=15.3cm,clip]{1205fig5.eps} \end{figure} Figure 5: Major-axis kinematics of FS373. a) velocity dispersion, b) mean velocity. The bottom panels zoom in on the central region around the KDC to show the velocity dispersion c) and mean velocity d) in more detail. The linear distance scale in kiloparsecs is indicated above the top panels (assuming H0=70 km s-1 Mpc-1). The slit position on the sky is indicated in panel a). FS373 shows a pronounced bump in the mean velocity profile around $\sim $1'' and falls to zero at $\sim $2'' before rising again; this is characteristic of a KDC. The dispersion has a central depression, within the inner arcsecond, of $\sim $7 km s-1, which could hint at the presence of a cold stellar disk.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=15cm,clip]{1205fig6.eps} \end{figure} Figure 6: Major-axis kinematics of FS76. Same layout as in Fig. 5. The giant elliptical NGC 5044 is at a projected distance of 50 kpc towards the east (i.e. positive radii are closest to NGC 5044). FS76 shows a pronounced bump in the mean velocity profile around $\sim $0.8''. The velocity dispersion remains approximately flat at $\sim $50 km s-1 within the inner 2'' and rises rather sharply outside this radius, indicative of a cold stellar disk.
Open with DEXTER

The systemic velocity of FS373, $v_{\rm sys}=2415 \pm 1$ km s-1, lies within 1 $\sigma_{\rm gal}$ of the mean recession velocity of the NGC 3258 group, confirming it as a group member. Judging from panels b and d in Fig. 5, FS373 has a complex mean velocity profile. The KDC's solid body rotation dominates the central kinematics and reaches a peak velocity of $6 \pm 2$ km s-1 around 200 pc (or 1/8 $R_{\rm e}$) while outside the KDC the velocity rises to $20 \pm 5$ km s-1 at about 1 $R_{\rm e}$. The velocity changes sign again around 2.2 kpc $~~ \approx 1.5~R_{\rm e}$. The velocity dispersion, presented in panels a and c in Fig. 5, rises from $48 \pm 2$ km s-1 up to $90 \pm 12$ km s-1 at 1 $R_{\rm e}$ and remains flat beyond that radius (the outermost data points suggest that the dispersion may decline further out). Within the inner arcsecond, the velocity dispersion shows a pronounced drop of about 7 km s-1, suggestive of the presence of a dynamically cold sub-component.

Table 1: Basic photometric parameters of FS76 and FS373: reddening-corrected V magnitude mV0, exposure time tV(seconds), seeing FWHMV (arcsec), and their R and I band analogs, and the R-band effective radius $R_{\rm e}$.

FS76 has a systemic velocity $v_{\rm sys}=2726 \pm 2$ km s-1 that places it within 1 $\sigma_{\rm gal}$ of the mean NGC 5044 group velocity. NGC 5044 has almost the same systemic velocity:  $v_{\rm sys}^{\rm N5044}=2704 \pm 33$ km s-1 (Nicolaci da Costa et al. 1998). The kinematics of FS76, presented in Fig. 6, are equally intriguing as those of FS373. The major axis velocity rises rapidly to $10 \pm 3$ km s-1 at a radius of about 200 pc $~ ~ \approx 1/4 ~R_{\rm e}$ while the bulk rotation flattens off at $15 \pm 6$ km s-1 beyond 600 pc $~~ \approx 1 ~ R_{\rm e}$. The velocity dispersion is virtually constant at $50 \pm 3$ km s-1 within the inner $2'' \approx 0.5~R_{\rm e}$ and rises up to $75 \pm 8$ km s-1 at $1~R_{\rm e}$. Surprisingly, the velocity dispersion declines beyond that radius and drops to $50 \pm 15$ km s-1at $2~R_{\rm e}$. There is a hint of minor-axis rotation (<5 km s-1), which could be attributed to an inclined embedded disk (De Rijcke et al. 2001). Outside 1 $~R_{\rm e}$, the velocity and velocity dispersion profiles are asymmetric, suggestive of a past gravitational interaction, most likely with NGC 5044.

3.2 Photometry and CaT* index

We measured the surface-brightness profile, position angle, and ellipticity $\epsilon = 1-b/a$ of FS373 and FS76 as a function of the geometric mean of major and minor axis distance, denoted by a and b respectively. These were obtained using our own software. Basically, the code fits an ellipse through a set of positions where a given surface brightness level is reached. The shape of an isophote, relative to the best fitting ellipse with semi-major axis a and ellipticity $\epsilon$, is quantified by expanding the intensity variation along this ellipse in a fourth order Fourier series with coefficients S4, S3, C4 and C3:

 
$\displaystyle I(a,\theta) = I_0(a) \left[ 1 + C_3(a) \cos(3\theta)+ C_4(a) \cos(4\theta)) + S_3(a)\sin(3\theta))+ S_4(a) \sin(4\theta) \right].$     (1)

Here, I0(a) is the average intensity of the isophote and the angle $\theta$ is measured from the major axis. The basic photometric parameters of the two galaxies are presented in Table 1. The surface-brightness, position angle, ellipticity, and C4 profiles are presented in Fig. 7.

We fitted a seeing-convolved Sérsic profile to the R-band surface brightness profile $\mu_{R}(r) = \mu_{R,\rm0} + 1.086(r/r_0)^{1/n}$, or equivalently $\mu_{R}(r) = \mu_{R,\rm0} + 2.5 b_n (r/R_{\rm e})^{1/n}$, with r0 the scale-length, $R_{\rm e}$ the half-light radius, $b_n \approx 0.848 n - 0.142$, radius $r=\sqrt{ab}$, measured from the central nucleus or intensity peak. The seeing characteristics were estimated from about 10 stars in each image. We simply minimized the quadratic difference between the observed surface brightness profile and the seeing-convolved Sérsic profile using a non-linear minimization routine. The formal error bars are approximated by the diagonal elements of the estimated covariance matrix of this non-linear problem. The results of this fit are presented in Fig. 7 and Table 2. Since both galaxies have a central brightness peak that cannot be fitted with a Sérsic profile, the inner 2'' were excluded from the fit. The value n=4corresponds to a de Vaucouleurs profile, typical for massive ellipticals; n=1 corresponds to the diffuse exponential profile, typical for the faintest dwarf ellipticals. The n values found by us agree with the dE classification of these galaxies.

FS373 has a systematically positive C4 and its isophotes are consequently slightly disky. Moreover, the ellipticity does not decline all the way to the center but instead rises inwardly inside the inner 2''. If the true flattening were constant all the way to the center, convolution with a circularly symmetric Gaussian seeing profile would make the inner isophotes steadily rounder as one approaches the center. In order to understand the observed behavior of the ellipticity profile, we calculated the appearance of a galaxy with a flattening varying smoothly between $\epsilon =0$ in the very center and $\epsilon=2.3$ at 6'' and beyond, to which an exponential disk with $\epsilon=9$ and radial scale-length hR=0.3'' is added. This model was then convolved with a Gaussian to simulate 1.2'' FWHM seeing conditions and sampled with $0.2''\times 0.2''$ pixels in order to reproduce the FORS2 CCD sampling. Both the position angle and the surface brightness profile match the R-band characteristics of FS373. Without attempting to reconstruct the appearance of FS373 in detail, this toy model (grey full line in Fig. 8) is able to reproduce the central rise of the observed ellipticity profile.

  \begin{figure} \par\includegraphics[width=7.9cm]{1205fig7.eps}\hspace*{3mm} \includegraphics[width=7.9cm]{1205fig8.eps} \end{figure} Figure 7: Photometry of FS373 ( left column), photometry of FS76 ( right column). From the bottom up: R-band surface brightness, $\mu _R$, overplotted with the best fitting seeing-convolved Sérsic profile $\mu _R^S$ in grey; the residual from the Sérsic fit, $\Delta \mu _R =\mu _R - \mu _R^S$; ellipticity, $\epsilon = 1-b/a$; position angle, PA; and C4, measuring the deviations of the isophotes from a pure elliptical shape (these photometric quantities have all been derived from the R-band image). Vertical dotted lines indicate the seeing FWHM. The central nucleus, which sits in the center of the outer isophotes, has been used as zero-point for the distance scale (we use the geometric mean of the semi-major and semi-minor axes of each isophotal ellipse, $\sqrt {ab}$, as radius). The positivity of the C4 parameter indicates that FS373 has disky isophotes. Top panels: R-I, V-R, and V-I color profiles as a function of major-axis distance a. For each color index, the image with the best seeing was convolved with a Gaussian to match the seeing of the other image (vertical dotted lines indicate where the seeing correction becomes important, with the V-R and V-I colors having a worse seeing (grey line) than the R-I color (black line) in the case of FS373). In the case of FS373, the V-band image suffers from variable extinction by thin cirrus, affecting the V-band surface brightness level but not the shape of the surface-brightness profile nor that of the color profiles. The uncorrected color profiles are drawn in full lines. The seeing correction is quite substantial, especially in the profiles involving the V-band image (0.2-0.3 mag). For FS76, the seeing corrections are small; 0.05 at most.
Open with DEXTER

The R-I, V-R, and V-I color profiles of FS373 are presented in Fig. 7 (top panel). These are constructed by first fitting a cubic spline to the various surface brightness profiles as a function of radius $r=\sqrt{ab}$ so they can all be evaluated at any given position. The errorbars take into account photon shot noise and sky-subtraction uncertainties. For each color, the image with the best seeing was convolved with a two-dimensional Gaussian to match the seeing of the other image (see Table 1 for the basic photometric data). For FS373 this correction towards equal seeing was quite substantial ( 0.10-0.25 mag near the center). The V-band image suffers from variable extinction by thin cirrus, affecting the surface brightness level but not the shape of the surface-brightness profile nor that of the color profiles. Outside the central region, FS373 has slightly rising color profiles, an effect best seen in the V-I profile. This outward reddening has been observed in many dEs and is usually interpreted as a metallicity effect (Mori & Yoshii 1999). Inside the inner 2'', all color profiles show a pronounced bump before declining inward, although one has to take into account the uncertainty that comes with the large seeing correction that was applied. Nonetheless, this behavior correlates with the strength of the Ca II lines as measured by the CaT* index (Cenarro et al. 2001). CaT* first rises outwards but appears to decline outside a radius of 2'' until the index can no longer be measured reliably (amongst other due to residuals of the ubiquitous strong sky emission lines that make it difficult to properly measure the continuum level). If CaT* traces metallicity in a composite stellar population, which is still the subject of debate, then one would indeed expect the KDC to be slightly redder than its immediate surroundings.

Photometric parameters for FS76 are presented in Fig. 7 and Table 1. The isophotes of FS76 do not deviate significantly from ellipses ( $C_4 \approx 0$). Within the inner 1.2'', the position angle shows a pronounced twist. Color profiles for this galaxy are shown in Fig. 7. The V-I color varies almost linearly with radius, going from V-I=1.0 mag at 0.5'' to V-I=1.1 mag at 10''. This outward reddening is also visible in the R-I profile, although less obvious, going from R-I=0.45 mag at 2.0'' to R-I=0.50 mag at 10''. The inner 2''appear to be slightly redder again in R-I but bluer in V-R and V-I. The CaT* index profile, presented in Fig. 10, shows approximately the same behavior as that of FS373: the strength of the Ca II lines rises outwardly out to about 1.5'' and declines further out. The higher CaT* value near the position where the KDC dominates the kinematics may either point to a slightly more metalrich (a few tens of a dex) or an older stellar population. Taken at face value, the colors and line-strengths are roughly consistent with a metalpoor ([Fe/H] $~~\approx -0.7$) and old (T>6 Gyr) star population (Vazdekis et al. 1996, 1997).

Table 2: R-band Sérsic parameters of FS373 and FS76: extrapolated central surface brightness $\mu _{\rm R,0}$ (at zero seeing), scale-length r0 (arcsec), and shape-parameter n.

Clearly, imaging at much higher spatial resolution, e.g. with HST, is required to obtain more reliable colors close to the center and to corroborate the presence of a disky subcomponent. Also, spectroscopy in a wavelength region better suited for constraining the mean age and metallicity of the stellar population is prerequisite to fully understand the origin of these KDCs. Finally, it should be noted that neither galaxy shows any dust features.

   
4 Dynamical models

The internal dynamics of a steady-state axisymmetric stellar system are described by a gravitational potential $\psi(\varpi,z)$, that determines the stellar orbits, and the distribution function (DF) $F(\vec{r},\vec{v})~{\rm d}\vec{r}~{\rm d}\vec{v}$, which gives the number density of stars in phase space ( $(\varpi,z)$ are cylindrical coordinates). Roughly speaking, the DF distributes the stars over all possible orbits. According to the Jeans theorem, the DF can be written as a function of the isolating integrals of motion. An axisymmetric potential generally allows only two such integrals; the binding energy E and the z-component of the angular momentum Lz. More freedom to distribute stars over phase space can be gained if a third integral of motion exists. Therefore, we work in spheroidal coordinates and approximate the gravitational potential by a Stäckel potential which allows the existence of a third integral, denoted by I3. Round galaxies are modeled more efficiently in a spherical geometry, in which case the DF is conveniently taken to be a function of E, Lz, and L, the total angular momentum. The Lz-dependence of the DF allows the construction of rotating and slightly flattened stellar systems. FS373, which has a significantly flattened appearance on the sky, is modeled using an axisymmetric Stäckel potential while FS76 is treated as a system with a spherical gravitational potential. Of course, a galaxy with a KDC need not be axisymmetric but in the context of equilibrium models such an assumption is inevitable; also, the isophotes do not indicate that these galaxies are significantly non-axisymmetric.


  \begin{figure} \par\includegraphics[width=8.8cm]{1205fig9.eps} \end{figure} Figure 8: Simulated ellipticity profile of FS373. A flat disk with $\epsilon =1-b/a=0.9$ was added to a host galaxy with a flattening varying smoothly between $\epsilon =0$ in the very center and $\epsilon =0.23$ at 6'' and beyond. This model was then convolved with a Gaussian to simulate FWHM = 1.2'' seeing conditions and sampled with $0.2''\times 0.2''$ pixels in order to reproduce the FORS2 CCD sampling. Both the position angle and the surface brightness profile match the R-band characteristics of FS373. Without attempting to reconstruct the appearance of FS373 in detail, this toy model (grey full line) is able to reproduce the central rise of the observed ellipticity profile (black dots).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=6.2cm,clip]{1205fig10.eps} %\end{figure} Figure 9: The strength of the Ca II triplet lines, corrected for contamination by the Pa lines, as measured by the CaT* index along the major axis of FS373.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=6cm,clip]{1205fig11.eps} %\end{figure} Figure 10: The strength of the Ca II triplet lines, corrected for contamination by the Pa lines, as measured by the CaT* index along the major axis of FS76.
Open with DEXTER

A detailed account of the method we employed to construct the spheroidal coordinate system and Stäckel potential that give the best fit to a given axisymmetric potential can be found in Dejonghe & de Zeeuw (1988), Dejonghe et al. (1996), and De Bruyne et al. (2001). In brief, we deproject the observed surface brightness distribution, derived from an I-band image, assuming the galaxy to be axisymmetric and viewed edge-on. The total mass density, including dark matter, is parameterized as the spatial luminosity density multiplied by a spatially varying mass-to-light ratio

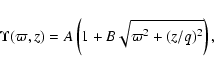\begin{displaymath}\Upsilon(\varpi,z) = A \left(1 + B \sqrt{\varpi^2 + (z/q)^2}\right), \end{displaymath} (2)

with the parameters A and B to be estimated from the data and qthe axis ratio of the luminosity density distribution. The gravitational potential is obtained by decomposing the total mass density in spherical harmonics. Finally, we fit a Stäckel potential to this gravitational potential. For a spherical galaxy (q=1), the deprojection of the surface brightness profile reduces to solving an Abel's integral equation (Binney & Tremaine 1987, Eq. (1B-57b)). The gravitational potential follows from Binney & Tremaine 1987, Eq. (2-22).

For a given potential, we wish to find the DF that best reproduces the kinematical information. The DF is written as a weighted sum of basis functions $F = \sum_i c_i ~ F_i$ and the coefficients ci are determined by minimizing the quantity

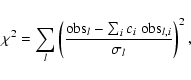\begin{displaymath}\chi^2 = \sum_l \left( \frac{ {\rm obs}_l - \sum_i c_i ~{\rm obs}_{l,i} }{\sigma_l} \right)^2, \end{displaymath} (3)

with ${\rm obs}_l$ an observed data point, $\sigma_l$ the 1-$\sigma$errorbar on that data point, and ${\rm obs}_{l,i}$ the corresponding value calculated from the ith basis function, subject to the constraint that the DF be positive everywhere in phase space. For a spherical potential, we used the basis functions $F_i(E,L) = E^{\alpha_i} L^{\beta_i}$ and $F_j(E,L_z) = E^{\alpha_j} L_z^{\beta_j}$, with integer powers, to construct the DF (De Bruyne et al. 2004). The three-integral DF in a Stäckel potential on the other hand was built with basis functions of the form $F_i(E,L_z,I_3) = E^{\alpha_i} L_z^{\beta_i} I_3^{\gamma_i}$, with integer powers (Dejonghe et al.  1996). In the case of FS76, the models are fitted directly to the observed major and minor axis spectra (De Rijcke & Dejonghe 1998), making the best possible use of all the kinematical information contained in the spectra. The axisymmetric models for FS373 are much more complex and computationally time-consuming and we opted to use the observed surface brightness distribution and the velocity dispersion and mean velocity profiles along both major and minor axis (i.e. the central second and first order moments of the LOSVDs, not the Gaussian parameters) as kinematical input for the modeling code. As a further constraint, we used the central fourth order moment of the LOSVDs, calculated from the kinematic parameters up to h4. We use a Quadratic Programming technique to find the optimal values for the ci using a library of hundreds of linearly independent basis functions, making this method essentially non-parametric. This is repeated for about 100 different (A,B)-pairs, covering the relevant part of parameter space. This allows us to define the range of models (and hence mass distributions) that are consistent with the data and to determine which model gives the best fit to the data.

The major-axis velocity dispersion and mean velocity profiles of the best models for FS373 and FS76 are compared with the observed kinematics in Fig. 11. From these best models, we estimate the mass within a 1.5 $R_{\rm e}$ sphere of FS76 at $2.9^{{+0.5}}_{{-1.7}} \times 10^9 ~M_\odot$(at the 90% confidence level) and that of FS373 at $6.2^{{+2.3}}_{{-1.3}} \times 10^9 ~M_\odot$. Both galaxies require the presence of a dark matter halo, albeit not a very massive one, in order to reproduce the observed outwardly rising velocity dispersion profiles. For FS76 we find a B-band mass-to-light ratio $M/L_B = 7.8^{{+1.3}}_{{-4.6}} ~M_\odot/L_{B,\odot}$ while for FS373 we find $M/L_B = 7.4^{{+2.8}}_{{-1.5}}~ M_\odot/L_{B,\odot}$. These models agree very well with the data and reproduce the central dip in the velocity dispersion, the bump in the velocity profile, and, in the case of FS373, the inward rise of the ellipticity profile. In both galaxies, this requires the presence of a fast rotating cold subcomponent in the models. The DFs of the best models for FS373 and FS76 are presented in Figs. 12 and 13, respectively. We plot the DF in the equatorial plane in turning-point space. Each orbit in this plane is labeled uniquely by its pericenter distance $R_{\rm peri}$ and apocenter distance $R_{\rm apo}$ if  $R_{\rm peri}$ is given the same sign as Lz. Circular orbits lie on two straight lines with $R_{\rm apo} = \pm R_{\rm peri}$. Radial orbits lie on the vertical line with $R_{\rm peri}=0$. In both galaxy models, an excess phase-space density of stars on near-circular orbits, forming the KDC, is clearly visible. Moreover, the KDC is obviously disjunct from the central nucleus or density cusp. Since the KDCs form a distinct subcomponent within their host galaxies, the stars that make up a KDC can be singled out of the DF and be studied separately (especially in the case of FS373, it was very clear which basis functions in the expansion of the DF formed the KDC). In order to roughly estimate the stellar mass of the KDC, we assumed a stellar mass-to-light ratio of $M/L_B = 2{-}4 ~M_\odot/L_{B,\odot}$, which agrees with the observed colors and line-strengths. Thus, we find $M_{\rm KDC} \approx 1{-}5 \times 10^7~ M_\odot$ for both galaxies or a few percent at most of the total mass. The adopted M/LB is both typical for a 10 Gyr old, metal-poor (-1 < [Fe/H] < -0.5) stellar population (which would agree with dEs being primordial stellar systems) and for a 5 Gyr old, more metal-rich (-0.5 < [Fe/H] < 0.0) stellar population (which would agree with dEs being harassed late-type spirals that experienced a starburst) (Worthey 1994).

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{1205fig12.eps} \end{figure} Figure 11: Major axis velocity dispersion and mean velocity of FS373 (panels a) and c), respectively) and of FS76 (panels b) and d)), folded around the center of the galaxy. The corresponding profiles of the best fit models are plotted with a full line. The models for FS373 were fitted to these kinematics. On the other hand, the models for FS76 were fitted directly to the spectra and are independent from the kinematics determined by a Gauss-Hermite fit to the LOSVDs. Still, the model agrees excellently with the kinematics, as it should of course.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.6cm,clip]{1205fig13.eps} \end{figure} Figure 12: The distribution function of FS373 in the equatorial plane in turning-point space. The pericenter distance, $R_{\rm peri}$, has the same sign as the z-component of the angular momentum, Lz. Circular orbits have $R_{\rm apo} = \pm R_{\rm peri}$(dashed lines); radial orbits are characterized by $R_{\rm peri}=0$(dotted line). The KDC is visible in phase-space as an excess of stars on near-circular orbits, indicated by an arrow.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.6cm,clip]{1205fig14.eps} \end{figure} Figure 13: The distribution function of FS76 in the equatorial plane in turning-point space. The KDC is visible in phase-space as an excess of stars on near-circular orbits. Its locus is indicated by an arrow.
Open with DEXTER

   
5 Discussion

The key question is whether KDCs in dwarf elliptical galaxies are produced the same way as in massive ellipticals. We explore two possible avenues to KDC formation in dEs. The first is the merger hypothesis, as in giant ellipticals; the second is the harassment scenario, which posits that gravitational interactions play an important role in the evolution of dEs. The analytical arguments given below are strictly speaking only valid for fast and distant encounters. An encounter between to galaxies, with masses M1 and M2, qualifies as distant if, at closest approach, the change in the potential energy of the pair is much smaller than the initial orbital kinetic energy. In a fast encounter, the relative velocity of the galaxies is much larger than the internal stellar velocities. This translates into the following constraints on the impact parameter b and the internal velocity dispersion  $\sigma_{\rm int}$:

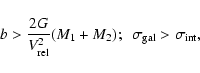\begin{displaymath}b > \frac{2G}{V_{\rm rel}^2}(M_1+M_2); ~~ \sigma_{\rm gal} > \sigma_{\rm int}, \end{displaymath} (4)

with $V_{\rm rel}$ the relative velocity of the interacting galaxies. For $M_2 \approx 5 \times 10^9 ~M_\odot$, a typical dE mass, and $M_1 = M_{\rm KDC} \ll M$, we find b > 250 - 500 pc for $V_{\rm rel} = \sigma_{\rm gal} = 300 {-} 400$ km s-1. Also, $\sigma_{\rm gal} > \sigma_{\rm int}$. Hence, any non-penetrating encounter between a dE and a much smaller dwarf galaxy classifies as a fast and distant encounter (even if we take the dwarf galaxy to be originally 10 times more massive than  $M_{\rm KDC}$, the minimum impact parameter would change by only 10%). In the case of a giant elliptical with $M_2 \approx 5 \times 10^{11} ~M_\odot$ and $M_1 = M_{\rm dE} \ll M_2$, the condition for a fast flyby becomes b > 25- 50 kpc, again rather unsensitive to $M_{\rm dE}$. In a group or cluster environment, galaxies keep respectable distances of a few tens of kpc (Moore et al. 1996). With this in mind, we can discuss possible mechanism of producing KDCs in dEs.

5.1 The merger hypothesis

While the merger origin of KDCs in bright ellipticals is well accepted, a number of facts argue against the merger hypothesis in the case of dEs.

The change of the forward velocity of a galaxy with mass M1 induced by a fast, distant hyperbolic encounter with a galaxy with mass M2with a relative velocity  $V_{\rm rel}$ is given by

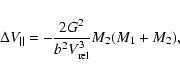\begin{displaymath}\Delta V_{\vert\vert} = - \frac{2 G^2}{b^2 V_{\rm rel}^3} M_2 (M_1+M_2), \end{displaymath} (5)

(Sparke & Gallagher 2000; Binney & Tremaine 1987). The closer and the slower the encounter, the more orbital energy is converted into internal (stellar) kinetic energy. For an encounter between a typical $M_2 =5 \times 10^9 ~M_\odot$ dE and a $M_1 =5 \times 10^7~ M_\odot$ dwarf galaxy with a relative velocity $V_{\rm rel} = \sigma_{\rm gal} = 300$ km s-1, $\Delta V_{\vert\vert}$ is very small (e.g. $\Delta V_{\vert\vert} \sim 35$ km s-1 for a collision with b=1 kpc). In the case of an encounter between a $M_2=5 \times 10^{11} ~M_\odot$ elliptical and a $M_1=5 \times 10^9 ~M_\odot$ dE, on the other hand, the velocity change is substantial :  $\Delta V_{\vert\vert} \sim V_{\rm rel}$, even for impact parameters of a few tens of kiloparsecs. This suggests that a dE, in a group or cluster environment, has virtually no chance of slowing down and capturing another (smaller) dwarf galaxy, contrary to a more massive elliptical galaxy. Hence, once the galaxy group or cluster is in place, the chance of forming a KDC in a dE by a merger is exceedingly small. Also, it is unclear how the merger scenario can explain the complex velocity profile of FS373, particularly the velocity changing sign around a radius of 12'' = 2.4 kpc.

Alternatively, the merger could have taken place before the group or cluster virialized, in an environment where relative velocities were smaller than the present values. The low galaxy density in such an environment argues against this idea. Also, it remains to be seen, e.g. using high-resolution N-body simulations, whether a KDC formed this way can survive the dE's falling into a group or cluster and the subsequent gravitational interactions with giant group or cluster members.

5.2 The harassment scenario


  \begin{figure} \par\includegraphics[angle=-90,width=8.5cm,clip]{1205fig15.eps} \end{figure} Figure 14: The estimated maximum change in the rotation velocity of a dwarf galaxy after an encounter with a giant elliptical of mass $M_2 = 5 \times 10^{11} M_\odot $ as a function of impact parameter b and axis ratio q. Full lines: FS373 (top to bottom:  q=0.3, 0.5, 0.7), dotted lines: FS76 (top to bottom:  q=0.5, 0.7, 0.9). We used $V_{\rm rel}=300$ km s-1 in the case of FS76 and $V_{\rm rel} =400$ km s-1 for FS373. Clearly, interactions with impact parameters smaller than $b \sim 20$ kpc can signifanctly change the streaming velocity of these slowly rotating systems.
Open with DEXTER

A plausible alternative is the spin-up of a dE's halo by fly-by encounters with other galaxies. The impulse approximation and the tensor virial theorem yield the following expression for the maximum amount of angular momentum that can be transfered to a galaxy with mass M1 during an encounter with a galaxy with mass M2:

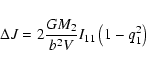\begin{displaymath}\Delta J = 2 \frac{G M_2}{ b^2 V} I_{11} \left( 1-q_1^2 \right) \end{displaymath} (6)

with q1 the axis ratio and I11 a component of the inertial tensor (Som Sunder & Kochhar 1990). Using $\Delta J \sim M_1 R_{\rm e,1} \Delta v_{\rm rot}$ to roughly estimate $\Delta v_{\rm rot}$, the maximum possible change in the rotation velocity after re-virialization, this translates into

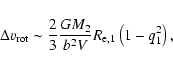\begin{displaymath}\Delta v_{\rm rot} \sim \frac{2}{3} \frac{G M_2}{ b^2 V} R_{\rm e,1} \left( 1-q_1^2 \right), \end{displaymath} (7)

with $R_{\rm e,1}$ the half-light radius of the galaxy with mass M1(we have used $I_{11} \sim M_1 R_{\rm e,1}^2/3$). This $\Delta v_{\rm rot}$ is plotted in Fig. 14 as a function of impact parameter b and axis ratio q. Clearly, interactions with impact parameters small than $b \sim 20$ kpc can significantly alter the streaming velocity of these slowly rotating systems, especially in the case of FS373, which is apparently more flattened than FS76.

According to the harassment scenario, some dEs may stem from late-type spirals, inflated by high-speed gravitational interactions (Moore et al. 1996; Mayer et al. 2001). During this metamorphosis, which in the case of a late-type spiral orbiting a massive galaxy, e.g. in a small group, takes only 2-3 pericenter passages, a disk and a spheroidal envelope co-exist. The N-body simulations presented by Hau & Thomson (1994) show that flyby interactions impart angular momentum preferentially to the outer parts of a galaxy (stars close to the galaxy's center have much shorter orbital periods and respond adiabatically to the perturbing forces during the interaction). The outer envelope's acquired angular momentum is most likely not aligned with that of the embedded disk and this results in a KDC-like signature in the velocity profile. Multiple interactions with different impact parameters and orbital angular momenta may produce the complex velocity profile observed in FS373, with the rotation velocity changing sign. Moreover, upon the first pericenter passage, the bar instability triggered in the progenitor spiral galaxy funnels almost all the gas to the center where it is consumed in a starburst. This process depletes the gas within roughly 2 Gyr (Mayer et al. 2001), effectively turning a gas-rich late-type galaxy into a gas-poor dE.

   
6 Conclusions

We have presented evidence for the discovery of two dwarf elliptical galaxies with kinematically decoupled cores. The presence of a cold, rotationally flattened subcomponent is supported by the photometry, kinematics, and the dynamics of these galaxies. This is the first time kinematically decoupled cores have been detected in dwarf elliptical galaxies.

KDCs in dwarf galaxies are not likely produced by mergers since the gravitational field of a dwarf elliptical galaxy is not strong enough for dynamical friction to sufficiently slow down another dwarf galaxy at the relative velocities and impact parameters that are typical for a group or cluster environment. In the field, relative velocities are much lower but the galaxy density is prohibitively low for mergers to occur. The harassment scenario is able to offer an alternative explanation: the angular momentum, transfered to the dwarf galaxy during an encounter by the tidal forces, can result in the observed peculiar kinematics. The fact that these two objects, the only ones in a sample of 15 dEs with measured kinematics to host a KDC, are found in a group environment (in which mergers are unlikely but interactions are slow enough to transfer significant amounts of energy and angular momentum) and not in a cluster environment (in which mergers are unlikely and interactions are much too fast to transfer significant amounts of angular momentum) agrees with this interpretation.

Acknowledgements
Based on observations made at the European Southern Observatory, Chile (ESO Large Programme No. 165.N-0115). S.D.R. thanks P. Prugniel and F. Simien for the hospitality and fruitful discussions during a stay at the Observatoire de Lyon. W.W.Z. acknowledges the support of the Austrian Science Fund (project P14753). We like to thank the referee J. A. L. Aguerri for his useful comments and suggested improvements. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.

References

 
Copyright ESO 2004