A&A 426, 333-341 (2004)
DOI: 10.1051/0004-6361:20041018
J. I. Sakai - K. Shimada
Laboratory for Plasma Astrophysics, Faculty of Engineering, Toyama University, 3190, Gofuku, Toyama, 930-8555, Japan
Received 4 April 2004 / Accepted 21 June 2004
Abstract
We investigate the plasma dynamics during coalescence of two parallel current loops in solar flares by using a resistive three-dimensional MHD simulation code, paying particular attention finding the most effective electromagnetic fields for the production of high-energy protons. Next we investigate the orbit of many protons in the electromagnetic fields obtained from the MHD simulations. We investigate two cases of the coalescence process: (1) co-helicity reconnection where only the poloidal magnetic
field produced from the axial currents dissipates and (2) counter-helicity reconnection where both poloidal and axial magnetic fields dissipate. We found a bump-on-tail distribution in the same direction as the original loop current for
both the cases of co-helicity and counter-helicity. It is shown that the maximum proton energy exceeds the energy (2.223 MeV) of the observed prompt nuclear de-excitation lines of gamma-ray, and that proton energy spectrum is neither a pure power-law type nor a pure exponential type.
We may conclude that anisotropic proton acceleration
along the loop can be realized both for co-helicity and counter-helicity reconnection during the
coalescence of two parallel loops.
Key words: acceleration of particles - magnetohydrodynamics (MHD) - Sun: flares
When energetic protons accelerated during impulsive flares collide with the solar atmosphere, they produce excited nuclei, which emit prompt nuclear de-excitation lines, as well as secondary neutrons and positrons, which results in the delayed 2.223 MeV neutron-capture and 511 keV positron-annihilation line emission. In most strong flare events the time profile of the prompt gamma-ray line emission is observed to be very similar to that of the bremsstrahlung hard X-rays emitted by energetic electrons. This suggests that the acceleration and propagation of the flare-accelerated protons and electrons are closely related. The most typical event among these events is the 1980 June 7 flare observed by the SMM (Forrest & Chupp 1983), which was explained by the current loop coalescence model (Tajima et al. 1982; Sakai & Ohsawa 1987; Sakai & De Jager 1996; Aschwanden 2002). Sakai & de Jager (1996) gave a review of the high-resolution observations of solar plasma loops with simulations of current-carrying loops and tried to arrive at an understanding of solar flare phenomena. In Chapter 7 in their review, they summarized the understanding of high-energy particle acceleration processes during and after solar flares. There are two types of solar flares: Confined/Impulsive and Eruptive/Dynamic flares. Confined/Impulsive flares are spatially compact and as a fairly general rule they show impulsive hard X-ray and/or microwave bursts. Eruptive/Dynamic flares, on the other hand, are spatially more extended and last longer. As proposed by de Jager (1988) and Sakai & de Jager (1991), there are three phases of acceleration in a fully developed eruptive/dynamic flare. The relevant observations regarding the first two phases are:
However, the location, size and geometry of the accelerated proton collision region has remained unknown until now. A recent paper by Hurford et al. (2003) presents the first gamma-ray images of a solar flare taken from the Reuven Ramaty High Energy Solar Spectroscopic Imager (RHESSI) for the X4.8 flare of 2002 July 23. The result shows that the
centroid of the 2.223 MeV image was found to be displaced by 20 ![]() 6 arcsec from that of the 0.3-0.5 MeV, implying a difference in acceleration and /or propagation between the accelerated electron and proton population near the Sun. The fact that the proton-associated gamma-ray source does not coincide with the electron-bremsstrahlung
sources suggests that the protons are accelerated in one direction by the DC electric field and can subsequently interact in spatially separate sources. Therefore it is important to investigate in detail the proton acceleration processes for different types of flares.
6 arcsec from that of the 0.3-0.5 MeV, implying a difference in acceleration and /or propagation between the accelerated electron and proton population near the Sun. The fact that the proton-associated gamma-ray source does not coincide with the electron-bremsstrahlung
sources suggests that the protons are accelerated in one direction by the DC electric field and can subsequently interact in spatially separate sources. Therefore it is important to investigate in detail the proton acceleration processes for different types of flares.
Sakai (1990) showed that, during 3D X-type current loop coalescence and under suitable assumptions
for the size and other physical parameters in the region of acceleration, protons and electrons may be accelerated promptly (i.e., within less than 1 s) to ![]() 100 GeV and
100 GeV and ![]() 100 MeV, respectively. De Jager & Sakai (1991) showed that the duration of impulsive phase bursts (5-25 s) observed during the impulsive phases of flares can be explained quantitatively by the
mechanism of X-type current-loop coalescence. Sakai (1992) developed a model for
long-duration gamma-ray/proton flares (the "gradual GR/P flares'') in order to explain prompt proton and electron
acceleration during the impulsive phase. He determined the electric fields during the implosion
phase of the current sheet from the MHD equations, and investigated the motion of test protons and electrons. The results showed that, under reasonable assumptions for the size and velocities in the
reconnection area, both protons and electrons can be accelerated promptly
within 1 s to
100 MeV, respectively. De Jager & Sakai (1991) showed that the duration of impulsive phase bursts (5-25 s) observed during the impulsive phases of flares can be explained quantitatively by the
mechanism of X-type current-loop coalescence. Sakai (1992) developed a model for
long-duration gamma-ray/proton flares (the "gradual GR/P flares'') in order to explain prompt proton and electron
acceleration during the impulsive phase. He determined the electric fields during the implosion
phase of the current sheet from the MHD equations, and investigated the motion of test protons and electrons. The results showed that, under reasonable assumptions for the size and velocities in the
reconnection area, both protons and electrons can be accelerated promptly
within 1 s to ![]() 70 MeV and
70 MeV and ![]() 200 MeV, respectively.
However, the above studies
did not give the energy spectrum of the accelerated particles.
In the first phase of acceleration, current loop coalescence is
one of the most plausible models of solar flares.
Although the triggering mechanisms of most of the complex flares are still puzzling so far,
several examples of solar flares triggered by current loop coalescence
were observed by Yohkoh (see for a review, Sakai & de Jager 1996).
In the case of partial reconnection of kink-unstable
loops coalescence (Nishikawa et al. 1994), it seems that electrons can be promptly accelerated to
relativistic energies, while the problem of proton acceleration has not been investigated
because of the limitation of full proton dynamics by using a particle simulation model.
200 MeV, respectively.
However, the above studies
did not give the energy spectrum of the accelerated particles.
In the first phase of acceleration, current loop coalescence is
one of the most plausible models of solar flares.
Although the triggering mechanisms of most of the complex flares are still puzzling so far,
several examples of solar flares triggered by current loop coalescence
were observed by Yohkoh (see for a review, Sakai & de Jager 1996).
In the case of partial reconnection of kink-unstable
loops coalescence (Nishikawa et al. 1994), it seems that electrons can be promptly accelerated to
relativistic energies, while the problem of proton acceleration has not been investigated
because of the limitation of full proton dynamics by using a particle simulation model.
Bulanov (1980) first showed the energy spectrum of accelerated particles in a simple
X-type configuration near the reconnection region, which is given by
![]() for
for
![]() .
Deeg et al. (1991) investigated the same problem using numerical simulation. Their results were in good agreement with the theory by Bulanov (1980).
.
Deeg et al. (1991) investigated the same problem using numerical simulation. Their results were in good agreement with the theory by Bulanov (1980).
Mori et al. (1998) investigated the behavior of protons near an X-type magnetic reconnection region
by numerical simulations. The magnetic field is taken to be hyperbolic and time
stationary with a uniform electric field perpendicular to the magnetic field.
They also studied the effects of the magnetic field along the uniform electric field. From many parametric runs, they found that the energy spectrum of accelerated protons near an X-type
magnetic reconnection region is universal with a power-law spectrum
![]() ,
where
the power-law index
,
where
the power-law index ![]() is about 2.0-2.2. The acceleration time of protons with
an energy range of 1-20 MeV is very rapid and within
is about 2.0-2.2. The acceleration time of protons with
an energy range of 1-20 MeV is very rapid and within ![]()
![]() which is much less than 1 s for solar flare plasmas. Heerikhuisen et al. (2002) and Craig et al. (2002) investigated
the proton dynamics under a self-consistent MHD reconnection solution and found that the proton
energy spectrum approximates a power law E-1.5 nonrelativistically, but steepens slightly at higher energies. Hamilton et al. (2003) studied the proton energy spectra for the model fields obtained from solutions of the linearized MHD equations for the reconnecting region. They showed that in some cases the energy distributions
exhibit a bump-on-tail in the MeV range, but in general the shape of the distribution is sensitive to the model parameters. The previous model fields used to obtain the proton energy spectrum during coalescence process were limited by the simple spatial configurations near the reconnection region and by the lack of self-consistent MHD solutions.
which is much less than 1 s for solar flare plasmas. Heerikhuisen et al. (2002) and Craig et al. (2002) investigated
the proton dynamics under a self-consistent MHD reconnection solution and found that the proton
energy spectrum approximates a power law E-1.5 nonrelativistically, but steepens slightly at higher energies. Hamilton et al. (2003) studied the proton energy spectra for the model fields obtained from solutions of the linearized MHD equations for the reconnecting region. They showed that in some cases the energy distributions
exhibit a bump-on-tail in the MeV range, but in general the shape of the distribution is sensitive to the model parameters. The previous model fields used to obtain the proton energy spectrum during coalescence process were limited by the simple spatial configurations near the reconnection region and by the lack of self-consistent MHD solutions.
In this paper we investigate the plasma dynamics during the coalescence of two parallel current loops using a resistive three-dimensional MHD simulation code developed by Sokolov et al. (1999, 2002), paying particular attention findiing the most effective electromagnetic fields for the production of high-energy protons. This approach is very important for obtaining the proton energy spectrum that depends on the model electromagnetic fields, as shown by Mori et al. (1998) and Hamilton et al. (2003). Next we investigate the orbit of many protons in the electromagnetic fields obtained from the MHD simulations. We investigate two cases of the coalescence process: (1) co-helicity reconnection where only the poloidal magnetic field produced from the axial currents dissipates; and (2) counter-reconnection where both poloidal and axial magnetic fields dissipate. We found that for the proton acceleration co-helicity reconnection is more efficient than counter-helicity reconnection. The protons can be accelerated mostly in one direction along the loop axis near where magnetic reconnection occurs. There appears a weak bump-on-tail proton distribution in the middle energy region, not in the high-energy region as shown by Nagao et al. (2000) and Hamilton et al. (2003). Therefore the proton energy spectrum is neither pure power-law type nor pure exponential type.
In Sect. 2 we present our methods to obtain the proton energy spectra during coalescence of two parallel current loops. In Sect. 3 we present our MHD simulation results to obtain the most effective electric fields for accelerating the protons. In Sect. 4 we investigate many proton orbits under the electromagnetic fields during two types of coalescence to find their energy spectra. In the final section we summarize our results.
In this section we describe two simulation methods for obtaining the energy spectrum of the protons accelerated during the coalescence of two parallel current loops. Firstly we briefly present a model of a two-loop coalescence flare by using a three-dimensional resistive MHD simulation to obtain the electromagnetic fields during the loop coalescence. Next we present the simulation method to obtain the orbits of many protons in the electromagnetic fields obtained from the MHD simulations.
We use a resistive 3-D MHD code with the recently proposed Artificial Wind (AW) numerical scheme (Sokolov et al. 1999, 2002) with splitting over the spatial coordinates. The basis of the AW scheme is the fact that fundamental physical invariance, Galilean (or more general, Lorentz) invariance, make it possible to solve the governing equation in different steadily moving frames. The principle of the AW scheme is that the frame of reference may be chosen in such a way that the flow under simulation is supersonic. The problem of upwinding becomes trivial and considerably simplified versions of discontinuity-capturing schemes may be employed. An extra velocity (Artificial Wind) is added to the velocity of the flow under simulation when the system of coordinates is changed.
The MHD equations are numerically solved in a conservative form as follows:
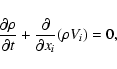 |
(1) |
![\begin{displaymath}%
\frac{\partial (\rho V_i)}{\partial t}+\frac \partial {\par...
...rho V_iV_j+\left(p+B^2\right)\delta _{ij}-
2B_iB_j\right]
=0,
\end{displaymath}](/articles/aa/full/2004/40/aa1018/img14.gif) |
(2) |
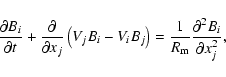 |
(3) |
![$\displaystyle \frac \partial{\partial t}\left(\frac{\rho V^2}2+\frac p{\gamma
-...
...\rho
V^2}{2}+\frac{\gamma
p}{\gamma -1}+2{B^2}\right)-2B_iB_jV_j+q_i\right]
=0,$](/articles/aa/full/2004/40/aa1018/img16.gif) |
(4) |
Magnetic reconnection takes place through finite conductivity. The conductivity due to microturbulence (Vasyliunas 1975) may be written by the expression
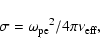 |
(5) |
For resistive MHD with a large but finite value of ![]() the
energy equation Eq. (4) should be obtained as the sum of the equation
for plasma energy, in which the Joule heating term is present as
follows:
the
energy equation Eq. (4) should be obtained as the sum of the equation
for plasma energy, in which the Joule heating term is present as
follows:
![]() ,
and the equation for magnetic energy
which is given by Eq. (3) multiplied by the magnetic field
,
and the equation for magnetic energy
which is given by Eq. (3) multiplied by the magnetic field
![]() (none of
the variables is normalized here). The
dissipation of the magnetic field energy is hence given by the following term:
(none of
the variables is normalized here). The
dissipation of the magnetic field energy is hence given by the following term:
![]() .
So in Eq. (4) for the
total energy the Joule heating is compensated by the magnetic
energy dissipation in the following way:
.
So in Eq. (4) for the
total energy the Joule heating is compensated by the magnetic
energy dissipation in the following way:
![\begin{eqnarray*}\frac{c^2}{(4\pi)^2\sigma}\left[B_i\Delta B_i+({\rm rot}{\vec B...
...^2}{(4\pi)^2\sigma}{\rm div}[{\vec B}\times {\rm rot}{\vec B}].
\end{eqnarray*}](/articles/aa/full/2004/40/aa1018/img35.gif)
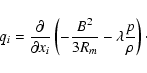 |
(6) |
![\begin{figure}
\par\includegraphics[width=5.4cm,clip]{1018f1.eps} %\end{figure}](/articles/aa/full/2004/40/aa1018/Timg44.gif) |
Figure 1: A schematic picture of two parallel current loops and the coordinate system. |
| Open with DEXTER | |
Magnetic reconnection during the coalescence of two current loops produces strong electric fields in the plasma and, as a result, charged particles can be accelerated. In this paper we concentrate on the proton dynamics around an X-point. During two current loops coalescence, there are two types of magnetic reconnection possible: one is complete reconnection ( we call here counter-helicity case), where the By component is null, while for partial magnetic reconnection (we call here co-helicity case) the By component is not zero. Here we take a system size of Ny=100 and Nx=Nz=300, as shown in Fig. 1.
Each current loop (i=1, 2) located parallel to the y-axis is assumed to be in an
equilibrium state (
![]()
![]()
![]() ). This means that the initial state with two current loops is not in equilibrium.
The magnetic field and pressure for each loop are given as
). This means that the initial state with two current loops is not in equilibrium.
The magnetic field and pressure for each loop are given as
| Bx=qi By (z-zci)/a, | (7) |
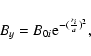 |
(8) |
| Bz=- qi By (x-xci)/a, | (9) |
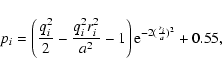 |
(10) |
Using the electromagnetic fields obtained from the above MHD equations during the coalescence of two parallel
current loops, we investigate the proton dynamics to obtain their energy spectrum.
The normalized relativistic equations of the motion of a proton are given by
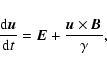 |
(11) |
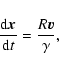 |
(12) |
To solve numerically the equation of motion of a test particle in an electric and
magnetic field, we used a centered-difference form of the
Newton-Lorentz equations of motions (Buneman 1993; Birdsall & Langdon 1991), namely
![\begin{displaymath}%
{\vec u}^{{\rm new}} - {\vec u}^{{\rm old}} = \frac{q{\delt...
...m new}} + {\vec u}^{{\rm old}}\right) \times {\vec B} \right],
\end{displaymath}](/articles/aa/full/2004/40/aa1018/img61.gif) |
(13) |
The protons are randomly distributed with two protons per cell. We changed the test particle number just twice, namely from one to two particles per each cell. We found that the results are almost the same. The initial velocity distribution function for protons is Maxwellian with thermal
velocity
![]() .
The simulation time step is
.
The simulation time step is
![]() .
The boundary conditions for protons are periodic in the y-direction and open
in the x- and z-directions.
.
The boundary conditions for protons are periodic in the y-direction and open
in the x- and z-directions.
The basic physical evolution of reconnection between two loops with parallel axial currents is known to be as follows (see for a review, Sakai & de Jager 1996). Each of the two current loops is in an equilibrium state as long as the distance between them is much greater than the loop radius a. While the loops approach to each other, they are no longer in the equilibrium state and the whole non-equilibrium system tends to a new equilibrium state. In more detail, due to attraction, the two initially static current loops begin to move and approach to each other. Then they meet, merge, and form a new single loop. Our present simulation is performed to investigate the phenomena accompanying this reconnection process.
The simulation result for the co-helicity reconnection can be described as follows. In the early stage, while the two loops begin to approach each other, the reconnection of the poloidal magnetic field is important. As the two current loops approach each other, the original magnetic field lines break and join to new ones, the reconnected magnetic field lines being strongly bent. Due to magnetic stress, the magnetic field lines tend to shorten and drive the surrounding plasma moving towards in the z and -z directions. Thus a pair of jet-like flows is formed.
On the contrary, for the counter-helicity which proceeds in the form of a comparatively
fast oscillation, the period of the oscillations is governed by MHD processes and is comparable
with the
![]() transient time. This means that the dynamics of the system enter the axial field reconnection phase.
transient time. This means that the dynamics of the system enter the axial field reconnection phase.
First we present the simulation results of coalescence of the two current loops for the co-helicity and counter-helicity cases, paying particular attention to the time period on which the induced electric field becomes strongest in order to find the most efficient proton acceleration phase. In Fig. 2 we show the time evolution of magnetic fields ((a), (b), (c)) and electric fields ((d), (e), (f)) in the x-z plane for y=50 for co-helicity at three different times: 3.8 ![]() ((a) and (d)), 4.7
((a) and (d)), 4.7 ![]() ((b) and (e)) and 6.6
((b) and (e)) and 6.6 ![]() ((c) and (f)). The gray scale in Figs. 2a-c shows the spatial distribution of the magnetic field By along the current loop, while the gray scale in Figs. 2d-f shows the spatial distribution of the electric field Ey along the current loop. The vectors in the x-z plane show the Bx -Bz in Figs. 2a-c and the Ex -Ez in Figs. 2d-f, respectively.
((c) and (f)). The gray scale in Figs. 2a-c shows the spatial distribution of the magnetic field By along the current loop, while the gray scale in Figs. 2d-f shows the spatial distribution of the electric field Ey along the current loop. The vectors in the x-z plane show the Bx -Bz in Figs. 2a-c and the Ex -Ez in Figs. 2d-f, respectively.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1018f2.eps}
\end{figure}](/articles/aa/full/2004/40/aa1018/Timg67.gif) |
Figure 2:
The time evolution of magnetic fields ( a), b), c)) and electric fields ( d), e), f)) in the x-z plane for y=50 for the co-helicity case at three different times: 3.8 |
| Open with DEXTER | |
As seen in Figs. 2a-c, the reverse current that flows against the original loop currents (positive y-direction) is generated in the middle region of the two loops as they approach each other. The magnetic reconnection is triggered in the induced current region whose shape becomes elongated in the z-direction, as seen from the structure of the magnetic vector fields in Fig. 2c. If the original loop currents were stronger than at present case, the elongated
current structure in the x-direction is again formed with some oscillation period. As seen in Fig. 2e, the strongest electric fields can be induced just where the two loops begin to merge with magnetic recconnetion at about
![]() .
The electric field in the x-z plane is characterized by a quadru-pole like structure. Therefore we will use
the electromagnetic fields (Figs. 2b and 2e) at
.
The electric field in the x-z plane is characterized by a quadru-pole like structure. Therefore we will use
the electromagnetic fields (Figs. 2b and 2e) at
![]() to study the proton acceleration for co-helicity reconnection.
to study the proton acceleration for co-helicity reconnection.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1018f3.eps}
\end{figure}](/articles/aa/full/2004/40/aa1018/Timg69.gif) |
Figure 3:
The time evolution of magnetic fields ( a), b), c)) and electric fields ( d), e), f)) in the x-z plane for y=50 for the counter-helicity case at three different times: 3.8 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1018f4.eps}
\end{figure}](/articles/aa/full/2004/40/aa1018/Timg70.gif) |
Figure 4:
Proton energy spectra at three different times, a) at
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1018f5.eps}
\end{figure}](/articles/aa/full/2004/40/aa1018/Timg71.gif) |
Figure 5:
The proton velocity distribution functions of three components, a) Vx, b) Vy and c) Vz. The dot-dashed , dotted and solid curves show the initial proton velocity distribution, and the proton velocity distribution for the counter-helicity case and for the co-helicity case at
|
| Open with DEXTER | |
A remarkable phenomenon in the counter-helicity case (Zhang et al. 2001) is the oscillation of the axial component of the magnetic field By, and the velocity Vy. The reconnection and oscillation mechanism can be clarified as follows. As the two current loops approach each other, the By reconnection begins. After reconnection (the original magnetic field lines break and join new ones) the magnetic field lines appear to be strongly bended. Due to magnetic stress, the magnetic field lines tend to shorten and drive the surrounding plasma motion in the y or -y directions. As the magnetic field lines shorten, the surrounding plasma gets momentum in the y-direction. After the magnetic field lines have reached their balance point, the moving surrounding plasma begins to drive and stretch the magnetic field lines. Thus, the interaction between magnetic field and surrounding plasma leads to the oscillation.
In Fig. 3 we show the time evolution of magnetic fields (Figs. 3a-c) and electric fields (Figs. 3d-f) in the x-z plane on the plane y=50 for the counter-helicity case at three different times: 3.8 ![]() (Figs. 3a and d), 4.7
(Figs. 3a and d), 4.7 ![]() (Figs. 3b and e) and 6.6
(Figs. 3b and e) and 6.6 ![]() (Figs. 3c and f). The gray scale in Figs. 3a-c shows the spatial distribution of the magnetic field By along the current loop, while the gray scale in
Figs. 3d-f shows the spatial distribution of the electric field Ey along the current loop. The vectors in the x-z plane show the Bx -Bz in Figs. 3a-c and the Ex -Ez in Figs. 3d-f, respectively. As seen in Fig. 3e, the strongest
electric fields can be induced just where the two loops begin to merge with magnetic recconnetion at about
(Figs. 3c and f). The gray scale in Figs. 3a-c shows the spatial distribution of the magnetic field By along the current loop, while the gray scale in
Figs. 3d-f shows the spatial distribution of the electric field Ey along the current loop. The vectors in the x-z plane show the Bx -Bz in Figs. 3a-c and the Ex -Ez in Figs. 3d-f, respectively. As seen in Fig. 3e, the strongest
electric fields can be induced just where the two loops begin to merge with magnetic recconnetion at about
![]() .
The electric field in the x-z plane perpendicular to the loops is dominant in the negative x-direction . Therefore we will use the electromagnetic fields (Figs. 3b and 2e) at
.
The electric field in the x-z plane perpendicular to the loops is dominant in the negative x-direction . Therefore we will use the electromagnetic fields (Figs. 3b and 2e) at
![]() to study the proton acceleration for
counter-helicity reconnection. The electric field strength (Ey) along the loops for the counter-helicity case is slightly weaker than that for the co-helicity case.
to study the proton acceleration for
counter-helicity reconnection. The electric field strength (Ey) along the loops for the counter-helicity case is slightly weaker than that for the co-helicity case.
In this section we investigate the proton dynamics in the electromagnetic fields obtained from the resistive MHD simulation for both cases of co-helicity and counter-helicity reconnection.
In Fig. 4 we show the proton energy spectra at three different times: at
![]() (Fig. 4a), at
(Fig. 4a), at
![]() (Fig. 4b) and at
(Fig. 4b) and at
![]() (Fig. 4c). The solid and dotted curves show the co-helicity and counter-helicity case, respectively.
E=(Vx2+Vy2+Vz2)/VA2.
(Fig. 4c). The solid and dotted curves show the co-helicity and counter-helicity case, respectively.
E=(Vx2+Vy2+Vz2)/VA2.
In contrast with the result shown by Mori et al. (1998) who showed that the energy distribution of the accelerated protons has a power-law spectrum, we find that the proton energy spectrum is more complicated. There appears a weak bump-on-tail in the midium energy region, not in the high-energy tail shown by Hamilton et al. (2003). The reason may be related to the fact that the induced electric fields are not simple as compared with the model fields used by Mori et al. (1998) and Hamilton et al. (2003). Except for the weak bump-on-tail, the global proton spectrum seems to be exponential as predicted by Bulanov (1980). The fact that the production of high-energy protons in the counter-helicity case is less weak than in the co-helicity case is mainly due to the following reason. As shown by Mori et al. (1998) and Hamilton et al. (2003), the magnetic field component along the reverse current is more effective for high-energy proton production, because the guiding magnetic field plays a role in keeping the protons within the accelerating region for a long time, while in a weak guiding field like in the counter-helicity case the accelerated protons may escape from the strong electric field region. The production of the proton bump-on-tail in the medium energy region is also related to the electric fields perpendicular to the reverse current, as shown by the test proton simulation (Nagao et al. 2000) including both parallel electric field (Ey) and perpendicular electric fields (Ex and Ez).
Next we show the proton velocity distributions to see the details of the direction of acceleration of the protons. In Fig. 5 we present the proton velocity distribution functions for the three components, (a) Vx, (b) Vy and (c) Vz. The dot-dashed, dotted and solid curves show the initial proton velocity distribution, proton velocity distribution for the counter-helicity case and for the co-helicity case at
![]() ,
respectively.
As seen in Fig. 5b, strong anisotropic acceleration in the negative y-direction is observed for the co-helicity case, while for the counter-helicity case, almost symmetric acceleration in the y-direction occurs and the maximum proton velocity in the y-direction is small compared with what it is in the co-helicity case. The proton bump-on-tail appears in the positive y-direction for both co-helicity and counter-helicity, as seen in Fig. 5b. Therefore the origin of the bump-on-tail may be related to the acceleration by the combination of three electric field components as shown by Nagao et al. (2000), not simply only to the acceleration by the electric field parallel to the reverse current.
,
respectively.
As seen in Fig. 5b, strong anisotropic acceleration in the negative y-direction is observed for the co-helicity case, while for the counter-helicity case, almost symmetric acceleration in the y-direction occurs and the maximum proton velocity in the y-direction is small compared with what it is in the co-helicity case. The proton bump-on-tail appears in the positive y-direction for both co-helicity and counter-helicity, as seen in Fig. 5b. Therefore the origin of the bump-on-tail may be related to the acceleration by the combination of three electric field components as shown by Nagao et al. (2000), not simply only to the acceleration by the electric field parallel to the reverse current.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{1018f6.eps}
\end{figure}](/articles/aa/full/2004/40/aa1018/Timg72.gif) |
Figure 6:
The phase-diagrams of protons: a) the x-Vy plane and b) the z-Vy plane at
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=10cm]{1018f7.eps}
\end{figure}](/articles/aa/full/2004/40/aa1018/Timg73.gif) |
Figure 7:
The phase-diagrams of protons: a) the x-Vy plane and b) the z-Vy plane at
|
| Open with DEXTER | |
Next we investigate the location where the high-energy protons can be accelerated.
We show the phase-diagrams of protons of the x-Vy plane in Fig. 6a, and the z-Vy plane in Fig. 6b at
![]() for the co-helicity case.
In Fig. 6c we show the spatial distribution of the electric field Ey with gray scale and vector plots (Ex -Ez) at 4.7
for the co-helicity case.
In Fig. 6c we show the spatial distribution of the electric field Ey with gray scale and vector plots (Ex -Ez) at 4.7 ![]() for the co-helicity case. We found that the high-energy protons in the negative y-direction can be produced near the center of the reversed
current sheet and the midium energy proton in the positive y-direction can be accelerated near the region where the electric field Ez is strong in the positive z-direction. Therefore the protons with medium energy can be produced mostly in one loop such as the right-hand loop seen in Fig. 6c.
for the co-helicity case. We found that the high-energy protons in the negative y-direction can be produced near the center of the reversed
current sheet and the midium energy proton in the positive y-direction can be accelerated near the region where the electric field Ez is strong in the positive z-direction. Therefore the protons with medium energy can be produced mostly in one loop such as the right-hand loop seen in Fig. 6c.
In Figs. 7a and b we show the phase-diagrams of protons of the x-Vy plane and the z-Vy plane at
![]() for the counter-helicity case, respectively.
Fig. 7c shows the spatial distribution of the electric field Ey with gray scale and vector plots (Ex -Ez) at 4.7
for the counter-helicity case, respectively.
Fig. 7c shows the spatial distribution of the electric field Ey with gray scale and vector plots (Ex -Ez) at 4.7 ![]() for the counter-helicity case. As in Fig. 7a, the proton acceleration near the center of the reverse current sheet is weak compared with the previous co-helicity case. The reason is due to the fact that the guiding magnetic field By near the reverse current sheet is weak by its magnetic reconnection. As seen in Figs. 7a and b, the high-energy protons can be accelerated in the positive y-direction mainly near the inner part of the right-handed loop. Therefore, for the counter-helicity case there is no strong anisotropic proton acceleration in the y-direction along the loop.
for the counter-helicity case. As in Fig. 7a, the proton acceleration near the center of the reverse current sheet is weak compared with the previous co-helicity case. The reason is due to the fact that the guiding magnetic field By near the reverse current sheet is weak by its magnetic reconnection. As seen in Figs. 7a and b, the high-energy protons can be accelerated in the positive y-direction mainly near the inner part of the right-handed loop. Therefore, for the counter-helicity case there is no strong anisotropic proton acceleration in the y-direction along the loop.
Since the aim of this study is to investigate the acceleration of protons by magnetic
reconnection in solar flares, we establish physical links between the scaling of
the basic parameters in the simulations and solar flare conditions.
As the initial given value of
![]() ,
the Alfvén velocity is about
,
the Alfvén velocity is about
![]() .
Also, the proton thermal velocity is assumed to be equal to 0.4Va,
or
.
Also, the proton thermal velocity is assumed to be equal to 0.4Va,
or
![]() ,
which corresponds to the
,
which corresponds to the ![]() 1.6 keV ambient ions. The temperature
is acceptable for a well-developed flare in the preflare phase.
Those
1.6 keV ambient ions. The temperature
is acceptable for a well-developed flare in the preflare phase.
Those ![]() 1.6 keV ions can be accelerated to the MeV energy range,
whose maximum is about
1.6 keV ions can be accelerated to the MeV energy range,
whose maximum is about ![]() 7 MeV for co-helicity reconnection and
about
7 MeV for co-helicity reconnection and
about ![]() 5 MeV for counter-helicity reconnection, respectively. Therefore protons accelerated during co-helicity reconnection can produce the observed prompt nuclear de-excitation lines
of gamma-ray. The bump-on-tail proton energy corresponds to about 1 MeV.
5 MeV for counter-helicity reconnection, respectively. Therefore protons accelerated during co-helicity reconnection can produce the observed prompt nuclear de-excitation lines
of gamma-ray. The bump-on-tail proton energy corresponds to about 1 MeV.
We have investigated the behavior of protons near an X-type magnetic reconnection region
during the coalescence of two parallel loops for the two cases of co-helicity and counter-helicity.
The electromagnetic fields during the coalescence process were calculated from a three-dimensional resistive MHD simulation, to find the most effective electric fields for the proton acceleration.
In contrast to the result by Mori et al. (1998) who showed that the energy spectrum of accelerated protons near X-type magnetic reconnection regions is universal with a power-law spectrum
![]() ,
where the power-law index
,
where the power-law index ![]() is about 2.0-2.2, the proton energy spectrum found by us is neither purely exponential nor purely power-law, because of the more complicated structure of the electromagnetic fields during coalescence process.
We found a bump-on-tail distribution in the positive y-direction along the original loop current for both the cases of co-helicity and counter-helicity. While the high-energy protons producing the observed prompt nuclear de-excitation gamma-ray lines can be produced mostly in the direction opposite to the original loop current near the reverse current sheet only for co-helicity reconnection. Therefore we may conclude that the anisotropic proton acceleration
along the loop can be realized both for co-helicity and counter-helicity reconnection during two parallel loops coalescence. This result should be very important for understanding the recent gamma-ray images taken from the RHESSI observation (Hurford et al. 2003). The observation shows that the centroid of the 2.223 MeV image was found to be displaced by 20
is about 2.0-2.2, the proton energy spectrum found by us is neither purely exponential nor purely power-law, because of the more complicated structure of the electromagnetic fields during coalescence process.
We found a bump-on-tail distribution in the positive y-direction along the original loop current for both the cases of co-helicity and counter-helicity. While the high-energy protons producing the observed prompt nuclear de-excitation gamma-ray lines can be produced mostly in the direction opposite to the original loop current near the reverse current sheet only for co-helicity reconnection. Therefore we may conclude that the anisotropic proton acceleration
along the loop can be realized both for co-helicity and counter-helicity reconnection during two parallel loops coalescence. This result should be very important for understanding the recent gamma-ray images taken from the RHESSI observation (Hurford et al. 2003). The observation shows that the centroid of the 2.223 MeV image was found to be displaced by 20 ![]() 6 arcsec from that of the 0.3-0.5 MeV, implying a difference in acceleration and/or propagation between the accelerated electron and proton population near the Sun. The fact that the proton-associated gamma-ray source does not coincide with the electron-bremsstrahlung sources suggests
that the protons are accelerated in one direction by the DC electric field and could subsequently interact in spatially separated sources. One possible scenario to explain the above
observation is as follows. The single loop with
6 arcsec from that of the 0.3-0.5 MeV, implying a difference in acceleration and/or propagation between the accelerated electron and proton population near the Sun. The fact that the proton-associated gamma-ray source does not coincide with the electron-bremsstrahlung sources suggests
that the protons are accelerated in one direction by the DC electric field and could subsequently interact in spatially separated sources. One possible scenario to explain the above
observation is as follows. The single loop with ![]() in the center of the loop is supposed to be disrupted by the mechanism recently proposed by Sakai et al. (2002), then the disrupted part of the loop with high energy protons as well as hot thermalized
protons could move up and interact with the overlying other loop. The interaction between the ascending magnetized plasma blobs and the other loop can lead to magnetic reconnection in the interaction region, where the proton could be accelerated further by the inductive electric field associated with the magnetic reconnection mostly in one direction
along the guiding magnetic field.
in the center of the loop is supposed to be disrupted by the mechanism recently proposed by Sakai et al. (2002), then the disrupted part of the loop with high energy protons as well as hot thermalized
protons could move up and interact with the overlying other loop. The interaction between the ascending magnetized plasma blobs and the other loop can lead to magnetic reconnection in the interaction region, where the proton could be accelerated further by the inductive electric field associated with the magnetic reconnection mostly in one direction
along the guiding magnetic field.
Acknowledgements
We thank the referee for constructive comments that improved our original paper. This work was completed when one of authors (Sakai) stayed in Warwick University, supported by the exchange program between the JSPS and the Royal Society. He thanks V. Nakariakov and G. Rowlands for their hospitality during his stay.