A&A 426, 75-80 (2004)
DOI: 10.1051/0004-6361:20035669
The Pleiades mass function: Models
versus observations
E. Moraux1,2 - P. Kroupa3,4,5 - J. Bouvier1
1 - Laboratoire d'Astrophysique, Observatoire de Grenoble, BP
53, 38041 Grenoble Cedex 9, France
2 - Institut of Astronomy, Cambridge, CB3 0HA, UK
3 - Institut für Theoretische Physik und Astrophysik der Universität
Kiel, 24098 Kiel, Germany
4 - Sternwarte der Universität Bonn, Auf dem Hügel 71, 53121
Bonn, Germany
5 - Heisenberg Fellow
Received 12 November 2003 / Accepted 23 June 2004
Abstract
Two stellar-dynamical models of binary-rich embedded
proto-Orion-Nebula-type clusters that evolve to Pleiades-like
clusters are studied with an emphasis on comparing the stellar mass
function with observational constraints. By the age of the Pleiades
(about 100 Myr) both models show a similar degree of mass
segregation which also agrees with observational constraints. This
thus indicates that the Pleiades is well relaxed and that it is
suffering from severe amnesia. It is found that the initial mass
function (IMF) must have been indistinguishable from the standard or
Galactic-field IMF for stars with mass
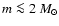 ,
provided the Pleiades precursor had a central density of about
104.8 stars/pc3. A denser model with 105.8 stars/pc3 also leads to reasonable agreement with observational constraints,
but owing to the shorter relaxation time of the embedded cluster it
evolves through energy equipartition to a mass-segregated condition
just prior to residual-gas expulsion. This model consequently
preferentially loses low-mass stars and brown dwarfs (BDs), but the
effect is not very pronounced. The empirical data indicate that the
Pleiades IMF may have been steeper than the Salpeter for stars with
,
provided the Pleiades precursor had a central density of about
104.8 stars/pc3. A denser model with 105.8 stars/pc3 also leads to reasonable agreement with observational constraints,
but owing to the shorter relaxation time of the embedded cluster it
evolves through energy equipartition to a mass-segregated condition
just prior to residual-gas expulsion. This model consequently
preferentially loses low-mass stars and brown dwarfs (BDs), but the
effect is not very pronounced. The empirical data indicate that the
Pleiades IMF may have been steeper than the Salpeter for stars with
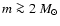 .
.
Key words: stars: low-mass, brown dwarfs - stars: luminosity function, mass function -
Galaxy: open clusters and associations: general
Because of its richness and proximity (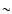 120 pc, Robichon et al. 1999), the Pleiades cluster with an age of 120 Myr (Stauffer et al. 1998; Martín et al. 1998) is one of the best studied young
open clusters. It has a mass of about
120 pc, Robichon et al. 1999), the Pleiades cluster with an age of 120 Myr (Stauffer et al. 1998; Martín et al. 1998) is one of the best studied young
open clusters. It has a mass of about
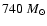 ,
contains
,
contains
 1000 stars and has a tidal radius of about 13.1 pc, a half mass
radius of about 3.66 pc (Pinfield et al. 1998), and a binary-rich
population with properties similar to that in the Galactic field
(Bouvier et al. 1997). Recent stellar-dynamical computations suggest
that the Pleiades-precursor may have been very similar to the about
1 Myr old Orion Nebula cluster (ONC) (Kroupa et al. 2001,
hereinafter KAH), opening the possibility of seeing the same kind of
object at two very different evolutionary stages.
1000 stars and has a tidal radius of about 13.1 pc, a half mass
radius of about 3.66 pc (Pinfield et al. 1998), and a binary-rich
population with properties similar to that in the Galactic field
(Bouvier et al. 1997). Recent stellar-dynamical computations suggest
that the Pleiades-precursor may have been very similar to the about
1 Myr old Orion Nebula cluster (ONC) (Kroupa et al. 2001,
hereinafter KAH), opening the possibility of seeing the same kind of
object at two very different evolutionary stages.
Several surveys have been performed to date to measure its stellar
mass function which is now well constrained from the stellar to the
sub-stellar domain. Recent estimates extend as deep as
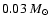 (Moraux et al. 2003). A pressing issue in star formation is to know
whether this mass function (MF) observed at an age of
(Moraux et al. 2003). A pressing issue in star formation is to know
whether this mass function (MF) observed at an age of  100 Myr is
representative of the initial mass function (IMF). In other words, is
the observed Pleiades population representative of the cluster
population at the time it formed and how did it evolve within 100 Myr?
100 Myr is
representative of the initial mass function (IMF). In other words, is
the observed Pleiades population representative of the cluster
population at the time it formed and how did it evolve within 100 Myr?
KAH present calculations of the formation of Galactic clusters using
Aarseth's NBODY6 variant GASEX (Aarseth 1999). They
defined an initial model from a set of assumptions describing the
outcome of the star formation process and studied how it could lead to
the formation of the ONC and then to the Pleiades by dynamical and
stellar evolution. They found encouraging consistency with
observational constraints on the radial density profile, kinematics
and binary properties for both the ONC and the Pleiades. With this
contribution we compare the MF predicted by the models with currently
available data to test if the Pleiades IMF may have been compatible
with the "standard'' IMF (Kroupa 2001) or with the log-normal IMF found to match the Galactic field population down to the substellar
regime (Chabrier 2002).
In this paper, we describe briefly KAH's models in Sect. 2 before
comparing them to current estimates of the Pleiades MF and presenting
relevant results about the radial distribution and the evolution of
the cluster population in Sect. 3. The conclusions are given in
Sect. 4.
KAH develop stellar-dynamical models of cluster formation under
realistic conditions. Their computations are performed with Aarseth's
NBODY6-variant GASEX which allows accurate treatment of
close encounters without softening and multiple stellar systems in
clusters, incorporates stellar evolution and a Galactic tidal field in
the solar neighbourhood. In the models the initial stellar and
sub-stellar masses are distributed following the standard, or
Galactic-average, three-part power-law IMF
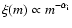 ,
where
,
where
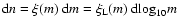 is the number of objects in the mass interval
is the number of objects in the mass interval
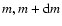 and log10m, log
and log10m, log
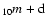 log10m, respectively.
log10m, respectively.
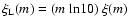 is the "logarithmic
IMF''. The standard IMF has (Kroupa 2001)
is the "logarithmic
IMF''. The standard IMF has (Kroupa 2001)
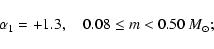 |
(1) |
Initially all objects, stars and brown dwarfs, are assumed to be in
binary systems with component masses chosen randomly from the IMF. The
total binary proportion
where
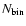 and
and
 are the number of binary and
single-star systems respectively, is then equal to unity. The models
initially consist of 104 stars and brown dwarfs in 5000 binaries.
are the number of binary and
single-star systems respectively, is then equal to unity. The models
initially consist of 104 stars and brown dwarfs in 5000 binaries.
Two models are constructed, both with a spherical Plummer density
profile for the stars and the gas initially. The half-mass radius is
R0.5=0.45 pc for model A with an initial central number density
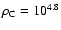 stars/pc3, and
R0.5=0.21 pc for
model B with
stars/pc3, and
R0.5=0.21 pc for
model B with
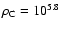 stars/pc3. Both models are
embedded in a gas potential with twice the mass in stars and with the
same density profile as the stellar component. The gas is removed due
to the action of the O stars after 0.6 Myr and the dynamical evolution
is integrated for 150 Myr. By assuming a star-formation efficiency of
33 per cent and removing the residual gas within a thermal time-scale,
the initially embedded cluster (the proto-ONC) expands rapidly,
matches the ONC by about 1 Myr, and by 100 Myr it forms a bound star
cluster which resembles the observed Pleiades and which forms the
nucleus of an expanding association.
stars/pc3. Both models are
embedded in a gas potential with twice the mass in stars and with the
same density profile as the stellar component. The gas is removed due
to the action of the O stars after 0.6 Myr and the dynamical evolution
is integrated for 150 Myr. By assuming a star-formation efficiency of
33 per cent and removing the residual gas within a thermal time-scale,
the initially embedded cluster (the proto-ONC) expands rapidly,
matches the ONC by about 1 Myr, and by 100 Myr it forms a bound star
cluster which resembles the observed Pleiades and which forms the
nucleus of an expanding association.
The MF measured in the Pleiades today may bear witness to these
events, because if the embedded cluster was significantly mass
segregated prior to gas removal, then mostly the low-mass stars will
have been lost, and the Pleiades would then be deficient in
very-low-mass stars.
The evolution of the two cluster models is discussed in KAH and
compared to observational constraints on the structure, kinematics and
binary-star properties for both the ONC and the Pleiades cluster. The
core radii as well as the number of stars within these radii predicted
at 0.9 Myr and 100 Myr by both models are in reasonable agreement with
observed values for the ONC and the Pleiades respectively. Available
velocity dispersion measurements are also consistent with the
models. The observed ONC radial density profile is well reproduced by
model B but not model A, whereas for the Pleiades the best fit is
given by model A. Concerning the period distribution for late-type
binaries, both models are consistent with the Pleiades data, although
an intermediate model in term of central density would be better. For
the ONC, only model B leads to agreement with the measured proportion
of binaries with periods
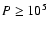 days, model A retaining too many
binaries. Overall though, both models fit the ONC and the Pleiades
data quite well, suggesting that the Pleiades cluster most probably
formed from an ONC-like object. Therefore the initial state of the
Pleiades will have been much more concentrated than presently observed
with a half-mass radius between 0.2 and 0.5 pc.
days, model A retaining too many
binaries. Overall though, both models fit the ONC and the Pleiades
data quite well, suggesting that the Pleiades cluster most probably
formed from an ONC-like object. Therefore the initial state of the
Pleiades will have been much more concentrated than presently observed
with a half-mass radius between 0.2 and 0.5 pc.
In this paper we extend this study by a comparison to the Pleiades MF
which is now constrained down to the sub-stellar regime. The system
MF which is constructed by counting only the system masses is compared
with the observed MF, because the observational surveys cannot resolve
binary stars. It is interesting to investigate the Pleiades MF to see
if it may have changed and whether it differed from the standard IMF,
given that the search for IMF variations constitutes one of the most
important issues of star formation work.
Moraux et al. (2003) performed a deep and extended survey of the
Pleiades cluster using the CFH-12K camera. The survey covered 6.4 sq.deg. reaching up to 3 degrees from the cluster's centre and the
covered mass range extends from 0.03 to 0.45 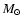 .
The authors
used the NextGen (Baraffe et al. 1998) and Dusty (Chabrier et al. 2000) models to convert their luminosity function into a mass
function and they used the Stauffer & Prosser open cluster
database
.
The authors
used the NextGen (Baraffe et al. 1998) and Dusty (Chabrier et al. 2000) models to convert their luminosity function into a mass
function and they used the Stauffer & Prosser open cluster
database![[*]](/icons/foot_motif.gif) to complete their data
for
to complete their data
for
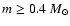 .
They thus computed the mass function from
.
They thus computed the mass function from
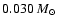 to
to
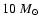 and found that it is reasonably well-fitted
by a log-normal function in logarithmic units (Moraux et al. 2003,
Fig. 9)
and found that it is reasonably well-fitted
by a log-normal function in logarithmic units (Moraux et al. 2003,
Fig. 9)
![\begin{displaymath}\xi_{\rm L}(m) = \frac{{\rm d}n}{{\rm d}\log m} \propto \exp\left[ -
\frac{(\log m - \log m_{0})^2}{2\sigma^{2}}\right]
\end{displaymath}](/articles/aa/full/2004/40/aa0669/img29.gif) |
(2) |
with
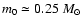 and
and
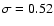 .
It is shown in
Fig. 1.
.
It is shown in
Fig. 1.
However, the lowest mass point of the MF looks a bit different and is
located much above the log-normal fit. Similar features are observed
for other clusters around the same spectral type (M7-M8) and Dobbie et al. (2002) argued this reflects a sharp local drop in the
luminosity-mass (L-M) relationship, due to the onset of dust formation
in the atmosphere around
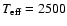 K. A change in the slope of
the L-M relationship implies that the masses of objects with spectral
types later than M7 may be significantly underestimated by the current
NextGen and Dusty models and that the number of objects in this lowest
mass bin may be overestimated. By applying the empirical
magnitude-mass relation given by Dobbie et al. (2002; their Fig. 3) for
the Pleiades low mass stars and brown dwarfs, we find that the lowest
mass point of the Pleiades MF goes down whereas higher mass points go
up (see Fig. 1). The log-normal fit does not change however
and becomes even better.
K. A change in the slope of
the L-M relationship implies that the masses of objects with spectral
types later than M7 may be significantly underestimated by the current
NextGen and Dusty models and that the number of objects in this lowest
mass bin may be overestimated. By applying the empirical
magnitude-mass relation given by Dobbie et al. (2002; their Fig. 3) for
the Pleiades low mass stars and brown dwarfs, we find that the lowest
mass point of the Pleiades MF goes down whereas higher mass points go
up (see Fig. 1). The log-normal fit does not change however
and becomes even better.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0669fig1.ps}
\end{figure}](/articles/aa/full/2004/40/aa0669/Timg33.gif) |
Figure 1:
The Pleiades mass function. The open triangles are from the
Prosser and Stauffer Open Cluster Database and the filled circles
are the data points from Moraux et al. (2003). The open squares
have been obtained by applying the empirical magnitude-mass
relation given by Dobbie et al. (2002). The log-normal fit
(Eq. (2)) found by Moraux et al. (2003) is shown as a
solid line. |
| Open with DEXTER |
Even if this dust effect has still to be investigated, it suggests
that the lowest mass point of the Pleiades MF may come down in the
future and we consider the log-normal distribution as a good
approximation of the observed MF in this mass domain.
For
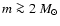 however, this fit does not seem to be steep
enough. The 2-4
however, this fit does not seem to be steep
enough. The 2-4 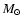 MF points are more than 2-sigma below the
log-normal fit.
MF points are more than 2-sigma below the
log-normal fit.
The system MFs at t=100 Myr resulting from the dynamical and stellar
evolution of KAH's models, assuming random pairing and a binary
fraction
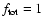 at t=0 are compared to the log-normal fit
of the observed Pleiades MF in Fig. 2 over the entire mass
range. The system MF from model A (resp. model B) is shown as a dashed
(resp. dotted) histogram.
at t=0 are compared to the log-normal fit
of the observed Pleiades MF in Fig. 2 over the entire mass
range. The system MF from model A (resp. model B) is shown as a dashed
(resp. dotted) histogram.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0669fig2.ps}
\end{figure}](/articles/aa/full/2004/40/aa0669/Timg36.gif) |
Figure 2:
Comparison of the log-normal fit of the observed Pleiades
MF (shown as a solid line) to the model MFs. The dashed (dotted)
histogram represents the system mass function at an age of 100 Myr
from model A (B) of KAH for all systems within 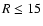 pc of the
model cluster center. They have been scaled to match the Pleiades
data around pc of the
model cluster center. They have been scaled to match the Pleiades
data around
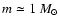 . . |
| Open with DEXTER |
Both models reproduce well the log-normal distribution for
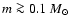 which indicates that the observed MF (data points in
Fig. 1) is also steeper than the model MF for
which indicates that the observed MF (data points in
Fig. 1) is also steeper than the model MF for
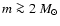 .
This discrepancy cannot be the effect of the
stellar evolution since the models include its treatment but may
indicate that the true stellar IMF in the Pleiades may have been
steeper than Salpeter (
.
This discrepancy cannot be the effect of the
stellar evolution since the models include its treatment but may
indicate that the true stellar IMF in the Pleiades may have been
steeper than Salpeter (
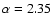 )
above
)
above 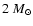 .
.
It is useful to note that the KAH models do not constitute a fit
but are a prediction of the Pleiades MF in the stellar and the
sub-stellar regime under the assumption that the Pleiades IMF was
identical to the standard IMF (Eq. (1); Kroupa 2001). Our
result here suggests that this may indeed have been the case except
for the possibly steeper IMF for
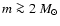 .
.
For
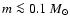 down to the sub-stellar regime, model A
yields a better fit than model B which suggests that the Pleiades may
not have formed from an embedded cluster as concentrated as model
B. The larger number of isolated BD systems predicted by model B
compared to model A in Fig. 2 results from the early release
of brown dwarf companions from their primary in the initially denser
environment of model B. The observed period-distribution of late-type
Pleiades binaries seems also to be better reproduced with model A for
down to the sub-stellar regime, model A
yields a better fit than model B which suggests that the Pleiades may
not have formed from an embedded cluster as concentrated as model
B. The larger number of isolated BD systems predicted by model B
compared to model A in Fig. 2 results from the early release
of brown dwarf companions from their primary in the initially denser
environment of model B. The observed period-distribution of late-type
Pleiades binaries seems also to be better reproduced with model A for
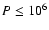 days (see KAH, their Fig. 11), although an intermediate
model in terms of central density would lead to improved agreement for
longer periods. Therefore, our results tend to favour model A but
model B cannot be excluded since it is still consistent with the
observational result within the uncertainties (especially for the
lower mass bins where the effect of dust formation still needs to be
investigated).
days (see KAH, their Fig. 11), although an intermediate
model in terms of central density would lead to improved agreement for
longer periods. Therefore, our results tend to favour model A but
model B cannot be excluded since it is still consistent with the
observational result within the uncertainties (especially for the
lower mass bins where the effect of dust formation still needs to be
investigated).
By 100 Myr the binary fraction is not equal to one any longer and
depends on mass. During the early stage of the cluster's life, many
binaries are disrupted because of gravitational interactions. The
binding energy being weak for low mass binaries, many brown dwarfs
(BDs) have been freed and the BD-BD binary fraction predicted by the
models is 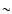
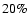 (see KAH, their Fig. 9) which is consistent with
current observational results ranging from 15-50%. Martín
et al. (2003) find
(see KAH, their Fig. 9) which is consistent with
current observational results ranging from 15-50%. Martín
et al. (2003) find 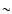
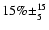 for resolved Pleiades
systems with separations from 7-12 AU but Pinfield et al. (2003)
suggest that the Pleiades total (i.e. unresolved in general) binary
fraction is from 30-50%. Overall, the observational constraints on
late-type binaries are in reasonable agreement with the models, as
shown by KAH. The binary proportion of the massive stars decreases
first through disruption and then increases as new companions are
captured.
for resolved Pleiades
systems with separations from 7-12 AU but Pinfield et al. (2003)
suggest that the Pleiades total (i.e. unresolved in general) binary
fraction is from 30-50%. Overall, the observational constraints on
late-type binaries are in reasonable agreement with the models, as
shown by KAH. The binary proportion of the massive stars decreases
first through disruption and then increases as new companions are
captured.
The mass function of all the objects counted individually is
represented by a histogram in Fig. 3 for both models.
It corresponds to the Pleiades MF we would observe if we were able to
resolve all the binaries. If we compare this single star MF with the
standard IMF indicated by the dots, we find that the overall shapes
are similar, although model B shows a marginal deficit of BDs compared
to model A. This indicates that the main difference between the
Pleiades MF observed at an age of 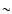 100 Myr and the Pleiades IMF
is mainly due to the binarity effect and that the cluster dynamical
evolution had little effect on its mass distribution.
100 Myr and the Pleiades IMF
is mainly due to the binarity effect and that the cluster dynamical
evolution had little effect on its mass distribution.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0669fig3.ps}
\end{figure}](/articles/aa/full/2004/40/aa0669/Timg46.gif) |
Figure 3:
The single object mass function for model A (dashed
histogram) and model B (dotted histogram) at t=100 Myr and
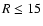 pc. The shaded region represents the field mass function
from Chabrier (2003) with uncertainties. The dots correspond to the
shape of the standard three-part power-law IMF. All models are
scaled to agree between pc. The shaded region represents the field mass function
from Chabrier (2003) with uncertainties. The dots correspond to the
shape of the standard three-part power-law IMF. All models are
scaled to agree between
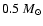 and
and
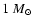 . . |
| Open with DEXTER |
The Galactic disk log-normal MF obtained by Chabrier (2003, Eq. (17)) by
fitting L and T dwarf samples (Chabrier 2002) is found to be slighty
above the histograms in the sub-stellar domain. This suggests that
either the Pleiades IMF is different from the Chabrier's field IMF in
this mass range or that the number of brown dwarfs in the field has
been overestimated. The ratio
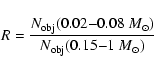
where
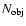 is the number of objects in the respective mass range
is found to be equal to
is the number of objects in the respective mass range
is found to be equal to
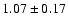 for Chabrier's Galactic disk
log-normal MF, whereas it is equal to
for Chabrier's Galactic disk
log-normal MF, whereas it is equal to
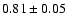 for the three-part
power-law standard Pleiades IMF.
for the three-part
power-law standard Pleiades IMF.
In Fig. 4, the fraction of systems per mass bin
contained in the cluster centre (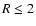 pc) and predicted by the
models at t=100 Myr is compared with observational constraints. The
solid line corresponds to model A and the dashed line to the initially
more concentrated model B. The observational results for the Pleiades
are indicated by the filled circles. The data points come from
Pinfield et al. (1998) for the stellar domain and from Moraux et al. (2003) for the sub-stellar regime. The King density profile found
by these authors for each mass bin has been de-projected, thus
providing the spatial density which has then been integrated between 0
and 2 pc to obtain the number of systems in the inner part of the
cluster.
pc) and predicted by the
models at t=100 Myr is compared with observational constraints. The
solid line corresponds to model A and the dashed line to the initially
more concentrated model B. The observational results for the Pleiades
are indicated by the filled circles. The data points come from
Pinfield et al. (1998) for the stellar domain and from Moraux et al. (2003) for the sub-stellar regime. The King density profile found
by these authors for each mass bin has been de-projected, thus
providing the spatial density which has then been integrated between 0
and 2 pc to obtain the number of systems in the inner part of the
cluster.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{0669fig4.ps}
\end{figure}](/articles/aa/full/2004/40/aa0669/Timg51.gif) |
Figure 4:
Ratio of the number of systems within 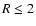 pc to the
total number of cluster systems ( pc to the
total number of cluster systems (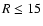 pc) per mass bin at
t=100 Myr. The solid line corresponds to model A and the dashed
line to model B. The stellar data points are from the observational
survey of Pinfield et al. (1998) and the sub-stellar one is from
Moraux et al. (2003) (filled circles). pc) per mass bin at
t=100 Myr. The solid line corresponds to model A and the dashed
line to model B. The stellar data points are from the observational
survey of Pinfield et al. (1998) and the sub-stellar one is from
Moraux et al. (2003) (filled circles). |
| Open with DEXTER |
Model predictions are consistent with observations. The more massive
stars are concentrated around the cluster centre whereas the low mass
objects are much more spread out throughout the cluster.
That the mass segregation at t=100 Myr is similar for the two models
indicates the cluster to be completely relaxed at this age, and that
the memory of the initial concentration has been lost. However, if we
compare the models after 1 Myr, mass segregation has not occurred yet
for model A whereas it is already present for model B (see KAH,
Fig. 15). This model evolved more rapidly than model A by virtue of
its larger initial density and thus shorter relaxation time.
In the previous sections it has been shown that the Pleiades cluster
is dynamically evolved and that mass segregation has occurred, as is
also found to be the case by Portegies Zwart et al. (2001). Here we
consider the detailed structure of the MF to infer if the preferential
loss of stars of a certain mass may be evident in the models. The
ratio of the present-day MF at t=100 Myr to the IMF is plotted for
models A and B in Fig. 5. The comparison between the
cluster population at 100 Myr and the initial cluster population shows
that the evolved population is depleted above about 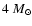 due
to stellar evolution. However there are no significant
evolutionary effects that deplete the population of stars having a
mass from
due
to stellar evolution. However there are no significant
evolutionary effects that deplete the population of stars having a
mass from
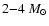 .
Therefore the difference between the observed
Pleiades mass function and the models in this mass range is more
likely due to binarity or a different IMF.
.
Therefore the difference between the observed
Pleiades mass function and the models in this mass range is more
likely due to binarity or a different IMF.
For model A the ratio is quite constant for less massive stars (and BDs) thus demonstrating that the same fraction of objects has been
lost from the cluster independently of mass and thus that energy
equipartition did not play a major role in de-populating the embedded
clusters but rather the violent process given by rapid gas expulsion
during which the model clusters lose about 2/3 of their population.
The larger ratio for model B comes about because this model is
initially more concentrated thus ultimately leading to a more massive
bound cluster because a larger fraction of the population evolves to a
more bound state due to energy equipartition before gas expulsion, as
already noted by KAH and considered in detail by Boily & Kroupa
(2003a,b). For model B the ratio decreases from 0.45 at
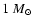 to 0.38 below
to 0.38 below
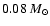 .
This comes about in this
model, which has a short equipartition time-scale, because
less-massive objects end up with a lower cluster binding energy due to
energy equipartition during the embedded phase. Gas expulsion then
leads to the low-mass objects being preferentially lost. The effect is
not very significant though, amounting to about 16 per cent.
.
This comes about in this
model, which has a short equipartition time-scale, because
less-massive objects end up with a lower cluster binding energy due to
energy equipartition during the embedded phase. Gas expulsion then
leads to the low-mass objects being preferentially lost. The effect is
not very significant though, amounting to about 16 per cent.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{0669fig5.ps}
\end{figure}](/articles/aa/full/2004/40/aa0669/Timg55.gif) |
Figure 5:
Fraction of individual objects remaining inside the cluster
(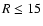 pc) at t=100 Myr compared to the initial number of objects at
t=0. The solid line corresponds to model A and the dashed line to
model B. The ratio of the individual object MFs is shown, not of the
system MFs. pc) at t=100 Myr compared to the initial number of objects at
t=0. The solid line corresponds to model A and the dashed line to
model B. The ratio of the individual object MFs is shown, not of the
system MFs. |
| Open with DEXTER |
The Pleiades is a young (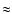 120 Myr) close-by (
120 Myr) close-by (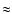 120 pc) Galactic cluster and therefore allows very detailed
observational scrutiny. The available data together with theoretical
work suggest that the Pleiades may have been born similar to the ONC,
and that its subsequent evolution passed a violent phase as a result
of rapid gas expulsion once the massive cluster stars provided
sufficient feedback to the young nebula. The theoretical models
suggest that initially highly concentrated states (model B), with
120 pc) Galactic cluster and therefore allows very detailed
observational scrutiny. The available data together with theoretical
work suggest that the Pleiades may have been born similar to the ONC,
and that its subsequent evolution passed a violent phase as a result
of rapid gas expulsion once the massive cluster stars provided
sufficient feedback to the young nebula. The theoretical models
suggest that initially highly concentrated states (model B), with
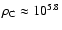 stars/pc3, evolve to significant
mass segregation prior to gas expulsion, while less-concentrated
models with
stars/pc3, evolve to significant
mass segregation prior to gas expulsion, while less-concentrated
models with
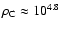 stars/pc3 (model A) do
not. As a result, the former loses slightly more of its low-mass
members relative to higher-mass ones than the latter
(Fig. 5).
stars/pc3 (model A) do
not. As a result, the former loses slightly more of its low-mass
members relative to higher-mass ones than the latter
(Fig. 5).
Both models are in good agreement with the observed MF in the Pleiades
(Fig. 2), although model A yields a better fit which may
suggest that the Pleiades precursor had a concentration near
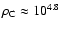 stars/pc3 rather than being more
concentrated. The cluster's stellar IMF could thus have been very
similar to the Galactic-field average IMF for stars with
stars/pc3 rather than being more
concentrated. The cluster's stellar IMF could thus have been very
similar to the Galactic-field average IMF for stars with
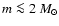 .
No significant stellar IMF variation can thus be
detected, in comparison to the Galactic-field. The sub-stellar part of
the Pleiades mass function also seems correctly reproduced by the
dynamical evolution of dense clusters. This suggests only marginal
evaporation of the lowest cluster members relative to higher mass
stars on a timescale of 100 Myr.
.
No significant stellar IMF variation can thus be
detected, in comparison to the Galactic-field. The sub-stellar part of
the Pleiades mass function also seems correctly reproduced by the
dynamical evolution of dense clusters. This suggests only marginal
evaporation of the lowest cluster members relative to higher mass
stars on a timescale of 100 Myr.
The Pleiades do appear to have a deficit of stars with
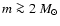 (Fig. 2) compared to the number expected from the
average IMF indicating that the Pleiades IMF may have been steeper,
(Fig. 2) compared to the number expected from the
average IMF indicating that the Pleiades IMF may have been steeper,
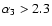 for
for
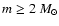 .
This is interesting, because
there exists evidence that the stellar IMF corrected for binarity for
massive stars is probably steeper than a Salpeter IMF (Sagar &
Richtler 1991; Kroupa & Weidner 2003). These authors found
.
This is interesting, because
there exists evidence that the stellar IMF corrected for binarity for
massive stars is probably steeper than a Salpeter IMF (Sagar &
Richtler 1991; Kroupa & Weidner 2003). These authors found
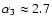 whereas an apparent Salpeter IMF indicates
whereas an apparent Salpeter IMF indicates
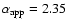 .
However, it will be necessary to compute
additional models with different values for the star-formation
efficiency and mass to map-out feasible Pleiades precursors and the
range of physical conditions within the solution space. For example, a
lower initial density and thus a presumably larger loss of massive
stars during gas expulsion may reduce the discrepancy found here of
the measured MF and the standard IMF.
.
However, it will be necessary to compute
additional models with different values for the star-formation
efficiency and mass to map-out feasible Pleiades precursors and the
range of physical conditions within the solution space. For example, a
lower initial density and thus a presumably larger loss of massive
stars during gas expulsion may reduce the discrepancy found here of
the measured MF and the standard IMF.
The Pleiades show very pronounced mass segregation
(Fig. 4) which is well reproduced by both models. This
indicates that the mass segregation that develops in model B prior to
gas expulsion is forgotten by 100 Myr. The Pleiades is therefore in a
completely relaxed state, having almost completely lost memory of its
initial condition. These, however, are reflected in the properties of
its binary population, because the initial concentration limits the
binary-star periods that survive to old cluster age (KAH).
Acknowledgements
P.K. acknowledges support through DFG grant KR1635/4-1 and thanks the
staff of the Observatoire de Grenoble for their very kind hospitality
during the summer of 2002. This work made use of Aarseth's
NBODY6 code.
- Aarseth, S. J.
1999, PASP, 111, 1333 [NASA ADS] [CrossRef] (In the text)
- Baraffe, I.,
Chabrier, G., Allard, F., & Hauschildt, P. H. 1998, A&A,
337, 403 [NASA ADS] (In the text)
- Boily, C. M., &
Kroupa, P. 2003a, MNRAS, 338, 665 [NASA ADS] [CrossRef] (In the text)
- Boily, C. M., &
Kroupa, P. 2003b, MNRAS, 338, 673 [NASA ADS] [CrossRef]
- Bouvier, J.,
Rigaut, F., & Nadeau, D. 1997, A&A, 323, 139 [NASA ADS] (In the text)
- Chabrier, G.
2003, PASP, 115, 763 [NASA ADS] [CrossRef] (In the text)
- Chabrier, G.
2002, ApJ, 567, 304 [NASA ADS] [CrossRef] (In the text)
- Chabrier, G.,
Baraffe, I., Allard, F., & Hauschildt, P. H. 2000, ApJ, 542,
464 [NASA ADS] [CrossRef] (In the text)
- Dobbie, P. D.,
Pinfield, D. J., Jameson, R. F., & Hodgkin, S. T. 2002, MNRAS,
335, L79 [NASA ADS] [CrossRef] (In the text)
- Kroupa, P. 2001,
MNRAS, 322, 231 [NASA ADS] [CrossRef] (In the text)
- Kroupa, P., &
Weidner, C. 2003, ApJ, 598, 1076 [NASA ADS] [CrossRef] (In the text)
- Kroupa, P.,
Aarseth, S., & Hurley, J. 2001, MNRAS, 321, 699 [NASA ADS] [CrossRef] (KAH)
- Kroupa, P.,
Bouvier, J., Duchêne, G., & Moraux, E. 2003, MNRAS, 346,
368 [NASA ADS]
- Martín, E. L.,
Barrado y Navascués, D., Baraffe, I., Bouy, H., & Dahm, S.
2003, ApJ, 594, 525 [NASA ADS] [CrossRef] (In the text)
- Martín, E. L.,
Basri, G., Gallegos, J. E., et al. 1998, ApJ, 499, L61 [NASA ADS] [CrossRef] (In the text)
- Moraux, E.,
Bouvier, J., Stauffer, J. R., & Cuillandre, J.-C. 2003,
A&A, 400, 891 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Pinfield, D.
J., Jameson, R. F., & Hodgkin, S. T. 1998, MNRAS, 299, 955 [NASA ADS] [CrossRef] (In the text)
- Portegies
Zwart, S. F., McMillan, S. L. W., Hut, P., & Makino, J. 2001,
MNRAS, 321, 199 [NASA ADS] [CrossRef]
- Robichon, N.,
Arenou, F., Mermilliod, J.-C., & Turon, C. 1999, A&A, 345,
471 [NASA ADS] (In the text)
- Sagar, R., &
Richtler, T. 1991, A&A, 250, 324 [NASA ADS] (In the text)
- Stauffer, J.
R., Schultz, G., & Kirkpatrick, J. D. 1998, ApJ, 499, L199 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2004
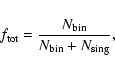
![\begin{displaymath}\xi_{\rm L}(m) = \frac{{\rm d}n}{{\rm d}\log m} \propto \exp\left[ -
\frac{(\log m - \log m_{0})^2}{2\sigma^{2}}\right]
\end{displaymath}](/articles/aa/full/2004/40/aa0669/img29.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0669fig1.ps}
\end{figure}](/articles/aa/full/2004/40/aa0669/Timg33.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0669fig2.ps}
\end{figure}](/articles/aa/full/2004/40/aa0669/Timg36.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0669fig3.ps}
\end{figure}](/articles/aa/full/2004/40/aa0669/Timg46.gif)
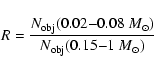
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{0669fig4.ps}
\end{figure}](/articles/aa/full/2004/40/aa0669/Timg51.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{0669fig5.ps}
\end{figure}](/articles/aa/full/2004/40/aa0669/Timg55.gif)