A&A 426, 267-277 (2004)
DOI: 10.1051/0004-6361:20040455

Temperature distribution in magnetized neutron star crusts

U. Geppert1 - M. Küker1 - D. Page2


1 - Astrophysikalisches Institut Potsdam An der Sternwarte 16 14482 Potsdam, Germany
2 - Instituto de Astronomía, UNAM, 04510 Mexico DF, Mexico

Received 16 March 2004 / Accepted 2 July 2004

Abstract
We investigate the influence of different magnetic field configurations on the temperature distribution in neutron star crusts. We consider axisymmetric dipolar fields which are either restricted to the stellar crust, "crustal fields'', or allowed to penetrate the core, "core fields''. By integrating the two-dimensional heat transport equation in the crust, taking into account the classical (Larmor) anisotropy of the heat conductivity, we obtain the crustal temperature distribution, assuming an isothermal core. Including classical and quantum magnetic field effects in the envelope as a boundary condition, we deduce the corresponding surface temperature distributions. We find that core fields result in practically isothermal crusts unless the surface field strength is well above 1015 G while for crustal fields with surface strength above a few times 1012 G significant deviations from crustal isothermality occur at core temperatures inferior or equal to 108 K. At the stellar surface, the cold equatorial region produced by the suppression of heat transport perpendicular to the field by the Larmor rotation of the electrons in the envelope, present for both core and crustal fields, is significantly extended by that classical suppression at higher densities in the case of crustal fields. This can result, for crustal fields, in two small warm polar regions which will have observational consequences: the neutron star has a small effective thermally emitting area and the X-ray pulse profiles are expected to have a distinctively different shape compared to the case of a neutron star with a core field. These features, when compared with X-ray data on thermal emission of young cooling neutron stars, would provide a first step toward a new way of studying the magnetic flux distribution within a neutron star.

Key words: stars: neutron - stars: magnetic fields - conduction - dense matter - X-rays: stars

1 Introduction

The presence of strong magnetic fields in neutron stars is one of their distinctive characteristics. In typical neutron stars the observed and/or inferred surface fields are of the order of 1012...13 G; for magnetars they even reach 1014...15 G (Vasisht & Gotthelf 1997; Kouveliotou et al. 1998). The strength, structure and topology, and time evolution of the magnetic field is intimately related to its origin, which is still an open problem and about which several scenarios have been proposed. During the supernova core collapse which produces the neutron star, the magnetic field possibly present in the progenitor is amplified by flux conservation and may reach values compatible with the observed ones (Woltjer 1964). Moreover, during the convective phase of the proton-neutron star efficient dynamo processes are likely to take place (Thompson & Duncan 1993). In these two scenarios one can expect the magnetic field to have a very complicated topology, the currents supporting it certainly span the whole stellar interior, and significant toroidal components generated by differential rotation can be expected. An alternative scenario had been proposed by Blandford et al. (1983) in which a small seed field is amplified in the upper (liquid) layers of the star through thermomagnetic processes. The currents producing this field are then located entirely in the stellar crust. Notice that these three types of scenarios are not exclusive at all, may act almost simultaneously and/or in succession, and may produce magnetic fields with a double or even triple structure.

Beyond the existence of a strong dipolar component, very little is known about the exact structure of a neutron star magnetic field. Several lines of evidence, both observational and theoretical as described by Arons (1993), indicate that non-dipolar (quadrupolar, octopolar, ...) components in pulsars have to be smaller than the dipolar one. On the other hand, the four-peaked shape of the light curve of the giant flare of August 27, 1998 from SGR 1900+14 (Feroci et al. 2001) is probably strong evidence for the presence of a large quadrupolar component in this magnetar.

A way to observe the structure of the star's surface magnetic field is provided with the observation of surface thermal emission in the soft X-ray band. The structure of the field in the envelope, a shallow layer below the surface, has a direct effect on the surface temperature and leads to a non-uniform distribution (Greenstein & Hartke 1983) with observational consequences (Page 1995) if its strength is above 1010 G. Modeling of the thermal X-ray pulse profile of the Geminga pulsar and PSR 1055-52 (Page & Sarmiento 1996) seemed to require the presence of a quadrupolar component with a strength compatible with the constraint that Arons (1993) had obtained for millisecond pulsars. (See, however, Harding & Muslimov 1998 for a different analysis with a purely dipolar field.) Moreover, Page & Sarmiento (1996) found that the superposition of an arbitrary quadrupolar component with a strength comparable to the dipole generally reduced the observable modulation of the soft thermal X-ray emission, much below observed values, simply due to the fact that it introduced more (up to four) magnetic poles and hence more warm regions at the surface. Together with the considerations of the previous paragraph, these results show that the surface and external field of radio pulsars could be, as a first approximation, reasonably well approximated by a dipolar field. In contrast, almost nothing in observationally known about the structure of the magnetic field inside the neutron star.

Considering physical processes in the interior of a neutron star, transport processes are the most affected by a magnetic field. The effects of the magnetic field onto the transport processes can be roughly divided into classical and quantum ones (see, e.g., Yakovlev & Kaminker 1994 for a review). The classical effects are due to the Larmor rotation of the electrons, the main carriers of charge and heat, and are determined by the magnetization parameter $\omega _{\scriptscriptstyle B} \tau $ where $\omega_{\scriptscriptstyle B} \equiv e B/m_{\rm e}^* c$ is the gyrofrequency of the electrons, $\tau$ being their relaxation time and $m_{\rm e}^*$ their effective mass. Quantized motion of the electrons transverse to the magnetic field causes the quantum effects which are of importance only if few Landau levels are occupied. Quantum effects play an important role for strong magnetic fields in the outermost layers of the neutron star crust - the thin low density shell of the envelope - but are negligible in the deeper layers. The deeper layers of the crust, as well as the envelope, can, however, be affected by classical effects in case of strong fields, i.e., large $\omega_{\scriptscriptstyle B}$, and/or low temperature, i.e., high $\tau$. In such a case the usual assumption of an isothermal crust could be questionable and this is the issue we want to address in this paper.

As a first step in this study, in the present paper we will compare two extreme field configurations referring to the old dichotomy of "core'' and "crustal'' fields. In the first case we have a field penetrating the whole star while the latter is characterized by having the field and its supporting currents restricted to the stellar crust (see, e.g., Chanmugam 1992). Moreover, for simplification, we also restrict ourselves to axisymmetric poloidal dipolar fields. For identical external field structure and strength, in the case of a crustal magnetic field its strength in the crust unavoidably exceeds its surface value by one to two orders of magnitude (see, e.g., Page et al. 2000) and its effects on heat transport can naturally be expected to be much stronger than in the case of a field permeating the whole star whose internal strength can perfectly be everywhere inferior to its external strength. To date, there is still no compelling observational evidence in favor of or against either of these two hypotheses of core or crustal field, but recently Link (2003) argued that long period pulsar precession, as observed in PSR B1828-11 (Stairs et al. 2000), may be impossible if the magnetic field penetrates regions of the core where neutrons are superfluid and proton superconducting (see, however, Jones 2004b for a different point of view).

Our results will show that the structure of the magnetic field deep in the crust can potentially control the distribution of temperature at the stellar surface. This may open a way to study the structure of the magnetic field in the crust and provide observational features which may allow us to discriminate between the above mentioned two types of hypothesized field structure, crustal vs. core. More complex field structure, as, e.g., superposition of core and crustal poloidal dipolar fields, toroidal components, quadrupolar poloidal components, will considered in future papers.

The paper is organized as follows: in the next Sect. 2 the basic equations are introduced which describe the magnetic field and the heat transport influenced by it. The components of the heat conductivity tensor are given and the outer boundary condition is discussed. The physical input as well as the numerical method are shortly described. In Sect. 3 the results of the numerical calculations are presented. For different core temperatures, magnetic field strengths and geometries the crustal temperature profiles, the surface temperature distributions and the corresponding luminosities are calculated. Section 4 is devoted to the discussion of the consequences of the magnetic effects on the crustal and surface temperature distributions.

   
2 Physics input

   
2.1 Heat transport and magnetic field

The thermal evolution of the crust is determined by the energy balance equation

 \begin{displaymath}C~\frac{\partial T}{\partial t} = {\rm Sources} - {\rm Sinks} - \vec{\nabla} \cdot \vec{F} \end{displaymath} (1)

and the heat transport equation

 \begin{displaymath}\vec{F} = - \hat{\kappa} \cdot \vec{\nabla} T \end{displaymath} (2)

where C denotes the specific heat per unit volume, $\vec{F}$ is the heat flux density and $\hat{\kappa}$ the tensor of heat conductivity.

In this paper we intend to consider only the effect of the crustal magnetic field onto the stationary temperature distribution in the crust, which, in a first approximation, is assumed to be free of heat sources and sinks. The cooling process itself as well as the back reaction of the now non-spherically symmetric temperature distribution upon the magnetic field decay are beyond the scope of this work.

  \begin{figure} \par\includegraphics[width=18cm,clip]{0455fig1.eps} \end{figure} Figure 1: Thermal conductivity $\kappa _0$, in cgs units, versus density $\rho $ and temperature T. The left panel shows the phonon-only contribution $\kappa_{0 \; \rm ph}$, the right one the impurity-only contribution $\kappa_{0 \; \rm imp}$, and the central panel the complete $\kappa _0$ (with an impurity concentration $Q_{\rm imp} = 0.1$).
Open with DEXTER

In the relaxation time approximation the components of $\hat{\kappa}$ parallel and perpendicular to the magnetic field, $\kappa_\Vert$ and $\kappa _\perp $ respectively, as well as the Hall component, $\kappa_\wedge$, are related to the scalar heat conductivity $\kappa _0$ and to the magnetization parameter $\omega _{\scriptscriptstyle B} \tau $ by (Yakovlev & Kaminker 1994)

 \begin{displaymath}\kappa_\Vert = \kappa_0 ~,\quad \kappa_\perp = \frac{\kappa_... ...{\wedge} = \omega_{\scriptscriptstyle B} \tau ~ \kappa_\perp . \end{displaymath} (3)

For $\kappa _0$ we use

 \begin{displaymath}\kappa_0 = \frac{\pi^2 k_B^2 T n_{\rm e}}{3 m_* \nu} \end{displaymath} (4)

where $\nu = 1/\tau$ is the effective electron collisional frequency and is given by the sum

\begin{displaymath}\nu = \nu_{\rm ph} + \nu_{\rm ion} + \nu_{\rm imp} \end{displaymath} (5)

where $\nu_{\rm ph}$ is the effective collisional frequency for electron-phonon, $\nu_{\rm ion}$ for electron-ion, and $\nu_{\rm imp}$ for electron-impurity collisions. Since for the range of densities and temperatures we are interested in the crust is always in the solid state we neglect  $\nu_{\rm ion}$and use the calculations of Baiko & Yakovlev (1996) for  $\nu_{\rm ph}$while we take $\nu_{\rm imp}$ from Yakovlev & Urpin (1980). Troughout this work we assume an "impurity parameter'' $Q \equiv x_{\rm imp} \overline{(\Delta Z)^2}$ equal to 0.1, where $x_{\rm imp}$ is the fractional number of impurities which have a mean square charge excess of $\overline{(\Delta Z)^2}$. Figure 1 shows the resulting $\kappa _0$: note that $\nu_{\rm imp}$ is almost temperature independent while $\nu_{\rm ph}$ scales approximately as T2 so that if $\nu = \nu_{\rm ph}$ then we have the "phonon-only conductivity'' $\kappa_{0 \; {\rm ph}} \sim T^{-1}$ (Fig. 1, left panel) but if $\nu = \nu_{\rm imp}$ we would have an "impurity-only conductivity'' $\kappa_{0 \; \rm imp}$ $\sim T^{+1}$ (Fig. 1, right panel) and the exact $\kappa _0$ (Fig. 1, central panel), which one could write as $\kappa_0 = (1/\kappa_{0 \; {\rm ph}} +1/\kappa_{0 {\rm imp}})^{-1}$, shows both types of behavior depending on which type of collision process dominates.
  \begin{figure} \par\includegraphics[width=8.3cm,clip]{0455fig2.eps} \end{figure} Figure 2: Magnetization parameter $\omega _{\scriptscriptstyle B} \tau $ vs. density at six different temperatures (as labeled on the curves) assuming a uniform magnetic field of strength B =1012 G. Its value for different field strengths scales linearly in B.
Open with DEXTER

Given the conductivities described above, the magnetization parameter $\omega _{\scriptscriptstyle B} \tau $ varies strongly throughout the crust by many orders of magnitude. In $\omega_{\scriptscriptstyle B}$ the values of both B and $m_{\rm e}^*$ span a large range of values throughout the crust and in $\tau$ there is also a strong dependence on the temperature T, chemical composition and the thermodynamic phase of the matter. For illustration we show, in Fig. 2, $\omega _{\scriptscriptstyle B} \tau $in the crust at various uniform temperatures and a uniform field strength: however, neither T nor B will be uniform in our realistic calculation presented below. Note that values of $\omega _{\scriptscriptstyle B} \tau $ at T= 105 and 106 K are very close to each other because at such low temperatures, $\nu$ is dominated by $\nu_{\rm imp}$ which is temperature independent while when going to increasingly higher temperatures $\nu_{\rm ph}$ contributes more and more and hence $\tau$ decreases. Finally, Fig. 3 shows the resulting $\kappa _\perp $: notice its very different T-$\rho $ behavior compared to $\kappa _0$due to the simple fact that at high $\omega _{\scriptscriptstyle B} \tau $we obtain $\kappa_\perp \propto \tau^{-1}$ while $\kappa_0 \propto \tau$.

Note, that the contribution of electron-impurity collisions to the collisional frequency is far from being understood. Moreover, Jones (2001, 2004a) argues that the crust is a glass rather than a bcc lattice, resulting in $Q\simeq10...100$. However, calculation of the effect of electron-impurity collisions (Flowers & Itoh 1976) assumes that impurity collisions are uncorrelated, which requires that impurities are randomly located. This raises the issue of how the impurities are arranged, besides their concentration. While well ordered impurities do not disturb significantly the electron motion, highly disordered impurities will (Yakovlev 2004, private communication). In the former case the conductivity would be close to the perfect lattice one while in the latter case it would approach the conductivity of a liquid, i.e. be dominated by electron-ion collisions. These qualitative different behaviors are not reflected by the "impurity parameter'' Q. In this investigation, as described in the previous paragraph, we will consider the crust to be a Coulomb crystal which is so far the only case studied in detail.

Conductive processes which are not affected by magnetic fields can increase the heat flux perpendicular to $\vec{B}$. Recently, Yakovlev (2004, private communication) pointed out that there are at least three processes which have to be considered carefully: the convective counterflow of superfluid neutrons in the inner crust, the diffusive transport by non-superfluid neutrons which may be present in certain regions of the crust and the phonon transport. These transport processes have not yet been considered in the context of cooling calculations of neutron stars up to now. They are beyond the scope of the present manuscript but should be seriously investigated.

  \begin{figure} \par\includegraphics[width=8.3cm,clip]{0455fig3.eps} %\end{figure} Figure 3: Thermal conductivity, in cgs units, perpendicular to the magnetic field, $\kappa _\perp $, vs. density $\rho $ and temperature T for a uniform magnetic field of strength $3\times 10^{12}$ G. For field strengths $\gg $1012 G, i.e., for $\omega _{\scriptscriptstyle B} \tau \gg 1$, $\kappa _\perp $ scales as B-2. The impurity parameter Q is assumed to be 0.1.
Open with DEXTER

2.2 The crustal magnetic field

A dipolar poloidal magnetic field can be conveniently described in terms of the (possibly time dependent) Stokes stream function S = S(r,t). The vector potential $\vec{A} = (0, 0, A_{\varphi})$ is written as $A_{\varphi} = S(r, t) \sin \theta /r$, where r, $\theta $ and $\varphi$ are spherical coordinates. The field components are then expressed as

 \begin{displaymath}B_r = + \frac{2 \cos \theta}{r^2} S(r,t) = B_0 \; \frac{\cos \theta}{x^2} \; s(x,t) \end{displaymath} (6)


 \begin{displaymath}B_\theta = - \frac{\sin \theta}{r} \frac{\partial S(r,t)}{\... ...; \frac{\sin \theta}{x} \; \frac{\partial s(x,t)}{\partial x} \end{displaymath} (7)


\begin{displaymath}B_\varphi = 0 \end{displaymath} (8)

where B0 is the field strength at the magnetic pole, and we have introduced normalized variables $S=s B_0 R_{\rm NS}^2/2$, with s=1 at the magnetic north pole, and $x=r/R_{\rm NS}$. The vacuum solution, outside the star, is simply s =1/x. At the surface, x=1, the standard boundary condition for matching to a vacuum dipole field should be fulfilled,

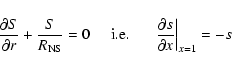\begin{displaymath}\frac{\partial S}{\partial r} + \frac{S}{R_{\rm NS}} = 0 \;\;... ...\; \left. \frac{\partial s}{\partial x}\right\vert _{x=1} = -s \end{displaymath} (9)

and at the center regularity requires $S(r=0,t) \equiv 0$.

For the present investigation we select for the crustal field configuration a snapshot of the evolution of S(x,t). The Stokes function S(x,t) was calculated by solving the induction equation, applying the above boundary conditions and an electric conductivity which reflects the same microphysics as the heat conductivity does for the model under consideration (see, e.g., Geppert & Urpin 1994 or Page et al. 2000).

  \begin{figure} \par\includegraphics[width=3.5cm,clip]{0455fig4.ps}\hspace*{3mm} \includegraphics[width=3.5cm,clip]{0455fig5.ps} \end{figure} Figure 4: Magnetic field lines of the core field ( left panel) and of the crustal field as applied in our calculations. Both field configurations match for $r \ge R_{\rm NS}$ with a dipolar poloidal vacuum field. They are presented in a meridional plane, of the crust for $\rho _n \ge \rho \ge \rho _{\rm b}$ (see Sects. 2.4 and 2.5). The polar surface value B0 is identical for both field types.
Open with DEXTER

The initial value S(x,t=0) is a priori unknown and depends on the field generation process. For a crustal magnetic field, the function S(x,t=0) initially vanishes in the core and, due to proton superconductivity, the Meissner-Ochsenfeld effect prevents the field from penetrating into the core (see, e.g. Page et al. 2000). A typical crustal field structure is shown in the right panel of Fig. 4. In case the magnetic field is maintained by electric currents circulating in the core the field penetrates the crust too but has a qualitatively different structure. Let us assume that for the core field there are no currents in the crust and the field is maintained in the core by axisymmetric currents circulating around the center of the star. Then a dipolar field will penetrate the crust with the components

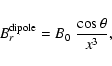\begin{displaymath}B_r^{\rm dipole} = B_0 \; \frac{\cos \theta}{x^3} , \end{displaymath} (10)


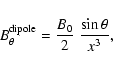\begin{displaymath}B_\theta^{\rm dipole} = \frac{B_0}{2} \; \frac{\sin \theta}{x^3} , \end{displaymath} (11)


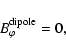\begin{displaymath}B_\varphi^{\rm dipole} = 0 , \end{displaymath} (12)

where B0 denotes again the polar surface value of the magnetic field. The crustal field lines of such a field are presented in the left panel of Fig. 4. A comparison of the geometries of both fields immediately suggests that the star-centered core field will not significantly affect the heat transport through the crust while a crustal field may cause drastic changes. Moreover, in the crust $B_\theta$ has to be much larger than $B_\theta^{\rm dipole}$, for a given identical external field, since the flux of a crustal field is compressed into a layer of thickness $\Delta r \sim \frac{1}{10} - \frac{1}{20}$ of $R_{\rm NS}$, while the flux of a core field can expand within the whole core, typically $B_\theta \sim 10 - 20 B_\theta^{\rm dipole}$.

2.3 The two-dimensional heat transport equation

Denoting the components of the temperature gradient $\vec{\nabla}T$parallel and perpendicular to the unit vector of the magnetic field, $\vec b$ as well as the Hall component by

$\displaystyle (\vec{\nabla} T)_\Vert = \vec{b} \; (\vec{\nabla} T \cdot \vec{b}) ,$   $\displaystyle \;\; (\vec{\nabla} T)_\perp = \vec{b} \times (\vec{\nabla} T \times \vec{b}) ,$ (13)
$\displaystyle (\vec{\nabla} T)_\wedge$ = $\displaystyle \vec{b} \times \vec{\nabla} T ,$  

the magnetic field-influenced heat flux can be expressed by
$\displaystyle \hat{\kappa} \cdot \vec{\nabla}T = \kappa_{\Vert} \; \vec{b} \; (... ...{\nabla} T \times \vec{b}) + \kappa_{\wedge} \; \vec{b} \times \vec{\nabla} T .$     (14)

This provides the following expression for the heat flux in terms of the scalar heat conductivity, the magnetization parameter, the temperature gradient, and the unit vector of the magnetic field:
$\displaystyle \vec{F} = - \hat{\kappa} \cdot \vec{\nabla} T = - \; \frac{\kappa... ...) + \omega_{\scriptscriptstyle B}\tau \; \vec{b} \times \vec{\nabla}T \right] .$     (15)

The last term on the r.h.s. represents the Hall component of the heat flux. Its divergence vanishes as long as the magnetic field and the temperature gradient are assumed to be axially symmetric, i.e. do not depend on the azimuthal angle $\varphi$. By use of the representation of the dipolar magnetic field in terms of the Stokes stream function s and its radial derivatives (see Eqs. (6), (7)) and by introducing the heat conductivity coefficients
 
$\displaystyle \chi_1= \frac{\kappa_0}{1+(\omega_{\scriptscriptstyle B}\tau)^2} ... ...mega_{\scriptscriptstyle B_0}\tau)^2}{1+(\omega_{\scriptscriptstyle B}\tau)^2},$     (16)

the radial and meridional components of the magnetic-field-dependent heat flux have the following form:
 
$\displaystyle F_x= -\chi_1\frac{\partial T}{\partial x} + \chi_2 \left( \frac{\... ...\theta} - \frac{\partial T}{\partial x} \frac{s^2}{x^4} \cos^2{\theta}\right) ,$     (17)


 
$\displaystyle F_{\theta}= -\chi_1\frac{1}{x} \frac{\partial T}{\partial \theta}... ...c{1}{4x^3} \left(\frac{\partial s}{\partial x}\right)^2 \sin^2{\theta}\right) ,$     (18)

where T is measured in units of $T_{\rm core}$ and the temperature gradient is normalized on $T_{\rm core}/R_{\rm NS}$. Note that in Eq. (16) the magnetization parameter $\omega_{\scriptscriptstyle B_0}\tau$ is calculated by use of the polar surface field strength B0.

Axial symmetry implies that, along the polar axis, $F_\theta$ and $\partial F_\theta/\partial \theta$ vanish while x2 Fx is constant. Mirror symmetry at the magnetic equator implies that $F_\theta$ vanishes (but $\partial F_\theta/\partial \theta$ can be very large).

Our aim in this paper will be to find stationary solutions for the temperature distribution in the neutron star crust, i.e. to solve the equation

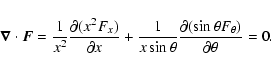\begin{displaymath}\vec{\nabla} \cdot \vec{F} = \frac{1}{x^2} \frac{\partial (... ... \frac{\partial (\sin \theta F_\theta)}{\partial \theta} = 0 . \end{displaymath} (19)

The boundary condition for this equation at the crust-core boundary is "T fixed and uniform'' and at the surface it as discussed in the following subsection.

2.4 Outer boundary: Tb(B)-Ts(B) relation

 

In the lowest-density layers, close to the surface, matter is no longer degenerate and the magnetic field affects the equation of state. Appropriate treatment of this layer requires solving for hydrostatic equilibrium simultaneously with heat transport. Moreover, quantum effects of the magnetic field become important. To avoid these problems, we separate this layer, called envelope, from the crust and incorporate it in the outer boundary condition.

Quantum effects become significant (see, e.g., Yakovlev & Kaminker 1994, for a review) when electrons occupy only few Landau levels, requiring thus densities

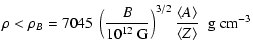$\displaystyle \rho < \rho_B = 7045 ~ \left(\frac{B}{10^{12} ~{\rm G}}\right)^{3/2} \frac{\langle A \rangle }{\langle Z \rangle} \;\; {\rm g \; cm}^{-3}$      

and temperatures
$\displaystyle T \ll T_B \approx 1.34 \times 10^8 \left(\frac{B}{10^{12}~ {\rm G}}\right) \;\; {\rm K}$      

(Potekhin et al. 2003) where $\langle A \rangle $ and $\langle Z \rangle$ are the average mass and charge numbers of the ions. From these numbers it becomes clear that quantum effects play an important role for strong magnetic fields in the outermost layers of the neutron star crust - the envelope - but are negligible in the deeper layers.

The thinness of this envelope justifies a study of heat transport in a plane parallel, one dimensional approximation and many such calculations have been performed (see, e.g., for the most recent one, Potekhin & Yakovlev 2001, hereafter PY01, and references therein). In such 1D envelope approximation, a surface temperature $T_{\rm s}$, and hence an out-coming flux $F^{\rm env} \equiv \sigma T_{\rm s}^4$, is chosen and hydrostatic equilibrium and heat transport are solved toward increasing densities up to $\rho_{\rm b}$ giving the temperature $T^{\rm env}_{\rm b}$ at that density. Varying $T_{\rm s}$ gives a " $T_{\rm b} - T_{\rm s}$ relationship''. Two-dimensional calculations of heat transport with magnetic field have been presented by Schaaf (1990a,b) who however restricted himself to the thin envelope and an uniform magnetic field. Tsuruta (1998) has presented results of two-dimensional cooling calculations of neutron stars which included the quantizing effect of a dipolar magnetic field in the envelope. These 2D calculations showed that the 1D approximation is indeed very good when the field affects heat transport only in the thin envelope. We will use the 1D results of PY01.

We stop the interior integration at an outer boundary density $\rho_{\rm b}$, at radius $r_{\rm b}$, and, for each latitude $\theta $, obtain a radial flux $F_{\rm r}(\rho_{\rm b}, \theta)$ and a temperature $T(\rho_{\rm b}, \theta)$ which we match to the envelope. At each point $(r_{\rm b},\theta)$ we apply an envelope with a magnetic field $\vec{B}$ equal to the field we have at that point (hence the " $T_{\rm b} - T_{\rm s}$ relationship'' should be called a " $T_{\rm b}(\vec B)-T_{\rm s}(\vec B)$ relationship''). The matching of the envelope with our interior calculation is simply obtained by imposing $T^{\rm env}_{\rm b} = T(\rho_{\rm b}, \theta)$and $F^{\rm env} \equiv \sigma T_{\rm s}^4 = F_{\rm r}(\rho_{\rm b}, \theta)$which is our outer boundary condition. YP01 place the bottom of the envelope at the neutron drip density, i.e., $\rho_{\rm b} \approx 4\times 10^{11}$ g cm-3, while we intend to apply lower values down to $\rho_{\rm b} = 10^{10}$ g cm-3 in order to extend the 2-dimensional transport calculation as far as possible while still being safely in the non-quantizing regime. Since the temperature profile in the 1D calculations of YP01 is quite flat between $4\times 10^{11}$ g cm-3 and 1010 g cm-3 the same $T_{\rm b} - T_{\rm s}$ relationship can be applied for the lower $\rho_{\rm b}$ which we consider a good approximation. Explicitly, we apply their Eqs. (26) to (30) but replace their $T_{\rm int}$, which they assume to be spherically symmetric, by our calculated angle-dependent $T_{\rm b}(\theta)$.

To illustrate the main features of this boundary condition, a good approximation (Greenstein & Hartke 1983; YP01) is to write it as

 \begin{displaymath}F_{\rm r}(\rho_{\rm b},\Theta_B,B,T_{\rm b}) \approx F_\Vert \cos^2 \Theta_B + F_\perp \sin^2 \Theta_B , \end{displaymath} (20)

which expresses $F_{\rm r}$, for an arbitrary angle $\Theta_B$ between $\vec{B}$ and the radial direction, in terms of the radial flux for a radial field $F_\Vert \equiv F_{\rm r}(\rho_{\rm b},\Theta_B=0,B,T_{\rm b})$and for a meridional field $F_\perp \equiv F_{\rm r}(\rho_{\rm b},\Theta_B=\pi/2,B,T_{\rm b})$. For a dipolar field $\Theta_B$ is related to the polar angle $\theta $ by $\tan \Theta_B = 0.5 \tan \theta$. Note that when $B \gg 10^{11}$ G one has $F_\perp \ll F_\Vert$, i.e. the envelope is blanketing the star much more strongly around the magnetic equator than around the poles.
  \begin{figure} \par\includegraphics[width=18cm,clip]{0455fig6.eps} \end{figure} Figure 5: The crustal temperature T (normalized on $T_{\rm core}$) as a function of the density within the crust at 4 different polar angles: $\theta =0$: dotted-dashed line (almost coincident with the upper limit of the figure), $\theta =30$: dashed line, $\theta =60\hbox {$^\circ $ }$: dotted line, and $\theta =90\hbox {$^\circ $ }$: full line, for a crustal field of strength $B_0=3\times 10^{12}$ G. The three panels correspond, from left to right, to $T_{\rm core}=10^8$ K, 107 K, and 106 K, respectively.
Open with DEXTER

   
2.5 Equation of state and chemical composition

We will consider a $1.4 ~M_{\odot}$ neutron star whose structure is obtained by integrating the Tolman-Oppenheimer-Volkoff equation of hydrostatic equilibrium. The core matter is described by the equation of state (EOS) calculated by Wiringa et al. (1988). We separate the crust from the core at the density $\rho = \rho_{n} \equiv 1.62 \times 10^{14}$ g cm-3(Lorenz et al. 1993) and use the EOS of Negele & Vautherin (1973) for the inner crust, at $\rho > \rho_{\rm drip} \equiv 4.4 \times 10^{11}$ g cm-3, and Haensel et al. (1989) for the outer crust. We assume that the chemical composition is that of cold catalyzed matter, as is the case for these two crustal EOSs.

The star so produced has a radius $R_{\rm NS} = 10.9$ km and the crust-core boundary is at radius $r_{n} = 0.925 R_{\rm NS} = 9.33$ km.

2.6 Numerical method

We solve the heat transport equation in its time-dependent form,

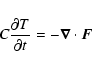\begin{displaymath}C \frac{\partial T}{\partial t} = - \vec{\nabla} \cdot \vec{F} \end{displaymath} (21)

starting with constant temperature, $T = T_{\rm core}$. As boundary condition at the lower boundary the temperature is kept fixed to the value  $T_{\rm core}$ at all times while at the outer boundary the radial heat flux is related to the temperature at the same point as described above. The code is then run until a stationary state is reached.

For the discretization of the spatial derivatives a staggered mesh method as described in Stone & Norman (1992) is used in spherical polar coordinates (r and $\theta $). For the integration in time the fully explicit method turned out to be prohibitively slow because the diffusion coefficients vary strongly in space in the case of strong magnetic fields. We therefore use the scheme in an operator-split implementation that treats the radial diffusion terms implicitly while the horizontal diffusion and the $ {\partial T}/\partial \theta $ term in $F_{\rm r}$ remain explicit. This keeps the computational effort per time step small as the equations to be solved are tridiagonal, but allows for a sufficiently large time step to reach a stationary state within several hours of computing time. For the evaluation of the transport coefficients and the outer boundary condition the temperature resulting from the last time step is always used, i.e., only the radial derivatives are treated implicitly.

   
3 Results

3.1 Internal temperature

The importance of the magnetic field-induced non-isothermality of the whole crust is illustrated in Figs. 5-8. The temperature profiles of Fig. 5, when compared with Fig. 6, show clearly the difference between a crustal and a core field, the latter inducing temperature variations in the crust of much less than 1% at $B_0=3\times 10^{12}$ G while the former can result in variations of a factor two for the same dipolar external field strength and $T_{\rm core}=10^7$ K, and even much larger at lower  $T_{\rm core}$.

For strong fields, when $\omega _{\scriptscriptstyle B} \tau \gg 1$, one has $\kappa_{\Vert} =\kappa_0 \gg \kappa_{\perp}$ and hence heat flows essentially along the field lines and, given the large values of $\kappa _0$, no large temperature gradient can build up along them, as illustrated in Fig. 7. Only extremely strong core fields may cause significant deviations from the isothermality of the crust; for B0 = 1016 G we could observe a difference of only 10% for $T(\rho_{\rm b})$ between pole and equator. The qualitative difference between core and crustal magnetic fields is then easily understood by observing that field lines are essentially radial in most of the crust in the case of a core field while they are predominantly meridional for a crustal field inhibiting radial heat flow in a large part of the crust. We could find significant differences to the isothermal crust model only if the polar surface field strength exceeds 1012 G. Additionally, the core temperature should be smaller than 108 K.

  \begin{figure} \par\includegraphics[width=7cm,clip]{0455fig7.ps} \end{figure} Figure 6: Same as Fig. 5 but for a dipolar core field with $T_{\rm core}=10^7$ K.
Open with DEXTER

In the case of a star-centered core field, Fig. 6 and the right panel of Fig. 7 show that the stellar equator is very slightly warmer than the pole. This is a direct consequence of the outer boundary condition, i.e., the envelope: magnetic-field-induced anisotropies are weak within the crust for such fields but are large in the envelope which is more insulating around the equator than around the poles.

A 3D representation of the crust temperature is shown in Fig. 8: it may be surprising in the sense that heat flows into the crust from the core, at a fixed  $T_{\rm core}$, and out of the crust at the surface and most of the heat comes out in the polar regions which are, first, warmer than the equator and where, second, the envelope is less insulating. So heat must be flowing from the equatorial regions toward the polar regions, i.e., apparently from cold regions toward warmer ones! That this situation cannot violate the second law of thermodynamics is built into the heat conductivity tensor $\hat{\kappa}$ which is positive definite and guarantees that $\vec{F} \cdot \vec{\nabla} T < 0$always. Figure 9 illustrates this situation: at a point in the northern hemisphere $\vec{\nabla}T$ is almost perpendicular to $\vec{B}$and $-(\vec{\nabla} T)_\theta$ is clearly pointing toward the equator. However, since $F_\Vert = -\kappa_\Vert (\vec{\nabla} T)_\Vert$, $F_\perp = -\kappa_\perp (\vec{\nabla} T)_\perp$, and $\kappa_\Vert \gg \kappa_\perp$ we have $\vert F_\Vert\vert \gg \vert F_\perp\vert$and the resulting $F_\theta$ is negative, i.e., pointing toward the pole: heat is flowing from the equator toward the poles but does it along the magnetic field lines from warmer regions toward colder ones. Our numerical results show that, e.g., in the northern hemisphere, $F_\theta$ is negative in large regions and is positive elsewhere depending on the orientation of $\vec{B}$.

  \begin{figure} \par\includegraphics[width=4cm,clip]{0455fig8.ps}\hspace*{3mm} \includegraphics[width=4cm,clip]{0455fig9.ps} \end{figure} Figure 7: Representation of both field lines and temperature distribution in the crust whose radial scale ( $r(\rho _n) \le r \le r(\rho _{\rm b})$) is stretched by a factor of 5, assuming $B_0=3\times 10^{12}$ G and $T_{\rm core}=10^6$ K. Left panel corresponds to a crustal field, right panel to a star-centered core field. Bars show the temperature scales in units of $T_{\rm core}$.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{0455fig10.eps} \end{figure} Figure 8: 3-D presentation of the temperature distribution in the crust for $T_{\rm core}=10^6$ K and a crustal field with strength $B_0=3\times 10^{12}$ G. (corresponding to the right panel of Fig. 5).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.3cm,clip]{0455fig11.eps} %\end{figure} Figure 9: Illustration of the magnetic-field-induced anisotropy (see text for details).
Open with DEXTER

The results shown in Fig. 5 for the crustal field configuration with the typical strength $B_0=3\times 10^{12}$ G confirms the statement that with increasing magnetization parameter the anisotropy of the temperature distribution within the crust increases too. The magnetization parameter increases with increasing magnetic field strength and with decreasing crustal temperature, i.e. with decreasing  $T_{\rm core}$, because the relaxation time of electron-phonon collisions grows strongly in the course of cooling. Therefore, while the temperature profile along the poles shows practically no gradient with decreasing  $T_{\rm core}$the ratio $T(\rho_{\rm b},\theta =90^\circ)/T(\rho_{\rm b},\theta = 0^\circ)$ decreases from 0.95 to 0.5 and 0.2 when  $T_{\rm core}$ decreases from 108 K to 107 and 106 K, respectively. Also, an increase of the magnetic field strength amplifies that difference. Applying the same field structure but B0=1013 G the temperature ratio becomes smaller than 0.1 for $T_{\rm core}=10^6$ K.

Note also that the highly unknown parameter of the impurity concentration (Q=0.1 throughout this paper) affects the relaxation time: the more impurities the shorter the relaxation time of electron-impurity collisions. Therefore, while in a highly impure crust the magnetic field effects on the crustal temperature distribution are reduced, in a very pure neutron star crust these effects will be even more pronounced.

3.2 Surface temperature distribution

The magnetic field permeating the envelope induces a non-uniform surface temperature distribution, mostly due to quantizing effects of the field at low densities, even in the case of a uniform crustal temperature (Schaaf 1990a,b; Page 1995). The non-isothermality of the crust produced by a crustal magnetic field will result in an even more pronounced non-uniformity of the surface temperature. These effects are shown quantitatively in Fig. 10 where the two cases of core and crustal fields are compared.

  \begin{figure} \par\mbox{\includegraphics[width=4cm,height=9.4cm,clip]{0455fig12... ...} \includegraphics[width=4cm,height=9.4cm,clip]{0455fig14.eps} } \end{figure} Figure 10: The surface temperature $T_{\rm s}$ as a function of the polar angle $\theta $ and for $T_{\rm core}=10^6$ K ( left panels), $T_{\rm core}=10^7$ K ( mid panels), or $T_{\rm core}=10^8$ K ( right panels) The dashed lines show the surface temperature distribution when an isothermal crust is assumed. The full lines represent the surface temperatures when the crust temperature distributions take into account the anisotropy of heat transport induced by a crustal magnetic field (the temperature at the crust-core interface being fixed at the $T_{\rm core}$). Almost indistinguishable from the isothermal crust model is the $T_{\rm s}$-distribution for a star-centered core field. It is shown by dot-dashed lines for $T_{\rm core}=10^8$ K; for lower $T_{\rm core}$ the differences are even smaller. The assumed polar surface field strengths B0 are 1012 G ( upper panels), $3\times 10^{12}$ G ( mid panels) and 1013 G ( lower panels).
Open with DEXTER

The different field structures do not only affect the relation between polar and equatorial surface temperature but also the setup and the extension of the warm polar regions. In Fig. 10 it is seen that the crustal field can cause a much smaller warm polar region than a star-centered core field of the same polar surface strength would do. While for the core field geometry with B0=1013 G and $T_{\rm core}=10^8$ K the surface temperature at a polar angle of $31.5\hbox{$^\circ$ }$is reduced only to 0.93 of its polar value, for the crustal field configuration the corresponding value is 0.82. With decreasing  $T_{\rm core}$ this difference becomes larger: thus for $T_{\rm core}=10^6$ K the corresponding values for the core and the crustal field are 0.93 and 0.77, respectively. The setup of a clearly distinct warm polar region becomes more and more pronounced with an increasing magnetization parameter (i.e. increasing field strength and/or decreasing crustal temperature and/or decreasing impurity concentration) for a crustal field configuration, while the shape of the surface temperature distribution is almost unaffected by the magnetization parameter in case of a core magnetic field.

3.3 Luminosity

Having a non-uniform surface temperature distribution, $T_{\rm s}=T_{\rm s}(\theta)$, the effective temperature $T_{\rm eff}$ can be calculated, from its definition, as

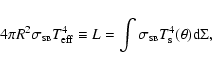\begin{displaymath}4\pi R^2\sigma_{\rm\scriptscriptstyle SB}T_{\rm eff}^4 \equiv... ..._{\rm\scriptscriptstyle SB} T_{\rm s}^4(\theta) {\rm d}\Sigma, \end{displaymath} (22)

where R is the circumferential neutron star radius and ${\rm d}\Sigma \equiv \sin\theta {\rm d}\phi {\rm d}\theta $ is the surface area element, so that finally the luminosity is given by

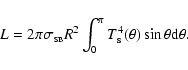\begin{displaymath}L = 2\pi \sigma_{\rm\scriptscriptstyle SB} R^2 \int^\pi_0 T_{\rm s}^4(\theta) \sin{\theta}{\rm d}\theta. \end{displaymath} (23)

The photon luminosities for the neutron star models under consideration with different magnetic field structures and strengths are listed in Table 1 for a model with $T_{\rm core}=10^8$ K, Table 2 for $T_{\rm core}=10^7$ K, and Table 3 for $T_{\rm core}=10^6$ K.

Table 1: Photon luminosities for a neutron star with $T_{\rm core}=10^8$ K. The differences between isothermal crust and star-centered field are negligible but significant between them and crustal fields larger than 1013 G.

Table 2: Photon luminosity for a neutron star with $T_{\rm core}=10^7$ K.

The almost identical luminosities obtained for the isothermal crust and a crust penetrated by a star-centered core field (Table 1) reflect the little effect even strong fields of that structure have onto the crustal temperature distribution. While for a star-centered magnetic field (both with isothermal and non-isothermal crust) the photon luminosity increases with increasing field strength, in neutron stars possessing a crustal magnetic field above a certain strength ($\approx $1012 G) the luminosity is reduced since then over the major part of the surface the heat insulating effect of such a field configuration dominates; its $\theta $-component causes strong meridional heat fluxes toward the polar region whose area, however, becomes smaller with increasing field strength. This effect impedes the radial heat transport strongly, finally less heat can be irradiated away from the surface and the photon cooling process will be decelerated significantly in comparison to a non-magnetized neutron star (here $B_0 \le 10^{12}$ G) or even to a strongly magnetized neutron star with a star-centered core field.

Table 3: Photon luminosity for a neutron star with $T_{\rm core}=10^6$ K.

   
4 Discussion and conclusions

A sufficiently strong magnetic field modifies the thermal insulation of the envelope by increasing the longitudinal thermal conductivity due to the Landau quantization of the electron motion and increases the insulation perpendicular to $\vec{B}$ because of the classical electron Larmor rotation which may diminish the transversal thermal conductivity considerably.

Here, importance of the classical (Larmor) effect for the heat transport through the whole crust has been demonstrated in the particular case of a specific magnetic field configuration, exclusively maintained by electric currents circulating in the crust, which does not penetrate the core of the star and, consequently, has a large tangential component in most of the crust. Besides its insulating effect, the tangential crustal magnetic field creates a meridional heat flux from the equatorial regions towards the high latitude ones. It transports the heat, which is dammed in the equatorial region, towards the poles where it can be much more easily irradiated away. Eventually this leads to an extended equatorial belt which is much cooler than the poles.

In case the magnetic field is allowed to penetrate the core of the star, and assuming a star-centered dipolar geometry in the crust, we have shown that the stationary thermal state of the crust is very close to isothermality. We are thus confirming, for this field geometry, the assumptions of the models of surface temperature distribution of magnetized neutron stars (e.g., Page 1995; Page & Sarmiento 1996; Shibanov & Yakovlev 1996) which considered only the effects of different magnetic field structures and strengths in the envelope and assumed the rest of the crust to be isothermal.

Recently, Svidzinsky (2003) argued that the accumulation of magnetic field lines along the proton superconductor at the crust-core boundary, due to the Meissner-Ochsenfeld effect, produces an insulating barrier preventing heat to flow between the crust and the core. Our results are in the same line of thought but they do not confirm his claims of insulation of the crust from the core. The field geometries, i.e., the Stokes stream functions (Eqs. (6), (7)), we used in our calculations come from field evolution models (Page et al. 2000) of crustal fields in which the migration, and accumulation, of the currents and the field lines toward the crust-core superconducting boundary was modeled in detail and, as illustrated in Fig. 7, they allow heat diffusion through the crust-core boundary. Nevertheless, other field evolution scenarios, e.g. the possible expulsion of the magnetic flux from the core by a proton type I superconductor (Link 2003; Buckley et al. 2004) may produce a much stronger piling up of field lines tangentially to the crust-core boundary and result in more efficient thermal insulation.

Our results have several observational consequences which will be explored in details in forthcoming papers. For both magnetic field structures considered here, the thermal emission of cooling neutron stars will show low amplitude pulsations due to the non-uniform surface temperature exhibited in Fig. 10. Even if the crust remains (almost) isothermal the effect of the magnetic field in the envelope still creates a significant meridional temperature gradient. However, in the presence of a purely crustal field, that temperature gradient will be considerably steeper than for a core field and pulse profiles of different shape and amplitude can be expected. Generally, the steeper meridional temperature gradient will enhance the pulsed fraction of the light curve. However, since it is strongly affected both by the inclination of the line of sight and by the gravitational light bending (see e.g. Page 1995; Heyl & Hernquist 2002), these influences on the light curve have to be taken into account. Clearly, the effect of a crustal magnetic field on the surface temperature distribution will counteract the reduction of the pulsed fraction by gravitational light bending.

A second observational consequence comes from the warm polar region which in case of a strong crustal field is much smaller than for star-centered and/or weak magnetic fields (see Fig. 10). This may open a new way to distinguish between crustal and core magnetic fields: a strong crustal magnetic field implies a smaller effective area for thermally emitting cooling neutron stars. For example, the "Three Musqueteers'' (PSR 0656+14, PSR 1055-52 and Geminga: Becker & Trümper1997) as well as RX J185635-3754 (Pons et al. 2002) all have $R_{\rm eff} \sim 5{-}7$ km when their thermal spectra are fitted with blackbody spectra. If these radii would coincide with the radius of the neutron star, the equation of state describing the state of the core matter would have to be extremely soft. A relatively small warm polar region, created by a strong crustal field and emitting almost all the thermal radiation would be a reasonable explanation for such small  $R_{\rm eff}$.

The differences in the photon luminosities for a star-centered or a crustal field will also affect the long term cooling of neutron stars. A neutron star having a magnetic field confined to its crust will stay warmer for a longer time, due to its lower photon luminosity, than a neutron star with a field penetrating its core. The strength of this effect has to be explored by 2D cooling calculations.

We also mention the consequences the non-isothermality of the crust may have for the crustal field itself. Since the electric conductivity in the hot polar region is much smaller than in the equatorial layer, the field decay will be affected too and may cause differences in the field structure. This "back reaction'' of the field onto its own decay via a field driven non-spherical symmetric crustal temperature distribution will be subject of future investigations.

As discussed in the introduction, the dichotomy "core'' versus "crustal'' magnetic field is probably an over simplification. More realistic cases, comprising a superposition of a core and a crustal field as well as including toroidal components will be considered in future work. The inclusion of higher order multipolar components will also be needed. Nevertheless, one can expect that any field configuration which presents strong meridional components in the crust will affect the surface temperature.

Acknowledgements
The authors thank the (anonymous) referee as well as D. G. Yakovlev whose comments helped to improve the first version of this manuscript. U.G. is grateful to M. Rheinhardt for discussions and to G. Ruediger, whose engagement enabled the realization of the DFG-project "The interaction of thermal and magnetic effects in neutron stars'' (RU 488/18-1). Part of this work is supported by a binational grant from DGF-Conacyt #444MEX113/4/0-2. D.P.'s work is partially supported by grants from UNAM-DGAPA (#IN112502) and Conacyt (#36632-E).

References

 
Copyright ESO 2004