A&A 426,145-149 (2004)
DOI: 10.1051/0004-6361:20040387

The progenitor of the "born-again'' core V605 Aql and the relation to its younger twin V4334 Sgr[*]

M. F. M. Lechner - S. Kimeswenger

Institut für Astrophysik der Universität Innsbruck, Technikerstr. 25, 6020 Innsbruck, Austria

Received 4 March 2004 / Accepted 22 June 2004

Abstract
We derived the properties of V605 Aql before the final helium flash pulse by studying its surrounding PN A58. Photoionizing models of our spectral data together with a new distance estimate and a closer look at the recombination timescales lead to a consistent model. Comparing our findings with the only hydrogen-poor twin, namely Sakurai's Object, we conclude that these born-again objects have normal PNe core masses. We are able to prove V605 Aql indeed to be, similar to V4332 Sgr, a very late thermal pulse object and to put constraints on the evolutionary time scales for the transition back to the AGB.

Key words: stars: AGB and post-AGB - stars: evolution - ISM: planetary nebulae: individual: Abell 58 - stars: individual: V605 Aql, V4334 Sgr

1 Introduction

Calculations done in the early 1980s demonstrated that luminous central stars of PNe could be undergoing a final helium shell flash before the final cooling of the white dwarf. It was reviewed by (Iben & MacDonald 1995) that this last thermal pulse brightens a white dwarf to AGB luminosity and results in a sudden change in abundances to heavier elements as the residual hydrogen envelope is consumed in the helium-burning convective shell. Back at the AGB, the central star of the PN (CSPN) pursues again its evolutionary path to become a white dwarf, but this time the main energy source is helium burning. This evolutionary behavior is called the born-again scenario. Born-again PNe helium-flash objects are characterized by highly processed hydrogen-deficient nebular material and dust and are of fundamental importance for the understanding of the late stages of stellar evolution. Due to the short timescales of the transition only few born again objects were discovered therein. At the moment there are only three objects - Sakurai's Object (V4334 Sgr), V605 Aql and FG Sge - where we can observe more than a final H-deficient PN. This makes individual detailed studies of these objects necessary, especially as they are also discussed as possible progenitors of [WC]-CSPNe, PG1195 type CSPNe and RCrB stars. For a review see Clayton (2001) and references therein.

Sakurai's Object (V4334 Sgr) is the proto-typical final helium shell flash object and had its flash in 1996 (Dürbeck & Benetti 1996). The old PN of V4334 Sgr has been found and its spectrum reveals it to be an ordinary PN (Pollacco 1999).

V605 Aql is often referred to as the "older twin of Sakurai's object'', as many similarities exist. It was discovered in 1919 as "Nova Aquilae No.4'' and later assigned V605 Aql. Only in the 1980s was it recognized to be a final helium flash object and thus it was observed less than Sakurai's object or FG Sge. It already had its flash in 1917, and therefore serves as pathfinder for future events in V4334 Sgr, which is still frozen in its reborn AGB resp. post-AGB state. A detailed historical review of the evolution of V605 Aql can be found in Clayton & de Marco (1997) and the photometric similarities between V605 Aql and V4334 Sgr are discussed in Dürbeck et al. (2002).

Different theoretical models exist to describe the born-again phenomenon, but there is not yet a consensus about the crucial parameters like convective mixing, opacities at high ionization energies, the importance of convective overshoot or surface cooling by means of stellar wind (e.g. Lawlor & MacDonald 2003; Herwig 2001).

We present here a detailed study of V605 Aql and compare our results to those found for V4334 Sgr.

2 Observations and data reduction

We obtained spectra using the ESO NTT telescope at LaSilla (August 4th to 6th 2002) with the multi mode instrument EMMI mounted. Also different narrow-band filter images were obtained there. The calibration (bias, flatfield, wavelength calibration and response curve for the spectra; bias and skyflats for the images) was done using usual procedures in MIDAS. The resolutions of the individual grisms used for the spectra can be found in Table 1.

Table 1: Grisms used for spectroscopy.


  \begin{figure} \par\includegraphics[width=7.7cm,clip]{0387f1.eps}\end{figure} Figure 1: These [OIII] ( left) and [NII] ( right) narrow-band images of PN A58 are not rotated to prevent information loss. The position angle to a north-east orientation is 132.381. The edge enhancement in [NII] gives the impression of an interaction with the ISM.
Open with DEXTER

Narrow-band direct images (see Fig. 1) show a strong dependence of the shape of PN A58 on the excitation level. The [OIII] image of the PN looks rather roundish, whereas in H$\beta$ and in [NII] a western rim is clearly visible. In all three images the nebula seems to consist of three parts; an inner central part and two "polar caps'', which is most obvious in the [OIII] image. According to the manual the EMMI CCD chip has a resolution of 0 $.\!\!^{\prime\prime}$333 per pixel, but the seeing was not sufficient to derive the size of the V605 Aql knot as done by Hinkle et al. (2001). On the basis of the CCD images our estimate for the size of the old PN A58 is 50 $^{\prime\prime}$ for the longitudinal axis and 38 $^{\prime\prime}$ for the secondary axis.

The edge enhancement suggests an interaction with the interstellar medium (ISM). Hence we determined the physical properties of the old nebula Abell 58 out of the inner part, nearer to V605 Aql.

The interstellar extinction had been derived from the Balmer decrement. Different regions show an E(B-V) with extrema of  $0\hbox{$.\!\!^{\rm m}$ }35$ and  $0\hbox{$.\!\!^{\rm m}$ }55$. A weighted average of $E(B-V)=0\hbox{$.\!\!^{\rm m}$ }5$ was adopted for the models.

   
3 Distance determination

There were several distance estimates for V605 Aql before, giving values between 2.7 and 6.0 kpc as reviewed by Clayton & de Marco (1997), who recommended a distance of 3.5 kpc.

We tried to determine the distance by the use of radio observations. The VLA Sky Survey by (Condon & Kaplan 1998) gives a S=2.7 mJy flux-density peak for PN A58 at 1.4 GHz (according to a wavelength of 21 cm), with an 0.8 mJy RMS uncertainty. Usually distances are calculated by the 6 cm radio fluxes (according to a frequency of 4885 MHz), but assuming free-free radiation with

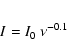
\begin{eqnarray*}I=I_0 ~\nu^{-0.1} \end{eqnarray*}


we translated this value into

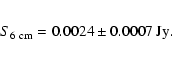
\begin{eqnarray*}S_{{\rm 6~cm}}=0.0024\pm0.0007~\rm Jy. \end{eqnarray*}


Now the method by Cahn et al. (1992) can be applied. The optical thickness parameter $\tau$ is given by

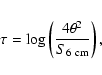
\begin{eqnarray*}\tau=\log\left(\frac{4\theta^2}{S_{{\rm 6~cm}}}\right), \end{eqnarray*}


with $S_{{\rm 6~cm}}$ in Jansky and $\theta$ in arcseconds. A mean value for the angular radius of the PN of 22 $^{\prime\prime}$ resulted in $\tau = 5.91$ $\pm$ 0.12. For $\tau>3.13$ the ionized mass $\mu$ of the PN can be described with

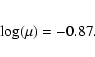
\begin{eqnarray*}\log(\mu)=-0.87. \end{eqnarray*}


Using these equations, the radius R and the distance D of the PN can be determined from the ionized mass by

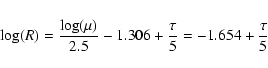
\begin{eqnarray*}\log(R)=\frac{\log(\mu)}{2.5}-1.306+\frac{\tau}{5}=-1.654+\frac{\tau}{5} \end{eqnarray*}


and

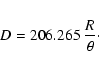
\begin{eqnarray*}D=206.265 ~ \frac{R}{\theta}\cdot \end{eqnarray*}


So the solutions using Condon & Kaplan (1998) and Cahn et al. (1992) are

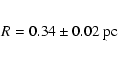
\begin{eqnarray*}R=0.34\pm0.02~{\rm pc } \end{eqnarray*}


and

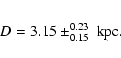
\begin{eqnarray*}D=3.15\pm^{0.23}_{0.15}~{\rm kpc}. \end{eqnarray*}


Alternatively the method of van de Steene & Zijlstra (1995) uses the radio continuum brightness temperature

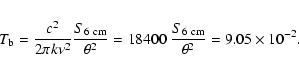
\begin{eqnarray*}T_{\rm b}=\frac{c^2}{2 \pi k \nu^2} \frac{S_{{\rm 6~cm}}}{\theta^2}=18400 ~ \frac{S_{{\rm 6~cm}}}{\theta^2} = 9.05\times10^{-2}. \end{eqnarray*}


From this temperature, which is a measure for the brightness of the nebula at radio frequencies, together with their fitted linear regression line through a sample of bulge PN they specify a radius R:

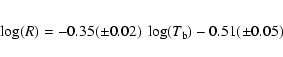
\begin{eqnarray*}\log(R)=-0.35(\pm0.02)~ \log(T_{\rm b}) - 0.51 (\pm0.05) \end{eqnarray*}


leading to R=0.71 pc and D=6.6 kpc. This approximation is generally a factor of 2 too big.

Normally the best and most faithful results (for a discussion see Schmeja & Kimeswenger 2002) are derived by the method of Schneider & Buckley (1996). Their equation is:

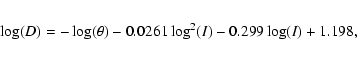
\begin{eqnarray*}\log(D)=-\log(\theta) -0.0261\log^2(I) - 0.299\log(I) + 1.198, \end{eqnarray*}


where the surface brightness $I=S_{{\rm 6~cm}}/(\theta^2 \pi)$ is measured in mJy arcsec-2. This leads to $D=3.08\pm^{0.17}_{0.12}$ kpc.

For all further calculations we therefore assumed a distance of D=3.1 kpc. This means that the radius R of the PN A58 equals 0.33 pc.

   
4 Photoionization models

On the basis of the line fluxes presented in Table 2 the old PN A58 was modelled with CLOUDY (Ferland 1996). The final goal was not to reproduce the ionization and thermal equilibria within the nebula in detail but to qualify the stellar continuum before the helium flash pulse. The low density PN sees still its old central star at the time, when it was sufficiently hot to ionize it. Thus a large grid of photoionizing models was calculated, giving us the position of V605 Aql in the Hertzsprung-Russell diagram (HRD) during its hidden past.

Table 2: Dereddened line fluxes for the PN A58.

Blackbody radiation usually is used for such calculations of other objects (e.g. van de Steene 1995; van Hoof & van de Steene 1999; Kerber et al. 1999; Nürnberger et al. 2001; Cuisinier et al. 2002). Armsdorfer et al. (2002) and Armsdorfer & Kimeswenger (2001) showed that the use of real stellar atmospheres especially changes the helium lines. Here we thus used NLTE central star models of Rauch (1997, 2003). The same grid of model atmospheres was used also by Pollacco (1999) for the twin object V4334 Sgr.

The temperature of the central star of the PN, its luminosity, the gas density and the filling factor of the gas were varied. While the range for the filling factor was selected to fit to the typical findings for evolved nebulae (Armsdorfer et al. 2002), the gas density range of 100 to 300 e- cm-3 was taken from the ratio of the [SII] doublet as in Osterbrock (1974). The distance of 3.1 kpc was adopted from Sect. 3, leading, with the average angular radius of 22 $^{\prime\prime}$, to the linear radius of the shell.

The strength of the helium lines is nearly independent of the CSPN luminosity. Thus this fixes the abundance of this element clearly. The variations of the parameters were chosen to get a optimized intersection of the solutions for the HeI5876, the [OIII] 4948+5007 and the [NII] 6548+6583 lines at the level of $I_{\tt observed}/I_{\tt model} = 1.0$. These solutions are not completely independent of the chosen abundance. The [NII]5755 line then should intersect there as well, if the resulting electron temperature is suited. This fixes the CSPN temperature and therefore the whole solution. The best fit model is shown in Fig. 2.


  \begin{figure} \par\includegraphics[width=7.6cm,clip]{0387f2.eps}\end{figure} Figure 2: The best fit model shows a good intersection of the solutions for the helium, oxygen and nitrogen lines at the level $I_{\tt observed}/I_{\tt model} = 1.0$. The resulting model is given in Table 3.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.6cm,clip]{0387f3.eps}\end{figure} Figure 3: The position of the CSPN in the HRD at the moment of the helium flash. The evolutionary tracks for the post-AGB evolution for a 0.605, 0.625 and 0.696 $M_\odot $ white dwarf from Blöcker (1995) are plotted. For comparison reasons also the results of Pollacco (1999) and of Kerber(1999) for Sakurai's Object are shown. Pollacco's error bars show the observational incertainties, he declares $\log(L/L_{\odot})<3$ to be consistent with the white dwarf cooling tracks. Kerber assumed a relative error of 10 percent in the intensities, but admits that the overall error bars are certainly larger. The grey line underneath represents the evolutionary model of Lawlor & MacDonald (2003).
Open with DEXTER

Table 3: Parameters of the best fit model.

The placement of the derived CSPN luminosity and temperature together with the theory of stellar post-AGB evolution by Blöcker (1995) yields the mass of the final white dwarf and the transition time t. The position of the CSPN in the HRD is shown in Fig. 3. The resulting model (see Table 3) is completely self consistent. In addition it is also supported by the velocity measurements of Pollacco et al. (1992), who derived for the expansion velocity of A58 $v_{{\rm exp}}=31$ $\pm$ 4 km s-1, giving with the dynamical age of 8200 years a dynamical radius of PN A58 of

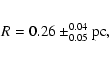
\begin{eqnarray*}R=0.26\pm^{0.04}_{0.05} {\rm pc}, \end{eqnarray*}


which matches extremely well our radius of $R=0.33~{\rm pc}$ as derived in Sect. 3. This is an especially good conjunction, if we take into account that the dynamical solution is usually a factor of 2 or 3 off target.

   
5 Recombination timescales in A58

There is clearly HeII4685 in the spectrum of A58. This fact, together with the knowledge of recombination timescales provides an estimate for the time between the ending of the UV radiation of the central star and the nova burst (position H or E in Fig. 3).

Using the same dielectric recombination coefficients $\alpha$ as Pollacco (1999) we calculated a table for the recombination time-scales for electron densities $n_{\rm e}$ of 100 and 200 e- cm-3 (see Table 4).

It can be seen that the recombination times for [OIII] are relatively low, but this table is only valid for single atomic systems. We have to take into account the Bowen HeII Lyman $\alpha$ - [OIII] resonance-fluorescence mechanism within the PN. This mechanism slightly decreases the HeII recombination times but enlarges the [OIII] recombination time-scales. For a more detailed study refer to Osterbrock (1974). The emphasis lies on HeII as the most common element, but NII also is important as it is not influenced by the Bowen HeII - [OIII] resonance-fluorescence mechanism.

Since we have to take the minimum of all the derived time-scales for a specific electron density as an upper limit for the lifetime of a nebula in this state, we can use a weighted average of 100 $\pm$ 50 years as a good estimate for the upper limit. This also justifies the use of photoionizing models with CLOUDY.

Table 4: Recombination time-scale for atomic states at  $T_{\rm e}=10~000$ K for electron densities $n_{\rm e}$ of 100 and 200 e- cm-3. An increase of the electron density to $n_{\rm e}=300$ e- cm-3 only lowers the upper limits. The terms "r'' and "d'' refer to the radiative and dielectronic components in the total recombination coefficient "t''.

6 Discussion and conclusion

The parameters used to calculate stellar evolution become crucial when we consider such subtleties as born-again objects. Hence the physical properties of born-agains in all stages provide a hard constraint on valid evolution theories. In general two different scenarios are discussed for the born again event:

For a more detailed discussion see Blöcker (2001) and references therein.

Based on recombination timescales we conclude that the time between the end of the UV radiation of the central star ( $t_{{\rm flash}} =$ the time of the late helium flash) and the observed bright Nova burst of V605 Aql in the 1920s (= $t_{{\rm nova}}$) has to be very short. Modelling the surrounding old PN A58 with CLOUDY, we obtain that the central star had a mass near 0.6 $M_\odot $(using the tracks of Blöcker (1995) as well as those of Herwig et al. (1999) and Herwig (2001)) and a temperature of 120 000 Kelvin before the final helium flash. The model of Herwig (2001) with lower masses is neither consistent with the photometric data of V4332 Sgr, as pointed out there already, nor with our model of the pre-outburst CSPN of V605 Aql. According to Blöcker (1995) the time since leaving the post-AGB is 8200 years. The distance of 3.1 $\pm$ 0.2 kpc from radio observations matches the constraints of the photoionization model and also matches the angular size for the derived age. Our observations obtained in 2002 (= $t_{{\rm obs}}$) and thus about 85 years after  $t_{{\rm nova}}$ and the finding that the age of the PN ( $t_{{\rm obs}}-t_{{\rm flash}}$) has to be around 100 years, lead to the conclusion that the transition time to either point H or E has to be less than 20 years - taking into account all types of uncertainties. This clearly excludes a LTP and accordingly is consistent with the CSPN position in the HRD. Our findings clearly - in luminosity and especially in temperature - exclude the possibility that the PN was excited in position D or F (see Fig. 3). In addition, test calculations with CLOUDY also exclude the possibility that the PN was excited additionally in between by a 40 000 < $T_{{\rm CSPN}}$ < 70 000 K source with a luminosity more than 1000 $L_\odot$. This would have revealed by special emission line ratios of [NII] and [SII]. Also, although checked by Fuhrmann (1981) on more than 430 Sonneberg and Heidelberg patrol plates taken after 1920 and by Dürbeck et al. (2002) on the Harvard patrol plates, no brightening has been detected since the 1917 outburst. This implies that the source is either in its first return to the AGB (position E), or not visible due to a thick dust shell during the transition E-F-H, or this second loop does not really occur. Whilst Iben et al. (1983) do not show such a loop at all, the transition time for the model of Lawlor & MacDonald (2003) gives timescales of only a few tens of years for the heating process after the first "Nova event'' for the transition E-F. The timescale in Herwig (2003) is even shorter. Then it stays near F for a long time at high luminosity and high temperature. This environment would have destroyed a dense dust shell built during the short evolution from leaving E towards F (Koller 2000; Koller & Kimeswenger 2001a,b; Kimeswenger & Koller 2002) and consequently V605 Aql should have been observable as a blue star on the POSS plates. This was found neither on the first generation POSS plates in the 1950s nor on the second generation in the 1980s and 1990s. We thus conclude that the object is at its first return to the AGB and the timescale for the transition has to be as short as given by Herwig (2001) and not as long as given by Lawlor & MacDonald (2003). Furthermore V605 Aql should have stayed at least several decades at the AGB before reheating to the temperature seen nowadays in the CIV lines (Kimeswenger 2003; Lechner & Kimeswenger 2003). This gives somewhat longer timescales than those predicted by Lawlor & MacDonald (2003) or by Herwig (2003).

The mass of the progenitor CSPN also was discussed heatedly. Dürbeck et al. (1997) derive $\geq$0.7 $M_\odot $using Paczynski's core-mass relationship. Dürbeck et al. (2000) argue, using the high luminosity and the evolution time span, that a mass of 0.8 $M_\odot $ should be a lower limit. However the outcomes here for V605 Aql and those of Pollacco (1999) and Kerber (1999) (see Fig. 3) place V605 Aql and V4334 Sgr clearly in the range of normal PNe core masses at or just below 0.6 $M_\odot $. Kerber (1999) calculated his models with the photoionization code GWYN and used only blackbody radiation. Pollacco (1999) used CLOUDY with different but comparable stellar atmospheres. It can be assumed that their spectra are from different regions in Sakurai's Object. In Fig. 3 we note the dependence on the distance with the aid of Kerber's results for 1.5 kpc and 5.5 kpc for Sakurai's Object. The mass of 0.6 $M_\odot $ also corresponds extremely well to the dynamic age of the old PN. A CSPN with a mass above 0.7-0.8 $M_\odot $ would evolve much faster than the observed PN. Thus, we conclude that the CSPN mass is very similar to that of Sakurai's object found by Herwig (2001).

References

 
Copyright ESO 2004