A&A 425, 1097-1106 (2004)
DOI: 10.1051/0004-6361:20041302

Automated recognition of coronal mass ejections (CMEs) in near-real-time data

E. Robbrecht - D. Berghmans

Royal Observatory of Belgium, Ringlaan 3, 1180 Brussels, Belgium

Received 17 May 2004 / Accepted 16 June 2004

Abstract
This paper presents a new method and first applications of software that we have developed to autonomously detect CMEs in image sequences from LASCO (Large Angle Spectrometric Coronagraph). The crux of the software is the detection of CMEs as bright ridges in (time, height) maps using the Hough transform. The next step employs clustering and morphological closing operations to mark out different CMEs. The output is a list of events, similar to the classic catalogs, with starting time, principle angle, angular width and velocity estimation for each CME. In addition we present a new type of CME overview map that clearly shows all detected CMEs in a (principal angle, time of occurrence) coordinate system. In contrast to catalogs assembled by human operators, these CME detections can be done without any human interference on real-time data 24 h per day (see http://sidc.oma.be/cactus for the real-time output with data covering the last 4 days). Therefore the detection is not only more immediate, but, more importantly, also more objective. In this paper we describe the software and validate its performance by comparing its output with the SOHO LASCO CME catalog. Experimental results on real-time data show that the developed technique can achieve excellent results in measuring starting time and principal angle and good results for the angular width and velocity measurement compared to the CMEs listed in the catalog. Its overall success rate is presently about 94%. The software also reveals CMEs or other features that have not been listed in the catalog. Such unreported cases might influence CME statistics and they demonstrate that also the present catalogs do not have a 100% success rate. This inevitably leads to a discussion on the definition of a CME. Prospects for improvement and exploitation are discussed.

Key words: Sun: corona - Sun: particle emission - Sun: coronal mass ejections (CMEs) - methods: data analysis - techniques: image processing - catalogs

1 Introduction

Over the past 8 years, coronal mass ejections have been routinely detected by visual inspection of each image from the Large Angle Spectrometric Coronagraph (LASCO) onboard SOHO (Brueckner et al. 1995). Event catalogs have been assembled continuously and are made publicly available (http://lasco-www.nrl.navy.mil/cmelist.html, http://cdaw.gsfc.nasa.gov/CME_list). Each observed CME is listed with its first time of appearance in the inner C2 coronagraph, central position angle, angular width, velocity and acceleration estimations. These catalogs are used as a reference and form a valuable resource for further statistical analysis on the nature of CMEs (St. Cyr et al. 2000; Vourlidas et al. 2002; Michalek 2002,2003; Moon et al. 2002; Gopalswamy et al. 2003).

The visual detection of CMEs in the flood of incoming new data is a labor intensive task. It is up till now essentially the human eye that detects a CME occurrence and a scientist that collects all the CME parameters in the catalogs. With the future coronagraphs on the STEREO spacecrafts this will become a big investment of manpower. Meanwhile, near-real-time alerts for halo CMEs are needed by the space weather community. In coronagraphic observations, halo CMEs appear as intensity enhancements surrounding the entire occulting disk (Howard et al. 1982). Although in typical cases such halo CMEs take a few days (3-4) to travel to the Earth, their timely detection is important as CPU-time intensive 3D MHD simulations are required to estimate their geo-effectiveness. Even much faster CMEs which arrived near earth within 24 h have been recorded. Remember the storm of October 29th 2003, in which a CME arrived near Earth in less than 19 h. This implies that halo CME alerts should be issued 24 h per day.

Also, the subjective interpretation by a human operator or scientist makes it doubtful whether this visual CME detection is stable over a solar cycle, as the operator gains experience or personnel is replaced. There is probably not much confusion for big, well-structured events, but small and/or weak events might be arbitrarily detected or not.

For these reasons, we have developed a software package called CACTus ("Computer Aided CME Tracking'') that detects CMEs in coronagraphic images. Early versions of the CACTus package were discussed in Berghmans et al. (2002a,b). In this paper we will present the inner machinery of the improved package. The method consists of two steps - image preprocessing and feature extraction, as is often the case. The preprocessing module (Sect. 2) merges the C2 and C3 images, cleans, rebins and reformats them with every step optimized for improving the CME contrast. This merging of C2 and C3 images is a delicate exercise in which attention should be drawn to the different spatial and temporal resolutions. Section 3 describes the image-recognition module. The most difficult part is the CME motion extraction since the signal-to-noise ratio becomes very low near the outer edge of the C3 coronagraph. After extraction of CME signals, they are grouped into different CMEs using clustering and morphological closing techniques. To estimate the performance of CACTus, we applied it on the most recent quicklook LASCO images available at the time of the first write-up of this paper (mid November 2003). The result of this test (Sect. 4) demonstrates the performance of CACTus operating in near-real-time. We summarize some ideas for further improvement and exploitation and formulate our conclusions in Sect. 5.

  
2 The preprocessing module

The default processing of the LASCO images (see e.g. latest images on http://sohowww.nascom.nasa.gov) is not optimized for CME detection. The CME signature is convolved with quasi-static K-corona streamer structures and with slowly moving stars, planets and comets as well as the instrumental stray light and F-corona backgrounds. Also, towards the edge of the field-of-view (FOV), the noise level increases sharply because the CME contrast diminishes, and this makes it difficult to follow features moving out. The images are relatively large with a spatial resolution far beyond what is needed for CME detection. A typical CME is only a relatively weak variation in intensity and only visible in a few subsequent images. All this means that the signal on which we want to trigger, is only very weakly present in the huge amount of incoming data. Straight application of image recognition techniques on the usual $1024\times1024$ images would therefore result in a very large computational overhead. Finally the different spatial and temporal resolution of C2 and C3 data make a combined analysis difficult. To avoid all these complications, a preprocessing module is applied that reformats the input images:

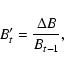
The output of this procedure is a $[\theta,r,t]$datacube that is much smaller than the total of the original input data, and in which most of the non-CME signal is removed or strongly attenuated.

  
3 The image recognition module

In order to apply feature recognition techniques to detect coronal mass ejections, a clear definition of a "CME'' is indispensable. Hundhausen et al. (1984; also Munro et al. 1979) defined a CME to be "an observable change in coronal structure that occurs on a time scale of a few minutes to several hours and involves the appearance of a new, discrete, bright, white-light feature in the coronagraph field-of-view''. In what follows we will implement this definition under a slightly modified form by requiring (necessary condition) that a CME is a new, discrete, bright, white-light feature in the coronagraph field-of-view with a radially outward velocity (Schwenn 1995). The discussion whether this is also a sufficient condition is postponed to Sect. 5.

It turned out not to be feasible to automatically identify in each separate image the location and extension of individual CMEs by segmentation techniques. The CMEs are too variable in appearance, they are often too weak to identify their extension (especially their trailing edge), and they might erroneously be merged with one another. Instead of trying to detect CMEs in each $[\theta ,r]$image, we look at [t,r] slices (Fig. 1, top) for each $\theta$ in the $[\theta,r,t]$ data cube. If a [t,r] slice at an angle $\theta$ cuts through a CME, an inclined bright ridge is seen in the [t,r] slice. Detecting CMEs in [t,r] slices was first introduced by Sheeley et al. (1999). Thanks to the preprocessing module however, our [t,r] slices, and the CME ridges in them, have a much better contrast and contain less noise. Working with [t,r] slices has the advantage that all CMEs look the same (inclined ridges), that even weak CMEs show up with a clear signature and that the detection of inclined ridges naturally satisfies the above specified necessary condition of radially outward moving features. Finally, as a bonus, the propagation speed of the CME can be determined from the inclination angle of the CME.

 

A well known technique for detecting straight lines in noisy data is the Hough transform (see Jähne 1997). The same transform has been used by LLebaria and Lamy (1999) to detect polar plumes in LASCO/C2 data. Every straight line in the [t, r] space as drawn in Fig. 2 can be parameterized by two variables t0 and $\Delta t$, t0 being the coordinate of the intersection point with the time-axis and $\Delta t$ being the distance along the t-axis, corresponding to a distance $r_{\rm max}-r_{\rm min}$ in the r-direction. The equation describing the line is then

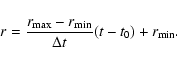
\begin{displaymath}r=\frac{r_{\rm max}-r_{\rm min}}{\Delta t}(t-t_0)+r_{\rm min}.\end{displaymath}

The modified Hough transform of this line is a point in the $[t_0,\Delta t]$ plane (the so-called accumulator space) with the intensity being the integral of the intensity along the corresponding line in the original image. Then local maxima in the $[t_0,\Delta t]$ space give the different straight lines present in the original image.
  \begin{figure} \par\includegraphics[width=7.8cm,clip]{images/1302f01.ps} \end{figure} Figure 1: Top: example of a (time, height) slice through the datacube at a given angle. Bottom: the corresponding ridges (set upside down) detected in this slice using the Hough transform. The horizontal range runs from 9 to 14 November 2003. In both panels the vertical range corresponds to the combined C2/C3 field of view (FOV). The inclination angle of the ridges corresponds to the propagation velocity.
Open with DEXTER

We make a modified Hough transform of every [t,r] slice. During this step we take into account the unequal spacing in time of the images, such that the ridge would look like a straight line if the images were equally spaced in time. In transformed space, we filter the most significant signals, which after inversion correspond to the required ridges (Fig. 1, bottom). Each ridge R in a [t,r] slice at an angle $\theta_R$ is characterized by its onset time tR, its velocity vR ($\sim$ $ \frac{1}{\Delta t}$) and its intensity IR. We can now build up a datacube $[v,\theta,t ]$ by setting for each ridge $[v_R,\theta_R,t_R]=I_R$.

Since a CME is a large scale structure, the onset time and velocity will differ only slightly from angle to angle. This means that a CME is represented in the $[v,\theta,t ]$ datacube as a dense cluster of data points. The problem of detecting CMEs has thus been reduced to identifying clusters in a 3D scatter plot. We simply integrate the $[v,\theta,t ]$ cube along the v-direction and identify the location of clusters in the resulting $[\theta,t]$ CME overview map as the time of occurrence and angular span of CMEs. The result of this is shown in Fig. 3. The colors are randomly chosen and are used to distinguish between different CMEs. The length of the "blob'' in the vertical direction indicates how long the outflow of the CME takes. Figure 4 is an illustration of how the CACTus output looks like. A sequence of 3 running difference $[\theta ,r]$-images is shown (top panel), containing 2 CMEs on 11 November 2003. The bottom panel shows the same information with the CACTus CME detections superimposed on it in green (CME No. 22) and in blue (CME No. 23).


 \begin{figure} \par\includegraphics[width=7.8cm,clip]{images/1302f02.eps} % \end{figure} Figure 2: Illustration of the modified Hough transform. Left: each line can be characterized by t0 and $\Delta t$. Right: $(t_0,\Delta t)$ is its corresponding point in the Hough space. $r_{\rm min}$ and $r_{\rm max}$ correspond to the edges of the FOV in the radial direction. $\Delta t$ is the time the CME spends in the FOV.
Open with DEXTER

At several places in the algorithm we have imposed thresholds to limit the number of false alerts. These thresholds restrict the detection to CMEs to cases that

  
4 Real-time performance test

We applied the above scheme to real-time data from a period from 9 to 14 November 2003. This just follows the period of the giant X17 and X25 flares on 28 October and 4 November. The dataset is limited to five days for practical reasons. We compared our results with the SOHO LASCO CME CATALOG (Yashiro et al.  2004) available online (http://lasco-www.nrl.navy.mil/cmelist.html). In this list each CME is listed with the time of appearance in the inner C2 coronagraph, the central position angle of the CME, the angular width, a velocity and acceleration estimation and a short morphological description. The catalog lists 16 CMEs in the period considered.


  \begin{figure} \par\includegraphics[width=8cm,clip]{images/1302f03.eps} \end{figure} Figure 3: CME overview map comparing the catalog CMEs (black lines) and those found by CACTus (colored shapes). The colors have no meaning itself but are used to distinguish between different CMEs. Time runs vertically from 9 to 14 November 2003. The poloidal angle runs counterclockwise from left (near the C3 pylon) to right. The catalog time of appearance corresponds to the bottom of the black lines. The thickness of the boxes is arbitrarily set to 30 min.
Open with DEXTER

The time series of November 2003 consists of 372 C2 and 246 C3 images. The median C2-cadence is 24 min and for C3 this is 36 min. This period is particularly useful as a test-case as it contains four halo CMEs.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{images/1302f04.eps} \end{figure} Figure 4: Illustration of detection of two CMEs. A sequence of 3 running difference $[\theta ,r]$-images is shown (top panel), containing 2 CMEs on 11 November 2003. The bottom panel shows the same information with the CACTus CME detections superimposed on it in green (CME No. 22) and in blue (CME No. 23).
Open with DEXTER

4.1 General results

In total the CACTus software found 47 events. They are shown as colored elongated regions in Fig. 3. The black lines are the corresponding CMEs listed in the catalog. The thickness of the boxes is arbitrarily set to 30 min. The overall distribution in the (angle, time) space is very similar. Comparing the two sets in more detail is a delicate exercise. The "success rate'' of our software obviously depends on the tolerance allowed on the deviations. In Appendix B, an overview is given of the correspondence of the catalog CMEs with the CACTus CMEs.

Of the 16 catalog CMEs, 15 CMEs (93.75%) are reproduced with nearly identical time of appearance and angular location. The first CME found by CACTus (see Fig. 3, CME No. 1), is detected as a marginal case (see Appendix B), since it is a very weak disturbance in the very beginning of the sequence (edge effect in temporal dimension).

The CACTus software found 47 events whereas there are only 16 CME entries in the catalog. Part of the difference between the two numbers can be explained by the cases in which subsequent parts of a CME are detected as separate events. Unfortunately the CME definition in Sect. 3 does not give a clear view on when one CME is finished and the next one starts. The definition only requires a CME to be a "new'' feature. Based on this, Fig. 11 (right, see Sect. 4.4 for a broader description of this CME) shows apparently a new small CME in the SE (around  $120^{\circ}$), but both the catalog and CACTus include this in CME No. 43.

There are also cases in which CACTus did split a CME in subsequent events (CME No. 23, followed by 24, 25, 26, 27) while the catalog only lists the occurrence of the first, main event (CME No. 23). In the LASCO quicklook CME catalog (http://lasco-www.nrl.navy.mil/cmelist.html), which is based on the daily observations of the operators, events No. 24-25-26-27 are described as "a ragged loop front with some gusty outflow, possible residual to some previous event''. Their detection by CACTus proves however that they do satisfy the CME definition as stated in Sect. 3. Again this highlights the shortcoming of the definition.

We also found small events that are "far from'' any catalog CME, but that do satisfy the CME definition given in Sect. 3. Some of these are due to false alerts generated by fast streamer evolution. In at least some cases, our software has found "unreported CMEs''. An example of such a case is shown in Fig. 5. This demonstrates again that also the catalogs do not have a 100% success rate.


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{images/1302f05.ps} \end{figure} Figure 5: The unreported CME No. 10, lifting off at 02h06 on November 10, 2003 is visible in the south-west of the C2 FOV. Two C2 difference images are shown, 1 h apart from each other. The straight lines limit the angular span given by CACTus.
Open with DEXTER

For space weather applications it is important to notice that all 4 halo CMEs listed in the catalog have been detected, three of them with an angular width larger than  $200^{\circ}$. Halo CMEs are particularly difficult to detect in white light images due to the nature of Thomson scattering (Hundhausen 1993).


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{images/1302f06.eps} \end{figure} Figure 6: Plot comparing the catalog starting times with the times found by CACTus. Of the 15 overlapping CMEs 12 have identical starting time. The times given are UT-times, the corresponding dates can easily be found on Fig. 3.
Open with DEXTER

4.2 Starting time

Figure 6 plots the difference in starting time of the 15 CMEs found by both, the catalog and CACTus. 12 of the 15 CMEs have identical starting time. In the three other cases the difference was only 1 C2 image (being 12 min for CMEs No. 9 and 46; and 24 min for CME No. 43).

4.3 Principal angle

In Fig. 7 the principal angle of the catalog is plotted versus the CACTus principal angle. Halo CMEs are not included since no principal angle is listed for them. All non-halo CMEs have a principal angle within  $18^{\circ}$ of the catalog principal angle. The mean difference in principal angle between the catalog and the CACTus values for all non-halo CMEs is  $7.80^{\circ }$.

  
4.4 Angular width

The comparison of the angular width of the CMEs is plotted in Fig. 8. In contrast to the parameters discussed in the previous subsections, Fig. 8 reveals apparently clear discrepancies between the catalog and the CACTus CMEs.

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{images/1302f07.eps} \end{figure} Figure 7: Plot comparing the principal angles. No halo CMEs are plotted since no principal angle can be measured for these CMEs. The mean difference in principal angle between the catalog and the CACTus values for all non-halo CMEs is  $7.80^{\circ }$.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{images/1302f08.eps} \end{figure} Figure 8: Plot comparing the angular widths. The four CMEs at the top (22, 4, 14 and 28) are all listed as halo CME in the catalog. At the contrary, CME 43 is found to be halo by CACTus, but not so listed in the catalog.
Open with DEXTER

For the CMEs with a small angular width (< $ 180^{\circ}$) there is still a relatively good correspondence between the catalog and the CACTus output. This is re-assuring as 94% of all CMEs listed between 1996 and 2003 in the catalog have indeed small (< $ 180^{\circ}$) angular widths. For wider CMEs the difference in angular width is larger. Let us take a closer look to CMEs No. 37, 23, 43, 22, 4 and 14 which show the strongest deviations.

In the case of CME No. 37 (Fig. 9) CACTus measures the same southern edge as mentioned in the catalog, but at the north it includes more outflow than only the bright core. Figure 10 shows the velocity profile versus the angle. In this plot we indeed can distinguish between two different parts: a dense part at the left, which corresponds to the brightest feature of the CME and a somewhat detached, scattered part at the right (=north). The only argument in favor of not including the northern extension is of morphological nature: Fig. 9 shows a suggestive nice round bow for CME No. 37 to which the detached side-outflows detected by CACTus do not "seem to belong''. Since no explicit morphological requirement has been programmed in CACTus, the software does include all the side-outflows. The underlying problem is that it is not at all obvious what is meant with the word "discrete'' in the CME definition in Sect. 3. The operator assembling the catalog has interpreted that the CME extension corresponds to the discrete region covered by the bright bow in Fig. 9, while CACTus has determined the CME extension to be the discrete region showing a clear velocity signal (Fig. 10). The same applies for CME No. 23, which erupts only 2 h after CME No. 22. Because of the remaining outflow of CME No. 22, CACTus groups this remaining outflow in CME No. 23. Another point to mention here is that due to taking running difference images, features outside the ejecta i.e. the compressed and deflected material around the real CME are overemphasized. That makes the measurements of angular extensions and even position angles dubious.

  \begin{figure} \par\includegraphics[width=7cm,clip]{images/1302f09.ps} \end{figure} Figure 9: C2 running difference images showing CME No. 37. The solid lines limit the angular span given by CACTus, the dashed lines limit the angular span listed in the catalog.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{images/1302f10.eps} \end{figure} Figure 10: CACTus Velocity profile of CME No. 37 as a function of the angle, which runs counterclockwise from the north. The dashed line represents the speed as listed in the catalog. On the left the boxplot is drawn: the vertical box contains the middle 50% of the measured speeds. The horizontal line in the box is the median speed, given in the CACTus output list. The whiskers at both ends indicate respectively the minimal and maximal detected speeds within 1.5 times the box length from the edge of the box, speeds further away are disregarded as outliers. (See Appendix A for a broader description of boxplot.)
Open with DEXTER

What makes CME No. 43 to deviate so much? CACTus found this CME to be halo, but the catalog only mentions an angular width of  $217^{\circ}$. Looking at two difference images (Fig. 11) the leading edge indeed seems to cover only a partial halo CME in the east. CACTus, however also detected higher speeds which come out later at the west. These data points indicate small features blown away along and in between the two streamers present.

  \begin{figure} \par\includegraphics[width=7cm,clip]{images/1302f11.ps} \end{figure} Figure 11: C2 running difference images showing CME No. 43. The dashed lines limit the angular span as listed in the catalog. CACTus found this CME to be halo.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7cm,clip]{images/1302f12.ps} \end{figure} Figure 12: C2 running difference images showing CME No. 22. The full lines limit the angular span given by CACTus. The catalog listed this CME as a halo.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7cm,clip]{images/1302f13.eps} \end{figure} Figure 13: CACTus velocity profile of CME No. 22 as a function of the angle, which runs counterclockwise from the north. The dashed line represents the speed as listed in the catalog. On the left the boxplot is drawn:the vertical box contains the middle 50% of the measured speeds. The horizontal line in the box is the median speed, given in the CACTus output list. The whiskers at both ends indicate respectively the minimal and maximal detected speeds within 1.5 times the box length from the edge of the box, speeds further away are disregarded as outliers. (See appendix A for a broader description of boxplot.)
Open with DEXTER

It is striking that in the case of CME No. 22, the discrepancy between the catalog and CACTus is reversed: it is listed as a full halo CME in the catalog while CACTus found an angular width of only  $150^{\circ}$. Figure 12 shows that it is indeed very difficult to define the edges of the CME. Figure 13 shows the velocity profile of the CME over the angular range were the CME was well detected by CACTus. Why did CACTus miss the rest of the CME? A similar problem occurs with halo CMEs 4, 14 and 28: CACTus found no sufficient signal of outflow velocities to conclude that these events where $360^{\circ}$-halo CMEs. However, it is instructive to note that between 1996 and 2004, the catalog lists 298 CMEs with an angular width larger than  $270^{\circ}$, of which 281 (94%!) are listed as halo CMEs. This indicates that the word "halo'' is not used in the strict  $360^{\circ}$ sense but that the halo-label is (almost always) given as soon as the angular width exceeds  $270^{\circ}$ (or even less). In this sense, we conclude that CACTus did find CMEs No. 14 and 28 to be halo CMEs.

4.5 Velocity measurement


  \begin{figure} \par\includegraphics[width=7.6cm,clip]{images/1302f14.eps} \end{figure} Figure 14: Comparative plot of the measured speeds. For each CME we have drawn a "box and whisker plot'' (or "boxplot''). The horizontal box contains the central 50% of the measured speeds. The vertical line inside the box is the median speed. The whiskers at both ends indicate respectively the minimal and maximal detected speeds within 1.5 $\times $ the box length from the edge of the box. See Appendix A for a broader explanation on the boxplot.
Open with DEXTER

The catalog attributes to each CME a single velocity value called the "primary speed'' of the CME. This primary speed is typically derived from tracking the leading edge. In contrast, our software determines a velocity in each direction $\theta$ within the angular span of the CME, resulting in velocity profiles such as Figs. 10 and 13. From these figures it is clear that describing a CME with only one speed does not reveal the complete picture: structure can be seen in the figures hinting at the internal configuration and velocity distribution of the CMEs. In order to approach human behavior in measuring speeds, CACTus calculates a reference velocity value for the CME as a whole by taking the median value of all detected speeds within the CME. Although we are aware of the fact that the median speed has no physical meaning itself, it is a proxy for the overall CME speed. This median CACTus speed is listed in Appendix B and typically differs significantly from the catalog speed. Since the leading edge speed usually is the highest speed present in a CME the CACTus speed usually is an underestimation compared to the catalog speed (see Figs. 10 and 13 for illustrations of this effect).

Figure 14 is a comparative plot of the measured speeds. For each CME we have drawn a "box and whisker plot'' (or "boxplot''). The horizontal box contains the central 50% of the measured speeds. The vertical line in the box is the median speed, given in the CACTus output list. The whiskers at both ends indicate respectively the minimal and maximal detected speeds within 1.5 times the box length from the edges of the box; speeds further away are disregarded as outliers. See Appendix A for a broader explanation of boxplot. Note that, apart from CME No. 9 (which has a "poor quality'' label in the catalog, see Appendix B), every boxplot crosses the diagonal. This indicates that the primary speed in the catalog is indeed found by CACTus somewhere along the CME.

The catalog also lists the acceleration of the CME. At the present time, this is not possible yet with the CACTus software since the Hough transform detects ridges in the [t,r] slices as straight lines. This implicitly assumes constant velocity CMEs. To better estimate the final CME-speed, we could apply the Hough transform to higher radial distances (>3 $R_{\odot}$) only, since from this point on CMEs are expected to have relatively constant speeds.

  
5 Discussion

This paper shows that it is possible to fully automatically detect CMEs in coronagraphic image sequences, estimate its main characteristics (time, principal angle, angular width, velocity) and produce a CME catalog just as currently human operators do it. The current version of our program recovers nearly (94%) all of the catalog CMEs on a real-time basis with nearly identical starting time and principal angle. Also the angular width and speed of the CMEs are determined, though with certain deviations from the SOHO LASCO CME catalog.

CACTus found nearly 3 times as many CMEs as there were listed in the catalog. In some cases, CACTus included a range of weak transients not included in the CME catalog because they were regarded as only "gusty outflow''. However they do satisfy the definition of a CME as given in Sect. 3. In some cases, CACTus has split up a CME in separate events where the catalog has only listed the main event. While this might seem only a matter of CME-bookkeeping, it can create significant biases when making a statistical analysis of a large number of CMEs. Finally, there were also moving features in which the software did detect indisputable CMEs that were missing in the catalog. This means that the reference catalog also does not have a 100% success rate.

By carefully studying the discrepancies between the catalog and the output of CACTus we found out that these discrepancies were usually not generated by imperfections in our software or by inattentive human operators, but instead by the vagueness of the concept "CME'' itself. It is, for example, basically undefined what the temporal and spatial extension of a CME is. When one CME follows immediately after another, it is hard to come up with observational criteria that define the split between the two CMEs. When does a CME end and when does the next one start? Also in the spatial domain ambiguity rules: is a CME limited to the region characterized by excess brightness or to the region showing clear outflow velocities? In a theoretical framework, the extension of a CME could be defined in terms of magnetic separatrix surfaces but, when having access to coronagraphic data only, such concepts are not applicable. A refinement of the concept of "CME'' is thus needed and an understanding of the 3D structure is required for this. A good prospect for this will be the upcoming STEREO mission, where the coronagraphic images of the same CME will be viewed from 2 viewpoints and be combined with MHD simulations.

CACTus is not perfect yet and a number of improvements are planned. These include the determination of the acceleration of a CME. For space weather applications, not only velocity but also intensity and mass of a CME are important parameters. We plan to list also these in a next version. The real-time output of CACTus for the last 4 days can be found on http://sidc.oma.be/cactus.


  \begin{figure} \par\includegraphics[width=7cm,clip]{images/1302f15.ps} \end{figure} Figure 15: Example of a composite image, combining an EIT195 image with CACTus CME detections for 4 days, represented by white arches. This image was produced by the Solar Weather Browser (SWB), which was developed in the frame of the ESA-Space Weather Applications Pilot Project (SWAPP). The SWB can be downloaded free of charge from http://sidc.oma.be/html/SWAPP/swb/swb.html.
Open with DEXTER

The output from the CACTus software can be used as input for several automatic near-real-time programs as support for daily space weather forecasts. As an example in Fig. 15 we plotted a composite image, combining an SOHO/EIT (19.5 nm) image with CACTus CME detections for 4 days, represented by white arches. This image was produced by the Solar Weather Browser (SWB), which was developed in the frame of the ESA-Space Weather Applications Pilot Project (SWAPP). The SWB can be downloaded free of charge from http://sidc.oma.be/html/SWAPP/swb/swb.html.

At the time of writing we are also testing automatic real-time halo CME alerts, triggered by CACTus. Whenever CACTus detects a CME with an angular width larger than  $ 180^{\circ}$, it sends out an alert via email to registered users.

Acknowledgements
We would like to thank our colleague Ronald Van der Linden for useful discussions and for his critical eye on the paper. Part of this work was performed while DB was a research fellow at ESTEC. The development of CACTus as a space weather tool was finalized under ESA contract 16913/03/NL/LvH in the ESA-Space Weather Applications Pilot Project (SWAPP). We would like to thank Seiji Yashiro for the fast processing of the SOHO LASCO CME catalog for the period we used. The SOHO LASCO CME catalog is generated and maintained by NASA and The Catholic University of America in cooperation with the Naval Research Laboratory. The SOHO/LASCO data used here are produced by a consortium of the Naval Research Laboratory (USA), Max-Planck-Institut fuer Aeronomie (Germany), Laboratoire d'Astronomie (France), and the University of Birmingham (UK). SOHO is a project of international cooperation between ESA and NASA.

  
Appendix A: The box-and-whisker plot


  \begin{figure} \par\includegraphics[width=7cm,clip]{images/1302f16.eps} \end{figure} Figure A.1: Illustration of a box-and-whisker plot.

A box-and-whisker plot (or boxplot) is a graphical way of summarizing a set of data measured on an interval scale. It is often used in exploratory data analysis. For an illustration see Fig. A.1. The median (point at 50%) of the dataset is indicated by the dashed line, the first and third quartiles define the edges of the box, of which the length is called the inter-quartile range (IQR). Hence, the box always contains the central 50% of the data. The smaller the IQR is, the less variable the measurements are. The whiskers at both ends of the box each cover another 25% of the data. They reach up to the extreme values within 1.5 times the IQR from the edges of the box. Data points at a greater distance are regarded as outliers.

cmenr t0 dt0 pa da v dv min v max v Catalog t0 pa da v Q
0001 Marginal case 02 234 024 0416 0722 0390 2101 2003/11/09 02:30:05 232 35 75 2
0002 2003/11/09 04:30 02 219 026 0372 0047 0286 0446          
0003 2003/11/09 06:06 03 226 036 1041 0624 0208 2174          
0004 2003/11/09 06:30 03 086 212 1041 0483 0440 2083 2003/11/09 06:30:05 Halo 360 2008 4
0005 2003/11/09 07:31 00 320 032 0637 0046 0578 0744          
0006 2003/11/09 09:30 05 225 038 0496 0642 0211 1743          
0007 Marginal case 03 104 068 0489 0235 0195 1177          
0008 2003/11/09 15:06 01 104 024 0440 0147 0220 0725          
0009 2003/11/09 16:54 02 292 012 0400 0035 0343 0427 2003/11/09 17:06:05 290 15 639 1
0010 2003/11/10 02:06 07 226 044 0248 0033 0192 0315          
0011 2003/11/10 16:54 03 047 038 0428 0063 0276 0548 2003/11/10 16:54:05 55 43 478 2
0012 2003/11/11 00:06 01 240 028 0529 0101 0303 0625 2003/11/11 00:06:29 235 40 553 3
0013 Marginal case 01 222 012 0844 0565 0664 1852          
0014 2003/11/11 02:30 08 270 300 0947 0374 0312 2083 2003/11/11 02:30:07 Halo 360 1359 5
0015 Marginal case 00 105 014 0833 0056 0762 0946          
0016 2003/11/11 03:30 01 062 012 1633 0511 0744 2403          
0017 2003/11/11 04:06 00 356 020 0393 0775 0252 2065          
0018 2003/11/11 05:54 03 104 072 0919 0408 0343 1953 2003/11/11 05:54:05 118 52 1445 3
0019 2003/11/11 06:06 01 051 038 0933 0493 0306 1838          
0020 2003/11/11 06:30 00 026 020 0889 0387 0212 1630          
0021 2003/11/11 10:06 01 204 016 0395 0067 0269 0496          
0022 2003/11/11 13:54 05 265 150 1041 0245 0558 1366 2003/11/11 13:54:05 Halo 360 1315 3
0023 2003/11/11 15:54 02 090 196 0993 0468 0231 2232 2003/11/11 15:54:05 87 128 1785 3
0024 2003/11/11 20:06 01 102 012 0505 0440 0306 1562          
0025 2003/11/11 21:54 02 110 048 1009 0431 0504 1953          
0026 Marginal case 01 108 020 0549 0422 0359 1497          
0027 Marginal case 01 111 030 0529 0144 0233 0588          
0028 2003/11/12 10:54 06 123 346 0801 0199 0460 1360 2003/11/12 10:54:06 Halo 360 1197 2
0029 2003/11/12 12:06 00 212 012 1116 0075 0976 1201          
0030 2003/11/12 12:30 00 299 014 0948 0196 0822 1302          
0031 2003/11/12 12:54 03 180 040 1116 0585 0271 2403          
0032 2003/11/12 12:30 01 301 022 1335 0323 0915 1838          
0033 2003/11/12 12:30 00 210 012 1008 0165 0889 1302          
0034 2003/11/12 14:54 04 120 040 0529 0412 0229 1644          
0035 2003/11/12 12:54 01 236 020 1562 0000 1562 1562          
0036 2003/11/12 16:06 02 076 020 0868 0711 0395 1953          
0037 2003/11/12 18:30 03 264 128 0694 0156 0339 0976 2003/11/12 18:30:05 246 88 891 4
0038 Marginal case 02 234 016 0589 0242 0228 0844          
0039 2003/11/12 22:30 01 165 026 0728 0169 0434 1041          
0040 2003/11/13 01:54 02 232 016 0600 0237 0229 0892          
0041 2003/11/13 05:30 03 116 028 0679 0092 0512 0892 2003/11/13 05:30:05 103 62 598 2
0042 2003/11/13 06:54 00 202 012 0466 0004 0466 0473 2003/11/13 06:54:05 202 18 444 1
0043 2003/11/13 09:54 05 - 360 1008 0476 0359 2083 2003/11/13 09:30:05 49 217 1141 4
0044 Marginal case 01 116 012 0346 0083 0279 0496          
0045 2003/11/13 22:30 05 136 104 0355 0131 0182 0744 2003/11/13 22:30:05 130 113 554 3
0046 2003/11/14 11:06 02 273 046 0651 0095 0413 0844 2003/11/14 10:54:05 282 57 683 2
0047 2003/11/14 15:26 00 127 014 0987 0641 0219 1838          

  
Appendix B: Comparative table of the CACTus and the catalog output

In the table above, the CACTus output is listed combined with the corresponding catalog outputs, as could be found on http://cdaw.gsfc.nasa.gov/CME_list at the time of writing. The different outputs given by CACTus are:
cmenr: cme identification number;
t0*: onset time, earliest indication of liftoff;
dt0: duration of liftoff (hours);
pa*: central axis, counterclockwise from north (degrees);
da*: angular width (degrees);
v*: median velocity (km s-1);
dv: variation of velocity over the width of the CME;
min v: lowest velocity detected within the CME;
max v: highest velocity detected within the CME.
The values for which we have found a corresponding measurement from the catalog are indicated with a "*''. The catalog speed mentioned is the linear fit. The last column "Q'' indicates the quality_index of the catalog running from 1 to 5, meaning

1
poor;
2
fair;
3
typical;
4
good;
5
Excellent.

A CME is indicated as "marginal case'', when the CME signal doesn't exceed the desired threshold ($2\sigma$) above the background.

References

 
Copyright ESO 2004