A&A 425, 1153-1159 (2004)
DOI: 10.1051/0004-6361:20041297
D. M. Mitnik 1 - N. R. Badnell 2
1 - Departamento de Física, FCEN, Universidad de Buenos Aires,
and Instituto de Astronomía y Física
del Espacio (IAFE), Casilla de Correo 67, Sucursal 28,
(C1428EGA) Buenos Aires, Argentina
2 - Department of Physics, University of Strathclyde, Glasgow G4 0NG, UK
Received 14 May 2004 / Accepted 23 June 2004
Abstract
Dielectronic recombination data for nitrogen-like ions
forming oxygen-like ions has been
calculated as part of the assembly of a level-resolved dielectronic
recombination database necessary for the modelling of dynamic finite-density
plasmas (Badnell et al. 2003). Dielectronic recombination
rate coefficients for a selection of ions from O+ to Xe47+ are
presented and the results discussed.
Key words: atomic data - plasmas - atomic processes
Our programme to generate a reliable DR database necessary for the spectroscopic modelling of dynamic finite-density plasmas, has been described by Badnell et al. (2003). Calculations are being carried-out initially to produce DR data for the isoelectronic sequences of all first and second row elements. So far, results have been published for the lithium (Colgan et al. 2004), beryllium (Colgan et al. 2003), boron (Altun et al. 2004), carbon (Zatsarinny et al. 2004a), oxygen (Zatsarinny et al. 2003), and neon (Zatsarinny et al. 2004b) isoelectronic sequences.
In this paper, we describe calculations and present results for DR data
for nitrogen-like ions forming oxygen-like ions.
The present calculations generated DR data for the total and final
level-resolved rate coefficients, in intermediate coupling (IC).
Total rate coefficients are presented in a compact form using a simple
fitting formula. Data are presented for several ions
applicable to astrophysics and magnetic fusion plasmas.
The large irregularity in Z-dependence of the total DR rate coefficients
makes scaling inaccurate. This is particularly problematic for
low temperatures, where the
![]() core transitions are dominant.
The reason for the irregular behaviour as a function of Z is due to
the fact that autoionizing levels that are just above threshold for
one value of Z (giving a high contribution to the DR cross section)
can move just below threshold for a neighboring Z+1 member of the
series, becoming a bound state and thus not contributing to DR.
The present data will form part of an Atomic Data and Analysis Structure
dataset (the ADAS project (Summers 1999),
comprising the adf09 files for each ion, detailing the
rate coefficients to each LSJ-resolved final level.
These data are also made available on-line at the
Oak Ridge Controlled Fusion
Atomic Data Center (http://www-cfadc.phy.ornl.gov).
core transitions are dominant.
The reason for the irregular behaviour as a function of Z is due to
the fact that autoionizing levels that are just above threshold for
one value of Z (giving a high contribution to the DR cross section)
can move just below threshold for a neighboring Z+1 member of the
series, becoming a bound state and thus not contributing to DR.
The present data will form part of an Atomic Data and Analysis Structure
dataset (the ADAS project (Summers 1999),
comprising the adf09 files for each ion, detailing the
rate coefficients to each LSJ-resolved final level.
These data are also made available on-line at the
Oak Ridge Controlled Fusion
Atomic Data Center (http://www-cfadc.phy.ornl.gov).
Although studies for a few elements of this sequence have been
made, there are no systematically determined DR rate coefficients
for the entire sequence. The first calculations of DR rate coefficients
for nitrogen-like ions were carried out by
Jacobs et al. (1977a) for Fe19+,
Jacobs et al. (1977b) for Si7+,
Jacobs et al. (1979) for Ne3+, Mg5+,
and S9+,
and Jacobs et al. (1980) for Ca13+ and Ni21+.
These data were fitted by Mazzotta et al. (1998)
with a single formula, tabulating the related coefficients.
Terao et al. (1991), and
Badnell (1992), calculated the DR rate coefficient for the
special case of O+.
The only detailed experimental DR measurements for nitrogen-like ions
are for Fe19+ (
![]() core transitions).
These experimental DR results, together with four different state-of-the-art
theoretical calculations, were published by
Savin et al. (2002).
More recently, Gu (2003) has reported result for Mg5+,
Si7+, S9+, Ar11+, Ca13+, Fe19+, and Ni21+.
We will compare our results with the detailed existing data in
Sect. 3.
core transitions).
These experimental DR results, together with four different state-of-the-art
theoretical calculations, were published by
Savin et al. (2002).
More recently, Gu (2003) has reported result for Mg5+,
Si7+, S9+, Ar11+, Ca13+, Fe19+, and Ni21+.
We will compare our results with the detailed existing data in
Sect. 3.
The plan for the remainder of the paper is as follows: in Sect. 2 we give a brief description of the theory used and the details of our calculations for the nitrogen-like ions. In Sect. 3 we present the results for the total DR rate coefficient for O+, F2+, Ne3+, Na4+, Mg5+, Al6+, Si7+, P8+, S9+, Cl10+, Ar11+, Ca13+, Ti15+, Cr17+, Fe19+, Ni21+, Zn23+, Kr29+, Mo35+, and Xe47+ nitrogen-like ions. We finish with a short summary in Sect. 4.
The theoretical details of our calculations have already been described in Badnell et al. (2003). Here we outline only the main points and describe the configurations included in the calculations.
The dielectronic recombination process
![]() can be symbolically represented by
can be symbolically represented by
In the independent-processes and isolated resonance approximations using
distorted waves (IPIRDW), the partial dielectronic
recombination rate coefficient
![]() from an initial
metastable level g into a final level f of an ion X+q is given by
from an initial
metastable level g into a final level f of an ion X+q is given by
The AUTOSTRUCTURE code (Badnell 1986; Badnell & Pindzola 1989; Badnell 1997) is used to calculate multi-configuration intermediate coupling energy levels, radiative rates and autoionization rates. The code can make use both of non-relativistic and semi-relativistic wavefunctions (Pindzola & Badnell 1990). The calculations have been produced in intermediate coupling (IC) approximation. As explained in Badnell et al. (2003), AUTOSTRUCTURE employs an interpolation technique which allows the calculation of very high-n orbitals. This approach avoids the extrapolation of low-n autoionization rates or, even worse, partial dielectronic recombination rate coefficients to high-n.
The "post-processing'' calculations, where the data is organized for the generation of final state level-resolved and total dielectronic recombination rate coefficients, are implemented in the ADASDR code. Radiative transitions between highly-excited Rydberg states are computed hydrogenically, and added-in during the post-processing. Also, observed energies for the core and parent levels are used at this stage to ensure accurate positioning of the resonances and, hence, accurate low-temperature rate coefficients. The ADASDR code outputs directly the adf09 file for use by ADAS.
Due to the complexity of the modelling involved in the DR calculation, we separate the calculations for different core-excitations generating different adf09 output files. This also enables selective upgrades of the database.
We calculated DR processes from the initial
![]() configuration, which consists of the
configuration, which consists of the
![]() ground level, and the
ground level, and the
![]() ,
,
![]() ,
and
,
and
![]() metastable levels.
(These states are fully-mixed with the
metastable levels.
(These states are fully-mixed with the ![]() configuration.)
The g, d and f configurations included (Eq. (1))
for the calculation of the DR process for nitrogen-like ions,
through the intermediate levels having
configuration.)
The g, d and f configurations included (Eq. (1))
for the calculation of the DR process for nitrogen-like ions,
through the intermediate levels having
![]() core transitions
(i.e., core transitions from
core transitions
(i.e., core transitions from
![]() to
to
![]() followed by a capture in a nl Rydberg orbital) are given by:
followed by a capture in a nl Rydberg orbital) are given by:
Radiative stabilization within the
![]() core is also described by the
presence of the middle group of configurations.
Depopulation via autoionization into the continua of levels of the
core is also described by the
presence of the middle group of configurations.
Depopulation via autoionization into the continua of levels of the
![]() and
and ![]() configurations was also accounted for.
In this case values of n from n=3 to n=20 were included,
and l up to l=15 are calculated. An approximation for the
high-level values of n orbitals (Badnell et al. 2003)
was used up to n=999.
configurations was also accounted for.
In this case values of n from n=3 to n=20 were included,
and l up to l=15 are calculated. An approximation for the
high-level values of n orbitals (Badnell et al. 2003)
was used up to n=999.
The calculation for the DR process
through the intermediate odd levels d produced by a
![]() core excitation (
core excitation (
![]() )
and a capture in an n=3 Rydberg orbital, included the
following intermediate d configurations:
)
and a capture in an n=3 Rydberg orbital, included the
following intermediate d configurations:
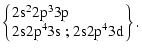 |
(5) |
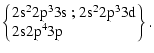 |
(6) |
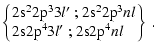 |
(7) |
Our calculations include full configuration mixing between the complexes listed for the target and intermediate configurations. For consistency, we allow the same configuration mixing on the continuum level calculations, in order to allow the appropriate autoionization pathways of the intermediate mixed states. Prior to the final DR calculations, the ionic thresholds were shifted to the known spectroscopic values (http://physics.nist.gov/cgi-bin/AtData/main_asd) by a small amount - typically in the range of 1-2 eV for high Z. The calculations for Ti15+, and beyond, were performed in the semirelativistic approximation for the radial wave functions, developed by Cowan & Griffin (1976) and implemented in AUTOSTRUCTURE as is explained in Pindzola & Badnell (1990). Non-relativistic radial functions were used otherwise.
The dielectronic recombination rate coefficients for
all the selected nitrogen-like ions calculated here
are available on-line at the Oak Ridge Controlled Fusion
Atomic Data Center (http://www-cfadc.phy.ornl.gov).
The adf09 files for each ion provide
detailed LSJ-resolved final level rates in a manner
useful to fusion and astrophysical modellers.
The results are given for a wide range of temperatures,
from
![]() K to
K to
![]() K,
where q is the residual charge of the initial ion.
All our total intermediate coupling DR rate coefficients
were also fitted with the formula:
K,
where q is the residual charge of the initial ion.
All our total intermediate coupling DR rate coefficients
were also fitted with the formula:
Table 1:
Fitting coefficients ci (cm3 s-1 K1.5)
and Ei (K), for Eq. (10),
for DR via
![]() core excitations,
for N-like ions forming O-like ions. X(Y) means
core excitations,
for N-like ions forming O-like ions. X(Y) means
![]() .
.
Table 2:
Fitting coefficients ci (cm3 s-1 K1.5)
and Ei (K), for Eq. (10),
for DR via
![]() core excitations,
for N-like ions forming O-like ions. X(Y) means
core excitations,
for N-like ions forming O-like ions. X(Y) means
![]() .
.
Figure 1 shows the DR rate coefficients for
O+ to Xe47+ ions through
![]() inner core transitions,
as a function of electron temperature.
As is shown in the figure, the DR rate coefficients behave rather
irregularly at lower temperatures. Only at electron temperatures
higher than
inner core transitions,
as a function of electron temperature.
As is shown in the figure, the DR rate coefficients behave rather
irregularly at lower temperatures. Only at electron temperatures
higher than
![]() K is the behaviour of the DR regular, allowing
for a systematic interpolation parametrization.
Figure 2 shows the DR rate coefficients for O+ to Xe47+ ions through
K is the behaviour of the DR regular, allowing
for a systematic interpolation parametrization.
Figure 2 shows the DR rate coefficients for O+ to Xe47+ ions through
![]() inner core transitions,
as a function of electron temperature.
In this case, the behaviour of the DR is regular, showing a progressive
increase in the DR rate from O+ to Xe47+.
inner core transitions,
as a function of electron temperature.
In this case, the behaviour of the DR is regular, showing a progressive
increase in the DR rate from O+ to Xe47+.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1297fig1.eps}
\end{figure}](/articles/aa/full/2004/39/aa1297/Timg41.gif) |
Figure 1:
Dielectronic recombination rate coefficients for
O+ to Xe47+ N-like ions forming O-like ions
through
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1297fig2.eps}
\end{figure}](/articles/aa/full/2004/39/aa1297/Timg42.gif) |
Figure 2:
Dielectronic recombination rate coefficients for
O+ to Xe47+ N-like ions forming O-like ions
through
|
| Open with DEXTER | |
We show some separate examples of the total,
![]() and
and
![]() total DR rate coefficients from the ground state
of different ions, in Figs. 3 to 7.
In all cases, excepting the O+ ion and
the high-Z elements beyond Ni,
we compare our data with results from the tables tabulated
by Mazzotta et al. (1998).
In many cases where theoretical data were not available,
they use the well known Burgess General Formula
(Burgess 1965).
Although only designed to be used for DR via
total DR rate coefficients from the ground state
of different ions, in Figs. 3 to 7.
In all cases, excepting the O+ ion and
the high-Z elements beyond Ni,
we compare our data with results from the tables tabulated
by Mazzotta et al. (1998).
In many cases where theoretical data were not available,
they use the well known Burgess General Formula
(Burgess 1965).
Although only designed to be used for DR via
![]() core
excitations (and H-like and H-like ions) it has been widely used
outside of its range of applicability, mainly due to the lack of
other data sources.
core
excitations (and H-like and H-like ions) it has been widely used
outside of its range of applicability, mainly due to the lack of
other data sources.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1297fig3.eps}
\end{figure}](/articles/aa/full/2004/39/aa1297/Timg43.gif) |
Figure 3:
Dielectronic recombination rate coefficients for O+
forming O
as a function of electron temperature.
Thick solid curve: total DR,
thick dotted curve: DR through
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1297fig4.eps}
\end{figure}](/articles/aa/full/2004/39/aa1297/Timg44.gif) |
Figure 4:
Dielectronic recombination rate coefficients for Ne3+
forming Ne2+
as a function of electron temperature.
Thick solid curve: total DR,
thick dotted curve: DR through
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1297fig5.eps}
\end{figure}](/articles/aa/full/2004/39/aa1297/Timg45.gif) |
Figure 5:
Dielectronic recombination rate coefficients for Si7+
forming Si6+ as a function of electron temperature.
Thick solid curve: total DR,
thick dotted curve: DR through
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1297fig6.eps}
\end{figure}](/articles/aa/full/2004/39/aa1297/Timg46.gif) |
Figure 6:
Dielectronic recombination rate coefficients for S9+
forming S8+ as a function of electron temperature.
Thick solid curve: total DR,
thick dotted curve: DR through
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1297fig7.eps}
\end{figure}](/articles/aa/full/2004/39/aa1297/Timg47.gif) |
Figure 7:
Dielectronic recombination rate coefficients for Fe19+
forming Fe18+
as a function of electron temperature.
Thick solid curve: total DR,
thick dotted curve: DR through
|
| Open with DEXTER | |
The case of O+ can be considered a special one because, as it was pointed out by Badnell (1992), an improved atomic structure calculation is needed for accurate results. For this special case, the correlation in the N-electron configuration-interaction expansion leads to very important changes in the dominant oscillator strengths. Therefore, parametric adjusted orbitals have been used for the structure calculation, as is explained in this previous work. In Fig. 3, the intermediate coupling DR results for O+ are also compared with the previous results obtained by Badnell (1992), showing very good agreement. These are about 25% larger than the total obtained in LS-coupling, which itself differs by less than 10% from the revised R-matrix results of Terao et al. (1991).
In Fig. 4 for Ne3+ we see the large low-temperature
enhancement of the rate coefficient due to DR via low-lying resonances,
typical of the
![]() core excitation. This is not described by
the data of Jacobs et al. (1979), which was fitted
by Mazzotta et al. (1998). This is of relevance for
the modelling of photoionized plasmas, but not collision dominated plasmas.
We see a similar trend for Si7+ in Fig. 5, with the low
temperature enhancement in close agreement with that described by Gu (2003).
core excitation. This is not described by
the data of Jacobs et al. (1979), which was fitted
by Mazzotta et al. (1998). This is of relevance for
the modelling of photoionized plasmas, but not collision dominated plasmas.
We see a similar trend for Si7+ in Fig. 5, with the low
temperature enhancement in close agreement with that described by Gu (2003).
The parametric data given by Mazzotta et al. (1998) for
S9+ (Fig. 6) is the result of fitting the data calculated
by Jacobs et al. (1979), which covers the
electron temperature range between 104 K to 107 K.
Since the fitting formula does not represent well the data of
Jacobs et al., we show also the original results together
with those of the fitting formula. Below
![]() K our
results start fall away from those of Gu (2003). At these
temperatures the DR rate coefficient is sensitive
to small differences in the position of near-threshold resonances.
The abundance of S9+ in a photoionized plasma is sharply
peaked at about
K our
results start fall away from those of Gu (2003). At these
temperatures the DR rate coefficient is sensitive
to small differences in the position of near-threshold resonances.
The abundance of S9+ in a photoionized plasma is sharply
peaked at about
![]() K (Kallman & Bautista 2001).
At
K (Kallman & Bautista 2001).
At
![]() K its abundance has fallen by a factor of 10
and S6+ and S7+ are the dominant ionization stages.
K its abundance has fallen by a factor of 10
and S6+ and S7+ are the dominant ionization stages.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1297fig8.eps}
\end{figure}](/articles/aa/full/2004/39/aa1297/Timg50.gif) |
Figure 8:
Dielectronic recombination rate coefficients for
Fe19+ forming Fe18+
through
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1297fig9.eps}
\end{figure}](/articles/aa/full/2004/39/aa1297/Timg51.gif) |
Figure 9:
Dielectronic recombination rate coefficients for
Mg5+ forming Mg4+ through
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1297fig10.eps}
\end{figure}](/articles/aa/full/2004/39/aa1297/Timg52.gif) |
Figure 10:
Dielectronic recombination rate coefficients for
Fe19+ forming Fe18+ through
|
| Open with DEXTER | |
In Fig. 7, the
![]() DR results for Fe19+
are also compared with the experimental results obtained by
Savin et al. (2002), showing an excellent agreement
for a very wide range of temperatures. The parametric data given by
Mazzotta et al. (1998) is based ultimately on
unpublished data from Roszman which, again, does not describe the
low temperature regime.
DR results for Fe19+
are also compared with the experimental results obtained by
Savin et al. (2002), showing an excellent agreement
for a very wide range of temperatures. The parametric data given by
Mazzotta et al. (1998) is based ultimately on
unpublished data from Roszman which, again, does not describe the
low temperature regime.
In general, DR from initial metastable levels is also required for
collisional-radiative modelling of dynamic plasmas. The reason for
this is that significant populations can build up in the metastables
and they are not necessarily in quasi-static equilibrium with the ground
state. An example of our initial level-resolved data is given in
Fig. 8, where DR rate coefficients for Fe19+ (through
![]() core transitions) are displayed. The figure shows DR from
the initial ground
core transitions) are displayed. The figure shows DR from
the initial ground
![]() and metastables
and metastables
![]() ,
,
![]() ,
and
,
and
![]() .
We show only the
.
We show only the
![]() contribution, because the
contribution, because the
![]() contribution (important only at high temperatures) is roughly the same
from all the initial metastable levels.
On the other hand, the
contribution (important only at high temperatures) is roughly the same
from all the initial metastable levels.
On the other hand, the
![]() contributions from each different initial
levels are quite different at low temperatures.
contributions from each different initial
levels are quite different at low temperatures.
As an example of the final-state level-resolved rate coefficients available,
we present in Fig. 9 DR rate coefficients for Mg5+
from the initial
![]() level to the final
level to the final
![]() (
(
![]() ), and
), and
![]() levels.
These are the dominant path contributions (among thousand of levels) to the
total DR through
levels.
These are the dominant path contributions (among thousand of levels) to the
total DR through
![]() core transitions.
core transitions.
In addition to the total DR rate coefficients, the adf09 files
also contain information about the population from DR of the resolved
final levels, bundled for different nl manifolds, which is required
for collisional-radiative modelling of dense plasmas.
As an example of the final bundled n rate coefficients available,
we present in Fig. 10 the
![]() DR rate coefficients
for Fe19+, for population of the final
DR rate coefficients
for Fe19+, for population of the final
![]() levels, with
given n quantum numbers. As is expected, the ion preferentially recombines
to the
levels, with
given n quantum numbers. As is expected, the ion preferentially recombines
to the
![]() levels (n=2), and in general, the contributions for
the different n manifolds smoothly decrease as n increases, until a
new autoionization channel is opened.
For this particular case, an n=7 resonant lying close to threshold produces
a very large contribution at low temperatures.
levels (n=2), and in general, the contributions for
the different n manifolds smoothly decrease as n increases, until a
new autoionization channel is opened.
For this particular case, an n=7 resonant lying close to threshold produces
a very large contribution at low temperatures.
In this paper we have described calculations of dielectronic recombination
data for the nitrogen-like isoelectronic sequence
forming oxygen-like ions as part of an
assembly of a dielectronic recombination database necessary for the
modelling of dynamic finite-density plasmas
(Badnell et al. 2003).
We have calculated LSJ final-state level-resolved dielectronic recombination
rate coefficients in a form which will prove of great use to
astrophysical and fusion plasma modellers.
We have calculated data over a wide temperature range and for a large
number of atomic ions in order to maximise the available information
for modelling work.
In order to facilitate the further application of our data,
we fitted the total DR results with a standart approximation
formula.
Our fits are accurate to better than 3% for all ions in the
temperature range
![]() K to
K to
![]() K,
where q is the residual charge of the initial ion.
Comparisons have been made with the fitting formulae of
Mazzotta et al. (1998), showing that their
approximation is not good for the low temperature range.
We found very good agreement with the results calculated
by Gu (2003), and for the only detailed experimental
data, Fe19+, by Savin et al. (2002).
K,
where q is the residual charge of the initial ion.
Comparisons have been made with the fitting formulae of
Mazzotta et al. (1998), showing that their
approximation is not good for the low temperature range.
We found very good agreement with the results calculated
by Gu (2003), and for the only detailed experimental
data, Fe19+, by Savin et al. (2002).