| (1) | |||
| (2) |
A&A 425, 773-781 (2004)
DOI: 10.1051/0004-6361:20035653
Z. Meliani 1,2 - C. Sauty 1,2 - K. Tsinganos 3 - N. Vlahakis 3
1 - Observatoire de Paris, L.U.Th., 5 place Jules Janssen, 92190 Meudon, France
2 - Université de Paris 7, APC, 2 place Jussieu, 75005 Paris, France
3 - IASA and Section of Astrophysics, Astronomy & Mechanics,
Department of Physics, University of Athens,
Panepistimiopolis 157 84, Zografos, Greece
Received 10 November 2003 / Accepted 23 June 2004
Abstract
Spherically symmetric hydrodynamical outflows accelerated thermally in the
vicinity of a compact object are studied by generalizing an equation of state
with a variable effective polytropic index, appropriate to describe
relativistic temperatures close to the central object and nonrelativistic ones
further away. Relativistic effects introduced by the Schwarzschild metric and
the presence of relativistic temperatures in the corona are compared with
previous results for a constant effective polytropic index and also with
results of the classical wind theory.
By a parametric study of the polytropic index and the location of the sonic
transition it is found that
space time curvature and relativistic temperatures tend to increase the
efficiency of thermal driving in accelerating the outflow.
Thus conversely to the classical Parker wind, the outflow is
accelerated even for polytropic indices higher than 3/2.
The results of this simple but fully relativistic extension of the
polytropic equation of state may be useful in simulations of outflows
from hot coronae in black hole magnetospheres.
Key words: stars: winds, outflows - ISM: jets and outflows - galaxies: jets - hydrodynamics - relativity
Relativistic outflows are commonly inferred from observations of collimated winds (jets) in Galactic X-ray binaries and supermassive black holes in active galactic nuclei and quasars (Biretta et al. 1999; Livio 2002). Also, observations infer coronae with rather high temperatures in microquasars (e.g., Corbel et al. 2003) and AGN (e.g., Rózanska & Czerny 2000, and Refs. therein). Although there are still some ambiguities in the interpretation of these observations, temperatures up to 109 K for electrons/positrons and 1012 K for protons are usually inferred. Nevertheless, even if such temperatures were to correspond to closed field line regions, by using the analogy with the solar corona, one may extrapolate that such high temperatures could also exist in the open field line regions where the outflow is accelerated. The heating mechanism to obtain these high temperatures can be of magnetic origin (Heinz & Begelman 2000). Alternatively, accreted material falling onto the central black hole may be decelerated via a shock, feeding the magnetosphere with a hot plasma. Discussions on the possibility of such shock formation in an accretion disk that leads to a heated corona have been already given in the literature in the so called CENBOL model (Chakrabarti et al. 1996; Chattopadhyay et al. 2004; Das 2000, and references therein). These papers have also discussed how radiation and coupling with the photon distribution has to be taken into account properly.
The inevitable result of such hot atmospheres is that they expand supersonically and at large distances thermal energy is converted to bulk flow kinetic energy. For example, Ferrari et al. (1985), Das (2000) and Chattopadhyay et al. (2004) have suggested that outflows can be thermally accelerated to relativistic speeds. However, such treatments assumed the classical polytropic equation of state which prevents from studying consistently the relativistic temperatures in the corona and the nonrelativistic ones farther away. The first effort to use an equation of state appropriate for outflows containing both ultrarelativistic and classical temperatures has been used only for studying spherical accretion flows and only in the adiabatic case (Mathews 1971; Blumenthal & Mathews 1976). Moreover, Blumenthal & Mathews (1976) discussed the topology of the Mach number variation in the solution of an adiabatic wind. However, as it is well known (Parker 1960) the topology of the Mach number does not give us information on whether the flow itself is accelerated or not.
In this paper we extend the equation of state used in Blumenthal & Mathews (1976) for nonadiabatic flows and our goal is to investigate the efficiency of thermal driving under extreme relativistic conditions. For example, in the classical polytropic solar wind theory, the polytropic index needs to be smaller than 3/2 in order to obtain an accelerated wind solution (Parker 1960). This means that a minimal extension of the corona is required. Here we explore how this value is changed under relativistic conditions. In order to simplify the study, we shall focus our attention on spherical, steady and radial hydrodynamic outflows at large distances from a stationary compact object. Also for simplicity we shall use Schwarzschild's metric. Furthermore, we will not discuss how the pressure and the heating may include coupling with the radiation field, especially in the case of pair production, as our goal is to keep the discussion at a basic level and this has already been done elsewhere (e.g., Chattopadhyay et al. 2004).
In the next section we outline the governing equations with particular emphasis to an equation of state appropriate to relativistic temperatures close to the base of the outflow and classical ones further away. In Sect. 3 we derive for a given asymptotic value of the polytropic index the range of allowed locations of the sonic surface and also the limits of the asymptotic speed. In Sect. 4 via a parametric study we present a comparison of our model with the nonrelativistic Parker wind and relativistic winds with constant polytropic index. An astrophysical application is outlined in Sect. 5 and the results are summarized in Sect. 6.
The flow of a relativistic fluid is governed by conservation of the number
of particles and energy-momentum,
The proper enthalpy per particle, w, is the sum
of the proper internal energy per particle (including the proper mass), e,
and the proper pressure P divided by n,
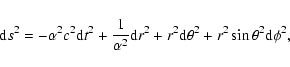 |
(4) |
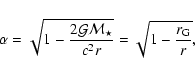 |
(5) |
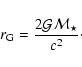 |
(6) |
To close the system of Eqs. (7)-(9) we
should specify an equation of state that
relates the entropy per particle
s=s(w,P)=s(e,P) to the pressure, P, and
the enthalpy per particle, w, or the internal energy per particle, e.
In the literature (e.g., Michel 1972; Chakrabarti et al. 1996; Das 1999) various authors have adopted a
classical adiabatic or polytropic equation to replace the equation of state
The scalar isotropic pressure of a single perfect fluid is given by
(Mathews 1971; Synge 1957)
By integrating Eqs. (8) and (12) we obtain
a generalized equation of state for an adiabatic (ideal) fluid
(see Blumenthal & Mathews 1976, Eq. (3.3)),
For studying stellar interiors, a classical trick to study different equations
of state and their hardness is to use the same equation, called
polytropic equation of state, with a
different value of the adiabatic index, assuming the number of degrees of
freedom of the particles has changed. In this case
![]() ,
but the system still evolves adiabatically.
E. Parker to study the solar wind proposed (Parker 1960)
to follow the same path using Eq. (10),
assuming
,
but the system still evolves adiabatically.
E. Parker to study the solar wind proposed (Parker 1960)
to follow the same path using Eq. (10),
assuming ![]() being any value
between 1 and the adiabatic value 5/3 to mimic the coronal heating in a
simple but hidden way. As explained in Sauty et al. (1999) this is equivalent to
use a generalized enthalpy and internal energy which includes the heating.
being any value
between 1 and the adiabatic value 5/3 to mimic the coronal heating in a
simple but hidden way. As explained in Sauty et al. (1999) this is equivalent to
use a generalized enthalpy and internal energy which includes the heating.
Following Parker's initial approach of the polytropic solar wind, we assume
also here that the enthalpy and the particle density are related by Eq. (8) but
relating e to the particle density via
By combining Eqs. (14) and (8) we get a
generalized relation between pressure and density which includes the proper
mass energy per particle,
![]() ,
,
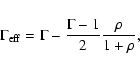 |
(16) |
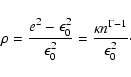 |
(17) |
Finally, the local sound speed
![]() can be written as
a function of
can be written as
a function of ![]() ,
,
In the limit of a nonrelativistic fluid,
![]() ,
we may calculate the thermal energy per particle or random thermal energy
(Mathews 1971),
,
we may calculate the thermal energy per particle or random thermal energy
(Mathews 1971),
| |
= | ||
| (21) |
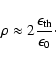 |
(22) |
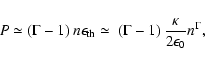 |
(23) |
On the other hand, in the ultrarelativistic domain where the thermal energy
is much larger than the mass energy (
![]()
![]()
![]() )
we have
)
we have
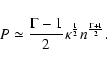 |
(24) |
The effective polytropic index and corresponding temperature for an adiabatic
flow with relativistic temperatures at the base and classical behavior further
away are plotted in Fig. 1.
These solutions are discussed in more detail later on. We simply note here
that for an adiabatic flow, the polytropic index increases from 4/3 at the
base where the thermal energy equals or exceeds the mass energy (i.e.
![]() for protons, or,
for protons, or,
![]() for positrons) to 5/3
asymptotically where the temperature is much lower (i.e.,
for positrons) to 5/3
asymptotically where the temperature is much lower (i.e.,
![]() for
protons or
for
protons or
![]() for positrons), as expected. To emphasize this property of the equation of state, we have plotted in Fig. 1 a case with ultrarelativistic
temperatures at the base. Note that the coronal temperature close to the compact object are very
sensitive to the value of the parameter
for positrons), as expected. To emphasize this property of the equation of state, we have plotted in Fig. 1 a case with ultrarelativistic
temperatures at the base. Note that the coronal temperature close to the compact object are very
sensitive to the value of the parameter ![]() ,
as discussed in the following.
,
as discussed in the following.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{0653fig1.ps}\end{figure}](/articles/aa/full/2004/39/aa0653/Timg79.gif) |
Figure 1:
a) Plot of the effective polytropic index
|
| Open with DEXTER | |
In the following all quantities are defined in dimensionless form. First,
velocities are normalized to the speed of light
![]() such that
such that
![]() is the (variable) dimensionless sound
speed. Second, distances could have been normalized at the gravitational
radius
is the (variable) dimensionless sound
speed. Second, distances could have been normalized at the gravitational
radius ![]() .
However, we found easier to normalize all quantities at the sonic
surface
.
However, we found easier to normalize all quantities at the sonic
surface ![]() ,
such that we can define a dimensionless radius,
,
such that we can define a dimensionless radius,
| (25) |
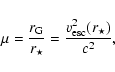 |
(26) |
The Euler equation and the continuity equation can be written in dimensionless
forms,
This model has two free parameters
that affect the solution of the differential Eqs. (27) and (28)![]() .
The first parameter,
.
The first parameter, ![]() ,
is the value of the effective polytropic index at infinity. The second parameter,
,
is the value of the effective polytropic index at infinity. The second parameter, ![]() ,
is the ratio of the Schwarzschild's radius to the radius at the sonic surface.
,
is the ratio of the Schwarzschild's radius to the radius at the sonic surface.
Equations (27) and (28) have a singularity corresponding to
the sonic surface, which we may call hydrodynamic horizon by analogy with the
black hole horizon. At the sonic surface the right hand sides of the two equations
vanish because the left hand sides vanish.
For a detailed discussion of the nature and position of the critical surfaces in astrophysical winds, see Tsinganos et al. (1996).
This gives the following criticality condition,
Since
![]() ,
the above criticality condition requires that we should always have
,
the above criticality condition requires that we should always have ![]() .
Furthermore, by combining Eqs. (20) and (29)
we find an upper value for
.
Furthermore, by combining Eqs. (20) and (29)
we find an upper value for ![]()
Thus, the criticality conditions for wind-type solutions reduces the
acceptable values of ![]() to a limited range:
to a limited range:
| (35) |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0653fig2.ps}\end{figure}](/articles/aa/full/2004/39/aa0653/Timg117.gif) |
Figure 2:
Contour plots of constant terminal Lorentz factor
|
| Open with DEXTER | |
The conservation of the number of particle can be integrated to give a first
constant of the system, which corresponds to the mass loss rate or the mass
flux ![]()
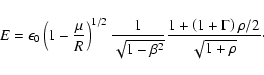 |
(37) |
Instead of integrating the differential equations which is the way we followed
after Parker (1960), we could also plot the isocontours of constant E and ![]() .
The two methods are equivalent. We have checked that
while integrating the differential equations E remained constant.
.
The two methods are equivalent. We have checked that
while integrating the differential equations E remained constant.
In the following we present the results of our parametric study for various
values of the polytropic index ![]() and the gravitational parameter
and the gravitational parameter ![]() .
We also compare them with the corresponding results in the analysis of
Blumenthal & Mathews (1976) for an adiabatic polytropic index
.
We also compare them with the corresponding results in the analysis of
Blumenthal & Mathews (1976) for an adiabatic polytropic index
![]() and studies using a classical equation of state with a constant polytropic
index
and studies using a classical equation of state with a constant polytropic
index ![]() .
.
We solved numerically the equations by using a Runge-Kutta scheme starting at the sonic surface and integrating both upstream towards the black hole and downstream to infinity.
The behavior of the solutions for various values of ![]() is displayed in Figs. 3.
is displayed in Figs. 3.
![\begin{figure}
\par\includegraphics[height=5.7cm,width=5.75cm,angle=180,clip]{06...
...cludegraphics[height=5.7cm,width=5.75cm,angle=180,clip]{0653fig5.ps}\end{figure}](/articles/aa/full/2004/39/aa0653/Timg125.gif) |
Figure 3:
For
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=8.45cm,width=6.1cm,angle=270,clip]{06...
...cludegraphics[height=8.45cm,width=6.1cm,angle=270,clip]{0653fig8.ps}\end{figure}](/articles/aa/full/2004/39/aa0653/Timg128.gif) |
Figure 4:
Comparison of the classical Parker solutions and the relativistic ones
for two sets of the parameters |
| Open with DEXTER | |
In the classical limit, the horizon goes to the center of the
gravitational well,
![]() and consequently
and consequently
![]() .
The index
.
The index ![]() is the only free parameter which is left together with
the mass loss rate. Then, in the classical limit the condition at the critical
point reduces to the usual expression,
is the only free parameter which is left together with
the mass loss rate. Then, in the classical limit the condition at the critical
point reduces to the usual expression,
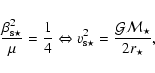 |
(39) |
For a classical polytropic wind there is no acceleration for
![]() (see Parker 1960) because then the acceleration at
the sonic surface becomes negative for both critical solutions and
no real wind-type solution exists. Conversely our relativistic solutions can
be accelerated even if
(see Parker 1960) because then the acceleration at
the sonic surface becomes negative for both critical solutions and
no real wind-type solution exists. Conversely our relativistic solutions can
be accelerated even if
![]() when
when ![]() increases. This is illustrated
in Figs. 4a,b where the topology of the adiabatic solution
(
increases. This is illustrated
in Figs. 4a,b where the topology of the adiabatic solution
(
![]() )
is displayed in the
classical and the relativistic cases. In the first case both critical solutions
are decelerated while in the second one there is an accelerated wind type
solution. This is also shown in Fig. 2: for
)
is displayed in the
classical and the relativistic cases. In the first case both critical solutions
are decelerated while in the second one there is an accelerated wind type
solution. This is also shown in Fig. 2: for ![]() (classical limit,
along the horizontal axis),
the highest value of
(classical limit,
along the horizontal axis),
the highest value of ![]() to have an accelerated wind-type solution
is 1.5. For non zero values of
to have an accelerated wind-type solution
is 1.5. For non zero values of ![]() (relativistic regime), the domain of
wind-type solutions extends to higher values of
(relativistic regime), the domain of
wind-type solutions extends to higher values of ![]() .
.
The relativistic wind is characterized
by the fact that from the compact object outwards the pressure decreases
faster. This is due to the presence of the redshift function ![]() in the
continuity Eq. (36). When matter flows away from the
central object the proper volume of the fluid increases faster than the
observed (spherical) volume because of
in the
continuity Eq. (36). When matter flows away from the
central object the proper volume of the fluid increases faster than the
observed (spherical) volume because of ![]() ,
which provokes the decrease of the proper density and consequently
of the pressure. The larger pressure gradient leads to higher acceleration. This is equivalent
to the well known acceleration due to overradial flaring in the
classical solar wind as studied in Kopp & Holzer (1976).
,
which provokes the decrease of the proper density and consequently
of the pressure. The larger pressure gradient leads to higher acceleration. This is equivalent
to the well known acceleration due to overradial flaring in the
classical solar wind as studied in Kopp & Holzer (1976).
In fact, expanding Euler's Eq. (27) to first order in the
relativistic effects, i.e. for ![]() and
and ![]() ,
we find
,
we find
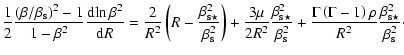 |
(40) |
Even for quasi-isothermal (
![]() )
flows we see that the relativistic winds are more rapidly accelerated than their classical counter part (Figs. 4c,d).
)
flows we see that the relativistic winds are more rapidly accelerated than their classical counter part (Figs. 4c,d).
Let us consider next relativistic winds with a constant effective polytropic.
In this approach the same free parameters exist,
![]() and
and ![]() .
However for a relativistic polytropic wind where
.
However for a relativistic polytropic wind where
![]() const., the expression of the sound speed and the
Bernoulli equation are written as
const., the expression of the sound speed and the
Bernoulli equation are written as
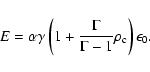 |
(42) |
For a fixed value of ![]() ,
we may compare the solutions of three
equations of state describing a relativistic wind. First, by using the
consistent equation of state with a variable
,
we may compare the solutions of three
equations of state describing a relativistic wind. First, by using the
consistent equation of state with a variable
![]() and second,
for a constant polytropic index, either
and second,
for a constant polytropic index, either
![]() ,
a value which is the limit of
,
a value which is the limit of
![]() in the ultrarelativistic domain, or, for a constant
in the ultrarelativistic domain, or, for a constant
![]() which is the limit of
which is the limit of
![]() in the classical regime (see Fig. 5). The consistent relativistic
equation of state gives a wind which is always more efficient than the
classical one corresponding to the constant value
in the classical regime (see Fig. 5). The consistent relativistic
equation of state gives a wind which is always more efficient than the
classical one corresponding to the constant value ![]() ,
but less
efficient than the ultrarelativistic one for the value
,
but less
efficient than the ultrarelativistic one for the value
![]() .
Using the value
.
Using the value ![]() will always underestimate the asymptotic speed, but
this difference becomes smaller as we approach the adiabatic value, as
illustrated in Fig. 5.
Conversely, it is appropriate to use the value
will always underestimate the asymptotic speed, but
this difference becomes smaller as we approach the adiabatic value, as
illustrated in Fig. 5.
Conversely, it is appropriate to use the value
![]() in the vicinity of the black hole where the temperatures are
ultrarelativistic. However it will always overestimate the asymptotic Lorentz
factor, especially in the adiabatic case.
As it can be seen in Fig. 5b, in some cases
the solutions can be slightly decelerated in the
super-sonic region, because the thermal energy is not sufficient
to overcome gravity in these distances.
in the vicinity of the black hole where the temperatures are
ultrarelativistic. However it will always overestimate the asymptotic Lorentz
factor, especially in the adiabatic case.
As it can be seen in Fig. 5b, in some cases
the solutions can be slightly decelerated in the
super-sonic region, because the thermal energy is not sufficient
to overcome gravity in these distances.
![\begin{figure}
\par\includegraphics[height=7.1cm,width=8.2cm,angle=180,clip]{0653fig9.ps}\end{figure}](/articles/aa/full/2004/39/aa0653/Timg142.gif) |
Figure 5:
Comparison between a variable and two constant |
| Open with DEXTER | |
In the ultrarelativistic limit (large ![]() and
and ![]() )
we can obtain analytically that our model is more efficient than the
classical one, by comparing the acceleration at the sonic point for the two models.
The condition is
)
we can obtain analytically that our model is more efficient than the
classical one, by comparing the acceleration at the sonic point for the two models.
The condition is
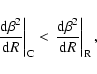 |
(43) |
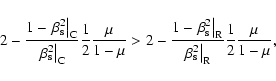 |
(44) |
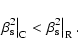 |
(45) |
At this point of the comparison, we should stress that a constant polytropic index, as it has been used in many models of relativistic thermal wind, is inconsistent with having both ultrarelativistic and classical temperatures in the flow. With the usual equation of state the thermodynamic regime is either ultrarelativistic or classical. In reality the outflow escapes from a very hot corona but cools down further out so there must be a smooth transition from one regime to the other.
In this section we apply our model using typical values for jets from compact
objects. We consider two cases, a supermassive black hole with
![]() ,
typical of a quasar (see Wang & Zhang 2003) and
a stellar size black hole with
,
typical of a quasar (see Wang & Zhang 2003) and
a stellar size black hole with
![]() ,
typical of a
microquasar (see Mirabel 1998).
,
typical of a
microquasar (see Mirabel 1998).
We choose the sonic surface to be close to the compact
object,
![]() ,
such that
,
such that
![]() .
This choice
of
.
This choice
of ![]() gives a sufficiently high asymptotic Lorentz factor of
gives a sufficiently high asymptotic Lorentz factor of
![]() ,
typical of those objects for sufficiently small
values of
,
typical of those objects for sufficiently small
values of ![]() (Fig. 6). For the solution with
(Fig. 6). For the solution with
![]() ,
the initial temperature is
,
the initial temperature is
![]() K in the case of electron-proton
gas and
K in the case of electron-proton
gas and
![]() K in the case of electron-positron pairs.
Note however, that for low values of
K in the case of electron-positron pairs.
Note however, that for low values of ![]() such as
such as
![]() the
temperature remains unrealistically high at large distances. Hence, a more
physical approach would be to avoid taking these solutions corresponding to
the
temperature remains unrealistically high at large distances. Hence, a more
physical approach would be to avoid taking these solutions corresponding to
![]() all the way to large distances, but instead match them with solutions with
a faster decrease of the temperature (
all the way to large distances, but instead match them with solutions with
a faster decrease of the temperature (
![]() ).
).
In both cases the solutions differ only in the density and mass loss rate.
Both solutions have the same Lorentz factor profile and the same energy
per particle in units of mass energy as this depends only on ![]() and not
on the mass of the central object or on the total mass loss rate. The result is
displayed on Fig. 6.
and not
on the mass of the central object or on the total mass loss rate. The result is
displayed on Fig. 6.
![\begin{figure}
\par\includegraphics[height=5.6cm,width=8.5cm,clip]{0653fig10.ps}\end{figure}](/articles/aa/full/2004/39/aa0653/Timg154.gif) |
Figure 6:
Plot of the Lorentz factor in a) and the thermal energy density
in b) versus radius for
|
| Open with DEXTER | |
For quasi-isothermal winds,
![]() ,
the Lorentz factor
,
the Lorentz factor ![]() can exceed a value of 5 if the thermal energy distribution in the vicinity of the central object is
roughly 10 times more than the mass energy.
The thermal content is spread along the
flow and not peaked close to the compact object such that it can accelerate
efficiently the flow with a lower maximum in temperature.
Such a quasi-isothermal outflow can occur if there is a
redistribution of energy by the highly
radiative initial field which cools the upstream flow and reheat the
down part in the subsonic part where the medium is still optically
thick (Das 2000; Tarafdar 1988).
The dissipation of disorganized magnetic field
could also occur to produce extended heating. Such a dissipation has
shown to be potentially important after the sonic surface and in the
asymptotic region (Heinz & Begelman 2000)
can exceed a value of 5 if the thermal energy distribution in the vicinity of the central object is
roughly 10 times more than the mass energy.
The thermal content is spread along the
flow and not peaked close to the compact object such that it can accelerate
efficiently the flow with a lower maximum in temperature.
Such a quasi-isothermal outflow can occur if there is a
redistribution of energy by the highly
radiative initial field which cools the upstream flow and reheat the
down part in the subsonic part where the medium is still optically
thick (Das 2000; Tarafdar 1988).
The dissipation of disorganized magnetic field
could also occur to produce extended heating. Such a dissipation has
shown to be potentially important after the sonic surface and in the
asymptotic region (Heinz & Begelman 2000)
![\begin{figure}
\par\includegraphics[height=4.9cm,width=8.5cm,clip]{0653fig11.ps}\end{figure}](/articles/aa/full/2004/39/aa0653/Timg157.gif) |
Figure 7:
Plot of density versus radius for
|
| Open with DEXTER | |
In Fig. 7 we plot the number density in units of n0 cm-3
as a function of distance, for a free density parameter n0.
For the quasar solution (Fig. 7a) the
corresponding mass loss rate is
![]() yr, while for the micro-quasar
solution (Fig. 7b)
yr, while for the micro-quasar
solution (Fig. 7b)
![]() yr.
yr.
We note that as the mass of the central compact object changes from
![]() to
to
![]() the solution is simply scaled
down spatially, a result consistent with the idea
that microquasars could be considered to zeroth order as
scaled down versions of quasars.
A more detailed treatment however, should take into account certain differences of the
two cases, e.g. pair production, different densities, etc., something beyond the scope of the
present analysis.
the solution is simply scaled
down spatially, a result consistent with the idea
that microquasars could be considered to zeroth order as
scaled down versions of quasars.
A more detailed treatment however, should take into account certain differences of the
two cases, e.g. pair production, different densities, etc., something beyond the scope of the
present analysis.
We have generalized a variable polytropic index equation of state for
the purpose of modelling relativistic flows, both in temperature and velocity
in the vicinity of a Schwarzschild black hole. This has enabled us to analyze
thermally driven winds having both ultrarelativistic temperatures
at the base of the central corona (
![]() )
and classical temperatures (
)
and classical temperatures (
![]() )
further
out. This equation of state is characterized
by a polytropic index
)
further
out. This equation of state is characterized
by a polytropic index ![]() such that pressure is related to density in
the form of Eq. (15).
such that pressure is related to density in
the form of Eq. (15).
For a given polytropic index ![]() ,
transonic wind solutions can be found
only within a limited range of radii of the sonic point, r*,
,
transonic wind solutions can be found
only within a limited range of radii of the sonic point, r*,
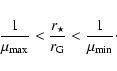
Schwarzschild's metric tends to enhance the effects of gravity. One
major effect of strong gravity is to have a more efficient De Laval nozzle
which allows to have accelerated winds even for polytropic indices larger
than the typical Parker's value, i.e.
![]() ,
conversely to the classical Parker's wind (Parker 1960).
This can be understood by computing the effective polytropic index
,
conversely to the classical Parker's wind (Parker 1960).
This can be understood by computing the effective polytropic index
![]() .
Enhanced gravity and also relativistic
temperatures tend to lower the effective polytropic index in the low corona
which gives a more efficient thermal driving of the wind.
.
Enhanced gravity and also relativistic
temperatures tend to lower the effective polytropic index in the low corona
which gives a more efficient thermal driving of the wind.
However, we note that despite its widespread use in the literature, the ordinary polytropic equation of state with a constant effective polytropic index seems not to be really consistent with a mixed regime of temperatures in the corona from ultra-relativistic to classical ones.
In order to reach very high Lorentz factors, in the adiabatic case, the internal energy of the plasma in the corona should exceed by a large factor its mass energy. This can be easily achieved if the total pressure is not limited to the kinetic pressure of the gas but also includes extra physical processes such as MHD waves or radiation. This result is somehow consistent with the usual low velocities obtained for classical winds. Quasi-isothermal winds reach higher Lorentz factors with a relatively lower - but still larger than the mass energy - internal energy.
Applying our model to typical values observed in microquasars and quasars we recover as expected that microquasar outflows may be seen as a scaled down version of their bigger extragalactic counterparts. We do not claim however that all jets are only thermally driven. A magnetic driving mechanism seems more efficient indeed to accelerate the outflow on parsec scales as shown by Vlahakis & Königl (2004), in agreement with some jet observations (Sudou et al. 2000). However, we simply emphasize that thermal driving may indeed play an important role alongside other mechanisms, when hot coronae are observed; in such cases, a consistent way of dealing with these relativistic temperatures is required.
Finally, this consistent generalization of the Parker polytrope for relativistic thermal winds could be implemented in numerical simulations, instead of the classical constant polytropic index equation of state to simulate the transition from relativistic to nonrelativistic temperatures along the flow. Nevertheless, as in any polytropic equation of state the source of heating is not specified on physical grounds and more detailed physics of the coronal heating is needed.
Acknowledgements
We acknowledge financial support from the French Foreign Office and the Greek General Secretariat for Research and Technology (Program Platon). K.T. and N.V. acknowledge partial support from the European Research and Training Networks PLATON (HPRN-CT-2000-00153) and ENIGMA (HPRN-CT-2001-0032).
Conversely to the usual polytropic equation of state used in studying stellar interiors, the use in classical as well as relativistic winds of a polytropic index different from the adiabatic one is an implicit way to mask extra heating in the corona as explained in Sauty et al. (1999). In all cases, the fluid remains a monoatomic plasma of electrons and protons with a ratio of specific heats 5/3.
Thus, by substituting Eq. (14) to Eq. (13),
we have
introduced implicitly that the external medium could give extra energy to the
fluid. e in Eq. (14) is the total internal energy of the gas.
It has two component, i.e.
![]() the internal energy of the plasma
itself calculated from Eq. (13)
the internal energy of the plasma
itself calculated from Eq. (13)
The global system plasma + external medium being isolated, it is adiabatic, so it is
usual to define e instead of
![]() in order to keep its simple
form to the energy conservation given by Eq. (2)
(e.g., Blumenthal & Mathews 1976; Mobarry & Lovelace 1986). It is
easy to calculate the heating transfered to the plasma during its expansion,
in order to keep its simple
form to the energy conservation given by Eq. (2)
(e.g., Blumenthal & Mathews 1976; Mobarry & Lovelace 1986). It is
easy to calculate the heating transfered to the plasma during its expansion,
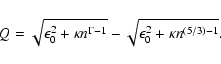 |
(A.3) |
 |
(A.4) |