A&A 425, 797-812 (2004)
DOI: 10.1051/0004-6361:20047157
F. La Barbera - P. Merluzzi - G. Busarello - M. Massarotti - A. Mercurio
INAF, Istituto Nazionale di Astrofisica, Osservatorio Astronomico di Capodimonte, via Moiariello 16, 80131 Napoli, Italy
Received 28 January 2004 / Accepted 10 June 2004
Abstract
We present a detailed analysis of the photometric
properties of galaxies in the cluster A 2163B at redshift
![]() .
R-, I- and K-band structural parameters, (half light
radius
.
R-, I- and K-band structural parameters, (half light
radius
![]() ,
mean surface brightness
,
mean surface brightness
![]() within
within
![]() and
Sersic index n) are derived for
and
Sersic index n) are derived for ![]() galaxies, and are
used to study their internal colour gradients. For the first time,
we use the slopes of optical-NIR Kormendy relations to study colour
gradients as a function of galaxy size, and we derive the
Photometric Plane at
galaxies, and are
used to study their internal colour gradients. For the first time,
we use the slopes of optical-NIR Kormendy relations to study colour
gradients as a function of galaxy size, and we derive the
Photometric Plane at
![]() in the K band. Colour
gradients are negligible at optical wavelengths, and are negative
in the optical-NIR, amounting on average to
in the K band. Colour
gradients are negligible at optical wavelengths, and are negative
in the optical-NIR, amounting on average to
![]() .
This result is in agreement with our previous measurements of
colour gradients at intermediate redshifts, and imply a metallicity
gradient in galaxies of
.
This result is in agreement with our previous measurements of
colour gradients at intermediate redshifts, and imply a metallicity
gradient in galaxies of
![]() per radial decade. The
analysis of the Kormendy relation suggests that its slope increases
from the optical to the NIR, implying that colour gradients do not
vary or even do become less steep in more massive galaxies. Such a
result is not simply accomodated within a monolithic collapse
scenario, while it can be well understood within a hierarchical
merging framework. Finally, we derive the first NIR Photometric
Plane at
per radial decade. The
analysis of the Kormendy relation suggests that its slope increases
from the optical to the NIR, implying that colour gradients do not
vary or even do become less steep in more massive galaxies. Such a
result is not simply accomodated within a monolithic collapse
scenario, while it can be well understood within a hierarchical
merging framework. Finally, we derive the first NIR Photometric
Plane at
![]() ,
accounting for both the correlations on
the measurement uncertainties and the selection effects. The
Photometric Plane at
,
accounting for both the correlations on
the measurement uncertainties and the selection effects. The
Photometric Plane at
![]() is consistent with that at
is consistent with that at
![]() ,
with an intrinsic scatter significantly smaller
than the Kormendy relation but larger than the Fundamental Plane.
,
with an intrinsic scatter significantly smaller
than the Kormendy relation but larger than the Fundamental Plane.
Key words: galaxies: clusters: individual: A 2163B - galaxies: photometry - galaxies: fundamental parameters - galaxies: evolution
Studies of galaxy populations in clusters at intermediate redshifts have been proved to be an effective tool to constrain the mechanisms underlying their formation and evolution. A pure photometric approach involves the analysis of galaxy Luminosity Functions (LFs), of galaxy colours, mainly via the colour magnitude (CM) diagrams, and of the internal light distribution of galaxies, i.e. their structural parameters.
The galaxy LF and its dependence on the waveband carry information
both on the stellar processes occurring in galaxies and on the
cosmological processes which determine their mass function. Since
Press & Schechter (1974), the shape of the LF has been seen as a basic test of
theories of structure formation and evolution. The luminosities of
early-type galaxies are also tightly correlated with their colours,
through the colour magnitude (CM) relation (Visvanathan & Sandage 1977; Bower et al. 1992). The
slope of this relation shows little evolution with redshift up to ![]() ,
while its zeropoint changes according to what is expected
for an old passively evolving stellar population (e.g.
Stanford et al. 1998, Kodama et al. 1998, hereafter KAB98). As shown by KAB98
(see also Merluzzi et al. 2003), the evolution of the CM sequence with
redshift sets strong constraints on the origin of this relation,
resolving the well known age-metallicity degeneracy (Worthey et al. 1996).
,
while its zeropoint changes according to what is expected
for an old passively evolving stellar population (e.g.
Stanford et al. 1998, Kodama et al. 1998, hereafter KAB98). As shown by KAB98
(see also Merluzzi et al. 2003), the evolution of the CM sequence with
redshift sets strong constraints on the origin of this relation,
resolving the well known age-metallicity degeneracy (Worthey et al. 1996).
The structural properties of galaxies at different redshifts provide a wealth of information by which galaxy evolution can be investigated, both through the study of the correlations and through the analysis of the waveband dependence of such quantities. The NIR light, in fact, is less sensitive to more recent star formation, to metallicity effects (though line blanketing) and to dust absorption, following more closely the luminous matter distribution.
The multi-waveband analysis gives information on the internal colour gradients (CGRs) of galaxies, and therefore on the radial gradients of the properties of their stellar populations (SPs), such as age, metallicity and dust content. Nearby galaxies have on average negative CGRs, their SPs becoming bluer toward the periphery (Peletier et al. 1990a, b). Due to the low evolution of colour gradients with redshift, metallicity seems to be the primary driver of the SP gradients in spheroidal galaxies, as demonstrated both by optical-optical studies (e.g. Tamura & Ohta 2000; Saglia et al. 2000) and by optical-NIR CG measurements (La Barbera et al. 2003a,2002, hereafter LBM02 and LBM03a). Age gradients, however, are not fully ruled out by the present data (Saglia et al. 2000, LBM03a), while the effects of dust absorption still remain substantially unresolved. The presence of metallicity gradients can be well explained in the monolithic formation scenario of early-type galaxies (Larson 1974), due to the later beginning of a galactic wind in the inner galaxy regions. However, it can also be accommodated within the hierarchical merging framework, since metallicity gradients are settled in disk galaxies at high redshifts, and more massive early-types form on average from the merging of larger disks (Kauffmann 1996).
Structural parameters, such as the effective (half-light) radius
![]() ,
the mean surface brightness
,
the mean surface brightness
![]() within
within
![]() and the Sersic index
n, are correlated by various relations, whose physical origins
reside both in the properties of the SPs of galaxies and in the
dynamical structure of these systems. For the early-type galaxies,
one of these correlations is that between
and the Sersic index
n, are correlated by various relations, whose physical origins
reside both in the properties of the SPs of galaxies and in the
dynamical structure of these systems. For the early-type galaxies,
one of these correlations is that between
![]() and
and
![]() ,
also known
as the Kormendy relation (KR). As shown by Capaccioli, Caon and
D'Onofrio (1992),
,
also known
as the Kormendy relation (KR). As shown by Capaccioli, Caon and
D'Onofrio (1992),
![]() form two
distinct families in the plane of effective parameters: that of the
bright early-types, following the KR, and another "ordinary'' family,
whose properties are more disperse and heterogeneous. Recently,
Graham & Guzmàn (2003) showed that a real dichotomy does not exist between the
two families, but their observed properties are well explained by a
systematic change in the profile shape with galaxy luminosity. The
evolution of the zeropoint of the KR has been largely investigated at
optical wavebands to constrain the major formation epoch of galaxy SPs
and to perform the Tolman test for the cosmological expansion
(Lubin & Sandage 2001; Sandage & Perelmuter 1991; Barger et al. 1998; Sandage & Lubin 2001; Ziegler et al. 1999; Pahre et al. 1996). On the other hand,
the slope of the KR is an interesting tool to gain insight into the
properties of the galaxy SPs as a function of galaxy size
(Ziegler et al. 1999; La Barbera et al. 2003b, hereafter LBM03b), which is a
crucial prediction of hierarchical merging scenarios. As recently
shown by Graham (2002, hereafter GRA02), early-type galaxies also
follow a three-dimensional relation between
form two
distinct families in the plane of effective parameters: that of the
bright early-types, following the KR, and another "ordinary'' family,
whose properties are more disperse and heterogeneous. Recently,
Graham & Guzmàn (2003) showed that a real dichotomy does not exist between the
two families, but their observed properties are well explained by a
systematic change in the profile shape with galaxy luminosity. The
evolution of the zeropoint of the KR has been largely investigated at
optical wavebands to constrain the major formation epoch of galaxy SPs
and to perform the Tolman test for the cosmological expansion
(Lubin & Sandage 2001; Sandage & Perelmuter 1991; Barger et al. 1998; Sandage & Lubin 2001; Ziegler et al. 1999; Pahre et al. 1996). On the other hand,
the slope of the KR is an interesting tool to gain insight into the
properties of the galaxy SPs as a function of galaxy size
(Ziegler et al. 1999; La Barbera et al. 2003b, hereafter LBM03b), which is a
crucial prediction of hierarchical merging scenarios. As recently
shown by Graham (2002, hereafter GRA02), early-type galaxies also
follow a three-dimensional relation between
![]() ,
,
![]() and
and ![]() ,
which is similar to the spectroscopic Fundamental Plane (FP), once
velocity dispersions are replaced by Sersic indices. This
"photometric plane'' (hereafter PHP) has an observed scatter comparable
to that of the Fundamental Plane (FP) relation, and carries
interesting information on the physical properties of galaxies and
their origin.
,
which is similar to the spectroscopic Fundamental Plane (FP), once
velocity dispersions are replaced by Sersic indices. This
"photometric plane'' (hereafter PHP) has an observed scatter comparable
to that of the Fundamental Plane (FP) relation, and carries
interesting information on the physical properties of galaxies and
their origin.
In the framework of a project aimed at investigating the optical-NIR
photometric properties of galaxies in the fields of ROSAT PSPC
extended sources, we have obtained multi-waveband data (BVRIK) for a
field of
![]() centered at
centered at
![]() and
and
![]() ,
at about 6.5' North (
,
at about 6.5' North (
![]() at
at ![]() with
with
![]() ,
,
![]() and
and
![]() )
)![]() of the
Abell cluster A 2163 at redshift z=0.201 (Arnaud et al. 1994). The
coordinates of this field correspond to the center of a secondary
extended emission in the X-ray map of A 2163, known as A 2163B
(Elbaz et al. 1995, hereafter EAB95), with an X-ray temperature
of the
Abell cluster A 2163 at redshift z=0.201 (Arnaud et al. 1994). The
coordinates of this field correspond to the center of a secondary
extended emission in the X-ray map of A 2163, known as A 2163B
(Elbaz et al. 1995, hereafter EAB95), with an X-ray temperature
![]() .
The cluster A 2163 (
.
The cluster A 2163 (
![]() ,
,
![]() )
)![]() is a very
rich and complex structure of galaxies, which has been extensively
studied for its exceptionally hot X-ray temperature,
is a very
rich and complex structure of galaxies, which has been extensively
studied for its exceptionally hot X-ray temperature,
![]() (see Markevitch et al. 1996, and references therein), and for its
huge radio halo, one of the most powerful known so far
(Feretti et al. 2001, hereafter FFG01). Our data show the presence of a
significant excess of galaxies at redshift
(see Markevitch et al. 1996, and references therein), and for its
huge radio halo, one of the most powerful known so far
(Feretti et al. 2001, hereafter FFG01). Our data show the presence of a
significant excess of galaxies at redshift
![]() in the field of
A 2163B, with a NIR spatial distribution typical for a cluster of
galaxies, with a main central overdensity and a secondary structure at
in the field of
A 2163B, with a NIR spatial distribution typical for a cluster of
galaxies, with a main central overdensity and a secondary structure at
![]() in the North-East direction.
in the North-East direction.
In the present work, we study the photometric and structural properties of the galaxy population of A 2163B, by discussing the constraints implied by our results on different galaxy evolution scenarios.
The layout of the paper is as follows. The data are presented in
Sect. 2, while the luminosity density map, the colour
magnitude relations and the K-band LF of A 2163B are studied in
Sect. 3. Cluster members are then selected by the
photometric redshift technique, as described in Sect. 4. The
derivation of structural parameters is outlined in Sect. 5. Section 6
deals with the comparison of structural parameters and with the
analysis of the internal colour gradients of galaxies. Sections 7 and 8
deal with the correlations between the structural parameters. In
Sect. 7, we attempt for the first time to perform an optical/NIR
comparative study of the
![]() -
-
![]() relation, while in Sect. 8 we
use the K-band data to analyze the PHP for the population of spheroids
in A 2163B. Discussion and conclusions follow in Sect. 9. Details on
data reduction are given in Appendix A, while the estimate of the
cluster redshift from the optical-NIR CM relations is detailed in
Appendix B. The catalogue, including all the photometric properties
of galaxies in the field of A 2163B, that is BVRIK total magnitudes,
colours, photometric redshifts and RIK structural parameters, is
described in Sect. 2.3.
relation, while in Sect. 8 we
use the K-band data to analyze the PHP for the population of spheroids
in A 2163B. Discussion and conclusions follow in Sect. 9. Details on
data reduction are given in Appendix A, while the estimate of the
cluster redshift from the optical-NIR CM relations is detailed in
Appendix B. The catalogue, including all the photometric properties
of galaxies in the field of A 2163B, that is BVRIK total magnitudes,
colours, photometric redshifts and RIK structural parameters, is
described in Sect. 2.3.
During three nights of run I, we obtained K-band imaging with the SOFI
instrument (pixel scale
![]() )
for a field of
)
for a field of
![]() .
The sky conditions were photometric for two nights and non
photometric for the third night. A total of 120 exposures were
collected, with a DIT of
.
The sky conditions were photometric for two nights and non
photometric for the third night. A total of 120 exposures were
collected, with a DIT of ![]() ,
,
![]() ,
and
a dithering box of
,
and
a dithering box of
![]() .
Due to the non photometric
conditions, only 85 exposures were retained, resulting in a total
integration time of
.
Due to the non photometric
conditions, only 85 exposures were retained, resulting in a total
integration time of
![]() .
Standard stars from
Persson et al. (1998) were observed during each night, each at five different
positions on the chip. In order to perform the illumination
correction (see Sect. A.2), we also observed a standard star at
different positions on a
.
Standard stars from
Persson et al. (1998) were observed during each night, each at five different
positions on the chip. In order to perform the illumination
correction (see Sect. A.2), we also observed a standard star at
different positions on a
![]() grid across the frame. In the
same period, we also obtained V-, R-, and I-band photometry with the
EMMI instrument for a region of
grid across the frame. In the
same period, we also obtained V-, R-, and I-band photometry with the
EMMI instrument for a region of
![]() (pixel scale
(pixel scale
![]() ), under non photometric conditions. On April 2002, the
field A 2163B was re-observed in B, V, R and I band with EMMI under
photometric conditions. The relevant information on the observations
are summarized in Table 1. The total exposure times amount to
600, 3000, 1200 and
), under non photometric conditions. On April 2002, the
field A 2163B was re-observed in B, V, R and I band with EMMI under
photometric conditions. The relevant information on the observations
are summarized in Table 1. The total exposure times amount to
600, 3000, 1200 and
![]() for the B, V, R and I bands,
respectively.
for the B, V, R and I bands,
respectively.
| Run | Date | Note | Waveband |
|
|
FWHM |
| (s) | ('') | |||||
| I | 25/08/2000 | NP | V | 3 | 900 | 1.3 |
| I | 24/08/2000 | NP | R | 2 | 450 | 1.0 |
| I | 26/08/2000 | NP | I | 2 | 450 | 1.0 |
| I | 08,10/09/2000 | P | K | 70 | 60 | 0.6-1.0 |
| I | 09/09/2000 | NP | K | 50 | 60 | 1.0 |
| II | 09/04/2002 | P | B | 2 | 300 | 1.5 |
| II | 09/04/2002 | P | V | 1 | 300 | 1.2 |
| II | 09/04/2002 | P | R | 1 | 300 | 0.9 |
| II | 09/04/2002 | P | I | 1 | 300 | 1.0 |
![\begin{figure}
\par\includegraphics[width=18cm,height=8.1cm,clip]{0157fi01.ps} \end{figure}](/articles/aa/full/2004/39/aa0157-04/Timg83.gif) |
Figure 1:
K-band image ( left panel) and luminosity-weighted map
( right panel) for the field of galaxies A 2163B. The image is
centered at
|
The BVRIK photometric catalogue for the N=131 galaxies with
photometric redshift estimate (see Sect. 4)![]() is shown in Table 2.
is shown in Table 2.
The catalogue is organized as follows. Two rows correspond to each galaxy. The first one provides the measured quantities, while the second one gives the relative uncertainties (one sigma standard intervals). All the photometric quantities have been corrected for galactic extinction by using the photometric redshift estimates and adopting E(B-V)=0.415, with the extinction law from SFD98. The typical uncertainties on the structural parameters are discussed in Sect. 6.1.
Column 1: running number of the catalogue.
Column 2: photometric redshift.
Columns 3, 4: right ascension and
declination referred to J2000. The astrometric solution was computed
by using a list of stars from the USNO catalogue. The rms of the
residuals to the astrometric solution is ![]() .
.
Columns
5-9: B-, V-, R-, I- and K-band total magnitudes.
Columns 10-13:
optical-NIR galaxy colours in the aperture of 3.5'' corrected for
seeing effects.
Columns 14-16: mean surface brightness
![]() within the effective radius
within the effective radius
![]() ,
logarithm of
,
logarithm of
![]() (in arcsec) and
Sersic index n for the R-band.
(in arcsec) and
Sersic index n for the R-band.
Columns 17-19: the same of
Cols. 14-16 for the I-band.
Columns 20-22: the same of Cols. 14-16 for the K-band.
Columns 23, 24: axis ratio and position
angle in degrees obtained from the K-band surface photometry.
In order to derive the redshift ![]() of the galaxy population of
A 2163B we compared the BVRIK photometry with predictions of
stellar population models from the GISSEL00 code (Bruzual & Charlot 1993). In
particular, we used (1) the optical-NIR colour magnitude (hereafter
CM) relations (Sect. 3.1); (2) the K-band LF
(Sect. 3.2) and (3) the photometric redshift technique
(Sect. 4). We point out that, although it is known that
broad-band colours are degenerate in age, metallicity and redshift,
and that uncertainties exist among stellar population models (e.g.
Charlot et al. 1996), the large wavelength baseline provided by our
photometry (from U to NIR restframe) and the use of the GISSEL
synthesis code allow to obtain a reliable redshift estimate of
galaxies at intermediate redshifts by using purely photometric
techniques, as shown by other studies (e.g., de Propris & Pritchet 1998;
Busarello et al. 2002; La Barbera et al. 2003c). Another important point for
estimating
of the galaxy population of
A 2163B we compared the BVRIK photometry with predictions of
stellar population models from the GISSEL00 code (Bruzual & Charlot 1993). In
particular, we used (1) the optical-NIR colour magnitude (hereafter
CM) relations (Sect. 3.1); (2) the K-band LF
(Sect. 3.2) and (3) the photometric redshift technique
(Sect. 4). We point out that, although it is known that
broad-band colours are degenerate in age, metallicity and redshift,
and that uncertainties exist among stellar population models (e.g.
Charlot et al. 1996), the large wavelength baseline provided by our
photometry (from U to NIR restframe) and the use of the GISSEL
synthesis code allow to obtain a reliable redshift estimate of
galaxies at intermediate redshifts by using purely photometric
techniques, as shown by other studies (e.g., de Propris & Pritchet 1998;
Busarello et al. 2002; La Barbera et al. 2003c). Another important point for
estimating ![]() is the effect of the galactic reddening E(B-V). The main sources for the reddening of the Milky Way are
based on
is the effect of the galactic reddening E(B-V). The main sources for the reddening of the Milky Way are
based on ![]() measurements from Burstein & Heiles (1984, hereafter BH84) and
on COBE/DIRBE and IRAS/ISSA FIR data from Schlegel et al. (1998, hereafter
SFD98). Generally, the estimates of E(B-V) from SFD98
are systematically higher than those of BH84. For A 2163B, BH84 and
SFD98 predict very different extinction values,
E(B-V)=0.18 and
E(B-V)=0.415, respectively. In the next section, we obtain a
simultaneous estimate of the galactic reddening as well as of the
cluster redshift from the optical-NIR colour magnitude relations.
This procedure gives an extinction value which is in remarkable
agreement with that of SFD98 and a redshift estimate of
measurements from Burstein & Heiles (1984, hereafter BH84) and
on COBE/DIRBE and IRAS/ISSA FIR data from Schlegel et al. (1998, hereafter
SFD98). Generally, the estimates of E(B-V) from SFD98
are systematically higher than those of BH84. For A 2163B, BH84 and
SFD98 predict very different extinction values,
E(B-V)=0.18 and
E(B-V)=0.415, respectively. In the next section, we obtain a
simultaneous estimate of the galactic reddening as well as of the
cluster redshift from the optical-NIR colour magnitude relations.
This procedure gives an extinction value which is in remarkable
agreement with that of SFD98 and a redshift estimate of
![]() ,
which concides within the uncertainties with that obtained from
the K-band LF (Sect. 3.2), for which extinction effects are
negligible. The difference between BH84 and SFD98 reddening values,
therefore, does not affect the present analysis.
,
which concides within the uncertainties with that obtained from
the K-band LF (Sect. 3.2), for which extinction effects are
negligible. The difference between BH84 and SFD98 reddening values,
therefore, does not affect the present analysis.
The zeropoints of the CM relation were used to obtain a simultaneous
estimate of the cluster redshift ![]() and of the galactic
reddening in the direction of A 2163, fitting the values of
and of the galactic
reddening in the direction of A 2163, fitting the values of
![]() with the colours expected from old stellar population
models (see Appendix B for details). In this approach, we took into
account the degeneracy among metallicity and the other stellar
population parameters exploiting the fact that the CM relation mainly
origins from a mass-metallicity relation (see Merluzzi et al. 2003 and
references therein). This procedure gives
with the colours expected from old stellar population
models (see Appendix B for details). In this approach, we took into
account the degeneracy among metallicity and the other stellar
population parameters exploiting the fact that the CM relation mainly
origins from a mass-metallicity relation (see Merluzzi et al. 2003 and
references therein). This procedure gives
![]() and
and
![]() .
It is quite remarkable that (1) the
estimate of E(B-V) is in very good agreement with that of SFD98,
E(B-V)=0.415; and (2) the value of
.
It is quite remarkable that (1) the
estimate of E(B-V) is in very good agreement with that of SFD98,
E(B-V)=0.415; and (2) the value of ![]() coincides with that
obtained from the K-band LF, which is virtually unaffected by galactic
reddening. For this reason, we adopted in the following
E(B-V)=0.415, and applied the corresponding absorption corrections to
our photometry
coincides with that
obtained from the K-band LF, which is virtually unaffected by galactic
reddening. For this reason, we adopted in the following
E(B-V)=0.415, and applied the corresponding absorption corrections to
our photometry![]() . Repeating the zeropoint fitting with
E(B-V)=0.415gives
. Repeating the zeropoint fitting with
E(B-V)=0.415gives
![]() ,
which is fully consistent with the redshift
of the main cluster structure (A 2163 ) at
,
which is fully consistent with the redshift
of the main cluster structure (A 2163 ) at
![]() .
.
We used these results in order to obtain a further estimate of the
redshift of A 2163B. The K-band LF was obtained by correcting our
number counts with field galaxy counts from the Calar Alto Deep
Imaging Survey (CADIS, see Huang et al. 2001), which is the largest
medium deep K-band survey to date, with a total area of
![]() and a completeness magnitude of
and a completeness magnitude of
![]() .
Since our
K-band photometry is complete down to
.
Since our
K-band photometry is complete down to
![]() (see
Sect. 2.2), the CADIS data are the most suitable dataset for
the estimate of field galaxy counts. The LF of A 2163B is shown in
Fig. 3. The error bars take into account Poissonian
uncertainties on both field and cluster counts, while the different
curves show the SF fits of the LF. In order to account for the finite
size of the magnitude bins, the fits were performed by the convolution
of a SF with the bin size. Following dPS99 and de Propris & Pritchet (1998, hereafter
dPP98), we fitted the galaxy counts down to
(see
Sect. 2.2), the CADIS data are the most suitable dataset for
the estimate of field galaxy counts. The LF of A 2163B is shown in
Fig. 3. The error bars take into account Poissonian
uncertainties on both field and cluster counts, while the different
curves show the SF fits of the LF. In order to account for the finite
size of the magnitude bins, the fits were performed by the convolution
of a SF with the bin size. Following dPS99 and de Propris & Pritchet (1998, hereafter
dPP98), we fitted the galaxy counts down to
![]() (
(
![]() ,
see below) by a SF with
,
see below) by a SF with
![]() ,
excluding the
three brightest cluster galaxies. The fit provided a good description
of the counts of bright galaxies
,
excluding the
three brightest cluster galaxies. The fit provided a good description
of the counts of bright galaxies![]() ,
giving the following estimate of the characteristic magnitude:
,
giving the following estimate of the characteristic magnitude:
![]() .
In order to estimate
.
In order to estimate ![]() ,
we
minimized the function:
,
we
minimized the function:
![\begin{displaymath}{
\chi^2= \left[ K^*_{0.9}(z)- K^*_{0.9} \right]^2,
}
\end{displaymath}](/articles/aa/full/2004/39/aa0157-04/img120.gif) |
(2) |
In order to study the faint end of the LF, we performed a SF fit for
![]() by treating both
by treating both ![]() and K* as free
parameters. As shown in Fig. 3, the SF, whose best-fit
parameters are
and K* as free
parameters. As shown in Fig. 3, the SF, whose best-fit
parameters are
![]() and
and
![]() ,
provides a good description of the LF of A 2163B. The cluster counts
show some deviation from the SF fit only for the two bins at
,
provides a good description of the LF of A 2163B. The cluster counts
show some deviation from the SF fit only for the two bins at
![]() and
and
![]() .
Although this could be an indication
of a bimodal behaviour of the LF, as found by previous studies (see
Mercurio et al. 2003, and references therein), the deviations are only at
the levels of
.
Although this could be an indication
of a bimodal behaviour of the LF, as found by previous studies (see
Mercurio et al. 2003, and references therein), the deviations are only at
the levels of ![]() and
and ![]() ,
respectively, and are
therefore not very significant. The value of
,
respectively, and are
therefore not very significant. The value of ![]() is in very good
agreement with the value of -1.18 found by Andreon (2001) for a rich
cluster of galaxies at z=0.3 in an area of
is in very good
agreement with the value of -1.18 found by Andreon (2001) for a rich
cluster of galaxies at z=0.3 in an area of
![]() ,
which is similar to that analyzed in the present study (
,
which is similar to that analyzed in the present study (
![]() ), and is also consistent with values of the faint end slope
of the NIR LF for the Coma cluster,
), and is also consistent with values of the faint end slope
of the NIR LF for the Coma cluster,
![]() (dPP98) and
(dPP98) and
![]() (Andreon & Pellò 2000), and for field galaxies,
(Andreon & Pellò 2000), and for field galaxies,
![]() (Kochanek et al. 2001). We also analyzed the dependence of the LF of A 2163B
on environment, by performing the SF fits separately for the
galaxies inside the higher density region, defined by the circles in
Fig. 1, and for the galaxies outside that region. The two
LFs are shown in Fig. 4 with the corresponding SF fits.
Interestingly, we found that the values of
(Kochanek et al. 2001). We also analyzed the dependence of the LF of A 2163B
on environment, by performing the SF fits separately for the
galaxies inside the higher density region, defined by the circles in
Fig. 1, and for the galaxies outside that region. The two
LFs are shown in Fig. 4 with the corresponding SF fits.
Interestingly, we found that the values of ![]() vary from
vary from
![]() (higher density) to
(higher density) to
![]() (lower density),
implying a steepening of the faint end slope at lower densities, in
agreement with the findings of other studies (see Haines et al. 2004,
and references therein). This steepening is due to the fact
that, as shown in Fig. 4, the lower density environment is
characterized by a higher fraction of faint galaxies, with a
significant difference (
(lower density),
implying a steepening of the faint end slope at lower densities, in
agreement with the findings of other studies (see Haines et al. 2004,
and references therein). This steepening is due to the fact
that, as shown in Fig. 4, the lower density environment is
characterized by a higher fraction of faint galaxies, with a
significant difference (
![]() )
in the low- and high- density
counts at
)
in the low- and high- density
counts at
![]() .
.
In order to select cluster members, we used the photometric redshift
technique, which has been proven to be an effective tool to estimate
the redshift of cluster galaxies at intermediate redshifts (e.g.
Busarello et al. 2002; La Barbera et al. 2003c, and references therein).
Photometric redshifts were estimated according to the Spectral Energy
Distribution fitting method (see Massarotti et al. 2001a,b, and references
therein). In order to achieve a reasonable accuracy, we considered
galaxies with signal-to-noise ratio
![]() in at least three
bands, limiting the sample to the N=131 galaxies brighter than
in at least three
bands, limiting the sample to the N=131 galaxies brighter than
![]() .
Since the percentage of galaxies
.
Since the percentage of galaxies![]() at redshift z > 1 with K < 17.5 is
expected to be negligible (
at redshift z > 1 with K < 17.5 is
expected to be negligible (![]() ), we looked for redshifts in the
range
), we looked for redshifts in the
range
![]() with a step of 0.01, imposing that at a given
redshift galaxy templates were younger than the age of the universe in
the adopted cosmology. We used the GISSEL00 code in order to produce
galaxy templates with a Scalo IMF and an exponential SFR
with a step of 0.01, imposing that at a given
redshift galaxy templates were younger than the age of the universe in
the adopted cosmology. We used the GISSEL00 code in order to produce
galaxy templates with a Scalo IMF and an exponential SFR
![]() .
The colours of E/S0, Sa/Sb, and Sc/Sd spectra were
modeled by choosing
.
The colours of E/S0, Sa/Sb, and Sc/Sd spectra were
modeled by choosing
![]() and
and
![]() ,
respectively,
while early-type galaxies with different metallicities were described
by using E/S0 models with
,
respectively,
while early-type galaxies with different metallicities were described
by using E/S0 models with
![]() ,
0.4, 1 and 2.5. The
differential dust extinction of the Milky Way was included in the
computation of model colours by adopting the extinction curve of
Cardelli et al. (1989) and a colour excess of
E(B-V)=0.415 (see
Sect. 3.1). The uncertainty on the photometric redshift
,
0.4, 1 and 2.5. The
differential dust extinction of the Milky Way was included in the
computation of model colours by adopting the extinction curve of
Cardelli et al. (1989) and a colour excess of
E(B-V)=0.415 (see
Sect. 3.1). The uncertainty on the photometric redshift ![]() was estimated by performing numerical simulations, taking
into account the measurement errors on galaxy colours. The mean value
of
was estimated by performing numerical simulations, taking
into account the measurement errors on galaxy colours. The mean value
of ![]() is
is
![]() ,
varying from
,
varying from
![]() at
at
![]() to
to
![]() at
at
![]() .
.
As shown in Fig. 5, the distribution of photometric
redshifts is dominated by the peak around
![]() ,
indicating
that most galaxies with
,
indicating
that most galaxies with
![]() are actually cluster members.
Applying the bi-weight statistics, we obtained the following estimate
of the cluster redshift:
are actually cluster members.
Applying the bi-weight statistics, we obtained the following estimate
of the cluster redshift:
![]() ,
in agreement
with the values obtained in Sects. 3.1 and 3.2.
Galaxies with photometric redshift in a range of
,
in agreement
with the values obtained in Sects. 3.1 and 3.2.
Galaxies with photometric redshift in a range of
![]() around
around ![]() were defined as cluster members, resulting in a
final list of N=102 objects
were defined as cluster members, resulting in a
final list of N=102 objects![]() . This value is in good agreement with
that predicted from the LF of cluster galaxies, N=112 (see
Sect. 3.2).
. This value is in good agreement with
that predicted from the LF of cluster galaxies, N=112 (see
Sect. 3.2).
Surface photometry was derived for all the galaxies brighter than
![]() in the R and I bands, and for the galaxies brighter than
in the R and I bands, and for the galaxies brighter than
![]() in the K band. These selection criteria were chosen
in order to obtain reliable structural parameters from the A 2163B
photometry, and were the results of numerical simulations performed as
described in LBM02. A further selection was performed a
posteriori by excluding few faint galaxies in the I and K bands
because of the strong contamination from close stars. The resulting
samples include N=64, 62 and 58 galaxies for the R, I and K bands, respectively, with N=62 objects in common between the Rand I bands, and N=58 galaxies in common between the R and K bands. Structural parameters for these galaxies are given in the
catalogue (see Sect. 2.3).
in the K band. These selection criteria were chosen
in order to obtain reliable structural parameters from the A 2163B
photometry, and were the results of numerical simulations performed as
described in LBM02. A further selection was performed a
posteriori by excluding few faint galaxies in the I and K bands
because of the strong contamination from close stars. The resulting
samples include N=64, 62 and 58 galaxies for the R, I and K bands, respectively, with N=62 objects in common between the Rand I bands, and N=58 galaxies in common between the R and K bands. Structural parameters for these galaxies are given in the
catalogue (see Sect. 2.3).
Galaxy images were fitted with 2D models convolved with the PSF, as
detailed in LBM02. As shown in that paper, the 2D approach allows
reliable structural parameters to be obtained for galaxies at
intermediate redshifts (
![]() )
from ground based data taken
under ordinary observing conditions (seeing
)
from ground based data taken
under ordinary observing conditions (seeing
![]() and
pixel scale
and
pixel scale
![]() ).
Galaxy models were parametrized by the Sersic law:
).
Galaxy models were parametrized by the Sersic law:
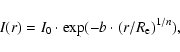 |
(3) |
![\begin{figure}
\par\includegraphics[angle=0,width=13.7cm,height=11.7cm,clip]{0157fi06.ps} \end{figure}](/articles/aa/full/2004/39/aa0157-04/Timg173.gif) |
Figure 6: 2D fits of galaxies in the K-band image. For each plot, from left to right, the galaxy image, the 2D model and the residual map are shown. The size of the horizontal white bar is 5''. |
Figure 6
plots, as an example, the K-band 2D fitting of some galaxies in the
cluster field. The models turned out to give a very good description
of the galaxy images.
![\begin{figure}
\par\includegraphics[angle=0,width=10cm,height=10cm,clip]{0157fi08.ps} \end{figure}](/articles/aa/full/2004/39/aa0157-04/Timg176.gif) |
Figure 8: Same of Fig. 7 for the R- and K-band parameters. |
Differences between R- and K-band structural parameters are shown in
Fig. 8. We note that the differences of mean surface
brightnesses,
![]() ,
were obtained by
subtracting the R-K galaxy colours, that is:
,
were obtained by
subtracting the R-K galaxy colours, that is:
![]() .
The mean values of the distributions show that cluster galaxies are
more concentrated in the NIR than in the optical, having NIR effective
radii which are on average
.
The mean values of the distributions show that cluster galaxies are
more concentrated in the NIR than in the optical, having NIR effective
radii which are on average
![]() smaller than in the R-band
(
smaller than in the R-band
(
![]() ), and Sersic indices slightly
larger in the K band, although the last difference is not very
significant. The mean difference of
), and Sersic indices slightly
larger in the K band, although the last difference is not very
significant. The mean difference of
![]() can be fully explained by using the definition of total magnitude
can be fully explained by using the definition of total magnitude
![]() ,
and
computing the difference between R- and K-band total magnitudes:
,
and
computing the difference between R- and K-band total magnitudes:
The dispersion of the distributions in Fig. 8 is due (1) to
the uncertainties on both the R- and K-band parameters; and (2) to
the intrinsic scatter of the optical-NIR properties of galaxies. We
verified by numerical simulations (performed as described in LBM02)
that the uncertainties on the K-band structural parameters are as
large as or smaller than those estimated for the optical wavebands.
This suggests that the dispersions of the histograms in
Fig. 8 have mainly an intrinsic origin. In Sects. 7
and 8, in order to describe the uncertainties on
![]() ,
,
![]() and
and ![]() ,
we adopted the same covariance matrix for both the
optical and the NIR data. By looking at Fig. 8, we stress
again the small dispersion in the
,
we adopted the same covariance matrix for both the
optical and the NIR data. By looking at Fig. 8, we stress
again the small dispersion in the
![]() variable, that amounts to
variable, that amounts to
![]() .
.
The distributions of colour gradients for the galaxies of A 2163B
are shown in Fig. 9, we wrote the R-I and R-K colour gradients as V-R and V-K restframe gradients,
respectively. By using different galaxy templates from the GISSEL00
code, we verified, in fact, that the conversion from R-I (R-K) at z=0.2 into V-R (V-K) at z=0 is
independent of the spectral type (for ![]() ), with
), with ![]() variations of 0.01 and
variations of 0.01 and
![]() between different spectral
models for the optical-optical and the optical-NIR colours,
respectively. As expected on the basis of the structural parameters,
galaxies show optical-optical colour gradients which are fully
consistent with zero, while the V-K colour gradients are negative for
most galaxies, implying that their SPs are on average redder in the
center. The mean value of the optical-NIR gradient is -0.48, which
implies that galaxies become
between different spectral
models for the optical-optical and the optical-NIR colours,
respectively. As expected on the basis of the structural parameters,
galaxies show optical-optical colour gradients which are fully
consistent with zero, while the V-K colour gradients are negative for
most galaxies, implying that their SPs are on average redder in the
center. The mean value of the optical-NIR gradient is -0.48, which
implies that galaxies become
![]() bluer per decade of
radius toward the periphery. The value of grad(V-K) is fully
consistent with the colour gradient estimate of LBM03a (
bluer per decade of
radius toward the periphery. The value of grad(V-K) is fully
consistent with the colour gradient estimate of LBM03a (
![]() ).
).
![\begin{figure}
\par\includegraphics[angle=0,width=12.2cm,height=6.2cm,clip]{0157fi09.ps} \end{figure}](/articles/aa/full/2004/39/aa0157-04/Timg202.gif) |
Figure 9: Distributions of V-R and V-K colour gradients. The mean values are marked by a solid line. |
The
![]() -
-
![]() diagrams for the galaxies of A 2163B are shown in
Fig. 10 for the R and K bands. We note that the I-band data
provide almost the same spectral information as the R-band photometry,
and therefore are not discussed in the following. For each band, we
excluded the disks (n < 2) and the galaxies for which the total
magnitude estimated by the structural parameters is fainter than the
completeness magnitude. This selection results in N=52 and N=53 galaxies in the R and K bands, respectively. For what concerns
the NIR data, we also excluded two galaxies that have small radii and
low surface brightness and for which, therefore, structural parameters
are possibly affected by a larger uncertainty. The K-band sample
consists of N=51 objects.
In order to describe the
diagrams for the galaxies of A 2163B are shown in
Fig. 10 for the R and K bands. We note that the I-band data
provide almost the same spectral information as the R-band photometry,
and therefore are not discussed in the following. For each band, we
excluded the disks (n < 2) and the galaxies for which the total
magnitude estimated by the structural parameters is fainter than the
completeness magnitude. This selection results in N=52 and N=53 galaxies in the R and K bands, respectively. For what concerns
the NIR data, we also excluded two galaxies that have small radii and
low surface brightness and for which, therefore, structural parameters
are possibly affected by a larger uncertainty. The K-band sample
consists of N=51 objects.
In order to describe the
![]() -
-
![]() sequence, we consider the
following equation for each waveband
sequence, we consider the
following equation for each waveband ![]() :
:
The
other panels of Fig. 12 show different projections of the
so-called Photometric Plane (PHP). For comparison with GRA02, we
adopted the following representation of the PHP:
The slopes and the scatter of the
NIR PHP at
![]() turn out to be in remarkable agreement
with those derived by GRA02 for galaxies in the Fornax and Virgo
clusters:
turn out to be in remarkable agreement
with those derived by GRA02 for galaxies in the Fornax and Virgo
clusters:
![]() ,
,
![]() and
and
![]() .
We point out that the magnitude
selection significantly affects the
.
We point out that the magnitude
selection significantly affects the ![]() coefficient and that,
therefore, it would be very interesting to use a sample of galaxies
spanning a larger magnitude range in order to better constrain this
coefficient. The selection effects can be further illustrated by
looking at the face-on projection of the PHP in Fig. 12d.
Due to the finite dispersion of the galaxies around the PHP, its
intersection with the plane
coefficient and that,
therefore, it would be very interesting to use a sample of galaxies
spanning a larger magnitude range in order to better constrain this
coefficient. The selection effects can be further illustrated by
looking at the face-on projection of the PHP in Fig. 12d.
Due to the finite dispersion of the galaxies around the PHP, its
intersection with the plane
![]() results in a "strip'', whose
"upper'' border marks the limits of the dashed area in
Fig. 12d. As consequence, the distribution of galaxies in
this area is not "complete''.
results in a "strip'', whose
"upper'' border marks the limits of the dashed area in
Fig. 12d. As consequence, the distribution of galaxies in
this area is not "complete''.
In order to estimate the intrinsic
dispersions of the
![]() -
-![]() relation and of the PHP, we
subtracted to the observed dispersion in
relation and of the PHP, we
subtracted to the observed dispersion in
![]() the amount of scatter
expected from the measurement errors on the observed parameters,
taking into account the covariance terms between the uncertainties on
the amount of scatter
expected from the measurement errors on the observed parameters,
taking into account the covariance terms between the uncertainties on
![]() ,
,
![]() and
and ![]() .
The intrinsic dispersions of the
.
The intrinsic dispersions of the
![]() -
-![]() relation and of the PHP turn out to be
relation and of the PHP turn out to be
![]() and
and
![]() ,
respectively. Interestingly, we find that the
measurement errors account only for few percents of the observed
dispersion around the PHP, because, as shown in Fig. 12b,
their correlation is almost parallel to the plane, in the same way as
for the KR.
,
respectively. Interestingly, we find that the
measurement errors account only for few percents of the observed
dispersion around the PHP, because, as shown in Fig. 12b,
their correlation is almost parallel to the plane, in the same way as
for the KR.
The K-band luminosity density map of A 2163B presents a main
central overdensity of radius
![]() ,
and a secondary
structure
,
and a secondary
structure
![]() from the center. The colour-magnitude
diagrams show a sharp red sequence whose slope flattens at longer
wavelengths: galaxy colours become bluer by
from the center. The colour-magnitude
diagrams show a sharp red sequence whose slope flattens at longer
wavelengths: galaxy colours become bluer by
![]() per
magnitude in the B-K vs.
per
magnitude in the B-K vs. ![]() diagrams, and by
diagrams, and by
![]() in the I-K vs.
in the I-K vs. ![]() plane. These values
agree with the predictions of a mass-metallicity model of the CM relation (KAB98). By introducing a suitable procedure to account for
the Milky Way reddening, we find that the zeropoints of the CM
sequence are consistent with those expected for a red galaxy
population at redshift
plane. These values
agree with the predictions of a mass-metallicity model of the CM relation (KAB98). By introducing a suitable procedure to account for
the Milky Way reddening, we find that the zeropoints of the CM
sequence are consistent with those expected for a red galaxy
population at redshift
![]() ,
implying that A 2163B is a
cluster of galaxies likely involved in a merging event with A 2163. The value of
,
implying that A 2163B is a
cluster of galaxies likely involved in a merging event with A 2163. The value of ![]() is also confirmed by the analysis of
the K-band LF and by the photometric redshift technique, which is used
to select cluster members. The luminosity segregation of A 2163B
is investigated by means of the K-band LF. The global LF is well
described by a single Schecter function with a faint end slope of
is also confirmed by the analysis of
the K-band LF and by the photometric redshift technique, which is used
to select cluster members. The luminosity segregation of A 2163B
is investigated by means of the K-band LF. The global LF is well
described by a single Schecter function with a faint end slope of
![]() ,
in agreement with other studies of the NIR LF both in
clusters and in the field (e.g. Andreon 2001; Kochanek et al. 2001). On the other hand, the faint end slope depends on
environment, varying from about -1 in the two higher density clumps,
to about -1.4 into the outer region, implying that the population of
dwarf galaxies is less abundant in the denser environments. This
behaviour of the LF suggests that some mechanism, such as tidal
disruption or cannibalism, is working in the higher density
environments, decreasing the number of faint galaxies (Haines et
al. 2004).
,
in agreement with other studies of the NIR LF both in
clusters and in the field (e.g. Andreon 2001; Kochanek et al. 2001). On the other hand, the faint end slope depends on
environment, varying from about -1 in the two higher density clumps,
to about -1.4 into the outer region, implying that the population of
dwarf galaxies is less abundant in the denser environments. This
behaviour of the LF suggests that some mechanism, such as tidal
disruption or cannibalism, is working in the higher density
environments, decreasing the number of faint galaxies (Haines et
al. 2004).
Surface photometry has been derived in the R, I and K bands for ![]() cluster galaxies, and has been used:
cluster galaxies, and has been used:
The population of spheroids in A 2163B
has null colour gradients at optical wavelengths (V-Rrestframe) and optical-NIR gradients that are significantly negative
(
![]() ), consistently with the quoted
differences among the effective radii. As shown by LBM03a, the
optical-NIR gradients do not evolve significantly with redshift,
amounting to
), consistently with the quoted
differences among the effective radii. As shown by LBM03a, the
optical-NIR gradients do not evolve significantly with redshift,
amounting to
![]() .
As detailed in that work, the redshift
dependence of both optical-NIR and UV-optical colour gradients
strongly constrains the age and metallicity of the inner and outer
galaxy stellar populations. Using the colour gradient model of LBM03a
(see model Z1, Table 6), the quoted colour gradients imply a
metallicity gradient in spheroids of
.
As detailed in that work, the redshift
dependence of both optical-NIR and UV-optical colour gradients
strongly constrains the age and metallicity of the inner and outer
galaxy stellar populations. Using the colour gradient model of LBM03a
(see model Z1, Table 6), the quoted colour gradients imply a
metallicity gradient in spheroids of
![]() per decade
of radius. This result is in agreement with that reported from other
studies of colour gradients for both nearby and intermediate redshift
galaxies (Idiart et al. 2002; Saglia et al. 2000).
per decade
of radius. This result is in agreement with that reported from other
studies of colour gradients for both nearby and intermediate redshift
galaxies (Idiart et al. 2002; Saglia et al. 2000).
Monolithic collapse models predict that early-type galaxies are more metal rich in the center than in the outskirts. During galaxy formation, the gas dissipates its kinetic energy carrying the heavy elements ejected from the evolved stars into the inner region (Larson 1974). Numerical simulations predict a metal abundance gradient of about -0.5 (e.g. Carlberg 1984; Kawata 2001, see their models B1/B2 which correspond to the magnitude range of our samples). This value is not consistent with our results, although some caution is needed due to scatter present both in the observed data and in the simulation results (see Kawata 2001). The difference of observed and predicted metallicity gradients suggests that gas dissipation has a minor role in monolithic collapse models. We note, however, that dissipation is required in order to reproduce the mass-metallicity relation of early-type galaxies and their moderate orbital anisotropies. We argue, therefore, that some tuning of the parameters driving the physics of gas dissipation would be required in order to fit all the observed properties into the monolithic scenario. A likely explanation of the observed metallicity gradients resides in the merging processes, which mix the SPs inside galaxies. It has been shown that both dissipationless merging of spheroidal systems (White 1980) and dissipative merging of disk galaxies (Bekki & Shioya 2001) produce more shallow stellar population gradients.
The slope and the zeropoint of the optical
![]() -
-
![]() relation are
consistent with those obtained in LBM03b. For what concerns the NIR
KR, we compared its slope and zeropoint with the optical values by
taking into account (i) the colour magnitude relation; and (ii) the
mean value of the ratio of optical/NIR effective radii. These factors
fully explain the difference among the optical and NIR zeropoints.
The most interesting result is that the slope of the R-band KR,
corrected for the effects (i) and (ii), is lower by
relation are
consistent with those obtained in LBM03b. For what concerns the NIR
KR, we compared its slope and zeropoint with the optical values by
taking into account (i) the colour magnitude relation; and (ii) the
mean value of the ratio of optical/NIR effective radii. These factors
fully explain the difference among the optical and NIR zeropoints.
The most interesting result is that the slope of the R-band KR,
corrected for the effects (i) and (ii), is lower by
![]() than the K-band value. We show that this difference can be explained
if the ratio of optical to NIR effective radii (the optical/NIR colour
gradient) decreases (flattens) for larger galaxies. A direct
inspection of the
than the K-band value. We show that this difference can be explained
if the ratio of optical to NIR effective radii (the optical/NIR colour
gradient) decreases (flattens) for larger galaxies. A direct
inspection of the
![]() and the grad(V-K) vs.
and the grad(V-K) vs.
![]() diagrams shows that such trend exists. Our data do
not favour a steepening of colour gradients with galaxy size, that
would imply a larger discrepancy between the R- and K-band KR slopes.
A steepening of colour gradients with galaxy luminosity (size)
is a natural expectation of the monolithic collapse model, due to the
galactic wind mechanism (Larson 1974). The galactic wind blows early
in less massive galaxies, preventing gas dissipation to carry heavy
metals in the center, and producing, therefore, a less steep gradient
in these systems. A steepening of colour gradients with galaxy
luminosity has been unfruitfully looked for by various studies (e.g.
Peletier et al. 1990a; Bartholomew et al. 2001). Recently, Tamura & Ohta (2003) measured
the optical colour gradients for N=36 galaxies at
diagrams shows that such trend exists. Our data do
not favour a steepening of colour gradients with galaxy size, that
would imply a larger discrepancy between the R- and K-band KR slopes.
A steepening of colour gradients with galaxy luminosity (size)
is a natural expectation of the monolithic collapse model, due to the
galactic wind mechanism (Larson 1974). The galactic wind blows early
in less massive galaxies, preventing gas dissipation to carry heavy
metals in the center, and producing, therefore, a less steep gradient
in these systems. A steepening of colour gradients with galaxy
luminosity has been unfruitfully looked for by various studies (e.g.
Peletier et al. 1990a; Bartholomew et al. 2001). Recently, Tamura & Ohta (2003) measured
the optical colour gradients for N=36 galaxies at ![]() .
They found that the optical colour gradient of very bright
early-types (
.
They found that the optical colour gradient of very bright
early-types (
![]() )
can steepen with galaxy luminosity,
while an opposite trend was suggested for fainter galaxies. A similar
bimodal behaviour was found by (Balcells & Peletier 1994) for the colour gradients
of early-type spiral bulges. We note that our data do not allow us to
distinguish the behaviour of colour gradients for the very bright
early-types, while they allow a larger magnitude range in both optical
and NIR to be analyzed. In hierarchical merging models, more massive
galaxies form from larger disk systems, which have stronger internal
gradients. Since merging dilutes the stellar population gradients
(White 1980), if galaxies with larger size have experienced a higher
merging rate (Capaccioli et al. 1992), their colour profile can be as flat as or
even less steep than those of smaller systems. The data of A 2163B
seem to favour this interpretation.
)
can steepen with galaxy luminosity,
while an opposite trend was suggested for fainter galaxies. A similar
bimodal behaviour was found by (Balcells & Peletier 1994) for the colour gradients
of early-type spiral bulges. We note that our data do not allow us to
distinguish the behaviour of colour gradients for the very bright
early-types, while they allow a larger magnitude range in both optical
and NIR to be analyzed. In hierarchical merging models, more massive
galaxies form from larger disk systems, which have stronger internal
gradients. Since merging dilutes the stellar population gradients
(White 1980), if galaxies with larger size have experienced a higher
merging rate (Capaccioli et al. 1992), their colour profile can be as flat as or
even less steep than those of smaller systems. The data of A 2163B
seem to favour this interpretation.
Finally, we have analyzed the so-called Photometric Plane (PHP) of
spheroids at
![]() .
We find that galaxies follow a
bivariate relation between K-band effective parameters and the
logarithm of the Sersic index:
.
We find that galaxies follow a
bivariate relation between K-band effective parameters and the
logarithm of the Sersic index:
![]() .
Accounting for the correlations
among the uncertainties on structural parameters as well as for the
selection effects, we find
.
Accounting for the correlations
among the uncertainties on structural parameters as well as for the
selection effects, we find
![]() and
and
![]() ,
and an observed dispersion of
,
and an observed dispersion of
![]() in
in
![]() .
These values are consistent with the optical PHP coefficients
found by GRA02 for early-types in the Fornax and Coma clusters. We
have discussed how the magnitude cut affects the distribution of
galaxies in the space of the structural parameters: the
.
These values are consistent with the optical PHP coefficients
found by GRA02 for early-types in the Fornax and Coma clusters. We
have discussed how the magnitude cut affects the distribution of
galaxies in the space of the structural parameters: the ![]() term
of the PHP turns out to be significantly affected by the magnitude
selection, indicating that it would be very interesting to analyze a
larger, deeper sample of galaxies to further constrain the
coefficients of this relation. Interestingly, we find that the
correlation of the uncertainties on the structural parameters is
almost parallel to the PHP, analogously to what happens for the KR.
This implies that the intrinsic scatter of the PHP amounts to about
term
of the PHP turns out to be significantly affected by the magnitude
selection, indicating that it would be very interesting to analyze a
larger, deeper sample of galaxies to further constrain the
coefficients of this relation. Interestingly, we find that the
correlation of the uncertainties on the structural parameters is
almost parallel to the PHP, analogously to what happens for the KR.
This implies that the intrinsic scatter of the PHP amounts to about
![]() ,
which is only few percents smaller than the observed
scatter, but
,
which is only few percents smaller than the observed
scatter, but
![]() lower than that of the KR (
lower than that of the KR (
![]() ). Therefore, although the observed scatter around the plane
seems to be similar to that of the spectroscopic Fundamental Plane
(
). Therefore, although the observed scatter around the plane
seems to be similar to that of the spectroscopic Fundamental Plane
(
![]() )
as found by GRA02, the present data indicate that
its intrinsic dispersion can be significantly larger. This point will
have to be further analyzed by studying samples of galaxies for which
both velocity dispersions and Sersic indices are available.
)
as found by GRA02, the present data indicate that
its intrinsic dispersion can be significantly larger. This point will
have to be further analyzed by studying samples of galaxies for which
both velocity dispersions and Sersic indices are available.
Instrumental
magnitudes for the Landolt stars were computed within an aperture of
diameter 10'' by means of S-Extractor (Bertin & Arnout 1996). For each band,
in order to obtain the zeropoint and the colour term of the
photometric calibration, we performed a robust least square
fit. Colour terms were found to be small and were neglected, while the
zeropoints turned out to be
![]() ,
,
![]() ,
,
![]() ,
,
![]() (scaled to 1 s exposure time).
(scaled to 1 s exposure time).
| (B.1) |
![\begin{displaymath}{ \chi^2 [ z_{\rm c}, z_{\rm f}, E(B-V) ] = \sum_M \left[ \Gamma_{K_\odot{(z)}}-
(N-K)_t + (A_N-A_K) \right]^2 }
\end{displaymath}](/articles/aa/full/2004/39/aa0157-04/img312.gif) |
(B.2) |