In this paper, we have made an accurate investigation of proton acceleration in GRBs and we have predicted a possible signature of cosmic rays, in a sufficiently baryon-loaded fireball, via GeV
D. Gialis 1 - G. Pelletier1,2
1 - Laboratoire d'Astrophysique de Grenoble, 414 rue de la Piscine, Domaine Universitaire, BP 53, 38041 Grenoble Cedex 9, France
2 -
Institut Universitaire de France
Received 10 September 2003 / Accepted 27 February 2004
Abstract
In this paper, we have made an accurate investigation of proton acceleration in GRBs and we have predicted a possible signature of cosmic rays, in a sufficiently baryon-loaded fireball, via GeV ![]() -ray emission produced by
-ray emission produced by ![]() -meson decay. If two ungrounded assumptions are removed, namely, Bohm's scaling and a slow magnetic field decrease, the usual Fermi processes are unable to generate ultra high energy cosmic rays (UHECRs) in GRBs. We propose to develop another scenario of relativistic Fermi acceleration in the internal shock stage. We present the results of a realistic Monte-Carlo simulation of a multi-front acceleration which clearly shows the possible generation of UHECR. The amount of energy converted into UHECRs turns out to be a sizeable fraction of the magnetic energy.
-meson decay. If two ungrounded assumptions are removed, namely, Bohm's scaling and a slow magnetic field decrease, the usual Fermi processes are unable to generate ultra high energy cosmic rays (UHECRs) in GRBs. We propose to develop another scenario of relativistic Fermi acceleration in the internal shock stage. We present the results of a realistic Monte-Carlo simulation of a multi-front acceleration which clearly shows the possible generation of UHECR. The amount of energy converted into UHECRs turns out to be a sizeable fraction of the magnetic energy.
Key words: gamma rays: bursts - ISM: cosmic rays - acceleration of particles
Gamma Ray Bursts (hereafter GRBs) have been considered as promising sources of Ultra High Energy Cosmic Rays (UHECRs) either through the external ultrarelativistic shock (Vietri 1995) or through the internal shocks (Waxman 1995). The acceleration at the external shock does not achieve this goal when the external medium is a standard interstellar medium (Gallant & Achterberg 1999). As for the internal shocks, first and second order Fermi processes would achieve this goal with the extreme assumption of a cosmic ray mean free path of the order of its Larmor radius (so-called Bohm's scaling). In a previous paper (Gialis & Pelletier 2003), we have shown that such scaling is physically inconsistent for two reasons; first, the law is not validated by numerical simulations (Casse et al. 2001) and second, even if inappropriately used, it would lead to tremendously fast magnetic energy depletion in the fireball. We also have considered a more realistic Kolmogorov scaling but a severe expansion loss limitation does not make it possible. These arguments are developed in Sects. 2 and 3 of this paper, together with the important issue of the magnetic field profile. Because both the global energy budget of the fireball and the Hillas criterium are in favour of the generation of UHECRs, we have made a detailed investigation of a different Fermi process proposed by Pelletier & Kersalé (2000) and Pelletier (1999). In this kind of Fermi process, reviewed in Sect. 4, the sheets invoked in the internal shock model are considered as relativistic hydromagnetic fronts that scatter cosmic rays. Thus, cosmic rays undergo a relativistic Fermi acceleration, similar to a kind of second order process through multiple interactions with all the fronts in the relativistic wind. Actually, this is not a second order Fermi process because no expansion is allowed in the relativistic regime, the energy jump being large at each scattering. The generation of cosmic rays resulting from these multiple scatterings is very different from generation obtained by a superposition of the individual first order contributions of each shock.
In Sect. 5 we describe a realistic Monte-Carlo simulation of this process, taking into account several dynamical parameters in a conical expanding fireball, for several intensities and profiles of the average magnetic field. The results are presented in Sect. 6; they suggest a good efficiency of the process of acceleration of UHECRs and give a prediction of the time at which they are created during the internal shock stage. Finally, we establish a possible diagnosis of cosmic rays in GRBs through ![]() -ray emission by
-ray emission by ![]() -meson decay which would be easily detected by HESS observatory, 5@5 experiment and GLAST.
-meson decay which would be easily detected by HESS observatory, 5@5 experiment and GLAST.
The goal of the generation oif UHECRs in GRBs is to reach a maximum energy close to the confinement energy limit above which the Larmor radius becomes larger than the correlation length of the magnetic field, namely
The Fermi acceleration of supra-thermal particles at the external ultrarelativistic shock was suggested by Vietri (1995) and it has recently been reviewed by Vietri et al. (2003). As mentioned before, a 100 G magnetic field is required to obtain UHECRs. If the usual interstellar medium is considered, with a ![]() G magnetic field, even with the shortening of the acceleration time due to the ultrarelativistic shockfront, namely
G magnetic field, even with the shortening of the acceleration time due to the ultrarelativistic shockfront, namely
![]() ,
as shown by Gallant & Achterberg (1999), UHECRs cannot be produced. Moreover the amplification of the pre-existing cosmic ray distribution does not provide enough UHECR flux. The only hope is through the consideration of a different external medium, as for instance a pulsar wind bubble such as considered by Gallant & Achterberg (1999).
,
as shown by Gallant & Achterberg (1999), UHECRs cannot be produced. Moreover the amplification of the pre-existing cosmic ray distribution does not provide enough UHECR flux. The only hope is through the consideration of a different external medium, as for instance a pulsar wind bubble such as considered by Gallant & Achterberg (1999).
The internal shock model has been designed (Mészáros et al. 1993) to account for variability observed in the light curve. Indeed millisecond variability, as observed in some GRB light curves, cannot be explained in the framework of a single sheet colliding with the interstellar medium. The most interesting feature of the multiple sheet model is that the time variability at the origin of the flow is observable thanks to the following scheme. Let us consider two sheets that leave the central engine separated by a time interval ![]() ,
respectively with Lorentz factor
,
respectively with Lorentz factor
![]() and
and
![]() .
A collision occurs when
.
A collision occurs when
![]() at a time
that can be expressed by
at a time
that can be expressed by
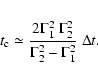
The Fermi acceleration (first or second order) in the internal shock model is usually considered (Waxman 1995) as mildly or sub-relativistic with a characteristic time proportional to the Larmor radius (Bohm scaling). However, in a recent paper (Gialis & Pelletier 2003), we have shown that this assumption is not realistic regarding the magnetic energy depletion time. Moreover, the Fermi acceleration time depends on the mean free path,
![]() ,
of the particle in an irregular magnetic field. This length depends on two other lengths, namely the Larmor radius,
,
of the particle in an irregular magnetic field. This length depends on two other lengths, namely the Larmor radius, ![]() ,
and the correlation length,
,
and the correlation length,
![]() :
for a turbulence spectrum of magnetic perturbations that follows a power law of index
:
for a turbulence spectrum of magnetic perturbations that follows a power law of index ![]() the following law, which is known in weak turbulence theory, has been extended into the regime of strong turbulence and large rigidities such that
the following law, which is known in weak turbulence theory, has been extended into the regime of strong turbulence and large rigidities such that
![]() (Casse et al. 2001):
(Casse et al. 2001):
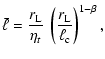 |
(3) |
According to a Kolmogorov scaling with
![]() ,
we have shown (Gialis & Pelletier 2003) that GRBs are unable to produce UHECRs with this acceleration process because of a strong expansion limitation in energy
,
we have shown (Gialis & Pelletier 2003) that GRBs are unable to produce UHECRs with this acceleration process because of a strong expansion limitation in energy
The flow that reaches the beginning of the acceleration range is disconnected from the source if
![]() .
In that case, the sheets that compose the flow start to expand with carrying a magnetic field that decays like r-2, as argued by Mészáros et al. (1993). This is the most severe assumption on the evolution of the magnetic field in the attempt to accelerate particles. Some authors (Waxman 2003) claimed that it decays like r-1, because this would be consistent with the synchrotron interpretation of the GRB spectrum; this would require an amplification of the magnetic field in the vicinity of the shocks. We think that this would occur only in narrow layers behind the internal shocks and would be beneficial for electron acceleration. As for the high energy protons, especially those candidates for UHECRs, they necessarily explore a major part of the flow because of their large Larmor radii, and they experience a magnetic field that decays faster than r-1, unless the flow is still connected with the source and carries a current associated with a toroidal field. In computations, for the sake of compromise, we have considered a field that decays like r-3/2, which means that the magnetic energy is conserved in the shells. However, to demonstrate the capability of GRBs to produce UHECRs, we will also investigate the conservative case of a magnetic field decaying like r-2.
.
In that case, the sheets that compose the flow start to expand with carrying a magnetic field that decays like r-2, as argued by Mészáros et al. (1993). This is the most severe assumption on the evolution of the magnetic field in the attempt to accelerate particles. Some authors (Waxman 2003) claimed that it decays like r-1, because this would be consistent with the synchrotron interpretation of the GRB spectrum; this would require an amplification of the magnetic field in the vicinity of the shocks. We think that this would occur only in narrow layers behind the internal shocks and would be beneficial for electron acceleration. As for the high energy protons, especially those candidates for UHECRs, they necessarily explore a major part of the flow because of their large Larmor radii, and they experience a magnetic field that decays faster than r-1, unless the flow is still connected with the source and carries a current associated with a toroidal field. In computations, for the sake of compromise, we have considered a field that decays like r-3/2, which means that the magnetic energy is conserved in the shells. However, to demonstrate the capability of GRBs to produce UHECRs, we will also investigate the conservative case of a magnetic field decaying like r-2.
Because we will need some magnetic field intensity at the beginning of the acceleration range, we need to assume
![]() G at the black hole scale
G at the black hole scale
![]() cm. However, for the work presented in this paper, we do not consider a situation where the magnetic field would dominate during the adiabatic expansion. The case of a magnetic field dominated expansion is interesting from the point of view of particle acceleration, but requires different modeling, postponed for future work.
cm. However, for the work presented in this paper, we do not consider a situation where the magnetic field would dominate during the adiabatic expansion. The case of a magnetic field dominated expansion is interesting from the point of view of particle acceleration, but requires different modeling, postponed for future work.
In this paper, we will introduce an acceleration process additionnal to the usual internal shock acceleration. However we will consider this additionnal process as operating above 1 GeV and below the expansion cut off mentioned in Sect. 2.2 (see Eq. (4)). This yields an
![]() -spectrum in the frame
-spectrum in the frame
![]() moving with a Lorentz factor
moving with a Lorentz factor ![]() ,
in which the distribution function is almost isotropized. In fact, we will see later on that the highest energy part, especially that part accelerated by the additional process, is not fully isotropized. Because we will present numerical results in the observer frame (or, more properly, in the stationary frame of the source
,
in which the distribution function is almost isotropized. In fact, we will see later on that the highest energy part, especially that part accelerated by the additional process, is not fully isotropized. Because we will present numerical results in the observer frame (or, more properly, in the stationary frame of the source
![]() ), it is useful to show how this truncated distribution looks in this frame.
), it is useful to show how this truncated distribution looks in this frame.
In the co-moving frame
![]() ,
the distribution is almost isotropized by turbulence, at least for the lower energy part, and the phase-space distribution function can be written
,
the distribution is almost isotropized by turbulence, at least for the lower energy part, and the phase-space distribution function can be written
| (5) |
In the stationary frame
![]() ,
the distribution is highly anisotropic, since the proton energy,
,
the distribution is highly anisotropic, since the proton energy, ![]() ,
is such that
,
is such that
![]() where
where
![]() .
The angular distribution is such that
.
The angular distribution is such that
The Lorentz invariance of the phase-space distribution function leads to an energy distribution function ![]() such that
such that
In the frame
![]() ,
one can summarize the effect of the anisotropy on the shape of
the energy distribution function produced by the internal shocks as follows (see Appendix):
,
one can summarize the effect of the anisotropy on the shape of
the energy distribution function produced by the internal shocks as follows (see Appendix):
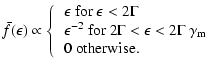 |
(8) |
In this section, we present the properties of hydromagnetic fronts in GRBs and we show that the Fermi acceleration process resulting from scattering off relativistic magnetized fronts constitutes an interesting solution for UHECR generation.
The internal shock model accounts for the light curves of GRBs that display fast variations, sometimes on a millisecond scale. This typically requires a number ![]() of sheets around 10-100, with Lorentz factors
of sheets around 10-100, with Lorentz factors ![]() (
(
![]() )
between 102-103 with respect to the frame
)
between 102-103 with respect to the frame
![]() (Daigne & Mochkovitch 1998). This means that they are mildly relativistic in the co-moving frame
(Daigne & Mochkovitch 1998). This means that they are mildly relativistic in the co-moving frame
![]() with Lorentz factors
with Lorentz factors
![]() ,
and we will refer to an average value
,
and we will refer to an average value
![]() .
For instance, assume that half of the sheets run forwards at a velocity
.
For instance, assume that half of the sheets run forwards at a velocity
![]() with respect to
with respect to
![]() ,
and half of them run backwards at a velocity
,
and half of them run backwards at a velocity
![]() ,
then we have a lower Lorentz factor
,
then we have a lower Lorentz factor
![]() and an upper Lorentz factor
and an upper Lorentz factor
![]() with respect to
with respect to
![]() .
.
The cosmic rays can be scattered by these sheets provided that they carry a sufficiently high magnetic field. Indeed they are scattered by magnetic sheets if and only if their Larmor radius is smaller than the thickness ![]() of the magnetic profile of the considered sheet. Particles of larger Larmor radius cross the front with just a small pitch angle jump of order
of the magnetic profile of the considered sheet. Particles of larger Larmor radius cross the front with just a small pitch angle jump of order
![]() .
We assume that
.
We assume that ![]() is of the order of the thickness of the sheet and follows its evolution. Therefore, we assume an average thickness
is of the order of the thickness of the sheet and follows its evolution. Therefore, we assume an average thickness
![]() measured in the stationary frame
measured in the stationary frame
![]() .
Consequently, particles of energy larger than
.
Consequently, particles of energy larger than
![]() ,
where
,
where ![]() is the average magnetic field in a sheet located at
radius r, have a negligible interaction with the magnetic front. Thus, it is important to specify the interaction limit,
is the average magnetic field in a sheet located at
radius r, have a negligible interaction with the magnetic front. Thus, it is important to specify the interaction limit,
![]() ,
for each sheet along the flow. We adopted the following scheme: we assume a prescribed value of the magnetic field
,
for each sheet along the flow. We adopted the following scheme: we assume a prescribed value of the magnetic field
![]() for each sheet at the distance
for each sheet at the distance ![]() and then any sheet carries a magnetic field of intensity decreasing with the distance r like
and then any sheet carries a magnetic field of intensity decreasing with the distance r like
![]() with
with
![]() (we will look at the case
(we will look at the case
![]() and
and ![]() for the reason explained in Sect. 2.3). Now in the frame of each sheet, the particles are scattered with no preferred direction and we can adopt either a mirror reflection or a random scattering. Both will give similar energy gains as will be seen later on; however we will choose the random scattering for the numerical simulation.
for the reason explained in Sect. 2.3). Now in the frame of each sheet, the particles are scattered with no preferred direction and we can adopt either a mirror reflection or a random scattering. Both will give similar energy gains as will be seen later on; however we will choose the random scattering for the numerical simulation.
Very high intensities of the magnetic field are allowed if we consider that the fireball results from the merging/collapse of a compact neutron star, namely 1015 G. For instance, a decrease of the magnetic field with
![]() and an average Lorentz factor of 300, lead to
and an average Lorentz factor of 300, lead to
![]() G for 100 sheets. We emphasize that this is a maximum value for a given number of sheets. Thus the specification of the magnetic field is crucial, for it controls both the acceleration through scattering of particles having an energy lower than the interaction limit
G for 100 sheets. We emphasize that this is a maximum value for a given number of sheets. Thus the specification of the magnetic field is crucial, for it controls both the acceleration through scattering of particles having an energy lower than the interaction limit
![]() and the spreading and decimation of the scattering sheets, responsible of both acceleration and expansion loss.
and the spreading and decimation of the scattering sheets, responsible of both acceleration and expansion loss.
Because of the forward and backward, mildly relativistic, motions of the sheets with respect to the co-moving frame
![]() ,
no isotropic distribution function can be built, only an axisymmetric and mirror-symmetric distribution is obtained. Assuming for instance a random scattering scheme (i.e. tendency of isotropization by each sheet), we obtain an angular distribution in this frame which is close to a superposition of two anisotropic distributions generated through the isotropic scattering by both forward (moving at
,
no isotropic distribution function can be built, only an axisymmetric and mirror-symmetric distribution is obtained. Assuming for instance a random scattering scheme (i.e. tendency of isotropization by each sheet), we obtain an angular distribution in this frame which is close to a superposition of two anisotropic distributions generated through the isotropic scattering by both forward (moving at
![]() )
and backward (moving at
)
and backward (moving at
![]() )
perturbations:
)
perturbations:
![\begin{figure}
\par\includegraphics[angle=-90,width=5.8cm,clip]{0301fig1.ps}\hsp...
...e*{3mm}
\includegraphics[angle=-90,width=5.8cm,clip]{0301fig4.ps}
\end{figure}](/articles/aa/full/2004/38/aa0301-03/Timg97.gif) |
Figure 1:
The proton repartition in the stationary frame
|
| Open with DEXTER | |
The efficiency of the Fermi process with relativistic scattering fronts for the acceleration of supra-thermal particles was emphasized by Pelletier (1999). This process consists in an interaction of a relativistic particle having an initial 4-vector momentum
![]() in the stationary frame
in the stationary frame
![]() with a magnetized front of velocity
with a magnetized front of velocity
![]() (with corresponding
(with corresponding ![]() ). We denote by primes physical quantities in the magnetized front frame
). We denote by primes physical quantities in the magnetized front frame
![]() and we define the angle between
and we define the angle between
![]() and
and ![]() by its cosine
by its cosine ![]() just before the interaction. The Lorentz transformation gives us the following equations:
just before the interaction. The Lorentz transformation gives us the following equations:
The scattering does not change the particle energy in the magnetized front frame and the pitch angle (cosine) ![]() is randomly changed into
is randomly changed into ![]() .
Denoting by 2 the physical quantities after the interaction, the reversed Lorentz transformation leads to
.
Denoting by 2 the physical quantities after the interaction, the reversed Lorentz transformation leads to
We have considered a conical box representing the ultrarelativistic flow around the broadening radius ![]() (
(![]() 1012 cm). In the stationary frame
1012 cm). In the stationary frame
![]() ,
the initial box height, corresponding to the flow length, is given by
,
the initial box height, corresponding to the flow length, is given by
![]() and the transversal size of the flow is equal to
and the transversal size of the flow is equal to
![]() with
with
![]() ,
the opening angle of the flow.
Using a Monte-Carlo simulation, we randomly put in the flow a set of identical (same mass) baryonic layers (or sheets) with an uniform Lorentz factor distribution between 102 and 103 considered by several authors (Piran 2000; Daigne & Mochkovitch 1998) to reproduce the GRB light curves from internal shocks. Following previous simulations (Kobayashi et al. 1997), we consider a number of layers of about several times ten. For a layer with a Lorentz factor of
,
the opening angle of the flow.
Using a Monte-Carlo simulation, we randomly put in the flow a set of identical (same mass) baryonic layers (or sheets) with an uniform Lorentz factor distribution between 102 and 103 considered by several authors (Piran 2000; Daigne & Mochkovitch 1998) to reproduce the GRB light curves from internal shocks. Following previous simulations (Kobayashi et al. 1997), we consider a number of layers of about several times ten. For a layer with a Lorentz factor of
![]() at a distance r the width is equal to
at a distance r the width is equal to
![]() and the transverse radius is the same as that of the flow.
The isotropic suprathermal proton population is initially injected in each layer with an energy spectrum in the co-moving frame proportional to
and the transverse radius is the same as that of the flow.
The isotropic suprathermal proton population is initially injected in each layer with an energy spectrum in the co-moving frame proportional to
![]() between 1 GeV and a cut-off energy
between 1 GeV and a cut-off energy
| (15) |
For each proton, we initially define a random pitch angle cosine as defined in Sect. 3 (see Eq. (6)). We have plotted in Fig. 1, for
![]() G and
G and
![]() G, the initial energy repartition of the proton population, in the observer frame, which depends on three independent random parameters namely
G, the initial energy repartition of the proton population, in the observer frame, which depends on three independent random parameters namely
![]() ,
,
![]() and
and ![]() .
.
We describe here the temporal evolution in our Monte-Carlo simulation. The Lorentz factor distribution leads to collisions of different sheets during the numerical process between ![]() and
and
![]() (about
(about
![]() for
for
![]() cm or
cm or
![]() for
for
![]() cm) which is sufficient to determine the fraction of UHECRs according to the confinement limit (see Sect. 2). We have considered the simple case where the result of a collision of two identical sheets is a single sheet having a Lorentz factor defined
by
cm) which is sufficient to determine the fraction of UHECRs according to the confinement limit (see Sect. 2). We have considered the simple case where the result of a collision of two identical sheets is a single sheet having a Lorentz factor defined
by
![]() where
where
![]() and
and
![]() are the Lorentz factors of the sheets before colliding. The total number of sheets decreases with time and this reduces the interaction probability with protons in the flow even if the sheet width and the transversal radius increase like r in our model.
are the Lorentz factors of the sheets before colliding. The total number of sheets decreases with time and this reduces the interaction probability with protons in the flow even if the sheet width and the transversal radius increase like r in our model.
The first collision of a sheet defines the time from which its protons are released into the flow and can interact with all sheets. After a proton-sheet interaction, which is spatially defined by comparing respective positions, we randomly assign a new pitch angle for the proton and its energy is changed according to the Eq. (12). We assume that all interactions are instantaneous. Indeed, the magnetic scattering duration inside a sheet,
![]() ,
can be neglected; for a proton with energy
,
can be neglected; for a proton with energy ![]() in the co-moving frame, it can be expressed by
in the co-moving frame, it can be expressed by
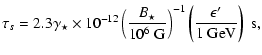 |
(16) |
The proton energy limitation for an interaction (or magnetic scattering) is given by the interaction limit calculated in each layer (see Sects. 2 and 4.1); for a given proton, the higher its energy is, the more transparent the medium is to it and its escape probability becomes important. This limitation is far more important than the transverse escape.
We also have neglected the synchrotron losses for protons because the synchrotron limitation, in the co-moving frame
![]() ,
is over 105 GeV at
,
is over 105 GeV at ![]() and next, increases like r2 for
and next, increases like r2 for
![]() and r11/8 for
and r11/8 for
![]() (Gialis & Pelletier 2003).
(Gialis & Pelletier 2003).
The numerical Monte-Carlo simulation clearly shows that a sizeable part of cosmic rays is produced by the relativistic Fermi process stretching the initial distribution tail up into the UHE range (see Fig. 2); for any magnetic field intensity higher than 104 G at ![]() ,
the relativistic Fermi acceleration by multiple fronts leads to a production of UHECRs with a fraction larger than 10-6 for a given initial proton distribution as prescribed in Sect. 5. Table 1 summarizes the results for different values of
,
the relativistic Fermi acceleration by multiple fronts leads to a production of UHECRs with a fraction larger than 10-6 for a given initial proton distribution as prescribed in Sect. 5. Table 1 summarizes the results for different values of
![]() and of the flow duration. We have chosen a typical number of sheets,
and of the flow duration. We have chosen a typical number of sheets, ![]() ,
of 50 at the beginning of the process and, first, a magnetic field that decreases like r-3/2, second, a magnetic field that decreases like r-2.
,
of 50 at the beginning of the process and, first, a magnetic field that decreases like r-3/2, second, a magnetic field that decreases like r-2.
| |
Figure 2:
The initial proton distribution ( left figure) is strongly modified by the Fermi acceleration process in the high energy range where an UHECR population appears ( right figure) with
|
| Open with DEXTER | |
Table 1: The UHECR (>1010 GeV) fraction generated by relativistic Fermi acceleration in the Monte-Carlo simulation. A number of 50 layers is considered here and the flow duration varies from 0.5 s (short GRB) to 10.0 s (long GRB). The magnetic field decreases as r-3/2.
The determination of the time of UHECR creation which has been made for different values of the wind duration and the magnetic field (see Fig. 4) shows that UHECR generation mainly happens at the very beginning of the internal shock phase; more precisely, UHECR generation can be achieved before ![]()
![]() (or
(or ![]() 104 s) which corresponds to only a few percent of the internal shock phase duration (
104 s) which corresponds to only a few percent of the internal shock phase duration (![]() 105 s).
There are two conditions that govern the ending of the multi-front acceleration: first, the maximum value of the interaction limit
105 s).
There are two conditions that govern the ending of the multi-front acceleration: first, the maximum value of the interaction limit
![]() assigned at the radius
assigned at the radius ![]() through the value of the magnetic field there; and second, the decrease of the interaction energy limit with distance. Indeed, the lowest interaction energy limit (see Sect. 2) to get UHECRs is about 1019 eV at
through the value of the magnetic field there; and second, the decrease of the interaction energy limit with distance. Indeed, the lowest interaction energy limit (see Sect. 2) to get UHECRs is about 1019 eV at ![]() for
for
![]() G; the difference between this energy and the UHE range
(
G; the difference between this energy and the UHE range
(![]() 1020 eV) is almost at the maximum possible value of the energy jump (the maximum gain being about 16), and then the gap quickly becomes too high with time to be jumped by a proton in a single proton-sheet interaction, since the interaction limit decreases like
1020 eV) is almost at the maximum possible value of the energy jump (the maximum gain being about 16), and then the gap quickly becomes too high with time to be jumped by a proton in a single proton-sheet interaction, since the interaction limit decreases like
![]() .
However, we have shown (see Sect. 4) that only a small number of interactions (
.
However, we have shown (see Sect. 4) that only a small number of interactions (![]() 10) is necessary to achieve the UHE range. The simulation directly provides this number per proton: whatever the flow duration between 0.5 and 10 s and for a magnetic field of 104 G at
10) is necessary to achieve the UHE range. The simulation directly provides this number per proton: whatever the flow duration between 0.5 and 10 s and for a magnetic field of 104 G at ![]() ,
the results confirm that a sizeable fraction of protons (>
,
the results confirm that a sizeable fraction of protons (>
![]() )
undergoes more than 10 interactions with the hydromagnetic fronts and, consequently, can easily achieve the UHE range (see Fig. 3).
Moreover, Table 1 indicates that the energy amount converted into UHECRs at the beginning of the Fermi process is high enough to constitute a sizeable fraction of the total magnetic energy.
)
undergoes more than 10 interactions with the hydromagnetic fronts and, consequently, can easily achieve the UHE range (see Fig. 3).
Moreover, Table 1 indicates that the energy amount converted into UHECRs at the beginning of the Fermi process is high enough to constitute a sizeable fraction of the total magnetic energy.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{0301fig6.ps}
\end{figure}](/articles/aa/full/2004/38/aa0301-03/Timg155.gif) |
Figure 3:
The proton repartition as a function of the number of interactions (or scatterings) for a magnetic field at |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{0301fig7.ps}\hspac...
...ace*{3mm}
\includegraphics[angle=-90,width=7cm,clip]{0301fig10.ps} \end{figure}](/articles/aa/full/2004/38/aa0301-03/Timg156.gif) |
Figure 4:
The UHECR repartition (in |
| Open with DEXTER | |
Finally, a magnetic field decreasing in r-2 leads to a lower resulting fraction of UHECRs but a sizeable one again: for instance, for a magnetic field
![]() G, this fraction is about
G, this fraction is about
![]() with
with
![]() s and
s and
![]() with
with
![]() s.
s.
Let us now give arguments concerning the number of sheets required to produce UHECRs. The numerical simulation shows that the acceleration stops because of the decimation of the sheets due to expansion (the mean free path increases like
![]() )
and mostly due to decrease of the interaction energy limits (
)
and mostly due to decrease of the interaction energy limits (
![]() for
for
![]() )
which rarefies the scattering medium for increasing energies. Since
)
which rarefies the scattering medium for increasing energies. Since
![]() is given by the number of sheets
is given by the number of sheets ![]() ,
namely
,
namely
![]() ,
a simple estimate of the minimum number of sheets can be given. At each scattering, a particle migrates towards a region of lower interaction limit and roughly, after n scatterings
,
a simple estimate of the minimum number of sheets can be given. At each scattering, a particle migrates towards a region of lower interaction limit and roughly, after n scatterings
![]() ,
where
,
where
![]() and
and
![]() denotes the local scattering energy limit, rather than the interaction limit associated to a specific sheet. So the acceleration stops when the number of scatterings is such that
denotes the local scattering energy limit, rather than the interaction limit associated to a specific sheet. So the acceleration stops when the number of scatterings is such that
![]() ,
which leads to the following number of scatterings:
,
which leads to the following number of scatterings:
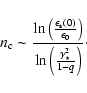 |
(17) |
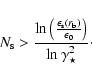 |
(18) |
Since the process tends to produce cosmic rays that reach an energy close to the local scattering limit, the integrated distribution function reflects the evolution of the scattering limit, which is directly given by the magnetic field decay. For an intensity of the magnetic field decreasing
like r-2, the scattering limit decreases like r-1, and for a continuous flow during
![]() ,
the cosmic ray density decreases like r-2. Therefore the integrated energy distribution function is
,
the cosmic ray density decreases like r-2. Therefore the integrated energy distribution function is
There are two possible types of neutrino emission due to the generation of cosmic rays (Gialis & Pelletier 2003). The most expected one results from the ![]() -process where the total energy radiated by neutrinos in the co-moving flow is given by
-process where the total energy radiated by neutrinos in the co-moving flow is given by
The other possibility is low energy emission between 5 GeV and 150 GeV resulting from pp-collisions. We predicted significant emission due to the standard Fermi acceleration at internal shocks when ![]() is smaller than
is smaller than
![]() where
where
![]() is reached when the photospheric radius is equal to
is reached when the photospheric radius is equal to ![]() (Gialis & Pelletier 2003). The improvement of the acceleration by the process presented in this paper does not significantly change the order of magnitude of our previous estimate. The number of pp-neutrinos is greater and could allow the formation of a spectrum, since we could get 108 neutrinos under the same conditions.
(Gialis & Pelletier 2003). The improvement of the acceleration by the process presented in this paper does not significantly change the order of magnitude of our previous estimate. The number of pp-neutrinos is greater and could allow the formation of a spectrum, since we could get 108 neutrinos under the same conditions.
The pp-process generates ![]() -mesons that decay into two
-mesons that decay into two ![]() -photons. This emission deserves more attention because of a possible detection in the GeV range, which would constitute an interesting diagnosis. For a
-photons. This emission deserves more attention because of a possible detection in the GeV range, which would constitute an interesting diagnosis. For a
![]() spectrum of cosmic rays, the gamma flux due to
spectrum of cosmic rays, the gamma flux due to ![]() -decay is estimated by
-decay is estimated by
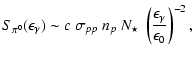 |
(21) |
The ![]() -decay spectrum must be compared with the SSC-spectrum. The latter can be written;
-decay spectrum must be compared with the SSC-spectrum. The latter can be written;
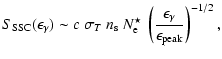 |
(22) |
The diagnosis of the ![]() -decay should be fairly easy since it radiates at much higher energy than the synchrotron emission and at much lower energy than the SSC-emission. When
-decay should be fairly easy since it radiates at much higher energy than the synchrotron emission and at much lower energy than the SSC-emission. When
![]() ,
the fraction of the energy radiated by
,
the fraction of the energy radiated by ![]() -decay is quite significant, a few percent; indeed
-decay is quite significant, a few percent; indeed
| (23) |
Such a detection (by HESS observatory, 5@5 experiment and GLAST) would provide a very nice estimate of the baryon load together with evidence of cosmic ray generation.
We have shown through accurate investigation of scattering properties that the usual Fermi processes are unable to generate UHECRs in GRBs. First of all, it is well known that the highly relativistic external shock with a standard interstellar medium cannot achieve the goal of UHECR generation. The hope that it could do so was mostly based on the internal shock model but the irrelevant Bohm's scaling was used; moreover, a slowly decreasing magnetic field was assumed. Removing these extreme assumptions made the goal impossible (Gialis & Pelletier 2003).
However, because the global energy budget is in favour of copious cosmic ray generation, we thought it interesting to design an additional Fermi process that would stretch the cosmic ray distribution tail. Indeed, the acceleration through multi-scattering off magnetized relativistic fronts turns out to be more efficient even with a field decreasing in r-2. In this paper, we found that a sizeable fraction (![]() 10-5) of the cosmic ray population reaches the UHE range, which is even more than necessary.
10-5) of the cosmic ray population reaches the UHE range, which is even more than necessary.
There is another important physical issue, namely the escape of the UHECRs from the fireball towards the observer. The relativistic Fermi process that we proposed generates UHECRs in a thin layer located at the very beginning of the internal shock phase. The question arises whether these particles suffer a further expansion loss. In fact, because the magnetic field decreases faster
than r-1, the interaction energy limit with the magnetic fronts decreases and the UHECRs are no longer scattered by them. Thus, because of the lack of scattering, they cannot experience the expansion loss, contrarily to models expecting
![]() .
Therefore, they directly travel across the shells, benefiting of the Lorentz boost. For a magnetic field decreasing as r-2, the integrated spectrum is in
.
Therefore, they directly travel across the shells, benefiting of the Lorentz boost. For a magnetic field decreasing as r-2, the integrated spectrum is in
![]() over 4 decades.
over 4 decades.
In our previous paper (Gialis & Pelletier 2003), we predicted a possible double neutrino emission; even though this improvement of the acceleration process does not significantly change the estimated fluxes, the collimation allows detectable events, especially with pp-neutrinos. However, we found a possible diagnosis of cosmic ray generation in some numerous class of GRBs, having
![]() ,
associated with the signature of
,
associated with the signature of ![]() -decay in the GeV
-decay in the GeV ![]() -ray spectrum. This seems to be really observable, with a few percent of the GRB energy, for GRBs having a sufficient baryon load. This signature (in the GeV range by HESS observatory, 5@5 experiment and GLAST) would be easily distinguished from the synchrotron bump and the SSC-bump with a flux as high as a few percent of the fireball global energy flux.
-ray spectrum. This seems to be really observable, with a few percent of the GRB energy, for GRBs having a sufficient baryon load. This signature (in the GeV range by HESS observatory, 5@5 experiment and GLAST) would be easily distinguished from the synchrotron bump and the SSC-bump with a flux as high as a few percent of the fireball global energy flux.
This study gives a new chance to GRBs as sources of UHECRs. But their contribution to the diffuse background spectrum might not be dominant compared to the AGN contribution. This is an important issue that is under intense debate in the literature (Stecker 2000; Bahcall & Waxman 2003; Berezinsky et al. 2003).
From Eq. (7), we deduce the following expression
| (24) |
According to Eq. (2) and for a typical magnetic field of 105 G at ![]() ,
we have supposed that
,
we have supposed that
![]() .
It is noteworthy that the following calculation leads to the same result for the hypothesis
.
It is noteworthy that the following calculation leads to the same result for the hypothesis
![]() .
Let us distinguish two cases: the first one for
.
Let us distinguish two cases: the first one for
![]() gives
gives
![]() and
and
![]() .
The distribution function becomes
.
The distribution function becomes
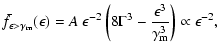 |
(25) |
The second case is considered for
![]() and it can be divided in two sub cases: first, for
and it can be divided in two sub cases: first, for
![]() ,
the distribution function can be simplified and becomes such that
,
the distribution function can be simplified and becomes such that
| (26) |
| (27) |