A&A 425, 591-594 (2004)
DOI: 10.1051/0004-6361:20034245

On rotational mixing in stars

R. Q. Huang

National Astronomical Observatories / Yunnan Observatory, the Chinese Academy of Sciences, Kunming 650011, PR China

Received 1 September 2003 / Accepted 16 March 2004

Abstract
A method to treat rotational mixing in stars is proposed. The evolution of a 8 $M_\odot $ star with rotation is studied, and the effects of rotation on the interior structure and evolution of the star are discussed.

Key words: stars: evolution - stars: interiors - stars: rotation

1 Introduction

To construct a model for a rotating star, we have to take into account two effects of rotation: centrifugal force and that of meridian circulation. Due to the first effect, the structure of a star changes from sphericaly symmetric to non-sphericaly symmetric, and the stellar model becomes two-dimensional. Owing to the second effect, a radial flow of mass occurs in the star. As a result of radial mass flow, the transport of angular momentum and chemical composition takes place in the star. The sum of the two effects makes the structure and evolution of a rotating star differ from that of a non-rotating star.

The effect of centrifugal force and the changes in the stellar model have been studied by many investigators (Kippenhahn & Thomas 1970; Endal & Sofia 1976; Pinsonneault et al. 1989, 1990, 1991; Charboyer et al. 1995a,b; Langer 1998; Heger & Langer 1998; Meynet & Maeder 1997; Maeder & Meynet 2000). Among these investigations the study of Kippenhahn & Thomas (1970) has attracted special attention because they introduced a method to simplify the two-dimensional model with conservative rotation to a one-dimensional model, and gave the structure equations. Without a detailed study of the properties of stellar rotation, we make a simple assumption that the method developed by Kippenhahn & Thomas (1970) can be used in our model. The effect of meridian circulation and the radial mass flow in a star have also been studied in many investigators (Endal & Sofia 1976; Tassoul 1978; Schatzman et al. 1981; Langer 1991, 1992; Chaboyer & Zahn 1992; Zahn 1992; Heger et al. 2000; Maeder & Meynet 2000). The calculations of meridian circulation and the radial mass flow are quite complicated. Here we propose a simple method to treat the transport of angular momentum and the chemical composition of a star.

In Sect. 2, we discuss the rotational mixing and the model for a rotating star. In Sect. 3, the evolution a 8 $M_\odot $ star with rotation is studied, and the differences between the results for the evolution with and without the effects of rotation are discussed in detail.

2 Rotational mixing and the stellar model

2.1 Rotational mixing

The effect of rotation causes an outward mass flow along the rotational axis and an inward mass flow along the equatorial plane. Such an outward and inward mass flow in a star is called meridian circulation (Kippenhahn & Weigert 1990; Maeder & Meynet 2000). As a result of the meridian circulation and the shear turbulence, a transport of angular momentum and chemical composition occurs in the star. We can treat this transport process approximately as an advection process. The meridian circulation is caused by the effect of rotation, and the strength of rotation of a mass layer in the star can be expressed by the difference between the gravity gi and the mean effective gravity  $\langle g_{{\rm eff}} \rangle_i$ of this layer. The shear turbulence is caused by the differential rotation, so that the rate of the change in the composition of the $\alpha$ element can be expressed as

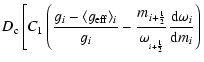$\displaystyle % \frac{{\rm d}X_{\alpha i}}{{\rm d}t}$ = $\displaystyle D_{\rm c} \left[ C_1\left( \frac{g_i-\langle g_{{\rm eff}} \rangl... ...}}{\omega _{_{i+\frac 12}}}% \frac{{\rm d}\omega _i}{{\rm d}m_i}\right) \right.$$\displaystyle \left. -C_2\frac{m_{i+\frac 12}}{X_{_{i+\frac 12}}}% \frac{{\rm d... ...d}m_i}\right] +\left( \frac{{\rm d}X_{\alpha i}}{{\rm d}t}\right) _{{\rm nuc}},$ (1)

where $D_{\rm c}$ is a coefficient ( $D_{\rm c}=\frac{X_{\alpha i}}{\tau _{{\rm adv}}}$), the advection time scale can be given as (Maeder & Meynet 2000) $\tau _{{\rm adv}}=\tau _{k{\rm h}}\frac{GM}{R^3\omega ^2},\tau _{k{\rm h}}=\frac q2\frac{GM^2}{RL}$, C1 and C2 are the dimensionless parameters, miand $\omega _i$ are the mass and angular velocity of the ith layer. The quantity with the subscript  $i+\frac 12$ in Eq. (1) is defined as

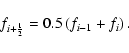\begin{displaymath}% f_{i+\frac 12}=0.5\left(f_{i-1}+f_i\right). \end{displaymath} (2)

The first and second terms on the right hand side of Eq. (1) correspond to the contributions of the meridian circulation and the shear turbulence, respectively. The third and the fourth terms correspond to the contributions of the gradient of the chemical composition and the nuclear reactions, respectively.

At the outer and inner boundary, reflecting conditions are used:

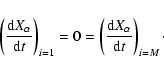\begin{displaymath}% \left( \frac{{\rm d}X_\alpha }{{\rm d}t}\right) _{i=1}=0=\left( \frac{{\rm d}X_\alpha }{{\rm d}t}\right) _{i=M}\cdot \end{displaymath} (3)

The change in the composition of the $\alpha$ element is obtained as:

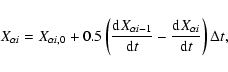\begin{displaymath}% X_{\alpha i}=X_{\alpha i,0}+0.5\left(\frac{{\rm d}X_{\alpha... ...{\rm d}t}-\frac{{\rm d}X_{\alpha i}}{{\rm d}t}\right)\Delta t, \end{displaymath} (4)

where the subscript 0 refers to the values of the last evolutionary model, $\Delta t$ is the time difference between the two successive evolutionary models.

Another result of the meridian circulation and the shear turbulence is the transport of angular momentum in the star.

If Ji is the angular momentum of the ith layer, the rate of the change in angular momentum can be expressed as:

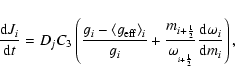\begin{displaymath}% \frac{{\rm d}J_i}{{\rm d}t}=D_jC_3\left( \frac{g_i- \langle... ...a _{_{i+\frac 12}}}\frac{{\rm d}\omega _i}{{\rm d}m_i}\right), \end{displaymath} (5)

where Dj is the coefficient ( $D_j=\frac{J_i}{\tau _{{\rm adv}}}$), C3 is a dimensionless parameter. The first and second terms on the right hand side of Eq. (5) correspond to the contributions of the meridian circulation and the shear turbulence, respectively.

At the outer and inner boundary reflecting conditions are used:

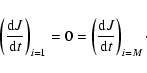\begin{displaymath}% \left( \frac{{\rm d}J}{{\rm d}t}\right) _{i=1}=0=\left( \frac{{\rm d}J}{{\rm d}t}\right) _{i=M}\cdot \end{displaymath} (6)

The change in the angular momentum of the ith layer is obtained as:

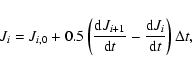\begin{displaymath}% J_i=J_{i,0}+0.5\left(\frac{{\rm d}J_{i+1}}{{\rm d}t}-\frac{{\rm d}J_i}{{\rm d}t}\right)\Delta t, \end{displaymath} (7)

where the subscript 0 refers to the values of the last evolutionary model. The variation of the angular velocity $\omega _i$ can be obtained as

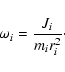\begin{displaymath}% \omega _i=\frac{J_i}{m_ir_i^2}\cdot \end{displaymath} (8)

2.2 Stellar model

The stellar model for rotating stars is based on the method developed by Kippenhahn & Thomas (1970). The structure equations are the following:

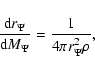\begin{displaymath}% \frac{{\rm d}r_\Psi }{{\rm d}M_\Psi }=\frac 1{4\pi r_\Psi ^2\rho }, \end{displaymath} (9)


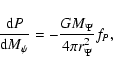\begin{displaymath}% \frac{{\rm d}P}{{\rm d}M_\psi }=-\frac{GM_\Psi }{4\pi r_\Psi ^2}f_P, \end{displaymath} (10)


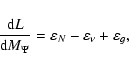\begin{displaymath}% \frac{{\rm d}L}{{\rm d}M_\Psi }=\varepsilon _N-\varepsilon _\nu +\varepsilon _g, \end{displaymath} (11)


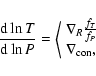\begin{displaymath}% \frac{{\rm d}\ln T}{{\rm d}\ln P}= \left \langle \begin{arr... ..._R\frac{f_T}{f_P} \\ \nabla _{{\rm con}}, \end{array} \right. \end{displaymath} (12)

where

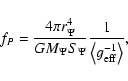\begin{displaymath}% f_P=\frac{4\pi r_\Psi ^4}{GM_\Psi S_\Psi }\frac 1{\left\langle g_{{\rm eff}}^{-1} \right\rangle}, \end{displaymath} (13)


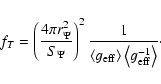\begin{displaymath}% f_T=\left( \frac{4\pi r_\Psi ^2}{S_\Psi }\right) ^2\frac 1{... ...}} \rangle \left\langle g_{{\rm eff}}^{-1} \right\rangle}\cdot \end{displaymath} (14)

Here, $\langle g_{{\rm eff}} \rangle, \langle g_{{\rm eff}}^{-1} \rangle$ are the mean values of the effective gravity and its inverse over the equipotential surface.

The equipotentials are defined by the equation of

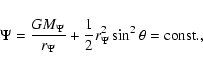\begin{displaymath}% \Psi =\frac{GM_\Psi }{r_\Psi }+\frac 12r_\Psi ^2\sin ^2\theta = {\rm const.}, \end{displaymath} (15)

$S_\Psi $ is the surface area of the equipotential. $\nabla_R,\nabla _{{\rm con}}$ in Eq. (12) are the radiate and the convective temperature gradients.


  \begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{0245fig1.ps}\end{figure} Figure 1: The evolutionary tracks in the HR diagram of a 8$~M_\odot $ star for the sequences with and without rotation. The solid and dotted curves correspond to the tracks for the STD sequence and the ROT sequence, respectively.
Open with DEXTER

3 Evolutionary computations and results

The evolution of a 8 $M_\odot $ star is studied. Two evolutionary sequences corresponding to the cases with and without the effects of rotation are calculated. The sequence denoted as STD corresponds to the evolution without the effects of rotation, while the sequence denoted as ROT corresponds to that with the effects of rotation. The initial chemical composition of X=0.70, Z=0.02 is adopted for both sequences. The effects of mass loss due to stellar winds and convective overshooting (0.22l over the Schwartzschield border) are considered for both sequences. The initial rotating velocity for the 8 $M_\odot $ star has a value of 150.49 km s-1. The parameters C1 and C2 in Eq. (1) have the values of 0.02 and 0.1, while the parameter C3 in Eq. (5) has the value of 0.05.


  \begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{0245fig2.ps}\end{figure} Figure 2: The time dependent variation of the border of the burning core of the 8 $M_\odot $star. The solid and dotted curves have the same meanings as in Fig. 1.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{0245fig3.ps}\end{figure} Figure 3: he evolution of the ratio $\langle g_{{\rm eff}} \rangle_i/g_i$ as a function of the mass fraction in the star. X(c) is the hydrogen composition at the center.
Open with DEXTER

Table 1: The parameters at different evolutionary points a, b, c and d of the STD and ROT sequences.

The evolutionary tracks in the HR diagram for the 8 $M_\odot $ star of two sequences are illustrated in Fig. 1. The solid curve corresponds to the track for the STD sequence, while the dotted curve corresponds to that of the ROT sequence. From the difference between the solid and the dotted curves in Fig. 1 one finds that rotation causes the evolutionary track in the HR diagram to shift towards lower luminosity.

Figure 2 shows the time dependent variation at the border of the burning core of a 8 $M_\odot $ star. The solid and the dotted curves correspond to the sequences STD and ROT respectively. From Fig. 2 one finds that the ends of the H- and He-burning phases are at later times for the ROT sequence than for the STD sequence. This means that the effect of rotation causes the star to evolve more slowly. In addition, Fig. 2 shows that the border of the H-burning core of the ROT sequence is slightly smaller than that of the STD sequence. This explains the fact that the evolutionary track in the HR diagram of the star with rotation shifts towards lower luminosity in Fig. 1, because the luminosity of the star is dependent on the size of the burning core.

In Table 1 we list the ages, masses, effective temperatures, luminosities, the central hydrogen and helium compositions, the compositions of helium and heavy elements on the surface, and the rotating velocities at the critical evolutionary points of the sequences. From the compositions of helium and heavy elements on the surface of the ROT sequence at the points b, c and d, we find the effect of the rotational mixing. However, it is quite small.

Figure 3 illustrates the time-dependent variation in the rotating velocity of the ROT sequence. From Fig. 3 we find that the rotating velocity of the star decreases progressively during the central hydrogen burning phase, and reduces rapidly to very small values during the H-shell burning phase. This shows that the effects of rotation have an influence on the structure and evolution of the star mainly in the main sequence phase.

Acknowledgements
This work is supported by the Chinese National Science Foundation No. 10073020.

References

 
Copyright ESO 2004