A&A 425, L9-L12 (2004)
DOI: 10.1051/0004-6361:200400053
Planets opening dust gaps in gas disks
S.-J. Paardekooper 1 - G. Mellema 2,1
1 - Leiden Observatory, Postbus 9513, 2300 RA Leiden,
The Netherlands
2 -
ASTRON, Postbus 2, 7990 AA Dwingeloo, The Netherlands
Received 7 July 2004 / Accepted 10 August 2004
Abstract
We investigate the interaction of gas and dust in a protoplanetary
disk in the presence of a massive planet using a new two-fluid
hydrodynamics code. In view of future observations of planet-forming
disks we focus on the condition for gap formation in the dust fluid.
While only planets more massive than 1 Jupiter mass (
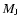 )
open up a
gap in the gas disk, we find that a planet of 0.1
)
open up a
gap in the gas disk, we find that a planet of 0.1
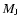 already creates
a gap in the dust disk. This makes it easier to find lower-mass planets
orbiting in their protoplanetary disk if there is a significant population
of mm-sized particles.
already creates
a gap in the dust disk. This makes it easier to find lower-mass planets
orbiting in their protoplanetary disk if there is a significant population
of mm-sized particles.
Key words: hydrodynamics - stars: planetary systems
Resolved images of protoplanetary disks can reveal density structures in
gas and dust hinting at the presence of embedded planets. It is therefore
important to investigate the response of a dusty circumstellar disk on
planets, as opposed to for example radiation pressure effects in optically
thin disks (Takeuchi & Artymowicz 2001).
The most dramatic disk structure a planet can create is an annular gap
(Papaloizou & Lin 1984), and these planet-induced gaps can be used
as tracers for recent giant planet formation.
Recently, Wolf et al. (2002) showed that the Atacama Large
Millimeter Array (ALMA) will be able to detect a gap at 5.2 AU caused
by the presence of a Jupiter mass planet in a disk 140 pc away in the
Taurus star-forming region. However, they assumed a constant dust-to-gas
mass ratio of 1:100, whereas in the presence of large pressure gradients
the gas and the dust evolution will decouple to some extent
(Takeuchi & Lin 2002). Due to radial pressure support
the gas orbits at sub-Keplerian velocity, and when the dust particles are
slowed down by drag forces they move inward.
In this letter we present the first results of two-dimensional numerical
simulations where we treat the gas and the dust as separate but coupled
fluids. These two-fluid calculations take into account the full interaction
of gas and dust, and can be used to simulate observations in a better way.
In Sect. 2 we briefly discuss the physics of gas-dust
interaction. We describe the numerical method in Sect. 3,
and the initial conditions in Sect. 4. We present the
results in Sect. 5 and we conclude in Sect. 6.
2 Basic equations
Protoplanetary disks are fairly thin, i.e. the vertical thickness His small compared with the distance r from the centre of the disk.
Typically we use
H/r = h = 0.05. Therefore it is convenient to average
the equations of motion vertically, and work with vertically averaged
quantities only. The governing equations as well as the gas disk model are
the ones described in detail in Kley (1999).
We treat the dust as a pressureless fluid, and its evolution is governed
by conservation of mass and conservation of linear and angular momentum.
The major difference between the equations for the gas and the dust is the
absence of pressure in the latter. In this sense the dust fluid behaves
like a gas that is moving always with supersonic velocity. This implies that
near shock waves, where the gas goes from sonic to supersonic flow and large
density and velocity gradients are present, dust and gas behave in a very
different way.
The interaction between the gas and dust fluids occurs only through
drag forces. The nature of the drag force depends on the size of the
particles with respect to the mean free path of the gas molecules. We
consider only spherical particles with radius s, and for the particle
sizes we are interested in (
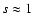 mm) we can safely use Epsteins
drag law (Takeuchi & Artymowicz 2001). In the limit of small relative
velocities of gas and dust compared to the local sound speed, the drag
forces are written as:
mm) we can safely use Epsteins
drag law (Takeuchi & Artymowicz 2001). In the limit of small relative
velocities of gas and dust compared to the local sound speed, the drag
forces are written as:
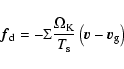 |
(1) |
where
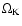 is the Keplerian angular velocity, and
is the Keplerian angular velocity, and 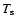 is the non-dimensional stopping time (Takeuchi & Lin 2002):
is the non-dimensional stopping time (Takeuchi & Lin 2002):
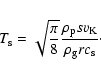 |
(2) |
Here,
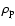 is the particle internal density, s is the radius
of the particle and
is the particle internal density, s is the radius
of the particle and 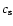 is the sound speed. We have used
is the sound speed. We have used
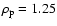
 ,
and the gas density
,
and the gas density
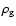 is found by using
is found by using
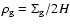 .
During simulations we have always checked whether Eq. (1) applied.
.
During simulations we have always checked whether Eq. (1) applied.
3 Numerical method
For the evolution of the gas component, we use the method described by
Paardekooper & Mellema (2004). It is a second-order Eulerian hydrodynamics
code which uses an approximate Riemann solver (Roe 1981).
It derives from a general relativistic method (Eulderink & Mellema 1995),
from which it inherits the capability to deal with non-Cartesian, non-inertial
coordinate systems. We work in a cylindrical coordinate frame 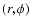 ,
corotating with the embedded planet that has a Keplerian angular velocity.
A module for Adaptive Mesh Refinement (AMR) can be used
to obtain very high resolution near the planet. We use basically the same
method to follow the evolution of the dust, but without the pressure terms.
This is a very different approach than for example in
Klahr & Henning (1997), who solve the equations of motion of particles
instead of the fluid equations. All the source terms except the drag forces
are integrated using stationary extrapolation (Paardekooper & Mellema 2004). The drag
forces are incorporated separately using an ordinary differential equation:
,
corotating with the embedded planet that has a Keplerian angular velocity.
A module for Adaptive Mesh Refinement (AMR) can be used
to obtain very high resolution near the planet. We use basically the same
method to follow the evolution of the dust, but without the pressure terms.
This is a very different approach than for example in
Klahr & Henning (1997), who solve the equations of motion of particles
instead of the fluid equations. All the source terms except the drag forces
are integrated using stationary extrapolation (Paardekooper & Mellema 2004). The drag
forces are incorporated separately using an ordinary differential equation:
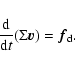 |
(3) |
Separating the drag forces from the advection in this way puts constraints
on the time step. Basically the assumption is that no drag force acts on the
dust during the advection, and this is clearly not correct when the drag
force source terms are very stiff. The time step is set by the hydrodynamic
Courant-Friedrichs-Lewy (CFL) condition, and therefore one has to make sure
that the typical time scale for the drag forces (the stopping time) is not
much smaller than this time step. Switching the order of integration
every time step yields a second order accurate update for the state
(Strang 1968). If the stopping time is very small (well-coupled particles) the dust can not
be assumed to move free of drag during a dust update. This puts
a lower limit on the particle size that we can put into the simulations. For
a typical disk, this limit is about 0.1 mm. The time step can however be
reduced to include smaller particles.
4 Initial and boundary conditions
The standard numerical resolution is
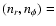 (128,384).
This way, the cells close to the planet have equal size in the radial
and in the azimuthal direction. We do not resolve the Roche lobe at this
resolution, but since we are interested only in the large scale evolution
of the disk, this is not important. We will discuss the flow within the
Roche lobe and accretion processes in future papers. Using a low resolution
allows us to run longer simulations, which is important because the
drift velocities can be very low.
We take a constant initial surface density
(128,384).
This way, the cells close to the planet have equal size in the radial
and in the azimuthal direction. We do not resolve the Roche lobe at this
resolution, but since we are interested only in the large scale evolution
of the disk, this is not important. We will discuss the flow within the
Roche lobe and accretion processes in future papers. Using a low resolution
allows us to run longer simulations, which is important because the
drift velocities can be very low.
We take a constant initial surface density
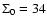 g
g
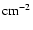 .
This surface density corresponds to the value at 5.2 AU in a disk
with 0.01
.
This surface density corresponds to the value at 5.2 AU in a disk
with 0.01
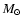 within 100 AU and a surface density profile that
falls off as r-1/2, or to about 13 AU in the Minimum Mass Solar Nebula.
The initial dust-to-gas ratio is 0.01. Using the radius of the planet's
orbit as our unit distance, the inner boundary is at r=0.4
and the outer boundary at r=2.5. The gas rotates with a slightly
sub-Keplerian velocity due to the radial pressure gradient. The dust
rotates exactly with the Keplerian velocity, initially. All radial
velocities are taken to be zero. The constant kinematic viscosity is set so
that the Shakura & Sunyaev (1973)
within 100 AU and a surface density profile that
falls off as r-1/2, or to about 13 AU in the Minimum Mass Solar Nebula.
The initial dust-to-gas ratio is 0.01. Using the radius of the planet's
orbit as our unit distance, the inner boundary is at r=0.4
and the outer boundary at r=2.5. The gas rotates with a slightly
sub-Keplerian velocity due to the radial pressure gradient. The dust
rotates exactly with the Keplerian velocity, initially. All radial
velocities are taken to be zero. The constant kinematic viscosity is set so
that the Shakura & Sunyaev (1973) 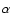 parameter equals 0.004 at r=1.
For a disk described above, the critical planet mass for gap opening is about 1 Jupiter mass (1
parameter equals 0.004 at r=1.
For a disk described above, the critical planet mass for gap opening is about 1 Jupiter mass (1
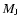 )
(Bryden et al. 1999). We varied the mass
of the planet between 0.001
)
(Bryden et al. 1999). We varied the mass
of the planet between 0.001
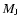 and 0.5
and 0.5
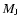 .
The boundary conditions are
as in Paardekooper & Mellema (2004), deriving from Godon (1996). They
are non-reflecting, so that all waves generated in the simulated region leave
the computational domain without further influencing the interior.
.
The boundary conditions are
as in Paardekooper & Mellema (2004), deriving from Godon (1996). They
are non-reflecting, so that all waves generated in the simulated region leave
the computational domain without further influencing the interior.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{Gg071_f1.eps}
\end{figure}](/articles/aa/full/2004/37/aagg071/Timg22.gif) |
Figure 1:
Dust flow near a 0.1
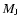 planet. Left panel: grey-scale plot of
the logarithm of the dust surface
density after 400 planetary orbits. Middle panel: logarithm of the
dust-to-gas ratio. Right panel: radial cut at
planet. Left panel: grey-scale plot of
the logarithm of the dust surface
density after 400 planetary orbits. Middle panel: logarithm of the
dust-to-gas ratio. Right panel: radial cut at  (opposite to the
planet). Solid line: gas surface density, dashed line: dust surface density
(opposite to the
planet). Solid line: gas surface density, dashed line: dust surface density
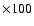 .
The filled circles indicate the 3:2, the 2:1 and the 3:1 mean
motion resonances. .
The filled circles indicate the 3:2, the 2:1 and the 3:1 mean
motion resonances. |
| Open with DEXTER |
5 Results
The evolution of the gas component is described in detail in
Paardekooper & Mellema (2004), and the drag forces on the gas are too small to
alter the flow. Therefore we focus on the evolution of the dust particles.
For the standard case we use a planet of 0.1
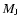 ,
and we
consider dust particles of 1 mm. In the left panel of Fig. 1
we can see that the dust particles are opening a gap, which leads to
variations in the dust-to-gas ratio of more than an order of magnitude
(middle panel). For this small planet these variations in dust density
are so large that the spiral waves are no longer visible.
The radial cut (right panel) shows that this planet is
not able to open up a gap in the gas, while the dust reacts more strongly
and shows a very dense ring at r=1.3 just outside a very low density gap.
,
and we
consider dust particles of 1 mm. In the left panel of Fig. 1
we can see that the dust particles are opening a gap, which leads to
variations in the dust-to-gas ratio of more than an order of magnitude
(middle panel). For this small planet these variations in dust density
are so large that the spiral waves are no longer visible.
The radial cut (right panel) shows that this planet is
not able to open up a gap in the gas, while the dust reacts more strongly
and shows a very dense ring at r=1.3 just outside a very low density gap.
Also shown in the right panel of Fig. 1 are positions of the 3:2, the 2:1 and the 3:1 mean motion resonances. Especially the 3:2
resonance (at r=1.25) plays a role in structuring the disk, while
only faint features can be seen at the other resonances. There also
exists a small density bump at corotation (r=1.0).
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{Gg071_f2.eps}
\end{figure}](/articles/aa/full/2004/37/aagg071/Timg23.gif) |
Figure 2:
Close-up on the gas density near the planet for a high resolution
AMR simulation (3 levels of refinement, so a resolution that is 8 times higher
than our standard resolution). The arrows indicate the relative velocity of
the dust compared to the gas. The typical relative velocity across the shocks
is 0.035
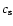 .
Note that the color scale is reversed with respect
to Fig. 1. .
Note that the color scale is reversed with respect
to Fig. 1. |
| Open with DEXTER |
Figure 2 shows a close-up on the gas density near the planet
in a high-resolution simulation. The high-density core can be seen, as
well as the spiral shocks. The arrows indicate the relative velocity
of the dust compared to the gas, showing that the dust decouples from
the gas near the spiral shocks. In the shocks the gas velocity is
reduced, and the gas is also deflected. The dust particles do not feel
the shock directly, but notice its presence by the drag forces
in the post-shock region. Figure 2 shows that it takes a
certain distance before the velocity difference between dust and gas
has disappeared again. Because of this, the flux of dust particles
streaming into the spiral wave is larger than in the case of a
perfectly coupled gas-dust mixture. Since the wave is responsible for
gradually pushing the gas and dust particles away from the orbit of
the planet this leads to a depletion of dust particles, and hence a
deeper gap in the dust distribution. The dust density is affected most
where the waves are the strongest, which is approximately at a radial
distance h from the orbit of the planet. This is where a low density
gap starts to form, leaving the particles at r=1 largely
unaffected. The particles moving to larger radii seem to get trapped in the 3:2 and the 2:1 mean motion resonances, creating the dense rings at
r=1.3 and r=1.6. Interestingly, it has been found that the Kuiper Belt
Objects also tend to accumulate at the the 3:2 and 2:1 mean motion resonances
with Neptune (Luu & Jewitt 2002). Whether this is related to the
effect we find, requires further study. Inside corotation, the combined
inward force due
to the spiral waves, the imposed radial temperature gradient and the
viscous gas flow is so large that basically all particles move over
the resonances quickly and end up near the wave-damping boundary where they
are absorbed completely, leaving an almost featureless inner disk.
Simulations with different planetary masses showed that the minimum planetary
mass for this mechanism to operate is 0.05
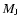 with particles of 1 mm.
with particles of 1 mm.
5.2 Simulated observations
![\begin{figure}
\par\includegraphics[width=17.3cm,clip]{Gg071_f3.eps}
\end{figure}](/articles/aa/full/2004/37/aagg071/Timg24.gif) |
Figure 3:
Logarithm of flux densities at 1 mm, normalized by the maximum and
convolved with a Gaussian of FWHM 2.5 AU, corresponding to a resolution of
12 mas at 140 pc.
Left panel: all particles follow the gas exactly (static dust evolution).
Middle panel: particles larger than the critical size decouple from the gas
(dynamic dust evolution). Right panel: the corresponding radial flux
densities. |
| Open with DEXTER |
To investigate the observational effects of the gas-dust decoupling we
simulate an image taken at a wavelength of 1 mm. The disk is optically thin at
this wavelength, and we put the planet at 5.2 AU. Calculations with different particle sizes showed that the minimum grain size
for gap formation is approximately 0.1 mm, with a very sharp transition.
We therefore assume that all particles larger than this critical size create
a gap, and smaller particles follow the gas exactly. To estimate the relative
amount of mass in these two families of particles we take an MRN size
distribution (Mathis et al. 1977), in which the number density of
particles is a power law in s with exponent -3.5. For a maximum particle
size of 5 mm most mass is in particles larger than our critical size, and as
a conservative assumption we take an equal amount of mass in the particles
smaller than 0.1 mm and in the larger particles. But since the opacity at
1 mm is dominated by particles with
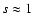 mm (Miyake & Nakagawa 1993),
the emission will be dominated by the larger particles. We used the size-dependent opacity data from Miyake & Nakagawa (1993) to calculate the flux
densities. In Fig. 3 the resulting flux densities are shown, convolved with
a Gaussian of FWHM 2.5 AU, which corresponds to an angular resolution of 12 mas at 140 pc (the Taurus star forming region). This resolution is
comparable to the maximum resolution of 10 mas that ALMA will achieve. In the
left panel of Fig. 3 we computed the flux under the assumption that
all particles move with the gas, as was done for example by
Wolf et al. (2002). There is a little dip visible due to the decrease
in density in the gas, but only when we include the density distribution of
Fig. 1 for the larger particles a clear gap emerges (middle panel
of Fig. 3). The right panel of Fig. 3 shows the radial
dependence of the flux density. From this panel we can see that the contrast
between the inside of the gap and the gap edges is enhanced from almost a
factor of two (dashed line) to more than an order of magnitude (solid line).
So the impact of the dynamics of the larger particles on the appearance of a
low-mass planet in a disk is considerable.
mm (Miyake & Nakagawa 1993),
the emission will be dominated by the larger particles. We used the size-dependent opacity data from Miyake & Nakagawa (1993) to calculate the flux
densities. In Fig. 3 the resulting flux densities are shown, convolved with
a Gaussian of FWHM 2.5 AU, which corresponds to an angular resolution of 12 mas at 140 pc (the Taurus star forming region). This resolution is
comparable to the maximum resolution of 10 mas that ALMA will achieve. In the
left panel of Fig. 3 we computed the flux under the assumption that
all particles move with the gas, as was done for example by
Wolf et al. (2002). There is a little dip visible due to the decrease
in density in the gas, but only when we include the density distribution of
Fig. 1 for the larger particles a clear gap emerges (middle panel
of Fig. 3). The right panel of Fig. 3 shows the radial
dependence of the flux density. From this panel we can see that the contrast
between the inside of the gap and the gap edges is enhanced from almost a
factor of two (dashed line) to more than an order of magnitude (solid line).
So the impact of the dynamics of the larger particles on the appearance of a
low-mass planet in a disk is considerable.
6 Summary
We have presented the first two-fluid calculations of a circumstellar disk
with an embedded planet. These models allow us to make predictions on the dust
distributions that will be observed in protoplanetary disks in the near
future.
For a reasonable disk mass (0.01
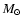 within 100 AU) the strong spiral
shocks near the planet are able to decouple the
larger
particles (
within 100 AU) the strong spiral
shocks near the planet are able to decouple the
larger
particles (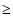 0.1 mm) from the gas. This leads to the formation of an
annular gap in the dust, even if there is no gap in the gas density. Because
the opacity at millimeter wavelengths is dominated by these larger particles,
the signatures of low-mass planets in disks can be stronger than previously
thought. The minimum mass for a planet to open a gap this way was found to
be 0.05
0.1 mm) from the gas. This leads to the formation of an
annular gap in the dust, even if there is no gap in the gas density. Because
the opacity at millimeter wavelengths is dominated by these larger particles,
the signatures of low-mass planets in disks can be stronger than previously
thought. The minimum mass for a planet to open a gap this way was found to
be 0.05
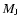 for 1 mm particles.
for 1 mm particles.
Acknowledgements
We wish to thank Carsten Dominik for carefully reading the manuscript. S.P.
and G.M. acknowledge support from the European Research
Training Network "The Origin of Planetary Systems'' (PLANETS, contract number
HPRN-CT-2002-00308).
- Bryden, G., Chen, X.,
Lin, D. N. C., Nelson, R. P., & Papaloizou,
J. C. B. 1999, ApJ, 514, 344 [NASA ADS] [CrossRef]
- Eulderink, F., &
Mellema, G. 1995, A&AS, 110, 587 [NASA ADS]
- Godon, P. 1996, MNRAS,
282, 1107 [NASA ADS]
- Klahr, H. H.,
& Henning, T. 1997, Icarus, 128, 213 [NASA ADS] [CrossRef]
- Kley, W. 1999, MNRAS,
303, 696 [NASA ADS] [CrossRef]
- Luu, J. X.,
& Jewitt, D. C. 2002, ARA&A, 40, 63 [NASA ADS]
- Mathis, J. S.,
Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef]
- Miyake, K., &
Nakagawa, Y. 1993, Icarus, 106, 20 [NASA ADS] [CrossRef]
-
Paardekooper, S.-J., & Mellema, G. 2004, A&A, in
preparation
(In the text)
- Papaloizou, J., &
Lin, D. N. C. 1984, ApJ, 285, 818 [NASA ADS] [CrossRef]
- Roe, P. L. 1981,
J. Comp. Phys., 43, 357 [NASA ADS] [MathSciNet]
- Shakura, N. I.,
& Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS]
- Strang, G. 1968,
Siam. J. Num. Analysis, 5, 506 [NASA ADS] [MathSciNet]
- Takeuchi, T., &
Artymowicz, P. 2001, ApJ, 557, 990 [NASA ADS] [CrossRef]
- Takeuchi, T., &
Lin, D. N. C. 2002, ApJ, 581, 1344 [NASA ADS] [CrossRef]
- Wolf, S., Gueth, F.,
Henning, T., & Kley, W. 2002, ApJ, 566, L97 [NASA ADS] [CrossRef]
Copyright ESO 2004
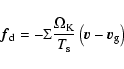
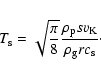
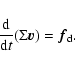
![\begin{figure}
\par\includegraphics[width=17cm,clip]{Gg071_f1.eps}
\end{figure}](/articles/aa/full/2004/37/aagg071/Timg22.gif)
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{Gg071_f2.eps}
\end{figure}](/articles/aa/full/2004/37/aagg071/Timg23.gif)
![\begin{figure}
\par\includegraphics[width=17.3cm,clip]{Gg071_f3.eps}
\end{figure}](/articles/aa/full/2004/37/aagg071/Timg24.gif)