A&A 425, 287-299 (2004)
DOI: 10.1051/0004-6361:20040521
S. J. Bradshaw1 - G. Del Zanna2 - H. E. Mason2
1 - Blackett Laboratory, Imperial College London, Prince
Consort Road, London SW7 2BZ, UK
2 -
Department of Applied Mathematics and Theoretical Physics, Centre
for Mathematical Sciences, University of Cambridge, Wilberforce
Road, Cambridge CB3 0WA, UK
Received 25 March 2004 / Accepted 1 June 2004
Abstract
We carry out a hydrodynamic simulation of a compact flare and find
significant non-equilibrium distributions for the ionisation balance
during the impulsive and gradual phases, which can strongly alter the
radiative emission. This has major implications for attempts to derive
the theoretical intensities of emission lines used for spectroscopic
diagnostic analyses of the plasma properties.
During the impulsive phase we find that the emissivities of He I, He II and C IV in the transition region can be strongly enhanced above their expected equilibrium values, followed by a significant reduction which increases the amount of chromospheric plasma ablated into the corona. Furthermore, during the flare heating the overall charge state of the coronal ions can be significantly lower than is suggested by an equilibrium ionisation balance and, therefore, line ratio measurements will yield plasma temperatures that are much greater than the formation temperature of the emitting ion.
During the gradual phase the emissivity at transition region temperatures remains suppressed, compared with its equilibrium value, with correspondingly reduced downflow velocities and increased radiative cooling time-scales.
Finally, we synthesise the emission as it would be detected by TRACE in its 171 Å and 195 Å wavelength bands, and find that the filter ratio technique can give reasonably good estimates of the plasma temperature in quiescence, though when the populations of Fe VIII, Fe IX, Fe X and Fe XII exhibit departures from equilibrium the temperatures derived from filter ratio measurements become unreliable.
Key words: Sun: flares - hydrodynamics - atomic processes - Sun: UV radiation
The current paper is the final of a series of three in which the consequences of a non-equilibrium ionisation balance for observations and theoretical models of the solar atmosphere are investigated. In Bradshaw & Mason (2003a, hereafter BM1) we simulated a loop cooling from coronal to transition region temperatures and in Bradshaw & Mason (2003b, hereafter BM2) we simulated a small-scale heating event with properties characteristic of a nanoflare. We used a new hydrodynamic code (HYDRAD), which is designed to couple the time-dependent ionisation balance equations to the hydrodynamic equations in a self-consistent manner. We found that non-equilibrium effects can become important in both scenarios, which are commonly assumed to occur in the solar atmosphere, and studied the consequences of a non-equilibrium ionisation balance for the radiative emission and the dynamics of the plasma. In the current paper we simulate a compact flare of moderate energy and follow the evolution of the plasma through the impulsive and gradual phases. The term compact flare describes a strong heating event that takes place in a closed magnetic loop and the field remains essentially unchanged for its duration.
Among the first self-consistent compact flare models were those of MacNeice et al. (1984), Nagai & Emslie (1984) and Fisher et al. (1985). Their computational codes modelled a chromosphere and a corona coupled via thermal conduction across a thin transition region, and followed the hydrodynamic response of an initially hydrostatic atmosphere to thick-target heating of the chromosphere. The simulations of MacNeice et al. (1984) and Nagai & Emslie (1984) under-resolved the transition region, whereas the computational code used by Fisher et al. (1985) included an adaptive regridding scheme (McClymont & Canfield 1983) to ensure sufficient resolution everywhere along the loop.
Several thermal heating models of compact flares have also been published. Nagai (1980), Nagai et al. (1983), Cheng et al. (1983), Pallavicini et al. (1983) and MacNeice (1986) have all investigated the effect of depositing the flare energy at the loop apex. The transition region was under-resolved by all of these authors with the exception of MacNeice (1986), who incorporated an adaptive regridding scheme into the computational code.
The constraints imposed on the allowable time-step by the spatial-scale of a properly resolved transition region mean that it can be prohibitively expensive (in terms of real-time and the monetary cost of computing time) to carry out a complete hydrodynamic simulation of a flare from the initial input of heat, through the downward propagation of the transition region and the upward evaporation of chromospheric material, to the eventual cooling and condensation of the evaporated material back onto the chromosphere (MacNeice 1986).
A major consequence of insufficient resolution in the transition region is the under-estimation of the conducted heat flux, which is due to the artificial limitation of the temperature gradient to a resolution dependent maximum value. This leaves energy bottled up in the corona and may result in the over-estimation of coronal temperatures, as well as the under-estimation of chromospheric ablation velocities and coronal densities, in numerical simulations.
The physical treatment of the conducted heat flux in the transition region was considered in detail by MacNeice et al. (1984), Nagai & Emslie (1984) and Fisher et al. (1985). The classical treatment of Spitzer (1962), a common feature of both hydrostatic and hydrodynamic models to-date, allows the conducted heat flux to increase without limit as the temperature gradient steepens. Eventually the conducted flux calculated in this way will become unphysical because its upper limit is prescribed by the free-streaming value, which occurs when all of the electrons move at the thermal speed in the same direction. MacNeice et al. (1984) and Nagai & Emslie (1984) used the lesser of the classical (Spitzer) heat flux and the saturated flux as the actual conducted heat flux. However, there are associated problems because the derivative of the conducted heat flux, which appears in the energy balance, is not treated self-consistently. Fisher et al. (1985) adopted a scheme whereby there is a smooth transition between the values for the classical and saturated regimes. Karpen & Devore (1987) included the effects of non-local thermal transport in their simulations of solar flares.
Antiochos & Krall (1979), Doschek et al. (1982) and Gan & Fang (1990) have
studied the gradual or cooling phase of a flare, while circumventing
consideration of the impulsive phase, by simulating the cooling of a
flare loop in an initial hydrostatic
equilibrium. Antiochos & Krall (1979) and Doschek et al. (1982)
took as their initial conditions an apex temperature of
![]() K, a density of
K, a density of
![]() cm-3 and a total loop
length of
cm-3 and a total loop
length of
![]() cm. Gan & Fang (1990) used an initial apex
temperature of
cm. Gan & Fang (1990) used an initial apex
temperature of
![]() K, a density of 1010 cm-3 and
a total loop length of
K, a density of 1010 cm-3 and
a total loop length of
![]() cm.
cm.
To simulate the onset of the gradual phase Antiochos & Krall (1979) and Doschek et al. (1982) simply switched off the heating term in the energy balance, whereas Gan & Fang (1990) added a flare heating component to the energy balance and linearly decreased it to zero during the first 10 s of their simulation. During the earliest part of the gradual phase thermal conduction continued to drive chromospheric evaporation and all of the models predicted similar velocities for the ablated material. This is consistent with observations, which have shown that the peak in emission measure is reached after the peak in temperature.
Cargill et al. (1995) derived analytical formulae relating the total
cooling time to the loop half-length and the pressure or density (in
the corona) when cooling commences. They assumed that cooling of the
flare plasma is first dominated by conduction and then by radiation,
giving formulae for the cooling time-scales of both phases:
There are a number of possibilites that may explain the
different cooling time-scales obtained by Antiochos & Krall (1979) and
Doschek et al. (1982), and Gan & Fang (1990). The earlier two papers
adopted very different initial conditions to the latter paper, which
could influence the nature of the plasma cooling. For example, from
Eq. (1) above, it would appear that Antiochos & Krall (1979) and
Doschek et al. (1982) should have obtained the longest cooling
time-scales because of the higher density used in their initial
conditions, however, this is clearly not the case and Eq. (2)
suggests that in fact radiative cooling dominates in their
simulations. This is further supported by the fact that
Gan & Fang (1990) used a loop length an order of magnitude greater than
the other two papers and Eq. (1) shows that
![]() .
A
reasonably self-consistent picture then emerges from these
considerations, where conductive cooling quickly gives way to an
extremely rapid radiative cooling in the case of Antiochos & Krall (1979) and
Doschek et al. (1982), whereas in the case of Gan & Fang (1990) both the
conductive and radiative cooling time-scales are greater.
.
A
reasonably self-consistent picture then emerges from these
considerations, where conductive cooling quickly gives way to an
extremely rapid radiative cooling in the case of Antiochos & Krall (1979) and
Doschek et al. (1982), whereas in the case of Gan & Fang (1990) both the
conductive and radiative cooling time-scales are greater.
The results of Antiochos & Krall (1979) and Doschek et al. (1982) may have been influenced by substantially over-estimating the chromospheric radiative energy loss and under-resolving the transition region. Gan & Fang (1990) carried out a careful investigation of the chromospheric radiative losses in order to choose an appropriate radiative loss function for low temperature and high density plasma, and they also employed a higher resolution computational grid. If radiation is over-estimated in the transition region and the chromosphere then more heat via thermal conduction from the corona is required to balance the energy loss. If the transition region is under-resolved then it may not be able to handle the necessary heat flux and this results in its rapid ascent along the loop (as in Doschek et al. 1982) because the plasma beneath it quickly cools to chromospheric temperatures. In Gan & Fang (1990) the transition region continued to move downward during the early part of the gradual phase and then remained stationary for a long while, before beginning to ascend at the latter stages of the gradual phase.
Evidently it is necessary to carry out hydrodynamic simulations for the entire duration of a flare in order to perform a self-consistent study. The nature of cooling clearly depends upon the properties of the flare plasma, which in turn depend upon the details of how the plasma was heated.
In light of the work reviewed above we decided to apply HYDRAD to the problem of self-consistently modelling a solar flare throughout every phase of its evolution and to investigate the effects of non-equilibrium processes on the ion populations and their associated radiative emission. Thus, quantitative predictions can be made regarding the consequences of these non-equilibrium processes for theoretical and observational studies of flaring plasma.
The paper is structured as follows: Sect. 2 gives details of our model; Sect. 3 describes the results from the impulsive phase of the flare; Sect. 4 describes the results from the gradual phase of the flare; Sect. 5 discusses the observational consequences by synthesising the emission detectable by the TRACE 171 Å and 195 Å wavelength bands; and Sect. 6 gives an overall summary of the results and conclusions.
The nature of the flare heating mechanism chosen for the current work is a thermal perturbation at the apex of the loop, rather than a mechanism such as beam heating in the chromosphere. This choice was partly motivated by the conclusions of others that a thermal heating mechanism produces results more consistent with observations (Peres et al. 1987; Betta et al. 2001) and partly by observations themselves where evidence for heating via magnetic reconnection events taking place near the loop apex has been found (Masuda et al. 1995; Shibata et al. 1995). However, there is also evidence that some flares are driven by magnetic reconnection with newly emerging flux near loop footpoints (Fludra et al. 1995) and consequently the hydrodynamic simulations performed here are applicable only to compact flares driven by an assumed thermal input of energy in the apex region of the loop.
The thermal perturbation applied to the initial loop atmosphere at
t>0 is of the form:
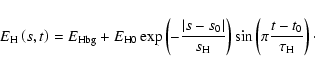 |
(3) |
The following values were adopted for the parameters:
![]() erg cm-3 s-1,
erg cm-3 s-1,
![]() erg cm-3 s-1,
erg cm-3 s-1,
![]() cm,
cm,
![]() cm, t0 = 0 s,
cm, t0 = 0 s,
![]() = 300 s,
= 300 s,
which describe a heating pulse delivered symmetrically about the loop
apex with a maximum volumetric heat input of
0.1 erg cm-3 s-1, a spatial-scale of
![]() cm and
a period of 300 s. Only one pulse is delivered to the loop in each
simulation and so only constant background heating remains after 300 s. The loop eventually returns to its initial hydrostatic
equilibrium. The amount of heat delivered to the loop by the pulse is
about
cm and
a period of 300 s. Only one pulse is delivered to the loop in each
simulation and so only constant background heating remains after 300 s. The loop eventually returns to its initial hydrostatic
equilibrium. The amount of heat delivered to the loop by the pulse is
about
![]() erg cm-2, which is toward the low-energy
regime of typical flares, though the plasma still reaches temperatures
characteristic of soft X-ray emission, and velocities of
200 km s-1.
erg cm-2, which is toward the low-energy
regime of typical flares, though the plasma still reaches temperatures
characteristic of soft X-ray emission, and velocities of
200 km s-1.
A new initial loop atmosphere was derived with extended chromospheric
regions of
![]() cm. The extended chromospheres are
necessary because the substantially increased conducted heat flux
means that the transition region can be expected to propagate further
than the
cm. The extended chromospheres are
necessary because the substantially increased conducted heat flux
means that the transition region can be expected to propagate further
than the
![]() cm depth of the chromospheres in the
initial atmosphere used in BM1 and BM2. Consequently, a deeper
chromosphere is required to avoid the numerical influence of boundary
effects such as wave reflections and the loss of mass and energy from
the loop.
cm depth of the chromospheres in the
initial atmosphere used in BM1 and BM2. Consequently, a deeper
chromosphere is required to avoid the numerical influence of boundary
effects such as wave reflections and the loss of mass and energy from
the loop.
The properties of the initial atmosphere are similar to the average
loop properties found by Aschwanden & Alexander (2001), Table 3, for
their study of the Bastille Day flare, and also used by
Tsiklauri et al. (2004) who carry out a hydrodynamical simulation of
this event. In summary: the length of the loop used in the present
study is
![]() cm (somewhat longer than the average length
of
cm (somewhat longer than the average length
of
![]() cm reported by Aschwanden & Alexander 2001); the coronal part of the loop has a temperature of
cm reported by Aschwanden & Alexander 2001); the coronal part of the loop has a temperature of
![]() K at its apex; and the electron number density is
approximately
K at its apex; and the electron number density is
approximately
![]() cm-3. Both the temperature and
the density are slightly greater than the initial values used by
Tsiklauri et al. (2004), though not significantly so. The duration of
the heating event in the present study (300 s) is also of the same
order as the longer time-scales in the range chosen by
Tsiklauri et al. (2004). However, it is not the intention of the
authors to attempt a simulation of the individual loops comprising
the Bastille Day event in the present study.
cm-3. Both the temperature and
the density are slightly greater than the initial values used by
Tsiklauri et al. (2004), though not significantly so. The duration of
the heating event in the present study (300 s) is also of the same
order as the longer time-scales in the range chosen by
Tsiklauri et al. (2004). However, it is not the intention of the
authors to attempt a simulation of the individual loops comprising
the Bastille Day event in the present study.
The response of the plasma to the flare heating was calculated by
solving the one-dimensional, conservative form of the hydrodynamic
equations in curvilinear coordinates (taken along the loop in the
direction of the magnetic field):
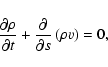 |
(4) |
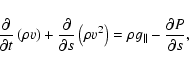 |
(5) |
![$\displaystyle \frac{ \partial E }{ \partial t } + \frac{ \partial }{ \partial s }
\left[\left(E+P\right)v\right]$](/articles/aa/full/2004/37/aa0521-04/img26.gif) |
= | 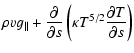 |
(6) |
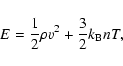 |
(7) |
| (8) |
Details of the boundary conditions, the numerical methods employed, and the results of numerical tests designed to assess the stability and the accuracy of the hydrodynamic code are given in BM1 and BM2.
As in BM1 and BM2, two simulations were performed: one employing a straightforward equilibrium treatment of the ion populations (simulation A) and the associated radiative emission; and the other employing a full non-equilibrium treatment (simulation B). The equilibrium ionisation balances were calculated using the same ionisation and recombination rates (Mazzotta et al. 1998) as those used to solve the system of time-dependent ionisation balance equations for each element and the element abundances were assumed to be coronal. The individual ion emissivities were calculated using the CHIANTI atomic database (Dere et al. 1997; Young et al. 2003).
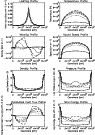 |
Figure 1: Time series of the heating, temperature, velocity, sound speed, density, pressure, conducted heat flux and total energy along the length of the loop at: 0 s (solid), 60 s (dotted), 90 s (dashed), 120 s (dash-dot), 150 s (dash-dot-dot-dot) and 210 s (long-dashed). The profiles are taken from simulation A. |
| Open with DEXTER | |
The impulsive phase of the flare for the purposes of the current work is defined as the period during which the plasma reaches its maximum temperature and the ablated chromospheric material reaches its maximum velocity. Thereafter, the flare plasma begins to cool and enters its gradual phase. Figure 1 shows the heating profile which decays exponentially in space either side of the maximum at the loop apex and obeys a sinusoidal variation in time. The rate of energy input rises from zero, reaches its peak at 150 s and returns to zero at 300 s. Figure 1 also shows time series of the profiles for a number of physical properties of the plasma between 0 s and 210 s. Figure 2 shows an enlarged view of the same profiles in the left-hand footpoint region of the loop. There are no discernible differences in the profiles of these properties between simulations A and B, during the impulsive phase of the flare, because the energy balance in the coronal region of the loop is dominated by heating, thermal conduction and, toward the end of the impulsive phase, convection. Though the dynamical evolution of the loop plasma is almost identical in simulations A and B, there remain consequences for the overall radiative emission and the diagnostic line intensities, which will affect the results and conclusions drawn from observations and are discussed in the following sections.
 |
Figure 2: Time series of the heating, temperature, velocity, sound speed, density, pressure, conducted heat flux and total energy in the left-hand footpoint region of the loop at: 0 s (solid), 60 s (dotted), 90 s (dashed), 120 s (dash-dot), 150 s (dash-dot-dot-dot) and 210 s (long-dashed). The profiles are taken from simulation A. |
| Open with DEXTER | |
After 60 s of evolution the temperature, pressure and the total energy
in the coronal region of the loop have dramatically increased, by a
factor of 3 at the apex, and downflows of around
![]() cm s-1 have developed. The sound speed has also increased
in response to the rising temperature and is never exceeded by the
plasma velocity in the coronal region. The density remains almost
constant since the downflows are not substantial enough to carry a
significant amount of material away. The conducted heat flux has also
increased, by more than an order of magnitude at its peak, in response
to the increasing coronal temperature and the steepening coronal
temperature gradient.
cm s-1 have developed. The sound speed has also increased
in response to the rising temperature and is never exceeded by the
plasma velocity in the coronal region. The density remains almost
constant since the downflows are not substantial enough to carry a
significant amount of material away. The conducted heat flux has also
increased, by more than an order of magnitude at its peak, in response
to the increasing coronal temperature and the steepening coronal
temperature gradient.
Figure 2 shows that after 90 s the conduction front associated with the coronal heating event has propagated into the chromosphere to a depth of about 500 km and increased the temperature of the plasma to values on the order of 105 K. The density and pressure profiles show that a large amount of chromospheric material has been ablated into the corona due to the inability of the chromosphere to efficiently radiate the excess energy. Material has also been pushed further down into the chromosphere by the oppositely directed flows that arise in response to the ablation.
The temperature, the conducted heat flux and the total energy continue
to increase between 90 s and 210 s in the coronal region of the loop
as the ablation accelerates and fills it with material. The
temperature in the apex region of the loop reaches
![]() K;
the conducted heat flux peaks at
K;
the conducted heat flux peaks at
![]() erg cm-2 s-1 compared with a peak value at t = 0 s
of
erg cm-2 s-1 compared with a peak value at t = 0 s
of
![]() erg cm-2 s-1; and the pressure increases
by a factor
erg cm-2 s-1; and the pressure increases
by a factor ![]() in most of the coronal region (as does the total
energy). The upflows reach velocities close to
in most of the coronal region (as does the total
energy). The upflows reach velocities close to
![]() cm s-1 and substantially increase the density of the
coronal plasma. The upflowing material in each half of the loop
eventually collides, producing a localised enhancement in the density,
pressure and total energy in the apex region. The density enhancement
is a factor of 3 greater than the initial apex value. The pressure and
total energy enhancement is a factor of 16. The observational
consequences would be a localised enhancement in the measured
intensity of radiative emission.
cm s-1 and substantially increase the density of the
coronal plasma. The upflowing material in each half of the loop
eventually collides, producing a localised enhancement in the density,
pressure and total energy in the apex region. The density enhancement
is a factor of 3 greater than the initial apex value. The pressure and
total energy enhancement is a factor of 16. The observational
consequences would be a localised enhancement in the measured
intensity of radiative emission.
In the footpoint region the conduction front continues to propagate
into the chromosphere, reaching a depth of 750 km at 210 s, as the
temperature of the initially chromospheric material rises to a maximum
value of
![]() K. The conducted heat flux carried by the
transition region increases to values on the order of 106 to
107 erg cm-2 s-1, which forces it to steepen
dramatically. The pressure and the total energy in the chromosphere
and the transition region are enhanced by a maximum factor of about 8
to 10 over their initial values. The maximum chromospheric density
enhancement is by a factor of 6. The downward propagating compression
wave associated with the conduction front is eventually damped due to
the increasing density as a function of depth in the chromosphere,
which acts to decelerate the condensation.
K. The conducted heat flux carried by the
transition region increases to values on the order of 106 to
107 erg cm-2 s-1, which forces it to steepen
dramatically. The pressure and the total energy in the chromosphere
and the transition region are enhanced by a maximum factor of about 8
to 10 over their initial values. The maximum chromospheric density
enhancement is by a factor of 6. The downward propagating compression
wave associated with the conduction front is eventually damped due to
the increasing density as a function of depth in the chromosphere,
which acts to decelerate the condensation.
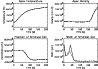 |
Figure 3: Plots of apex temperature, apex density, the position of the smallest grid cell and the width of the smallest grid cell as a function of time. The results from simulation A are plotted as a solid line and those from simulation B are plotted as a dashed line. |
| Open with DEXTER | |
Figure 3 shows the change in the apex temperature and density as a function of time for simulations A and B. The ablated material does not reach the apex of the loop until about 170 s, at which time the density begins to increase extremely rapidly as the material ablated from each chromosphere collides. The peak density at the apex reaches a slightly greater value in simulation B than in simulation A. The physical reason for this will be discussed later.
Figure 3 also shows the response of the adaptive regridding scheme to the flare heating by plotting the position of the smallest grid cell and its size as functions of time. The qualitative behaviour is much the same in simulations A and B. Between 0 s and 60 s the coronal conduction front propagates toward the chromosphere and the position of the smallest grid cell remains fixed at the base of the transition region. At 60 s the conduction front reaches the base of the transition region and forces it to propagate into the chromosphere. Between 60 s and 100 s the adaptive regridding scheme tracks the transition region as it penetrates to greater depths in the chromosphere and ensures that it is always well-resolved by placing grid cells of the required size at its base. The position of the smallest grid cell remains approximately constant between 100 s and 210 s. The width of the smallest grid cell fluctuates in time between 0 s and 40 s as the equilibrium solution in the footpoint region relaxes slightly, though there are clearly no quantitative changes to the physical properties of the plasma.
The smallest cell-width in both simulations is reached at about
120 s. In simulation A it is about
![]() cm and in
simulation B about 103 cm. According to Craig et al. (1982), a heat
flux on the order of 108 erg cm-2 s-1 carried by the
transition region requires a resolution of less than
cm and in
simulation B about 103 cm. According to Craig et al. (1982), a heat
flux on the order of 108 erg cm-2 s-1 carried by the
transition region requires a resolution of less than
![]() cm. In Fig. 2 the conducted heat flux peaks at just
below 108 erg cm-2 s-1. Therefore, the results from
HYDRAD represent a substantial improvement over earlier work since the
transition region structure has been successfully resolved on the
required spatial-scales of just a few metres, rather than kilometres.
cm. In Fig. 2 the conducted heat flux peaks at just
below 108 erg cm-2 s-1. Therefore, the results from
HYDRAD represent a substantial improvement over earlier work since the
transition region structure has been successfully resolved on the
required spatial-scales of just a few metres, rather than kilometres.
Table 1: Peak population fractions and corresponding temperatures, in equilibrium, for the selected transition region ions.
The behaviour of the most strongly emitting ions can be investigated
with HYDRAD and the consequences of non-equilibrium effects for the
observable line intensities and the overall radiative emission can be
assessed. The transition region ions selected for the current study,
the peak population fractions and corresponding temperatures, in
equilibrium, are given in Table 1.
(a) Helium
In equilibrium, the population fraction of He I decreases from 1 to
become almost negligible over a temperature interval of
![]() K and He II mostly exists over a temperature interval
of
K and He II mostly exists over a temperature interval
of
![]() K.
K.
Figure 4 shows that at 60 s the conduction front reaches the chromosphere and the emissivities of He I and He II in simulation B are increased by an order of magnitude in comparison with simulation A. This is extremely significant as there are well-known intensity enhancements of helium emission lines in the solar atmosphere (Jordan 1975) that have been difficult to account for. Smith & Jordan (2002) found that when non-thermal motions in the transition region carry helium ions across the strong temperature gradient and expose them to collisional excitation by high temperature electrons, the observed intensities of the resonance lines of He I and He II can be explained. A similar effect is operating in simulation B, though in this case the ions are stationary and the conduction front is propagating through the plasma, exposing the slowly ionising He I and He II to high temperatures, and thus enhancing the intensities of the resonance lines.
The decrease in the emissivities of He I and He II after 90 s is due to the downflows that transport He III from higher temperature regions, while carrying He I and He II into the dense chromosphere where He II quickly recombines and where He I emits only weakly. By 120 s the He I and He II ionisation fronts have actually propagated farthest in simulation B, which demonstrates the potential importance of accounting for convective transport when calculating ion populations.
He II is one of the strongest emitters at 105 K (the peak of the
optically-thin radiative loss function) and this depletion in its
population results in a significant decrease in the overall helium
emission.
(b) Carbon
Figure 5 shows the response of the C III and C IV populations
and their associated emissivities as the conduction front reaches and
heats the chromosphere. The emission from C III (
![]() K) peaks at about 104.9 K and the emission from C IV
(
K) peaks at about 104.9 K and the emission from C IV
(
![]() K) peaks at about 105.1 K in
equilibrium.
K) peaks at about 105.1 K in
equilibrium.
At 60 s C III exhibits qualitatively the same behaviour as He II. There is close agreement between simulations A and B in terms of the peak population fraction and the same broadening of the population distribution toward higher temperatures, as a result of the non-zero ionisation time-scale, is evident. The agreement also remains close at 80 s, though the C III ionisation front clearly trails the conduction front in simulation B.
By 90 s there is a substantial decrease in the population of C III in simulation B and by 120 s the ionisation front has again propagated to a greater depth than in simulation A. The C III emissivity profiles follow the behaviour of the ion populations at the corresponding times and the total C III emissivity is reduced by a factor of 4 at 120 s in simulation B compared with its value in simulation A.
The behaviour of C IV is rather different. At 60 s the population of C IV is greater by a factor of 2 in simulation B than in simulation A, with a corresponding increase in its emissivity. A factor of 2 enhancement of the population of C IV, under similar circumstances, was also found by Sarro et al. (1999). At later times the population of C IV dramatically decreases in simulation B, becoming a factor of 3 less than in simulation A between 90 s and 120 s. As with He II the depletion of C III and C IV is due to the downflows that transport higher ionisation stages from further up the loop, while carrying lower ionisation stages into the chromosphere where they quickly recombine. Again, this depletion in the populations of such strongly emitting ions results in a significant decrease in the overall carbon emission.
One question naturally arises: why is there such a large enhancement in the population of C IV at 60 s? The answer lies in the shape of the equilibrium population distribution. The C IV population distribution is asymmetric, with a high temperature wing that extends significantly further up the loop than that of C III. In fact, asymmetric distributions, with a high temperature wing, are a common feature of Li-like ion populations. For example, the population distributions of O VI and Si XII also possess such a distribution. In simulation B ions are transported from the high temperature wing of the distribution, by the downflows, and are added to the peak population. Thus, a large enhancement of the ion population ensues, with a corresponding increase in the emissivity.
These results provide further evidence that a substantial increase or
spike in the intensity of C IV (or indeed any Li-like ion) emission,
over and above that which one might expect from density effects alone,
could act as a signature for the presence of non-equilibrium ion
populations.
(c) Peak emissivities as a function of time
Figure 6 shows the peak emissivities of carbon and helium, together with oxygen and magnesium for the purpose of comparison. An initial increase in the peak emissivity can be expected from the transition region ions as the plasma is heated by the downward propagating conduction fronts. However, the overall tendency for the transition region ions that emit close to the peak of the optically-thin radiative loss curve to become depleted at later times, when non-equilibrium effects are taken into account, acts to reduce the peak emissivity.
Recall that in Fig. 3 the peak density at the apex reaches a slightly greater value in simulation B than in simulation A. The physical reason for this is due to the supressed radiative emission in simulation B. The additional energy provided by the conducted heat flux cannot be radiated as efficiently, consequently convection is enhanced and the upflows reach higher velocities. Thus, more material is ablated into the corona.
Table 2: Peak population fractions and corresponding temperatures, in equilibrium, for the selected coronal ions.
The coronal ions selected for the current study are all different
charge states of iron since it is by far the strongest emitter at
coronal temperatures. The particular ions, peak population fractions
and corresponding temperatures are listed in Table 2. The
choice of ions provides comprehensive temperature coverage between
105.8 and 106.9 K. The ability to follow successive
ionisation stages of elements as the plasma evolves provides a
powerful tool for spectroscopic diagnostics, and relating the
ionisation history of the plasma to its current ionisation state
provides useful clues to understanding its evolution and
properties. The usefulness of this approach will become particularly
apparent when the non-equilibrium behaviour of Fe XIV to Fe XIX is
investigated.
(a) Fe IX to Fe XIII
Figure 7 shows enhanced peak population fractions at 60 s in simulation B for all of these ions, except Fe IX, and a broadening of the population distributions toward higher temperatures, which increases with the ionisation stage. By 90 s the upper coronal region is entirely depleted of Fe IX to Fe XIII in both simulations. At 210 s in the cooler and denser regions of the loop, the population distributions of Fe IX and Fe X are in fairly close agreement between simulations A and B. However, the peak population fractions of Fe XII and Fe XIII in simulation B are lower than their equilibrium values.
Figure 9 shows the total Fe IX to Fe XIII (excluding Fe XI)
emissivity profile for simulations A and B. At 60 s the emissivity is
clearly increased in simulation B and exhibits a fairly broad plateau
at around s = 109 cm, compared with its more sharply peaked profile
in simulation A. However, as expected from the behaviour of the ion
populations, the emission from the cooler and denser regions of the
loop remains in equilibrium. By 210 s the entire emissivity profile in
simulation B is close to equilibrium.
(b) Fe XIV to Fe XVII
Figure 8 follows the ionisation of successive stages of iron
from Fe XIV to Fe XVII, between 0 s and 210 s. The ionisation fronts
of the higher stages follow the lower stages as they propagate down
the loop. At 60 s, in simulation B, the populations of both Fe XIV and
Fe XV are substantially enhanced over their equilibrium distributions
in the upper corona. The difference between the Fe XIV populations at
![]() cm (
cm (
![]() K) is a factor of
28. The difference between the Fe XV populations at the same location
is a factor of 6. The Fe XIV and Fe XV populations are considerably
depleted below s = 109 cm, compared with their equilibrium
distributions. The population of Fe XVI at 60 s in simulation B is
also enhanced toward higher temperatures and depleted toward lower
temperatures compared with its equilibrium distribution.
K) is a factor of
28. The difference between the Fe XV populations at the same location
is a factor of 6. The Fe XIV and Fe XV populations are considerably
depleted below s = 109 cm, compared with their equilibrium
distributions. The population of Fe XVI at 60 s in simulation B is
also enhanced toward higher temperatures and depleted toward lower
temperatures compared with its equilibrium distribution.
The behaviour of Fe XVII in simulation B is markedly different, as its
population at 60 s is significantly depleted everywhere along the loop
in comparison with its equilibrium distribution. The slight bump in
the Fe XVII population at
![]() cm in simulation B is
coincident with the peak downflow velocity and could therefore be due
to the transport of Fe XVII from further up the loop. The reason for
the substantial departure of Fe XVII from its equilibrium distribution
can be easily understood in terms of the behaviour of the lower
ionisation stages, which, as mentioned above, demonstrates the
usefulness of the capability to follow the ionisation history of the
plasma. The enhanced populations of Fe XIV, Fe XV and Fe XVI at 60 s
in simulation B have consequences for the populations of the higher
ionisation stages. Clearly, they can't all be enhanced because of the
requirement that the total number of ions belonging to a particular
element must be conserved. Therefore, an enhancement of the lower
ionisation stages must result in a depletion of the higher ionisation
stages at the same location.
cm in simulation B is
coincident with the peak downflow velocity and could therefore be due
to the transport of Fe XVII from further up the loop. The reason for
the substantial departure of Fe XVII from its equilibrium distribution
can be easily understood in terms of the behaviour of the lower
ionisation stages, which, as mentioned above, demonstrates the
usefulness of the capability to follow the ionisation history of the
plasma. The enhanced populations of Fe XIV, Fe XV and Fe XVI at 60 s
in simulation B have consequences for the populations of the higher
ionisation stages. Clearly, they can't all be enhanced because of the
requirement that the total number of ions belonging to a particular
element must be conserved. Therefore, an enhancement of the lower
ionisation stages must result in a depletion of the higher ionisation
stages at the same location.
At later times the populations of Fe XIV to Fe XVII exhibit significant departures from equilibrium, though as the coronal density increases, due to the ablation of chromospheric material, the population distributions in simulations A and B begin to agree more closely. At 210 s, when the coronal density has increased by a factor of 3, the population distributions of Fe XIV, Fe XV and Fe XVI are in good agreement between simulations A and B. The population distribution of Fe XVII in simulation B is near equilibrium in the cooler and denser regions of the loop, below s = 109 cm, and it is enhanced in the upper coronal region.
Figure 9 also shows the total emissivity profiles for Fe XIV
to Fe XVII. At 60 s the emissivity is considerably greater toward
higher temperatures in simulation B than in simulation A, and
significantly reduced toward lower temperatures. At later times in
simulation B the emissivity profile approaches equilibrium toward
lower temperatures, as the density increases, though remains slightly
increased toward higher temperatures. This is a result of the greater
proportion of more strongly emitting lower ionisation stages in
simulation B.
(c) Fe XVIII to Fe XIX
The top four panels of Fig. 10 show the population distributions of Fe XVIII and Fe XIX from 160 s to 210 s for simulations A and B. In simulation A the population of Fe XVIII is significant in the upper coronal region of the loop and does not change appreciably between 160 s and 210 s. In contrast, the population of Fe XVIII in simulation B remains negligible until 190 s, at which time the ionisation rate increases sufficiently, due to the ablated chromospheric material filling the corona, that the population of Fe XVIII begins to increase. The differences in the Fe XIX population profiles between simulations A and B are especially interesting because Fe XIX makes no appearance at all in simulation B.
This is of particular relevance because Fe XIX contains an important flare line (592 Å) and were it not to be observed during a flare, then, under the assumption that the ion populations remain in equilibrium, one might conclude that much lower temperatures than those characteristic of Fe XIX emission were reached. In reality, however, simulation B has demonstrated that extremely high temperatures could be accompanied by emission characterised by relatively low temperature lines. Furthermore, if emission from Fe XIX is observed, then, based upon the assumption of an equilibrium ionisation balance, one might also conclude that the plasma temperature is much cooler than in reality. This is because significantly higher temperatures need to be reached in simulation B before the population of Fe XIX becomes significant.
The behaviour of successive ionisation stages in simulation B also
indicates that the departures from equilibrium become larger with
increasing ionisation stage, so these considerations may be even more
important for understanding the flare lines emitted by Fe XXIV, for
example. The reason for this is that line intensities
generally tend to increase with increasing temperature and, since the
time-scales for excitation and decay are shorter than for ionisation
and recombination, the intensities of lines emitted by Fe XXIV could
be underestimated, particularly if the peak non-equilibrium ion
population is greater than the peak equilibrium ion
population. Furthermore, for the same reason, the intensity ratio of
two lines emitted by an ion of high charge state would yield plasma
temperatures much greater than the equilibrium formation temperature
of the emitting ion.
(d) Total iron emissivity
The bottom two panels of Fig. 10 show the total iron emissivity profile for simulations A and B. The greater proportion of lower ionisation stages to higher stages in the coronal region that arises in simulation B acts to substantially enhance the emissivity over that in simulation A for the first 90 s. After 90 s, as the density begins to increase toward lower coronal temperatures due to the chromospheric evaporation, the emissivity profiles in simulation B tend toward equilibrium and by 210 s they match almost exactly with simulation A.
However, at later times and higher coronal temperatures the density does not increase as rapidly because the ablated material takes longer to reach the upper regions of the loop. At 210 s, in simulation B, the emissivity at the apex remains slightly enhanced over its equilibrium value, despite the significant local density increase as the material ablated from each chromosphere collides.
The gradual phase of the flare, for the purposes of the current study,
is defined as the period of evolution after the peak temperature has
been reached (Cargill et al. 1995). In Sect. 3 this
was seen to be 210 s after the impulsive heating mechanism was
switched on. Figures 11 to 13 show the evolution of
the flare plasma in terms of its temperature, velocity and density,
between 300 s and 8000 s (5000 s for simulation B due to time
constraints), as it cools from its peak temperature of
![]() K and gradually returns to hydrostatic equilibrium.
K and gradually returns to hydrostatic equilibrium.
Between 300 s and 800 s the coronal region of the loop cools to
approximately its initial temperature of
![]() K at the
apex. The rate of cooling is greater in simulation A than in
simulation B because the non-equilibrium processes act to suppress the
radiative losses from the transition region.
K at the
apex. The rate of cooling is greater in simulation A than in
simulation B because the non-equilibrium processes act to suppress the
radiative losses from the transition region.
At 300 s the upflows remain substantial and reach almost 107 cm s-1. The maximum velocity in simulation B is greater than in simulation A as a consequence of the suppressed radiative emission. The work of Antiochos & Krall (1979), Doschek et al. (1982) and Gan & Fang (1990), discussed in Sect. 1, also found that the ablation continued well into the gradual phase and significantly increased the coronal density. The results from HYDRAD are in good agreement with this previous work and are consistent with observations, which show the peak in the emission measure from a flaring loop is reached after the peak in temperature.
By 500 s material has begun to drain out of the upper coronal region,
reaching peak downflow velocities of almost
![]() cm s-1 at 700 s in simulation A and just under
cm s-1 at 700 s in simulation A and just under
![]() cm s-1 in simulation B. At 800 s the loop reaches its
initial apex temperature, though the coronal density is far greater
than at t = 0 s. It was also shown in BM1 that loops tend to cool
more quickly than they drain. The over-density of loops observed by
TRACE at temperatures around 106 K, compared with hydrostatic
equilibrium models, could thus be explained by cooling from much
greater temperatures after a period of chromospheric evaporation, in
agreement with the findings of Warren et al. (2002) and
Spadaro et al. (2003).
cm s-1 in simulation B. At 800 s the loop reaches its
initial apex temperature, though the coronal density is far greater
than at t = 0 s. It was also shown in BM1 that loops tend to cool
more quickly than they drain. The over-density of loops observed by
TRACE at temperatures around 106 K, compared with hydrostatic
equilibrium models, could thus be explained by cooling from much
greater temperatures after a period of chromospheric evaporation, in
agreement with the findings of Warren et al. (2002) and
Spadaro et al. (2003).
One problem remains: the persistence of these loops for periods longer than the characteristic cooling time (Lenz et al. 1999) is difficult to explain satisfactorily, though it seems likely that it could be accounted for by a more slowly decaying rate of heating. However, theoretically predicted cooling times of compact flares are in reasonably good agreement with observationally measured values and so it is unclear whether additional heat input during the gradual phase is necessary (Wu et al. 1986).
Beyond 800 s the catastrophic cooling of coronal material to transition region temperatures takes place. Catastrophic cooling after a strong heating event was also shown by Spadaro et al. (2003). In simulation A the total cooling time from the peak temperature at 210 s to the minimum temperature reached at 1400 s is 1190 s, or 19.8 min, which is in excellent agreement with the cooling time of 20 min found by Gan & Fang (1990).
By 1400 s the downflows have drained sufficient material from the coronal region that it is close to its initial density and so the constant background heating begins to recover the initial hydrostatic equilibrium. Between 1600 s and 8000 s the temperature and the density return to their initial values everywhere along the loop. The plasma flows gradually decay away, eventually becoming negligible in comparison with the sound speed and have no further influence upon the evolution of the loop.
Figures 14 and 15 show the population distributions
and the total emissivity of helium between 300 s and 1400 s, as the
loop cools from its peak apex temperature of
![]() K to
temperatures below
K to
temperatures below
![]() K.
K.
The population fractions of He I and He II are everywhere reduced in simulation B when compared with simulation A. The population fraction of He I is effectively 1.0 in the low temperature, high density chromosphere in both simulations, though the gradient across the ionisation front is much less severe at later times in simulation B. The erosion of the strong gradients and the broadening of the population distributions is a consequence of the transportation of ions by the bulk flows. Convection generally acts to smooth out gradients and discontinuities.
The total emissivity profile of helium tells a similar story to the
ion population profiles. The peak emissivity is considerably lower at
all times in simulation B and extends to greater heights. This reduced
emissivity is one of the main contributors to the differences in the
radiative cooling time-scales and the bulk flow velocities that arise
between the simulations.
(b) Carbon
Figures 16 and 17 show the population distributions and the total emissivity of C III and C IV during the gradual phase of the flare. As for helium, the population fractions remain strongly reduced in simulation B. In fact, the magnitude of the reduction is over a factor of 4 at most times for both C III and C IV. This has clear implications for the theoretical calculation of spectral line intensities.
The total C III and C IV emissivity profiles demonstrate the effect of the severely depleted ion populations. They are reduced by almost an order of magnitude in simulation B, compared with the corresponding emissivities in simulation A. As for helium, the decreased emissivity has extremely important consequences for the radiative cooling time-scale and the bulk flow velocity of the plasma. The C III and C IV emissivity profiles, in common with He I and He II, are also broadened when the lowest temperatures are reached, though the spatial extent of the broadening is considerably greater in simulation A.
It is interesting to note that while the peak emissivity of C III and
C IV is larger than that of He I and He II, the spatial extent of the
latter is greater at all times in both simulations. Between 300 s and
800 s the emissivity of the carbon ions is strongly peaked, whereas
the emissivity of the helium ions is relatively broad. Between 900 s
and 1400 s the emissivity profile of the carbon ions broadens
slightly, but remains considerably narrower than that of the helium
ions. The somewhat surprising consequence of this is that He I and
He II emit more strongly further up the loop, at higher temperatures,
than C III and C IV. For example, in simulation B at 1400 s and
![]() cm, the total helium emissivity is around
10-23.4 erg cm3 s-1, whereas the total C III and C IV
emissivity has fallen far below this amount. The same effect is
present in simulation A, though to a far lesser extent. Therefore,
given sufficient spatial resolution, it is possible that one may
observe significant emission from helium overlying emission from
carbon, from the same magnetic structure in the presence of a
non-equilibrium ionisation balance.
cm, the total helium emissivity is around
10-23.4 erg cm3 s-1, whereas the total C III and C IV
emissivity has fallen far below this amount. The same effect is
present in simulation A, though to a far lesser extent. Therefore,
given sufficient spatial resolution, it is possible that one may
observe significant emission from helium overlying emission from
carbon, from the same magnetic structure in the presence of a
non-equilibrium ionisation balance.
(c) Total emissivity
Figure 18 shows the total emissivity profiles in the left-hand footpoint region of the loop between 300 s and 1400 s for simulations A and B. The differences in the emissivity profiles are exactly as expected from the discussion above. The peak radiative emission at lower transition region temperatures is strongly reduced at all times in simulation B compared with simulation A. At 300 s the total emissivity at upper transition region temperatures is slightly enhanced in simulation B because of the greater abundance of more strongly emitting lower ionisation stages, though by 800 s the total emissivity curves agree more closely in this region.
Between 900 s and 1400 s the peak of the total emissivity curve in simulation A broadens considerably due to the behaviour of ions such as C III and C IV, discussed above. However, the total emissivity profiles in the upper region of the footpoint remain in fairly good agreement. A significant contribution to the total emissivity in the upper footpoint region is made by the higher ionisation stages such as C V, which have fewer stages to recombine through as the plasma cools. It was shown in BM1 that the very highest ionisation stages persist for the longest periods of time as the plasma cools, which results in the depletion of the lower ionisation stages and consequently reduces the overall radiative emission. However, the coronal densities in the post-flare plasma are greater and so the populations of these ions are able to remain closer to equilibrium.
Figures 19 and 20 show the population distributions of
the upper transition region and coronal ions Fe VIII, Fe IX, Fe X and
Fe XII between 300 s and 1400 s for simulations A and B. As the plasma
cools between 300 s and 800 s the population distributions of Fe VIII
and Fe IX broaden. The peak population of Fe VIII descends the loop,
whereas the peak population of Fe IX ascends the loop. The differences
between simulations A and B can be reasonably pronounced, with the
population fraction of Fe IX at 800 s and
![]() cm a
factor of 3 greater in simulation A than in simulation B. However, as
the density decreases further down the loop the differences between
simulations A and B in the vicinity of the peak populations become
relatively small.
cm a
factor of 3 greater in simulation A than in simulation B. However, as
the density decreases further down the loop the differences between
simulations A and B in the vicinity of the peak populations become
relatively small.
The Fe X and Fe XII population distributions also broaden between 300 s and 800 s, although toward higher temperatures only and the peak population fractions ascend the loop. At 800 s the apex population of Fe X is a factor of 4 greater in simulation A than in simulation B. The peak population of Fe XII increases slightly with time in simulation B because the downflows are sufficiently strong to allow convection to make a contribution.
Between 900 s and 1400 s the population of Fe VIII increases and the
peak population ascends the loop slightly as lower ionisation stages
become more abundant further down. There is a significant amount of
Fe IX present in both simulations where the temperatures have fallen
to values around
![]() K. The population of Fe IX is greater
in simulation B and a small amount of Fe X persists.
K. The population of Fe IX is greater
in simulation B and a small amount of Fe X persists.
The enhanced presence in relatively cool plasma of ions that are commonly assumed to be most abundant at coronal temperatures may be sufficient to increase the intensity of their emission above equilibrium values and, furthermore, may lead one to overestimate the temperature of the plasma when an equilibrium ionisation balance is assumed.
Figure 21 shows the total Fe VIII, Fe IX, Fe X and Fe XII emissivity profiles between 300 s and 1400 s for simulations A and
B. As the loop begins to cool, the higher ionisation stages (such as
Fe XIV to Fe XVIII) dominate the contribution to the emissivity. The
lower ionisation stages (such as Fe VIII to Fe XII) gradually become
more important as lower temperatures are reached and dominate by 800 s.
(b) Total emissivity
Figure 22 shows the total emissivity in the coronal region of the loop between 300 s and 1400 s. The total emissivity qualitatively follows the behaviour of the selection of ions already discussed and can be understood in terms of these. At 300 s the total emissivity is greater in simulation B because of the enhancement in the population of lower ionisation stages, compared with simulation A, which emit more strongly.
At 800 s there is an enhanced population of more weakly emitting higher ionisation stages in simulation B, due to the finite recombination time-scale, and so the total emissivity is greater in simulation A. The total emissivity remains greater in simulation A after 800 s, as can be seen in the bottom two panels of Fig. 22. As time progresses and the loop relaxes back toward its initial hydrostatic equilibrium configuration, the differences between simulations A and B become negligible.
Figure 23 shows profiles of the synthesised counts in the
171 Å and 195 Å wavelength bands of TRACE at key stages during
the impulsive and the gradual phases of the compact flare. The counts
in the 171 Å range are mostly due to emission from Fe IX and Fe X,
though we also include lines from O IV, O V and O VI. The 195 Å range is dominated by Fe VIII and Fe XII, with contributions from O IV
and O V. In order to sythesise the counts an estimate of the
line-of-sight depth of the emitting plasma is required. We adopt a
value of
![]() cm, which is similar to the observationally
measured value of
cm, which is similar to the observationally
measured value of
![]() cm given by Del Zanna & Mason (2003).
cm given by Del Zanna & Mason (2003).
The temperatures attained along most of the coronal region of the loop during the impulsive phase exceed the upper limit to the range of sensitivity of both filters. However, the transition region and lower coronal region of the loop remain brightly visible, so the loop would perhaps be observed as a vertical structure with no apparent overlying emission if viewed from the side, or as a patch of emission on the order of 106 K if viewed from above, especially if there were several footpoints of similarly flaring loops embedded within the same region of strong magnetic field. The nature of the so-called active region moss observed by TRACE (Berger et al. 1999; Fletcher & de Pontieu 1999) is akin to the description of the latter.
At 90 s the predicted peak intensities of emission detected by both filters increase by over an order of magnitude compared with their values at t = 0 s in simulations A and B. The maximum and minimum in emission detected by the 195 Å filter are predicted by simulation B to be closer in value. The deeper minimum in simulation A is due to the instantaneous ionisation of Fe VIII, whereas in simulation B the ionisation time-scale is non-zero. The enhanced maximum in simulation A is due to the instantaneous ionisation of lower stages to Fe XII. The predicted emission detectable by both filters also extends further along the loop in simulation B due to the non-zero ionisation time-scales of Fe IX, Fe X and Fe XII. At 210 s and 400 s the maxima and minima in both filters are in very close agreement between simulations A and B, which is due to the enhanced densities resulting from the chromospheric evaporation. The detectable emission in both filters extends further along the loop at 210 s in simulation B, though at 400 s the location of the cut-off is in almost exact agreement between simulations A and B.
At 800 s the predicted emission detected by the 171 Å filter is
reduced in simulation B along most of the coronal region of the loop
due to the delay in recombination to Fe IX and Fe X. The predicted
emission detected by the 195 Å filter is in relatively close
agreement between simulations A and B because the delay in
recombination to Fe XII is somewhat less. At 1400 s the predicted
emission in the 171 Å filter is greater in simulation B due to the
delay in the recombination of Fe IX and Fe X to lower ionisation
stages. The predicted emission in the 195 Å filter is also greater
and extends further along the loop in simulation B due to the delay in
the recombination of Fe VIII. The results of simulation B at 1400 s
and
![]() K (along most of the coronal region of
the loop), show that more intense emission from ions such as Fe IX and
Fe X than would be predicted by a conventional equilibrium treatment,
can be observed from plasma at temperatures well below their formation
temperatures. In fact, the intensity of emission in the 171 Å filter at 1400 s is actually greater than at t = 0 s along the upper
part of the loop. The persistence of the loop in the TRACE filters at
these relatively low temperatures might go some way toward explaining
the longevity of cooling loops observed by TRACE. If they remain
visible at such low temperatures and subsequently during the recovery
of their initial equilibrium after a thermal perturbation, then the
longevity of the observed loops can be reconciled with the time-scales
involved in this process. The loops themselves may only disappear from
view when some other process, perhaps related to the magnetic field, acts to destabilise them.
K (along most of the coronal region of
the loop), show that more intense emission from ions such as Fe IX and
Fe X than would be predicted by a conventional equilibrium treatment,
can be observed from plasma at temperatures well below their formation
temperatures. In fact, the intensity of emission in the 171 Å filter at 1400 s is actually greater than at t = 0 s along the upper
part of the loop. The persistence of the loop in the TRACE filters at
these relatively low temperatures might go some way toward explaining
the longevity of cooling loops observed by TRACE. If they remain
visible at such low temperatures and subsequently during the recovery
of their initial equilibrium after a thermal perturbation, then the
longevity of the observed loops can be reconciled with the time-scales
involved in this process. The loops themselves may only disappear from
view when some other process, perhaps related to the magnetic field, acts to destabilise them.
Forward modelling the detectable emission in the TRACE wavelength bands in the manner carried out here provides a very powerful tool. The consequences of assuming an equilibrium ionisation balance when deriving temperatures using the filter ratio technique can be investigated and the potential for misinterpreting observational data assessed.
Figure 24 shows profiles of the predicted filter ratios for
simulations A and B, which exhibit clear differences and will lead to
discrepancies between the actual and derived plasma temperatures. At
90 s the temperature at
![]() cm is about
cm is about
![]() K (Fig. 2), however, assuming that simulation B
describes the properties of the observed loop the filter ratio
technique yields a value of
K (Fig. 2), however, assuming that simulation B
describes the properties of the observed loop the filter ratio
technique yields a value of
![]() K. The ratio, as a
function of temperature, of the response functions of the 171 Å and
195 Å filters was taken from Del Zanna & Mason (2003), who use atomic
data from version 4.01 of the CHIANTI database
(Young et al. 2003; Dere et al. 1997), the
ionisation balance of Mazzotta et al. (1998), coronal element abundances
and the TRACE ground calibration.
K. The ratio, as a
function of temperature, of the response functions of the 171 Å and
195 Å filters was taken from Del Zanna & Mason (2003), who use atomic
data from version 4.01 of the CHIANTI database
(Young et al. 2003; Dere et al. 1997), the
ionisation balance of Mazzotta et al. (1998), coronal element abundances
and the TRACE ground calibration.
At 210 s the temperature at
![]() cm is about
cm is about
![]() K, whereas the filter ratio technique yields two possible
temperatures of
K, whereas the filter ratio technique yields two possible
temperatures of
![]() K and
K and
![]() K. This is
because the filter ratio is close to a local maximum in the curve of
the ratio of the filter response functions versus
temperature. Differences between the filter ratios at 90 s and 210 s
in simulations A and B also exist further down the loop.
K. This is
because the filter ratio is close to a local maximum in the curve of
the ratio of the filter response functions versus
temperature. Differences between the filter ratios at 90 s and 210 s
in simulations A and B also exist further down the loop.
At 400 s the filter ratio curves in Fig. 24 actually exhibit relatively good agreement when one considers that the transition region propagates further into the chromosphere in simulation B, which naturally results in a displacement of the filter ratio curve relative to the curve given by simulation A.
At 800 s the differences in the filter ratio curves between
simulations A and B, particularly along most of the coronal region,
appear to be quite pronounced. However, the high densities present
actually ensure that the filter ratio temperatures derived using these
curves agree relatively well with the simulated temperatures. For
example, in simulation A the temperature at
![]() cm is
about
cm is
about
![]() K (Fig. 11) and the filter ratio
temperature is
K (Fig. 11) and the filter ratio
temperature is
![]() K, although a considerably higher
value of
K, although a considerably higher
value of
![]() K could not be discounted due to the
non-uniqueness of the ratio value as a function of temperature. In
simulation B the temperature at
K could not be discounted due to the
non-uniqueness of the ratio value as a function of temperature. In
simulation B the temperature at
![]() cm is about
cm is about
![]() K and the filter ratio temperature is
K and the filter ratio temperature is
![]() K, although, again, a value of
K, although, again, a value of
![]() K could not be
discounted from the observational data alone.
K could not be
discounted from the observational data alone.
Clearly, though the filter ratio technique is not as accurate as spectroscopic techniques that use line ratios from the same ion for deriving the plasma temperature, it yields acceptable results for qualitative purposes when the assumption of an equilibrium ionisation balance is valid, with uncertainties in the derived temperature of around 10%.
HYDRAD has been used to simulate a compact flare of moderate energy,
driven by a thermal mechanism depositing heat in the corona, with due
account taken of the departure from equilibrium of the ion populations
and their associated radiative emission. The evolution of the plasma
in terms of its thermal properties, dynamics and ion populations has
been followed through the impulsive phase, the gradual phase and the
subsequent recovery of the initial hydrostatic equilibrium. Thus, a
self-consistent analysis of the interdependent phases of a compact
flare has been carried out. The results from HYDRAD have been shown to
be consistent with the work of others in terms of the overall,
qualitative behaviour of the system, although important quantitative
differences have emerged as a consequence of the non-equilibrium
processes that affect the ion populations and the radiative emission.
(a) The impulsive phase
During the impulsive phase, an ablation of chromospheric material is
evident when the plasma is conductively heated, with upflows reaching
peak velocities of
![]() cm s-1. An oppositely directed
compression wave is also observed to propagate toward the
chromosphere, where it eventually becomes damped out in the high
density plasma. The coronal density increases by a factor of about 3
at the apex when the ablated material in each half of the loop
collides. A factor of 3 increase in the density will result in almost
an order of magnitude increase in the intensity of emission since it
is proportional to n2. The adaptive regridding scheme is shown to
successfully track and resolve the transition region as it steepens
dramatically and propagates into the chromosphere. The smallest
cell-width is only
cm s-1. An oppositely directed
compression wave is also observed to propagate toward the
chromosphere, where it eventually becomes damped out in the high
density plasma. The coronal density increases by a factor of about 3
at the apex when the ablated material in each half of the loop
collides. A factor of 3 increase in the density will result in almost
an order of magnitude increase in the intensity of emission since it
is proportional to n2. The adaptive regridding scheme is shown to
successfully track and resolve the transition region as it steepens
dramatically and propagates into the chromosphere. The smallest
cell-width is only
![]() cm, which represents an improvement
of several orders of magnitude over the resolution achieved in
previous work.
cm, which represents an improvement
of several orders of magnitude over the resolution achieved in
previous work.
In the lower transition region strong non-equilibrium enhancements are present in the ion populations when the conduction front reaches the chromosphere, particularly for the Li-like C IV. These enhancements are due to the extended high temperature wing of the population distribution and the downflows contributing to the peak population fraction via convection. The high temperature wing of the distribution remains slightly enhanced due to the non-zero ionisation time-scale. The emissivities of lower transition region ions such as He I, He II and C IV are increased by up to an order of magnitude as these ions find themselves emitting at considerably higher temperatures. Strong emission lines are always observed during flares, which may be due to both density enhancements and the influence of a non-equilibrium ion population. The evidence therefore suggests that accounting for non-equilibrium ion populations is necessary in order to make theoretically calculated line intensities more consistent with their observationally measured values. The inclusion of non-equilibrium effects in the present case certainly alters the predicted intensity of the He I, He II and C IV emission in the way necessary to bring them into closer agreement with observations (Jordan 1975; Del Zanna et al. 2002).
An over-abundance of lower ionisation stages compared with their equilibrium populations is evident in the corona as the plasma temperature increases. Therefore, the coronal emissivity is enhanced away from equilibrium because lower ionisation stages are generally stronger emitters at high temperatures than the higher ionisation stages that would exist there in equilibrium. The non-zero ionisation time-scale also means that the departures from equilibrium become increasingly important for higher ionisation stages because the delay between events accumulates. It has been seen that, for example, the population of Fe XIX is severely depleted at the maximum temperature reached by the plasma when non-equilibrium effects are accounted for. However, according to the equilibrium ionisation balance it should be relatively abundant.
This depletion of high ionisation stages has important implications for the analysis of observational data. The results from HYDRAD have shown that high temperatures can be reached without the corresponding emission one would expect to see in equilibrium, which could result in a severe underestimation of the temperature if non-equilibrium effects were omitted from the analysis. Furthermore, the results from HYDRAD have shown that significantly higher temperatures (than indicated by the assumption of equilibrium) need to be reached before the populations of the highest ionisation stages of iron are sufficient for their emission to become significant. This also means that measurements made using the ratio of two lines emitted from the same ion would yield significantly greater plasma temperatures than the equilibrium formation temperature of the emitting ion.
The ablation of material is seen to continue well into the gradual
phase, thus verifying the results of Antiochos & Krall (1979),
Doschek et al. (1982) and Gan & Fang (1990). Since the density continues
to increase, the peak in the emission measure occurs after the peak in
temperature is reached, which is consistent with observations.
(b) The gradual phase
During the gradual phase the populations of the strongest transition region emitters are substantially reduced from their equilibrium values, as are the lower ionisation stages of elements such as neon and magnesium, due to the non-zero recombination time-scale of the higher ionisation stages. Therefore, the radiative emission from the transition region is also reduced, which results in lower downflow velocities and a somewhat increased time-scale of cooling.
The total emissivity in the corona is higher than one would expect in equilibrium at the beginning of the gradual phase, due to the over-abundance of strongly emitting, lower ionisation stages of iron. It is reduced thereafter due to the greater abundance of weakly emitting, higher ionisation stages than one would expect in equilibrium.
When the loop cools to its temperature at t=0 s, the coronal density remains substantially enhanced over the density one would expect to find in hydrostatic equilibrium. Therefore, the cooling process after an initial dynamic heating event provides a likely explanation for the over-density of loops observed by TRACE at temperatures around 106 K. This is in close agreement with the findings of Warren et al. (2002) and Spadaro et al. (2003). However, the persistence of these loops over periods considerably greater than their characteristic cooling times remains unresolved. It appears that including non-equilibrium effects when calculating the radiative energy loss does not decrease the rate of cooling sufficiently to enhance the longevity of the loop, making only a few minutes difference at most to the cooling time. Plausible suggestions include a multi-thread loop model with individual filaments at different stages in their evolution. However, estimates of the loop filling factor (the fraction of the resolved volume of plasma actually emitting) on the order of 1.0 (Del Zanna & Mason 2003) means that there could be too few unresolved filaments to make this explanation viable.
Alternatively, since the loop cools from Fe XII to Fe VIII in the TRACE filters and it has only recently been realised that Fe VIII is a strong emitter in the 195 Å passband (Del Zanna 2003, private communication), Fe VIII emission could previously have been mistaken for hotter Fe XII emission. This would result in the overestimation of the cooling time since the loop would appear to be maintained at higher temperatures for longer. A further possibility is that after the initial impulse of energy the rate of heating could decay more slowly and provide sufficient energy to increase the cooling time. These lines of enquiry will be pursued in future work with HYDRAD.
During the final stages of the gradual phase the coronal plasma cools
catastrophically to transition region temperatures, due to the
enhanced density, before the downflows drain sufficient material away
to allow the initial hydrostatic equilibrium to be recovered. This
behaviour was also found by Spadaro et al. (2002) and
Spadaro et al. (2003).
(c) Observational consequences for TRACE
Finally, the intensity of emission that would be detected by the TRACE 171 Å and 195 Å filters has been synthesised. During the impulsive phase only the low lying, relatively low temperature, regions of the loop would be visible with no discernible overlying emission, perhaps reminiscent of the active region moss observations of others. The filter ratio technique for the determination of temperatures has been shown to underestimate the temperature of the plasma in the low lying regions of the loop during the impulsive phase as a consequence of departures of the ionisation balance from equilibrium, which may have important implications for the observationally derived properties of moss-like regions.
During the gradual phase, the enhanced densities ensure that the ionisation balance in simulation B remains fairly close to equilibrium and therefore the filter ratio technique may do a reasonably good job of estimating the plasma temperature under these circumstances only. As the ablated material drains back into the chromosphere the departures from equilibrium of the ionisation balance become more pronounced.
The synthesised emission in both filters shows that the loop should remain visible at much lower temperatures than would be indicated by a purely equilibrium treatment of the ion populations and the radiative emission. Therefore, the longevity of observed loops in these TRACE filters can potentially be reconciled with a non-equilibrium population of emitting ions. The loop is predicted to remain visible as it cools to low temperatures and as it recovers its equilibrium after the thermal perturbation. This process takes several hours, in agreement with the time-scales for which similar loops persist (Lenz et al. 1999), and eventually another process, perhaps related to the magnetic field, may act to destabilise the loop and cause it to disappear from view.
Acknowledgements
The authors acknowledge the financial support of PPARC and wish to thank the anonymous referee for their careful reading of the original manuscript, and for their suggestions for improvements.
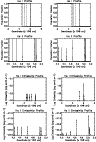 |
Figure 4: Time series of the He I and He II population fractions and emissivities at: 0 s (solid), 60 s (dotted), 80 s (dashed), 90 s (dash-dot), 100 s (dash-dot-dot-dot) and 120 s (long-dashed). The left-hand panels show the results for simulation A and the right-hand panels show the results for simulation B. |
| Open with DEXTER | |
 |
Figure 5: Time series of the C III and C IV population fractions and emissivities at: 0 s (solid), 60 s (dotted), 80 s (dashed), 90 s (dash-dot), 100 s (dash-dot-dot-dot) and 120 s (long-dashed). The left-hand panels show the results for simulation A and the right-hand panels show the results for simulation B. |
| Open with DEXTER | |
 |
Figure 6: Plots of the peak helium, carbon, oxygen and magnesium emissivities as a function of time. The results from simulation A are plotted as a solid line and those from simulation B are plotted as a dashed line. |
| Open with DEXTER | |
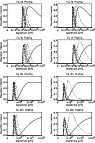 |
Figure 7: Time series of the Fe IX, Fe X, Fe XII and Fe XIII population fractions at: 0 s (solid), 60 s (dotted), 90 s (dashed), 120 s (dash-dot), 150 s (dash-dot-dot-dot) and 210 s (long-dashed). The left-hand panels show the results for simulation A and the right-hand panels show the results for simulation B. |
| Open with DEXTER | |
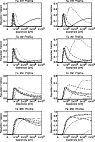 |
Figure 8: Time series of the Fe XIV, Fe XV, Fe XVI and Fe XVII population fractions at: 0 s (solid), 60 s (dotted), 90 s (dashed), 120 s (dash-dot), 150 s (dash-dot-dot-dot) and 210 s (long-dashed). The left-hand panels show the results for simulation A and the right-hand panels show the results for simulation B. |
| Open with DEXTER | |
 |
Figure 9: Time series of the total Fe IX, Fe X, Fe XII and Fe XIII emissivity, and the total Fe XIV, Fe XV, Fe XVI and Fe XVII emissivity at: 0 s (solid), 60 s (dotted), 90 s (dashed), 120 s (dash-dot), 150 s (dash-dot-dot-dot) and 210 s (long-dashed). The left-hand panels show the results for simulation A and the right-hand panels show the results for simulation B. |
| Open with DEXTER | |
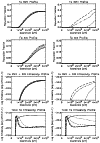 |
Figure 10: The top six panels show time series of the Fe XVIII and Fe XIX population fractions and emissivities at: 160 s (solid), 170 s (dotted), 180 s (dashed), 190 s (dash-dot), 200 s (dash-dot-dot-dot) and 210 s (long-dashed). The bottom two panels show time series of the total iron emissivity at: 0 s (solid), 60 s (dotted), 90 s (dashed), 120 s (dash-dot), 150 s (dash-dot-dot-dot) and 210 s (long-dashed). The left-hand panels show the results for simulation A and the right-hand panels show the results for simulation B. |
| Open with DEXTER | |
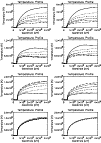 |
Figure 11: Time series of the temperature profile for the left-hand region of the loop. Row 1: 300 s (solid), 400 s (dotted), 500 s (dashed), 600 s (dash-dot), 700 s (dash-dot-dot-dot) and 800 s (long-dashed). Row 2: 900 s (solid), 1000 s (dotted), 1100 s (dashed), 1200 s (dash-dot), 1300 s (dash-dot-dot-dot) and 1400 s (long-dashed). Row 3: 1600 s (solid), 1800 s (dotted), 2000 s (dashed), 2200 s (dash-dot), 2400 s (dash-dot-dot-dot) and 2600 s (long-dashed). Row 4: 3000 s (solid), 4000 s (dotted), 5000 s (dashed), 6000 s (dash-dot), 7000 s (dash-dot-dot-dot) and 8000 s (long-dashed). The left-hand panels show the results for simulation A and the right-hand panels show the results for simulation B. |
| Open with DEXTER | |
 |
Figure 12: Time series of the velocity profile for the left-hand region of the loop at the same times as in Fig. 11. |
| Open with DEXTER | |
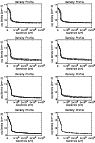 |
Figure 13: Time series of the density profile for the left-hand region of the loop at the same times as in Fig. 11. |
| Open with DEXTER | |
 |
Figure 14: Time series of the He I and He II population fractions. The first row of plots for each ion shows the population fractions at: 300 s (solid), 400 s (dotted), 500 s (dashed), 600 s (dash-dot), 700 s (dash-dot-dot-dot) and 800 s (long-dashed). The second row of plots for each ion shows the population fractions at: 900 s (solid), 1000 s (dotted), 1100 s (dashed), 1200 s (dash-dot), 1300 s (dash-dot-dot-dot) and 1400 s (long-dashed). The left-hand panels show the results for simulation A and the right-hand panels show the results for simulation B. |
| Open with DEXTER | |
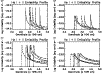 |
Figure 15: Time series of the total He I and He II emissivity. Row 1: 300 s (solid), 400 s (dotted), 500 s (dashed), 600 s (dash-dot), 700 s (dash-dot-dot-dot) and 800 s (long-dashed). Row 2: 900 s (solid), 1000 s (dotted), 1100 s (dashed), 1200 s (dash-dot), 1300 s (dash-dot-dot-dot) and 1400 s (long-dashed). The left-hand panels show the results for simulation A and the right-hand panels show the results for simulation B. |
| Open with DEXTER | |
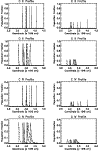 |
Figure 16: Time series of the C III and C IV population fractions. The first row of plots for each ion shows the population fractions at: 300 s (solid), 400 s (dotted), 500 s (dashed), 600 s (dash-dot), 700 s (dash-dot-dot-dot) and 800 s (long-dashed). The second row of plots for each ion shows the population fractions at: 900 s (solid), 1000 s (dotted), 1100 s (dashed), 1200 s (dash-dot), 1300 s (dash-dot-dot-dot) and 1400 s (long-dashed). The left-hand panels show the results for simulation A and the right-hand panels show the results for simulation B. |
| Open with DEXTER | |
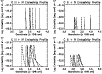 |
Figure 17: Time series of the total C III and C IV emissivity. Row 1: 300 s (solid), 400 s (dotted), 500 s (dashed), 600 s (dash-dot), 700 s (dash-dot-dot-dot) and 800 s (long-dashed). Row 2: 900 s (solid), 1000 s (dotted), 1100 s (dashed), 1200 s (dash-dot), 1300 s (dash-dot-dot-dot) and 1400 s (long-dashed). The left-hand panels show the results for simulation A and the right-hand panels show the results for simulation B. |
| Open with DEXTER | |
 |
Figure 18: Time series of the total emissivity in the left-hand footpoint region of the loop. Row 1: 300 s (solid), 400 s (dotted), 500 s (dashed), 600 s (dash-dot), 700 s (dash-dot-dot-dot) and 800 s (long-dashed). Row 2: 900 s (solid), 1000 s (dotted), 1100 s (dashed), 1200 s (dash-dot), 1300 s (dash-dot-dot-dot) and 1400 s (long-dashed). The left-hand panels show the results for simulation A and the right-hand panels show the results for simulation B. |
| Open with DEXTER | |
 |
Figure 19: Time series of the Fe VIII and Fe IX population fractions. The first row of plots for each ion shows the population fractions at: 300 s (solid), 400 s (dotted), 500 s (dashed), 600 s (dash-dot), 700 s (dash-dot-dot-dot) and 800 s (long-dashed). The second row of plots for each ion shows the population fractions at: 900 s (solid), 1000 s (dotted), 1100 s (dashed), 1200 s (dash-dot), 1300 s (dash-dot-dot-dot) and 1400 s (long-dashed). The left-hand panels show the results for simulation A and the right-hand panels show the results for simulation B. |
| Open with DEXTER | |
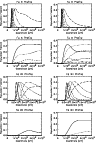 |
Figure 20: Time series of the Fe X and Fe XII population fractions. The first row of plots for each ion shows the population fractions at: 300 s (solid), 400 s (dotted), 500 s (dashed), 600 s (dash-dot), 700 s (dash-dot-dot-dot) and 800 s (long-dashed). The second row of plots for each ion shows the population fractions at: 900 s (solid), 1000 s (dotted), 1100 s (dashed), 1200 s (dash-dot), 1300 s (dash-dot-dot-dot) and 1400 s (long-dashed). The left-hand panels show the results for simulation A and the right-hand panels show the results for simulation B. |
| Open with DEXTER | |
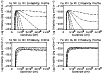 |
Figure 21: Time series of the total Fe VIII to Fe XII emissivity. Row 1: 300 s (solid), 400 s (dotted), 500 s (dashed), 600 s (dash-dot), 700 s (dash-dot-dot-dot) and 800 s (long-dashed). Row 2: 900 s (solid), 1000 s (dotted), 1100 s (dashed), 1200 s (dash-dot), 1300 s (dash-dot-dot-dot) and 1400 s (long-dashed). The left-hand panels show the results for simulation A and the right-hand panels show the results for simulation B. |
| Open with DEXTER | |
 |
Figure 22: Time series of the total emissivity in the left-hand coronal region of the loop. Row 1: 300 s (solid), 400 s (dotted), 500 s (dashed), 600 s (dash-dot), 700 s (dash-dot-dot-dot) and 800 s (long-dashed). Row 2: 900 s (solid), 1000 s (dotted), 1100 s (dashed), 1200 s (dash-dot), 1300 s (dash-dot-dot-dot) and 1400 s (long-dashed). The left-hand panels show the results for simulation A and the right-hand panels show the results for simulation B. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=4cm]{0521figs/fig38a.ps}\includegraphic...
...521figs/fig38e.ps}\includegraphics[width=4cm]{0521figs/fig38e_ne.ps}\end{figure}](/articles/aa/full/2004/37/aa0521-04/Timg94.gif) |
Figure 23: Profiles of counts in the TRACE 171 Å (solid) and 195 Å (dashed) filters for simulation A (left-hand column) and simulation B (right-hand column). Row 1: 90 s. Row 2: 210 s. Row 3: 400 s. Row 4: 800 s. Row 5: 1400 s. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=5.0cm]{0521figs/fig39a.ps}\par\vspace*{...
...}\par\vspace*{3mm}
\includegraphics[width=5.0cm]{0521figs/fig39e.ps}\end{figure}](/articles/aa/full/2004/37/aa0521-04/Timg95.gif) |
Figure 24: Profiles of the filter ratio for simulation A (solid) and simulation B (dashed). Top-left: 90 s. Top-right: 210 s. Middle-left: 400 s. Middle-right: 800 s. Bottom: 1400 s. |
| Open with DEXTER | |