A&A 425, 217-228 (2004)
DOI: 10.1051/0004-6361:20040327
Effects of rotation on the helium burning shell source in accreting white dwarfs
S.-C. Yoon1 - N. Langer1 - S. Scheithauer2,3
1 - Astronomical Institute, Utrecht University, Princetonplein 5,
3584 CC, Utrecht, The Netherlands
2 -
Institut für Physik, Universität
Potsdam, 14415 Potsdam, Germany
3 -
Present address: ZARM, University of Bremen Am Fallturm, 28359 Bremen, Germany
Received 25 February 2004 / Accepted 3 June 2004
Abstract
We investigate the effects of rotation on the behavior of the helium-burning shell source
in accreting carbon-oxygen white dwarfs,
in the context of the single degenerate Chandrasekhar mass progenitor scenario
for type Ia supernovae (SNe Ia). We model the evolution of helium-accreting white
dwarfs of initially 1
 ,
assuming four different constant accretion rates
(2, 3, 5 and
,
assuming four different constant accretion rates
(2, 3, 5 and
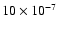
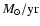 ). In a one-dimensional
approximation, we compute the mass accretion and subsequent nuclear
fusion of helium into carbon and oxygen, as well as angular momentum accretion,
angular momentum transport inside the white dwarf, and rotationally induced
chemical mixing. Our models show two major effects of rotation:
a) The helium-burning nuclear shell source in the rotating models
is much more stable than in corresponding non-rotating models -
which increases the likelihood that accreting white dwarfs reach the stage
of central carbon ignition.
This effect is mainly due to rotationally induced mixing at the CO/He
interface which widens the shell source, and due to the centrifugal force
lowering the density and degeneracy at the shell source location.
b) The C/O-ratio in the layers which experience helium shell burning
- which may affect the energy of an SN Ia explosion - is
strongly decreased by the rotationally induced mixing of
). In a one-dimensional
approximation, we compute the mass accretion and subsequent nuclear
fusion of helium into carbon and oxygen, as well as angular momentum accretion,
angular momentum transport inside the white dwarf, and rotationally induced
chemical mixing. Our models show two major effects of rotation:
a) The helium-burning nuclear shell source in the rotating models
is much more stable than in corresponding non-rotating models -
which increases the likelihood that accreting white dwarfs reach the stage
of central carbon ignition.
This effect is mainly due to rotationally induced mixing at the CO/He
interface which widens the shell source, and due to the centrifugal force
lowering the density and degeneracy at the shell source location.
b) The C/O-ratio in the layers which experience helium shell burning
- which may affect the energy of an SN Ia explosion - is
strongly decreased by the rotationally induced mixing of
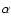 -particles into the carbon-rich layers.
We discuss implications of our results for the evolution of SNe Ia progenitors.
-particles into the carbon-rich layers.
We discuss implications of our results for the evolution of SNe Ia progenitors.
Key words: nuclear reactions, nucleosynthesis, abundances - stars: evolution - stars: white dwarf - stars: rotation - supernovae: individual: type Ia
Accreting white dwarfs in close binary systems are considered to be responsible
for such important astrophysical phenomena as nova explosions,
cataclysmic variables and super-soft X-ray sources.
Especially, there is general agreement that accreting
CO white dwarfs are progenitors of type Ia supernovae (SNe Ia)
(e.g., Woosley & Weaver 1986; Branch et al. 1995;
Wheeler 1996; Nomoto et al. 1997,
Hillebrandt & Niemeyer 2000; Livio 2001).
The fairly homogeneous properties of light curves and spectra of SNe Ia have made
them a valuable distance indicator for determining cosmological
parameters (e.g., Hamuy et al. 1996; Branch 1998; Leibundgut 2001).
One of the most intriguing results obtained from SNe Ia data may be the recent suggestion of a
finite cosmological constant, which implies that the universe is currently accelerating its
expansion (Perlmutter et al. 1999; Riess et al. 2000).
The observational properties of SNe Ia demand a thermonuclear explosion of
a CO white dwarf as their origin.
However, despite the far-reaching observational achievements,
self-consistent progenitor evolution model calculations which explain the existence
of SNe Ia are still lacking (but see Yoon & Langer 2003).
Models for the evolution of SN Ia progenitors studied until now can be
divided into two groups, one where the white dwarf explosion is
triggered close to the center, and the other where the white dwarf
explosion is triggered in the helium shell
(see Livio 2001, for a review).
Two scenarios exist for close-to-center ignition.
One is the double degenerate scenario, in which two CO white dwarfs in a binary system
merge due to the angular momentum loss by gravitational wave radiation.
If the system mass exceeds the Chandrasekhar mass, carbon must ignite,
with the possible outcome of a thermonuclear explosion.
Although there is observational evidence for double white dwarf systems
(e.g., Koester et al. 2001; Karl et al. 2003),
including one sdB star plus a CO white dwarf system which might
result in a double white dwarf system having a total mass beyond the Chandrasekhar limit
(Maxted et al. 2000),
this scenario is criticized mainly by the fact
that the merging of two white dwarfs is likely to end in an accretion-induced
collapse rather than an SN explosion (Saio & Nomoto 1985, 1998).
The currently favored scenario for close-to-center ignition is the
single degenerate scenario, in which a CO white dwarf in a close binary system
accretes hydrogen-rich or helium-rich matter from a non-degenerate companion at
a relatively high accretion rate (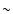 10-7
10-7
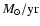 ).
The super-soft X-ray sources, which are believed to consist of a non-degenerate
star and a white dwarf, are promising observed counterparts
of this scenario. The idea of steady nuclear burning due to a
high accretion rate fits well to these sources (e.g., Li & van den Heuvel 1997;
Kahabka & van den Heuvel 1997; Langer et al. 2000;
Yoon & Langer 2003).
Symbiotic systems (e.g., Hachisu et al. 1999) and recurrent novae
(e.g., Hachisu & Kato 2001; Thoroughgood et al. 2001)
may also belong to this scenario.
However, it is still not clear whether this scenario
can explain the observed SN Ia frequency since the accretion rates which
allow steady burning are limited to a very narrow range.
Furthermore, helium shell burning is generally found to be unstable:
strong helium shell flashes might lead to strong mass loss by
optically thick winds, or to a strong expansion of the
white dwarf envelope to a red-giant phase which will result in a possible merging of the binary
(e.g., Nomoto 1982a; Hachisu et al. 1996; Cassisi et al. 1998;
Kato & Hachisu 1999; Langer et al. 2002).
).
The super-soft X-ray sources, which are believed to consist of a non-degenerate
star and a white dwarf, are promising observed counterparts
of this scenario. The idea of steady nuclear burning due to a
high accretion rate fits well to these sources (e.g., Li & van den Heuvel 1997;
Kahabka & van den Heuvel 1997; Langer et al. 2000;
Yoon & Langer 2003).
Symbiotic systems (e.g., Hachisu et al. 1999) and recurrent novae
(e.g., Hachisu & Kato 2001; Thoroughgood et al. 2001)
may also belong to this scenario.
However, it is still not clear whether this scenario
can explain the observed SN Ia frequency since the accretion rates which
allow steady burning are limited to a very narrow range.
Furthermore, helium shell burning is generally found to be unstable:
strong helium shell flashes might lead to strong mass loss by
optically thick winds, or to a strong expansion of the
white dwarf envelope to a red-giant phase which will result in a possible merging of the binary
(e.g., Nomoto 1982a; Hachisu et al. 1996; Cassisi et al. 1998;
Kato & Hachisu 1999; Langer et al. 2002).
In the so called "Edge Lit Detonation'' models, corresponding to
sub-Chandrasekhar mass models, helium ignites at the bottom of
a helium layer of a few tenths of a solar mass, accumulated on a CO white dwarf
at a relatively low accretion rate (
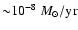 )
(e.g., Nomoto 1982b; Limongi & Tornambé 1991;
Woosley & Weaver 1994; Livne & Arnett 1995).
These models are favored in terms of
statistics (e.g., Iben & Tutukov 1991; Tout et al. 2001) but disfavored by the fact that
the spectra and light curves produced by these models are
not in agreement with observations (Höflich et al. 1996; Nugent et al. 1997;
Pinto et al. 2001). Yoon & Langer (2004b)
showed that
a helium detonation in such models may be avoided altogether due to a strong shear layer
inside an accreting white dwarf.
)
(e.g., Nomoto 1982b; Limongi & Tornambé 1991;
Woosley & Weaver 1994; Livne & Arnett 1995).
These models are favored in terms of
statistics (e.g., Iben & Tutukov 1991; Tout et al. 2001) but disfavored by the fact that
the spectra and light curves produced by these models are
not in agreement with observations (Höflich et al. 1996; Nugent et al. 1997;
Pinto et al. 2001). Yoon & Langer (2004b)
showed that
a helium detonation in such models may be avoided altogether due to a strong shear layer
inside an accreting white dwarf.
Most previous studies of accreting white dwarfs as SN Ia progenitors have
assumed spherical symmetry.
However, in a close binary system which contains a white dwarf,
an accretion disk is formed around the white dwarf.
The matter coming from the accretion disk
which is incorporated into the white dwarf
carries high specific angular momentum, i.e. up to the value
corresponding to Keplerian rotation at the white dwarf equator.
Consequently, not only the accreted layer may be spinning very rapidly,
but also the rest of the white dwarf, as
angular momentum may be transported
into the stellar interior (e.g., Ritter 1985; Langer et al. 2000).
Recent polarization observations provide evidence
for the aspherical nature of SNe Ia
(SN 1999by, Howell et al. 2001; SN 2001el, Wang et al. 2003).
A plausible explanation for this asphericity may be a rapidly rotating
progenitor, while clumpiness of supernova ejecta or binarity of the
progenitors could be
another possible cause for the observed polarization (Kasen et al. 2003).
The observation that white dwarfs in Cataclysmic Variables rotate much faster than
isolated ones (Sion 1999; Starrfield 2003) supports the idea
that accreting white dwarfs are indeed spun up.
In this picture, differential rotation inside the
accreting white dwarf is inevitable, unless the angular momentum
transport in the white dwarf is extremely efficient such that
rigid body rotation may be maintained throughout the white dwarf interior
(Yoon & Langer 2004a).
Rotationally induced instabilities such as the shear instability
may lead to chemical mixing
between the CO white dwarf material and the accreted matter.
This effect has been discussed
by several authors mainly with respect to the chemical
enrichment of CNO and other heavier elements observed in nova
ejecta (e.g., Kippenhahn & Thomas 1978; MacDonald 1983;
Livio & Truran 1987; Fujimoto 1988; Fujimoto & Iben 1997).
In this paper, we investigate
the effects of rotation on the evolution of accreting white dwarfs
in relation to the single degenerate Chandrasekhar mass scenario for SNe Ia progenitors.
For this purpose, we carry out numerical simulations of helium burning white dwarfs
considering high accretion rates (
>10-7
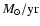 )
which allow steady shell burning
for hydrogen or helium.
Our discussions in this study are focused on the rotationally induced
chemical mixing and its consequences for the behavior of the helium burning shell source.
Comprehensive discussions of the rotational induced hydrodynamic instabilities
and their role in the redistribution of angular momentum in accreting
white dwarfs are given in a separate paper (Yoon & Langer 2004a).
Effects of rotation on sub-Chandrasekhar mass models, i.e., on accreting
white dwarfs with relatively low accretion rates (
)
which allow steady shell burning
for hydrogen or helium.
Our discussions in this study are focused on the rotationally induced
chemical mixing and its consequences for the behavior of the helium burning shell source.
Comprehensive discussions of the rotational induced hydrodynamic instabilities
and their role in the redistribution of angular momentum in accreting
white dwarfs are given in a separate paper (Yoon & Langer 2004a).
Effects of rotation on sub-Chandrasekhar mass models, i.e., on accreting
white dwarfs with relatively low accretion rates (
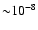
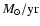 ),
are discussed in Yoon & Langer (2004b).
Our computational method is introduced in Sect. 2, and
the initial model and physical assumptions are discussed in Sect. 3.
In Sect. 4 we present the evolution of various physical quantities of
our white dwarf models. We discuss rotationally
induced chemical mixing and the stability of shell burning in
Sects. 5 and 6 respectively.
Finally, we discuss our results in Sect. 7.
),
are discussed in Yoon & Langer (2004b).
Our computational method is introduced in Sect. 2, and
the initial model and physical assumptions are discussed in Sect. 3.
In Sect. 4 we present the evolution of various physical quantities of
our white dwarf models. We discuss rotationally
induced chemical mixing and the stability of shell burning in
Sects. 5 and 6 respectively.
Finally, we discuss our results in Sect. 7.
2 Method
The numerical models have been computed with a hydrodynamic stellar evolution
code (cf., Langer 1998; Heger et al. 2000).
Opacities are taken from Iglesias & Rogers (1996).
Changes in the chemical composition
are computed using a nuclear network with more than 60 nuclear
reactions, of which 31 reactions are
relevant to helium burning such as 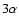 ,
,
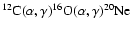 and
and
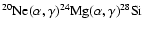 reactions.
For the
reactions.
For the
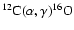 reaction rate, which has an important role in our study,
we use the rate of Caughlan et al. (1985) reduced by a factor of 0.63,
as suggested by Weaver & Woosley (1993).
reaction rate, which has an important role in our study,
we use the rate of Caughlan et al. (1985) reduced by a factor of 0.63,
as suggested by Weaver & Woosley (1993).
The effect of the centrifugal force on the stellar structure,
and rotationally induced transport of angular momentum and chemical species
are treated in a one-dimensional approximation (Heger et al. 2000).
We consider rotationally induced transport processes such as
Eddington-Sweet circulations, the Goldreich-Schubert-Fricke
instability, and the dynamical and secular shear instability,
by solving a non-linear diffusion equation, with diffusion coefficients
for each of the instabilities computed as in Heger et al. (2000)
and Yoon & Langer (2004a).
The viscous dissipation of the rotational energy
is also considered as described by Yoon & Langer (2004a).
More details about the
numerical methods are given in Yoon & Langer (2004a).
A comparison of our method with previously used ones for rotating white dwarf models
has already been given in Yoon & Langer (2004a) in detail.
Here we give some additional comments on the rotation physics
in relation to helium-accreting white dwarfs.
Our approach to include rotation is based on the method given
by Kippenhahn & Thomas (1970),
with the mass shells of a star defined by isobars instead of spherical shells.
In describing effects of rotationally induced chemical mixing,
the chemical abundances are assumed to be constant on isobars.
This has been justified by theoretical achievements of Zahn (1975), Chaboyer & Zahn (1992)
and Zahn (1992), who showed that anisotropic turbulence acts much more efficiently
in the horizontal than in the vertical direction. Shellular rotation
and chemical homogeneity on isobars can thus be achieved (Meynet & Maeder 1997), enabling
us to use a one dimensional approximation (see also Maeder 2003).
Our assumption of shellular rotation may be questionable for
helium-accreting white dwarfs, on two accounts.
Kippenhahn & Thomas (1978) argued that the accreted matter
cannot spread over the whole surface of the white dwarf but rather forms an accretion belt,
since the angular momentum transport time scale based on the electron viscosity
is longer than the accretion time scale.
However, calculations by Sparks & Kutter (1987)
failed to obtain classical nova outbursts when the prescription of accretion belts
was employed. Livio & Truran (1987) argued that if turbulent
viscosity is used, the angular momentum transport becomes much more efficient
than discussed by Kippenhahn & Thomas.
They concluded that the accreted matter
can spread over the entire star with the consequence that
mass accretion onto white dwarfs may result in nova outbursts,
which was not possible in the accretion belt prescription due to
the too strong centrifugal force at the equator.
A local stability analysis by MacDonald (1983) and a theoretical study
by Fujimoto (1988) also concluded
that the accreted matter will not remain confined to the equatorial belt
due to efficient angular momentum transport toward the poles.
We therefore conclude that the assumption of shellular rotation
employed in our study may still be well-grounded,
at least in the non-degenerate helium envelope,
although multi-dimensional simulations are ultimately required
for its justification (cf. Hujeirat 1995).
Secondly,
as degenerate matter is barotropic, perturbations which create
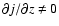 ,
with j as specific angular momentum
and z being the distance to
the equatorial plane, are eliminated on a short time scale. Thus,
cylindrical rotation may be enforced in the inner CO core
(e.g., Kippenhahn & Möllenhoff 1974; Durisen 1977).
This means that accreting white dwarfs may consist of two different
rotation laws: shellular in the non-degenerate envelope and
cylindrical rotation in the degenerate core.
However, our numerical models can still represent
the cylindrically rotating degenerate inner core to some degree,
since most of the total angular momentum is confined
at the equatorial plane in both the shellular and the cylindrical cases.
It is harder to estimate the angular momentum transport efficiency
in the semidegenerate transition layer, as non-barotropic perturbations in the degenerate core may
induce dynamical meridional flows
(Kippenhahn & Möllenhoff 1974; Müller 2003, private communication).
Since it is poorly known
how these meridional flows may affect the angular momentum redistribution,
we have to leave the detailed investigation of this effect to future work.
,
with j as specific angular momentum
and z being the distance to
the equatorial plane, are eliminated on a short time scale. Thus,
cylindrical rotation may be enforced in the inner CO core
(e.g., Kippenhahn & Möllenhoff 1974; Durisen 1977).
This means that accreting white dwarfs may consist of two different
rotation laws: shellular in the non-degenerate envelope and
cylindrical rotation in the degenerate core.
However, our numerical models can still represent
the cylindrically rotating degenerate inner core to some degree,
since most of the total angular momentum is confined
at the equatorial plane in both the shellular and the cylindrical cases.
It is harder to estimate the angular momentum transport efficiency
in the semidegenerate transition layer, as non-barotropic perturbations in the degenerate core may
induce dynamical meridional flows
(Kippenhahn & Möllenhoff 1974; Müller 2003, private communication).
Since it is poorly known
how these meridional flows may affect the angular momentum redistribution,
we have to leave the detailed investigation of this effect to future work.
Finally, the accuracy of our results for very rapid
rotation is limited due to the one-dimensional approximation.
In computing the effective gravitational potential in a rotating star,
the potential is expanded in terms of spherical harmonics,
of which we only consider terms up to the second order
(Kippenhahn & Thomas 1970; Endal & Sofia 1976).
This method can
reproduce the shapes of rigidly rotating polytropes accurately
up to a rotation rate of about 60% of the critical value, corresponding
to correction factors of
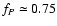 and
and
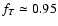 in the stellar structure equations (Fliegner 1993; Heger et al. 2000).
We therefore limit these factors to the quoted values,
with the consequence that we underestimate the effect
of the centrifugal force in layers that rotate more rapidly than
about 60% critical. We shall see below that this affects
only a very small fraction of our stellar models.
However,
as the surface layers are always very close to critical rotation,
the stellar radius of our models may be somewhat underestimated.
A better description of the equilibrium structure of rapidly rotating stars which
may deviate significantly from spheres
requires multi-dimensional techniques
such as the self-consistent field method (Ostriker & Mark 1968; Hachisu 1986).
In addition, since our models are rotationally symmetric,
three-dimensional effects such as triaxial
deformation cannot be described with our numerical code.
in the stellar structure equations (Fliegner 1993; Heger et al. 2000).
We therefore limit these factors to the quoted values,
with the consequence that we underestimate the effect
of the centrifugal force in layers that rotate more rapidly than
about 60% critical. We shall see below that this affects
only a very small fraction of our stellar models.
However,
as the surface layers are always very close to critical rotation,
the stellar radius of our models may be somewhat underestimated.
A better description of the equilibrium structure of rapidly rotating stars which
may deviate significantly from spheres
requires multi-dimensional techniques
such as the self-consistent field method (Ostriker & Mark 1968; Hachisu 1986).
In addition, since our models are rotationally symmetric,
three-dimensional effects such as triaxial
deformation cannot be described with our numerical code.
Table 1:
Properties of the computed models. The first column denotes
the sequence number, where "NR'', "R'' and "RT'' denote
the non-rotating models and rotating models with
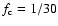 and 1/3 respectively.
The second column gives the accretion rate in units of 10-7
and 1/3 respectively.
The second column gives the accretion rate in units of 10-7
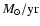 .
The third column denotes the factor
.
The third column denotes the factor 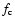 for the chemical mixing efficiency in rotating models.
Columns 4-7 give mass, central density, central temperature and
for the chemical mixing efficiency in rotating models.
Columns 4-7 give mass, central density, central temperature and
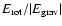 of the last computed model
of each evolutionary sequence. The eighth column gives the amount of accreted
material until the onset of the helium shell instability.
The column with
of the last computed model
of each evolutionary sequence. The eighth column gives the amount of accreted
material until the onset of the helium shell instability.
The column with
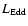 indicates whether the last computed model reached the Eddington limit or not.
The last column gives the total number of the computed models for each sequence.
indicates whether the last computed model reached the Eddington limit or not.
The last column gives the total number of the computed models for each sequence.
We begin with a hot carbon-oxygen white dwarf
of
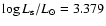 to avoid
the numerical difficulty of a strong initial helium shell flash.
The initial mass of our model is 0.998
to avoid
the numerical difficulty of a strong initial helium shell flash.
The initial mass of our model is 0.998
 .
The central temperature and density
are initially such that
.
The central temperature and density
are initially such that
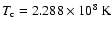 and
and
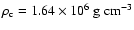 ,
respectively.
Although in reality white dwarfs may be much colder when mass accretion starts,
the thermal evolution of the white dwarf core is not influenced by the
different initial conditions due to the self heating of white dwarfs
(cf. Yoon & Langer 2003).
Since observations (Heber et al. 1997; Koester et al. 1998; Kawaler 2003)
and stellar evolution models (Langer et al. 1999) find small spin rates of isolated white dwarfs,
we adopt a slow and rigid rotation in our initial model: the initial rotation velocity
at the white dwarf equator is set to 1.0
,
respectively.
Although in reality white dwarfs may be much colder when mass accretion starts,
the thermal evolution of the white dwarf core is not influenced by the
different initial conditions due to the self heating of white dwarfs
(cf. Yoon & Langer 2003).
Since observations (Heber et al. 1997; Koester et al. 1998; Kawaler 2003)
and stellar evolution models (Langer et al. 1999) find small spin rates of isolated white dwarfs,
we adopt a slow and rigid rotation in our initial model: the initial rotation velocity
at the white dwarf equator is set to 1.0
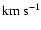 .
.
We consider 4 different accretion rates:
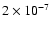 ,
,
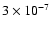 ,
,
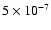 and 10-6
and 10-6
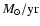 .
The accreted matter is assumed to be helium-rich with Y=0.98 and Z=0.02.
The abundances for heavier elements are chosen to be the same as
in a helium core which results from core hydrogen burning in a
main sequence star through the CNO cycle.
.
The accreted matter is assumed to be helium-rich with Y=0.98 and Z=0.02.
The abundances for heavier elements are chosen to be the same as
in a helium core which results from core hydrogen burning in a
main sequence star through the CNO cycle.
The specific angular momentum of the accreted matter is assumed to have the
local Keplerian value, as most white dwarfs with a non-degenerate companion
are believed to accrete matter through an accretion disk.
However, analytic considerations can show this to cause an angular momentum problem.
Assuming rigid rotation and a usual white dwarf mass-radius relation,
the white dwarf reaches overcritical rotation
long before reaching the Chandrasekhar limit
(Livio & Pringle 1998; Langer et al. 2000).
For finite angular momentum redistribution times, as realized by
our preliminary calculations (Yoon & Langer 2002),
overcritical rotation is even reached earlier.
Livio & Pringle (1998) suggested nova explosions as a possible mechanism
for angular momentum loss to explain the white dwarf rotation velocity in typical CV systems.
However, within the single degenerate SNe Ia progenitor scenario in which
the white dwarf must grow to the Chandrasekhar limit by mass accretion,
we need another mechanism to solve the angular momentum
problem. To prevent the white dwarf from rotating over-critically,
in our calculations, we limited the angular momentum gain
in a simple way as follow.
If the surface velocity at the white dwarf equator
is below the Keplerian value, the specific angular momentum of the accreted matter
is assumed to have the Keplerian value. Otherwise, no angular
momentum is allowed to be accreted onto the white dwarf while mass is still accreted:
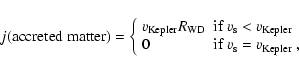 |
(1) |
where
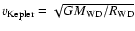 ,
and
,
and
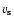 is the surface rotation velocity of the accreting white dwarf at its equator.
This assumption may be justified by considerations of Paczynski (1991)
and Popham & Narayan (1991) to allow angular momentum transport from the white dwarf
surface through the boundary layer into the accretion disk by turbulent viscosity
when the spin rate of the white dwarf reaches the Keplerian value, without preventing efficient
mass accretion.
is the surface rotation velocity of the accreting white dwarf at its equator.
This assumption may be justified by considerations of Paczynski (1991)
and Popham & Narayan (1991) to allow angular momentum transport from the white dwarf
surface through the boundary layer into the accretion disk by turbulent viscosity
when the spin rate of the white dwarf reaches the Keplerian value, without preventing efficient
mass accretion.
As discussed in Heger et al. (2000), the contribution of the rotationally
induced instabilities to the chemical diffusion is considered
by introducing a factor 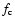
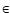 [0, 1], which
describes the ratio of the chemical diffusion coefficient to turbulent viscosity.
Heger et al. (2000) and Heger & Langer (2000) chose a value of
[0, 1], which
describes the ratio of the chemical diffusion coefficient to turbulent viscosity.
Heger et al. (2000) and Heger & Langer (2000) chose a value of
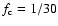 following Chaboyer & Zahn (1992) (see also Pinsonneault et al. 1989).
In the present study, we consider two different values for
following Chaboyer & Zahn (1992) (see also Pinsonneault et al. 1989).
In the present study, we consider two different values for 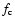 ,
i.e., 1/30 and
1/3 (see Table 1), in order to investigate how the strength of chemical mixing affects
the nuclear shell burning.
,
i.e., 1/30 and
1/3 (see Table 1), in order to investigate how the strength of chemical mixing affects
the nuclear shell burning.
For a comparative study, rotating and non-rotating
models with the same initial conditions have been investigated.
The properties of all computed models are summarized in Table 1.
4 Evolution
![\begin{figure}
\par\resizebox{7.8cm}{!}{\includegraphics[clip]{0327fg1a.ps}}\par...
...pace*{-2mm}\resizebox{7.5cm}{!}{\includegraphics[clip]{0327fg1c.ps}}\end{figure}](/articles/aa/full/2004/37/aa0327-04/Timg49.gif) |
Figure 1:
Evolution of nuclear luminosity due to helium burning in the helium-accreting white
dwarf models with
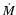 =
=
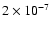
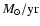 .
The box in panel a) gives
the result from the non-rotating case (NR1)
while the results from the rotating models with .
The box in panel a) gives
the result from the non-rotating case (NR1)
while the results from the rotating models with
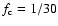 (R1) and (R1) and
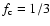 (RT1)
are shown in panels b) and c).
The abscissa denotes the total mass of the white dwarf, which serves as a measure of time. (RT1)
are shown in panels b) and c).
The abscissa denotes the total mass of the white dwarf, which serves as a measure of time.
|
| Open with DEXTER |
![\begin{figure}
\par\resizebox{7.8cm}{!}{\includegraphics[clip]{0327fg2a.ps}}\par\vspace*{3mm}
\resizebox{7.8cm}{!}{\includegraphics[clip]{0327fg2b.ps}}\end{figure}](/articles/aa/full/2004/37/aa0327-04/Timg50.gif) |
Figure 2:
Evolution of the white dwarf
in the sequences NR1 a) and R1 b) in the Hertzprung-Russell diagram.
The starting point
is marked by a filled circle. The endapoint, where the surface luminosity
reaches the Eddington limit, is marked by an asterisk for each case.
The raggedness which appears in some parts of the evolutionary tracks is due to the limited
number of digits in the numerical outputs.
|
| Open with DEXTER |
The results of our calculations are summarized in Table 1.
For sequences NR1, NR2, NR3, R1 and R2,
we followed the evolution until
the helium shell flashes become strong enough to drive the surface luminosity
to the Eddington limit.
For the remainder, calculations are stopped after a large number of models has been
calculated (cf. Table 1).
4.1 Helium shell burning and luminosity
In Fig. 1, the nuclear luminosity due to the helium burning in the sequences with
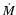 =
=
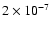
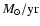 (NR1, R1 and RT1)
is shown as a function of the total mass of the white dwarf.
In sequence NR1,
helium shell burning is not stable but undergoes
thermal pulses, which are driven by the thin shell instability
(e.g., Schwarzshild & Härm 1965; Weigert 1966).
It is well known that this phenomenon occurs also in intermediate mass stars in
their thermally pulsating asymptotic giant branch (TP-AGB) phase
(e.g., Iben & Renzini 1983).
The thermal pulses in sequence NR1 become stronger as the white dwarf
accretes more matter (cf. Fujimoto & Sugimoto 1979). Finally,
the shell flash at the sixth pulse drives the surface
luminosity to the Eddington limit when
(NR1, R1 and RT1)
is shown as a function of the total mass of the white dwarf.
In sequence NR1,
helium shell burning is not stable but undergoes
thermal pulses, which are driven by the thin shell instability
(e.g., Schwarzshild & Härm 1965; Weigert 1966).
It is well known that this phenomenon occurs also in intermediate mass stars in
their thermally pulsating asymptotic giant branch (TP-AGB) phase
(e.g., Iben & Renzini 1983).
The thermal pulses in sequence NR1 become stronger as the white dwarf
accretes more matter (cf. Fujimoto & Sugimoto 1979). Finally,
the shell flash at the sixth pulse drives the surface
luminosity to the Eddington limit when

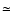 1.002
1.002
 (cf. Fig. 2), at which point we stop the calculation.
Perhaps, the white dwarf would experience a radiation-driven
optically thick outflow at this stage,
which would reduce the mass accumulation efficiency
(Kato & Hachisu 1999). It is beyond the purpose of this paper to
consider the ensuing evolution in detail.
(cf. Fig. 2), at which point we stop the calculation.
Perhaps, the white dwarf would experience a radiation-driven
optically thick outflow at this stage,
which would reduce the mass accumulation efficiency
(Kato & Hachisu 1999). It is beyond the purpose of this paper to
consider the ensuing evolution in detail.
In the rotating sequence R1 with the same accretion rate,
thermal pulses become significantly weaker than in the non-rotating case.
For instance, the helium shell source reaches
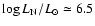 in the non-rotating case
when the white dwarf has accreted about 0.004
in the non-rotating case
when the white dwarf has accreted about 0.004
 ,
while the rotating sequence only reaches
,
while the rotating sequence only reaches
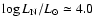 at the
same epoch (see Fig. 1).
As a consequence, the white dwarf can accrete more mass (
at the
same epoch (see Fig. 1).
As a consequence, the white dwarf can accrete more mass (
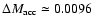
 )
than in sequence NR1 (
)
than in sequence NR1 (
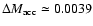
 )
before the surface luminosity reaches the Eddington limit.
In the HR diagram (Fig. 2), the rotating sequence is located at lower effective
temperatures than
the non-rotating sequence, since the white dwarf envelope is expanded by the centrifugal force.
)
before the surface luminosity reaches the Eddington limit.
In the HR diagram (Fig. 2), the rotating sequence is located at lower effective
temperatures than
the non-rotating sequence, since the white dwarf envelope is expanded by the centrifugal force.
The helium shell source becomes more
stable with stronger chemical mixing. Results of sequence RT1 in Fig. 1c,
where the chemical mixing is 10 times stronger than in sequence R1,
show that the helium is burned more or less steadily until

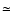 1.01
1.01
 .
More than 100 pulses were followed thereafter,
but the surface luminosity still did not reach the Eddington limit.
.
More than 100 pulses were followed thereafter,
but the surface luminosity still did not reach the Eddington limit.
The evolution of sequence NR2 (
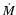 =
=
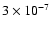
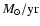 )
shown in Fig. 3
is similar to that of NR1, only
the white dwarf reaches the Eddington limit somewhat later, i.e., when
)
shown in Fig. 3
is similar to that of NR1, only
the white dwarf reaches the Eddington limit somewhat later, i.e., when

 1.004
1.004
 .
The thermal pulses are weakened in
the corresponding rotating sequence with
.
The thermal pulses are weakened in
the corresponding rotating sequence with
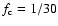 (R2, Fig. 3b),
and about 4 times more mass could be accreted in the white dwarf of sequence R2 before
the Eddington limit was reached.
With a stronger chemical mixing (
(R2, Fig. 3b),
and about 4 times more mass could be accreted in the white dwarf of sequence R2 before
the Eddington limit was reached.
With a stronger chemical mixing (
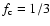 ,
RT2, Fig. 3c), steady
helium shell burning continues until
,
RT2, Fig. 3c), steady
helium shell burning continues until

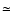 1.01
1.01
 ,
and weak thermal pulses with
,
and weak thermal pulses with
 follow.
The evolution of this sequence was stopped when
follow.
The evolution of this sequence was stopped when

 1.15
1.15
 ,
as the number of thermal pulses before reaching the Chandrasekhar mass
would exceed 104.
,
as the number of thermal pulses before reaching the Chandrasekhar mass
would exceed 104.
The stabilizing effect of rotation
appears more prominently at
 =
=
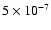
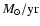 .
In the non-rotating case (NR3),
the helium shell burning is still unstable even with such a high
accretion rate, as shown in Fig. 4a, and
the white dwarf reaches the Eddington limit when
.
In the non-rotating case (NR3),
the helium shell burning is still unstable even with such a high
accretion rate, as shown in Fig. 4a, and
the white dwarf reaches the Eddington limit when

 1.013
1.013
 .
In the corresponding rotating sequence (R3), very weak thermal pulses
appear when
.
In the corresponding rotating sequence (R3), very weak thermal pulses
appear when

 1.005
1.005
 ,
but are suppressed when
,
but are suppressed when

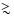 1.02
1.02
 .
Steady helium shell burning continues until
.
Steady helium shell burning continues until

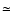 1.14
1.14
 ,
from which point the shell source becomes again unstable.
The thermal pulses shown
in Fig. 4b look like noise, but
actually each pulse is resolved by about 103 models.
,
from which point the shell source becomes again unstable.
The thermal pulses shown
in Fig. 4b look like noise, but
actually each pulse is resolved by about 103 models.
With an accretion rate of
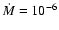
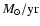 ,
the non-rotating white dwarf undergoes unstable helium shell burning
after
,
the non-rotating white dwarf undergoes unstable helium shell burning
after

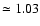
 (NR4, Fig. 4c).
We have followed the evolution until
(NR4, Fig. 4c).
We have followed the evolution until
 = 1.2
= 1.2
 and find that thermal pulses do not become strong enough to lead
the white dwarf to the Eddington limit.
On the other hand, in the rotating sequence R4 (Fig. 4d),
the white dwarf
can grow up to
and find that thermal pulses do not become strong enough to lead
the white dwarf to the Eddington limit.
On the other hand, in the rotating sequence R4 (Fig. 4d),
the white dwarf
can grow up to

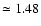
 without encountering significant
thermal pulses.
without encountering significant
thermal pulses.
![\begin{figure}
\par\resizebox{7.8cm}{!}{\includegraphics[clip]{0327fg4a.ps}}\hsp...
...pace*{7mm}
\resizebox{7.9cm}{!}{\includegraphics[clip]{0327fg4d.ps}}\end{figure}](/articles/aa/full/2004/37/aa0327-04/Timg62.gif) |
Figure 4:
Evolution of nuclear luminosity due to helium burning in the helium-accreting white
dwarf models for
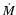 =
=
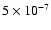
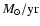 (NR3 a) and R3 b))
and
(NR3 a) and R3 b))
and
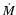 = 10-6
= 10-6
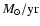 (NR4 c) and R4 d)).
The abscissa denotes the total mass of the white dwarf, which serves as a measure of time.
Note that what appears to look like noise in the plots for R3 and NR4
corresponds to many successive thermal pulses, each as well resolved in time
(i.e., by roughly 103 time steps) as those in the plots in Figs. 1 and 3.
(NR4 c) and R4 d)).
The abscissa denotes the total mass of the white dwarf, which serves as a measure of time.
Note that what appears to look like noise in the plots for R3 and NR4
corresponds to many successive thermal pulses, each as well resolved in time
(i.e., by roughly 103 time steps) as those in the plots in Figs. 1 and 3.
|
| Open with DEXTER |
The evolution of the white dwarf of sequence R4 in HR diagram is shown
in Fig. 5.
The surface luminosity
remains nearly constant at
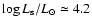 ,
while the surface temperature increases from
,
while the surface temperature increases from
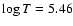 to
to
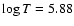 .
Therefore, the white dwarf will appear as a super-soft X-ray source throughout
the accretion phase
(e.g., Kahabka & van den Heuvel 1997; Greiner 2000).
.
Therefore, the white dwarf will appear as a super-soft X-ray source throughout
the accretion phase
(e.g., Kahabka & van den Heuvel 1997; Greiner 2000).
The results presented in this section show that
the helium shell source becomes more stable with rotation, and
that the stronger the chemical mixing the more stable
the shell burning becomes. We discuss the physical reasons
for this behavior in Sect. 6.
4.2 White dwarf spin and angular momentum transport
According to Yoon & Langer (2004a), who considered accretion of
carbon-oxygen rich matter,
non-magnetic accreting white dwarfs with
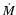
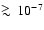
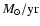 show the following features in relation to the angular momentum
redistribution.
a) Eddington-Sweet circulations,
the secular shear instability, and the GSF instability are
dominating the angular momentum redistribution in the non-degenerate outer envelope,
while the dynamical shear instability is the most important in the degenerate core.
b) The degree of differential rotation in the degenerate core
remains strong throughout the evolution, with a shear strength
near the threshold value for the onset of the dynamical shear instability.
c) The resulting differential rotation changes
the white dwarf structure such that the center
does not reach carbon ignition
even when the white dwarf reaches the Chandrasekhar limit (
show the following features in relation to the angular momentum
redistribution.
a) Eddington-Sweet circulations,
the secular shear instability, and the GSF instability are
dominating the angular momentum redistribution in the non-degenerate outer envelope,
while the dynamical shear instability is the most important in the degenerate core.
b) The degree of differential rotation in the degenerate core
remains strong throughout the evolution, with a shear strength
near the threshold value for the onset of the dynamical shear instability.
c) The resulting differential rotation changes
the white dwarf structure such that the center
does not reach carbon ignition
even when the white dwarf reaches the Chandrasekhar limit (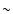 1.4
1.4
 ).
d) More than 60% of the angular momentum of the accreted matter
is rejected because of the condition that the white dwarf should not gain
angular momentum when its surface rotates critically (Eq. (1)).
).
d) More than 60% of the angular momentum of the accreted matter
is rejected because of the condition that the white dwarf should not gain
angular momentum when its surface rotates critically (Eq. (1)).
![\begin{figure}
\par\resizebox{7.8cm}{!}{\includegraphics[clip]{0327fg5.ps}}\end{figure}](/articles/aa/full/2004/37/aa0327-04/Timg69.gif) |
Figure 5:
Evolution of the white dwarf
in sequence R4 in the Hertzsprung-Russell diagram.
The region with
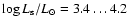 and and
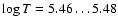 represents the epoch from the onset of
helium accretion to the first mild helium shell flash (cf. Fig. 4d).
represents the epoch from the onset of
helium accretion to the first mild helium shell flash (cf. Fig. 4d).
|
| Open with DEXTER |
It is found that all these features remain the same
in the present study, where helium accretion is considered.
Figure 6 shows angular velocity profiles throughout white
dwarf models of sequence RT1, R3 and R4, at various times,
where the angular velocity is given in units
of the local Keplerian value (i.e.,
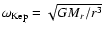 ).
Note that the spin rate remains well below the local Keplerian value
throughout the whole star in all cases.
).
Note that the spin rate remains well below the local Keplerian value
throughout the whole star in all cases.
The white dwarf model with

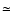 1.4
1.4
 in
sequence R4 has a central density of
in
sequence R4 has a central density of
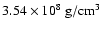 ,
which is still far from the carbon ignition density.
(cf. Ostriker & Bodenheimer 1968; Durisen 1975; Durisen & Imamura 1981).
As shown in the mentioned papers, a differentially rotating
white dwarf can be dynamically stable up to
,
which is still far from the carbon ignition density.
(cf. Ostriker & Bodenheimer 1968; Durisen 1975; Durisen & Imamura 1981).
As shown in the mentioned papers, a differentially rotating
white dwarf can be dynamically stable up to 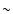 4.0
4.0
 .
As discussed in Yoon & Langer (2004a), this suggests that the secular
instability to the gravitational wave radiation reaction, which
is often called as the "CFS instability'' (Chandrasekhar 1970; Friedman & Schutz 1978),
might be important for the final fate of accreting white dwarfs
near or above the Chandrasekhar limit.
The ratio of the rotational energy to the gravitational energy (
.
As discussed in Yoon & Langer (2004a), this suggests that the secular
instability to the gravitational wave radiation reaction, which
is often called as the "CFS instability'' (Chandrasekhar 1970; Friedman & Schutz 1978),
might be important for the final fate of accreting white dwarfs
near or above the Chandrasekhar limit.
The ratio of the rotational energy to the gravitational energy (
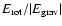 ),
which determines the growth time scale of the CFS instability via
the bar-mode or the r-mode (see Yoon & Langer 2004a), remains smaller than 0.1
in the white dwarf models of sequence R4, and the last
model (
),
which determines the growth time scale of the CFS instability via
the bar-mode or the r-mode (see Yoon & Langer 2004a), remains smaller than 0.1
in the white dwarf models of sequence R4, and the last
model (
 = 1.48
= 1.48
 )
has
)
has
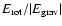 = 0.06.
Since in white dwarfs with strong differential rotation
= 0.06.
Since in white dwarfs with strong differential rotation
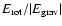
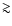 0.1 is required for the onset of the bar-mode instability (Imamura et al. 1995),
only the r-mode may be relevant at this point.
The expected growth time of the r-mode instability
in this model is about
0.1 is required for the onset of the bar-mode instability (Imamura et al. 1995),
only the r-mode may be relevant at this point.
The expected growth time of the r-mode instability
in this model is about
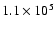 yr
(see Yoon & Langer 2004a; cf. Lindblom 1999).
We refer to Yoon & Langer (2004a)
for a detailed discussion of the final fate of rapidly
rotating massive white dwarfs.
yr
(see Yoon & Langer 2004a; cf. Lindblom 1999).
We refer to Yoon & Langer (2004a)
for a detailed discussion of the final fate of rapidly
rotating massive white dwarfs.
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[clip]{0327fg6a.ps}}\par\v...
...vspace*{2mm}
\resizebox{8cm}{!}{\includegraphics[clip]{0327fg6c.ps}}\end{figure}](/articles/aa/full/2004/37/aa0327-04/Timg74.gif) |
Figure 6:
Spin velocity at different white dwarf masses,
normalized to the local Keplerian value, as a function
of the mass coordinate for RT1, R3 and R4.
|
| Open with DEXTER |
5 Chemical mixing and nucleosynthesis
![\begin{figure}
\par\resizebox{7.8cm}{!}{\includegraphics[clip]{0327fg7a.ps}}\par\vspace*{2mm}
\resizebox{7.8cm}{!}{\includegraphics[clip]{0327fg7b.ps}}\end{figure}](/articles/aa/full/2004/37/aa0327-04/Timg75.gif) |
Figure 7:
Logarithm of the mass fractions of helium and carbon as a function
of the mass coordinate (solid line), in the white dwarf models of sequences NR4
( upper panel) and R4 ( lower panel) at a time when
 = 1.0305
= 1.0305
 .
The dotted and dashed lines denote
the corresponding energy generation rate (right scale)
for the .
The dotted and dashed lines denote
the corresponding energy generation rate (right scale)
for the 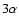 and
and
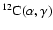 reactions respectively. reactions respectively.
|
| Open with DEXTER |
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[clip]{0327fg8.ps}}\end{figure}](/articles/aa/full/2004/37/aa0327-04/Timg76.gif) |
Figure 8:
Carbon mass fraction as a function of the mass coordinate
for the last computed models of sequences R4 (dashed line) and NR4
(dotted line). The thin solid line corresponds to the initial model.
Note that the mass of the helium envelope is
only of the order of 10-4
 ,
which is not resolved
in this figure. The sharp peak in the carbon abundance near
the surface in each white dwarf model is due to the active ,
which is not resolved
in this figure. The sharp peak in the carbon abundance near
the surface in each white dwarf model is due to the active
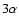 reaction at the bottom of the helium envelope
(cf. Fig. 7). reaction at the bottom of the helium envelope
(cf. Fig. 7).
|
| Open with DEXTER |
The mixing of 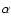 -particles into the CO-core and of carbon into
the helium envelope has consequences for the helium
burning shell source. Here, we discuss the resulting changes in
chemical structure of the white dwarf, while in the next section
we analyze how rotation and rotationally induced chemical mixing
affects the stability properties of the shell source.
-particles into the CO-core and of carbon into
the helium envelope has consequences for the helium
burning shell source. Here, we discuss the resulting changes in
chemical structure of the white dwarf, while in the next section
we analyze how rotation and rotationally induced chemical mixing
affects the stability properties of the shell source.
Figure 7 shows the chemical structure
and the nuclear energy generation rate
in the helium burning shell in the white dwarf
models of sequences R4 and NR4 when
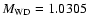
 .
The helium layer in the rotating model extends farther into the CO core
than in the non-rotating case, due to the rotationally induced
chemical mixing. This renders the
.
The helium layer in the rotating model extends farther into the CO core
than in the non-rotating case, due to the rotationally induced
chemical mixing. This renders the
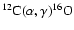 reaction more active in the rotating model,
with two main consequences.
reaction more active in the rotating model,
with two main consequences.
Firstly, the contribution of the
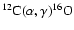 reaction to
the total energy production is considerably increased.
In the given models in Fig. 7,
the rotating model gives
reaction to
the total energy production is considerably increased.
In the given models in Fig. 7,
the rotating model gives
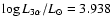 and
and
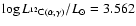 ,
while the non-rotating model gives
,
while the non-rotating model gives
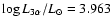 and
and
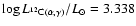 ,
where
,
where
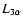 and
and
 are the integrated nuclear energy generation rates over the shell source,
due to the triple alpha reaction and the
are the integrated nuclear energy generation rates over the shell source,
due to the triple alpha reaction and the
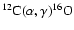 reaction, respectively.
The
reaction, respectively.
The 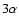 reaction is weaker in the rotating model than
in the non-rotating one
due to a lower density
in the helium envelope
(cf. Fig. 9)
and due to a smaller mass fraction of helium at the peak of the nuclear energy generation rate
caused by rotationally induced mixing (Fig. 7).
However, the increase of the energy generation by the
reaction is weaker in the rotating model than
in the non-rotating one
due to a lower density
in the helium envelope
(cf. Fig. 9)
and due to a smaller mass fraction of helium at the peak of the nuclear energy generation rate
caused by rotationally induced mixing (Fig. 7).
However, the increase of the energy generation by the
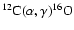 reaction
is more important on the whole,
leading to a higher nuclear luminosity in the rotating model
(
reaction
is more important on the whole,
leading to a higher nuclear luminosity in the rotating model
(
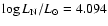 )
than in the corresponding non-rotating case (
)
than in the corresponding non-rotating case (
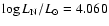 ),
for the models given in Fig. 7.
Furthermore, the shell source is hotter in the rotating model
[
),
for the models given in Fig. 7.
Furthermore, the shell source is hotter in the rotating model
[
 ]
than in the comparable non-rotating model [
]
than in the comparable non-rotating model [
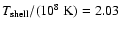 ],
which affects its stability as
discussed in Sect. 6.
],
which affects its stability as
discussed in Sect. 6.
Secondly, the enhanced
 -efficiency results in
an increased oxygen abundance in the ashes of the helium burning shell,
at the expense of carbon. Figure 8 shows the carbon mass fraction
throughout the white dwarf for the last computed models of sequences NR3 and R3.
In the non-rotating model, the carbon mass fraction produced by the shell
source reaches almost
-efficiency results in
an increased oxygen abundance in the ashes of the helium burning shell,
at the expense of carbon. Figure 8 shows the carbon mass fraction
throughout the white dwarf for the last computed models of sequences NR3 and R3.
In the non-rotating model, the carbon mass fraction produced by the shell
source reaches almost
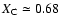 at a white dwarf mass of
1.03
at a white dwarf mass of
1.03
 .
At this time, the helium shell source becomes unstable
and develops thermal pulses. As the layers at and above the shell source
become convectively unstable during each pulse, the resulting carbon abundance
is reduced. The convective mixing becomes
more and more significant as thermal pulses become stronger (cf. Fig. 4c),
which is reflected in the drop of
.
At this time, the helium shell source becomes unstable
and develops thermal pulses. As the layers at and above the shell source
become convectively unstable during each pulse, the resulting carbon abundance
is reduced. The convective mixing becomes
more and more significant as thermal pulses become stronger (cf. Fig. 4c),
which is reflected in the drop of 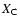 from about 0.68
to 0.55 in the range 1.03
from about 0.68
to 0.55 in the range 1.03

 in Fig. 8.
A comparison with the rotating model shows that the carbon mass fraction is
mostly below 0.5, even though the rotating model does not suffer from thermal
pulses for most of the time.
While the average carbon mass fraction in the accreted layer is
0.58 in the non-rotating model, it is 0.45 in the
layer with
in Fig. 8.
A comparison with the rotating model shows that the carbon mass fraction is
mostly below 0.5, even though the rotating model does not suffer from thermal
pulses for most of the time.
While the average carbon mass fraction in the accreted layer is
0.58 in the non-rotating model, it is 0.45 in the
layer with
 of the
rotating model. The mean value of
of the
rotating model. The mean value of 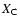 throughout the
accreted layer in the rotating model (i.e.,
throughout the
accreted layer in the rotating model (i.e.,
 )
is 0.38.
)
is 0.38.
The carbon and oxygen mass fractions in the accreted envelope of
a SN Ia progenitor are important from the point of view of nucleosynthesis
and supernova spectroscopy, and may even affect
the peak brightness of the supernova explosion
(cf. Umeda et al. 1999; Höflich et al. 2000; Domínguez et al. 2001).
6 Stability of helium shell burning
![\begin{figure}
\par\resizebox{11.8cm}{!}{\includegraphics[clip]{0327fg9.ps}}\end{figure}](/articles/aa/full/2004/37/aa0327-04/Timg94.gif) |
Figure 9:
Evolution of the helium shell source in the sequences NR4 and
R4 during the stable shell burning phase, in the plane spanned by
the degeneracy parameter 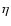 and the relative thickness of the shell source
and the relative thickness of the shell source
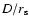 .
Here D denotes the thickness of the shell source and .
Here D denotes the thickness of the shell source and 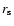 its radius. Each asterisk and black dot represents one selected stellar model
in sequences NR4 and R4, respectively.
The white dwarf mass in solar masses and the temperature of the shell source
in units of 108 K are indicated for various models.
The thin lines separate the stable and unstable regimes,
for its radius. Each asterisk and black dot represents one selected stellar model
in sequences NR4 and R4, respectively.
The white dwarf mass in solar masses and the temperature of the shell source
in units of 108 K are indicated for various models.
The thin lines separate the stable and unstable regimes,
for
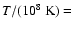 2.0 (dotted line), 2.2 (short dashed line), 2.4 (dotted-dashed line),
2.6 (three dotted - dashed line) and 2.8 (long dashed line)
according to the analytic stability criterion of Yoon et al. (2004).
I.e., helium shell burning is predicted to be stable (unstable) above (below) the lines,
while thermal pulses become significant from
2.0 (dotted line), 2.2 (short dashed line), 2.4 (dotted-dashed line),
2.6 (three dotted - dashed line) and 2.8 (long dashed line)
according to the analytic stability criterion of Yoon et al. (2004).
I.e., helium shell burning is predicted to be stable (unstable) above (below) the lines,
while thermal pulses become significant from
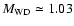
 in sequence NR4, and weak thermal pulses appear
from
in sequence NR4, and weak thermal pulses appear
from
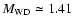
 in sequence R4.
in sequence R4.
|
| Open with DEXTER |
Our results show that helium shell burning is more stable with rotation,
than in the non-rotating case (Figs. 1, 3 and 4).
The stability of a helium shell source is mainly determined
by three factors: geometrical thickness, degree of degeneracy
and temperature of the shell source.
In other words, a helium shell source is more stable if it is thicker,
less degenerate and hotter. While a general and quantitative stability criterion
for shell sources has been worked out in a separate paper (Yoon et al. 2004), we discuss the qualitative effects of rotation on the
shell source stability of the models presented in Sect. 3 in the following.
Figure 9 shows the evolution of the helium shell
sources of sequences NR4 and R4
in the plane of the degeneracy parameter 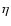 (
(
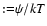 ,
e.g., Clayton 1968)
and the relative thickness of the shell source
,
e.g., Clayton 1968)
and the relative thickness of the shell source
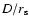 ,
where
D and
,
where
D and 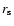 are the thickness and the radius of the shell source, respectively.
Here, the energy generation rate
weighted mean over the shell source is used for the degeneracy parameter.
The thickness of the shell source is defined such that
the energy generation rate at each boundary is
are the thickness and the radius of the shell source, respectively.
Here, the energy generation rate
weighted mean over the shell source is used for the degeneracy parameter.
The thickness of the shell source is defined such that
the energy generation rate at each boundary is
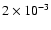 times its peak value.
Figure 9 illustrates the evolution toward instability for
the example of sequences NR4 and R4.
In sequence NR4, the mean temperature in the shell source
remains nearly constant, around
times its peak value.
Figure 9 illustrates the evolution toward instability for
the example of sequences NR4 and R4.
In sequence NR4, the mean temperature in the shell source
remains nearly constant, around
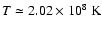 during
the stable shell burning phase.
Figure 9 shows the border between stability
and instability for
during
the stable shell burning phase.
Figure 9 shows the border between stability
and instability for
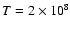 K, as obtained by Yoon et al. (2004), as a dotted line.
The shell source becomes more degenerate and thinner
as the white dwarf mass grows, and finally enters
the unstable regime when
K, as obtained by Yoon et al. (2004), as a dotted line.
The shell source becomes more degenerate and thinner
as the white dwarf mass grows, and finally enters
the unstable regime when

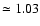
 ,
resulting
in the onset of thermal pulses as shown in Fig. 4c.
,
resulting
in the onset of thermal pulses as shown in Fig. 4c.
As already discussed in Sect. 5, the shell source in the rotating models
extends over a wider mass range due to rotationally induced chemical mixing. I.e.,
significant amounts of 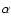 -particles are mixed into the CO core and participate
in the
-particles are mixed into the CO core and participate
in the
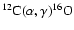 reaction. The presence of the centrifugal force
lowers the density, and were it not for the effect of mixing the shell source temperature
would decrease with rotation. However, due to the enhanced
reaction. The presence of the centrifugal force
lowers the density, and were it not for the effect of mixing the shell source temperature
would decrease with rotation. However, due to the enhanced
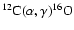 reaction,
temperature and nuclear energy production are increased, despite the lower density.
In summary, rotation changes all three physical properties
which affect the stability - thickness, degeneracy and temperature - such that
stability becomes more likely.
Figure 9 shows that this effect is quite significant.
While the evolutionary tracks of sequences NR4 and R4 are close to each other in the
shell thickness-degeneracy plane, at a given mass the shell thickness
is much larger and the degeneracy much lower in the rotating models.
For example, at
reaction,
temperature and nuclear energy production are increased, despite the lower density.
In summary, rotation changes all three physical properties
which affect the stability - thickness, degeneracy and temperature - such that
stability becomes more likely.
Figure 9 shows that this effect is quite significant.
While the evolutionary tracks of sequences NR4 and R4 are close to each other in the
shell thickness-degeneracy plane, at a given mass the shell thickness
is much larger and the degeneracy much lower in the rotating models.
For example, at
 = 1.01
= 1.01
 ,
the non-rotating model
gives
,
the non-rotating model
gives
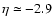 and
and
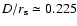 and
the corresponding rotating model gives
and
the corresponding rotating model gives
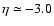 and
and
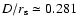 .
Furthermore,
we have
.
Furthermore,
we have
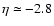 and
and
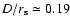 at
at
 = 1.03
= 1.03
 ,
from which point
thermal pulses become significant in the non-rotating sequence,
while
,
from which point
thermal pulses become significant in the non-rotating sequence,
while
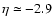 and
and
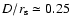 even
when
even
when
 is as large as 1.14
is as large as 1.14
 in the rotating model (Fig. 9).
in the rotating model (Fig. 9).
Additionally, the instability border which is given by
the thin lines in Fig. 9 is located lower
at a given mass in the rotating case,
due to the higher shell source temperature in the rotating models,
which leads to a later onset of the instability even for
a given shell source thickness and degeneracy.
For instance, the shell source temperature in the rotating model
when
 = 1.01
= 1.01
 is about
is about
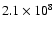 K, which is higher
than in the non-rotating models, where
K, which is higher
than in the non-rotating models, where
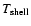 remains at
remains at
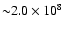 K
during the steady shell burning phase.
The last analyzed model in sequence NR4 is already in the unstable regime
(i.e., below the dotted line;
K
during the steady shell burning phase.
The last analyzed model in sequence NR4 is already in the unstable regime
(i.e., below the dotted line;
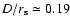 )
and thermal pulses become significant right after as expected from the stability criterion.
On the other hand, in sequence R4, the shell source temperature increases up to
)
and thermal pulses become significant right after as expected from the stability criterion.
On the other hand, in sequence R4, the shell source temperature increases up to
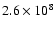 K
when
K
when
 = 1.41
= 1.41
 ,
which explains why the shell source
is stable until
,
which explains why the shell source
is stable until

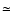 1.41
1.41
 even though
even though
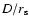 at this moment is smaller than in the last analyzed model of NR4.
As shown in Fig. 4d (see also Fig. 5),
the ensuing thermal pulses which appear when
at this moment is smaller than in the last analyzed model of NR4.
As shown in Fig. 4d (see also Fig. 5),
the ensuing thermal pulses which appear when

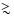 1.41
1.41
 in sequence R4
remain very weak until the last model
(
in sequence R4
remain very weak until the last model
(
 = 1.48
= 1.48
 with
with
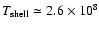 K),
which is still near the stability border line for
K),
which is still near the stability border line for
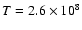 K
in Fig. 9.
K
in Fig. 9.
In summary, rotation stabilizes the instability of the
helium shell burning in our models significantly. The shell sources in
realistic white dwarfs, however, may be even more stable than
our models predict, for two reasons.
Firstly, as outlined in Sect. 2, our method
forces us to limit the structural effects of rotation to that
obtained at about 60% of critical rotation. This means that we underestimate
the centrifugal force in the layers which contain the shell source.
Secondly, our models are one-dimensional, which restricts
the pressure response due to any perturbation to the radial direction -
which is generally not true in the realistic situation. In a rapidly rotating
star, the pressure can also respond to a perturbation
horizontally, unless the shell source is located at the poles.
We believe that this multi-dimensional effects can stabilize the shell source further.
We have performed numerical simulations of helium-accreting CO white dwarfs
with an initial mass of 0.998
 and 4 different
mass accretion rates (2, 3, 5 and
and 4 different
mass accretion rates (2, 3, 5 and
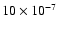
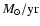 ),
considering spin-up by mass accretion.
The main feature of the spin-up is
the angular momentum transport from the accreted matter into the white dwarf,
which creates differential rotation in the white dwarf interior.
This induces transport of chemical species from the accreted matter into the CO core,
through the shear instability, Eddington-Sweet circulations, and the GSF instability.
),
considering spin-up by mass accretion.
The main feature of the spin-up is
the angular momentum transport from the accreted matter into the white dwarf,
which creates differential rotation in the white dwarf interior.
This induces transport of chemical species from the accreted matter into the CO core,
through the shear instability, Eddington-Sweet circulations, and the GSF instability.
It is shown that the helium burning layer
becomes spatially more extended than in the non-rotating case,
since the accreted 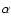 -particles
are mixed into the carbon enriched layer, participating actively
in the
-particles
are mixed into the carbon enriched layer, participating actively
in the
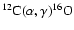 reaction (Sect. 5).
The carbon-to-oxygen ratio is significantly reduced
in the accreted layer.
The centrifugal force lowers the density in the shell source and degeneracy
is significantly lifted.
The total energy generation in the helium shell source increases with rotation,
due to the increased contribution from the
reaction (Sect. 5).
The carbon-to-oxygen ratio is significantly reduced
in the accreted layer.
The centrifugal force lowers the density in the shell source and degeneracy
is significantly lifted.
The total energy generation in the helium shell source increases with rotation,
due to the increased contribution from the
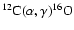 reaction, rendering
the helium shell source as hot as in the non-rotating cases, despite
the decreased density.
All these effects contribute to stabilizing the helium shell burning
significantly (Sect. 6).
Thermal pulses, if they occur, are considerably weakened with rotation.
reaction, rendering
the helium shell source as hot as in the non-rotating cases, despite
the decreased density.
All these effects contribute to stabilizing the helium shell burning
significantly (Sect. 6).
Thermal pulses, if they occur, are considerably weakened with rotation.
As mentioned previously, and as discussed by Cassisi et al. (1998),
Kato & Hachisu (1999) and Langer et al. (2002),
a high mass accumulation efficiency
on a white dwarf by hydrogen accretion has been seriously questioned
due to the unstable helium shell burning which is found
when helium is accreted at
a rate which gives steady hydrogen shell burning.
Note that the accretion rate of
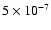
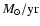 corresponds roughly
to the maximum rate for the steady hydrogen burning
in a 1.0
corresponds roughly
to the maximum rate for the steady hydrogen burning
in a 1.0
 white dwarf (Nomoto 1982a).
Our results indicate that even if hydrogen is
accreted and burned steadily, the subsequent helium shell burning
may be unstable, with strong helium shell flashes driving the stellar envelope
to the Eddington limit, unless effects of rotation are considered.
Kato & Hachisu (1999) suggested that
if the new OPAL opacities are adopted, an optically thick wind
can remove mass from the system without the white dwarf filling its Roche lobe.
They also suggested that the effective mass accumulation rate can remain
high enough for the white dwarf to grow to the Chandrasekhar limit.
However, their results are based on a very massive white dwarf model of 1.3
white dwarf (Nomoto 1982a).
Our results indicate that even if hydrogen is
accreted and burned steadily, the subsequent helium shell burning
may be unstable, with strong helium shell flashes driving the stellar envelope
to the Eddington limit, unless effects of rotation are considered.
Kato & Hachisu (1999) suggested that
if the new OPAL opacities are adopted, an optically thick wind
can remove mass from the system without the white dwarf filling its Roche lobe.
They also suggested that the effective mass accumulation rate can remain
high enough for the white dwarf to grow to the Chandrasekhar limit.
However, their results are based on a very massive white dwarf model of 1.3
 .
Cassisi et al. (1998), on the other hand, showed
that hydrogen-accreting white dwarfs with initial masses of 0.56
.
Cassisi et al. (1998), on the other hand, showed
that hydrogen-accreting white dwarfs with initial masses of 0.56
 and 0.8
and 0.8
 fill their Roche lobe
once helium flashes occur,
leaving doubts about the efficient mass increase of the white dwarf
from a relatively low mass
by hydrogen accretion.
fill their Roche lobe
once helium flashes occur,
leaving doubts about the efficient mass increase of the white dwarf
from a relatively low mass
by hydrogen accretion.
Our results imply that rotation may help white dwarfs
to grow in mass by stabilizing helium shell burning.
In the canonical single degenerate
scenario, however,
a main sequence star or a red giant is supposed to
transfer hydrogen-rich matter onto the white dwarf
(Li & van den Heuvel 1997; Hachisu et al. 1999;
Langer et al. 2000).
We still need to investigate the case of hydrogen accretion,
in order to answer the question whether rotation may be a potential solution
in explaining the observed SNe Ia rate from the considered binary systems.
Since the stability conditions for hydrogen shell burning
are not qualitatively different from that for helium shell burning
(Yoon et al. 2004),
we expect that the effects of rotation on the hydrogen shell source
are likely to give a similar conclusion
as for the helium shell burning.
On the other hand, hydrogen accretion with a rate of
10-6
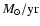 is supposed to expand a 1.0
is supposed to expand a 1.0
 white dwarf into a red giant phase (Nomoto 1982a; Nomoto & Kondo 1991;
Cassisi et al. 1998).
In a close binary system, the hydrogen envelope expanded to the red giant phase
will fill the Roche lobe, causing significant mass loss or the merging of both stars,
unless the mass accretion rate is reduced by an optically
thick stellar wind, as suggested by Hachisu et al. (1996, 1999).
However, steady helium accretion with such a high accretion rate can be realized, for example,
in a binary system which consists of a white dwarf and a helium giant star
("helium Algols'', Iben & Tutukov 1994), in which
the mass transfer rate can amount to
10-6 - 10-5
white dwarf into a red giant phase (Nomoto 1982a; Nomoto & Kondo 1991;
Cassisi et al. 1998).
In a close binary system, the hydrogen envelope expanded to the red giant phase
will fill the Roche lobe, causing significant mass loss or the merging of both stars,
unless the mass accretion rate is reduced by an optically
thick stellar wind, as suggested by Hachisu et al. (1996, 1999).
However, steady helium accretion with such a high accretion rate can be realized, for example,
in a binary system which consists of a white dwarf and a helium giant star
("helium Algols'', Iben & Tutukov 1994), in which
the mass transfer rate can amount to
10-6 - 10-5
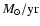 ,
as shown by Yoon & Langer (2003).
Our results indicate clearly that the mass accumulation
efficiency can be significantly enhanced by rotation for helium giant star + white dwarf binary systems.
Although the calculated production rate of SNe Ia via this route is currently
rather uncertain (Iben & Tutukov 1994; Branch et al. 1998),
consideration of rotation may increase it strongly.
,
as shown by Yoon & Langer (2003).
Our results indicate clearly that the mass accumulation
efficiency can be significantly enhanced by rotation for helium giant star + white dwarf binary systems.
Although the calculated production rate of SNe Ia via this route is currently
rather uncertain (Iben & Tutukov 1994; Branch et al. 1998),
consideration of rotation may increase it strongly.
In the present study, we did not consider stellar winds from white dwarfs,
on which rotation might cause significant effects. When the stellar surface approaches
the critical velocity, the mass loss due to radiation-driven winds could
increase dramatically (Friend & Abbott 1986; Langer 1997).
Since stellar winds may also carry a large amount of angular momentum
(Langer 1998),
this would involve a complicated history
of angular momentum gain or loss in accreting white dwarfs:
accretion will spin up white dwarfs, while stellar winds will brake them.
It is also possible that the physical conditions in the shell source
in a rapidly rotating white dwarf
vary with latitude, which may lead to interesting
consequences such as non-spherical stellar winds
(cf. Owocki & Gayely 1997; Maeder 1999).
We will investigate these effects systematically in the near future.
Finally, we note that an increase in the uncertain efficiency of
rotationally induced chemical mixing results in more stable
shell burning (Figs. 1 and 3), than
when the calibration by Heger et al. (2000) and
Heger & Langer (2000) is adopted.
Their calibration gives
a chemical mixing efficiency similar to that in
Pinsonneault et al. (1989) who made a calibration to reproduce
the solar surface
 abundance,
as well as to the theoretical estimate by Chaboyer & Zahn (1992).
The physical conditions in the helium shell source in white dwarfs
do not differ qualitatively from those in main sequence stars.
However, for accreting white dwarfs,
another mixing mechanism which was not considered in the present study
may be important: magnetic instability induced by
differential rotation in radiative layers (Spruit 2002).
Heger et al. (2003) and Maeder & Meynet (2003) show that
the turbulent diffusion can become stronger by several
orders of magnitude
due to the magnetic instability, than in
the case where only rotational effects are considered.
The differential-rotation-induced magnetic instability
can be even more important in accreting white dwarfs,
in which a strong shear motion is retained
due to the continuous angular momentum
transport from the accreted matter, as shown in Sect. 4.2.
The efficiency of the chemical mixing may increase accordingly,
which may stabilize the shell source even further than in the present study.
This possibility is currently under investigation.
abundance,
as well as to the theoretical estimate by Chaboyer & Zahn (1992).
The physical conditions in the helium shell source in white dwarfs
do not differ qualitatively from those in main sequence stars.
However, for accreting white dwarfs,
another mixing mechanism which was not considered in the present study
may be important: magnetic instability induced by
differential rotation in radiative layers (Spruit 2002).
Heger et al. (2003) and Maeder & Meynet (2003) show that
the turbulent diffusion can become stronger by several
orders of magnitude
due to the magnetic instability, than in
the case where only rotational effects are considered.
The differential-rotation-induced magnetic instability
can be even more important in accreting white dwarfs,
in which a strong shear motion is retained
due to the continuous angular momentum
transport from the accreted matter, as shown in Sect. 4.2.
The efficiency of the chemical mixing may increase accordingly,
which may stabilize the shell source even further than in the present study.
This possibility is currently under investigation.
Acknowledgements
We would like to thank the anonymous referee for useful comments
and careful reading of the manuscript, which led to significant
improvement of the text.
We are grateful to Peter Höflich for enlightening discussions.
This research has been supported in part by the Netherlands Organization for
Scientific Research (NWO).
- Branch, D., Livio,
M., Yungelson, L. R., Boffi, F. R., & Baron, E. 1995, PASP,
107, 1019 [NASA ADS] [CrossRef] (In the text)
- Branch, D. 1998,
ARA&A, 36, 17 [NASA ADS] (In the text)
- Cassisi, S.,
Iben, I., & Tornambé, A. 1998, ApJ, 496, 376 [NASA ADS] [CrossRef] (In the text)
- Caughlan, G.
R., Fowler, W. A., Marris, M. J., & Zimmerman, B. A. 1985,
Atomic Dat. Nuc. Dat. Tables, 32, 197 [NASA ADS] (In the text)
- Chaboyer, B.,
& Zahn, J.-P. 1992, A&A, 253, 173 [NASA ADS] (In the text)
-
Chandrasekhar, S. 1970, Phys. Rev. Lett., 24, 611 [NASA ADS] [CrossRef] (In the text)
- Clayton, D. D.
1968, Principles of Stellar Evolution and Nucleosynthesis (New
York: MacGraw-Hill)
(In the text)
-
Domínguez, I., Höflich, P., & Straniero, O. 2001,
ApJ, 557, 279 [NASA ADS] [CrossRef] (In the text)
- Durisen, R. H.
1975, ApJ, 199, 179 [NASA ADS] [CrossRef] (In the text)
- Durisen, R. H.
1977, ApJ, 213, 145 [NASA ADS] [CrossRef] (In the text)
- Durisen, R. H.,
& Imamura, J. N. 1981, ApJ, 243, 612 [NASA ADS] [CrossRef] (In the text)
- Endal, A. S., &
Sofia, S. 1976, ApJ, 210, 184 [NASA ADS] [CrossRef] (In the text)
- Fliegner, J.
1993, Diplomarbeit, University of Göttingen
(In the text)
- Friedman, J.
L., & Schutz, B. 1978, ApJ, 222, 281 [NASA ADS] [CrossRef] (In the text)
- Friend, D. S.,
& Abbott, D. C. 1986, ApJ, 311, 701 [NASA ADS] [CrossRef] (In the text)
- Fujimoto, M. Y.
1988, A&A, 198, 163 [NASA ADS] (In the text)
- Fujimoto, M.
Y., & Iben, I. 1997, in Advances in Stellar Evolution
(Cambridge University Press)
(In the text)
- Fujimoto, M.
Y., & Sugimoto, D. 1979, PASJ, 31, 1 [NASA ADS] (In the text)
- Greiner, J. 2000,
New Astron., 5, 137 [NASA ADS] (In the text)
- Hachisu, I. 1986,
ApJS, 62, 461 [NASA ADS] [CrossRef] (In the text)
- Hachisu, I.,
& Kato, M. 2001, ApJ, 558, 323 [NASA ADS] [CrossRef] (In the text)
- Hachisu, I.,
Kato, M., & Nomoto, K. 1996, ApJ, 470, L97 [NASA ADS] [CrossRef] (In the text)
- Hachisu, I.,
Kato, M., & Nomoto, K. 1999, ApJ, 522, 487 [NASA ADS] [CrossRef] (In the text)
- Hamuy, M.,
Phillips, M. M., & Suntzeff, N. B., et al. 1996, ApJ, 519,
314 [NASA ADS] (In the text)
- Heber, U.,
Napiwotzki, R., & Reid, I. N. 1997, A&A, 323, 819 [NASA ADS] (In the text)
- Heger, A., &
Langer, N. 2000, ApJ, 544, 1016 [NASA ADS] [CrossRef] (In the text)
- Heger, A., Langer,
N., & Woosley, S. E. 2000, ApJ, 528, 368 [NASA ADS] [CrossRef] (In the text)
- Heger, A., Woosley,
S., Langer, N., & Spruit, H. C. 2003, in Stellar Rotation, ed.
A. Maeder, & P. Eenens (San Francisco: ASP), Proc. IAU-Symp.,
215, in press
(In the text)
-
Hillebrandt, W., & Niemeyer, J. C. 2000, ARA&A, 38,
191 [NASA ADS] (In the text)
- Höflich,
P., Khokhlov, A., Wheeler, J. C., et al. 1996, ApJ, 472, 81 [NASA ADS] [CrossRef] (In the text)
- Höflich,
P., Nomoto, K., Umeda, H., & Wheeler, J. C. 2000, ApJ, 528,
590 [NASA ADS] [CrossRef] (In the text)
- Howell, D. A.,
Höflich, P., Wang, L., & Wheeler, J. C. 2001, ApJ, 556,
302 [NASA ADS] [CrossRef] (In the text)
- Hujeirat, A.
1995, A&A, 295, 268 [NASA ADS]
- Iben, I. Jr., &
Renzini, A. 1983, ARA&A, 27, 271 [NASA ADS] (In the text)
- Iben, I. Jr., &
Tutukov, A. V. 1991, ApJ, 370, 615 [NASA ADS] [CrossRef] (In the text)
- Iben, I. Jr., &
Tutukov, A. V. 1994, ApJ, 431, 264 [NASA ADS] [CrossRef] (In the text)
- Iglesias, C.
A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] (In the text)
- Imamura, J. N.,
Toman, J., Durisen, R. H., Pickett, B., & Yang, S. 1995, ApJ,
444, 363 [NASA ADS] [CrossRef] (In the text)
- Kahabka, P.,
& van den Heuvel, E. P. J. 1997, ARA&A, 35, 69 [NASA ADS] (In the text)
- Karl, C. A.,
Napiwotzki, R., & Nelemans, G., et al. 2003, A&A, 410,
663 [EDP Sciences] [NASA ADS] (In the text)
- Kasen, D., Nugent,
P., & Wang, L., et al. 2003, ApJ, 593, 788 [NASA ADS] [CrossRef] (In the text)
- Kato, M., &
Hachisu, I. 1999, ApJ, 513, L41 [NASA ADS] [CrossRef] (In the text)
- Kawaler, S. D.
2003, in Stellar Rotation, ed. A. Maeder, & P. Eenens, Proc.
IAU Symp., 215
(In the text)
- Kippenhahn,
R., & Möllenhoff, C. 1974, Ap&SS, 31, 117 [NASA ADS] (In the text)
- Kippenhahn,
R., & Thomas, H.-C. 1970, in Stellar Rotation, ed. A. Slettebak
(Dortrecht: Reidel), IAU Coll., 4
(In the text)
- Kippenhahn,
R., & Thomas, H.-C. 1978, A&A, 63, 265 [NASA ADS] (In the text)
- Koester, D.,
Dreizler, S., Weidemann, V., & Allard, N. F. 1998, A&A,
338, 617 [NASA ADS] (In the text)
- Koester, D.,
Napiwotzki, R., & Christlieb, N., et al. 2001, A&A, 378,
556 [EDP Sciences] [NASA ADS] (In the text)
- Langer, N. 1997, in
Luminous Blue Variables: Massive Stars in Transition, ed. A. Nota,
& H. J. G. L. M. Lamers, ASP Conf. Ser., 120, 83
(In the text)
- Langer, N. 1998,
A&A, 329, 551 [NASA ADS] (In the text)
- Langer, N., Heger
A., Wellstein, S., & Herwig, F. 1999, A&A, 346, L37 [NASA ADS] (In the text)
- Langer, N.,
Deutschmann, A., Wellstein, S., & Höflich, P. 2000,
A&A, 362, 1046 [NASA ADS] (In the text)
- Langer, N., Yoon,
S.-C., Wellstein, S., & Scheithauer, S. 2002, in The Physics of
Cataclysmic Variables and Related Objets, ASP Conf. Proc., 261
(In the text)
- Leibundgut,
B. 2001, ARA&A, 39, 67 [NASA ADS] (In the text)
- Li, X.-D., & van den
Heuvel, E. P. J. 1997, A&A, 322, L9 [NASA ADS] (In the text)
- Limongi, M.,
& Tornambé, A. 1991, ApJ, 371, 317 [NASA ADS] [CrossRef] (In the text)
- Lindblom, L.
1999, Phys. Rev. D, 60, 4007 [NASA ADS] (In the text)
- Livio, M. 2001, in
Cosmic evolution, ed. E. Vangioni, R. Ferlet, & M. Lemoine (New
Jersey: World Scientific)
(In the text)
- Livio, M., &
Pringle, J. E. 1998, ApJ, 505, 339 [NASA ADS] [CrossRef] (In the text)
- Livio, M., &
Truran, J. 1987, ApJ, 318, 316 [NASA ADS] [CrossRef] (In the text)
- Livne, E., &
Arnett, D. 1995, ApJ, 452, 62 [NASA ADS] [CrossRef] (In the text)
- MacDonald, J.
1983, ApJ, 273, 289 [NASA ADS] [CrossRef] (In the text)
- Maeder, A. 1999,
A&A, 347, 185 [NASA ADS] (In the text)
- Maeder, A. 2003,
A&A, 399, 263 [EDP Sciences] [NASA ADS] (In the text)
- Maeder, A, &
Meynet, G. 2003, A&A, 411, 543 [EDP Sciences] [NASA ADS] (In the text)
- Maxted, P. F. L.,
March, T. R., & North, R. C. 2000, MNRAS, 317, L41 [NASA ADS] [CrossRef] (In the text)
- Meynet, G., &
Maeder, A. 1997, A&A, 321, 465 [NASA ADS] (In the text)
- Nomoto, K. 1982a,
ApJ, 253, 798 [NASA ADS] [CrossRef] (In the text)
- Nomoto, K. 1982b,
ApJ, 257, 780 [NASA ADS] [CrossRef] (In the text)
- Nomoto, K.,
Iwamoto, K., & Kishimoto, N. 1997, Science, 276, 1378 [NASA ADS] [CrossRef] (In the text)
- Nomoto, K., &
Kondo, Y. 1991, ApJ, 367, L19 [NASA ADS] [CrossRef] (In the text)
- Nugent, P., Baron,
E., Branch, D., Fisher, A., & Hauschildt, P. H. 1997, ApJ, 485,
812 [NASA ADS] [CrossRef] (In the text)
- Ostriker, J.
P., & Bodenheimer, P. 1968, ApJ, 151, 1089 [NASA ADS] [CrossRef] (In the text)
- Ostriker, J.
P., & Mark, J. W.-K. 1968, ApJ, 151, 1075 [NASA ADS] [CrossRef] (In the text)
- Owocki, S. P.,
& Gayley, K. G. 1997, in Luminous Blue Variables: Massive stars
in Transition, ed. A. Nota, & H. J. G. L. M. Lamers, ASP Conf.
Ser., 120
(In the text)
- Paczynski, B.
1991, ApJ, 370, 597 [NASA ADS] [CrossRef] (In the text)
-
Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517,
565 [NASA ADS] [CrossRef] (In the text)
-
Pinsonneault, M. H., Kawaler, S. D., Sofia, S., & Demarque, P.
1989, ApJ, 338, 424 [NASA ADS] [CrossRef] (In the text)
- Pinto, P. A.,
Eastman, R. G., & Rogers, T. 2001, ApJ, 551, 231 [NASA ADS] (In the text)
- Popham, R., &
Narayan, R. 1991, ApJ, 370, 604 [NASA ADS] [CrossRef] (In the text)
- Riess, A. G.,
Filippenko, A. V., Liu, M. C., et al. 2000, ApJ, 536, 62 [NASA ADS] [CrossRef] (In the text)
- Ritter, H. 1985,
A&A, 148, 207 [NASA ADS] (In the text)
- Saio, H., & Nomoto,
K. 1985, A&A, 150, L21 [NASA ADS] (In the text)
- Saio, H., & Nomoto,
K. 1998, ApJ, 500, 388 [NASA ADS] [CrossRef] (In the text)
- Sion, E. M. 1999, PASP,
111, 532 [NASA ADS] [CrossRef] (In the text)
- Sparks, W. M.,
& Kutter, G. S. 1987, ApJ, 321, 394 [NASA ADS] [CrossRef] (In the text)
-
Schwarzshild, M., & Härm, R. 1965, ApJ, 142, 855 [NASA ADS] [CrossRef] (In the text)
- Starrfield,
2003, in Stellar Rotation, ed. A. Maeder, & P. Eenens, Proc.
IAU Symp., 215
(In the text)
- Spruit, H. C. 2002,
A&A, 381, 923 [EDP Sciences] [NASA ADS] (In the text)
-
Thoroughgood, T. D., Dhillon, V. S., Littlefair, S. P., Marsh, T.
R., & Smith, D. A. 2001, MNRAS, 327, 1323 [NASA ADS] [CrossRef] (In the text)
- Tout, C. A.,
Regös, E., Wickramasinghe, D., Hurley, J., & Pols, O. R.
2001, in Evolution of Binary and Multiple Star Systems, ed. Ph.
Podsialdlowski et al., ASP Conf. Ser., 229
(In the text)
- Umeda, H., Nomoto,
K., Kobayashi, C., Hachisu, I., & Kato, M. 1999, ApJ, 522,
L43 [NASA ADS] [CrossRef] [MathSciNet] (In the text)
- Wang, L., Baade, D.,
Höflich, P., et al. 2003, ApJ, 591, 1110 [NASA ADS] [CrossRef] (In the text)
- Weaver, T. A.,
& Woosley, S. E. 1993, Phys. Rep., 227, 65 [NASA ADS] (In the text)
- Weigert, A. 1966,
Z. Astrophys., 64, 395 [NASA ADS] (In the text)
- Wheeler, C. J.
1996, in Evolutionary Processes in Binary Stars (Dordrecht:
Kluwer)
(In the text)
- Woosley, S. E.,
& Weaver, T. A. 1986, ARA&A, 24, 205 [NASA ADS] (In the text)
- Woosley, S. E.,
& Weaver, T. A. 1994, ApJ, 423, 371 [NASA ADS] [CrossRef] (In the text)
- Yoon, S.-C., &
Langer, N. 2002, in The Physics of Cataclysmic Variables and
Related Objets, ed. B. T. Gaensicke et al., ASP Conf. Proc.,
261
(In the text)
- Yoon, S.-C., &
Langer, N. 2003, A&A, 412, L53 [EDP Sciences] [NASA ADS] (In the text)
- Yoon, S.-C., &
Langer, N. 2004a, A&A, 419, 623 [EDP Sciences] [NASA ADS] (In the text)
- Yoon, S.-C., &
Langer, N. 2004b, A&A, 419, 645 [EDP Sciences] [NASA ADS] (In the text)
- Yoon, S.-C., Langer,
N., & van der Sluys, M. 2004, A&A, 425, 207 [EDP Sciences] [NASA ADS] (In the text)
- Zahn, J.-P. 1975, Mem.
Soc. Roy. Liège, 8, 31 [NASA ADS] (In the text)
- Zahn, J.-P. 1992,
A&A, 265, 115 [NASA ADS] (In the text)
Copyright ESO 2004
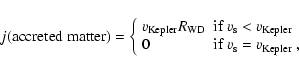
![\begin{figure}
\par\resizebox{7.8cm}{!}{\includegraphics[clip]{0327fg1a.ps}}\par...
...pace*{-2mm}\resizebox{7.5cm}{!}{\includegraphics[clip]{0327fg1c.ps}}\end{figure}](/articles/aa/full/2004/37/aa0327-04/Timg49.gif)
![\begin{figure}
\par\resizebox{7.8cm}{!}{\includegraphics[clip]{0327fg2a.ps}}\par\vspace*{3mm}
\resizebox{7.8cm}{!}{\includegraphics[clip]{0327fg2b.ps}}\end{figure}](/articles/aa/full/2004/37/aa0327-04/Timg50.gif)
![\begin{figure}
\par\resizebox{7.6cm}{!}{\includegraphics[clip]{0327fg3a.ps}}\par...
...pace*{3mm}
\resizebox{7.6cm}{!}{\includegraphics[clip]{0327fg3c.ps}}\end{figure}](/articles/aa/full/2004/37/aa0327-04/Timg51.gif)
![\begin{figure}
\par\resizebox{7.8cm}{!}{\includegraphics[clip]{0327fg4a.ps}}\hsp...
...pace*{7mm}
\resizebox{7.9cm}{!}{\includegraphics[clip]{0327fg4d.ps}}\end{figure}](/articles/aa/full/2004/37/aa0327-04/Timg62.gif)
![\begin{figure}
\par\resizebox{7.8cm}{!}{\includegraphics[clip]{0327fg5.ps}}\end{figure}](/articles/aa/full/2004/37/aa0327-04/Timg69.gif)
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[clip]{0327fg6a.ps}}\par\v...
...vspace*{2mm}
\resizebox{8cm}{!}{\includegraphics[clip]{0327fg6c.ps}}\end{figure}](/articles/aa/full/2004/37/aa0327-04/Timg74.gif)
![\begin{figure}
\par\resizebox{7.8cm}{!}{\includegraphics[clip]{0327fg7a.ps}}\par\vspace*{2mm}
\resizebox{7.8cm}{!}{\includegraphics[clip]{0327fg7b.ps}}\end{figure}](/articles/aa/full/2004/37/aa0327-04/Timg75.gif)
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[clip]{0327fg8.ps}}\end{figure}](/articles/aa/full/2004/37/aa0327-04/Timg76.gif)
![\begin{figure}
\par\resizebox{11.8cm}{!}{\includegraphics[clip]{0327fg9.ps}}\end{figure}](/articles/aa/full/2004/37/aa0327-04/Timg94.gif)