A&A 425, 353-360 (2004)
DOI: 10.1051/0004-6361:20040298
S. Ivarsson 1 - G. M. Wahlgren1 - Z. Dai2 - H. Lundberg2 - D. S. Leckrone3
1 - Lund Observatory, Lund University, PO Box 43,
22100 Lund, Sweden
2 - Department of Physics, Lund Institute of Technology, PO Box 118, 22100 Lund, Sweden
3 - Laboratory for Astronomy and Solar Physics, Code 681, NASA
Goddard Space Flight Center, Greenbelt, MD, USA, 20771
Received 18 February 2004 / Accepted 11 April 2004
Abstract
The determination of elemental abundances plays an important role
in understanding the atmospheric processes that lead to
anomalies in spectra of chemically peculiar stars. Ongoing
study of the HgMn star ![]() Lupi has defined
much of the elemental abundance distribution but progress
is dependent upon the availability and accuracy of the atomic data.
Here we present experimentally determined wavelengths and oscillator
strengths for 27 Os II and 23 Ir II transitions. The oscillator
strengths have been determined by combining radiative lifetimes
measured using the laser-induced fluorescence technique with branching
fractions determined from Fourier transform spectrometer emission
line intensities. The new data were used in a synthetic spectrum analysis
of high-resolution ultraviolet spectra of
Lupi has defined
much of the elemental abundance distribution but progress
is dependent upon the availability and accuracy of the atomic data.
Here we present experimentally determined wavelengths and oscillator
strengths for 27 Os II and 23 Ir II transitions. The oscillator
strengths have been determined by combining radiative lifetimes
measured using the laser-induced fluorescence technique with branching
fractions determined from Fourier transform spectrometer emission
line intensities. The new data were used in a synthetic spectrum analysis
of high-resolution ultraviolet spectra of ![]() Lupi obtained
with the Hubble Space Telescope. Weak abundance enhancements were
determined for both elements, [Os/H] = +1.3 dex and [Ir/H] = +0.7 dex,
which now clearly defines the heavy element abundance peak in this star
to be comprised of only the four elements Pt, Au, Hg, and Tl. This
result offers a new constraint on theoretical efforts to explain
the observed spectrum anomalies.
Lupi obtained
with the Hubble Space Telescope. Weak abundance enhancements were
determined for both elements, [Os/H] = +1.3 dex and [Ir/H] = +0.7 dex,
which now clearly defines the heavy element abundance peak in this star
to be comprised of only the four elements Pt, Au, Hg, and Tl. This
result offers a new constraint on theoretical efforts to explain
the observed spectrum anomalies.
Key words: atomic data - stars: abundances - stars: chemically peculiar - stars: individual: ![]() Lupi
Lupi
The chemically peculiar (CP) stars of the upper main sequence are renowned for peculiarities in their spectral lines. Among the HgMn class of CP stars these peculiarities reveal themselves in the observed line strengths and profiles. Line depths are generally interpreted in terms of elemental abundances in the region of line formation with both deficiencies and enhancements being inferred. Examples of abundance deficiencies are provided by the elements boron (Leckrone et al. 1999 and references therein) and zinc (Smith 1994) while enhancements are typical of all elements heavier than the iron group for which lines can be studied. For the sharpest-lined stars, the line profiles of certain heavy elements show the influence of peculiar isotopic compositions. Of particular note in this regard are the spectral lines from the elements platinum, mercury and thallium. The explanation put forward for these spectral peculiarities is currently described in terms of diffusion processes in stellar atmospheres (Michaud et al. 1976; Richer et al. 1998).
Table 1: Experimental radiative lifetimes in Os II.
One particular HgMn star, the binary system ![]() Lupi (B9.5Vp HgMn + A2Vm), has been the subject of intensive study at both optical and ultraviolet wavelengths to identify its spectral features and define its elemental abundance distribution. This star would therefore serve as a standard among HgMn stars and provide observational constraints for testing theoretical paradigms aimed at explaining the observed spectral peculiarities. The tenets of this study have been outlined in what has been termed the
Lupi (B9.5Vp HgMn + A2Vm), has been the subject of intensive study at both optical and ultraviolet wavelengths to identify its spectral features and define its elemental abundance distribution. This star would therefore serve as a standard among HgMn stars and provide observational constraints for testing theoretical paradigms aimed at explaining the observed spectral peculiarities. The tenets of this study have been outlined in what has been termed the ![]() Lupi Pathfinder Project (Leckrone et al. 1999). This project has been successful in determining abundances for more than 50 elements. An understated goal of this project has been to inspire the collection of accurate atomic data for the interpretation of spectral lines, and has resulted in the collection of wavelength and oscillator strength data for many heavy elements. These efforts have included not only those elements for which strong spectral lines are observed, but also those cloaked within spectral blends at ultraviolet wavelengths. As these data have been collected, and continue to be collected, the abundance distribution of heavy elements has been defined with increasing clarity.
Lupi Pathfinder Project (Leckrone et al. 1999). This project has been successful in determining abundances for more than 50 elements. An understated goal of this project has been to inspire the collection of accurate atomic data for the interpretation of spectral lines, and has resulted in the collection of wavelength and oscillator strength data for many heavy elements. These efforts have included not only those elements for which strong spectral lines are observed, but also those cloaked within spectral blends at ultraviolet wavelengths. As these data have been collected, and continue to be collected, the abundance distribution of heavy elements has been defined with increasing clarity.
In the realm of the heaviest stable elements the derived abundance pattern for ![]() Lupi is highlighted by line (abundance) enhancements for the elements platinum, gold, mercury, and thallium. These elements appear to define a peak in the elemental abundance distribution. However, the uncertainties in atomic data for lines of Os II and Ir II were sufficiently large that it could not be certain that large abundance enhancements did not start with these elements. A small abundance enhancement for osmium had been determined from lesser quality atomic data (Leckrone et al. 1999) and the abundance of iridium had remained undetermined. Whether the abundances of osmium and iridium reflected a gradual,
continuous rise between the lighter 5d elements and those of the peak
or a more precipitous rise between iridium and platinum was a question
that could be resolved by the acquisition of better quality atomic data.
Lupi is highlighted by line (abundance) enhancements for the elements platinum, gold, mercury, and thallium. These elements appear to define a peak in the elemental abundance distribution. However, the uncertainties in atomic data for lines of Os II and Ir II were sufficiently large that it could not be certain that large abundance enhancements did not start with these elements. A small abundance enhancement for osmium had been determined from lesser quality atomic data (Leckrone et al. 1999) and the abundance of iridium had remained undetermined. Whether the abundances of osmium and iridium reflected a gradual,
continuous rise between the lighter 5d elements and those of the peak
or a more precipitous rise between iridium and platinum was a question
that could be resolved by the acquisition of better quality atomic data.
In this contribution to the study of ![]() Lupi we have undertaken acquisition of accurate wavelengths and oscillator strengths from laboratory experiments for select lines of Os II and Ir II. We then determined the abundance of osmium and iridium from the comparison of high spectral resolution data obtained at ultraviolet wavelengths with the Hubble Space Telescope (HST) using synthetic spectra generated with the new atomic data. The abundance distribution for heavy elements (73
Lupi we have undertaken acquisition of accurate wavelengths and oscillator strengths from laboratory experiments for select lines of Os II and Ir II. We then determined the abundance of osmium and iridium from the comparison of high spectral resolution data obtained at ultraviolet wavelengths with the Hubble Space Telescope (HST) using synthetic spectra generated with the new atomic data. The abundance distribution for heavy elements (73 ![]() Z
Z ![]() 83) in
83) in ![]() Lupi has now been fully defined.
Lupi has now been fully defined.
In this paper we present oscillator strengths for 27 Os II and 23 Ir II transitions from recordings in the region 1900-3800 Å. These were derived using emission line intensities recorded with the Lund UV Fourier Transform Spectrometer (FTS) capable of a spectral range of roughly 1900-6500 Å. The radiative lifetimes were measured at the Lund Laser Centre (LLC). For all of the transitions measured we also present centre-of-gravity wavelengths.
Second spectrum osmium lines observed with the FTS show the effects of unresolved isotopic shifts and in some cases weak hyperfine components from the most abundant odd isotope. The main observed feature consists of the two most abundant isotopes A= 192 (41.0%) and 190 (26.4%). The remaining isotopes are distributed according to the normal terrestrial abundance used in our light source, A= 184 (0.02%), 186 (1.6%), 187 (1.6%), 188 (13.3%), 189 (16.1%). More general information about the atomic structure of singly-ionized osmium can be found in Van Kleef & Klinkenberg (1961).
Iridium has two stable isotopes, A=191 and 193, with relative terrestrial abundances of 37.3% and 62.7%, respectively. The spectral lines of Ir II have a slightly asymmetric appearance in the FTS spectrum as a result of unresolved blends of hyperfine structure and/or isotope shift components. The term structure of singly-ionized iridium had been studied by Van Kleef & Metsch (1978) using both experimental data and theoretical atomic structure calculations.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{0298fig1.eps}
\end{figure}](/articles/aa/full/2004/37/aa0298-04/Timg8.gif) |
Figure 1:
FTS recording of the a6D7/2-z6F9/2 Os II |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{0298fig2.eps}
\end{figure}](/articles/aa/full/2004/37/aa0298-04/Timg9.gif) |
Figure 2:
FTS recording of the a5F4-z5D3 Ir II |
| Open with DEXTER | |
Table 2: Experimental radiative lifetimes in Ir II.
Using the laser-induced fluorescence (LIF) technique, we have measured the radiative lifetime for eight levels in Os II and nine levels of Ir II, as reported in Tables 1 and 2, respectively. A rotating pellet of the target element was ablated by a high-power laser to produce a plasma cone of atoms and ions. Ions in the cone were selectively photo-excited and probed by light from a pulsed tuneable dye laser, working on a red dye and pumped by a Nd:YAG laser. The dye laser light was shifted to the desired wavelengths in the near UV and using frequency-doubling and mixing crystals and Raman shifting in a hydrogen cell. A fast detection system measured the fluorescence due to the decay of the excited levels. The experimental set-up is described in detail by Li et al. (2000).
Measurement uncertainties are based upon random scatter between different recordings and possible systematic effects. The photon shot noise in the individual recordings may be reduced by increasing the power of the ablation laser pulse or reducing the delay between the ablation and exciting laser pulses. These methods result in a denser plasma and higher light intensity at the moment of excitation, hence in an increased photon flux. The penalty for this gain is an increased component of collisional de-excitation, immediately visible as a systematic reduction of the measured lifetime.
Before determining branching fractions (BF) for one line divided by the sum of all lines from the same upper level, the measured intensity of the lines must be corrected for the wavelength-dependent instrumental response. For both Os II and Ir II spectra we used Ar II lines with well-known branching ratios (BR) (Whaling et al. 1993) to define the instrumental response function. The uncertainty in the intensity calibration derived from known Ar II branching ratios is estimated to be 10%.
Intensities for strong transitions involving low-lying states, especially the ground state, can be affected by self absorption in the hollow cathode light source. To check for any systematic errors from this effect, we investigated the intensity ratio of line pairs of different strength from the same upper level as a function of the discharge current through the lamp. This method is discussed in more detail by Sikström et al. (2002). Several intensities of transitions involving low-lying states were corrected for self absorption, noted by SA in Tables 3 and 4.
One disadvantage of the limited wavelength coverage is that not all transitions from a given upper level may be recorded, as a result of spectral lines falling outside the recorded wavelength interval. In this work we estimate this missing intensity, or Residual, by means of theoretical atomic structure calculations using the COWAN code (Cowan 1981). The uncertainty of the intensity determination for a line with SNR < 5 becomes as large as the total residual and in this work these transitions are instead represented by their calculated counterpart. Calculated residuals are added to the sum of the measured BRs to form the BF. The final BFs and the calculated residual for all measured lines are given in Table 3 for Os II and Table 4 for Ir II. The configurations included in the calculation for Os II were the 5d7, 5d66s, 5d56s2, 5d67s, 5d66d, 5d66p and 5d56s6p. For Ir II the configurations were 5d8, 5d76s, 5d66s2, 5d76p, 5d66s6p, 5d6s26p, 5d77s and 5d76d.
Table 3: Improved wavelengths, branching fractions and transition probabilities for Os II.
Table 4: Improved wavelengths, branching fractions and transition propabilities for Ir II.
Using the radiative lifetime, ![]() ,
and the derived BF one can obtain the transition probability, Aik, for lines belonging to an upper level i and lower level k, through the relation:
,
and the derived BF one can obtain the transition probability, Aik, for lines belonging to an upper level i and lower level k, through the relation:
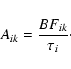 |
(1) |
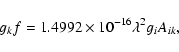 |
(2) |
Table 5: Finding list.
The last column of Tables 3 and 4 presents uncertainties in the A-values. These uncertainties were determined using a method described in detail by Sikström et al. (2002). In principal the method combines the individual errors of the measured quantities according to the law of propagating errors.
When comparing the derived gf-values for the singly-ionized species of both osmium and iridium to values available in atomic spectra databases we discovered a large discrepancy (see Fig. 3). The values in the databases KURUCZ (Kurucz & Bell 1995) and VALD (Kupka et al. 1999) differ by up to three orders of magnitude from our experimental values and are not consistent with any values expected from recorded spectra with intensity calibrated instruments or values derived from the atomic structure calculations. (For Os II and Ir II the entries in the VALD database are taken from Kurucz & Bell 1995). The source of the systematic discrepancy is likely to be related to the measurement and treatment of experimental line intensities and their conversion to gf values. The gf values for Os II lines were presented by Corliss & Bozman (1962) along with a general discussion about their technique. For the Ir II lines the intensities presented by Meggers et al. (1975) were transformed into gf values by R. Kurucz. Figure 3 shows that there is a clear trend where the discrepancy becomes enhanced for weaker lines. The general behaviour of this trend appears to be similar for both ions.
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{0298fig3.eps}
\end{figure}](/articles/aa/full/2004/37/aa0298-04/Timg17.gif) |
Figure 3: Comparison of log(gf) values from this work and data from Kurucz & Bell (1995). |
| Open with DEXTER | |
The determination of abundance for osmium and iridium has followed the techniques used in previous analyses for this star (Wahlgren et al. 1995). Since the observed spectrum is a combination of spectra from both stars of the binary system, a synthetic spectrum was generated for each star for short wavelength intervals that included each of the spectral lines studied. However, it is only for the primary star, ![]() Lup A, that we have identified spectral lines of Os II and Ir II. The lower flux level of the secondary star, as evidenced by the light ratio at ultraviolet wavelengths, combined with the cooler nature of the secondary effective temperature and the less dramatic nature of the peculiarities conspired to prevent detection of lines from the Os II and Ir II spectra for the secondary.
Lup A, that we have identified spectral lines of Os II and Ir II. The lower flux level of the secondary star, as evidenced by the light ratio at ultraviolet wavelengths, combined with the cooler nature of the secondary effective temperature and the less dramatic nature of the peculiarities conspired to prevent detection of lines from the Os II and Ir II spectra for the secondary.
For each star we use a model atmosphere that has been generated by the ATLAS9 code (Kurucz 1993) for the assumptions of a LTE plane-parallel atmosphere. The model parameters (Wahlgren et al. 1994) for the primary and secondary stars, respectively, are: effective temperature 10 650, 9200 K; log gravity = 3.8, 4.2; and micro turbulent velocity 0.0, 2.0 km s-1. The elemental abundances are solar for the model atmosphere opacity distribution. Synthetic spectra for each star were computed using the SYNTHE code (Kurucz 1993), the general line list data of Kurucz & Bell (1995) with the exception of data presented in this study for Os II and Ir II, elemental abundances as presented by Leckrone et al. (1999), and projected equatorial rotational velocity, vsin i of 1.0 and 2.0 km s-1 for the primary and the secondary, respectively. The synthetic spectra for the two stellar components were co-added after 1) shifting the secondary star spectrum by an amount appropriate for the orbital radial velocity of the system, as presented by Dworetsky (1972), at the phase of the observation; and 2) weighting of the spectra by the wavelength dependent luminosity ratio (
![]() /
/
![]() ). The observations were then shifted in wavelength in order that the rest wavelength scale coincides with the primary star. After co-addition the resultant synthetic spectrum was convolved with the instrumental profile, defined as a Gaussian function appropriate for the spectral resolution.
). The observations were then shifted in wavelength in order that the rest wavelength scale coincides with the primary star. After co-addition the resultant synthetic spectrum was convolved with the instrumental profile, defined as a Gaussian function appropriate for the spectral resolution.
The observations were obtained with the Goddard High Resolution Spectrograph (GHRS) onboard the HST. The data are described and presented in atlas format by Brandt et al. (1999). The spectral data from the atlas are comprised of small wavelength segments, typically 10 Å and totaling nearly 300 Å, located at wavelengths that were chosen for the study of particular spectral lines. Complete coverage of the ultraviolet spectrum at high resolving power (R = 90 000) does not exist for this star. As this pertains to the study of Os II and Ir II lines, very few strong (detectable) lines were identified in the available data. Other, presumably detectable lines, exist at wavelengths for which no HST data exists for this star or any other HgMn star. The more extensive wavelength coverage afforded by the IUE satellite is of an insufficient resolution and signal-to-noise for the study of Os II and Ir II in ![]() Lupi.
Lupi.
The osmium abundance was determined from fitting three lines of Os II (
![]() 2067.229, 2070.693, 2282.279 Å) with synthetic spectra that utilized the gf values presented in Table 5. The isotopic shifts for the three lines are quite small, and are undetectable as resolved components at the resolution of the GHRS spectra. Tests of any influence upon the observed line profiles arising from non-symmetric line profiles or shifts due to hyperfine structure and isotopic shifts were performed; however, no such information could be extracted from the observations. Suggestions made earlier that an isotope anomaly exists for osmium in
2067.229, 2070.693, 2282.279 Å) with synthetic spectra that utilized the gf values presented in Table 5. The isotopic shifts for the three lines are quite small, and are undetectable as resolved components at the resolution of the GHRS spectra. Tests of any influence upon the observed line profiles arising from non-symmetric line profiles or shifts due to hyperfine structure and isotopic shifts were performed; however, no such information could be extracted from the observations. Suggestions made earlier that an isotope anomaly exists for osmium in ![]() Lupi (Wahlgren et al. 1998) have not been verified in this study. The earlier and current studies both employ the same GHRS data and analysis techniques but differ in the laboratory FTS data used for the Os II wavelengths. The new laboratory spectrum was obtained at a slightly higher spectral resolution, which results in a center-of-gravity wavelength displacement that is similar to the isotopic shift of the two most prominent isotopes, relative to the spectrum of slightly lower resolution. While the new data does not verify a wavelength shift resulting from an isotopic anomaly it also cannot disprove its existence because of the line blending in the stellar spectrum. For now, though, we do not advocate the existence of an isotope anomaly for osmium. Based upon the fitting of the three Os II lines (see Figs. 4-6), an abundance of (Os/H) = log(
Lupi (Wahlgren et al. 1998) have not been verified in this study. The earlier and current studies both employ the same GHRS data and analysis techniques but differ in the laboratory FTS data used for the Os II wavelengths. The new laboratory spectrum was obtained at a slightly higher spectral resolution, which results in a center-of-gravity wavelength displacement that is similar to the isotopic shift of the two most prominent isotopes, relative to the spectrum of slightly lower resolution. While the new data does not verify a wavelength shift resulting from an isotopic anomaly it also cannot disprove its existence because of the line blending in the stellar spectrum. For now, though, we do not advocate the existence of an isotope anomaly for osmium. Based upon the fitting of the three Os II lines (see Figs. 4-6), an abundance of (Os/H) = log(
![]() ) - log(
) - log(
![]() ) = 2.67
) = 2.67 ![]() 0.1 dex, on a scale where log
0.1 dex, on a scale where log
![]() = 12.00. This abundance represents an enhancement over the solar system value (Lodders 2003) of +1.3 dex. It produces good fits to the lines at 2067 and 2282 Å and is supported by the 2070 Å line fit.
= 12.00. This abundance represents an enhancement over the solar system value (Lodders 2003) of +1.3 dex. It produces good fits to the lines at 2067 and 2282 Å and is supported by the 2070 Å line fit.
In the case of iridium only one reasonably unblended line of Ir II was identified in our stellar spectra. Its analysis followed a similar method as for the lines of Os II. The fit to the line Ir II ![]() 2152.706 is presented in Fig. 7, with the best fit abundance value of (Ir/H) = 2.05, representing an abundance enhancement of +0.7 dex with respect to the solar system. We consider the newly derived abundance to be an upper limit as a result of missing absorption in the synthetic spectrum.
2152.706 is presented in Fig. 7, with the best fit abundance value of (Ir/H) = 2.05, representing an abundance enhancement of +0.7 dex with respect to the solar system. We consider the newly derived abundance to be an upper limit as a result of missing absorption in the synthetic spectrum.
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{0298fig4.eps}
\end{figure}](/articles/aa/full/2004/37/aa0298-04/Timg23.gif) |
Figure 4:
Synthetic spectrum fitting of Os II |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{0298fig5.eps}
\end{figure}](/articles/aa/full/2004/37/aa0298-04/Timg24.gif) |
Figure 5:
Synthetic spectrum fitting of Os II |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{0298fig6.eps}
\end{figure}](/articles/aa/full/2004/37/aa0298-04/Timg25.gif) |
Figure 6:
Synthetic spectrum fitting of Os II |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{0298fig7.eps}
\end{figure}](/articles/aa/full/2004/37/aa0298-04/Timg26.gif) |
Figure 7:
Synthetic spectrum fitting of Ir II |
| Open with DEXTER | |
We present new wavelength and oscillator strength data from laboratory analyses for selected lines in spectra of Os II and Ir II. The spectral transitions studied occur for the most part at ultraviolet wavelengths with a few Os II lines located at short optical region wavelengths. The lines studied show no resolved structure at spectral resolutions typical of astronomical observations, and only a small amount of hyperfine structure. The newly derived oscillator strengths are markedly different from those found in data bases of spectral line data. For Os II lines there is a trend where the new gf values are reduced by between one and three orders of magnitude. For the Ir II lines the trend is similar but not as well defined due to fewer lines in the comparison. The impact of the new oscillator strengths on abundance determinations is therefore to roughly increase the abundances by these amounts.
We apply these new atomic data to the determination of the abundances
of osmium and iridium in the chemically peculiar star ![]() Lupi
and find small enhancements over the solar system values:
[Os/H] = +1.3 dex and [Ir/H] = +0.7 dex. The iridium abundance
determination is the first for this star. These enhancements remain
considerably lower than those comprising the peak (Pt, Au, Hg, Tl).
Figure 8 presents the abundance distribution for
Lupi
and find small enhancements over the solar system values:
[Os/H] = +1.3 dex and [Ir/H] = +0.7 dex. The iridium abundance
determination is the first for this star. These enhancements remain
considerably lower than those comprising the peak (Pt, Au, Hg, Tl).
Figure 8 presents the abundance distribution for ![]() Lup A for the
heaviest stable elements (Adelman et al. 2004, for Au; Eriksson et al. 2002, for Ta; Leckrone et al. 1999, for W, Re, Pt, Hg, Tl, Pb; Wahlgren et al. 2001, for Bi). All data points in the figure except for lead from the second spectrum, which is the prominent one for these
elements at the effective temperature of
Lup A for the
heaviest stable elements (Adelman et al. 2004, for Au; Eriksson et al. 2002, for Ta; Leckrone et al. 1999, for W, Re, Pt, Hg, Tl, Pb; Wahlgren et al. 2001, for Bi). All data points in the figure except for lead from the second spectrum, which is the prominent one for these
elements at the effective temperature of ![]() Lup A. The lead abundance
has been determined from a single line, Pb III
Lup A. The lead abundance
has been determined from a single line, Pb III ![]() 1553.0 (Leckrone et al. 1999).
(Lines of Pb II in the available ultraviolet data suffer
from line blending.) Similarly large abundance enhancements
have been determined from minority ionization states for platinum, gold
and mercury (see Leckrone et al. 1999, for discussion). Minority
ionization state (neutral and third spectrum) lines have not been
detected in this star for the other elements in this grouping.
1553.0 (Leckrone et al. 1999).
(Lines of Pb II in the available ultraviolet data suffer
from line blending.) Similarly large abundance enhancements
have been determined from minority ionization states for platinum, gold
and mercury (see Leckrone et al. 1999, for discussion). Minority
ionization state (neutral and third spectrum) lines have not been
detected in this star for the other elements in this grouping.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0298fig8.eps}
\end{figure}](/articles/aa/full/2004/37/aa0298-04/Timg27.gif) |
Figure 8:
The abundance pattern of |
| Open with DEXTER | |
Figure 8 represents a milestone in the study of ![]() Lupi, both
for the definition of the abundance peak and the acquisition of
atomic data for heavy elements, which are applicable to a variety
of studies. A tighter constraint is now placed upon theoretical
efforts to model the line enhancements in at least one HgMn star.
This surface constraint is only appropriate for the atmospheric
conditions of
Lupi, both
for the definition of the abundance peak and the acquisition of
atomic data for heavy elements, which are applicable to a variety
of studies. A tighter constraint is now placed upon theoretical
efforts to model the line enhancements in at least one HgMn star.
This surface constraint is only appropriate for the atmospheric
conditions of ![]() Lupi at its present stage of evolution.
Also, by itself, this snapshot in time may not be particularly
revealing as to the origins of line enhancements, which are
postulated to occur at deeper layers of the atmosphere where
the temperatures would mandate a higher ionization state. To fully
interpret Fig. 8 requires a large amount of atomic data for
the higher ion states of these elements for conducting diffusion
calculations. Further constraints can also be placed on the modeling
by continued efforts to fully define the elemental abundance
distribution in the photosphere in this star and similar study
of other CP stars will help determine how the spectral
peculiarities are related to stellar mass and atmospheric structure.
Lupi at its present stage of evolution.
Also, by itself, this snapshot in time may not be particularly
revealing as to the origins of line enhancements, which are
postulated to occur at deeper layers of the atmosphere where
the temperatures would mandate a higher ionization state. To fully
interpret Fig. 8 requires a large amount of atomic data for
the higher ion states of these elements for conducting diffusion
calculations. Further constraints can also be placed on the modeling
by continued efforts to fully define the elemental abundance
distribution in the photosphere in this star and similar study
of other CP stars will help determine how the spectral
peculiarities are related to stellar mass and atmospheric structure.
Acknowledgements
We gratefully acknowledge the excellent conditions at the Lund Laser Centre and the support by its Director, Prof. Sune Svanberg, for this research.