A&A 424, 919-925 (2004)
DOI: 10.1051/0004-6361:20040470
A. Claret
Instituto de Astrofísica de Andalucía, CSIC, Apartado 3004, 18080 Granada, Spain
Received 18 March 2004 / Accepted 11 May 2004
Abstract
We present new stellar models based on updated physics
(opacities, expanded nuclear network and mass loss rates). We compute
stellar models suitable for the mean solar
neighborhood, i.e. for Z=0.02 and X=0.70. The covered mass range is from 0.8 up to
125 ![]() and the models are followed until the exhaustion of
carbon in the core, for the more massive ones. In addition, the effective
temperatures of the more massive models are corrected for the effects of
stellar winds, while models with lower effective temperatures are computed using
a special treatment of the equation of state (CEFF). Convective core overshooting
is assumed to be moderate and is modelled with
and the models are followed until the exhaustion of
carbon in the core, for the more massive ones. In addition, the effective
temperatures of the more massive models are corrected for the effects of
stellar winds, while models with lower effective temperatures are computed using
a special treatment of the equation of state (CEFF). Convective core overshooting
is assumed to be moderate and is modelled with
![]() .
.
Besides the classical ingredients of stellar models, we also provide the
internal structure constants needed to investigate apsidal motion and tidal evolution
in close binaries. The latter constants are made public for the
first time. According to the current theories of tidal evolution, the time
scales for synchronization and circularization for cool stars depend - apart from
the mass, radius and effective temperature - on the depth of the convective
envelope
![]() and on the radius of gyration
and on the radius of gyration ![]() .
For stars with higher effective
temperatures, these dependencies are mainly incorporated in the tidal torque constant E2. All these parameters are steep functions of mass and time, and thus
require a special numerical treatment. The new mass loss formalism produces more mass
concentrated configurations than previously, especially for more massive and more
evolved stellar models. As the present grid is designed mainly for the study of
double-lined eclipsing binaries, the gravity-darkening exponents necessary to
calculate the surface brightness distribution in rotationally and/or tidally distorted
stars are computed following the method described recently by Claret (1998), and
made available for each point of every evolutionary track.
.
For stars with higher effective
temperatures, these dependencies are mainly incorporated in the tidal torque constant E2. All these parameters are steep functions of mass and time, and thus
require a special numerical treatment. The new mass loss formalism produces more mass
concentrated configurations than previously, especially for more massive and more
evolved stellar models. As the present grid is designed mainly for the study of
double-lined eclipsing binaries, the gravity-darkening exponents necessary to
calculate the surface brightness distribution in rotationally and/or tidally distorted
stars are computed following the method described recently by Claret (1998), and
made available for each point of every evolutionary track.
Key words: stars: binaries: close - stars: evolution - stars: interiors - stars: fundamental parameters - stars: abundances - stars: rotation
Since the first investigations on stellar structure one of the most exciting goals was to look into the interior of stars. Oscillating stars, in principle, offer such an opportunity, but generally do not yet have sufficiently accurate mass determinations. An accurate view inside the interior of a star is therefore not yet possible at this time. Double-lined eclipsing binaries (DLEB), on the other hand, have average errors in masses and radii of the order of 1%, which allow us to investigate stellar interiors using two different techniques: apsidal motion and tidal evolution.
Until very recently, systematic investigations of DLEB were restricted to the comparison between the observed radii, masses and effective temperatures with their theoretical counter-parts derived from evolutionary models. The only serious constraint was the coevity of the components. This situation has now changed drastically: in addition to these primary conditions, present-day studies are also oriented towards the properties of the stellar interior. The series of recent papers by Lacy, Torres and collaborators (Torres et al. 1999, 2000; Lacy et al. 2000, 2002, 2003) is a good example of the new systematics. On the other hand, extragalactic DLEB are now being investigated in different chemical environments such as the Magellanic Clouds or M 31 (for example, Fitzpatrick et al. 2003). Concerning direct investigations of the interior of extragalactic stars, North & Zahn (2003) performed an analysis of the critical fractional radius for the circularization of detached binaries in the SMC and LMC using data from OGLE and MACHO.
On the other hand, the study of rapidly rotating stars requires knowledge of how
the flux is distributed over the stellar surface. The brightness distribution depends
on the gravity-darkening exponent ![]() .
The first investigations are due to
von Zeipel (1924) who determined that, for stars with radiative envelopes, the flux is
directly proportional to the local gravity, i.e.
.
The first investigations are due to
von Zeipel (1924) who determined that, for stars with radiative envelopes, the flux is
directly proportional to the local gravity, i.e.
![]() ,
with
,
with
![]() .
Kippenhahn (1977) and Maeder (1999) later generalized the functional
relationship between the flux and the local gravity. More than 40 years after the
pioneering work by von Zeipel, Lucy (1967) investigated the case of stars with convective
external layers and found that
.
Kippenhahn (1977) and Maeder (1999) later generalized the functional
relationship between the flux and the local gravity. More than 40 years after the
pioneering work by von Zeipel, Lucy (1967) investigated the case of stars with convective
external layers and found that ![]() was, on average, of the order of 0.3. In 1998,
Claret made use of a new numerical method based on the triangle strategy of
Kippenhahn to derive
was, on average, of the order of 0.3. In 1998,
Claret made use of a new numerical method based on the triangle strategy of
Kippenhahn to derive ![]() as a function of mass, age, chemical composition, and effective
temperature. These calculations superseded the traditional values of 1 and 0.32 for radiative
and convective envelopes, and provided a smooth transition in
as a function of mass, age, chemical composition, and effective
temperature. These calculations superseded the traditional values of 1 and 0.32 for radiative
and convective envelopes, and provided a smooth transition in ![]() for the two mechanisms
of transport of energy. Claret (2000) later also extended the method to be applicable to brown
dwarfs. In the latter paper the effect of differential
rotation was also considered for more complicated systems, such as those presenting an accretion
disk. Since investigations of rapidly rotating stars acquire more and more importance,
gravity-darkening exponents are also presented for all models in this paper.
for the two mechanisms
of transport of energy. Claret (2000) later also extended the method to be applicable to brown
dwarfs. In the latter paper the effect of differential
rotation was also considered for more complicated systems, such as those presenting an accretion
disk. Since investigations of rapidly rotating stars acquire more and more importance,
gravity-darkening exponents are also presented for all models in this paper.
These new challenges support the necessity of ongoing updates of stellar evolution codes to provide new and more accurate theoretical material to be compared with observations. The main objective of the grid of stellar models presented in this paper is therefore to serve as a theoretical tool to explore the commented possibilities.
The four main differences between the present code and the 1995 version are: the opacities,
the nuclear network, the mass loss rates and the mass range for which the models are
computed. For radiative opacities we adopted the calculations by Iglesias & Rogers (1996)
completed with Alexander & Ferguson (1994) results for lower temperatures. This set of opacities
forced a revision in the calibration of the mixing-length parameter ![]() for the Sun.
For X = 0.684 and Y = 0.296, the new calibration yields
for the Sun.
For X = 0.684 and Y = 0.296, the new calibration yields
![]() .
Core overshooting is
considered through the parametrization
.
Core overshooting is
considered through the parametrization
![]() ,
where
,
where ![]() is the
pressure scale height and
is the
pressure scale height and
![]() is the overshooting parameter. For the latter, we adopt
the value 0.20 which seems to fit with acceptable accuracy the DLEB (Ribas 1999; Lastennet
& Valls-Gabaud 2002; Claret & Willems 2002). Other mixing processes are not considered, like
semiconvection or that due to rotation. In particular, semiconvection poses an interesting problem:
in an intermediate region above the convective core, the mean molecular weight decreases with
the distance and depending on the conditions, the zone should be mixed due to the differences between
the radiative and the adiabatic gradients. On the other hand, if this zone is mixed,
the chemical profile may change yielding a reverse situation. The equilibrium is achieved by means of
a slow mixing (semiconvection), which is really a diffusion process. Semiconvection is important
in massive stars but its effects are more notable in later evolutionary phases. We plan to implement
semiconvection to investigate the effects of partial mixing in the stellar internal structure, specially
the influence on the size of the convective core, as pointed out by Langer (1991).
is the overshooting parameter. For the latter, we adopt
the value 0.20 which seems to fit with acceptable accuracy the DLEB (Ribas 1999; Lastennet
& Valls-Gabaud 2002; Claret & Willems 2002). Other mixing processes are not considered, like
semiconvection or that due to rotation. In particular, semiconvection poses an interesting problem:
in an intermediate region above the convective core, the mean molecular weight decreases with
the distance and depending on the conditions, the zone should be mixed due to the differences between
the radiative and the adiabatic gradients. On the other hand, if this zone is mixed,
the chemical profile may change yielding a reverse situation. The equilibrium is achieved by means of
a slow mixing (semiconvection), which is really a diffusion process. Semiconvection is important
in massive stars but its effects are more notable in later evolutionary phases. We plan to implement
semiconvection to investigate the effects of partial mixing in the stellar internal structure, specially
the influence on the size of the convective core, as pointed out by Langer (1991).
In order to extend our investigation on stellar evolution of massive binary stars, we have implemented a more extensive nuclear network than before. We follow the evolution of 13 isotopes: 1H, 4He, 12C, 13C, 14N, 16O, 17O, 18O, 20Ne, 22Ne, 24Mg, 25Mg, and 26Mg. A more elaborate network is available as an option in the code in case the production/destruction of light elements as Li and Be or when more advanced stages of nucleosynthesis are required. This optional version is an adaptation of the routine written by Timmes (Timmes, private communication) for a general network with 47 isotopes. The calculations performed with our network and with the adaptation of the TORCH routine are compatible, at least for the evolutionary stages we have explored in this paper. However, this routine is very CPU intensive so that we only use it in special cases.
In our 13 isotope nuclear network we have used the usual reactions of the pp chains and the CNO tri-cycle. For helium burning the following reactions were introduced:
4He(
![]() )8Be(
)8Be(
![]() )12C(
)12C(
![]() )16O(
)16O(
![]() )20 Ne
)20 Ne
17O(![]() ,
n)20Ne
,
n)20Ne
20Ne(
![]() )24Mg
)24Mg
13C(![]() ,
n)16O
,
n)16O
22Ne(![]() ,
n)25Mg
,
n)25Mg
22Ne(
![]() )26Mg
)26Mg
14N((
![]() )18F(
)18F(![]() )18O(
)18O(
![]() )22Ne.
)22Ne.
Carbon burning was followed using the reactions:
12C(12C, ![]() )20Ne
)20Ne
12C(12C, p)23Na
23Na(p, ![]() )20Ne
)20Ne
12C(
![]() )16O
)16O
16O(
![]() )20Ne
)20Ne
20Ne(
![]() )24Mg.
)24Mg.
The basic nuclear reactions rates are from Caughlan & Fowler (1988), while the screening
factors are taken from Graboske et al. (1973). The loss of energy due to neutrinos was
considered using the work by Itoh et al. (1989). For cooler models, the adopted equation
of state was CEFF (Däppen 2000, private communication), while for hotter ones partial
ionization was taken into account for the same elements as in CEFF (H, He, C, N, O, Ne,
Na, Mg, Al, Si, Ar, Fe) by interacting the Saha equations. The Fermi-Dirac integrals are
used where necessary.
For the more massive models, the mass loss rates are the main determinants acting on the
evolutionary path of a given model. We adopted the formalism by Nieuwenhuijzen & de
Jager (1990) for all models except in two situations: Wolf-Rayet stars and red giants
with masses smaller than 4 ![]() .
In the latter case, we used the work by Reimers
(1977). The parametrization by Langer (1989) was used for WNE and WC Wolf-Rayet stars
while for WNL Wolf-Rayet stars, we use the mass-loss rates given by Conti (1988).
.
In the latter case, we used the work by Reimers
(1977). The parametrization by Langer (1989) was used for WNE and WC Wolf-Rayet stars
while for WNL Wolf-Rayet stars, we use the mass-loss rates given by Conti (1988).
If one compares our stellar models of 1995 with the present ones, the differences in the tracks are evident, mainly for more massive stars. In part, this is due to the fact that in the previous work the calculations were interrupted during the first stages of helium burning which renders a direct comparison impossible. In addition, more advanced evolutionary stages such as the WR stages were not computed with the 1995 code. The principal differences, however, are the mass range and the implications of the updated physics for the internal structure (see next sections).
Another parameter that influences the calculation of the apsidal-motion constants, the tidal-torque constant, and the depth of the convective envelope is obviously the radius of the stellar configuration. In stars with high mass-loss rates, the optical thickness of the winds are finite. In order to introduce this effect in the code, we follow the recipe given in Schaller et al. (1992), and references therein. The corrections are mainly important for WR stars, and are almost negligible during early evolutive phases. Although such a scheme is consistent (the opacity flux weighted, for example), there are still large uncertainties in the theory of stellar winds. We therefore consider these models to be less reliable than those located near the Main-Sequence.
The theoretical HR diagram corresponding to our grid of evolutionary tracks is represented in
Fig. 1. The basic differences between our calculation and those for example by Schaller et al.
(1992) are associated with the morphology of the tracks of more massive stars during later
evolutionary phases: our tracks predict, generally, cooler configurations. Recent comparisons
between several grids of stellar models (Lastennet & Valls-Gabaud 2002) indicate that the models
from Geneve, Padova and Granada give very similar results. However, the sample of known DLEB is
still limited in mass range as it contains only few systems with components more massive
than 25 ![]() .
Unfortunately, there are no sufficient massive DLEB to help to elucidate the question.
Hence, as mentioned above, we should take these advanced phases with caution: only when a systematic
comparison with observational data becomes possible (mainly using DLEB) will we be able draw
definitive conclusions.
.
Unfortunately, there are no sufficient massive DLEB to help to elucidate the question.
Hence, as mentioned above, we should take these advanced phases with caution: only when a systematic
comparison with observational data becomes possible (mainly using DLEB) will we be able draw
definitive conclusions.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig1.eps}
\end{figure}](/articles/aa/full/2004/36/aa0470-04/Timg17.gif) |
Figure 1: The theoretical HR diagram. The numbers below the tracks indicate the stellar masses in solar units. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig2.eps}
\end{figure}](/articles/aa/full/2004/36/aa0470-04/Timg18.gif) |
Figure 2:
The evolution of the apsidal-motion constant k2 for 5 and 40 |
| Open with DEXTER | |
The well known apsidal-motion phenomenon has been used for decades to test evolutionary models (see Claret & Giménez 1993 for a historic review). Briefly, the distortions in the shape of the components of an eccentric binary due to rotation and tides lead to secular changes in the position of the periastron. These distortions can be described in terms of the mass distribution of the stars, and can thus be directly derived from the theoretical stellar models. In addition to the contribution of the stellar shape distortions, there is also a general relativistic contribution which makes some systems (mainly those with high orbital eccentricity) particularly interesting as tests to the theory of General Relativity. The historic discrepancies between theory and observations seems to be reduced to acceptable levels after the introduction of modern stellar models which take into account the effects of dynamic tides (Claret & Willems 2002). However, some systems are yet to be explained (DI Her, for example) and require further refinements in the calculation of the theoretical internal structure constants (k2, k3 and k4).
As usual, the apsidal-motion constants are derived by integrating the Radau equation. Figure 2
shows the comparison between the present calculations (solid lines) and those by Claret (1995)
(dashed ones) for 5 and 40 ![]() models. The mass distributions are very similar for
both 5
models. The mass distributions are very similar for
both 5 ![]() models, at least up to exhaustion of hydrogen in the core. The present
model was computed until later stages, which is reflected by the peak in
log k2 around
models, at least up to exhaustion of hydrogen in the core. The present
model was computed until later stages, which is reflected by the peak in
log k2 around
![]() .
The situation for the 40
.
The situation for the 40 ![]() model is very different.
The mass distributions are only comparable during the early evolutionary stages, while during
the later ones the present models are much more mass concentrated than the previous ones.
Although the new opacities and the expansion of the nuclear network play some role, the main
cause of these differences is due to the higher mass-loss rates adopted for the present
models (Claret & Giménez 1991 showed that mass loss increases the grade of mass concentration).
The differences may achieve 0.5 dex near core-hydrogen exhaustion for the 40
model is very different.
The mass distributions are only comparable during the early evolutionary stages, while during
the later ones the present models are much more mass concentrated than the previous ones.
Although the new opacities and the expansion of the nuclear network play some role, the main
cause of these differences is due to the higher mass-loss rates adopted for the present
models (Claret & Giménez 1991 showed that mass loss increases the grade of mass concentration).
The differences may achieve 0.5 dex near core-hydrogen exhaustion for the 40 ![]() model.
These differences further improve the comparison between
theory and observations.
model.
These differences further improve the comparison between
theory and observations.
Concerning tidal evolution, the situation is not so clear but this is compensated for the
presence of an additional scenario besides the case of isolated binaries: the critical
time scales for the circularization of binaries belonging to clusters. Spectroscopic observations
(radial velocity curves) of binary systems in clusters indicate the presence of a cut-off
period (
![]() )
below which the binaries present circular orbits (Mathieu et al. 1992, for example).
In addition, there seems to be a relationship between the age of the cluster and the cut-off periods.
Dealing with cut-off periods of binaries in clusters is a very interesting and iterative exercise
since the age of the cluster (which can be used as an upper limit for the critical time scales) needs
to be computed,and, simultaneously, the differential equations governing the tidal evolution for the
most representative close binaries need to be integrated in order to compare the theoretical
)
below which the binaries present circular orbits (Mathieu et al. 1992, for example).
In addition, there seems to be a relationship between the age of the cluster and the cut-off periods.
Dealing with cut-off periods of binaries in clusters is a very interesting and iterative exercise
since the age of the cluster (which can be used as an upper limit for the critical time scales) needs
to be computed,and, simultaneously, the differential equations governing the tidal evolution for the
most representative close binaries need to be integrated in order to compare the theoretical
![]() with the observed
with the observed
![]() -age relationship (Claret, in preparation).
-age relationship (Claret, in preparation).
The stellar interior/envelope conditions dictate what mechanism will be responsible for
tidal braking. For stars with convective envelopes this agent is turbulent dissipation.
The associated time scale is of the order of R2/![]() and the convective friction time is,
following Zahn (1966),
and the convective friction time is,
following Zahn (1966),
![\begin{displaymath}{t_{\rm f}}= {\left[{MR^{2}\over{L}}\right]^{1/3}}
\end{displaymath}](/articles/aa/full/2004/36/aa0470-04/img22.gif) |
(1) |
where M is the stellar mass, R the radius, and L the luminosity. The differential
equations for synchronization and circularization can be written as (Zahn 1984):
| |
= | ||
| = | 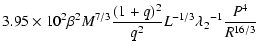 |
(2) |
| |
= | ||
| = | 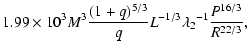 |
(3) |
where ![]() is the rotational angular frequency,
is the rotational angular frequency, ![]() the orbital angular
frequency,
the orbital angular
frequency, ![]() the radius of gyration, e the orbital eccentricity, q the mass
ratio, P the orbital period, and the time scales are expressed in years. The constant
the radius of gyration, e the orbital eccentricity, q the mass
ratio, P the orbital period, and the time scales are expressed in years. The constant ![]() depends on the depth of the convective envelope
depends on the depth of the convective envelope
![]() in normalized
units
and, when the convective turnover time is small in comparison to the tidal period, is given by the
following expression (Zahn 1989):
in normalized
units
and, when the convective turnover time is small in comparison to the tidal period, is given by the
following expression (Zahn 1989):
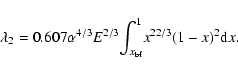 |
(4) |
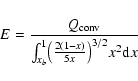 |
(5) |
The parameter ![]() is a steep function of the effective temperature. In fact,
the precision in the determination of the depth of the convective envelopes depends
strongly on the convergence criterions used to compute the stellar models. Moreover, the
triangle used to define an envelope in the HR diagram must be as small as possible
to avoid numerical oscillations in
is a steep function of the effective temperature. In fact,
the precision in the determination of the depth of the convective envelopes depends
strongly on the convergence criterions used to compute the stellar models. Moreover, the
triangle used to define an envelope in the HR diagram must be as small as possible
to avoid numerical oscillations in
![]() .
We typically use
.
We typically use ![]() log
log
![]() and
and ![]() log L = 0.004 or smaller, depending on the numerical conditions.
This numerical consistency is, however, only possible at the expense of more CPU time. Even
taking into account the mentioned precaution, we still detected small numerical oscillations
but these do not have a significant influence on the time scales. Figure 3 shows the behavior of
the depth of the convective envelope (0 means a fully convective model) as a function of the
effective temperature for a 1.41
log L = 0.004 or smaller, depending on the numerical conditions.
This numerical consistency is, however, only possible at the expense of more CPU time. Even
taking into account the mentioned precaution, we still detected small numerical oscillations
but these do not have a significant influence on the time scales. Figure 3 shows the behavior of
the depth of the convective envelope (0 means a fully convective model) as a function of the
effective temperature for a 1.41 ![]() model. The "zig-zag'' around
log
model. The "zig-zag'' around
log
![]() is due to the red hook. The constant E is represented in Fig. 4 for the same model and
presents similar features: the smaller the depth of the convective envelope, the smaller the
corresponding values of E. The integral which appears in Eq. (4) is a simple one and users
can easily compute the time scales and thus integrate the differential equations for e and
is due to the red hook. The constant E is represented in Fig. 4 for the same model and
presents similar features: the smaller the depth of the convective envelope, the smaller the
corresponding values of E. The integral which appears in Eq. (4) is a simple one and users
can easily compute the time scales and thus integrate the differential equations for e and ![]() directly from the files providing
directly from the files providing ![]() and
and
![]() .
As a final note on the
turbulent dissipation mechanism, it is worth to mention that
.
As a final note on the
turbulent dissipation mechanism, it is worth to mention that ![]() ,
as expected, also
depends on the chemical composition. Such a dependency may have some implications for the
levels of synchronization and circularization of some problematic systems.
,
as expected, also
depends on the chemical composition. Such a dependency may have some implications for the
levels of synchronization and circularization of some problematic systems.
![\begin{figure}
\par\includegraphics[height=8cm,width=8.8cm,clip]{fig3.eps}
\end{figure}](/articles/aa/full/2004/36/aa0470-04/Timg39.gif) |
Figure 3:
The depth of the convective envelope (normalized radius) as
a function of the effective temperature for a 1.41 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=8cm,width=8.8cm,clip]{fig4.eps}
\end{figure}](/articles/aa/full/2004/36/aa0470-04/Timg40.gif) |
Figure 4: The constant E characterizing a polytropic envelope (Eq. (5)) as a function of the effective temperature. Same models as in Fig. 3. |
| Open with DEXTER | |
The case of more massive stars with convective cores and radiative envelopes is somewhat
different. The dominant mechanism for tidal braking in this kind of stars is radiative
damping, characterized by the tidal torque constants En. The time scales for synchronization
and circularization are:
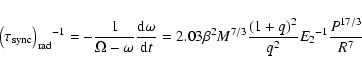 |
(6) |
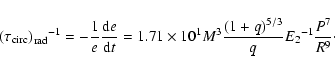 |
(7) |
![\begin{displaymath}{E_n} =
{3^{8/3}{\left(\Gamma(4/3)\right)^2}\over{(2n+1)\left...
...B\over
{x^{2}}}\right)^
{\prime}_{f}\right]^{-1/3}} {H_{n}^2}
\end{displaymath}](/articles/aa/full/2004/36/aa0470-04/img43.gif) |
(8) |
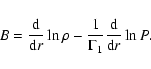 |
(9) |
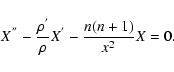 |
(11) |
In Eq. (10), Y(1) is the solution of the Clairaut equation. The differential equations
were solved for each configuration using a fourth order Runge-Kutta method.
We restrict the calculations to n=2 since for larger n the contribution to the dynamic
tide is not significant. The above parameters are more complicated to derive than the depth of
a convective envelope mentioned before: among other calculations, they depend on the
derivative of the Brunt-Väisäla frequency at the boundary of the convective core.
For less evolved models, the derivatives are rather simple but as the star evolves, the
convective core begins to recede, increasing the chemical composition gradient. The
situation is worst near the border of the convective core. In these conditions,
additional shell points have to be added by changing the convergence criterions. In some cases up to 6000-7000 mesh points were used.
![\begin{figure}
\par\includegraphics[height=8cm,width=8.8cm,clip]{fig5.eps}
\end{figure}](/articles/aa/full/2004/36/aa0470-04/Timg48.gif) |
Figure 5:
The behavior of the tidal torque constant E2 as a function of the
logarithm of the age. The models shown are for 2 and 10 |
| Open with DEXTER | |
The behavior of E2 is illustrated in Fig. 5 for 2 and
10 ![]() stellar models. The influence of the size of the convective core is obvious: the tidal torque
constant for the more massive model is about 2 orders of magnitude larger than
that for the 2
stellar models. The influence of the size of the convective core is obvious: the tidal torque
constant for the more massive model is about 2 orders of magnitude larger than
that for the 2 ![]() model. The tidal torque constant E2 is furthermore more sensitive to stellar
evolution than, for example, the apsidal-motion constants. Indeed, from the Main-Sequence
up to the last stages of carbon burning, log E2 changes from -5.5 to -16, which is
almost 10 orders of magnitude. In the same interval, k2 changes by less than 2 orders
of magnitude.
model. The tidal torque constant E2 is furthermore more sensitive to stellar
evolution than, for example, the apsidal-motion constants. Indeed, from the Main-Sequence
up to the last stages of carbon burning, log E2 changes from -5.5 to -16, which is
almost 10 orders of magnitude. In the same interval, k2 changes by less than 2 orders
of magnitude.
There is also a strong discussion on the validity of the hydrodynamical mechanism proposed by Tassoul (Rieutord 1992; Tassoul & Tassoul 1996, for example). According to this formalism, the distortions due to the proximity effects in close binaries cause hydrodynamical currents which tend to circularize their orbits. A full discussion of this controversy is outside the scope of this paper, but we would like to remark that our tables provide all the necessary material to compute the critical time scales of circularization and synchronization for the hydrodynamical mechanism as well.
By examining Eqs. (2), (3), (6) and (7) we note that the time scales for synchronization and
circularization also depend on the moment of inertia, through the radius of gyration ![]() .
The moment of inertia and the potential energy have additional important applications in stellar physics,
as for example in investigations of Jacobi dynamics (Ferronsky et al. 1987). The
later authors have shown that the product
.
The moment of inertia and the potential energy have additional important applications in stellar physics,
as for example in investigations of Jacobi dynamics (Ferronsky et al. 1987). The
later authors have shown that the product
![]() (
(
![]() ,
where
,
where
![]() is the potential energy) is almost constant for
several laws of mass distribution.
However, we have found that this product is not constant for the physical
conditions in stellar interiors. In Fig. 6, we show how
is the potential energy) is almost constant for
several laws of mass distribution.
However, we have found that this product is not constant for the physical
conditions in stellar interiors. In Fig. 6, we show how
![]() varies with the
evolution for 3 selected stellar models: 1, 20 and 125
varies with the
evolution for 3 selected stellar models: 1, 20 and 125 ![]() .
The general aspect of
Fig. 6 is independent of the mass of the models. As predicted by
Ferronsky et al., the product is around 0.4, but only up to core-hydrogen exhaustion, which
is indicated by an asterisk. After this
evolutionary phase, it increases steeply, breaking the constant tendency.
.
The general aspect of
Fig. 6 is independent of the mass of the models. As predicted by
Ferronsky et al., the product is around 0.4, but only up to core-hydrogen exhaustion, which
is indicated by an asterisk. After this
evolutionary phase, it increases steeply, breaking the constant tendency.
![\begin{figure}
\par\includegraphics[height=8cm,width=8.8cm,clip]{fig6.eps}
\end{figure}](/articles/aa/full/2004/36/aa0470-04/Timg51.gif) |
Figure 6:
The product
|
| Open with DEXTER | |
As commented in the Introduction, the rapid rotators and/or components of close binaries
are subject to distortions which will alter the brightness surface distribution.
The flux depends on the local gravity following the formula by von Zeipel. However,
the gravity-darkening exponent ![]() depends on which mechanism of transport of
energy is dominant and on the evolutionary status of the configuration.
Therefore, adopting the value 1 for envelopes in radiative equilibrium and 0.32 for envelopes in
convective equilibrium is not a fully correct procedure.
depends on which mechanism of transport of
energy is dominant and on the evolutionary status of the configuration.
Therefore, adopting the value 1 for envelopes in radiative equilibrium and 0.32 for envelopes in
convective equilibrium is not a fully correct procedure.
The numerical method used to derive ![]() is based on the triangles strategy (Claret 1998).
If the external boundary conditions are unchanged during the evolution, the integrations in the outer layers
will be the same, provided that the corresponding triangles in the HR diagram are small. By generalizing
this concept to several
points, we can simulate distorted configurations with different effective temperature distributions over
the surface. By numerically differentiating these envelopes, we finally obtain
is based on the triangles strategy (Claret 1998).
If the external boundary conditions are unchanged during the evolution, the integrations in the outer layers
will be the same, provided that the corresponding triangles in the HR diagram are small. By generalizing
this concept to several
points, we can simulate distorted configurations with different effective temperature distributions over
the surface. By numerically differentiating these envelopes, we finally obtain ![]() .
It is important
to emphasize that the triangles must be as small as possible in order to guarantee that the external
integrations be really unchanged and also to guarantee the validity of the definition
.
It is important
to emphasize that the triangles must be as small as possible in order to guarantee that the external
integrations be really unchanged and also to guarantee the validity of the definition
![]() ,
where K is the equation of an adiabate.
,
where K is the equation of an adiabate.
![\begin{figure}
\par\includegraphics[height=8cm,width=8.8cm,clip]{fig7.eps}
\end{figure}](/articles/aa/full/2004/36/aa0470-04/Timg53.gif) |
Figure 7:
The evolution of the gravity-darkening exponent |
| Open with DEXTER | |
Figure 7 shows how ![]() depends on the effective temperature for a fixed mass
(10
depends on the effective temperature for a fixed mass
(10 ![]() ). We selected this model because it crosses the radiative-convective boundary
three times, thus presenting envelopes with different physical conditions. For higher effective
temperatures the value of
). We selected this model because it crosses the radiative-convective boundary
three times, thus presenting envelopes with different physical conditions. For higher effective
temperatures the value of ![]() is 1.0, as predicted by von Zeipel. However, when
convection begins to dominate the situation changes drastically and
is 1.0, as predicted by von Zeipel. However, when
convection begins to dominate the situation changes drastically and ![]() decreases
rapidly. During the loops in the HR-diagram the gravity-darkening exponent increases-decreases and finally,
during the last stages of Carbon burning, it recovers the typical value for convective envelopes
(around 0.3). The auxiliary figure within Fig. 7 helps us to connect the chemical-
decreases
rapidly. During the loops in the HR-diagram the gravity-darkening exponent increases-decreases and finally,
during the last stages of Carbon burning, it recovers the typical value for convective envelopes
(around 0.3). The auxiliary figure within Fig. 7 helps us to connect the chemical-![]() evolution.
evolution.
The first five columns of the tables contain the age (in years), log L
(in solar units), log g,
log
![]() and the mass (in solar units). Columns 6-9 contain the logarithm of the mass-loss rate
(
and the mass (in solar units). Columns 6-9 contain the logarithm of the mass-loss rate
(![]() /year), the logarithm of the central temperature, of the density and the size of the convective
core
/year), the logarithm of the central temperature, of the density and the size of the convective
core ![]() .
Columns 10-35 contain the central and surface chemical composition
of X, Y, 12C, 13C, 14N, 16O, 17O, 18O, 20Ne, 22Ne,
24Mg, 25Mg, and 26Mg. In the next three columns we have log k2, log k3 and
log k4.
The depth of the convective envelope
.
Columns 10-35 contain the central and surface chemical composition
of X, Y, 12C, 13C, 14N, 16O, 17O, 18O, 20Ne, 22Ne,
24Mg, 25Mg, and 26Mg. In the next three columns we have log k2, log k3 and
log k4.
The depth of the convective envelope
![]() is given in Col. 39, while log E2 is given in
Col. 40. The constant E, the form factor
is given in Col. 39, while log E2 is given in
Col. 40. The constant E, the form factor
![]() and
and ![]() are given in positions 41, 42 and 43, and
finally, Col. 44 is reserved for the gravity-darkening exponent
are given in positions 41, 42 and 43, and
finally, Col. 44 is reserved for the gravity-darkening exponent ![]() .
We furthermore provided two kinds of
tables: more complete ones with our computed models and more restricted ones containing only
equivalent evolutionary points (usually more adequate for the computation of isochrones).
.
We furthermore provided two kinds of
tables: more complete ones with our computed models and more restricted ones containing only
equivalent evolutionary points (usually more adequate for the computation of isochrones).
Acknowledgements
I am grateful to B. Willems, who helped to improve the paper. The Spanish MCYT (AYA2003-04651) is gratefully acknowledged for its support during the development of this work.