A&A 424, 447-454 (2004)
DOI: 10.1051/0004-6361:20047183

Ionized gas and stellar kinematics of seventeen nearby spiral galaxies^,,

A. Pizzella¹ - E. M. Corsini¹ - J. C. Vega Beltrán² - F. Bertola¹

1 - Dipartimento di Astronomia, Università di Padova, vicolo dell'Osservatorio 2, 35122 Padova, Italy
2 - Instituto Astrofísico de Canarias, Calle Vía Láctea s/n, 38200 La Laguna, Spain

Received 2 February 2004 / Accepted 21 April 2004

Abstract
Ionized gas and stellar kinematics have been measured along the major axes of seventeen nearby spiral galaxies of intermediate to late morphological type. We discuss the properties of each sample galaxy, distinguishing between those characterized by regular or peculiar kinematics. In most of the observed galaxies, ionized gas rotates more rapidly than stars and has a lower velocity dispersion, as is to be expected if the gas is confined in the disc and supported by rotation while the stars are mostly supported by dynamical pressure. In a few objects, gas and stars show almost the same rotational velocity and low velocity dispersion, suggesting that their motion is dominated by rotation. Incorporating the spiral galaxies studied by Bertola et al. (1996), Corsini et al. (1999, 2003) and Vega Beltrán et al. (2001) we have compiled a sample of 50 S0/a-Scd galaxies, for which the major-axis kinematics of the ionized gas and stars have been obtained with the same spatial ($\approx$1'') and spectral ($\approx$50  $\rm km\;s^{-1}$) resolution, and measured with the same analysis techniques. This allowed us to address the frequency of counter-rotation in spiral galaxies. It turns out that less than $12\%$ and less than $8\%$ (at the $95\%$ confidence level) of the sample galaxies host a counter-rotating gaseous and stellar disc, respectively. The comparison with S0 galaxies suggests that the retrograde acquisition of small amounts of external gas gives rise to counter-rotating gaseous discs only in gas-poor S0s, while in gas-rich spirals the newly acquired gas is swept away by the pre-existing gas. Counter-rotating gaseous and stellar discs in spirals are formed only from the retrograde acquisition of large amounts of gas exceeding that of pre-existing gas, and subsequent star formation, respectively.

Key words: galaxies: kinematics and dynamics - galaxies: spiral - galaxies: structure

   
1 Introduction

Studying the interplay between ionized gas and stellar kinematics allows us to address different topics concerning the dynamical structure of disc galaxies and to constrain the processes leading to their formation and evolution. These topics include the study of the mass distribution of luminous and dark matter (see Sofue & Rubin 2001 for a review), the ubiquity of supermassive black holes and their relationship to the large-scale properties of the host galaxies (see Merritt & Ferrarese 2001 for a review), the discovery of kinematically decoupled components (see Bertola & Corsini 1999 for a review), the origin of disc heating (Merrifield et al. 2001 and references therein), and the presence of pressure-supported ionized gas in bulges (Bertola et al. 1995; Cinzano et al. 1999).

Table 1: Parameters of the sample galaxies.

All these issues will greatly benefit from a survey devoted to the comparative measurements of ionized gas and stellar kinematics in S0s and spiral galaxies. Since these are available only for a limited number of objects, we began a scientific programme aimed at deriving detailed velocity curves and velocity dispersion radial profiles of ionized gas and stars along the major axes of disc galaxies (Bertola et al. 1995, 1996; Corsini et al. 1999, 2003; Vega Beltrán et al. 2001; Funes et al. 2002) to be used for mass modelling (Corsini et al. 1999; Cinzano et al. 1999; Pignatelli et al. 2001).

This paper is organized as follows. An overview of the properties of the sample galaxies as well as the spectroscopic observations and data analysis are presented in Sect. 2. The resulting ionized gas and stellar kinematics are given and interpreted in Sect. 3. In particular, we derived the central velocity dispersion of stars of all the sample galaxies with the aim of studying the relationship between that the disc circular velocity and bulge velocity dispersion (Ferrarese 2002; Baes et al. 2003) in a forthcoming paper (but see also Pizzella et al. 2003). The fraction of spiral galaxies hosting a counter-rotating component is estimated in Sect. 4 by analysing the major-axis kinematics of all the spiral galaxies we have observed in recent years. Our conclusions are discussed in Sect. 5.

   
2 Sample selection, spectroscopic observations and data reduction

   
2.1 Sample selection

All the observed galaxies are bright ( $B_T\leq13.5$) and nearby ( $V_\odot < 5900$  $\rm km\;s^{-1}$) with an intermediate-to-high inclination ( $40^\circ\leq i \leq 85^\circ$). The Hubble morphological type of the sample galaxies ranges from Sb to Scd (de Vaucouleurs et al. 1991, RC3 hereafter) with eight unbarred, seven weakly barred and two strongly barred galaxies (RC3). The galaxies have been chosen for their strong emission lines. An overview of the basic properties of the sample galaxies is given in Table 1. The distribution of their absolute magnitudes, which brackets the M$^\ast$ value for spiral galaxies (Marzke et al. 1998, for H₀ = 75  $\rm km\;s^{-1}\;Mpc^{-1}$) is shown in Fig. 1.

   
2.2 Spectroscopic observations

The spectroscopic observations of our sample galaxies were carried out at the ESO in La Silla with the 1.52 m ESO telescope on January 22-27, 1996 (run 1 hereafter), and on August 9-14, 1996 (run 2 hereafter).

The Boller & Chievens Spectrograph was mounted on the telescope. The grism No. 26 with 1200  $\rm grooves~mm^{-1}$ blazed at 5730 Å was used in the first order in combination with the  $2\hbox{$.\!\!^{\prime\prime}$ }5\times4\hbox{$.\mkern-4mu^\prime$ }2$ slit and the Loral CCD No. 24 with  $2048 \times 2048$ pixels of $15\times15$  $\rm\mu m^2$. The wavelength range between 4940 Å and 6940 Å was covered with a reciprocal dispersion of 0.98 Å pixel^-1, which guarantees adequate oversampling of the instrumental broadening function. Indeed, the instrumental resolution, obtained by measuring the width of emission lines of a comparison spectrum after the wavelength calibration, was 2.59 Å (FWHM). This corresponds to an instrumental velocity dispersion of  $\sigma = 1.10$ Å (i.e. $\approx$70 and $\approx$50  $\rm km\;s^{-1}$ at the blue and red edges of the spectra, respectively). The angular sampling was $0\hbox{$.\!\!^{\prime\prime}$ }81$ pixel^-1.

At the beginning of each exposure, the slit was centred on the galaxy nucleus using the guiding TV camera and aligned along the galaxy major axis. Details of the slit position and spectra exposure times are given in Table 2. Comparison lamp exposures were obtained before and/or after each object integration to allow an accurate wavelength calibration. Quartz lamp and twilight sky flat-fields were used to map pixel-to-pixel sensitivity variations and large scale illumination patterns. A dozen late G and early K stars were observed with the same set up to serve as templates in measuring the stellar kinematics. The value of the seeing FWHM during the different observing runs ranged between  $1\hbox{$.\!\!^{\prime\prime}$ }0$ and  $2\hbox{$.\!\!^{\prime\prime}$ }0$, as measured by fitting a two-dimensional Gaussian to the guide star.

	Figure 1: Absolute magnitude distribution for the sample galaxies. A line marks  MBT0 = -20.05, which corresponds to M$^\ast$ for spiral galaxies as derived by Marzke et al. (1998) and assuming H0 = 75  $\rm km\;s^{-1}\;Mpc^{-1}$. The dashed region identifies galaxies classified barred or weakly barred in RC3.
Open with DEXTER

   
2.3 Routine data reduction

The spectra were bias subtracted, flat-field corrected, cleaned for cosmic rays and wavelength calibrated using standard MIDAS routines. Cosmic rays were identified by comparing the counts in each pixel with the local mean and standard deviation (as obtained from the Poisson statistics of the photons knowing the gain and readout noise of the detector), and then corrected by interpolating a suitable value. In the central regions (typically for $\vert r\vert\la5''$) cosmic rays were removed by manually editing the spectra.

The instrumental resolution as a function of wavelength was derived as the Gaussian FWHMs measured for several unblended arc lamp lines distributed over the whole spectral range of a wavelength-calibrated comparison spectrum. Finally, the spectra of the same galaxy were aligned and co-added using the centers of their stellar continua as reference. In the resulting spectra, the contribution from the sky was determined by interpolating along the outermost  10''-20'' at the edges of the slit, where galaxy light was negligible. The sky level was then subtracted. Since the spatial extension of the emission lines can exceed that of the stellar continuum, different ranges for sky subtraction have been considered in ionized gas and stellar kinematic measurements. In a few cases the galaxy emission lines extended through the whole slit length. The sky level was derived by scaling the sky frame derived for a different galaxy to match the intensity of the relevant night sky emission lines.

   
2.4 Measuring ionized gas and stellar kinematics

Table 2: Log of spectroscopic observations.

The ionized gas kinematics were measured by the simultaneous Gaussian fit of the emission lines present in the spectra (namely [N  II] $~\lambda6583$, H$\alpha$, and [S  II] $~\lambda\lambda6716,~6731$). The galaxy continuum was removed from the spectra, as was done for measuring the stellar kinematics. We fitted a Gaussian to each emission line in each row of the continuum-subtracted spectrum, assuming them to have the same line-of-sight velocity ($v_{\rm g}$), and velocity dispersion ( $\sigma_{\rm g}$). Velocities and velocity dispersions were corrected for heliocentric velocity and instrumental FWHM, respectively. An additional absorption Gaussian was added to the fit to take into account the presence of the H$\alpha$ absorption line and the flux ratio of the [N  II] lines have been fixed at 1:3. Far from the galaxy centre (for  $\vert r\vert\ga10''$) we averaged adjacent spectral rows to increase the signal-to-noise ratio of the relevant emission lines. We checked for a few galaxies that the error in the kinematic parameter determination derived by Monte Carlo simulations did not differ significantly from the formal errors given as output by the least-squares fitting routine. We therefore decided to assume the latter as error bars on the gas kinematics. For each galaxy we derive the heliocentric systemic velocity, $V_{\odot}$, as the velocity of the centre of symmetry of the ionized gas rotation curve (Table 1).

The stellar kinematics were measured from the galaxy absorption features present in the wavelength range running from 5050 Å to 5550 Å and centred on the Mg line triplet ( $\lambda\lambda~5164,5173,5184$ Å). We used the Fourier correlation quotient method (FCQ, Bender 1990) following the prescriptions of Bender et al. (1994). The spectra were binned along the spatial direction to obtain a nearly constant signal-to-noise ratio larger than 20 per resolution element. The galaxy continuum was removed row by row by fitting a fourth to sixth order polynomial as in Bender et al. (1994). The K1 III star HR 5777 was adopted as a kinematic template. This allowed us to derive, for each spectrum, the line-of-sight stellar velocity ($v_\star$), and velocity dispersion (ß) by fitting a Gaussian to the line-of-sight velocity distribution (LOSVD) at each radius. Velocities were corrected for heliocentric velocity. We derived errors for the stellar kinematics from photon statistics and CCD read-out noise, calibrating them by Monte Carlo simulations as done by Gerhard et al. (1998). These errors do not take into account possible systematic effects due to any template mismatch.

The ionized gas and stellar kinematics of all the sample galaxies are tabulated in Tables 3 and 4, respectively, and plotted in Fig. 2.

   
3 The ionized gas and stellar kinematics

3.1 Velocity curves and velocity dispersion profiles of ionized gas and stars

The resulting ionized gas and stellar kinematics of all our sample galaxies are shown in Fig. 2. For each object the plot is organized as follows:

1.

In the upper panel we display the galaxy image obtained from the Digitized Sky Survey. The galaxy image has been rotated and the slit position has been plotted to allow a better comparison between morphological and kinematic properties. The slit width and length correspond to those adopted in obtaining the spectra.

2.

In the middle panel we plot the velocity curves of the gaseous (open circles) and stellar (filled circles) components. The velocity scale on the left of the plot indicates the observed velocity after subtraction of the systemic velocity given in Table 1. The velocity scale on the right indicates the rotation velocity after deprojection for the galaxy inclination given in Table 1. Error bars are not plotted when smaller than symbols. The position angle of the slit is specified.

3.

In the lower panel we plot in radial profiles the velocity dispersion of the gaseous (open circles) and stellar (filled circles) components. Error bars are not plotted when smaller than their symbols.

The kinematic measurements obtained for the sample galaxies extend typically to $\approx$ $0.9\;R_{25}$ for the gaseous and $\approx$ $0.5\;R_{25}$ for the stellar component. The curves are generally regular and symmetric about the centre.

	Figure 2: Ionized gas ( open circles) and stellar ( filled circles) kinematics measured along the major axes of the sample galaxies. Error bars smaller than their symbols are not plotted.
Open with DEXTER

3.2 Comparison with the literature

The ionized gas and/or stellar kinematics of some of the sample galaxies have been measured by other authors. We used these data sets to assess the accuracy and reliability of our measurements. In most cases differences between different authors are due to slit centring and/or positioning, different analysis techniques, or both (see Fisher 1997, for a discussion).

Ionized gas velocity curves have been measured along the major axes of NGC 615, NGC 1620, NGC 2708, NGC 2815, NGC 3054, NGC 3200, NGC 4682, NGC 6118, NGC 7083 and NGC 7531. However, these measurements had previously been obtained with a lower spatial and/or velocity resolution with respect to ours. In Fig. 3 we plot our kinematic measurements compared to the available data. The agreement is good and the discrepancies ( $\Delta V\la20$  $\rm km\;s^{-1}$) are due to the different spatial sampling and accuracy of velocity measurements. Only in the case of NGC 7083 do we notice a systematic difference ( $\Delta V\approx80$  $\rm km\;s^{-1}$) on the north-east side of the rotation curve between our data and those of Rubin et al. (1982). We attribute such a discrepancy to the wavelength calibration of Rubin et al. (1982) since it is not present when we consider the data of Mathewson et al. (1992).

In Fig. 4 we compared our kinematic measurements for the stellar component of NGC 615, NGC 2815 and NGC 3200 to the data derived by Bottema (1992), Sil'chenko et al. (2001) and Vega Beltrán et al. (2001), respectively. The overall agreement is good both for velocities and velocity dispersions, except for NGC 2815. Indeed, we measured on the south-east side of this galaxy lower rotation velocities and higher velocity dispersions with respect to those of Bottema (1992).

   
3.3 The central velocity dispersion of stars

A tight correlation between the central velocity dispersion of the spheroid and the galaxy circular velocity has recently been found for a sample of elliptical and spiral galaxies (Ferrarese 2002; Baes et al. 2003). Since the bulge velocity dispersion and circular velocity are related to the masses of the central black hole (Ferrarese & Merritt 2000; Gebhardt et al. 2000) and dark matter halo (e.g. Bullock et al. 2001), respectively, the correlation between velocity dispersion and circular velocity is equivalent to unity between the mass of the black hole and the mass of the dark halo (Ferrarese 2002).

With the aim of exploring this correlation in a forthcoming paper (Pizzella et al. 2004, in preparation, but see also Pizzella et al. 2003), we tested how the central stellar velocity dispersion $\sigma_\star(0)$ depends on the radius of the aperture in which it has been measured. Indeed when comparing the values of $\sigma_\star(0)$ to those derived by other authors it is necessary to take this effect into account. Ferrarese (2002) took as reference aperture that corresponding to  $R_{\rm e}/8$ where $R_{\rm e}$ is the effective radius of the bulge, and adopted the aperture correction by Jorgensen et al. (1995).

To test the reliability this correction when applied to spiral galaxies, we measured the value of $\sigma_\star(0)$ for each sample galaxy in different radial bins obtained by averaging the central 1, 3, ..., 31 rows of the spectrum (corresponding to  $x=0\hbox{$.\!\!^{\prime\prime}$ }81$,  $2\hbox{$.\!\!^{\prime\prime}$ }43$, ..., and  $25\hbox{$.\!\!^{\prime\prime}$ }1$, respectively). In Fig. 5 the resulting profiles of $\sigma_\star(0)$ as a function of the radius of the circularized aperture are compared to that obtained for a galaxy with  $\sigma_\star(0)$ =150  $\rm km\;s^{-1}$ and  $R_{\rm e}=8\hbox{$.\!\!^{\prime\prime}$ }0$ by applying the aperture correction by Jorgensen et al. (1995). These are typical values for the central velocity dispersions and the bulge effective radii of our sample galaxies (Baggett et al. 1998).

It turns out that in most of cases the observed $\sigma_\star(0)$ profile is not centrally peaked and is nearly constant or even rising for large-aperture radii. This suggests that the empirical correction by Jorgensen et al. (1995), which was originally proposed for elliptical galaxies with centrally peaked velocity dispersions but negligible rotation velocities, is no longer valid for our late-type spiral galaxies. In this case the slit aperture is positioned along the galaxy major axis; therefore, the contribution of the rotation velocity (which remains spatially unresolved after the binning process) to the measured velocity dispersion increases with radius. The contribution of the rotation velocity makes the actual orientation of the slit a critical parameter when the aperture correction is applied.

We therefore decided to not apply any aperture correction to the measured value of  $\sigma_\star(0)$. However, as shown in Fig. 5, there is no strong dependence of  $\sigma_\star(0)$ on aperture for all the sample galaxies, except for NGC 4682. This peculiar behaviour is due to the low signal-to-noise ratio ($\approx$10) for the innermost two radial bins.

Figure 5: Percentage variation in the central velocity dispersion, $\sigma _0$, of the sample galaxies as a function of the radial bin, x (or of the circularized aperture,  $r_{\rm ap}$) in which it has been measured. The dotted line is the percentage variation obtained for an elliptical galaxy with  $\sigma _\ast (0)=150$  $\rm km\;s^{-1}$ and  $R_{\rm e}=8''$ by applying the empirical correction by Jorgensen et al. (1995).

Open with DEXTER

   
3.4 Interplay between kinematics of ionized gas and stars

Building a complete dynamical model to address the question of the mass distribution of the sample galaxies is beyond the scope of this paper. However, it is possible to derive some hints about their structure directly from the analysis of the interplay between the kinematics of their gas and stars. At each radius, $V_\star$ ($\equiv$ $\vert v_\star-V_\odot\vert$) and $V_{\rm g}$ ($\equiv$ $\vert v_{\rm g}-V_\odot\vert$) are the observed rotational velocities of the stars and the ionized gas, respectively. Following Vega Beltrán et al. (2001), we distinguished two classes in the sample galaxies, according to their kinematics and assuming that the gaseous and stellar discs are coplanar:

(i)

Galaxies in which ionized gas rotates faster than stars and has a lower velocity dispersion than the stars (i.e., $V_{\rm g}$$\;>\;$$V_\star$ and $\sigma_{\rm g}$$\;<\;$ß): NGC 210, NGC 615, NGC 1620, NGC 2590, NGC 2708 (although it has asymmetric rotation curves for both gas and stars), NGC 2815, NGC 3200, NGC 3717, NGC 6118, NGC 6878, NGC 6895 and NGC 7083. The different kinematic behaviour of the gaseous and stellar components can be explained by a model where the gas is confined in the disc and supported by rotation, while the stars are mostly supported by dynamical pressure. This is consistent with the application of the asymmetric drift (e.g. Binney & Tremaine 1987).

(ii)

Galaxies for which $V_{\rm g}$ $\;\simeq\;$$V_\star$ and $\sigma_{\rm g}$$\;\la\;$ß: NGC 4682, NGC 5530 and NGC 7412. The observed difference between the velocity dispersion of the two components is  $\Delta \sigma\leq50$ $\rm km\;s^{-1}$. The motions of both ionized gas and stars are dominated by rotation.

The weakly barred spirals NGC 3054 and NGC 7531 show peculiar kinematics that are unexpected if the gas is moving in circular orbits in a disc coplanar to the stellar one. In NGC 3054 $V_{\rm g}$$\;\leq\;$$V_\star$ and $\sigma_{\rm g}$$\;<\;$ß for  $\vert r\vert\la10''$, and $V_{\rm g}$$\;>\;$$V_\star$ and $\sigma_{\rm g}$ $\;\simeq\;$ß at larger radii, while NGC 7531 has intermediate properties between the two classes. It is characterized by $V_{\rm g}$ $\;\simeq\;$$V_\star$ and  $\sigma_{\rm g}$$\;<\;$ß for  $\vert r\vert\la10''$, and $V_{\rm g}$$\;>\;$$V_\star$ and  $\sigma_{\rm g}$ $\;\simeq\;$ß for |r|>10''. These cases cannot be explained without invoking a warp in the gaseous disc or non-circular gas motions.

   
4 The frequency of counter-rotation in spiral galaxies

   
4.1 Detectability of counter-rotation

The presence of counter-rotation in disc galaxies is generally interpreted as the signature of the external origin of the gaseous component (Bertola et al. 1992). Since we are going to discuss the frequency of counter-rotation in disc galaxies, it is necessary to establish our capability of detecting a counter-rotating component when it is present.

In order to estimate the frequency of counter-rotating components we considered the sample of spiral galaxies obtained from Bertola et al. (1996; one Sa galaxy), Corsini et al. (1999; six Sa galaxies), Vega Beltrán et al. (2001; sixteen Sa-Scd galaxies, NGC 224 and NGC 3031 have been excluded from this analysis since the available kinematic data do not extend to the disc region), Corsini et al. (2003; ten S0/a-Sa galaxies), and this paper (seventeen Sb-Sc galaxies). The sample consists of 50 spiral galaxies ( $0\leq T \leq 6$), with apparent magnitude  $10.1\leq B_T \leq 13.9$, inclination  $i \geq 35^\circ~$and systemic velocity  $V_\odot \leq 6000$  $\rm km\;s^{-1}$. Their major-axis ionized gas and stellar kinematics have been obtained with the same spatial ( ${\it FWHM} \approx1''$) and spectral ( $\sigma_{\rm instr} \approx 50$  $\rm km\;s^{-1}$) resolution, and measured with the same analysis technique. These 50 spiral galaxies represent our qualified sample, for which we are confident that we are able to detect any counter-rotating or kinematically decoupled gaseous and/or stellar component.

Revealing the presence of ionized gas that is counter-rotating with respect to the stellar component is straightforward. Indeed in most a cases visual inspection of the shape and orientation of spectral emission and absorption lines enables us to detect when the gas and stars are rotating opposite directions (e.g. NGC 4450; Rubin et al. 1992). The techniques we adopted to derive the gaseous and stellar kinematics allowed us to measure differences of a few  $\rm km\;s^{-1}$ in the rotation velocities of the two components. We are therefore confident that we are able to detect all the counter-rotating gaseous components hosted in our sample galaxies.

Disentangling a counter-rotating stellar component is a more difficult task. The kinematics of two counter-rotating stellar populations are measured from the same absorption features and depend on the dynamical status of the components, as well as on the spectral resolution of the available data. We estimated the upper limit on the fraction of counter-rotating stars we can detect assuming that the counter-rotating components are discs with the same scale length and different luminosity as follows. We assumed the stars in the disc of NGC 615 as the prograde component of the model. We selected the spectrum of NGC 615 since the absorption lines in the wavelength and radial ranges where we are going to measure the stellar kinematics are nearly symmetric with respect to the centre, have a large radial extension and are characterized by a high signal to noise ratio ($S/N\ga30$ per Å for |r|>20'', and $S/N\geq50$ per Å for  $\vert r\vert\leq20''$). We obtained the retrograde component of model by flipping the spectrum of NGC 615 about the centre of the slit. This corresponds to inverting all the line-of-sight velocities of the prograde component with respect to the systemic velocity of the galaxy. We built a series of synthetic spectra with a different fraction of counter-rotating stars ( $f_{\rm CR}= 5\%$, $10\%$, ..., $50\%$) by means of a linear superposition of the prograde and retrograde models. The retrograde model has been divided by its own continuum and then multiplied by the continuum of the prograde model to remove asymmetries in the continuum shape on the two sides of the galaxy disc. We measured the stellar kinematics in the disc-dominated region and derived the radial profile of LOSVD of the synthetic spectra by applying the FCQ method as described in Sect. 2.4. We recognized the signature of the presence of two counter-rotating components, namely the splitting of the LOSVD into two peaks, for  $f_{\rm CR} \geq 15\%$. We assume this value to be our limiting sensitivity for the detection of counter-rotating stars in the galaxy disc. We did not consider the bulge-dominated region, where disentangling the fraction of counter-rotating stars requires further constraints on the dynamical status of the bulge. We conclude that no more than $15\%$ of the stars in the disc of our sample galaxies reside in retrograde orbits.

A similar analysis has been done by Kuijken et al. (1996) who found an upper limit of $5\%$ on counter-rotating stars. We attribute this difference to the fact that they created the prograde and retrograde models by convolving the spectrum of a kinematic template with the appropriate LOSVD while we adopted a real (and therefore more noisy) spectrum. It has to be noted that this is a limit on the relative surface brightness of the prograde and retrograde component. If the retrograde component is more radially concentrated than the prograde one (e.g. NGC 3593; Bertola et al. 1996), it could be detected even if its luminosity is less than $15\%$ of the galaxy luminosity.

   
4.2 Fraction of disc galaxies hosting a counter-rotating gas component

We found that ionized gas is counter-rotating with respect to stars in 2 out 50 galaxies. They are the Sa NGC 3593 (Bertola et al. 1996) and S0/Sa NGC 7377 (Corsini et al. 2003), which corresponds to a frequency of $4\%$. Applying Poisson distribution statistics, this means that less than $12\%$ (at the $95\%$ confidence level) of the sample galaxies have a counter-rotating gaseous component. Only a few other spirals are known to host a counter-rotating gaseous disc (NGC 3626, Ciri et al. 1996; Haynes et al. 2000; NGC 4138, Jore et al. 1996; Haynes et al. 2000; NGC 7217, Merrifield & Kuijken 1994) or a kinematically decoupled gas component (NGC 5854, Haynes et al. 2000; and the spirals hosting an inner polar disc listed by Corsini et al. 2003).

For comparison, a similar analysis can be done for the lenticular galaxies. Combining the data of Bertola et al. (1992, 1995), Kuijken et al. (1996), and Kannappan & Fabricant (2001) with those for the S0 NGC 980 of Vega Beltrán et al. (2001), we obtained a sample of 53 S0 galaxies for which the kinematics of the ionized gas and stellar components have been measured along (at least) the major axis. A counter-rotating or kinematically decoupled gaseous component has been found found in seventeen of these galaxies. We also took into account the galaxies whose ionized gas angular momentum is misaligned with respect to that of the stellar component since we aimed at deriving the fraction of S0 galaxies hosting a gaseous component of external origin. This fraction corresponds to  $32\%^{+19}_{-11}$ (at the $95\%$ confidence level) from Poisson distribution statistics and is consistent with previous results by Bertola et al. (1992), Kuijken et al. (1996) and Kannappan & Fabricant (2001).

   
4.3 Fraction of disc galaxies hosting a counter-rotating stellar component

In our restricted sample of 50 spiral galaxies we found the presence of a counter-rotating stellar disc in the Sa NGC 3593 (Bertola et al. 1996). Applying Poisson distribution statistics this means that less that $8\%$ (at the $95\%$ confidence level) of the sample galaxies have a counter-rotating stellar component. Only two other spirals are known to host two counter-rotating stellar discs, one of these is corotating with the gaseous disc as observed in NGC 3593. They are the Sa NGC 4138 (Jore et al. 1996; Haynes et al. 2000) and the Sab NGC 7217 (Merrifield & Kuijken 1994). A kinematically decoupled stellar component orthogonally rotating with respect to the galaxy disc has been observed in the bulge of the early-type spirals NGC 4698 (Corsini et al. 1999; Bertola et al. 1999) and NGC 4672 (Sarzi et al. 2000).

Kuijken et al. (1996) estimated that less than $10\%$ (at the $95\%$ confidence level) of their S0 galaxies host a significant fraction of counter-rotating stars. This is actually the case for NGC 4550 (Rubin et al. 1992; Rix et al. 1992) where half of the disc stars are moving in retrograde orbits.

   
5 Summary and conclusions

We have measured the ionized gas and stellar kinematics along the major axes of seventeen intermediate- to late-type spiral galaxies. The rotation curves and velocity dispersion profiles of ionized gas and stars typically extend out to $\approx$ 0.9 R₂₅ and $\approx$ 0.5 R₂₅, respectively.

In most cases the different kinematic behaviour of ionized gas and stars can be easily explained if the gas is confined in the disc and supported by rotation while the stars belong mostly to the bulge and are supported by dynamical pressure. However, kinematic peculiarities have been observed at least in NGC 3054 and NGC 7531.

In addition, we discussed the frequency of counter-rotation in disc galaxies. We considered our seventeen spiral galaxies with those studied in previous papers (Bertola et al. 1996; Corsini et al. 1999, 2003; Vega Beltrán et al. 2001) to build a restricted sample of 50 bright and nearby spirals, ranging from S0/a to Scd for which the ionized gas and stellar kinematics have been measured along the major axis with the same analytical technique. We found that less than $12\%$ and less than $8\%$ (at the $95\%$ confidence level) of these galaxies host a counter-rotating gaseous and stellar disc, respectively. For comparison, we found that $\sim$$30\%$ of S0s host a counter-rotating gaseous disc, and Kuijken et al. (1996) estimated that less than $10\%$ (at $95\%$ confidence level) host a significant fraction of counter-rotating stars.

To interpret the observed frequencies of the gaseous and stellar counter-rotating components of disc galaxies, we suggest a scenario in which S0 and spiral galaxies are subject to external gas acquisition with equal probability.

The retrograde acquisition of small amounts of external gas gives rise to counter-rotating gaseous discs only in S0 galaxies, since in spiral galaxies the acquired gas is swept away by the pre-existing gas. The formation of counter-rotating gaseous discs is favoured in S0 galaxies since they gas-poor systems, while spiral discs host large amounts of gas (Roberts & Haynes 1994; Bettoni et al. 2003), which is corotating with the stellar component. When they acquire external gas in retrograde orbits, the gas clouds of the new retrograde and pre-existing prograde components collide, lose their centrifugal support, and accrete toward the galaxy centre. A counter-rotating gaseous disc will be observed only if the mass of the newly supplied gas exceeds that of the pre-existing one (Lovelace & Chou 1996; Thakar & Ryden 1998). A counter-rotating stellar disc is the end-result of star formation in the counter-rotating gas disc. For this reason we observe a larger fraction of counter-rotating gaseous disks in S0s than in spirals. This also explains why the mass of counter-rotating gas in most S0 galaxies is small compared to that of the stellar counter-rotating components (Kuijken et al. 1996). The fraction of S0s with a kinematically decoupled gas disc is consistent with the $50\%$ that we expect if all the gas in S0s is of external origin (Bertola et al. 1992).

Counter-rotating gaseous and stellar discs in spirals are both the result of retrograde acquisition of large amounts of gas, and they are observed with the same frequency. In this framework stellar counter-rotation is the end result of star formation in a counter-rotating gaseous disc.

Acknowledgements

This research has made use of the Lyon-Meudon Extragalactic Database (LEDA) and of the NASA/IPAC Extragalactic Database (NED). We thank Sheila Kannappan for providing us her kinematic data and Giuseppe Galletta for useful discussions.

References

• Baes, M., Buyle, P., Hau, G. K. T., & Dejonghe, H. 2003, MNRAS, 341, L44 [NASA ADS] (In the text)
• Baggett, W. E., Baggett, S. M., & Anderson, K. S. J. 1998, AJ, 116, 1626 [NASA ADS] (In the text)
• Bender, R. 1990, A&A, 229, 441 [NASA ADS] (In the text)
• Bender, R., Saglia, R. P., & Gerhard, O. E. 1994, MNRAS, 269, 785 [NASA ADS] (In the text)
• Bertola, F., & Corsini, E. M. 1999, in Galaxy interactions at low and high redshift, ed. J. E. Barnes, & D. B. Sanders (Dordrecth: Kluwer), IAU Symp., 186, 149 (In the text)
• Bertola, F., Buson, L. M., & Zeilinger, W. W. 1992, ApJ, 401, L79 [NASA ADS] (In the text)
• Bertola, F., Cinzano, P., Corsini, E. M., Rix, H., & Zeilinger, W. W. 1995, ApJ, 448, L13 [NASA ADS] (In the text)
• Bertola, F., Cinzano, P., Corsini, E. M., et al. 1996, ApJ, 458, L67 [NASA ADS] (In the text)
• Bertola, F., Corsini, E. M., Vega Beltrán, J. C., et al. 1999, ApJ, 519, L127 [NASA ADS] (In the text)
• Bettoni, D., Galletta, G., & García-Burillo, S. 2003, A&A, 405, 5 [EDP Sciences] [NASA ADS] (In the text)
• Binney, J., & Tremaine, S. 1987, Galactic dynamics (Princeton: Princeton University Press) (In the text)
• Bottema, R. 1992, A&A, 257, 69 [NASA ADS] (B92) (In the text)
• Bullock, J. S., Kolatt, T. S., Sigad, Y., et al. 2001, MNRAS, 321, 559 [NASA ADS] (In the text)
• Buta, R. 1987, ApJS, 64, 1 [NASA ADS] (B87) (In the text)
• Cinzano, P., Rix, H.-W., Sarzi, M., et al. 1999, MNRAS, 307, 433 [NASA ADS] (In the text)
• Ciri, R., Bettoni, D., & Galletta, G. 1995, Nature, 375, 661 [NASA ADS] [CrossRef]
• Corsini, E. M., Pizzella, A., Sarzi, M., et al. 1999, A&A, 342, 671 [NASA ADS] (In the text)
• Corsini, E. M., Pizzella, A., Coccato, L., & Bertola, F. 2003, A&A, 408, 873 [EDP Sciences] [NASA ADS] (In the text)
• Courteau, S. 1997, AJ, 114, 2402 [NASA ADS] (C97) (In the text)
• de Vaucouleurs, G., de Vaucouleurs, A., Corwin, H. G. Jr., et al. 1991, Third reference catalogue of bright galaxies (New York: Springer-Verlag) (RC3) (In the text)
• Ferrarese, L. 2002, ApJ, 578, 90 [NASA ADS] (In the text)
• Ferrarese, L., & Merritt, D. 2000, ApJ, 539, L9 [NASA ADS] (In the text)
• Fisher, D. 1997, AJ, 113, 950 [NASA ADS] (In the text)
• Funes, J. G., Corsini, E. M., Cappellari, M., et al. 2002, A&A, 388, 50 [EDP Sciences] [NASA ADS] (In the text)
• Gerhard, O., Jeske, G., Saglia, R. P., & Bender, R. 1998, MNRAS, 295, 197 [NASA ADS] (In the text)
• Gebhardt, K., Bender, R., Bower, G., et al. 2000, ApJ, 539, L13 [NASA ADS] (In the text)
• Guthrie, B. N. G. 1992, A&AS, 93, 255 [NASA ADS]
• Haynes, M. P., Jore, K. P., Barrett, E. A., Broeils, A. H., & Murray, B. M. 2000, AJ, 120, 703 [NASA ADS] (In the text)
• Jore, K. P., Broeils, A. H., & Haynes, M. P. 1996, AJ, 112, 438 [NASA ADS] (In the text)
• Jorgensen, I., Franx, M., & Kjaergaard, P. 1995, MNRAS, 276, 1341 [NASA ADS] (In the text)
• Kannappan, S. J., & Fabricant, D. G. 2001, AJ, 121, 140 [NASA ADS] (In the text)
• Kuijken, K., Fisher, D., & Merrifield, M. R. 1996, MNRAS, 283, 543 [NASA ADS] (In the text)
• Lovelace, R. V. E., & Chou, T. 1996, ApJ, 468, L25 [NASA ADS] (In the text)
• Mathewson, D. S., Ford, V. L., & Buchhorn, M. 1992, ApJS, 81, 413 [NASA ADS] (MFB92) (In the text)
• Marzke, R. O., da Costa, L. N., Pellegrini, P. S., Willmer, C. N. A., & Geller, M. J. 1998, ApJ, 503, 617 [NASA ADS] (In the text)
• Merrifield, M. R., & Kuijken, K. 1994, ApJ, 432, 575 [NASA ADS] (In the text)
• Merrifield, M. R., Gerssen, J., & Kuijken, K. 2001, in Galaxy disks and disk galaxies, ed. J. G. Funes, & E. M. Corsini (San Francisco: ASP), ASP Conf. Ser., 230, 221 (In the text)
• Meyssonnier, N. 1984, A&AS, 58, 351 [NASA ADS] (M84) (In the text)
• Merritt, D., & Ferrarese, L. 2001, The central kiloparsec of starbursts and AGN: The La Palma connection, ed. J. H. Knapen, J. E. Beckman, I. Shlosman, & T. J. Mahoney (San Francisco: ASP), ASP Conf. Ser., 249, 335 (In the text)
• Pignatelli, E., Corsini, E. M., Vega Beltrán, J. C., et al. 2001, MNRAS, 323, 188 [NASA ADS] (In the text)
• Pizzella, A., Dalla Bontà, E., Corsini, E. M., Coccato, L., & Bertola, F. 2003, in Dark matter in galaxies, ed. S. Ryder, D. J. Pisano, M. Walker, & K. Freeman (San Francisco: ASP), IAU Symp., 220, in press [arXiv:astro-ph/0311023] (In the text)
• Rix, H., Franx, M., Fisher, D., & Illingworth, G. 1992, ApJ, 400, L5 [NASA ADS] (In the text)
• Roberts, M. S., & Haynes, M. P. 1994, ARA&A, 32, 115 [NASA ADS] (In the text)
• Rubin, V. C., Thonnard, N., & Ford, W. K. 1980, ApJ, 238, 471 [NASA ADS] (RTF80) (In the text)
• Rubin, V. C., Thonnard, N., Ford, W. K., & Burstein, D. 1982, ApJ, 261, 439 [NASA ADS] (R+82) (In the text)
• Rubin, V. C., Graham, J. A., & Kenney, J. D. P. 1992, ApJ, 394, L9 [NASA ADS] (In the text)
• Sandage, A., & Tammann, G. A. 1981, A vevised Shapley-Ames catalog of bright galaxies (Washington: Carnegie Institution) (RSA)
• Sarzi, M., Corsini, E. M., Pizzella, A., et al. 2000, A&A, 360, 439 [NASA ADS] (In the text)
• Sil'chenko, O. K., Vlasyuk, V. V., & Alvarado, F. 2001, AJ, 121, 2499 [NASA ADS] (SVA01) (In the text)
• Sofue, Y., & Rubin, V. 2001, ARA&A, 39, 137 [NASA ADS] (In the text)
• Sofue, Y., Tomita, A., Tutui, Y., Honma, M., & Takeda, Y. 1998, PASJ, 50, 427 [NASA ADS] (S+98) (In the text)
• Thakar, A. R., & Ryden, B. S. 1998, ApJ, 506, 93 [NASA ADS] (In the text)
• Vega Beltrán, J. C., Pizzella, A., Corsini, E. M., et al. 2001, A&A, 374, 394 [EDP Sciences] [NASA ADS] (V+01) (In the text)

 

  
Online Material

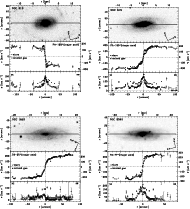	Figure 2: Ionized gas ( open circles) and stellar ( filled circles) kinematics measured along the major axes of the sample galaxies. Error bars smaller than their symbols are not plotted.
Open with DEXTER

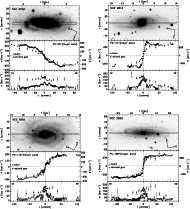	Figure 2: continued.
Open with DEXTER

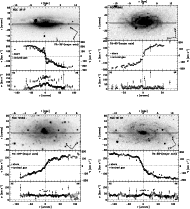	Figure 2: continued.
Open with DEXTER

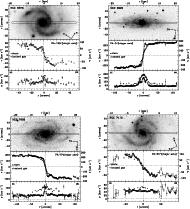	Figure 2: continued.
Open with DEXTER

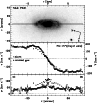	Figure 2: continued.
Open with DEXTER

	Figure 3: The ionized gas velocities derived in this study for NGC 615, NGC 1620, NGC 2708, NGC 2815 and NGC 3054 compared to those obtained by other authors: MFB92 = Mathewson et al. (1992); R+82 = Rubin et al. (1982); SVA01 = Sil'chenko et al. (2001); C97 = Courteau (1997); S+98 = Sofue et al. (1998).
Open with DEXTER

	Figure 3: continued. The ionized gas velocities derived in this study for NGC 3200, NGC 4682, NGC 6118, NGC 7083 and NGC 7531 compared to those obtained by other authors: V+01 = Vega Beltrán et al. (2001).; MFB92 = Mathewson et al. (1992); R+82 = Rubin et al. (1982); RTF80 = Rubin et al. (1980); B87 = Buta (1987); M84 = Meyssonnier (1984).
Open with DEXTER

	Figure 4: The stellar kinematics derived in this study for NGC 615, NGC 2815 and NGC 3200 compared to those obtained by other authors: B92 = Bottema (1992); SVA01 = Sil'chenko et al. (2001); V+01 = Vega Beltrán et al. (2001).
Open with DEXTER