A&A 424, 23-42 (2004)
DOI: 10.1051/0004-6361:20035626
A. Fontana 1 - L. Pozzetti 2 - I. Donnarumma 1 - A. Renzini 3 - A. Cimatti 4 - G. Zamorani 2 - N. Menci 1 - E. Daddi 4 - E. Giallongo 1 - M. Mignoli 2 - C. Perna 1 - S. Salimbeni 1 - P. Saracco 5 - T. Broadhurst 6 - S. Cristiani 7 - S. D'Odorico 3 - R. Gilmozzi 3
1 - INAF - Osservatorio Astronomico di Roma, via Frascati 33, Monteporzio, 00040, Italy
2 - INAF - Osservatorio Astronomico di Bologna, via Ranzani 1, 40127, Bologna, Italy
3 - European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748, Garching, Germany
4 - INAF - Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
5 - INAF - Osservatorio Astronomico di Brera, via E. Bianchi 46, Merate, Italy
6 - Racah Institute for Physics, The Hebrew University, Jerusalem, 91904, Israel
7 - INAF - Osservatorio Astronomico di Trieste, via G.B. Tiepolo 11,
34131, Trieste, Italy
Received 4 November 2003 / Accepted 20 April 2004
Abstract
We present a detailed analysis of the stellar mass
content of galaxies up to z=2.5 as obtained from the K20 spectrophotometric galaxy sample. We have applied and compared two
different methods to estimate the stellar mass M* from broad-band
photometry: a Maximal Age approach, where we maximize the age of the
stellar population to obtain the maximal mass
compatible with the observed R-K color, and a Best Fit model, where
the best-fitting spectrum to the complete
![]() multicolor
distribution is used.
We find that the M*/L ratio decreases with redshift: in particular,
the average M*/L ratio of early type galaxies decreases with z, with
a scatter that is indicative of a range of star-formation time-scales
and redshift of formation. More important, the typical M*/L ratio of
massive early type galaxies is larger than that of less massive ones,
suggesting that their stellar population formed at higher z.
We show that the final K20 galaxy sample spans a range of stellar
masses from
multicolor
distribution is used.
We find that the M*/L ratio decreases with redshift: in particular,
the average M*/L ratio of early type galaxies decreases with z, with
a scatter that is indicative of a range of star-formation time-scales
and redshift of formation. More important, the typical M*/L ratio of
massive early type galaxies is larger than that of less massive ones,
suggesting that their stellar population formed at higher z.
We show that the final K20 galaxy sample spans a range of stellar
masses from
![]() to
to
![]() :
massive
galaxies (
:
massive
galaxies (
![]() )
are common at 0.5<z<1, and are
detected also up to
)
are common at 0.5<z<1, and are
detected also up to ![]() .
We compute the Galaxy Stellar Mass
Function at various z, of which we observe only a mild evolution
(i.e. by 20-30%) up to
.
We compute the Galaxy Stellar Mass
Function at various z, of which we observe only a mild evolution
(i.e. by 20-30%) up to ![]() .
At z>1, the evolution in the
normalization of the GSMF appears to be much faster: at
.
At z>1, the evolution in the
normalization of the GSMF appears to be much faster: at ![]() ,
about 35% of the present day stellar mass in objects with
,
about 35% of the present day stellar mass in objects with
![]() appear to have assembled. We also detect a change in
the physical nature of the most massive galaxies: at
appear to have assembled. We also detect a change in
the physical nature of the most massive galaxies: at ![]() ,
all galaxies with
,
all galaxies with
![]() are early type, while at higher z a population of massive star-forming galaxies progressively
appears.
We finally analyze our results in the framework of
are early type, while at higher z a population of massive star-forming galaxies progressively
appears.
We finally analyze our results in the framework of ![]() -CDM
hierarchical models. First, we show that the large number of massive
galaxies detected at high z does not violate any fundamental
-CDM
hierarchical models. First, we show that the large number of massive
galaxies detected at high z does not violate any fundamental
![]() -CDM constraint based on the number of massive DM
halos. Then, we compare our results with the predictions of several
renditions of both semianalytic as well as hydro-dynamical models.
The predictions from these models range from severe underestimates to
slight overestimates of the observed mass density at
-CDM constraint based on the number of massive DM
halos. Then, we compare our results with the predictions of several
renditions of both semianalytic as well as hydro-dynamical models.
The predictions from these models range from severe underestimates to
slight overestimates of the observed mass density at ![]() 2. We
discuss how the differences among these models are due to the
different implementation of the main physical processes.
2. We
discuss how the differences among these models are due to the
different implementation of the main physical processes.
Key words: galaxies: evolution - galaxies: formation - galaxies: luminosity function, mass function
The recent consolidation of the "concordance'' cosmological scenario (Bennett et al. 2003), where several independent observational evidences have provided precise measures for the basic cosmological parameters, is opening an unique opportunity to understand the processes that led to galaxy formation and evolution. Without much residual ambiguity about the redshift-cosmic time relation and the dark energy/dark matter content of the universe, observations of galaxies at low and high redshift can better shed light on such processes as a function of both cosmological time and local over-density.
In the "concordance'' cosmological scenario, the history of galaxies
is driven by the build-up of the stellar population contained in their
dark matter halos. Hierarchical theories of galaxy formation are
characterized by a gradual enrichment of the star content of galaxies
as a result of gas cooling within dark matter halos, and of
progressive growth of the galaxy mass through merging events which may
also promote massive star-bursts. However, different renditions of the
hierarchical paradigm can differ dramatically in their predictions. In
some cases an extremely rapid decrease of the number density of massive
galaxies with increasing redshift is predicted (e.g., Baugh et al. 2003), while in other cases such decrease does not start until
beyond ![]() (e.g., Nagamine et al. 2001a,b; Hernquist & Springel
2003; Somerville et al. 2004a; Nagamine et al. 2004). Clearly, the
direct mapping of galaxy evolution through cosmic time can effectively
restrict the choice among such models.
(e.g., Nagamine et al. 2001a,b; Hernquist & Springel
2003; Somerville et al. 2004a; Nagamine et al. 2004). Clearly, the
direct mapping of galaxy evolution through cosmic time can effectively
restrict the choice among such models.
Within this framework, K-band surveys have long been recognized as ideal tools to study the process of mass assembly at high redshift (Broadhurst et al. 1992; Gavazzi et al. 1996; Madau et al. 1998). With respect to optical bands, indeed, the K band samples up to high z the rest frame optical and near-IR spectral range, and therefore it is less sensitive to the instantaneous star formation activity and to dust extinction. Albeit the relation between near-IR luminosity and stellar mass is not univocal, deep imaging and spectroscopic surveys have been carried on to test the cosmological scenarios on mass-selected galaxy samples (Songalia et al. 1994; Kauffmann & Charlot 1998; Fontana et al. 1999; Cohen et al. 1999; Drory et al. 2001; Firth et al. 2002).
The K20 survey (Cimatti et al. 2002a) has been designed to extend and
complement these studies, with the explicit aim of investigating the
high redshift evolution of massive galaxies. It is based on a sample
of about 500 galaxies to
![]() ,
for which a nearly complete
spectroscopic identification and a deep
,
for which a nearly complete
spectroscopic identification and a deep
![]() multicolor coverage
is available, which together make it an ideal dataset to study the
evolution of a mass-selected sample of galaxies up to
multicolor coverage
is available, which together make it an ideal dataset to study the
evolution of a mass-selected sample of galaxies up to ![]() .
In
the K20 dataset, the evolution of bright, massive galaxies has been
investigated up to
.
In
the K20 dataset, the evolution of bright, massive galaxies has been
investigated up to ![]() through the study of the K-limited
redshift distribution (Cimatti et al. 2002b) and the near-IR luminosity
functions (Pozzetti et al. 2003). The results of the K20 survey show that
galaxies selected in the K band are characterized by a modest luminosity
evolution up to
through the study of the K-limited
redshift distribution (Cimatti et al. 2002b) and the near-IR luminosity
functions (Pozzetti et al. 2003). The results of the K20 survey show that
galaxies selected in the K band are characterized by a modest luminosity
evolution up to ![]() ,
that seems well described by simple pure
luminosity evolution (PLE) models.
,
that seems well described by simple pure
luminosity evolution (PLE) models.
In this paper, we will use the K20 dataset to directly study the
evolution of the stellar mass content in galaxies up to ![]() .
Recently, various techniques have been developed to directly estimate
the stellar mass content of galaxies up to
.
Recently, various techniques have been developed to directly estimate
the stellar mass content of galaxies up to ![]() .
Some rely on
detailed spectral analysis (Kauffmann et al. 2003, for low zgalaxies), others on multi-wavelength imaging observations to remove
or reduce the uncertainties involved in the conversion between
near-IR luminosity and stellar mass (Giallongo et al. 1998;
Brinchmann & Ellis 2000; Cole et al. 2001; Papovich et al. 2001;
Shapley et al. 2001; Drory et al. 2001; Dickinson et al. 2003 - D03
hereafter -; Fontana et al. 2003 - F03 hereafter -; Rudnick et al. 2003;
Saracco et al. 2004).
.
Some rely on
detailed spectral analysis (Kauffmann et al. 2003, for low zgalaxies), others on multi-wavelength imaging observations to remove
or reduce the uncertainties involved in the conversion between
near-IR luminosity and stellar mass (Giallongo et al. 1998;
Brinchmann & Ellis 2000; Cole et al. 2001; Papovich et al. 2001;
Shapley et al. 2001; Drory et al. 2001; Dickinson et al. 2003 - D03
hereafter -; Fontana et al. 2003 - F03 hereafter -; Rudnick et al. 2003;
Saracco et al. 2004).
The applications of such techniques have been primarily driven by the
available datasets. On a relatively shallow dataset, Giallongo et al.
(1998) emphasized that at
![]() blue "faint'' galaxies are an
order of magnitude less massive than redder galaxies of comparable Bmagnitude, and attempted a first estimate of the evolution of the
cosmological mass density up to high z. Brinchmann & Ellis (2000)
used a multi-wavelength coverage of the CFRS galaxy sample (Lilly et al. 1995) to trace the stellar mass density in morphologically
selected galaxy samples up to z=1, while Drory et al. 2001 used a larger
set of galaxies with photometric redshifts to set an upper limit on
their mass density at
blue "faint'' galaxies are an
order of magnitude less massive than redder galaxies of comparable Bmagnitude, and attempted a first estimate of the evolution of the
cosmological mass density up to high z. Brinchmann & Ellis (2000)
used a multi-wavelength coverage of the CFRS galaxy sample (Lilly et al. 1995) to trace the stellar mass density in morphologically
selected galaxy samples up to z=1, while Drory et al. 2001 used a larger
set of galaxies with photometric redshifts to set an upper limit on
their mass density at ![]() .
Papovich et al. (2001) and Shapley
et al. (2001) pushed this technique to its limit to constrain the mass
of Lyman-break galaxies, showing that objects with stellar mass in
excess of
.
Papovich et al. (2001) and Shapley
et al. (2001) pushed this technique to its limit to constrain the mass
of Lyman-break galaxies, showing that objects with stellar mass in
excess of
![]() are commonly detected in the
are commonly detected in the ![]() universe. Recently, D03, F03 and
Rudnick et al. (2003) used extremely deep optical and near-IR data in
the HDF-N and HDF-S to derive the evolution of the
stellar mass density from z=0 to z=3. These studies have
derived a fast evolution of the stellar mass density in the redshift
range z=1-3, but have also shown that large ambiguities still
persist due to cosmic variance and uncertainties due to incomplete
spectroscopic redshift coverage.
universe. Recently, D03, F03 and
Rudnick et al. (2003) used extremely deep optical and near-IR data in
the HDF-N and HDF-S to derive the evolution of the
stellar mass density from z=0 to z=3. These studies have
derived a fast evolution of the stellar mass density in the redshift
range z=1-3, but have also shown that large ambiguities still
persist due to cosmic variance and uncertainties due to incomplete
spectroscopic redshift coverage.
The plan of the paper is as follows: in Sect. 2 we describe the data sample used in this paper. In Sect. 3 we discuss and compare the two methods we have applied to estimate the stellar masses of the K20 galaxies. Further details and validation tests of these procedures are deferred to Appendix A for the interested reader. In Sect. 4, we present the derived evolution of stellar masses and rest-frame M*/L ratios. In Sect. 5, we present the observed Galaxy Stellar Mass Functions and global Mass Density, for the total sample and for different spectral types, while a more technical discussion of the corrections required to take into account the effects of incompleteness is presented in Appendix B. In Sect. 6 we compare our results at different redshifts with the prediction of different renditions of the CDM models for galaxy formation. Finally, in Sect. 7 we summarize the results and discuss their validity and implications in the general scenario of galaxy formation.
A Salpeter IMF and the "concordance'' cosmology (H0=70 km s-1 Mpc-1,
![]() and
and
![]() )
are adopted
throughout the paper. In the following, we shall often refer
to the M*/L ratio, that is always computed in solar units adopting
)
are adopted
throughout the paper. In the following, we shall often refer
to the M*/L ratio, that is always computed in solar units adopting
![]() and
and
![]()
The K20 sample (Cimatti et al. 2002a) has been selected at
![]() (Vega system) over two independent fields, namely a sub-area of the
Chandra Deep Field South and the field around the z=3.7 QSO
Q0055-269, for a total of 546 objects over an area of 52 arcmin2.
Spectra have been obtained with the ESO-VLT, mostly using the optical
spectro-imagers FORS1 and FORS2, with the addition of a few redshifts
obtained in the IR with ISAAC. Besides the spectra already presented
in Cimatti et al. (2002a), we use here additional spectra recently
obtained with the same instruments, partly described in Daddi et al. (2004)
and Cimatti et al. (2003), and partly obtained within the ESO public
follow-up of the GOODS survey (Vanzella et al. 2004, in preparation).
(Vega system) over two independent fields, namely a sub-area of the
Chandra Deep Field South and the field around the z=3.7 QSO
Q0055-269, for a total of 546 objects over an area of 52 arcmin2.
Spectra have been obtained with the ESO-VLT, mostly using the optical
spectro-imagers FORS1 and FORS2, with the addition of a few redshifts
obtained in the IR with ISAAC. Besides the spectra already presented
in Cimatti et al. (2002a), we use here additional spectra recently
obtained with the same instruments, partly described in Daddi et al. (2004)
and Cimatti et al. (2003), and partly obtained within the ESO public
follow-up of the GOODS survey (Vanzella et al. 2004, in preparation).
In addition to the spectroscopic observations, we have used deep
multicolor coverage (
![]() )
of the whole galaxy sample obtained
from targeted and public observations with VLT and NTT made available
through the ESO Archive. From such detailed color information, we have
derived well calibrated photometric redshifts for the whole galaxy
sample, including those objects for which no spectroscopic redshift
could be obtained. The resulting photometric redshift dispersion is
)
of the whole galaxy sample obtained
from targeted and public observations with VLT and NTT made available
through the ESO Archive. From such detailed color information, we have
derived well calibrated photometric redshifts for the whole galaxy
sample, including those objects for which no spectroscopic redshift
could be obtained. The resulting photometric redshift dispersion is
![]() (Cimatti et al. 2002a).
(Cimatti et al. 2002a).
The K20 redshift survey is at present the most complete K-selected deep spectroscopic survey so far obtained. The spectroscopic coverage on the total sample is 92%, and excluding spectroscopically confirmed stars and AGNs, the total galaxy sample with either spectroscopic or accurate photometric redshift is made of 487 objects, 446 of which (i.e. 92%) have a spectroscopic redshift. Multicolor imaging in the UBVRIzJK bands is also available for all galaxies, with the exception of three galaxies in the CDFS field where only R-K is available.
In the following we shall also make use of a simple spectroscopic
classification: at ![]() ,
we have named "early type'' galaxies
as objects identified by absorption lines and with no detected
emission lines; "early+emission type'' galaxies, similar to early
type but with a weak [OII]
,
we have named "early type'' galaxies
as objects identified by absorption lines and with no detected
emission lines; "early+emission type'' galaxies, similar to early
type but with a weak [OII]![]() 3727 emission line; "late type'' galaxies,
i.e. star-forming objects with a strong [OII]
3727 emission line; "late type'' galaxies,
i.e. star-forming objects with a strong [OII]![]() 3727 emission line.
At z>1.6, where the [OII]
3727 emission line.
At z>1.6, where the [OII]![]() 3727 doublet is not observable, we
have classified three objects in the CDFS as early type, since
their spectra are dominated by features of evolved stellar
populations, and the others as late type since they are UV-bright
galaxies with far-UV absorption lines. Overall, the K20 sample
includes 107 early type, 44 early+emission type and 297 late type
galaxies.
3727 doublet is not observable, we
have classified three objects in the CDFS as early type, since
their spectra are dominated by features of evolved stellar
populations, and the others as late type since they are UV-bright
galaxies with far-UV absorption lines. Overall, the K20 sample
includes 107 early type, 44 early+emission type and 297 late type
galaxies.
In this study we have considered the whole K20 galaxy sample,
i.e. including also the galaxies located in the large structures at
z=0.65-0.73 in both the Q0055 and CDFS fields. Based on the number
and spatial distributions of members, on the X-ray luminosity and B
luminosity of the bright central elliptical, we indeed estimate that
at most one of these structures can be classified as a richness
0 cluster in the Abell classification scheme, while the others are
likely to be associated to either poorer clusters (e.g. groups) or
loose, extended, sheet-like structures (see, Gilli et al. 2003, for a
discussion of the K20 structures in the CDFS field). Based on recent
cluster catalogs we estimate that the number of clusters with Abell
richness ![]() 0 over the K20 area is of the order of 0.7 (see, for
example, Table 6 in Postman et al. 2002), similar to what predicted by
numerical simulations (Evrard et al. 2002). On the basis of this
comparison we conclude that the number of redshift peaks in our data
is in fair agreement with both existing data from large areas and
theoretical simulations, and we shall therefore use the whole K20
sample when computing mass functions and other integrated quantities.
0 over the K20 area is of the order of 0.7 (see, for
example, Table 6 in Postman et al. 2002), similar to what predicted by
numerical simulations (Evrard et al. 2002). On the basis of this
comparison we conclude that the number of redshift peaks in our data
is in fair agreement with both existing data from large areas and
theoretical simulations, and we shall therefore use the whole K20
sample when computing mass functions and other integrated quantities.
We finally note that all the magnitudes of the K20 sample are
estimated in "optimal'' Kron apertures, as obtained from the
SExtractor package (Bertin & Arnouts 1996). "Kron'' magnitudes are
prone to systematic underestimates of the total flux, by an amount
that depends on the morphology, sampling, redshift and S/N of the
objects. With detailed simulations we have shown that at ![]() the
underestimate is negligible for compact objects, and is about 10% for
spirals and 20% or even more for L>L* ellipticals
(Cimatti et al. 2002a).
We have decided not to apply any correction in the final
stellar mass distributions,
since the morphological mix is expected to change significantly across
the mass and redshift range that we sample, but we shall discuss
the effects of an average correction of
the
underestimate is negligible for compact objects, and is about 10% for
spirals and 20% or even more for L>L* ellipticals
(Cimatti et al. 2002a).
We have decided not to apply any correction in the final
stellar mass distributions,
since the morphological mix is expected to change significantly across
the mass and redshift range that we sample, but we shall discuss
the effects of an average correction of ![]()
![]() when comparing
our data with the theoretical predictions, as it has already been done
in our previous papers (e.g., Cimatti et al. 2002b; Pozzetti et al. 2003).
when comparing
our data with the theoretical predictions, as it has already been done
in our previous papers (e.g., Cimatti et al. 2002b; Pozzetti et al. 2003).
It is widely acknowledged that a close relationship exists between the
near-IR light and the stellar mass in local galaxies (e.g. Gavazzi et al. 1996; Madau et al. 1998). However, an accurate
estimate of the galaxy stellar mass at high z, when galaxies are
observed at various evolutionary stages, is more uncertain because of
the variation of the M*/LK ratio as a function of the age
and other parameters of the stellar population.
The typical M*/LK ratios for exponentially declining star
formation histories range from small values (
![]() )
at
young stellar ages
)
at
young stellar ages ![]() 0.1 Gyr to values about unity after 10 Gyr. This variation in the M*/LK ratio is larger than the scatter
induced (at a given age) by different metallicities or star formation
time-scales.
In addition, in the case of real galaxies the possibly complex star-formation
histories and in particular the presence of minor bursts of star
formation can affect the derived M*/LK and therefore their mass estimate.
0.1 Gyr to values about unity after 10 Gyr. This variation in the M*/LK ratio is larger than the scatter
induced (at a given age) by different metallicities or star formation
time-scales.
In addition, in the case of real galaxies the possibly complex star-formation
histories and in particular the presence of minor bursts of star
formation can affect the derived M*/LK and therefore their mass estimate.
Additional information on the spectral energy distribution of individual galaxies, as the multiband imaging available in our sample, can be used to overcome or at least minimize this problem. The use of the rest-frame optical and UV bands is a way to correct (at least conceptually) for the contribution of high-luminosity and low-mass young stellar population to the observed IR light.
Even with these additional data, however, the actual star-formation history of individual galaxies cannot be unambiguously recovered, and we are forced to rely on simplifying assumptions on the plausible star-formation histories. We will apply and compare here two different methods to estimate the stellar masses from the observed magnitudes, that are based on different assumptions on the previous star-formation history. For both we will adopt the Bruzual & Charlot (2003) code for spectral synthesis models, in its more recent rendition, using its low resolution version with the "Padova 1994'' tracks. We have investigated about possible systematic differences between this recent version and the previous one (GISSEL 2000) used in previous similar works we will compare with (D03; F03). We have found that the spectra obtained with the new version are remarkably similar to the previous ones, such that the integrated magnitudes are similar to a few hundreds of magnitude. As a result, the estimated stellar masses result comfortably similar to the BC00 ones, with an average offset of only -0.04 dex and a scatter of 0.12 dex. In the following, we shall therefore compare our results with those of previous surveys without any further re-normalization.
In our analysis we will adopt only the classical Salpeter IMF
(Salpeter 1955). The same IMF has been used in several previous works
that we shall compare with (e.g., Brinchmann & Ellis 2000;
Cole et al. 2001; D03; F03) as well as in
some of the theoretical predictions that will be tested with our
data. Unfortunately, scaling to different IMFs may not be simple, since
these corrections depend on the age of the stellar population. For
instance, for the simple case of simple stellar populations, the M*/L ratio of a Salpeter IMF at ages <1 Gyr is larger by a factor 1.3-1.5
with respect to the case of the frequently used Kennicutt IMF
(Kennicutt 1983), and by a factor up to ![]() 2.2 at larger ages
(this factors are largely independent of the wavelength).
With respect to the Kroupa IMF (Kroupa 2001), the M*/L ratio from a
Salpeter IMF is systematically larger by a factor
2.2 at larger ages
(this factors are largely independent of the wavelength).
With respect to the Kroupa IMF (Kroupa 2001), the M*/L ratio from a
Salpeter IMF is systematically larger by a factor ![]() 1.6, roughly
independent of the age of the population.
1.6, roughly
independent of the age of the population.
A first approach that we follow is to assume a simple scenario for the star-formation history of the different types of galaxies. This can be done adopting a limited set of evolutionary models, chosen in order to reproduce the colors of local galaxies, following the spirit of PLE models (e.g., Pozzetti et al. 2003) with a fixed redshift of formation.
In our case, we have adopted the parameterization used by Cole et al. (2001), a choice which is particularly useful for comparison with
their local GSMF. It consists of a set of models with exponentially
declining star formation rate, with time-scale
![]() Gyr,
metallicities ranging from 0.2
Gyr,
metallicities ranging from 0.2 ![]() to 2.5
to 2.5 ![]() ,
a constant
dust absorption taken from the Ferrara et al. (1999) model, all
computed assuming that the star-formation history of each galaxy
started at
,
a constant
dust absorption taken from the Ferrara et al. (1999) model, all
computed assuming that the star-formation history of each galaxy
started at
![]() .
The time-scale of star formation is then
determined for each galaxy by demanding to the model to reproduce the
observed
.
The time-scale of star formation is then
determined for each galaxy by demanding to the model to reproduce the
observed
![]() color, which is more sensitive to the spectral type
than the
color, which is more sensitive to the spectral type
than the
![]() color used by Cole et al. (2001).The mass is then
derived by normalizing the model to the observed K-band luminosity.
color used by Cole et al. (2001).The mass is then
derived by normalizing the model to the observed K-band luminosity.
We note that this approach maximizes the age of the stellar population (hence its M*/L ratio) as much as possible within the current CMB constraints. To emphasize this aspect, in the following we refer to these models as "Maximal Age'' (MA) models. We note that this choice is less extreme than the "Maximal Mass'' model of Drory et al. (2001), that fits the observed K band only assuming redshift-dependent maximal M*/LK, in practice ignoring the contribution of star-forming populations to the observed M*/LK ratio.
We have verified that the resulting values of the stellar mass are not
very sensitive to the particular set of parameters adopted in these
models. In particular, we have also explored the dust-free
"PLE-like'' star-formation histories of Pozzetti et al. (2003) with
![]() and solar metallicity, finding that the resulting
stellar masses in our sample are quite similar to those of the Cole et al. (2001) parameterization that we have adopted.
and solar metallicity, finding that the resulting
stellar masses in our sample are quite similar to those of the Cole et al. (2001) parameterization that we have adopted.
Adopting other colors from any of all the available bands we have found that the resulting masses do not vary by more than 5% (rms) on average.
In an effort to release as much as possible the underlying assumptions on star formation histories and other galaxy properties, we have also used a larger set of galaxy templates, spanning a much wider parameter space, and applied it to the full multicolor spectral energy distribution (SED) to constrain their allowed range for each object. This technique has already been widely applied in previous studies (e.g., Giallongo et al. 1998; Brinchann & Ellis 2000; Papovich et al. 2001; Shapley et al. 2001; D03; F03a) and will be only briefly summarized here. The main difference with respect to the MA method is that the galaxy ages are also allowed to vary at any z, with the only constraint that they are smaller than the Hubble time at that redshift.
The set of template stellar populations adopted in the present work
are listed in Table 1. For each galaxy, the best-fitting SED
to our multiband
![]() photometry is extracted from the grid at
the corresponding redshift with a
photometry is extracted from the grid at
the corresponding redshift with a ![]() minimization and used to
compute at once the stellar mass and all the rest frame
luminosities. In the following we refer to this as the "Best Fit'' (BF) method. A technique can be applied to estimate the confidence
levels on the estimated mass, taking into account the degeneracies
among the input parameters, as described in F03 and
in Appendix A.4. We explicitly note that while the "MA'' models are
designed to match the observed
minimization and used to
compute at once the stellar mass and all the rest frame
luminosities. In the following we refer to this as the "Best Fit'' (BF) method. A technique can be applied to estimate the confidence
levels on the estimated mass, taking into account the degeneracies
among the input parameters, as described in F03 and
in Appendix A.4. We explicitly note that while the "MA'' models are
designed to match the observed ![]() magnitude, the "BF'' mass
estimates are derived from the model that indeed "best fits'' the
global multicolor SED. In any case the average of the differences
between the observed
magnitude, the "BF'' mass
estimates are derived from the model that indeed "best fits'' the
global multicolor SED. In any case the average of the differences
between the observed ![]() magnitudes and those of the best fit model
is very small (<0.01 mag), with 10% rms fluctuations.
magnitudes and those of the best fit model
is very small (<0.01 mag), with 10% rms fluctuations.
Table 1: Parameters used for the library of template SEDs.
We are aware that, despite the wide parameter space covered by the "BF'' grid of templates, there is no guarantee that the best-fit solutions are, at least statistically, correct. First, several simplified assumptions are used in building the library grid: the most important are a monotonic, exponentially declining star-formation history and a single metallicity for each SED template. The adoption of a universal IMF and a single extinction law (and in particular our choice of the Salpeter IMF and the SMC law) may not be the most appropriate. Moreover, some models within the grid may be not physical (e.g. those implying large dust extinctions in absence of a significant star-formation rate).
In order to remove the most obvious unplausible - or at least less likely - models, we have not included in the libraries heavily extincted models ( E(B-V)>0.2) with no ongoing star formation activity.
Both MA and BF masses were also derived from a set of over 6000
galaxies using the publicly available multicolor catalogs of the SDSS
and 2MASS surveys, along with the SDSS redshifts, repeating a
procedure already adopted by Bell et al. (2003) to derive the local
stellar mass function. This allows us to compare in a
self-consistent fashion the K20 stellar mass function obtained at
high z with the BF method with the local one. To reduce the effects
of degeneracies among the models with short star-formation
time-scales, models with star-formation time-scales
![]() and
and
![]() were removed from the set of templates. Such a
choice matches also the model grid adopted by Kauffmann et al. (2003) in
their analysis of the SDSS spectra. Such a selection in the grid
models, for self-consistency, has been applied also on the estimates
of the K20 sample, but without appreciable effects, since most early
type galaxies are at z>0.5 and their best fit ages are independent
of this selection.
were removed from the set of templates. Such a
choice matches also the model grid adopted by Kauffmann et al. (2003) in
their analysis of the SDSS spectra. Such a selection in the grid
models, for self-consistency, has been applied also on the estimates
of the K20 sample, but without appreciable effects, since most early
type galaxies are at z>0.5 and their best fit ages are independent
of this selection.
We note that a small fraction of the K20 sample is made of the so-called "dusty'' ERO population (Cimatti et al. 2002c): these objects are characterized by strong emission line features and require large extinction (corresponding to E(B-V)=0.6-1.1 for a Calzetti et al. 2000 law). These objects are difficult to be modeled, since we expect them to be made of different stellar populations with a complex absorption geometry. On the one side, the adoption of a Calzetti attenuation curve is a coarse approximation, since is has been derived only on local starbursts, with a maximal extinction ( E(B-V)=0.7) lower than the one inferred in our EROs, and it has been show to be inapplicable to local Ultra Luminous IR starburst (Goldader et al. 2000), although these objects are probably more extreme than our EROs. On the other side, theoretical models allowing for a patchy, complex dust geometry (Granato et al. 2000) suggest that the outcoming attenuation curve may still be close to a single curve, similar to Calzetti one.
For simplicity, we have used for these objects the same set of
templates as in Table 1, searching for the best fit only among the
star-forming models with
![]() ,
but adopting both
the SMC and the Calzetti curve, and performed two simple tests.
First, we verified that the estimated stellar mass does not depend
dramatically on the assumed extinction law, since the SMC-based
estimates are typically 20-30% higher than the Calzetti-based
estimates. Second, we have found that the estimated star-formation
rates obtained adopting a Calzetti law are consistent with the X-ray
and radio luminosities of these objects (Daddi et al. 2004b),
suggesting that we are not missing a significant fraction of their
star-formation activity. In the following, we shall therefore adopt
the masses estimated with the Calzetti law.
,
but adopting both
the SMC and the Calzetti curve, and performed two simple tests.
First, we verified that the estimated stellar mass does not depend
dramatically on the assumed extinction law, since the SMC-based
estimates are typically 20-30% higher than the Calzetti-based
estimates. Second, we have found that the estimated star-formation
rates obtained adopting a Calzetti law are consistent with the X-ray
and radio luminosities of these objects (Daddi et al. 2004b),
suggesting that we are not missing a significant fraction of their
star-formation activity. In the following, we shall therefore adopt
the masses estimated with the Calzetti law.
The impact of different extinction curves on the mass estimates has
already been investigated by Papovich et al. (2001), D03 and F03, and
found to be small. In the HDFS, in particular, F03 found that adopting
the Calzetti extinction curve leads to mass estimates ![]() 20%
lower than those estimated by adopting the SMC law, with a typically
worse
20%
lower than those estimated by adopting the SMC law, with a typically
worse ![]() at
at ![]() .
We have repeated the same exercise on the
K20 data set, finding again that the typical
.
We have repeated the same exercise on the
K20 data set, finding again that the typical ![]() with a Calzetti
extinction curve is worse than that obtained with the SMC one, but
that the mass estimates are nevertheless similar, with an average
shift of 0.04 dex in the stellar mass (the SMC-based masses
being still larger than the Calzetti ones) with 0.2 dex of
dispersion. Likely, the difference between the two extinction curves
is lower in the K20 data set since it is richer in red, evolved
galaxies whose best fit spectra do not require a large amount
of extinction. We have also verified that the stellar mass densities
are not changed significantly by changing the extinction curves.
with a Calzetti
extinction curve is worse than that obtained with the SMC one, but
that the mass estimates are nevertheless similar, with an average
shift of 0.04 dex in the stellar mass (the SMC-based masses
being still larger than the Calzetti ones) with 0.2 dex of
dispersion. Likely, the difference between the two extinction curves
is lower in the K20 data set since it is richer in red, evolved
galaxies whose best fit spectra do not require a large amount
of extinction. We have also verified that the stellar mass densities
are not changed significantly by changing the extinction curves.
On the basis of these considerations we believe that the use of the SMC law is well justified, considering that our K-selected sample is not expected to contain a large fraction of starbursts, with the possible exception of the star-forming EROs which anyway have been also fitted with a Calzetti law.
We find that the typical error on the estimated masses is of the order
of
![]() (Appendix A.4), in agreement with the similar
results in the HDFN (D03) and HDFS (F03) at the same
redshifts. Therefore, there appears to be a core level of degeneracy
in the input models that cannot be eliminated within this approach.
Nevertheless, this uncertainty is smaller than that affecting the
stellar mass estimates at
(Appendix A.4), in agreement with the similar
results in the HDFN (D03) and HDFS (F03) at the same
redshifts. Therefore, there appears to be a core level of degeneracy
in the input models that cannot be eliminated within this approach.
Nevertheless, this uncertainty is smaller than that affecting the
stellar mass estimates at ![]() (Papovich et al. 2001;
Shapley et al. 2001), since at
(Papovich et al. 2001;
Shapley et al. 2001), since at ![]() we can rely on at least a
partial sampling of the rest-frame, near-IR side of the spectrum.
we can rely on at least a
partial sampling of the rest-frame, near-IR side of the spectrum.
It is beyond the aim of the present work to describe in detail the
results of the fitting procedures for all the parameters involved.
Nevertheless, it is worth mentioning that we have checked that their
distributions appear to be astrophysically reasonable, such that we do
not expect large systematic biases in the mass estimates. For
instance, the resulting distribution of metallicity is peaked at the
solar value, with only 10% of the objects at
![]() and
about 25% of them at
and
about 25% of them at
![]() .
The average dust extinction
on the whole sample is
.
The average dust extinction
on the whole sample is
![]() ,
and
,
and
![]() for the objects spectroscopically classified
as early type. The median (average)
for the objects spectroscopically classified
as early type. The median (average)
![]() is about 2 (2.8)
for spectroscopic early type and 1.3 (1.8) for spectroscopically late
type objects. We have also found that the "BF'' estimates reproduce the
amplitude of the 4000 Å spectral break, as measured in our
spectroscopic sample (see Appendix A.3).
is about 2 (2.8)
for spectroscopic early type and 1.3 (1.8) for spectroscopically late
type objects. We have also found that the "BF'' estimates reproduce the
amplitude of the 4000 Å spectral break, as measured in our
spectroscopic sample (see Appendix A.3).
However, from simulations fully described in Appendix A.2, we find
that the derived galaxy ages can significantly underestimate the
actual ages in cases of complex star-formation histories, although
this does not affect the mass estimate by more than 25%. In particular,
in simulations with a secondary starburst on top of an exponentially
declining star formation, the mass is on average underestimated by
![]()
![]() if the object is observed just during the starburst
itself. But 1-2 Gyr after the starburst the fits based on single
exponential laws are able to recover essentially all the stellar mass,
although the derived age may still be underestimated. This is
particularly important for the study of early type galaxies, that make
the bulk of the massive objects at
if the object is observed just during the starburst
itself. But 1-2 Gyr after the starburst the fits based on single
exponential laws are able to recover essentially all the stellar mass,
although the derived age may still be underestimated. This is
particularly important for the study of early type galaxies, that make
the bulk of the massive objects at ![]() .
.
As expected, the MA models provide mass estimates that on average are
larger by a factor ![]() 2 at low masses and
2 at low masses and ![]() 1.6 at high
masses (
1.6 at high
masses (
![]() ), although a large scatter
exists (see Appendix A.1). Such a mass difference is strongly
correlated with the age difference between the MA and BF estimates
(the median
), although a large scatter
exists (see Appendix A.1). Such a mass difference is strongly
correlated with the age difference between the MA and BF estimates
(the median
![]() for the total sample
resulting from the "BF'' approach is smaller than 2,
to be compared with the adopted fixed value
for the total sample
resulting from the "BF'' approach is smaller than 2,
to be compared with the adopted fixed value
![]() of the
MA models), while other parameters have a minor impact. This assumed
high redshift for the start of star formation is
indeed the main difference between the "Maximal Age'' MA models
and the BF models.
of the
MA models), while other parameters have a minor impact. This assumed
high redshift for the start of star formation is
indeed the main difference between the "Maximal Age'' MA models
and the BF models.
In addition, we have taken advantage of the
relation between MA and BF masses to obtain a "BF'' mass estimate of
the 3 objects in the CDFS field (that are at
z=0.366, 1.087, 1.277)
for which we do not have a full multicolor coverage, but only a MA
mass estimate from available
![]() color.
color.
Apart from systematic biases that would affect both methods in the same way (see Sect. 5.5), and based also on the results of the simulations and of the other tests described in Appendix A, we believe that considering the results of both methods gives an idea of the existing uncertainties and we will therefore consider both estimates in our subsequent analysis.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{0626f001.ps}
\end{figure}](/articles/aa/full/2004/34/aa0626/Timg69.gif) |
Figure 1:
Galaxy stellar masses in the K20 sample as a function of
redshift. Upper panel: estimates based on Maximal Age model.
Lower panel: estimates based on the Best Fit method. Filled circles: early
type galaxies; empty circles: early+emission type; crosses:
"star-forming'' type; triangles: objects with photometric redshifts.
A few very low redshift objects at
|
| Open with DEXTER | |
The derived masses for the K20 sample are shown in Fig. 1
as a function of redshift. For each object, both the MA (upper panel)
and the BF estimates (lower panel) are shown. It is immediately
apparent that very massive galaxies, in the range
![]() ,
are detected all the way to
,
are detected all the way to
![]() .
Besides the
.
Besides the
![]() galaxies within
the two
galaxies within
the two
![]() peaks, the most massive galaxy with
spectroscopic redshift in the K20 sample is CDF1-633 at
peaks, the most massive galaxy with
spectroscopic redshift in the K20 sample is CDF1-633 at
![]() ,
,
![]() ,
according to the BF
and the MA method, respectively.
,
according to the BF
and the MA method, respectively.
In the HDFN, the upper envelope of the mass distribution appears to decrease at high redshift (D03). Such a trend is much less clear in the similar analysis of the HDFS (F03), and even less so in the present K20 sample.
Conversely, the lower envelope is a result of the K<20 selection criteria, that prevents less massive objects to be detected. However, as already discussed by D03 and F03, IR-selected samples do not strictly correspond to mass-selected ones. Indeed, at any Hubble time (i.e. redshift), for each K-band luminosity there is a range in the possible M*/L ratios that is set by the range of allowable ages, metallicities and dust extinctions of the observed stellar population. This implies that at the low mass side the sample is progressively biased against the detection of high M*/L, such as old, passively evolving or highly extincted galaxies.
Because of the uncertainties in the modeling of such objects, it is
difficult to define a clear mass threshold as a function of redshift.
A very conservative way to estimate it corresponds to the minimum mass
that a
![]() galaxy at any given redshift may have, within the
adopted set of spectral templates. Such a threshold strongly depends
on the adopted library, and in particular on the allowed maximum
extinction. For both BF library, this threshold is shown as short
dashed lines in Fig. 1. In this case, this threshold
corresponds to the maximum extinction allowed in the set of templates
(which is entirely arbitrary) and it would eliminate a large fraction
of the sample from the statistical analysis. A more realistic
approach (already adopted by D03 and F03) is to consider only
dust-free, passively evolving models, such that the derived threshold
corresponds to the selection for early type galaxies. In the case of
both the MA and BF libraries, this is shown as a long dashed line in
Fig. 1. Our sample is therefore definitely incomplete
below this curve, where several objects of lower M*/L (typically
star-forming galaxies) are still detected, and reasonably complete
above, except for strongly obscured sources. The selection curves in
Fig. 1 shows that our sample is "mass-complete'', except
for strongly obscured sources, down to objects of
galaxy at any given redshift may have, within the
adopted set of spectral templates. Such a threshold strongly depends
on the adopted library, and in particular on the allowed maximum
extinction. For both BF library, this threshold is shown as short
dashed lines in Fig. 1. In this case, this threshold
corresponds to the maximum extinction allowed in the set of templates
(which is entirely arbitrary) and it would eliminate a large fraction
of the sample from the statistical analysis. A more realistic
approach (already adopted by D03 and F03) is to consider only
dust-free, passively evolving models, such that the derived threshold
corresponds to the selection for early type galaxies. In the case of
both the MA and BF libraries, this is shown as a long dashed line in
Fig. 1. Our sample is therefore definitely incomplete
below this curve, where several objects of lower M*/L (typically
star-forming galaxies) are still detected, and reasonably complete
above, except for strongly obscured sources. The selection curves in
Fig. 1 shows that our sample is "mass-complete'', except
for strongly obscured sources, down to objects of
![]() at
at ![]() ,
and of
,
and of
![]() up
up ![]() .
.
In principle, only objects above the long dashed lines of Fig. 1 should be used in statistical analyses that require mass-selected samples, such as average M*/L , mass densities or mass functions. In the Sect. 5.1 and in Appendix B we will describe how we have introduced a correction for the incompleteness in order to extend the construction of the mass function to lower masses. Thanks to this approach, we will be able to recover a significant fraction of our sample: the corresponding selection curves are shown as solid lines in Fig. 1.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0626f002.ps}
\end{figure}](/articles/aa/full/2004/34/aa0626/Timg76.gif) |
Figure 2: M*/LR ratios as a function of redshift, in the K20 sample. Upper panel shows the Maximal Age estimates, while lower one shows the Best Fit ones. In both panels the symbols correspond to different spectral types, as in Fig. 1. |
| Open with DEXTER | |
Table 2: Average M*/LR ratios as a function of redshift and spectral type, computed in the mass complete-sample, as defined by the thick solid curve of Fig. 1. All refers to all galaxies in the K20 sample, including also those with photometric redshift only. Early refer to early and early+emission spectroscopic types and late to late spectroscopic types, as defined in Sect. 2. Only objects with spectroscopic redshift are included in the last two columns. M*/L ratio in the V and K bands are available in electronic form at the web site http://www.arcetri.astro.it/~k20
Figure 2 shows the values of the M*/LR ratio for the K20
sample of galaxies as a function of redshift, as derived from the MA
and BF procedures. Here, LR is the absolute luminosity in the
rest-frame R band, in solar units, which is extracted from the
spectral template that best-fits the corresponding observables, and
that is well sampled by our multicolor photometry up to ![]() .
For the reasons described above, the M*/LR ratio tends to be
higher in the MA models than in the BF ones. Using the "mass
complete'' sample described in Appendix B, we have obtained the
average M*/LR ratio for the whole sample and for the two spectral
types as a function of redshift (in the redshift bins adopted to
compute the galaxy stellar mass function). The corresponding values
are shown in Table 2, along with the corresponding
dispersions in the data.
.
For the reasons described above, the M*/LR ratio tends to be
higher in the MA models than in the BF ones. Using the "mass
complete'' sample described in Appendix B, we have obtained the
average M*/LR ratio for the whole sample and for the two spectral
types as a function of redshift (in the redshift bins adopted to
compute the galaxy stellar mass function). The corresponding values
are shown in Table 2, along with the corresponding
dispersions in the data.
In the redshift range including most of the galaxies in the sample
(
![]() ), a correlation exists between the
average M*/LR ratio and the observed spectral type, with the
spectroscopic early type galaxies having on average a higher M*/LR ratio with respect to the late type, star-forming ones. In
addition, we also detect an overall trend of decreasing M*/LR with
increasing redshift, for both the early and the late type
galaxies.
), a correlation exists between the
average M*/LR ratio and the observed spectral type, with the
spectroscopic early type galaxies having on average a higher M*/LR ratio with respect to the late type, star-forming ones. In
addition, we also detect an overall trend of decreasing M*/LR with
increasing redshift, for both the early and the late type
galaxies.
It is of some interest to compare the observed M*/LR ratio of early
type galaxies with that expected in simple cases of PLE models. We
plot in Fig. 3 the M*/LR for spectroscopically early and
early+emission types as a function of redshift, differentiating
between brighter (MR<-22) and fainter (
![]() )
objects, and
compare the observed evolution with a set of single-exponential models
with
)
objects, and
compare the observed evolution with a set of single-exponential models
with
![]() and 20 and
and 20 and
![]() and 3 Gyr, all
computed with a Salpeter IMF and no dust extinction. For simplicity, we
plot only the BF estimates. It is shown that the observed M*/LR values are distributed over a significant range, suggesting that
coeval, single-exponential models are probably an oversimplified way
to describe the properties of spectroscopically early type galaxies.
A similar result was also presented on the EROs subsample (Cimatti et al. 2003), and is now extended to the whole early type population.
and 3 Gyr, all
computed with a Salpeter IMF and no dust extinction. For simplicity, we
plot only the BF estimates. It is shown that the observed M*/LR values are distributed over a significant range, suggesting that
coeval, single-exponential models are probably an oversimplified way
to describe the properties of spectroscopically early type galaxies.
A similar result was also presented on the EROs subsample (Cimatti et al. 2003), and is now extended to the whole early type population.
More interestingly, we show that the typical M*/LR of brighter
objects is significantly larger than that of the fainter ones at low
and intermediate redshifts. This implies that, while the M*/LR of the
bright population is consistent with either very short star-formation
time-scales or high
![]() ,
and some objects appear to
require both, the fainter population has experienced a more recent
history of assembly, witnessed by the larger
,
and some objects appear to
require both, the fainter population has experienced a more recent
history of assembly, witnessed by the larger ![]() and lower
and lower
![]() required to reproduce the typical M*/LR . So, the most
luminous and massive galaxies appear to reach near completion first,
while less massive ones keep growing in mass till later times. This
down-sizing effect was first noted by Cowie et al. (1996) for
required to reproduce the typical M*/LR . So, the most
luminous and massive galaxies appear to reach near completion first,
while less massive ones keep growing in mass till later times. This
down-sizing effect was first noted by Cowie et al. (1996) for
![]() ,
and then explicitly quantified by Brinchmann & Ellis
(2000) and F03 (see also Kodama et al. 2004). This tendency continues
all the way to
,
and then explicitly quantified by Brinchmann & Ellis
(2000) and F03 (see also Kodama et al. 2004). This tendency continues
all the way to ![]() ,
where the star-formation rate per unit mass
anti-correlates with galaxy mass (Gavazzi et al. 1996; Kauffman
et al. 2003).
,
where the star-formation rate per unit mass
anti-correlates with galaxy mass (Gavazzi et al. 1996; Kauffman
et al. 2003).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0626f003.ps}
\end{figure}](/articles/aa/full/2004/34/aa0626/Timg84.gif) |
Figure 3:
M*/LR ratios as a function of redshift for
spectroscopically early and early+emission spectral type galaxies of
the K20 sample. Large hollow circles are for bright (MR<-22) objects,
small filled circles for fainter (MR>-22) ones.
Lines show the M*/LR values computed with a set of single-exponential models with
|
| Open with DEXTER | |
Once the stellar mass has been obtained for each galaxy in the
sample, the building of the corresponding Galaxy Stellar Mass Function (GSMF) follows the traditional techniques used for
luminosity functions. We apply here both the classical
![]() formalism to obtain binned distributions, and the Maximum Likelihood
technique to estimate the best-fit Schechter parameters, using the
recipes described in Poli et al. (2001, 2003) and Pozzetti et al. (2003), and
references therein.
formalism to obtain binned distributions, and the Maximum Likelihood
technique to estimate the best-fit Schechter parameters, using the
recipes described in Poli et al. (2001, 2003) and Pozzetti et al. (2003), and
references therein.
With respect to the standard procedures adopted for luminosity
functions, an improvement is necessary to account for the
incompleteness in the mass census of galaxies. The adopted
procedure to obtain the correction fractions for incompleteness is
fully described in Appendix B. This correction factor is then
applied to the volume element
![]() of any galaxy, both in the
of any galaxy, both in the
![]() binned GSMF as well as in the Schechter best-fits.
binned GSMF as well as in the Schechter best-fits.
Another aspect requiring particular attention is the comparison of GSMFs
derived at the various redshifts with
the local, ![]() GSMF. In the following, we shall make use of the local
GSMFs derived by Cole et al. (2001) and
Bell et al. (2004) with the same Salpeter IMF. The former authors estimate the
spectral type by the observed J-K color, while the latter ones use the
complete set of ugrizJHK SDSS+2MASS colors. Since both authors use
a set of spectral synthesis models with star-formation rate
peaking at high redshifts, the two GSMFs agree quite well with each
other, especially for
GSMF. In the following, we shall make use of the local
GSMFs derived by Cole et al. (2001) and
Bell et al. (2004) with the same Salpeter IMF. The former authors estimate the
spectral type by the observed J-K color, while the latter ones use the
complete set of ugrizJHK SDSS+2MASS colors. Since both authors use
a set of spectral synthesis models with star-formation rate
peaking at high redshifts, the two GSMFs agree quite well with each
other, especially for
![]() ,
and the comparison with
our MA estimates at higher redshift is fair, since our MA method
mimics exactly the Cole et al. (2001) models.
,
and the comparison with
our MA estimates at higher redshift is fair, since our MA method
mimics exactly the Cole et al. (2001) models.
Conversely, the same may not hold for our BF estimates, that have no
constraint on age and typically yield lower
![]() for the K20
objects. To estimate the effect, we have repeated the Bell et al. (2004)
procedure, building a sample of 6332 SDSS+2MASS local galaxies, for
which we obtained both the MA and BF stellar masses with our
recipes. For this local sample we find that the BF mass estimates are
on average lower than MA by only about 20%, and even less for more
massive objects. Full details of this analysis are described in
Appendix A.5. Using this result to statistically convert the
Cole et al. (2001) mass function to a BF one, we have obtained a
"BF-scaled'' local GSMF that only marginally departs from the
original of Cole et al. (2001) in the massive tail, and that we will use
to compare with our "BF'' results at higher z.
for the K20
objects. To estimate the effect, we have repeated the Bell et al. (2004)
procedure, building a sample of 6332 SDSS+2MASS local galaxies, for
which we obtained both the MA and BF stellar masses with our
recipes. For this local sample we find that the BF mass estimates are
on average lower than MA by only about 20%, and even less for more
massive objects. Full details of this analysis are described in
Appendix A.5. Using this result to statistically convert the
Cole et al. (2001) mass function to a BF one, we have obtained a
"BF-scaled'' local GSMF that only marginally departs from the
original of Cole et al. (2001) in the massive tail, and that we will use
to compare with our "BF'' results at higher z.
Finally, the intrinsic uncertainty in the estimate of the stellar mass must be taken into account when computing the error budget in the GSMF. At this purpose, we have performed a set of MonteCarlo simulations where the input mass catalogs were randomly perturbed, allowing each galaxy in the sample to move around its best fit values of a quantity specified (for each galaxy) by the error analysis described in Appendix A.4. This includes also the uncertainty due to the redshift for galaxies with photometric redshifts only. We simulated 200 such catalogs, and computed the resulting GSMF. The dispersion in the derived values (both for the binned valued as well as for the fitted Schechter parameters) has been added in quadrature to the standard Poisson noise for each GSMF. We remark that a more global uncertainty - not shown in the following figures - is related to cosmic variance, that is much more difficult to treat. As we discuss in better detail in Sect. 5.5, the error budget due to cosmic variance is around 20-40% (depending on the assumed galaxy correlation length) of the total number densities.
![\begin{figure}
\par\includegraphics[angle=-90,width=15cm,clip]{0626f004.ps}
\end{figure}](/articles/aa/full/2004/34/aa0626/Timg88.gif) |
Figure 4: Galaxy stellar mass functions in the K20 sample, in four redshift ranges. Different symbols correspond to different methods adopted to estimate the stellar mass: triangles represent the Maximal Age estimates, and squares the Best Fit estimates. In the highest redshift bin, large hollow circles correspond to the GSMF measured by using only objects with spectroscopic redshift. Thick lines correspond to local galaxy mass functions: the solid line is the local galaxy mass function by Cole et al. (2001), the dot-dashed one is the same GSMF renormalized to our "BF'' method (See text and Appendix A for details). The same line types have been used to represent the Schechter fits to our "extended'' galaxy mass functions (thin lines). |
| Open with DEXTER | |
The resulting stellar mass functions of the K20 sample are shown in
Fig. 4. We have divided the sample into four redshift
bins: 0.2-0.7; 0.7-1.0; 1.0-1.5; and 1.5-2.0, having chosen the
two lowest redshift bins in such a way to distribute in two different
bins the impact of the two redshift peaks at z=0.67 and z=0.73,
and to have a similar comoving volume (about
![]() Mpc3). The two high redshift bins have also a comparable
comoving volume (
Mpc3). The two high redshift bins have also a comparable
comoving volume (
![]() Mpc3 and
Mpc3 and
![]() Mpc3,
respectively). We have restricted the estimate of the GSMF at z<2,
given the small number of objects and the limited mass range covered
by our sample beyond
Mpc3,
respectively). We have restricted the estimate of the GSMF at z<2,
given the small number of objects and the limited mass range covered
by our sample beyond ![]() .
The average redshift of the
galaxies in each bin is
0.52,0.83,1.17 and 1.72, respectively. In
terms of cosmic time, for the adopted cosmology these redshift
intervals correspond to an age of the Universe of
11.3-7.5,
7.5-6.1, 6.1-4.6 and 4.6-3.6, respectively. For each redshift
bin we have constructed the GSMF following the two different methods
described in the previous sections: Maximal Age and Best Fit. For each
bin, error bars include both the Poisson noise (computed using the
exact formulas for low counts given in Gehrels 1986) as well as the
uncertainty in mass estimates, obtained with the Monte Carlo procedure
described above.
.
The average redshift of the
galaxies in each bin is
0.52,0.83,1.17 and 1.72, respectively. In
terms of cosmic time, for the adopted cosmology these redshift
intervals correspond to an age of the Universe of
11.3-7.5,
7.5-6.1, 6.1-4.6 and 4.6-3.6, respectively. For each redshift
bin we have constructed the GSMF following the two different methods
described in the previous sections: Maximal Age and Best Fit. For each
bin, error bars include both the Poisson noise (computed using the
exact formulas for low counts given in Gehrels 1986) as well as the
uncertainty in mass estimates, obtained with the Monte Carlo procedure
described above.
In the highest z bin, the contribution by objects which have only a photometric redshift is significant. In order to provide a strict lower limit to the total GSMF, in this redshift bin we have also used only the spectroscopic sample with no correction for incompleteness (large hollow circles in Fig. 4).
At each redshift, the resulting GSMFs are compared to the local one by Cole et al. (2001) for the same Salpeter IMF, as well as to the one "rescaled'' to our BF estimates (see Appendix A.5, Fig. A.5). For simplicity, we do not plot the Bell et al. (2004) local GSMF, that is in excellent agreement with Cole et al. (2001) mass function.
In each panel of Fig. 4 we also plot the Schechter fits of
the "extended'' GSMFs. We remark that the Schechter parameters
derived by using the "strictly complete'' or the "extended''
selection criteria are statistically consistent with each other.
Unfortunately, at z>1, we cannot reliably estimate the slope of the GSMF because of the small range in mass covered by our sample. For
this reason, we have assumed in these bins the same slope that we
observe at
![]() ,
which may bias the estimate of the
characteristic mass in the high z bins. For this reason, and given
the size of the resulting statistical errors, one should not read too
much in these values, that should be primarily used as description of
our dataset in the range that we actually observe. The corresponding
best fit values are given in Table 3, with their
,
which may bias the estimate of the
characteristic mass in the high z bins. For this reason, and given
the size of the resulting statistical errors, one should not read too
much in these values, that should be primarily used as description of
our dataset in the range that we actually observe. The corresponding
best fit values are given in Table 3, with their ![]() uncertainties.
uncertainties.
The most relevant results that emerge from Fig. 4 are the following:
First, we note that the overall agreement between the GSMF derived with the BF and the MA procedures is fairly satisfactory. Albeit MA estimates provide higher normalizations than the BF estimates, as expected by their typically larger masses, the resulting scenarios are not significantly dependent on the adopted method of mass determination, and so are the conclusions that we shall draw in the following.
Table 3:
Best fit Schechter parameters of the Galaxy Stellar Mass
Functions in the K20 survey. Errors indicate ![]() confidence
levels. Parameters without error have been fixed to the best fit value
of the lower z bin.
confidence
levels. Parameters without error have been fixed to the best fit value
of the lower z bin.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0626f005.ps}
\end{figure}](/articles/aa/full/2004/34/aa0626/Timg94.gif) |
Figure 5: Ratio between the observed Galaxy Stellar Mass Functions in the K20 sample and the local GSMF. Data points refer to the ratio of the "Best Fit'' values to the corresponding "rescaled'' local GSMF. Filled symbols refer to points at z<1.0 (squares: 0.2<z<0.7; triangles 0.7<z<1.0); open symbols to z>1.0 (diamonds: 1.0<z<1.5, squares: 1.5<z<2). The data points at 1.5<z<2include objects with photometric redshifts. |
| Open with DEXTER | |
Up to ![]() there appears to be only a very mild evolution
of the GSMF (see Figs. 4 and 5), as
suggested by the corresponding near-IR luminosity function (Pozzetti
et al. 2003). Both the MA- and the BF-derived GSMFs are in agreement
with the local ones, at least in the range
there appears to be only a very mild evolution
of the GSMF (see Figs. 4 and 5), as
suggested by the corresponding near-IR luminosity function (Pozzetti
et al. 2003). Both the MA- and the BF-derived GSMFs are in agreement
with the local ones, at least in the range
![]() ,
where our statistics is reasonably accurate.
The low-mass end of the GSMF is rather flat in the first redshift bin,
where it is well determined (
,
where our statistics is reasonably accurate.
The low-mass end of the GSMF is rather flat in the first redshift bin,
where it is well determined (
![]() ), quite consistent
with the local estimates (
), quite consistent
with the local estimates (
![]() )
(Cole et al. 2001);
in addition, also the characteristic masses in the Schechter function
are consistent with local estimates.
)
(Cole et al. 2001);
in addition, also the characteristic masses in the Schechter function
are consistent with local estimates.
At higher redshifts, z>1, there appears to begin a decrease in the
normalization of the GSMF, which is particularly remarkable if we take
into account the relatively small range of cosmic time resulting from
our sampling. The decrease is particularly evident for
![]() ,
and is approximately constant up to
,
and is approximately constant up to ![]() .
This decrease in normalization is also shown in Fig. 5,
where we plot the ratio between the GSMF at the various redshifts and
the local GSMF for the BF case. The number density of objects around
.
This decrease in normalization is also shown in Fig. 5,
where we plot the ratio between the GSMF at the various redshifts and
the local GSMF for the BF case. The number density of objects around
![]() is (70-80%) of the local value up to
is (70-80%) of the local value up to
![]() ,
while it decreases to (30-40%) of the local value in the
two higher redshift bins. This suggests that the mass assembly of
objects with mass close to the local characteristic mass was quite
significant between z=2 and z=1, and was essentially complete by
,
while it decreases to (30-40%) of the local value in the
two higher redshift bins. This suggests that the mass assembly of
objects with mass close to the local characteristic mass was quite
significant between z=2 and z=1, and was essentially complete by
![]() .
.
The evidence presented in Sect. 4.2 of a differential evolution of early type galaxies, with more luminous (i.e. more massive) galaxies having formed earlier than less luminous one, should be reflected in a flattening of the observed GSMF at high z. In our data there is a tentative suggestion of this, since the massive tail of the GSMF appear to evolve in a slower fashion than the fainter. Given the present statistics, unfortunately, much wider surveys are required to confirm this potentially important item.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{0626f006.ps}
\end{figure}](/articles/aa/full/2004/34/aa0626/Timg98.gif) |
Figure 6: Galaxy stellar mass functions in the K20 sample for different spectral types. Empty points correspond to late spectral type, filled to early spectral type. The solid lines show the Schechter fits to the total GSMF of our sample at the corresponding redshifts. |
| Open with DEXTER | |
Figure 6 shows the GSMF for the two main broad galaxy
spectral types, early and late (we remark that early+emission type
have been omitted). Since only objects with spectroscopic redshift are
included, these were grouped into three bins rather than four as in
Fig. 4, thus ensuring a fairly good statistics in each
bin. We remind that the spectroscopic completeness of the K20 survey
is particularly high (![]()
![]() ), such that incompleteness effects
should play a minor role here. In any case, one expects galaxies
without a spectroscopic redshift to be preferentially at
), such that incompleteness effects
should play a minor role here. In any case, one expects galaxies
without a spectroscopic redshift to be preferentially at
![]() ,
for which the most prominent spectral features have moved out of
the observed spectral range. For z<1.3, indeed, we estimate the
spectroscopic completeness to be 97%, given the distribution of the
photometric redshifts of the unidentified objects.
,
for which the most prominent spectral features have moved out of
the observed spectral range. For z<1.3, indeed, we estimate the
spectroscopic completeness to be 97%, given the distribution of the
photometric redshifts of the unidentified objects.
We find that there is a clear difference in the GSMF for the two
spectral types (Fig. 6). Up to
![]() ,
early
type galaxies dominate the mass distribution, and in practice provide
the whole contribution to its most massive side. This can be
qualitatively appreciated by observing the GSMF of
Fig. 6 and by observing that all the more massive
galaxies at these redshift bins are early type. Although the latter
evidence may be somewhat affected by the prominent structures at
,
early
type galaxies dominate the mass distribution, and in practice provide
the whole contribution to its most massive side. This can be
qualitatively appreciated by observing the GSMF of
Fig. 6 and by observing that all the more massive
galaxies at these redshift bins are early type. Although the latter
evidence may be somewhat affected by the prominent structures at
![]() ,
that are dominated by early type galaxies, a scrutiny
of our catalogs reveals that early type galaxies are the most massive
galaxies also outside the structures (see Fig. 1).
Quantitatively, we find indeed that the stellar mass density due to
massive galaxies (i.e.
,
that are dominated by early type galaxies, a scrutiny
of our catalogs reveals that early type galaxies are the most massive
galaxies also outside the structures (see Fig. 1).
Quantitatively, we find indeed that the stellar mass density due to
massive galaxies (i.e.
![]() )
at
)
at
![]() and
and
![]() is of 1.68 and
is of 1.68 and
![]() Mpc-3, of which 85%
and 69%, respectively, is due to early type galaxies, and 0% and 16% is
due to late type galaxies.
When integrated over the whole observed range early type galaxies provide
about 60% of the whole stellar mass density at z<1.3.
A similar behavior was found in
the local GSMF by Bell et al. (2004), where the early-type/late-type
classification was based on morphology.
Mpc-3, of which 85%
and 69%, respectively, is due to early type galaxies, and 0% and 16% is
due to late type galaxies.
When integrated over the whole observed range early type galaxies provide
about 60% of the whole stellar mass density at z<1.3.
A similar behavior was found in
the local GSMF by Bell et al. (2004), where the early-type/late-type
classification was based on morphology.
In the highest redshift bin, star-forming galaxies appear to
contribute a significant fraction of the massive tail of the GSMF.
The measured stellar mass density at 1.3<z<2 due to star-forming
galaxies with
![]() is of the order of
is of the order of
![]() Mpc-3, corresponding to about 21% of the total
mass density in the same mass range, an amount nearly identical to the
contribution of early type galaxies (22%). This figure is a lower limit to the contribution of late-type galaxies to the total
stellar mass density, since it would correspond to assuming that all
the galaxies without spectroscopy in this redshift bin are passively
evolving objects (which implies that all photometric redshifts are
correct in this range and that all unidentified objects are
spectroscopically early type).
Mpc-3, corresponding to about 21% of the total
mass density in the same mass range, an amount nearly identical to the
contribution of early type galaxies (22%). This figure is a lower limit to the contribution of late-type galaxies to the total
stellar mass density, since it would correspond to assuming that all
the galaxies without spectroscopy in this redshift bin are passively
evolving objects (which implies that all photometric redshifts are
correct in this range and that all unidentified objects are
spectroscopically early type).
Irrespective of the nature of the unidentified objects, this result
suggests that a global physical change occurs at larger and larger z, with an increasing fraction of the stellar mass density being
contained in actively star-forming objects.
This is also supported by the upper limit to the global stellar
mass density in passively evolving galaxies at ![]() ,
that is
about 40% of the total (at
,
that is
about 40% of the total (at ![]() 3) in the HDFS (F03).
3) in the HDFS (F03).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0626f007.ps}
\end{figure}](/articles/aa/full/2004/34/aa0626/Timg108.gif) |
Figure 7:
Evolution of the cosmological mass density as a function of
redshift. Upper panel: observed cosmological mass density as
observed in the K20 data. Squares correspond to BF estimates,
Triangles to MA estimates. Empty points represent the observed
values, with the corresponding Poisson noise. Filled points represent
the values corrected for incompleteness, as obtained by integrating
the mass function over the whole range
|
| Open with DEXTER | |
Table 4: Observed and total stellar mass density in the K20 survey, as a function of redshift. Reference value are given for the BF estimates; lower errors take into account the Poisson noise and the uncertainties in the mass estimates. Upper limits have been computed with respect to the values provided by the MA method, to provide an estimate of the global uncertainties.
The upper panel of Fig. 7 shows the stellar mass density ![]() ,
as derived for the K20 sample with the two different
methods (BF and MA), both from the observed data, as well as
from the incompleteness-corrected GSMFs, i.e., integrating the
best-fit Schechter functions (Table 3) over the whole range
,
as derived for the K20 sample with the two different
methods (BF and MA), both from the observed data, as well as
from the incompleteness-corrected GSMFs, i.e., integrating the
best-fit Schechter functions (Table 3) over the whole range
![]() .
The same quantites
are given in Table 4. The correction is
marginal at z<1, but becomes a factor of
.
The same quantites
are given in Table 4. The correction is
marginal at z<1, but becomes a factor of ![]() 2 at
2 at ![]() ,
where this exercise is obviously prone to statistical as well as
systematic errors due to the limited mass range of the observed GSMF.
Figure 7 gives the statistical errors due to the
uncertainties in the best-fit parameters of the Schechter function.
,
where this exercise is obviously prone to statistical as well as
systematic errors due to the limited mass range of the observed GSMF.
Figure 7 gives the statistical errors due to the
uncertainties in the best-fit parameters of the Schechter function.
In the case of the two high redshift bins, where we have fixed the slope of the GSMF (see Table 3), these error estimates do not take into account the uncertainty in the slope of the GSMF: this systematic effect is discussed and quantified in Sect. 5.5, as well as the global uncertainty due to cosmic variance.
The global evolution of the stellar mass density from the K20 sample
is reported again in the lower panel of Fig. 7, along with
the results from other surveys at ![]() (Brinchmann & Ellis
2000; Cohen 2002), as well as at higher z from Glazebrook et al. (2004) and from the HDFN (D03) and HDFS (F03). The K20 survey data
show that the stellar mass density at
(Brinchmann & Ellis
2000; Cohen 2002), as well as at higher z from Glazebrook et al. (2004) and from the HDFN (D03) and HDFS (F03). The K20 survey data
show that the stellar mass density at
![]() is about 35% of
the local value, with a lower limit (given by the strictly observed
quantity) of 20%. This is well placed within the global trend that
witnesses a fast increase of the stellar mass density from
is about 35% of
the local value, with a lower limit (given by the strictly observed
quantity) of 20%. This is well placed within the global trend that
witnesses a fast increase of the stellar mass density from
![]() of the local value at 2<z<3 to about unity at
of the local value at 2<z<3 to about unity at
![]() ,
i.e. in a relatively short span of cosmic time. At z>2,
we cannot compute a reliable estimate of the total mass density since
most of the objects fall below the completeness threshold. For this
reason, we compute the same quantity on the observed data only, and
represent it as a lower limit. Interestingly, this quantity seems to
support the higher values observed in the HDFS rather than those in
the HDFN.
,
i.e. in a relatively short span of cosmic time. At z>2,
we cannot compute a reliable estimate of the total mass density since
most of the objects fall below the completeness threshold. For this
reason, we compute the same quantity on the observed data only, and
represent it as a lower limit. Interestingly, this quantity seems to
support the higher values observed in the HDFS rather than those in
the HDFN.
While the current, direct estimate is still affected by sizable
uncertainties, it is worth considering the indirect estimate of the
fraction of the stellar mass already in place at high redshift which
is provided by the low redshift "fossil'' evidence. Indeed, from the
fraction of the local stellar mass locked in passively evolving
spheroids (![]()
![]() ;
e.g., Persic & Salucci 1992;
Fukugita et al. 1998; Benson et al. 2002), and from the high redshift of formation
(
;
e.g., Persic & Salucci 1992;
Fukugita et al. 1998; Benson et al. 2002), and from the high redshift of formation
(![]() )
for the bulk of stars in such spheroids (Renzini 1999a),
it has been inferred that at least
)
for the bulk of stars in such spheroids (Renzini 1999a),
it has been inferred that at least ![]()
![]() of the local stellar
mass may well be already in place by z=3 (Renzini 1998, 2003).
of the local stellar
mass may well be already in place by z=3 (Renzini 1998, 2003).
Following the approach of Pozzetti et al. 1998, D03 and Cole et al. (2001), the lower panel of Fig. 7 shows a comparison
of ![]() from various surveys with the same quantity as obtained
by integrating over time the star-formation rate density from Steidel
et al. (1999), with two different assumptions for the dust extinctions
(i.e.,
E(B-V)=0.0 and 0.15). There appears to be a good agreement
between the observed evolution of
from various surveys with the same quantity as obtained
by integrating over time the star-formation rate density from Steidel
et al. (1999), with two different assumptions for the dust extinctions
(i.e.,
E(B-V)=0.0 and 0.15). There appears to be a good agreement
between the observed evolution of ![]() and the integrated
star-formation history due only to UV bright galaxies, after
allowing for a reasonable amount of dust.
and the integrated
star-formation history due only to UV bright galaxies, after
allowing for a reasonable amount of dust.
Given the uncertainties in the estimates of both the stellar masses
and the UV-corrected star-formation rates, it is still possible to
allocate space for other significant contributors to the global
star-formation rate, as could be the case of dust-enshrouded
sources. However, the overall agreement, and in particular the match
with the local value of the stellar mass density, as well as the
consistency with the luminosity densities at different wavelengths up
to ![]() (Madau et al. 1998), appear to support
the notion that the UV selection is able to recover a major fraction
of the star-formation activity at high redshift.
(Madau et al. 1998), appear to support
the notion that the UV selection is able to recover a major fraction
of the star-formation activity at high redshift.
In closing this section it is worth emphasizing that several systematic uncertainties still affect the mass estimates of individual galaxies as well as the current estimates of the global mass density at high redshift. Such uncertainties are cursorily listed below.
![]() initial mass function. The Salpeter IMF
(
initial mass function. The Salpeter IMF
(
![]() from 0.1 to 100
from 0.1 to 100 ![]() )
was adopted to
allow a direct comparison with other observational or theoretical
GSMFs. However, all empirical determinations of the IMF indicate that
its slope flattens to
)
was adopted to
allow a direct comparison with other observational or theoretical
GSMFs. However, all empirical determinations of the IMF indicate that
its slope flattens to ![]() -1.35 below
-1.35 below ![]()
![]() (Kroupa
2001), including data both in the Galactic disk (Gould et al. 1996) and in
the Galactic bulge (Zoccali et al. 2000). Compared to the single-slope
Salpeter IMF, such a two-slope IMF would give masses about a factor of
2 smaller, for a given galaxy luminosity. However, this correction
applies by about the same factor at all redshifts explored in this paper,
and the relative evolution of the GSMF is not affected. Of more
concern is the possibility of a different slope for
(Kroupa
2001), including data both in the Galactic disk (Gould et al. 1996) and in
the Galactic bulge (Zoccali et al. 2000). Compared to the single-slope
Salpeter IMF, such a two-slope IMF would give masses about a factor of
2 smaller, for a given galaxy luminosity. However, this correction
applies by about the same factor at all redshifts explored in this paper,
and the relative evolution of the GSMF is not affected. Of more
concern is the possibility of a different slope for
![]() .
The use of a top-heavy IMF would appreciably reduce
the estimated masses of actively star-forming galaxies at high
redshifts, and would appreciably modify the evolution of the GSMF
derived from the present data. On the other hand, a top-heavy IMF
would largely over produce metals compared to their observed amount in
galaxy clusters (Renzini 1999b), while probably leading to a too small
star mass density in the local universe. Nevertheless, a more
systematic exploration of other assumptions on the IMF may have been
in order, but this goes beyond the scope of the present paper.
.
The use of a top-heavy IMF would appreciably reduce
the estimated masses of actively star-forming galaxies at high
redshifts, and would appreciably modify the evolution of the GSMF
derived from the present data. On the other hand, a top-heavy IMF
would largely over produce metals compared to their observed amount in
galaxy clusters (Renzini 1999b), while probably leading to a too small
star mass density in the local universe. Nevertheless, a more
systematic exploration of other assumptions on the IMF may have been
in order, but this goes beyond the scope of the present paper.
![]() Spectral coverage.
As the redshift increases, a bluer and bluer portion of the rest-frame
spectrum is used, which is progressively dominated by the young-age,
low-mass components of galaxies, rather than by the older, more
massive components. This might lead to an underestimate of the stellar
mass at high redshift. A quantitative estimate of this effect should
soon become possible as the Spitzer observatory will directly
provide rest-frame K-band luminosities all the way to
Spectral coverage.
As the redshift increases, a bluer and bluer portion of the rest-frame
spectrum is used, which is progressively dominated by the young-age,
low-mass components of galaxies, rather than by the older, more
massive components. This might lead to an underestimate of the stellar
mass at high redshift. A quantitative estimate of this effect should
soon become possible as the Spitzer observatory will directly
provide rest-frame K-band luminosities all the way to ![]() for
galaxies in the GOODS fields (Dickinson 2002).
for
galaxies in the GOODS fields (Dickinson 2002).
![]() Highly obscured objects. A K-band selection of
galaxies to trace the build-up of stellar mass is certainly the least
biased approach to the problem, yet one not totally free from a
selection bias. Highly obscured objects at high z, such as SCUBA
sources (Chapman et al. 2003), may well be fainter than our threshold
at
Highly obscured objects. A K-band selection of
galaxies to trace the build-up of stellar mass is certainly the least
biased approach to the problem, yet one not totally free from a
selection bias. Highly obscured objects at high z, such as SCUBA
sources (Chapman et al. 2003), may well be fainter than our threshold
at
![]() and nonetheless they may contain a sizable fraction of the
stellar mass in the highest redshift bin, while experiencing extreme
starbursts. Again, this bias would introduce an underestimate of the total
stellar mass at high redshift.
and nonetheless they may contain a sizable fraction of the
stellar mass in the highest redshift bin, while experiencing extreme
starbursts. Again, this bias would introduce an underestimate of the total
stellar mass at high redshift.
![]() Shape of the mass function. The incomplete coverage of
the mass function increases with redshift, hence the uncertainty in
the slope
Shape of the mass function. The incomplete coverage of
the mass function increases with redshift, hence the uncertainty in
the slope ![]() of the GSMF increases with redshift (see Table 3),
such that we have been forced to fix the slope at z>1. In the case
that the high z GSMF is steeper than our assumption, this would lead
to an underestimate of the stellar mass density in the two high zbins, and to a (slight) overestimate in the opposite case. For
instance, the total mass density that we estimate in the redshift
range
z=1.0-1.5 would result
of the GSMF increases with redshift (see Table 3),
such that we have been forced to fix the slope at z>1. In the case
that the high z GSMF is steeper than our assumption, this would lead
to an underestimate of the stellar mass density in the two high zbins, and to a (slight) overestimate in the opposite case. For
instance, the total mass density that we estimate in the redshift
range
z=1.0-1.5 would result
![]() ,
108.34, 108.52 if the slope of GSMF is fixed to
,
108.34, 108.52 if the slope of GSMF is fixed to
![]() ,
respectively. Only substantially deeper data could
improve the present estimates of the GSMF.
,
respectively. Only substantially deeper data could
improve the present estimates of the GSMF.
![]() Cosmic variance. While some 10 times larger than HDF,
the area explored by the K20 survey is still quite small, likely to be
subject to sizable fluctuations in the number density of
highly-clustered massive galaxies. For example, field-to-field
variance is detected among COMBO-17 fields (Bell et al. 2004), each
of them almost 20 times the area covered by the K20 project. Indeed, as
mentioned in Sect. 2, the K20 sample exhibits redshift peaks that
appear to be significantly above the average distribution at
Cosmic variance. While some 10 times larger than HDF,
the area explored by the K20 survey is still quite small, likely to be
subject to sizable fluctuations in the number density of
highly-clustered massive galaxies. For example, field-to-field
variance is detected among COMBO-17 fields (Bell et al. 2004), each
of them almost 20 times the area covered by the K20 project. Indeed, as
mentioned in Sect. 2, the K20 sample exhibits redshift peaks that
appear to be significantly above the average distribution at ![]() ,
and strong clustering among early type red galaxies (EROs) is
detected in our sample at
,
and strong clustering among early type red galaxies (EROs) is
detected in our sample at ![]() (Daddi et al. 2002).
(Daddi et al. 2002).
For the reasons described in Sect. 2, however, the number of these structures is reasonably within the expectation, such that we do not have any reason to remove them nor any statistical argument to re-normalize their contribution.
Even in this case, the cosmic variance due to galaxy clustering
may affect our results. To estimate this effect, we have assumed two
possible values for the galaxy correlation lenghts,
r0 = 5 h
-1 Mpc and
r0 = 10 h -1 Mpc, respectively, and computed the
expected variance using Eq. (8) of Daddi et al. (2000). The value
r0 =
5 h -1 Mpc has been derived from an analysis of the clustering
observed in the K20 sample itself, of which we shall provide the
details elsewhere, while
r0 = 10 h -1 Mpc is a safe upper limit
taken from the EROs clustering amplitude (Daddi et al. 2001). We find
that the relative variances in our redshift bins are typically of
about 20-25% in the former case, and 40% in the latter. If we
restrict the computation to massive objects (
![]() ), which dominate the mass density, the expected
variance are only slightly larger, 30% and 45% respectively.
), which dominate the mass density, the expected
variance are only slightly larger, 30% and 45% respectively.
Ultimately, surveys over much wider areas will be necessary to fully average out the impact of cosmic variance. As a simple check, however, we have analyzed independently the stellar mass densities and GSMF in the CDFS or Q0055 field, that are separated by more that 45 degrees, finding a good agreement. In our redshift bins, the scatter between the stellar mass densities in the Q0055 and CDFS is typically of 0.1 dex, and the resulting GSMFs are consistent. In particular, the number density of massive galaxies and the decrease of the GSMF at z>1 are observed in each individual field. In addition, we note that also the GSMFs recently obtained with the wider MUNICS survey (Drory et al. 2004) result to be in excellent agreement with our, in the range where they overlap.
The aim of this section is to undertake a comparison of the present
findings on the evolution of the galaxy population up to ![]() with
the available predictions of some renditions of the CDM paradigm of
galaxy formation and evolution. This comparison will include both
semi-analytical as well as fully hydro dynamical models.
with
the available predictions of some renditions of the CDM paradigm of
galaxy formation and evolution. This comparison will include both
semi-analytical as well as fully hydro dynamical models.
As mentioned in Sect. 2, our total "Kron'' magnitudes are prone to systematic underestimates of the total flux, by an amount that depends on the morphology, sampling, redshift and S/N of the objects. In order to coarsely correct for this "photometric bias'', following Pozzetti et al. (2003) we have shifted all the empirical GSMF by 20% up in mass before proceeding to a comparison with theoretical models. Indeed, such models provide total galaxy luminosities, unaffected e.g., by the systematic bias introduced by systematics in the measured quantities.
We first examine whether the large number of massive galaxies that we
observe at high z is consistent with the fundamental properties of
![]() -CDM hierarchical scenarios, where
the mass assembly of galaxies is driven by the merging of DM
halos. After initial collapse the latter coalesce to form larger and
larger structures (from galaxies and small groups to rich clusters of
galaxies), at a rate well approximated by the Extended Press &
Schechter theory (Lacey & Cole 1993, and references therein).
-CDM hierarchical scenarios, where
the mass assembly of galaxies is driven by the merging of DM
halos. After initial collapse the latter coalesce to form larger and
larger structures (from galaxies and small groups to rich clusters of
galaxies), at a rate well approximated by the Extended Press &
Schechter theory (Lacey & Cole 1993, and references therein).
Thus, galaxies are included into progressively larger and larger host
DM structures, where they may merge with the central dominant galaxy
due to dynamical friction, or undergo binary aggregations with other
galaxies orbiting the same host halo. The analytic description of
these dynamical processes is bound by an a posteriori consistency with
high resolution N-body simulations. Once these processes have been
fixed, the distributions of galaxies as a function of their DM
circular velocity can be computed without further ambiguity, and is
only slightly dependent on the assumptions used to describe the
dynamical processes involved. Assuming that baryons smoothly follow
the DM condensations, one can then derive the expected distributions
of the available baryonic galaxy masses that corresponds to the
mass distribution of the DM halos. This is obviously an upper limit
to the actual GSMF. We have obtained such baryonic mass distributions
from the theoretical distribution of galaxy Dark Matter circular
velocities (from Menci et al. 2002, Fig. 3), by first computing the
corresponding DM mass as
![]() ,
where
,
where ![]() is the circular velocity of the galaxy DM halo and H(z) is the
Hubble constant at redshift z, and then applying a simple scaling
is the circular velocity of the galaxy DM halo and H(z) is the
Hubble constant at redshift z, and then applying a simple scaling
![]() ,
with
,
with
![]() from the best-fit WMAP parameters (Bennett et al. 2003), under the assumption that
from the best-fit WMAP parameters (Bennett et al. 2003), under the assumption that
![]() is constant down to galactic scales. As
discussed above, there are essentially no free parameters in deriving
these distributions, that depend primarily on the cosmological
parameters and on the dynamics of galactic sub-halos. These constitute
at present the most solid description of the hierarchical galaxy formation
models, so that the predicted distribution of
is constant down to galactic scales. As
discussed above, there are essentially no free parameters in deriving
these distributions, that depend primarily on the cosmological
parameters and on the dynamics of galactic sub-halos. These constitute
at present the most solid description of the hierarchical galaxy formation
models, so that the predicted distribution of
![]() can be
considered as a solid upper bound to the observed GSMF.
can be
considered as a solid upper bound to the observed GSMF.
The resulting distributions are then compared in
Fig. 8 with the empirical K20 stellar mass
distributions. The observed number density of massive
galaxies never exceeds this fundamental ![]() -CDM constraint. This
is equivalent to say that at all explored redshifts there are enough
massive DM halos to account for the observed comoving number density
of massive (in M*) galaxies (see also Gao et al. 2003). There is
a tendency for the most massive galaxies at
-CDM constraint. This
is equivalent to say that at all explored redshifts there are enough
massive DM halos to account for the observed comoving number density
of massive (in M*) galaxies (see also Gao et al. 2003). There is
a tendency for the most massive galaxies at ![]() to be somewhat
close to this limit but, as discussed in Sect. 5,
this may be due to
the impact of large scale structures in our sample.
From Fig. 8 one derives that massive galaxies have
already converted into stars
to be somewhat
close to this limit but, as discussed in Sect. 5,
this may be due to
the impact of large scale structures in our sample.
From Fig. 8 one derives that massive galaxies have
already converted into stars ![]()
![]() of the available baryon
reservoir, and therefore have a ratio
of the available baryon
reservoir, and therefore have a ratio
![]() ,
consistent with the observed properties of local massive ellipticals
(Padmanabahn et al. 2004). This efficiency of baryon-to-star conversion
drops rapidly with decreasing mass of the host DM halo, in agreement
with the naive expectation that star formation can proceed to a higher
level of completion in deep potential wells, while early winds or other
effects easily evacuate of most of their baryons the less massive DM halos
with shallower potential wells. Several interesting ramifications may
follow from this semi-empirical estimate of the baryons-to-star conversion
efficiency as a function of the mass of DM halos, but following them in
any detail goes beyond the scope of the present paper. We just notice here
the relevance of this aspect for the chemical evolution of galaxies, the IGM and the ICM, the run of the total mass to light ratio as a function
of galaxy mass, etc.
,
consistent with the observed properties of local massive ellipticals
(Padmanabahn et al. 2004). This efficiency of baryon-to-star conversion
drops rapidly with decreasing mass of the host DM halo, in agreement
with the naive expectation that star formation can proceed to a higher
level of completion in deep potential wells, while early winds or other
effects easily evacuate of most of their baryons the less massive DM halos
with shallower potential wells. Several interesting ramifications may
follow from this semi-empirical estimate of the baryons-to-star conversion
efficiency as a function of the mass of DM halos, but following them in
any detail goes beyond the scope of the present paper. We just notice here
the relevance of this aspect for the chemical evolution of galaxies, the IGM and the ICM, the run of the total mass to light ratio as a function
of galaxy mass, etc.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0626f008.ps}
\end{figure}](/articles/aa/full/2004/34/aa0626/Timg136.gif) |
Figure 8:
Observed Galaxy Stellar Mass Functions in the K20 sample,
compared with the baryonic mass function in a |
| Open with DEXTER | |
Another kind of constraint can be obtained from the Pure Luminosity
Evolution (PLE) models: by neglecting any merging, and requiring
consistency with the properties of present-day galaxies, these models
provide an upper limit on the stellar mass distribution within a given
cosmology. We have estimated the GSMF evolution for the PLE case
starting with the local K-band luminosity function for the various
morphological types (Kochaneck et al. 2001), and by evolving back in
time the mass of each galaxy according to the e-folding time of the
star formation rate appropriate for the corresponding morphological
types (Pozzetti et al. 1996, 1998). The full procedure is described in
Paper V of this series (Pozzetti et al. 2003), and the resulting PLE
predictions are shown in Fig. 8. At ![]() ,
these predictions are in excellent agreement with the observed data,
with the possible exceptions of the more massive bins, where there
appears to be an excess of galaxies in the data with respect to the
PLE prediction. However, in the two bins around z=0.7 most of the
contribution to the top end of the GSMF comes from the prominent
concentrations (clusters) at z=0.67 and 0.73.
At higher redshifts, the PLE
predictions are still well consistent with the data. At z=1.5-2, PLE
models are formally above the observed density by about 30% around
,
these predictions are in excellent agreement with the observed data,
with the possible exceptions of the more massive bins, where there
appears to be an excess of galaxies in the data with respect to the
PLE prediction. However, in the two bins around z=0.7 most of the
contribution to the top end of the GSMF comes from the prominent
concentrations (clusters) at z=0.67 and 0.73.
At higher redshifts, the PLE
predictions are still well consistent with the data. At z=1.5-2, PLE
models are formally above the observed density by about 30% around
![]() (see also Fig. 10), where the
statistics is good and the results of the spectroscopic sample matches
the photometric one.
(see also Fig. 10), where the
statistics is good and the results of the spectroscopic sample matches
the photometric one.
Overall, we conclude from this comparison that the evolution of the
massive galaxies in the K20 sample is consistent with the fundamental
constraints of the ![]() -CDM scenario, and that the more massive
galaxies have already converted into stars a significant fraction of
their baryonic reservoir. The actual success (or lack of) encountered
by theoretical models in populating the various DM halos with the
observed amount of stars is discussed next.
-CDM scenario, and that the more massive
galaxies have already converted into stars a significant fraction of
their baryonic reservoir. The actual success (or lack of) encountered
by theoretical models in populating the various DM halos with the
observed amount of stars is discussed next.
![\begin{figure}
\par\includegraphics[angle=-90,width=15cm,clip]{0626f009.ps}
\end{figure}](/articles/aa/full/2004/34/aa0626/Timg137.gif) |
Figure 9:
Observed Galaxy Stellar Mass Functions in the K20 sample,
compared with theoretical rendition in a |
| Open with DEXTER | |
Within the ![]() -CDM scenario, several attempts have already been
made to model the history of star formation within DM halos, that
is far more uncertain than that of the DM component because of
the highly non-linear behavior of the baryonic component.
-CDM scenario, several attempts have already been
made to model the history of star formation within DM halos, that
is far more uncertain than that of the DM component because of
the highly non-linear behavior of the baryonic component.
A first class of theoretical models have been developed using simple parametrized prescriptions to relate the star-formation rate to the properties of such halos, without attempting a physical modeling of the baryonic component. These semi-analytical models (SAM) include e.g., those of Cole et al. (2000), Somerville et al. (2001), and Menci et al. (2002, 2004).
Another class of models are those complementing N-body simulations for the dissipation-less components (DM and stars) with a full hydro-dynamical description of the baryonic gas component: we shall consider in the following the simulation of Nagamine et al. (2001a,b) based on the Cen & Ostriker (2000) models.
Finally, Granato et al. (2004) presented a semi-analytical type model, focused on the relationship between the early formation of AGNs and spheroids.
We shall proceed in this section to a comparison of the K20 results
with these theoretical models. Figure 9 displays in
separate panels the direct comparison of the various model GSMFs with
their K20 counterparts. As an alternative approach, we provide
another comparison with the theoretical models in
Fig. 10, where we plot the evolution the stellar mass
density contributed by galaxies in the range
![]() (i.e., around the Schechter
mass in the local mass function of Cole et al. 2001) which in the K20
sample can be computed with at most little extrapolations of the GSMF.
(i.e., around the Schechter
mass in the local mass function of Cole et al. 2001) which in the K20
sample can be computed with at most little extrapolations of the GSMF.
In making this exercise, we had to compensate for the different IMF
adopted in some of the theoretical models. This has been accomplished
by applying the appropriate scaling factor to our GSMF and stellar
mass densities, as described below.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0626f010.ps}
\end{figure}](/articles/aa/full/2004/34/aa0626/Timg139.gif) |
Figure 10:
Cosmological Stellar Mass Density for objects of
|
| Open with DEXTER | |
The main differences among the SAMs considered in this section concern the physical descriptions of processes such as the interactions among satellite galaxies orbiting the same host DM halos (groups or clusters), the star formation processes during galaxy interactions and merging events, the baryonic fraction, and the adopted stellar IMF. On the other hand, they all adopt the same standard parametric laws for the "quiescent'' star formation and the supernova feedback. In particular, we shall consider the following SAMs:
In the low-redshift bin all the SAM mass functions appear to be systematically steeper than the observed GSMF, with a pronounced excess of low-mass galaxies, and an incipient deficit of massive ones. The former discrepancy is a well known problem afflicting some SAMs also at zero redshift (e.g., Cole et al. 2000; Baugh et al. 2002), which is also directly noticeable in the comparison of the luminosity functions from UV to IR (Poli et al. 2001; Pozzetti et al. 2003; Poli et al. 2003).
Figure 9 shows that most SAMs do reproduce the bulk of the GSMF (i.e. the region around M*), although they often under-produce the very massive galaxies by an amount that increases with redshifts. Moreover, the various models show a remarkably large spread in the predicted GSMF, and progressively diverge from each other with increasing redshift, reaching differences by more than 2 orders of magnitudes at the highest explored redshifts.
The same results can be obtained by looking at the evolution of the
stellar mass density of galaxies in the range
![]() (Fig. 10). It is
worth noting that a significant decrease (
(Fig. 10). It is
worth noting that a significant decrease (![]()
![]() from z=0 to
z=2) is exhibited also by the PLE models, despite the large
from z=0 to
z=2) is exhibited also by the PLE models, despite the large
![]() adopted.
adopted.
Given the complexity of the baryonic physics involved in galaxy formation, all the parameterizations adopted by the various SAMs appear a priori equally plausible. Yet, as shown by Figs. 9 and 10, the results diverge dramatically with increasing redshift, offering a rather powerful opportunity for the direct observation of high redshift galaxies to discriminate between more or less viable SAMs, thus possibly giving useful hints for a better understanding of the dominant physical processes. For example, it appears that merging- or interaction-induced starbursts may be an essential ingredient in order to produce a number of massive galaxies at z>1, approaching the corresponding number that this survey has detected. On the other hand, the standard, "quiescent'' star formation regulated by the cooling time of baryons within the DM halos (as adopted e.g., in C00 and M02) appears to produce the most discrepant results compared to the observations presented in this paper. Also, the comparison suggests that the standard recipes for dynamical friction adopted by S04b and M04 tend to perform better than the "reduced'' merging treatment (S04a), that was introduced to improve the match with the density of bright galaxies in the local universe.
Unlike SAMs, the Nagamine et al. (2001a,b) simulation dynamically solves a full set of fluid equations for baryons, and includes physical processes such as radiative cooling and heating of the gas, star formation, and supernova feedback, with star particles being created out of the gas where it is contracting and cooling rapidly. To some extent, the effect on star formation of galaxy interactions is also automatically included in these simulations.
The published versions of these models provide GSMFs only for redshift bins centered at z=0.5, 1, and 2, that we compare in Fig. 9 with the empirical K20 GSMFs in the 0.2<z<0.7, 0.7<z<1.0 and 1.5<z<2 redshift bins, respectively. Since these models adopt the IMF from Gould et al. (1996), the K20 masses have been systematically scaled down by a factor 0.72, which is the appropriate correction to take into account to convert them to a Salpeter IMF (Nagamine, private communication).
Figure 9 shows that these models predict an evolution of the GSMF that is in very good agreement with the K20 results, avoiding both the low-mass excess and the high-mass deficit typical of SAMs. The good agreement in the low-mass range is likely to be due to the stronger feedback effect that in these models is tuned to match the X-ray background, resulting from the AGN activity.
Figure 10 shows that the Nagamine et al. models also
predict a very mild decrease with z of the high-mass contribution to
the stellar mass density, actually even milder than that derived from
the K20 data. We note also that these models predict that ![]()
![]() of the stellar mass is already in place by z=3 (Nagamine et al. 2004), in agreement with the expectation from the so-called
"fossil evidence'' (Renzini 1998, 2003).
of the stellar mass is already in place by z=3 (Nagamine et al. 2004), in agreement with the expectation from the so-called
"fossil evidence'' (Renzini 1998, 2003).
Yet another class of models has been developed specifically to explore the mutual feed-back between star formation in spheroids and the high-z QSO activity (Granato et al. 2001, 2004), largely neglected by classical SAM. In the latter paper, dark matter halos form at the rate predicted by the canonical hierarchical clustering scenario, and processes such as collapse, heating, cooling and supernovae feed-back are taken into account with techniques and recipes typical of other SAM. However, (i) it is assumed that angular momentum plays a negligible role in slowing down star formation activity in massive halos virialized at high redshift, which would be those leading to spheroid formation and are the only one accounted for in this model; (ii) the growth by accretion of a central SMBH is promoted by the resulting huge, and heavily obscured, star formation rate; and (iii) the feed-back on the ISM due to the ensuing AGN activity is taken into account with recipes inspired by the physics of Broad Absorption Line QSOs.
This model adopted a double-slope IMF that provides a M*/L ratio very close to Kennicutt. For this reason, we will plot this curve in the same panel with the Kennicutt models. We note that in the case of the second redshift bin (0.7<z<1), the model has been computed at z=1, and should therefore be considered as slightly underestimated.
The comparison with the K20 data suggests a good agreement in the
![]() range, and an overestimate of a factor about 2 of the mass
density of massive galaxies at z>1. In this redshift range, this
models predicts a fraction of massive galaxies to be strongly
extincted, and therefore to escape our K<20 selection criteria:
further modeling is required to assess whether this effect is able to
reconcile the model with our observations.
range, and an overestimate of a factor about 2 of the mass
density of massive galaxies at z>1. In this redshift range, this
models predicts a fraction of massive galaxies to be strongly
extincted, and therefore to escape our K<20 selection criteria:
further modeling is required to assess whether this effect is able to
reconcile the model with our observations.
Beyond ![]() the evolution of massive objects starts to accelerate
and by
the evolution of massive objects starts to accelerate
and by
![]() of the local density has been
locked in massive galaxies. This is associated with a change in the
physical properties of massive galaxies, among which star-forming
objects now become common, and contribute a much more substantial
fraction of the observed mass density (at least 21% in the K20 sample). So, several massive K<20 galaxies in the high-redshift tail
(
of the local density has been
locked in massive galaxies. This is associated with a change in the
physical properties of massive galaxies, among which star-forming
objects now become common, and contribute a much more substantial
fraction of the observed mass density (at least 21% in the K20 sample). So, several massive K<20 galaxies in the high-redshift tail
(![]() )
of the redshift distribution are star-bursting objects
showing irregular morphologies, and may be strongly clustered (Daddi
et al. 2004a), which makes them likely progenitors of local massive
early-type galaxies. While up to
)
of the redshift distribution are star-bursting objects
showing irregular morphologies, and may be strongly clustered (Daddi
et al. 2004a), which makes them likely progenitors of local massive
early-type galaxies. While up to ![]() PLE models still give an
acceptable fit to the data, at higher redshifts the massive starbursts
in the sample mark a departure from such models, and signal that one
may be entering the formation epoch of massive spheroids (Daddi et al. 2004; Somerville et al. 2004b). However, with the K20 survey we
have got just a first glimpse to the transition from the
passively-evolving to the active star-forming progenitors of the local
early-type galaxies. Wider areas and deeper spectroscopic surveys are
clearly required to thoroughly map this transition, that may extend up
to
PLE models still give an
acceptable fit to the data, at higher redshifts the massive starbursts
in the sample mark a departure from such models, and signal that one
may be entering the formation epoch of massive spheroids (Daddi et al. 2004; Somerville et al. 2004b). However, with the K20 survey we
have got just a first glimpse to the transition from the
passively-evolving to the active star-forming progenitors of the local
early-type galaxies. Wider areas and deeper spectroscopic surveys are
clearly required to thoroughly map this transition, that may extend up
to ![]() and beyond.
and beyond.
Overall, these features are in agreement with the basic elements of
the ![]() -CDM scenarios. In an accelerating universe, massive
galaxies have time to complete their assembly at
-CDM scenarios. In an accelerating universe, massive
galaxies have time to complete their assembly at ![]() ,
avoiding
too much merging at low redshifts. Thanks to the availability of gas,
shorter cooling time, and higher interaction and merging rates star
formation naturally occurs most efficiently at earlier times. The
anti-correlation of feedback with the halo mass, and the correlation
between high density peaks, boosts the star-formation rate in high
mass objects at high z, with respect to lower mass ones. Despite
these "built in'' features, most renditions of the
,
avoiding
too much merging at low redshifts. Thanks to the availability of gas,
shorter cooling time, and higher interaction and merging rates star
formation naturally occurs most efficiently at earlier times. The
anti-correlation of feedback with the halo mass, and the correlation
between high density peaks, boosts the star-formation rate in high
mass objects at high z, with respect to lower mass ones. Despite
these "built in'' features, most renditions of the ![]() -CDM
paradigm tend to delay the star formation and assembly of massive
galaxies well beyond the epochs favored by the present observations,
and several of them significantly fail to match the observed mass
densities. The reason is tied to the different physical processes
that are contained - or ignored - in the models and to the way they
are described.
-CDM
paradigm tend to delay the star formation and assembly of massive
galaxies well beyond the epochs favored by the present observations,
and several of them significantly fail to match the observed mass
densities. The reason is tied to the different physical processes
that are contained - or ignored - in the models and to the way they
are described.
At the time of writing, the Spitzer satellite is acquiring its first data: it is easy to predict that it will bring new, decisive information in this critical issue.
The M*/L ratio, stellar mass densities and GSMFs described in this papers are available in electronic form at the web site http://www.arcetri.astro.it/~k20
Acknowledgements
We warmly thank Carlton Baugh, G. L. Granato, Ken Nagamine, and Rachel Somerville for providing files with the predictions of their models, A. Grazian for a careful reading of the manuscript and precious suggestions, and the anonymous referee for very constructive comments that resulted in a significant improvement of the paper. We thank the VLT support astronomers for their kind assistance during the observations.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{0626fga1.ps}
\end{figure}](/articles/aa/full/2004/34/aa0626/Timg159.gif) |
Figure A.1: Comparison between the stellar masses estimated for the K20 galaxies with the Maximal Age and Best Fit techniques. Upper panel: the relation between MA (x-axis) and BF (y-axis) stellar masses in the K20 sample with full multicolor coverage. Different symbol refer to spectroscopic classification, as in Fig. 1: solid circles, early type; empty circles, early+emission type; crosses, late type; triangles, photometric redshifts. The dashed line shows the first-order fit to the observed relation. Lower panel: ratio between the MA and BF sample as a function of the redshift, for the same sample. Symbols have the same meaning of the upper panel. |
Figure A.1 shows the comparison between the stellar masses estimated
with the two different criteria. Beyond the obvious correlation, it
is immediately clear that the MA models provide an estimate that is
typically larger than the BF estimates, although a large scatter
exist. The ratio between the two methods is larger at intermediate
masses, and it is on average a factor
![]() at
at
![]() ,
and converges toward a
factor
,
and converges toward a
factor
![]() at
at
![]() .
We have found that this difference is mainly due to the
lower average ages that are inferred for the K20 galaxies in the
BF approach (the median
.
We have found that this difference is mainly due to the
lower average ages that are inferred for the K20 galaxies in the
BF approach (the median
![]() resulting from the "BF'' approach
is about 2). We have verified that this trend still holds if we fix
the metallicity to a solar value, or if we use different extinction
curves, like e.g. Calzetti (2000). A few BF models have larger stellar
masses than the corresponding MA estimates: these results from objects
fitted with large ages (comparable with the MA assumptions) and with
combinations of dust and/or metallicities that further enhance the M*/L
ratio. We also note that a contribution to the scatter (with a 10%
rms) results from the different normalizations (see Sect. 3.3).
resulting from the "BF'' approach
is about 2). We have verified that this trend still holds if we fix
the metallicity to a solar value, or if we use different extinction
curves, like e.g. Calzetti (2000). A few BF models have larger stellar
masses than the corresponding MA estimates: these results from objects
fitted with large ages (comparable with the MA assumptions) and with
combinations of dust and/or metallicities that further enhance the M*/L
ratio. We also note that a contribution to the scatter (with a 10%
rms) results from the different normalizations (see Sect. 3.3).
We have obtained a simple first order regression to the points in
Fig. A.1, finding that the relation
![]() provides a reasonable fit
to the observed relation, accurate to
provides a reasonable fit
to the observed relation, accurate to
![]() .
.
In order to check the reliability of the BF stellar masses estimates,
in particular during secondary starbursts, we have performed a set of
simulations.
We have computed a mock multicolor sample assuming a scenario where
galaxies were built during two major starbursts. During the first one,
characterized by an initial redshift
![]() and exponential
timescale
and exponential
timescale ![]() ,
a fraction 1-f of the total final mass is
assembled. All possible permutations of
,
a fraction 1-f of the total final mass is
assembled. All possible permutations of
![]() ,
,
![]() Gyr were adopted, to ensure a proper sampling of
any spectral type, including very red, passively evolving
galaxies. Solar metallicity and no dust was assumed in this case. In
addition, a younger starburst was summed, contributing for a fraction f of the final mass, with star-formation time scales
Gyr were adopted, to ensure a proper sampling of
any spectral type, including very red, passively evolving
galaxies. Solar metallicity and no dust was assumed in this case. In
addition, a younger starburst was summed, contributing for a fraction f of the final mass, with star-formation time scales
![]() Gyr and ages
0.1,0.2,..2 Gyr. Solar
metallicity and
E(B-V)=0.2 was adopted. The resulting mock spectral
distributions were computed with
f=0.1,0.3,0.5,0.7 at
z=0.5,0.6...1.3 to cover the main range of our observations, and
were analyzed with the same recipe of the K20 sample. In
Fig. A.2 we show the histogram of the recovered stellar mass
Gyr and ages
0.1,0.2,..2 Gyr. Solar
metallicity and
E(B-V)=0.2 was adopted. The resulting mock spectral
distributions were computed with
f=0.1,0.3,0.5,0.7 at
z=0.5,0.6...1.3 to cover the main range of our observations, and
were analyzed with the same recipe of the K20 sample. In
Fig. A.2 we show the histogram of the recovered stellar mass
![]() with respect to the input one
with respect to the input one
![]() ,
at different
starburst ages. It is shown that if the second burst is caught during
its early phase, within the first 0.2-0.3 Gyr from its start, the
BF estimated mass is typically lower than the actual one by a factor
of about 25% (average value). We have found that the effect is
larger when the fraction f is small (as shown from the
f=0.1 case in the histogram of Fig. A.2) and/or the first
starburst is peaked at high z. At larger ages, the BF estimated
mass approaches the input one, leading to a final average
underestimates of 20% at a starburst age of 1 Gyr and only 10%
after 2 Gyr. As a check,we have also verified that if we include only
single exponential laws (dashed line in Fig. A.2) the resulting
fit is essentially unbiased.
,
at different
starburst ages. It is shown that if the second burst is caught during
its early phase, within the first 0.2-0.3 Gyr from its start, the
BF estimated mass is typically lower than the actual one by a factor
of about 25% (average value). We have found that the effect is
larger when the fraction f is small (as shown from the
f=0.1 case in the histogram of Fig. A.2) and/or the first
starburst is peaked at high z. At larger ages, the BF estimated
mass approaches the input one, leading to a final average
underestimates of 20% at a starburst age of 1 Gyr and only 10%
after 2 Gyr. As a check,we have also verified that if we include only
single exponential laws (dashed line in Fig. A.2) the resulting
fit is essentially unbiased.
These simulation show that if the observed galaxy have a star-formation history significantly departing from single exponential, and are observed during a major starburst, the overall effect on the estimate of the stellar mass is relatively small, especially for the reddest galaxies, that dominate the massive tail of the GSMF.
We plot in Fig. A.3 the comparison between the D4000 break
measured from the K20 spectroscopic observations and the D4000 break
estimated from the Best Fit models. The comparison shows a relative
good agreement, with a nearly null average difference (that is
![]() )
and a dispersion of 0.2, that is smaller than the
average error on the spectroscopic D4000. Figure A.3 shows
that, as expected, the D4000 break of early-type galaxies is pretty
larger than for later types. In particular, we have found that the
average D4000 of the "old'' EROs population, derived from BF models,
is very close to the
value of the average spectrum, that is 1.9 (Cimatti et al. 2002c).
)
and a dispersion of 0.2, that is smaller than the
average error on the spectroscopic D4000. Figure A.3 shows
that, as expected, the D4000 break of early-type galaxies is pretty
larger than for later types. In particular, we have found that the
average D4000 of the "old'' EROs population, derived from BF models,
is very close to the
value of the average spectrum, that is 1.9 (Cimatti et al. 2002c).
Given the wide range of the free parameters involved in the BF estimate, and the relatively loose constraints that can be obtained
from broad band imaging only, the best fit solution to each galaxy is
far from being univocal. An advantage of the ![]() approach is
that it allows to take into account the resulting degeneracies among
the input parameters adopted and to provide an estimate of the range
of "acceptable'' models. At this purpose, we use a technique already
adopted in F03, and similar to the one adopted by
Papovich et al. (2001), based on the reduced chi-square
approach is
that it allows to take into account the resulting degeneracies among
the input parameters adopted and to provide an estimate of the range
of "acceptable'' models. At this purpose, we use a technique already
adopted in F03, and similar to the one adopted by
Papovich et al. (2001), based on the reduced chi-square ![]() (as
computed in Fontana et al. 2000). The
(as
computed in Fontana et al. 2000). The ![]() confidence levels on
the fitted parameters (such as mass, age and star-formation rate)
have been obtained by scanning the model grid and retaining only the
models that have
confidence levels on
the fitted parameters (such as mass, age and star-formation rate)
have been obtained by scanning the model grid and retaining only the
models that have
![]() .
Prior to this, as in
Papovich et al. (2001), we have rescaled the noise in bright objects order to have
.
Prior to this, as in
Papovich et al. (2001), we have rescaled the noise in bright objects order to have
![]() .
The scan is performed either at fixed redshift
(for objects with known spectroscopic redshift) or allowing the models
to move around the best-fitting photometric redshift.
.
The scan is performed either at fixed redshift
(for objects with known spectroscopic redshift) or allowing the models
to move around the best-fitting photometric redshift.
In general, the range of acceptable values will not be symmetric with
respect to the best-fit solution: we find that the typical range for
a galaxy of stellar mass M* is
0.6 M* - 1.6 M*. This
uncertainty is in agreement with the similar results in the HDFN
(D03) and HDFS (F03) at the same
redshifts and signals a core level of degeneracy in the input models,
that cannot be resolved without detailed spectroscopic informations.
This level is lower than the comparable estimates at ![]() (Papovich et al. 2001; Shapley et al. 2001), since we can rely on a better
sampling of the NIR side of the spectrum.
(Papovich et al. 2001; Shapley et al. 2001), since we can rely on a better
sampling of the NIR side of the spectrum.
To show how the uncertainty depends on the redshift and observed flux,
we use a simplified (symmetrical) estimator computed as
![]() ,
that we plot as a function of redshift
and K-band magnitude in Fig. A.4. For most of the objects,
this estimator is below 1, consistent with the average uncertainty
quoted above, showing that our mass estimates are overall robust
within a factor of 2. As expected, faintest objects have a typically
larger uncertainty, as well as objects with z>1.5, that begin to
suffer from the poor sampling of the IR side of the spectrum: longer
wavelengths data, as those provided by the recently launched
Spitzer satellite, are required to improve their estimates.
,
that we plot as a function of redshift
and K-band magnitude in Fig. A.4. For most of the objects,
this estimator is below 1, consistent with the average uncertainty
quoted above, showing that our mass estimates are overall robust
within a factor of 2. As expected, faintest objects have a typically
larger uncertainty, as well as objects with z>1.5, that begin to
suffer from the poor sampling of the IR side of the spectrum: longer
wavelengths data, as those provided by the recently launched
Spitzer satellite, are required to improve their estimates.
Finally, we have found that MA model typically lay close to the upper
confidence level. Quantitatively, we have found that about 40% of the MA values are lower than the upper ![]() confidence
level, and that the MA values are on average only 10% larger than the
upper
confidence
level, and that the MA values are on average only 10% larger than the
upper ![]() confidence level.
confidence level.
We address here the impact that our two different techniques to
estimate the stellar masses have on the estimate of the local stellar
mass functions and density (Cole et al. 2001), which are the pivots of
the evolutionary trends that we have analyzed. At this purpose, we
have followed the procedure described by Bell et al. (2004) to build a sample
of local galaxies (i.e.
![]() )
by cross-correlating the SDSS
and 2MASS public catalogs. Using a sub area of the SDSS EDR, we
obtained a catalog of 6332 galaxies with full ugrzJHK photometry,
from which we obtained the MA and BF stellar masses as described in
the main text. The main results of this comparisons are:
)
by cross-correlating the SDSS
and 2MASS public catalogs. Using a sub area of the SDSS EDR, we
obtained a catalog of 6332 galaxies with full ugrzJHK photometry,
from which we obtained the MA and BF stellar masses as described in
the main text. The main results of this comparisons are:
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0626fgb1.ps}
\end{figure}](/articles/aa/full/2004/34/aa0626/Timg182.gif) |
Figure B.1:
Relation between the observed |
As discussed in the main text, the building of the corresponding
stellar mass function follows the traditional techniques (
![]() and Maximal Likelihood) used for luminosity functions, although a
treatment must be included to correct for the incompleteness (in mass)
at the faintest levels, that arise from the not univocal conversion
from the observed K-band to the stellar mass. To emphasize this
issue, we plot in Fig. B.1 the stellar masses
and Maximal Likelihood) used for luminosity functions, although a
treatment must be included to correct for the incompleteness (in mass)
at the faintest levels, that arise from the not univocal conversion
from the observed K-band to the stellar mass. To emphasize this
issue, we plot in Fig. B.1 the stellar masses
![]() obtained in the K20 sample at the redshift of
obtained in the K20 sample at the redshift of
![]() as a function of the observed
as a function of the observed ![]() flux. The K20 sample is shown
with filled points. To ease the visual representation of the
incompleteness effect, we add with empty symbols the corresponding
points at
flux. The K20 sample is shown
with filled points. To ease the visual representation of the
incompleteness effect, we add with empty symbols the corresponding
points at
![]() from a similar analysis carried on in the HDFS (F03).
from a similar analysis carried on in the HDFS (F03).
The relation follows the expected correlation with a scatter of about
![]() ,
due to the intrinsic scatter in the
M*/LK ratios. We note that the
,
due to the intrinsic scatter in the
M*/LK ratios. We note that the
![]() limit cuts the galaxy
strip at a mass level that varies from
limit cuts the galaxy
strip at a mass level that varies from
![]() to
to
![]() .
The incompleteness at the faint M*levels becomes evident by observing the point distribution at a fixed
M* level. At, say,
.
The incompleteness at the faint M*levels becomes evident by observing the point distribution at a fixed
M* level. At, say,
![]() ,
about half
of the galaxies lay at
,
about half
of the galaxies lay at
![]() ,
and are therefore missed by a
,
and are therefore missed by a
![]() sample. To recover from this incompleteness, one can
make use of the distribution of the M*/L ratio, both as expected from
the library adopted and as observed in the data, as we describe below.
sample. To recover from this incompleteness, one can
make use of the distribution of the M*/L ratio, both as expected from
the library adopted and as observed in the data, as we describe below.
By construction, the points must lay between the minimum and maximum
mass that a galaxy at
![]() may have at a given
may have at a given ![]() magnitude: these limits can be obtained from the model grid that is
assumed to describe the galaxy properties. In the case of the BF
grid, we have computed these thresholds by scanning the output of the
spectral library defined in Table 1, which, as discussed in
the text, is particularly sensitive to the effects of dust. We plot in
Fig. B.1 both the upper limit corresponding to dusty objects
(dashed line) as well as the limit corresponding to passively evolving
dust-free models (dashed-dotted line). The lower limit (solid line)
is in both case resulting from a star-forming, dust-free young
population.
magnitude: these limits can be obtained from the model grid that is
assumed to describe the galaxy properties. In the case of the BF
grid, we have computed these thresholds by scanning the output of the
spectral library defined in Table 1, which, as discussed in
the text, is particularly sensitive to the effects of dust. We plot in
Fig. B.1 both the upper limit corresponding to dusty objects
(dashed line) as well as the limit corresponding to passively evolving
dust-free models (dashed-dotted line). The lower limit (solid line)
is in both case resulting from a star-forming, dust-free young
population.
Strictly speaking, the sample is therefore complete (in stellar mass)
only down to the horizontal dotted lines shown in Fig. B.1,
that correspond to the maximal mass allowable (at any redshift)
for a galaxy of magnitude equal to the faint limit of the sample. In
principle, stellar mass functions and other quantities should be
computed only on the subsample with
![]() .
At
masses smaller than this limit, any magnitude-selected sample will be
progressively incomplete, although objects of M*/L will still be
detected. We note that this effect has not been taken into account in
the local estimates of the GSMF (Cole et al. 2001; Bell et al. 2004), which
may explain the decrease of the local GSMF that is observed in their
faintest bins.
.
At
masses smaller than this limit, any magnitude-selected sample will be
progressively incomplete, although objects of M*/L will still be
detected. We note that this effect has not been taken into account in
the local estimates of the GSMF (Cole et al. 2001; Bell et al. 2004), which
may explain the decrease of the local GSMF that is observed in their
faintest bins.
However, as shown in Fig. B.1, the actual threshold sensitively depends on the choice of this "maximal mass'' model, and the strict adoption of a selection criteria would result in the loss of a significant fraction of our sample: for these reasons, we have introduced a correction for incompleteness that both allows to recover a significant fraction of the sample and, using the observed distribution of M*/L , removes the critical dependence on the upper and lower limits.
We also note, with that this formalism, we do not need to include any
term similar to the k-correction terms used in the computation of
standard luminosity functions, since the completeness curve by
definition allows to compute the maximum redshift used to estimate
![]() .
.
We remark that the correction is computed for each galaxy at the corresponding redshift, and that we will use here, at variance with the rest of the paper, the ratio between the stellar mass M* and the observed K-band flux k. The correction is computed as follows.
At a given mass
![]() ,
the observed K-band flux kcorresponding to a given stellar mass M* is encompassed between two
values, named
,
the observed K-band flux kcorresponding to a given stellar mass M* is encompassed between two
values, named
![]() and
and
![]() here (we have adopted in this
case of passively evolving, dust free objects). The key quantity is
the fraction
here (we have adopted in this
case of passively evolving, dust free objects). The key quantity is
the fraction
![]() of galaxies lost by effect of the incomplete
coverage of the M*/LK ratio, that reside in the shaded area of
Fig. B.1: in practice, the correction is based on the
computation of the fraction of observed galaxies
of galaxies lost by effect of the incomplete
coverage of the M*/LK ratio, that reside in the shaded area of
Fig. B.1: in practice, the correction is based on the
computation of the fraction of observed galaxies
![]() ,
that will
be used to correct for the accessible volume element
,
that will
be used to correct for the accessible volume element
![]() .
.
To show how we compute the fraction
![]() ,
let us first define the
number density N(M*,k) of objects (at redshift z) with observed
,
let us first define the
number density N(M*,k) of objects (at redshift z) with observed
![]() -band luminosity k and mass M: in principle, the fraction
-band luminosity k and mass M: in principle, the fraction
![]() (at given M) can be estimated from the number density of objects N(M,k) as
(at given M) can be estimated from the number density of objects N(M,k) as
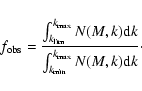 |
(B.1) |
In this case the number density N(M,k) can be written as
The simplest approach would be to assume that the distribution function ![]() is constant at fixed k: with this very coarse
assumption the correction factor
is constant at fixed k: with this very coarse
assumption the correction factor
![]() becomes
becomes
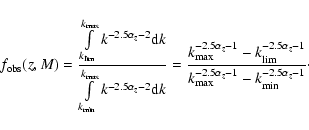 |
(B.5) |
With this assumptions, we have found that
the M*/L distribution function can be conveniently
expressed as
We have found that with
![]() (with n integer)
this expression provides an excellent fit to the M*/L
distribution at 19<K<20 and, most important, makes the fraction f (Eq. (1)) analytical: indeed, substituting Eqs. (B.4) into (B.3), and then inserting Eqs. (B.3) and (B.7) into (B.2), the fraction of observed objects
(with n integer)
this expression provides an excellent fit to the M*/L
distribution at 19<K<20 and, most important, makes the fraction f (Eq. (1)) analytical: indeed, substituting Eqs. (B.4) into (B.3), and then inserting Eqs. (B.3) and (B.7) into (B.2), the fraction of observed objects
![]() becomes:
becomes:
 |
(B.8) |
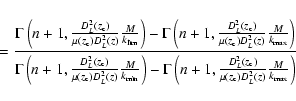 |
(B.9) |
The best fit values for n and
![]() have been found at each
redshift bin to be: n=4,4,5,6 and
have been found at each
redshift bin to be: n=4,4,5,6 and
![]() (when
masses are in units of
(when
masses are in units of
![]() and fluxes are in units of
10-29 erg/cm2/s/Hz) at
and fluxes are in units of
10-29 erg/cm2/s/Hz) at
![]() ,
respectively.
As stated before, the correction factor
,
respectively.
As stated before, the correction factor
![]() is then multiplied
to the volume element
is then multiplied
to the volume element
![]() of any galaxy with mass
of any galaxy with mass
![]() ,
both in the
,
both in the
![]() binned GSMF as
well as in the Schechter best-fit. The correction is applied until it
exceeds a factor of two. The selection curves shown in
Fig. 1 have been computed with this criteria.
binned GSMF as
well as in the Schechter best-fit. The correction is applied until it
exceeds a factor of two. The selection curves shown in
Fig. 1 have been computed with this criteria.
The practical effects of this correction are shown in Fig. B.2, where we compare the GSMF with and without the applied correction, where we show that if we entirely ignore the incompleteness effects, the GSMF appears to drop significantly in the low mass bins.