A&A 424, 73-78 (2004)
DOI: 10.1051/0004-6361:20040567

Influence of a generalized Eddington bias on galaxy counts

P. Teerikorpi

Tuorla Observatory, University of Turku, 21500 Piikkiö, Finland

Received 31 March 2004 / Accepted 11 May 2004

Abstract
We study the influence of the Eddington bias on measured distributions, in particular counts of galaxies when the accuracy of magnitude measurements is variable, e.g. when it changes towards fainter objects. Numerical experiments using different error laws illustrate the effect on the measured slope, helping one to decide if the variable Eddington bias is important, when the simple analytic correction is no longer valid. Common views on the origin and appearance of the Eddington bias are clarified and its relation to the classical Malmquist bias is briefly discussed. We illustrate the "Eddington shift'' approach with the counts of bright galaxies in the LEDA database.

Key words: galaxies: statistics

1 Introduction

Here we study the Eddington bias in a generalized form, keeping in mind applications for galaxy counts if the magnitude accuracy is variable. We assess how much these effects may influence the counts. For example, to be more immune to local structures, the counts of bright galaxies should be all-sky, but these are currently based on data with variable accuracy. In deep counts the accuracy may drop significantly within a few faintest magnitudes. The historical roots of the Eddington bias are in stellar parallaxes, see Sandage & Saha (2002) for an interesting discussion.

We review the classical Eddington bias (Sect. 2) and discuss its origin (Sect. 3) as a background to the more general cases when the sample is made of subsamples with different measurement accuracy (Sect. 5) or when the accuracy systematically depends on the magnitude (Sect. 7). In Sect. 4 "the Eddington shift'' is introduced as a way to treat the data in a special case. Numerical simulations illustrate some cases (Sect. 6) and different systematic error laws (Sect. 8). In Sect. 9 the ideas are applied to the LEDA galaxy sample. Main conclusions are found in Sect. 10. In the Appendices the Eddington and Malmquist biases are considered when they are coupled.

2 The classical Eddington bias

Eddington (1913) posed and briefly discussed the question: if the observed or experimental distribution function of quantities X with measured values x is EX(x), what is the true distribution of errorless quantities TX(x), when the errors of measurement $\epsilon$ are assumed to have a Gaussian distribution with dispersion $\sigma $? In Eddington (1940), he studied this issue in some detail, after a contribution by Dyson (1926).

Eddington derived the following general relation between the two distributions:

 \begin{displaymath}T(x) = E(x) - \frac{1}{2} \sigma^2{\rm d}^2E(x)/{\rm d}x^2 + ... ...(\frac{1}{2} \sigma^2\right)^2{\rm d}^4E(x)/{\rm d}x^4 - ... ~ \end{displaymath} (1)

Such an inverse problem, inferring the true distribution from the observed one, has in its general form special mathematical difficulties (see Lindegren 1995 for a discussion in the case of parallaxes). In practice, when we consider number counts of magnitudes, it is convenient to inspect the familiar approximate case $N_{{\rm obs}}(m) = k {\rm e}^{~\beta m}$. Then the errorless count N(m) is obtained as

 \begin{displaymath}N(m) = N_{{\rm obs}}(m) {\rm e}^{-\frac{1}{2} \sigma^2 \beta^2}. \end{displaymath} (2)

Transforming to the usual presentation $N_{{\rm obs}}(m) = k' 10^{\alpha m}$one obtains a link between observed and true counts:

 \begin{displaymath}\log N(m) = \log N_{{\rm obs}}(m) - \frac{1}{2} \sigma^2 \alpha^2 / \log e . \end{displaymath} (3)

When the dispersion $\sigma $ is constant, this formula shows that on a $\log~ N(m)$ vs. m diagram a linear counts curve with $\alpha > 0$ will shift upwards, preserving its slope. So in this case the slope $\alpha$can be directly obtained from the observed counts, and Eq. (3) gives the constant correction to the counts. Vice versa, one may predict the observed counts from a theoretical or expected law. This approach is especially useful when the dispersion $\sigma $ is variable.

3 Notes on the origin of the Eddington bias

As a background for the following discussion it is useful to inspect a little closer the origin of the Eddington bias. The reason why the measured distribution differs from the true one is not always clearly appreciated. Sometimes it is overly simply said that it is due to (in the case of magnitudes) the increase of the distribution towards faint magnitudes. Indeed, according to Eq. (1) the bias vanishes when the measured distribution is constant. But it also vanishes for a linearly increasing (or decreasing) distribution, because then the second (and further) derivatives are zero.

One may say that the galaxies at a fixed measured magnitude originate either from brighter or fainter true magnitudes, due to the symmetric Gaussian error distribution. Galaxies originally at $m \pm \frac{1}{2}{\rm d}m$ are lost equally to the right and left. If the distribution is constant, it is immediately clear that "incomers'' from the right and the left compensate for those losses. But also if the distribution is linear (and increasing to the right), the smaller number of incomers from the left are exactly compensated by the larger number from the right - their sum is the same as the loss[*]. The compensation may be incomplete and the bias in the counts appears, if the distribution function is not linear and has its 2nd derivative non-zero at m.

One sometimes reads that the Eddington bias is important only close to the magnitude limit. Actually it operates at all magnitudes, as is clear from the explanation above. It is a relative of the classical Malmquist (1920) bias, which also works at all m. A main result of Lutz & Kelker (1973) was that the bias in stellar parallaxes occurs at all parallaxes. In Appendix A we briefly compare the Eddington and Malmquist biases and ask what happens when they work in concert.

4 Constant dispersion

The exponential law of counts is convenient mathematically and is of course expected, when the number density law is $n(r) \propto r^{D-3}$: $N(m) \propto {\rm e}^{~\beta m} = {\rm e}^{\frac{D}{3} 1.382 m} = 10^{\frac{D}{3}0.6m}$, where $1.382 = 0.6/\log e$. D = 3 corresponds to a uniform spatial distribution (the well-known prediction for counts: 100.6m). Values D < 3 appear e.g. in fractal distributions.

4.1 The Eddington shift

Consider the observed magnitude interval $m \pm \frac{1}{2}{\rm d}m$. The galaxies counted at this magnitude window originate from different true magnitudes. In the case of an exponential (true) magnitude distribution $N(m) = k {\rm e}^{~\beta m}$it is easy to calculate (1) the number $N(m_{{\rm obs}})$ of galaxies at $m_{{\rm obs}}$, and (2) the distribution of the error $\epsilon$, when the original true magnitude is $m_{{\rm obs}} + \epsilon$ and the individual measurement errors follow a Gaussian law with the dispersion $\sigma $.

The result for (1) is essentially Eq. (2): $N_{{\rm obs}}(m) = N(m) {\rm e}^{\frac{1}{2} \sigma^2 \beta^2}$. This formula may be used to correct the counts by the constant factor. Note that the same corrected result is obtained if one increases each observed magnitude by the quantity $\frac{1}{2} \sigma^2 \beta = \frac{1}{2} \sigma^2 (\alpha /\log e) = 1.15 \sigma^2 \alpha$ and then repeats the counts, i.e.:

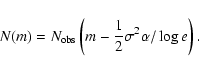\begin{displaymath}N(m) = N_{\rm obs}\left(m-\frac{1}{2}\sigma^2 \alpha / \log e\right). \end{displaymath} (4)

This quantity, the "Eddington shift'', is reminiscient of the classical Malmquist bias, but divided by two.

4.2 The Malmquist shift

The result for (2) above, also visible from Eq. (10) in Eddington (1940), is

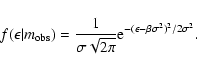\begin{displaymath}f(\epsilon \vert m_{\rm obs}) = \frac{1}{\sigma \sqrt{2\pi}} {\rm e}^{-(\epsilon - \beta \sigma^2)^2/2\sigma^2}. \end{displaymath} (5)

In other words, the galaxies counted at mhave their true original magnitude on the average at $m + \beta \sigma^2$. This is an analogue of the Malmquist bias in this case. One might be tempted to restore the true distribution by shifting each magnitude by this amount! In reality, the number of galaxies at the measured interval $m \pm \frac{1}{2}{\rm d}m$ is not the same as the number at the "Malmquist shifted'' (true) magnitude $m + \beta \sigma^2 \pm \frac{1}{2}{\rm d}m$. Only at the brighter magnitude $m + \frac{1}{2}\beta \sigma^2 = m + \frac{1}{2}(\alpha /\log e)\sigma^2$ is the true number the same as at the measured magnitude (Appendix B).

5 Non-constant dispersion

In practice, things are more complex if the sample is made from subsamples with different levels of precision, or standard deviation, $\sigma $ in measured magnitudes. Here two basic cases appear: 1) on average, the errors do not depend on the magnitude, or 2) there is a systematic change towards larger errors when the magnitude increases. We discuss in this section the first case.

Assume that one can assign to each galaxy two different mean errors $\sigma_1$ or $\sigma_2$ and these two classes are similarly (exponentially) distributed along m. Then one may apply to each magnitude its own Eddington shift, and then do the counts. The correction does not change the slope, but will lead to a more accurate amplitude and may reduce fluctuations. This may be generalized to the case when there are several classes with different $\sigma $. Also, if a catalogue contains magnitudes as weighted averages from two independent sources with different $\sigma $, one may use the weighted $\sigma $ in the correction.

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{0567_f1a.eps}\vspace*{3mm} \includegraphics[width=8.5cm,clip]{0567_f1b.eps} \end{figure} Figure 1: a) Differential counts for simulated uniform space distribution. Dots: no measurement error. Open circles: errors with $\sigma = 0.5$ mag. The straight line has the slope 0.6. At faint magnitudes the counts with error in the measured magnitudes become artificially distorted. The Eddington bias is seen at magnitudes brighter than 15.5. b) Counts for uniform space distribution. Open circles: measurement errors with randomly chosen $\sigma = 0.5, 0.7$, or 0.9 mag. Triangles: The measured magnitude of each galaxy is changed by the Eddington shift, then counted. The solid line is the initial regression line as in  a).
Open with DEXTER

6 Numerical simulations

We characterize the true radial space distribution of galaxies using the parameter D. It is like the fractal dimension only in the sense that the radial number density around us is $\propto$rD-3, which we generate with $0 < D \leq 3$.

6.1 Creating the magnitude distribution

If the variable $\xi$ is randomly and uniformly sampled from the interval (0, 1), then the probability distribution P(y) for the variable $y = \xi^d$(d > 0) is (Kalos & Whitlock 1986):

 \begin{displaymath}P(y) = y^{\frac{1}{d}-1}/d \end{displaymath} (6)

in which y also obtains values in (0, 1). Regarding P(y) as the number of galaxies within dy in this distance range, the exponent din the transformed variable y can be written in terms of Das d = 1/D.

In this way one may generate in a dimensionless distance interval (0, 1) a number density distribution corresponding to the assumed D. Transformation to a physical distance range from 0 to  $R_{\rm max}$ and then to distance moduli (and, hence, magnitudes) allows one to study the $\log~ N$ vs. m distribution, when one stays a few $\sigma $ (mag) away from the maximum distance modulus close to which the counts become distorted (in real galaxy space there is no such ultimate wall). We use sufficiently large numbers in these experiments to smooth out fluctuations.

6.2 Simulating the classical bias

Figure 1 shows a test simulation for the uniform distribution, without and with measurement error ( $\sigma = 0.5$ mag), on an arbitrary magnitude scale interval. The straight lines, actually regression lines, both are very close to the theoretical slope = 0.6. Note how the counts with measurement error are distorted at the faint end - this is an artifact - but along several magnitudes at the bright side they are shifted upwards by a constant amount in $\log~ N$. This is the classical Eddington bias. Its size is close to that expected from Eq. (3), or $\Delta \log N = 1.15 (0.5)^2 0.6^2 \approx 0.1$.

6.3 Simulating the correction by Eddington shifts

We generate counts for a uniform distribution, using three different $\sigma = 0.5$, 0.7, and 0.9 mag, randomly and equally likely chosen for each galaxy. Figure 1b shows that the resulting counts preserve the original slope. The counts made after the Eddington shifts (triangles) follow the counts without measurement errors well. This shows that applying the Eddington shift gives the correct counts.

7 Systematically varying error

Errors might increase towards faint magnitudes, so that $\sigma = \sigma (m)$. In such a case it is not allowed to use Eq. (3) or the Eddington shifts to correct the magnitudes and the counts, not even with $\sigma = \sigma (m)$. This is because the measuring errors at $m-\Delta m$ and $m + \Delta m$ are important for the resulting bias at m. If the errors are smaller at the bright side, then this makes the compensation, as discussed in Sect. 3, still more incomplete and thus enhances the Eddington effect and the attempt to correct it analytically will generally lead to an undercorrection. This makes numerical experimenting a necessary and efficient way to study the influence of the Eddington bias on counts when the error depends on the magnitude and may be large.

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{0567_f2a.eps}\vspace*{3mm} \includegraphics[width=8.5cm,clip]{0567_f2b.eps} \end{figure} Figure 2: $\log N(m)$ vs. m diagrams showing differential counts for a simulated space distribution thinning outwards with D = 2.2. The relation with the slope 0.44 was generated with no measurement error. The behaviour of  $\sigma~(m)$ is shown at the bottom of the diagrams. In  a) $\sigma $ increases linearly. In  b) a constant $\sigma $ is followed by an exponential increase.
Open with DEXTER

8 Some interesting initial slopes

In addition to the slope 0.6, we illustrate the effect with another input value 0.44 (such a smaller value is locally expected if $D \approx 2.2$). How much can systematically varying measurement errors change such slopes in counts?

We first experimented with a linear relation between $\sigma $ and m: $\sigma = \sigma_0 + a(m-m_0)$. We take $\sigma_0 = 0$, and put m0 = 11 mag. Figure 2a gives an example of the influence of this type of Eddington bias, when the input slope is 0.44. Inserted in the diagram is $\sigma (m)$ for a = 0.12. If the true $\alpha = 0.44$, then this a leads to an observed slope of 0.50.

A more realistic exponential law for the behaviour of the error leads to a slow increase at the beginning and a more rapid increase at faint magnitudes:

 \begin{displaymath}\sigma = \sigma_0, ~ (m \leq m_0); ~~ \sigma = \sigma_0 + a\left({\rm e}^{b(m-m_0)} - 1\right), ~( m > m_0). \end{displaymath} (7)

Figures 2b and 3 give examples of this case, with $\sigma_0 = 0.1$ and m0 = 13 mag. Now the observed slopes become somewhat steeper than in the case of a linear error law, for the same $\sigma $ at the faint end.

Furthermore, inspection of Fig. 2 illustrates how the Eddington bias is larger, say, at the magnitude where the increasing $\sigma (m)$ reaches 0.5 mag than for the case of the constant $\sigma = 0.5$ mag in Fig. 1. If one uses at the end of the magnitude interval ( $\Delta m = 4$) the simple formula based on Eq. (3) (cf. Huang et al. 1997) $\alpha_{\rm obs} \approx \alpha + 1.15\alpha^2 (\sigma_{{\rm m_2}}^2 {-} \sigma_{{\rm m_1}}^2) /\Delta m$with the constants $\sigma_{{\rm m_1}} = 0.1$ and $\sigma_{{\rm m_2}} = 0.6$ to calculate the change of the original slope 0.44, one obtains a too shallow slope of 0.46, instead of 0.53.

The increasing error at the faint magnitude end makes the counts there decline upwards leading to a steeper slope when a straight line is fitted for the whole magnitude range. Within the faintest two magnitudes the slope is still steeper, e.g. in Fig. 2b it approaches 0.55-0.6.

Figure 3 gives an example for the uniform distribution. Generally one expects a slope larger than 0.6. Vice versa, an observed slope of 0.6 does not necessarily imply a perfect agreement with a uniform spatial distribution, unless the measurement errors are quite small.

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{0567_f3.eps} \end{figure} Figure 3: $\log N(m)$ vs. m diagrams showing differential counts for a uniform space distribution. Dots mean no measurement error. Other symbols refer to errors increasing as in Fig. 2b.
Open with DEXTER

9 An application to the LEDA galaxy sample

The LEDA extragalactic database currently offers a catalogue of homogeneous parameters of galaxies for the largest available sample. Made from the amalgamation of all available catalogues and continually being completed with the flow of new data, the completeness of the LEDA sample has been studied over the years by inspecting the counts (Paturel et al. 1994; Paturel et al. 1997; Gabrielli et al. 2004; Courtois et al. 2004). Simultaneusly, the counts give information about the slope of the bright end of the galaxy counts, hence on the space density law. Here we briefly illustrate the above approach to LEDA counts. We are also interested in seeing if the counts are consistent with the radial density law $D \approx 2.2$(Teerikorpi et al. 1998).

We take all the galaxies from LEDA satisfying the following conditions: 1) The total B magnitude and its $\sigma $ are given. 2) It is found at galactic latitudes $\mid b \mid \ > 25$ deg. 3) Its B-magnitude is in the range from 9 to 16. The total number of such galaxies is 46 481, about equally divided between the two Galactic hemispheres.

Figure 4a shows the uncorrected counts for two subsamples, for the galaxies with $\sigma \leq 0.2$ and for those with $\sigma > 0.2$ ($\sigma $may reach 1 mag or even more). One sees that:

1)
In the magnitude range B < 14 both subsamples follow about the same linear $\log N$ line. This suggests (as may also be seen from $\sigma $ vs. B) that there is no significant systematic dependence of $\sigma $ on B in this range.

2)
At magnitudes fainter than $B \approx 14$ the two subsamples diverge: the galaxies with smaller assigned $\sigma $ are more numerous than those with apparently less accurate magnitudes with $\sigma > 0.2$.
The bifurcation probably reflects the fact that new additions to LEDA at these magnitudes are galaxies with accurate CCD photometry, while not all the old ones with poorer $\sigma $ have been reobserved. One may apply as a first approximation Eddington shifts $1.15\sigma^2 \alpha$when counting the brighter galaxies. This has been done in Fig. 4b, which also includes the linear regression result within the range $10.7 < B \leq 13.5$, giving the slope $\alpha = 0.44$. In this example the corrections are mostly not large (though they slightly decrease the scatter), but the procedure and inspection of the behaviour of errors are essential in general for a proper assesment of the result.
  \begin{figure} \par\includegraphics[width=8.6cm,clip]{0567_f4a.eps}\vspace*{3mm} \includegraphics[width=8.6cm,clip]{0567_f4b.eps} \end{figure} Figure 4: a) The counts within 10 < B < 16 for the all-sky LEDA galaxies with $\mid b \mid \ > 25$ deg. Those with assigned $\sigma \leq 0.2$ (triangle) and $\sigma > 0.2$ (open circle) have been shown separately. b) The counts after each galaxy has been Eddington shifted, using the slope = 0.44. The sum of the counts follows tightly the slope 0.44 above B = 10.5 up to 13.5. For problematic fainter magnitudes we show the uncorrected total counts.
Open with DEXTER

Qualitatively, the steepening of the slope at B > 13.5 is reminiscent of what happens in simulations (Fig. 2b). However, for it to be due to the Eddington effect, the accuracy should decrease significantly in this magnitude range, contrary to the behaviour of $\sigma $ as given in LEDA.

The shallow slope at brighter magnitudes could reflect either a local flattened inhomogeneity (Paturel et al. 1994) or more generally a fractal-like distribution of galaxies, with a fractal dimension around 2-2.2 (Sylos-Labini et al. 1998; Gabrielli et al. 2004). This slope is also consistent with the average radial space density law, derived using photometric distances to KLUN-galaxies and a method which accounts for incompleteness, corresponding to $D \approx 2.2$ from 20 Mpc up to about 100 Mpc (Teerikorpi et al. 1998). This is in agreement with the fractal analysis of the LEDA galaxies by Di Nella et al. (1996) who derived D = 2.2 within a similar scale. A new method of 2-point conditional density by Baryshev & Bukhmastova (2004) gave for the LEDA galaxies $D = 2.1 \pm 0.1$.

For the change of the slope, one may empirically find a typical distance for $B \approx 14$, from the radial velocity vs. magnitude diagram easily generated for the LEDA galaxies. The velocity turns out to be around 5000 km s-1, which means a distance 100/h50 Mpc. As the completeness of the sample and the behaviour of the accuracy at faint magnitudes needs further study, we leave open the interpretation of this feature (perhaps we are encountering a wall structure in the hypergalactic plane; Di Nella & Paturel 1994).

If one calculates the regression line up to 16 mag, one obtains a slope of about 0.5 (e.g. Gabrielli et al. 2004; Courtois et al. 2004). The present exercise suggests that at brighter magnitudes the slope is shallower. In particular, there is no evidence for the slope 0.6 in that magnitude range where the old counts by Hubble (1926) and Shapley & Ames (1932) were once regarded as showing an almost uniform distribution.

10 Conclusions

$\bullet$
Understanding the basic reason for the Eddington bias makes it more obvious that in galaxy counts it operates at all magnitudes and is affected by systematically varying measurement accuracy.
$\bullet$
When the counts follow an exponential law and the accuracies of measurements $\sigma $ do not depend on apparent magnitude, one may correct each magnitude by an Eddington shift depending on $\sigma $ for each galaxy and the slope $\alpha$ of the counts. Simulations show that the counts made after these corrections restore the counts expected without measurement errors.
$\bullet$
Numerical experiments show that magnitude errors increasing towards faint galaxies can change the slope of the counts more strongly than usually expected from the simple classical formula valid for a constant accuracy.
$\bullet$
The examples are useful guides when inspecting a set of counts. If one knows that the errors increase significantly (at least $\frac{1}{2}$ times those in Figs. 2 and 3) towards faint magnitudes, one should analyze its influence using numerical experiments tailored for that specific case.
$\bullet$
The approach via Eddington shifts was illustrated with LEDA galaxies, applicable at bright B magnitudes 10-14 where the slope in the counts (0.44) is the same for small and large $\sigma $.
$\bullet$
In the Appendices we discuss the coupling of Eddington and Malmquist biases in the case of an exponential m distribution. In particular, Appendix A shows that the average distance modulus for magnitude selected standard candles at observed magnitude m requires a correction $(\sigma_\epsilon^2 + \sigma_M^2)(\alpha / \log e)$.

Acknowledgements
I would like to thank Yu. Baryshev, A. Butkevich, H. Courtois, G. Paturel and F. Sylos Labini for inspiring discussions and comments on the manuscript. This study has been supported by the Academy of Finland (project "Fundamental questions of observational cosmology''). We have made use of the Lyon-Meudon Extragalactic Database (LEDA) supplied by the LEDA team at the CRAL-Observatoire de Lyon (France).

Appendix A: Eddington together with Malmquist

It is useful to see how the Eddington bias works with the classical Malmquist bias (or the Malmquist bias of the first kind, as termed in Teerikorpi 1997). In the former case one looks at galaxies through the "magnitude window'' $m \pm \frac{1}{2}{\rm d}m$ and counts their number. The magnitudes defining the window have Gaussian errors. However, in the latter case one may regard the measured magnitudes as without errors, but the galaxies in space have a Gaussian luminosity function with dispersion $\sigma_M$. Here one does not primarily count the galaxies, but considers their average absolute magnitude as seen through the magnitude window. The Malmquist bias depends on the derivative  ${\rm d}\ln N(m)/{\rm d}m$:

 \begin{displaymath}\langle M_m \rangle = M_0 - \sigma_M^2 {\rm d}\ln N(m)/{\rm d}m, \end{displaymath} (A.1)

hence it may be non-zero even in the situation when the Eddington bias is zero (N(m) linear). Indeed, for the Malmquist bias not only are the numbers important (as they are for the Eddington bias), but also the absolute magnitudes.

A question arises when there are measurement errors in m. How do these errors affect the initial Malmquist bias? In the general case when the derivative ${\rm d}\ln N(m)/{\rm d}m$ is not constant, the Eddington bias changes it, which causes error in $\langle M_{{\rm m}} \rangle$ if one uses the observed (measured) distribution of m in Eq. (A.1). In principle one should first restore the original distribution observed "from the sky'' (by making an Eddington correction) and only then use the Malmquist formula. In practice, this may be difficult.

Fortunately, an exponential distribution of m makes things again much easier. In that case the derivative in Eq. (A.1) will be constant and at all m the absolute magnitudes are similarly distributed. As random errors at a true m scatter the galaxies independently of their absolute magnitudes, the reorganized  $N(m_{{\rm obs}})$ distribution has the same distribution of absolute magnitudes at each  $m_{{\rm obs}}$ as the original one. Thus in this important special case the Eddington bias does not distort the Malmquist bias.

When one uses the Malmquist bias formula in distance determination, one calculates the distance modulus $m - \langle M \rangle _m$, having in mind the correct values of both m and $\langle M \rangle _m$. As was mentioned in Sect. 4.2, the objects found at m actually have their true average m fainter, just by the Malmquist shift. Hence, instead of the apparent distance modulus m-M0, the Eddington and Malmquist corrected modulus is:

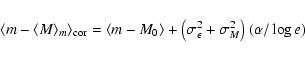\begin{displaymath}\langle m-\langle M \rangle _m \rangle_{{\rm cor}} = \langle ... ... \left(\sigma_\epsilon^2 + \sigma_M^2\right)(\alpha / \log e) \end{displaymath} (A.2)

in which $\sigma_\epsilon$ is the standard deviation of the measurement error. It is important to note that this formula applies on average to magnitude-selected standard candles at an observed magnitude m, say, in the Hubble diagram considered as $\log~ z$ versus m. It also assumes that the initial distribution N(m) is exponential.

Appendix B: Eddington and Malmquist shifts

As the difference between the Eddington and Malmquist shifts may still appear paradoxical, we show here, going backwards, that the individual Gaussians $G_{\sigma}(m_{{\rm obs}} + \sigma^2\beta -m)$ around $m_{{\rm obs}} + \sigma^2\beta$ (the Malmquist shift) sum up to the correct total N(m) at the errorless magnitude m (as predicted by the Eddington shift), when $m_{{\rm obs}}$ is taken from $-\infty$ to $\infty$ and the Gaussians are weighted by the exponential counts $k {\rm e}^{~\beta m_{{\rm obs}}}$:

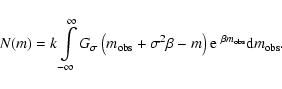\begin{displaymath}N(m) = k \int\limits_{-\infty}^{\infty}G_{\sigma} \left(m_{{\... ... -m\right) {\rm e}^{~\beta m_{{\rm obs}}}{\rm d}m_{{\rm obs}}. \end{displaymath} (B.1)

The dispersion $\sigma $ in the Gaussian and the exponent $\beta$ in the magnitude distribution become coupled and one can evaluate the integral as

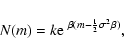\begin{displaymath}N(m) = k {\rm e}^{~\beta (m - \frac{1}{2}\sigma^2\beta)}, \end{displaymath} (B.2)

where the Eddington shift appears, and then the Eddington correction:

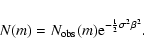\begin{displaymath}N(m) = N_{{\rm obs}}(m) {\rm e}^{-\frac{1}{2} \sigma^2 \beta^2}. \end{displaymath} (B.3)

References

 
Copyright ESO 2004