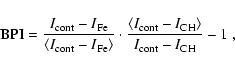 |
(1) |
A&A 423, 1147-1157 (2004)
DOI: 10.1051/0004-6361:20035879
K. Langhans 1,2 - W. Schmidt 1 - T. Rimmele 3
1 - Kiepenheuer-Institut für Sonnenphysik,
Schöneckstr. 6, 79104 Freiburg, Germany
2 -
The Institute for Solar Physics of the Royal Swedish Academy of Sciences, AlbaNova University Centre, 10691 Stockholm, Sweden
3 -
National Solar Observatory, PO Box 62, Sunspot, NM 88349, USA
Received 16 December 2003 / Accepted 18 May 2004
Abstract
A detailed analysis of high-resolution spectra obtained in three
different wavelength regions (at 430 nm, 526 nm and 569 nm) of G-band bright points in the solar photosphere is presented.
They show an average intensity contrast of 11% with respect to the
"quiet'' sun reference.
The CH lines are weakened in the bright point interior.
The atomic lines, too, e.g. the Fe I line at 569.15 nm, weaken
in the bright point interior.
In contrast thereto, the absorption line of single ionized iron at
526.48 nm remains almost constant between bright point interior and
the immediate surroundings.
Line-of-sight velocities show a stronger downflow
within bright points than in the close environment.
A net downflow relative to the intergranular surroundings of around 80 m/s is measured.
Filling factors are calculated from a comparison with synthesized spectra for different flux tube models and are used to estimate the "true'' velocity
in bright points with respect to their immediate surroundings.
We obtain up- and downflows in the order of one km s-1, in agreement with the magneto-convective picture of the formation and dispersal of magnetic flux tubes.
From the different behavior of the metallic lines and the CH lines we conclude that the line-weakening process that leads to the G-band bright points is mainly due to hot-wall radiation. This confirms that these bright points are indeed magnetic flux elements.
Key words: Sun: photosphere
Table 1: Top: specification of the spectral data. Bottom: specification of the image data. Abbreviations: FF - Flat Field, SNR - Signal-to-Noise Ratio.
In the basic theoretical picture of an isolated flux tube in magneto-hydrostatic equilibrium the magnetic pressure inside the tube is balanced by a reduced density of its atmosphere relative to the surrounding non magnetic atmosphere. This leads to a reduced opacity.
The iso-surfaces of optical depth are depressed at the location of the tube and hotter material of the exterior becomes exposed forming the "hot wall'' (e.g. Spruit & Zwaan 1981).
The radiation from the side may affect the tube interior in two ways: heating of the tube interior through radiative influx and photo-dissociation of the CH molecule by UV-radiation from the hot wall. The latter was first conjectured by Rutten (1999) and further discussed by e.g. Rutten et al. (2001) and Sánchez Almeida et al. (2001).
Rutten et al. (2001) conclude from LTE spectral synthesis based on a standard flux tube model that the evacuation of the flux tube leads to execss CH depletion within the tube. This results in a relatively more transparent flux tube, through which radiation from hot subsurface layers can escape. The G-bands contrast increases over the continuum due to an "enhanced hot wall effect''.
Further model calculations that relate G-band brightness and magnetic flux concentrations (all based on semi-empirical models) reproduce reasonably the observed bright point contrasts as well (Steiner et al. 2001; Sánchez Almeida et al. 2001; Kiselman et al. 2001).
Steiner et al. (2001) note that CH depletion due to collisional dissociation in the deep photospheric layers alone would be a sufficient mechanism to explain the enhanced G-band contrast. Sánchez Almeida et al. (2001) conclude further that the CH concentration is not controlled by radiation.
Ab-initio simulations of radiative magneto convection (Uitenbroek 2003; Schüssler et al. 2003) confirm this physical model of small scale magnetic flux concentrations as evacuated laterally heated structures.
That the CH lines indeed weaken in the spectrum of G-band brightenings was confirmed by Langhans et al. (2001) by recording the G-band
spectrum from 430.24 nm to 430.78 nm of a few isolated G-band bright points.
To measure the CH abundance variations from spectroscopic G-band data
Langhans et al. (2002) defined the Bright Point Index (BPI) as the ratio:
With the observations presented in this paper we improved and extended our previous observations (cf. Langhans et al. 2001,2002). Section 2 describes the observations, data characteristics and error sources. Section 3 deals with the method of analysis. Our results are presented and discussed in Sects. 4 and 5.
The HSG slit width was set to 40 ![]() m corresponding to 0.3 arcsec.
Spectral maps of
m corresponding to 0.3 arcsec.
Spectral maps of
![]() arcsec2 (slit length 40 arcsec) were obtained by repeated spatial scanning of the spectrograph slit across the region of interest.
The step size was 0.3 arcsec.
The detailed observing parameters are given in Table 1.
The NSO adaptive optics (AO) system (Rimmele 2000; Rimmele et al. 1999) was correcting the low order wave
front aberrations.
The system was tracking on a pore at heliographic
position N 20.2
arcsec2 (slit length 40 arcsec) were obtained by repeated spatial scanning of the spectrograph slit across the region of interest.
The step size was 0.3 arcsec.
The detailed observing parameters are given in Table 1.
The NSO adaptive optics (AO) system (Rimmele 2000; Rimmele et al. 1999) was correcting the low order wave
front aberrations.
The system was tracking on a pore at heliographic
position N 20.2![]() W 12.3
W 12.3![]() corresponding to
corresponding to ![]() .
An integration time of 1.5 s was required to achieve a sufficient signal-to-noise ratio of the G-band spectra.
The spectra at 526 nm and 569 nm, the broad band and slit jaw images were
taken with the same integration time as the G-band spectra. The combination of
white light image and G-band slit-jaw images allowed to identify the bright points (cf. Berger et al. 1998).
The sampling of the G-band spectra was 0.09 arcsec pixel-1 along the slit and
1.08 pm pixel-1 in wavelength.
.
An integration time of 1.5 s was required to achieve a sufficient signal-to-noise ratio of the G-band spectra.
The spectra at 526 nm and 569 nm, the broad band and slit jaw images were
taken with the same integration time as the G-band spectra. The combination of
white light image and G-band slit-jaw images allowed to identify the bright points (cf. Berger et al. 1998).
The sampling of the G-band spectra was 0.09 arcsec pixel-1 along the slit and
1.08 pm pixel-1 in wavelength.
Dark current subtraction and flat field corrections were done separately for each type of data. The spectra at 526 nm and 569 nm as well as the broadband continuum data and the slit jaw data were scaled and aligned with respect to the G-band spectra using images of a resolution target to determine image scale factors and image offsets. In Figs. 1 and 2 the common field-of-view (FOV) is displayed for the different data sets.
The data quality decreases continuously with distance from the tracking point (Fig. 1) The dashed box in Fig. 2 e marks the region, where the image quality in the broadband channel is close to the resolution limit of the telescope. The common area of both marked frames is used for further analysis. For the spectral data, the sampling along and perpendicular to the slit is given by the pixel size of the detector (0.2 arcsec) and the slit width (0.3 arcsec), respectively.
The measurement error of the observed broadband images consists of detector and photon noise and a contribution due to imperfect flat field correction. The same errors contribute to the error budget of the spectral data (cf. Table 1). The contribution of spatially scattered light within the spectrograph was estimated to 8.7% by a comparison of the contrast of the pore in the white light image and in the spectra. We estimate the contribution of spectral scattering to 4% in the line core, by comparing a high-resolution atlas-spectrum Wallace et al. (1998), convolved with the instrument profile of the HSG, to the observed data. A detailed error discussion can be found in Langhans (2003).
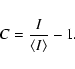 |
(2) |
Bright point identification is often based on the difference method developed by Berger et al. (1998). However, the spectral data presented here may offer more and better ways to identify bright points. For example, the difference of continuum intensity at 430.41 nm and the integrated G-band intensity or, alternatively, the CH-line core intensity can be used in order to enhance the contrast for easier identification of bright points. The BPI is used as an additional indicator to distinguish the brightenings of the two classes of bright points as defined by Langhans et al. (2002).
Physical properties of bright points are determined from our one-dimensional spectral data separately for
the bright point interior and its surroundings.
The interior of a bright point is defined as follows: data points with a BPI-value above two thirds of the maximum BPI define the size, S, of the bright point.
The adjacent data points within a range of ![]() define the immediate surroundings.
This definition is illustrated in Fig. 4 (dashed lines).
define the immediate surroundings.
This definition is illustrated in Fig. 4 (dashed lines).
![\begin{figure}
\par\includegraphics[width=7.4cm,height=10cm,clip]{0879fig1.eps}
\end{figure}](/articles/aa/full/2004/33/aa0879/Timg18.gif) |
Figure 1: Broadband data. One tick mark corresponds to 1 arcsec. Left: G-band image (broadband 1 nm at 430.5 nm, slit jaw camera), ritght: white light image (broadband 10 nm at 480 nm). Dashed box - region of reference. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=10cm,width=17.4cm,clip]{0879fig2.eps}
\end{figure}](/articles/aa/full/2004/33/aa0879/Timg19.gif) |
Figure 2: Spectral data. Example for one scan. One major tickmark corresponds to 1 arcsec. a) Continuum intensity at 430.41 nm, b)- e) Line core intensities of the analyzed absorption lines. Dashed box - region around tracking point of AO system with sufficient correction, solid box - exposures of high quality used for analysis. |
| Open with DEXTER | |
Table 2: Averaged properties of bright points, based on the spectral data (Int.: interior; Surr.: surroundings; Ref.: reference).
Spatial averages over all bright points within the sample were calculated for the interior and the immediate surroundings separately. The averaged bright point properties are listed in Table 2. The bright point sizes range from 0.18 arcsec to 0.63 arsec. The brightest point in the sample has a contrast of 28.3% and the weakest bright point shows a contrast of -2.3%. While the bright points on average stand out from their surroundings, they show no significant enhancement in the mean continuum intensity contrast. In the average over all bright points within the sample the continuum intensity contrast of interior and surroundings is almost equal. This confirms that the brightness of the G-band bright points is mainly a line effect. In particular this effect is observed in the CH lines. The depth of the CH lines in the bright point interior is (on average) reduced by 23% compared to the quiet sun value. A similar value is obtained for the weak Fe I line at 569.15 nm, while the line depression of the Fe II line is only slightly reduced.
The average value of all measured line widths and equivalent widths within the region of reference (as marked in Fig. 1) are used as reference.
In Figs. 3a,b the slit jaw and white light images of the
selected bright points are displayed. The FOV is
![]() ;
one tick mark corresponds to 0.25 arcsec.
We note that these images were not recorded strictly simultaneous with the spectral quantities shown in the graphs
(Figs. 3 d-k).
In the slit jaw images of the examples 1, 3 and 6 the slit is visible as a uniform gray bar across the image.
Black lines indicate the slit position for which the physical quantities were plotted in rows c
to k.
The spatial range of the line plots is indicated by grey vertical lines.
;
one tick mark corresponds to 0.25 arcsec.
We note that these images were not recorded strictly simultaneous with the spectral quantities shown in the graphs
(Figs. 3 d-k).
In the slit jaw images of the examples 1, 3 and 6 the slit is visible as a uniform gray bar across the image.
Black lines indicate the slit position for which the physical quantities were plotted in rows c
to k.
The spatial range of the line plots is indicated by grey vertical lines.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0879fig3.eps}
\end{figure}](/articles/aa/full/2004/33/aa0879/Timg21.gif) |
Figure 3: Individual Case Studies. a), b) Broadband images of the bright point examples in G-band (slit jaw images) and "white light''. c) Variation of G-band (dashed curve) and "white light'' intensity contrast along the slit (solid curve), taken from the broadband images. d) Continuum contrast. e) Contrast of integrated intensity. f) Doppler velocity. g) Bright Point Index. h) Variation in line core intensity. i) Variation in FWHM. k) Variation in equivalent width. Curve coding for d)- k): solid - CH, dashed - Fe I, dashed-dotted - Fe II, dotted - Ca I. |
| Open with DEXTER | |
The graphs in Fig. 3c show the intensity contrast of the white light (solid curve) and G-band images (dashed curve) along the slit. When intensity quantities based on spectral data are compared to quantities based on broadband intensities, the different spatial resolution should be taken into account. For clarity, the curves are displayed without error bars.
In the following we discuss properties of the selected individual bright point examples.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0879fig4.eps}
\end{figure}](/articles/aa/full/2004/33/aa0879/Timg22.gif) |
Figure 4: Illustration of the velocity measurements. Vertical dashed lines indicate the borders of bright point interior and immediate surroundings, respectively. Top: BPI. Bottom left: intensity contrast, continuum intensity (solid), integrated G-band intensity (dashed). Bottom right: flow velocity. |
| Open with DEXTER | |
Langhans et al. (2002) have shown that the bright points with an enhanced BPI are embedded in downflow regions. The comparison of the averaged interior and surroundings velocities for all bright points within our sample confirms those observations and in addition shows that the downflow within the bright point interior is stronger than in the immediate surroundings by about 73 m s-1 on average.
The location of a bright point does neither necessarily coincide with the minimal continuum
intensity nor with the strongest downflow in the intergranular lane.
The example shown in Fig. 4 illustrates this.
Due to insufficient resolution the velocity measurements in the interior and, espacially, in the immediate
surroundings of this bright point are most likely contaminated
by intergranular velocities on "both sides'' of the bright point. A clean separation of bright point velocity and intergranular
velocity is therefore not possible.
In addition, the influence of projected horizontal motions cannot be ignored: at the disk position of our observations (![]() )
a horizontal flow has a line-of sight component of 31%.
)
a horizontal flow has a line-of sight component of 31%.
Some bright point interiors show a clear velocity enhancement in comparison to their immediate surroundings.
Examples are shown in
Figs. 5b-d.
Figure 5a shows a bright point without any velocity variation correlated to BPI enhancement.
Instead the velocity variation is smooth and is typical for an intergranular lane.
Figures 5b-d show significant
variations of the line-of-sight velocity correlated to a BPI enhancement.
While in Fig. 5b the change is more
clear for the measurement based on the Fe I line shift, in
Fig. 5d the velocity based on the
Fe II-line shift shows the most significant variation toward an
upflow or at least a reduced downflow in the bright point interior.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0879fig5.eps}
\end{figure}](/articles/aa/full/2004/33/aa0879/Timg24.gif) |
Figure 5:
Four examples of velocity measurements of bright points.
Top: course of the BPI (solid curve, scale to the right) and the
G-band intensity contrast (dashed curve, scale to the left).
Bottom: velocity measurements (solid - CH, dashed - Fe I, dashed-dotted - Fe II).
The plotted error bars correspond to the 1 |
| Open with DEXTER | |
In Fig. 6 we compare the distribution of narrow-band continuum contrast, CH-line core contrast and
velocity vs. the BPI index for both the two-dimensional observations and the spectroscopic (one-dimensional) data.
The data points plotted in these scatter diagrams were selected according to the criterion:
intensity contrast
![]() .
The grey points represent the two-dimensional and the crosses the one-dimensional observations.
In both cases the the point clouds show very similar distributions.
The error ellipsoids in the correlation diagrams represent the rms-values of the total error
for the the one-dimensional data only.
The symbols refer to the examples described in Sect. 4.1.
The one-dimensional spectroscopic observations confirm the results of the two-dimensional spectral data, which had
slightly lower spatial resolution but better statistics.
.
The grey points represent the two-dimensional and the crosses the one-dimensional observations.
In both cases the the point clouds show very similar distributions.
The error ellipsoids in the correlation diagrams represent the rms-values of the total error
for the the one-dimensional data only.
The symbols refer to the examples described in Sect. 4.1.
The one-dimensional spectroscopic observations confirm the results of the two-dimensional spectral data, which had
slightly lower spatial resolution but better statistics.
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{0879fig6.eps}
\end{figure}](/articles/aa/full/2004/33/aa0879/Timg27.gif) |
Figure 6:
Correlation diagrams.
Criterion of data point selection is a G-band contrast
|
| Open with DEXTER | |
In comparison to the two-dimensional data the one-dimensional data produces slightly lower values of the line core contrast. This might be due to better spectral and spatial resolution achieved with the one-dimensional data, which results in a larger filling factor. A larger filling factor in turn causes an increase in the CH-line core intensity within a bright point.
The simulated and observed spectral quantities are plotted in the diagrams of Fig. 7. The bars indicate the range of values observed for bright point interiors. We conclude that the bright network model (FAL F) does not represent the observations of bright points. The bright network model predicts a rather low G-band contrast and a negative BPI, whereas observed bright points are characterized by a positive BPI. We note that due to spatial insufficient resolution the real G-band contrast is likely significantly higher than what we observe in our spectra, i.e., the discrepancy between bright network model and observations would be even more severe.
Both the G-band intensity contrast
![]() as well
as the BPI have the value 0 for the reference spectrum of the
quiet sun and the FAL C-spectrum, respectively.
Consequently both quantities can be used to calculate filling factors
as well
as the BPI have the value 0 for the reference spectrum of the
quiet sun and the FAL C-spectrum, respectively.
Consequently both quantities can be used to calculate filling factors
![]() based on the two remaining atmospheric models:
based on the two remaining atmospheric models:
The FAL P-model for a bright plage, which assumes unresolved magnetic elements, produces larger values for the BPI and the G-band intensity contrast than the observations do. In addition, the line depression and equivalent width show a larger reduction with respect to the reference model than what is observed.
Regarding the range of observed values, especially for the brighter bright points (large G-band contrast and high BPI), the observables match well with the FAL P-model predictions. We note again that due to insufficient resolution G-band contrast and BPI are likely underestimated in the observations.
The fairly good agreement between model and observations
is also reflected in the computed filling factors
![]() and
and
![]() .
The filling factors are close to unity for the maximum observables and 0.35 for the
averaged observed G-band contrast and 0.55 for the averaged BPI,
respectively.
.
The filling factors are close to unity for the maximum observables and 0.35 for the
averaged observed G-band contrast and 0.55 for the averaged BPI,
respectively.
The net-model represents an atmosphere of an isolated magnetic element with a hot atmosphere. This results in a strongly enhanced continuum intensity (cf. Steiner et al. 2001). The extraordinarily high BPI and G-band intensity contrast produced by this model is mainly caused by the large increase of the continuum intensity (cf. Table 3). The change in the CH-line depression is of the same order of magnitude as for the FAL P-model. The highest continuum intensity at 430.31 nm for an observed bright point reaches 7.9% of the continuum intensity predicted by the net-model.
In order to estimate an upper boundary for the actual observed continuum intensity we scale the observed contrast (7.9%)
with the lowest value for the computed filling factors (
![]() ). This results in an upper limit for
the actual intensity contrast of 0.76, which is still below the continuum intensity predicted by the the net-model.
This might be an indication that the net-model is actually too hot.
). This results in an upper limit for
the actual intensity contrast of 0.76, which is still below the continuum intensity predicted by the the net-model.
This might be an indication that the net-model is actually too hot.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0879fig7.eps}
\end{figure}](/articles/aa/full/2004/33/aa0879/Timg35.gif) |
Figure 7: Comparison of selected properties derived from synthetic spectra to observables. The bars indicate the range of values, observed for the bright point interior. Data points shifted to the left (thick symbols) refer to the CH line, data points shifted to the right (thin symbols) to Fe II and the centered symbols refer to Fe I. |
| Open with DEXTER | |
Table 3:
Top: continuum contrasts,
![]() ,
derived from synthetic spectra, with
respect to the FAL C-model atmosphere. The listed values from
observation refer to the average (maximum) over all observed bright point
interiors with respect to the spectrum of the reference region.
Bottom: filling factors derived from Eqs. (3) and (4).
,
derived from synthetic spectra, with
respect to the FAL C-model atmosphere. The listed values from
observation refer to the average (maximum) over all observed bright point
interiors with respect to the spectrum of the reference region.
Bottom: filling factors derived from Eqs. (3) and (4).
Taking the bright points as proxies for magnetic elements our measurements are in agreement with previous observations of red-shifted zero-crossing wavelengths of Stokes V profiles in network and plage regions (e.g. Sigwarth et al. 1999; Martinez Pillet et al. 1997). A net downflow of 0.5 km s-1 was measured from the average of all observed Stokes V profiles (cf. Sigwarth et al. 1999). For the smallest observed magnetic features the same authors observe "velocities of up to 5 km s-1 in both up- and downflows whereas for larger elements or clusters of several flux tubes the velocities become smaller and more uniform.'' Our sample of 46 bright points qualitatively gives the following results: both net downflows and upflows occur in individual bright points. However, the velocities we measured are much smaller than in the velocity measurements of Martinez Pillet et al. (1997) and Sigwarth et al. (1999), which refer only to the flow velocity of the magnetized part of the atmosphere.
Assuming that the observed bright points are the "white light'' signature of magnetic elements
and that the calculated filling factors
![]() and
and
![]() are correct the "real'' velocity difference of interior and immediate surroundings can be estimated.
This estimation is done in the following for two examples: (a) and (d) of
Fig. 5.
Example (a) coincides with a downflow.
The maximum BPI amounts to 0.193 and the maximum G-band contrast to 0.179.
This results in filling factors
are correct the "real'' velocity difference of interior and immediate surroundings can be estimated.
This estimation is done in the following for two examples: (a) and (d) of
Fig. 5.
Example (a) coincides with a downflow.
The maximum BPI amounts to 0.193 and the maximum G-band contrast to 0.179.
This results in filling factors
![]() and
and
![]() ,
respectively.
Taking these filling factors to scale the measured velocity difference
,
respectively.
Taking these filling factors to scale the measured velocity difference
![]() 100 ms-1results in an actual velocity difference of -700 ms-1 and -750 ms-1, respectively.
For example (d) the same estimation results in an upflow velocity of 1150 ms-1(
100 ms-1results in an actual velocity difference of -700 ms-1 and -750 ms-1, respectively.
For example (d) the same estimation results in an upflow velocity of 1150 ms-1(
![]() )
with respect to the immediate surroundings.
(Calculation based on
)
with respect to the immediate surroundings.
(Calculation based on
![]() m s-1, the maximum BPI of 0.209 and a maximum G-band contrast of 0.211.)
m s-1, the maximum BPI of 0.209 and a maximum G-band contrast of 0.211.)
A net downflow within magnetic elements is generally associated with the convective collapse of a magnetic element and according to
models occurs over time periods of a few minutes during a formation of a kG strength flux tube.
The upflow in magnetic elements might be explained by different
processes that can be distinguished by their temporal evolution.
Grossmann-Doerth et al. (1998) suggest that down-flowing gas might rebound in deeper
layers and result in upward propagating shocks.
Spruit & Zweibel (1979) conclude from convective stability analysis
that flux tubes with field strengths below a critical value (![]() 0.13 T) are unstable.
The instability may result in either a downflow or an upflow.
A downflow stabilizes the tube by intensifying the field strength
correspondingly the super-adiabatic effect.
An upflow reverses the process and causes flux tube dispersal.
Flux tubes at this state of evolution might also be candidates for the
observed bright points correlated with upflows.
0.13 T) are unstable.
The instability may result in either a downflow or an upflow.
A downflow stabilizes the tube by intensifying the field strength
correspondingly the super-adiabatic effect.
An upflow reverses the process and causes flux tube dispersal.
Flux tubes at this state of evolution might also be candidates for the
observed bright points correlated with upflows.
Rimmele (2004) presents results of flow field measurements of magnetic elements based on diffraction limited filtergram and image data. He finds strong narrow downflows at the edges of many small magnetic flux concentrations, while the plasma within the flux concentration is in rest at layers in the photosphere represented by Fe I 630.2 nm and 557.6 nm dopplergrams. Although we measure on average an increased downflow in the bright point interior in comparison to its immediate surroundings, the observations of Rimmele (2004) are in correspondence with a number of bright points within the observed sample (cf. velocity diagrams of bright points 2, 4 and 5 in Fig. 3). Rimmele (2004) points out that his sample of flux elements likely consists mostly of stable flux concentrations located in the vicinity of a small sunspot. Dynamic processes such as convective collapse or upward propagating shocks may not be present in this sample. Telescopes of larger aperture are needed to provide more quantitative measurements of the velocity flow field of small scale magnetic flux concentrations with sufficient time resolution to capture the dynamics.
This explains the extraordinarily strong weakening of the CH lines in magnetic flux tubes.
The high line density of both CH lines of the ![]() -
-![]() transition and the variety of neutral atomic lines enhances the line
weakening effect seen in the G band. Therefore the G-band intensity is an excellent tracer of small
scale magnetic field at the highest available spatial resolution.
transition and the variety of neutral atomic lines enhances the line
weakening effect seen in the G band. Therefore the G-band intensity is an excellent tracer of small
scale magnetic field at the highest available spatial resolution.
The BPI is a reliable tool to quantify the spectroscopic signature of G-band bright points and allows for a classification of G-band brightenings. Since the BPI is based on relative intensities, it is virtually independent on the photometric properties of the instrument used.
A comparison of the observed spectra with synthesized spectra produced with the net- and the FAL P-model indicates that the temperature effect in the models is overestimated in comparison to the line effect. In contrast to the synthesized spectra the observed spectra do not show a strongly enhanced continuum intensity at the bright points' locations. Most spectroscopic properties (e.g. BPI, G-band contrast and equivalent width) derived from the bright plage model (FAL P), or the net-model are within the range of the observed values (cf. Fig. 7). The modeled continuum intensities significantly exceed the observed values - especially for the net-model (cf. Table 3). These results indicate that the model atmospheres used are too hot. In part the observed continuum contrast might be caused by the fact that the small bright features are smeared out by the low intensity of the surrounding intergranular lanes due to the insufficient resolution. But the visibility of most bright points in the continuum and the high contrast observed in the integrated G-band intensity weaken this argument.
An additional hint that the direct temperature effect might be
less important than others is given by the behavior of the ionized iron
line at 526.48 nm and the CH line at 430.34 nm within the bright
points.
Based on the assumption that both lines form at similar height
- justified by model calculations using the radiation transfer code provided by Uitenbroek (1998) - the brightness
temperature obtained from the measured absolute intensity in the
Fe II-line core can be identified with the temperature at
![]() .
The unchanged Fe II-line core intensity within a G-band brightening
implies that the enhanced CH-line intensity most likely is not due to a direct temperature effect -
be it by means of the line source function or by enhanced dissociation of CH.
The CH dissociation is therefore most likely due to a process such as hot wall radiation.
The temperature gradient of the applied standard fluxtube models imply a considerable energy dissipation at very low heights of the fluxtube atmosphere that is hard to explain. Sideways irradiation avoids this problem but will require NLTE. This idea is discussed in more detail by Rutten (2002).
.
The unchanged Fe II-line core intensity within a G-band brightening
implies that the enhanced CH-line intensity most likely is not due to a direct temperature effect -
be it by means of the line source function or by enhanced dissociation of CH.
The CH dissociation is therefore most likely due to a process such as hot wall radiation.
The temperature gradient of the applied standard fluxtube models imply a considerable energy dissipation at very low heights of the fluxtube atmosphere that is hard to explain. Sideways irradiation avoids this problem but will require NLTE. This idea is discussed in more detail by Rutten (2002).
This explanation implies that G-band bright points are indeed magnetic flux tubes. Spectropolarimetric measurements of the small-scale magnetic field in and around bright points, with sufficient spatial and temporal resolution are needed to confirm our conclusions. In addition, more extensive simulations and modeling efforts will be needed in order to be able to interpret the observations.
Acknowledgements
J. Bruls provided useful hints and comments. Oskar Steiner generously offered his synthesized G-band data of the net-model atmosphere. Han Uitenbroek provided his radiation transfer code. K. Langhans' research was funded by the Deutsche Forschungsgemeinschaft (grant No. SCHM 1168/3). Now he is supported by the European Community's Human Potential Programme through the European Solar Magnetism Network (contract HPRN-CT-2002-00313). The DST data were obtained by K.L. as a visiting astronomer at the National Solar Observatory, operated by the Association of Universities for Research in Astronomy, Inc. (AURA), under cooperative agreement with the National Science Foundation.