A&A 423, 909-918 (2004)
DOI: 10.1051/0004-6361:20034431
L. C. Popovic1,2,3 - E. Mediavilla4 - E. Bon1,3 - D. Ilic5
1 - Astronomical Observatory, Volgina 7, 11160 Belgrade,
Serbia
2 -
Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482
Potsdam, Germany (Alexander von Humboldt fellow)
3 -
Isaac Newton Institute of Chile,
Yugoslavia Branch, Yugoslavia
4 -
Instituto de Astrofísica de Canarias C/ Vía Làctea,
s/n
38200 La Laguna, Tenerife, Spain
5 -
Department of Astronomy, Faculty of Mathematics, University of
Belgrade, Studentski trg 16, 11000 Belgrade, Serbia
Received 2 October 2003 / Accepted 3 May 2004
Abstract
We present an investigation of the
structure of the emission line region in a sample of 12
single-peaked Active Galactic Nuclei (AGNs). Using the high
resolution H![]() and H
and H![]() line profiles observed with the
Isaac Newton Telescope (La Palma) we study the substructure in the
lines (such as shoulders or bumps) which can indicate a disk or
disk-like emission in Broad Line Regions (BLRs). Applying
Gaussian analysis we found that both kinds of emission regions,
BLR and NLR, are complex. In this sample the narrow [OIII] lines
are composites of two components; NLR1 which have random
velocities from
line profiles observed with the
Isaac Newton Telescope (La Palma) we study the substructure in the
lines (such as shoulders or bumps) which can indicate a disk or
disk-like emission in Broad Line Regions (BLRs). Applying
Gaussian analysis we found that both kinds of emission regions,
BLR and NLR, are complex. In this sample the narrow [OIII] lines
are composites of two components; NLR1 which have random
velocities from ![]() 200 to 500 km s-1 and systematic velocities
toward the blue from 20 to 350 km s-1, and NLR2 with smaller random
velocities (
200 to 500 km s-1 and systematic velocities
toward the blue from 20 to 350 km s-1, and NLR2 with smaller random
velocities (![]() 100-200 km s-1) and a redshift corresponding to
the cosmological one. The BLR also have complex structure and we
apply a two-component model assuming that the line wings
originate in a very broad line region (VBLR) and the line core in an
intermediate line region (ILR). The VBLR is assumed to be an
accretion disk and the ILR a spherical emission region.
The model fits very well the H
100-200 km s-1) and a redshift corresponding to
the cosmological one. The BLR also have complex structure and we
apply a two-component model assuming that the line wings
originate in a very broad line region (VBLR) and the line core in an
intermediate line region (ILR). The VBLR is assumed to be an
accretion disk and the ILR a spherical emission region.
The model fits very well the H![]() and H
and H![]() line profiles of
the AGNs.
line profiles of
the AGNs.
Key words: galaxies: Seyfert - line: profiles - accretion, accretion disks
The concept of a disk geometry in the Broad Line Region (BLR) is
very attractive because the most widely accepted model for Active
Galactic Nuclei (AGNs) includes a super massive black hole fed by
an accretion disk. The detection and modeling of some
double-peaked Balmer lines has supported this idea
(Chen et al. 1989; Ho et al. 2000; Storchi-Bergmann et al. 1997; Chen & Halpern 1989; Rodríguez-Ardila et al. 1996; Eracleous & Halpern 1994; Shields et al. 2000; Eracleous & Halpern 2003; Perez et al. 1988; Strateva et al. 2003; Storchi-Bergmann et al. 2003; Livio & Xu 1997).
However, the
fraction of AGNs clearly showing double-peaked profiles is small
and statistically insignificant.
On the one hand, the existence of double-peaked lines should not
be required as a necessary condition for the existence of a disk
geometry in BLRs. Even if the emission in a spectral line comes
from a disk, the parameters of the disk (e.g. inclination) can be
such that one observes single-peaked lines
(Kollatschny 2003; Chen & Halpern 1989; Dumont & Collin-Souffrin 1990; Kollatschny & Bischoff 2002). Also, a Keplerian disk with
disk wind can produce single-peaked broad emission lines as
normally seen in most of the AGNs (Murray & Chiang 1997). On the other
hand, taking into account the complexity of emission line regions
of AGNs (see e.g. Sulentic et al. 2000), one might expect that the broad
emission lines are composed of radiation from two or more
kinematically and physically different emission regions, i.e. that
multiple BLR emission components with fundamentally different
velocity distributions are present (see e.g. Romano et al. 1996).
Consequently, one possibility could be that the emission of the
disk is masked by the emission of another emission line region.
Recently, Popovic (2003) investigated the physical processes in BLRs
using a Boltzmann-plot method, and found that probably "physical
conditions in regions which contribute to the line core and line
wings are different''. This supports the idea that the broad
optical lines originate in more than one emission region, i.e.
that the Broad Line Emission Region is complex and composed of at
least two regions. Moreover, Corbin & Boroson (1996) found that "the
difference between the Ly![]() and H
and H![]() full width at zero
intensity (FWZI) values provides additional evidence of an
optically thin very broad line region (VBLR) lying inside an
intermediate line region (ILR) producing the profile cores''.
Consequently we may expect that the VBLR can be formed in a disk
or disk-like emission region. Moreover, recently Wang et al. (2003)
investigated the central engines of 37 radio-loud QSOs and found
that their accretion rates suggest that most of the objects
possess standard optically thick, geometrically thin accretion
disks.
In fact, recently (Popovic et al. 2001,2002,2003) it was shown
that broad emission lines of at least three
AGNs (Akn 120, NGC 3516 and III Zw 2) can be well fitted with a model
which
has two
components: (i) an accretion disk and (ii) a region with a geometry
different from a disk.
full width at zero
intensity (FWZI) values provides additional evidence of an
optically thin very broad line region (VBLR) lying inside an
intermediate line region (ILR) producing the profile cores''.
Consequently we may expect that the VBLR can be formed in a disk
or disk-like emission region. Moreover, recently Wang et al. (2003)
investigated the central engines of 37 radio-loud QSOs and found
that their accretion rates suggest that most of the objects
possess standard optically thick, geometrically thin accretion
disks.
In fact, recently (Popovic et al. 2001,2002,2003) it was shown
that broad emission lines of at least three
AGNs (Akn 120, NGC 3516 and III Zw 2) can be well fitted with a model
which
has two
components: (i) an accretion disk and (ii) a region with a geometry
different from a disk.
The aim of this paper is to test the validity of the two-component
model of a BLR which contains an accretion disk and one additional
emission region, i.e. to try to find evidence that suggests that
the disk emission can contribute to the line emission even if the
line profiles are single-peaked. To do this, we observed 12 AGNs
in the H![]() and H
and H![]() wavelength region with the Isaac
Newton Telescope (Sect. 2, throughout). High resolution spectra
were analyzed first by Gaussian analysis (Sect. 3) and after that
we applied the two-component model for BLRs assuming that it is
composed of a VBLR and an ILR (Sect. 4).
wavelength region with the Isaac
Newton Telescope (Sect. 2, throughout). High resolution spectra
were analyzed first by Gaussian analysis (Sect. 3) and after that
we applied the two-component model for BLRs assuming that it is
composed of a VBLR and an ILR (Sect. 4).
It is very important to notice
that the two
peaks produced by the disk may appear like two bumps in the blue and red
parts of the H![]() and H
and H![]() line profiles. To find the
substructure connected with disk emission one should obtain the
spectral lines with a relatively high spectral resolution and S/N
ratio.
We observed with the Isaac Newton Telescope
(INT) 12 AGNs (see Table 1) which
have been previously observed in the X-ray band (Fe K
line profiles. To find the
substructure connected with disk emission one should obtain the
spectral lines with a relatively high spectral resolution and S/N
ratio.
We observed with the Isaac Newton Telescope
(INT) 12 AGNs (see Table 1) which
have been previously observed in the X-ray band (Fe K![]() line, see
e.g. Sulentic et al. 1998; Nandra et al. 1997) and
where, according to the X-ray results,
one can expect that a disk geometry is
present at least in the X-ray emitting region, i.e. that a disk exists
whose signature might be observed in
optical lines (emission of the outer part of the disk). The observed AGNs
have no double-peaked H
line, see
e.g. Sulentic et al. 1998; Nandra et al. 1997) and
where, according to the X-ray results,
one can expect that a disk geometry is
present at least in the X-ray emitting region, i.e. that a disk exists
whose signature might be observed in
optical lines (emission of the outer part of the disk). The observed AGNs
have no double-peaked H![]() and H
and H![]() lines.
lines.
The observations were performed with the 2.5 m INT at La Palma in
the period of 21-25 of January 2002.
The
Intermediate Dispersion Spectrograph (IDS) and the 235 camera
(with chip EEV10) in combination with the R1200Y (for the
H![]() wavelength region) and R1200B (for the H
wavelength region) and R1200B (for the H![]() wavelength region) gratings were used.
The list of the observed AGNs with the coordinates, redshift, central
wavelengths and the exposure times are given in Table 1. The
seeing was around
wavelength region) gratings were used.
The list of the observed AGNs with the coordinates, redshift, central
wavelengths and the exposure times are given in Table 1. The
seeing was around
![]() and the slit width was 1''. The
spectral resolution was
and the slit width was 1''. The
spectral resolution was ![]() 1 Å. As one can see from Table 1, we observed the H
1 Å. As one can see from Table 1, we observed the H![]() and H
and H![]() wavelength line region
for all galaxies, except Mrk 141 where only the H
wavelength line region
for all galaxies, except Mrk 141 where only the H![]() region
was observed. Also, after calibration of the spectra, the H
region
was observed. Also, after calibration of the spectra, the H![]() line of Mrk 493 was too weak and the red wing of the 3C 273
H
line of Mrk 493 was too weak and the red wing of the 3C 273
H![]() line was too noisy, so for these two spectra we use
the low resolution spectra observed with the HST (on Sep. 4, 1996
and Jan. 31, 1999) with G400 and G750L gratings, respectively.
line was too noisy, so for these two spectra we use
the low resolution spectra observed with the HST (on Sep. 4, 1996
and Jan. 31, 1999) with G400 and G750L gratings, respectively.
CuNe and CuAr lamps were used for the wavelength calibration. Standard reduction procedures including flat-fielding, wavelength calibration, spectral response, and sky subtraction were performed with the help of the IRAF software package.
The software package DIPSO was used for reducing the level of the local continuum (by using the DIPSO routine "cdraw 1'') fitted through the dots taken to be on the local continuum (see Fig. 1).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0431f1.ps} \includegraphics[width=8.8cm,clip]{0431f2.ps} \end{figure}](/articles/aa/full/2004/33/aa0431-03/Timg32.gif) |
Figure 1:
The estimate of the continuum (solid line) in the case of
Mrk 1040 H |
| Open with DEXTER | |
The redshifts of the considered AGNs were taken from Véron-Cetty & Véron (2000).
To analyze the shape of the H![]() and H
and H![]() lines, we
first fitted each line with the sum of Gaussian components. We
used a
lines, we
first fitted each line with the sum of Gaussian components. We
used a ![]() minimalization routine to obtain the best fit
parameters. We also assumed that the narrow emission lines can be
represented by one or more Gaussian components. In the fitting
procedure, we looked for the minimal number of Gaussian
components needed to fit the lines. To limit the number of free
parameters in the fit we set some a priori constraints
(Popovic et al. 2001,2002,2003):
minimalization routine to obtain the best fit
parameters. We also assumed that the narrow emission lines can be
represented by one or more Gaussian components. In the fitting
procedure, we looked for the minimal number of Gaussian
components needed to fit the lines. To limit the number of free
parameters in the fit we set some a priori constraints
(Popovic et al. 2001,2002,2003):
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{0431f3.ps}\vspace*{1.4cm}
\includegraphics[width=7.4cm,clip]{0431f4.ps} \end{figure}](/articles/aa/full/2004/33/aa0431-03/Timg34.gif) |
Figure 2:
Decomposition of the
H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0431f5.ps} \end{figure}](/articles/aa/full/2004/33/aa0431-03/Timg35.gif) |
Figure 3:
The estimated contribution of the H |
| Open with DEXTER | |
- For the H![]() line
in the fitting procedure we constrained the Gaussian parameters as
follows:
line
in the fitting procedure we constrained the Gaussian parameters as
follows:
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{0431f6.ps} \end{figure}](/articles/aa/full/2004/33/aa0431-03/Timg41.gif) |
Figure 4: Decomposition of the [OIII] lines. |
| Open with DEXTER | |
Table 2:
The parameters of the Gaussian components of the [OIII] lines. Gaussian widths (W) and
![]() are
given in km s-1. The intensity ratio
are
given in km s-1. The intensity ratio
![]() of the "blue component'' obtained from the Gaussian fit, the
measured flux ratio
of the "blue component'' obtained from the Gaussian fit, the
measured flux ratio
![]() and central intensity
ratio of the "blue'' and "central'' Gaussian components (
and central intensity
ratio of the "blue'' and "central'' Gaussian components (
![]() )
are also given (Cols. 2, 3 and 6). The data for the objects
denoted with stars should be taken with caution, because their
[OIII] lines are too weak.
)
are also given (Cols. 2, 3 and 6). The data for the objects
denoted with stars should be taken with caution, because their
[OIII] lines are too weak.
To find an acceptable fit of the [OIII] lines we first included
two more Gaussians which followed constraint (2). However, we
found that a satisfactory fit in some of the AGNs can be
obtained only if the intensity ratio of the [OIII]![]() 5007
and [OIII]
5007
and [OIII]![]() 4959 is left as a free parameter. Since our
main purpose is to find the best fit in order to subtract the
satellite and narrow lines from the H
4959 is left as a free parameter. Since our
main purpose is to find the best fit in order to subtract the
satellite and narrow lines from the H![]() and H
and H![]() line
profile, we therefore decided to leave as a free parameter the
intensity ratio of the blue-shifted gaussian components of the
[OIII]
line
profile, we therefore decided to leave as a free parameter the
intensity ratio of the blue-shifted gaussian components of the
[OIII]
![]() lines. As a rule we find that the
second Gaussian of the [OIII]
lines. As a rule we find that the
second Gaussian of the [OIII]
![]() lines is
shifted to the blue and more broadened than the central narrow one
(see Fig. 2).
To check our results for the different
components of the [OIII] lines, we subtracted the contributions of
Fe II and He I as well as the H
lines is
shifted to the blue and more broadened than the central narrow one
(see Fig. 2).
To check our results for the different
components of the [OIII] lines, we subtracted the contributions of
Fe II and He I as well as the H![]() red wing from [OIII]
using the DIPSO procedure for the continuum (see Fig. 3). Then we
fitted the [OIII] lines using two Gaussians and the ratio of the
[OIII] lines 1:3.03. In this case we can fit the [OIII] lines of
some of the AGNs in an adequate way (e.g. the [OIII] lines of 3C 120, Mrk 817, NGC 3227). There were
small differences in the residue for Mrk 110, NGC 4253 and PG 1211. But
for the remaining two AGNs (Mrk 1040 and Mrk 841) we could obtain
a satisfactory fit only with the intensity ratio of
[OIII]
red wing from [OIII]
using the DIPSO procedure for the continuum (see Fig. 3). Then we
fitted the [OIII] lines using two Gaussians and the ratio of the
[OIII] lines 1:3.03. In this case we can fit the [OIII] lines of
some of the AGNs in an adequate way (e.g. the [OIII] lines of 3C 120, Mrk 817, NGC 3227). There were
small differences in the residue for Mrk 110, NGC 4253 and PG 1211. But
for the remaining two AGNs (Mrk 1040 and Mrk 841) we could obtain
a satisfactory fit only with the intensity ratio of
[OIII]![]() 5007 and [OIII]
5007 and [OIII]![]() 4959 left as a free
parameter (see Fig. 4). Indeed, we have measured the fluxes of the
[OIII] lines and found that in these two AGNs the intensity ratio
tends to be smaller than 3.03. The results of the Gaussian
fitting analysis for the [OIII]
4959 left as a free
parameter (see Fig. 4). Indeed, we have measured the fluxes of the
[OIII] lines and found that in these two AGNs the intensity ratio
tends to be smaller than 3.03. The results of the Gaussian
fitting analysis for the [OIII]
![]() lines
are presented in Fig. 4, and in Table 2.
lines
are presented in Fig. 4, and in Table 2.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{0431f7.ps}\vspace*{1.4cm}
\includegraphics[width=7.4cm,clip]{0431f8.ps} \end{figure}](/articles/aa/full/2004/33/aa0431-03/Timg48.gif) |
Figure 5:
The same as in Fig. 2. but for the H |
| Open with DEXTER | |
- For the H![]() line, we assumed that [NII]
line, we assumed that [NII]
![]() and the H
and the H![]() narrow component have the same
redshift, and Gaussian widths proportional to their wavelengths.
Taking into account that the two [NII]
narrow component have the same
redshift, and Gaussian widths proportional to their wavelengths.
Taking into account that the two [NII]
![]() lines belong to a transition within the same multiplet we assume
an intensity ratio of 1:2.96 (see e.g. Wiese 1966). The fits of
the H
lines belong to a transition within the same multiplet we assume
an intensity ratio of 1:2.96 (see e.g. Wiese 1966). The fits of
the H![]() lines are presented in Fig. 5.
One can expect that other narrow lines in the optical
spectra
have the same shape as the [OIII] ones, but as the
[NII]
lines are presented in Fig. 5.
One can expect that other narrow lines in the optical
spectra
have the same shape as the [OIII] ones, but as the
[NII]
![]() lines are heavily blended
we are not able to resolve their
fine structure. Hence, each of them has been fitted by only one
Gaussian. On the other hand, we include the He I
lines are heavily blended
we are not able to resolve their
fine structure. Hence, each of them has been fitted by only one
Gaussian. On the other hand, we include the He I![]() 6678.15 Å and SiII
6678.15 Å and SiII![]() 6371 lines
(Véron et al. 2002), and each line has been represented by one
Gaussian. Also, one can expect a contribution of Fe II lines in
the H
6371 lines
(Véron et al. 2002), and each line has been represented by one
Gaussian. Also, one can expect a contribution of Fe II lines in
the H![]() wavelength region, but on the bases of the
calculation given by Sigut & Pradhan (2003) there are no Fe II lines
wavelength region, but on the bases of the
calculation given by Sigut & Pradhan (2003) there are no Fe II lines![]() that can significantly
contribute to the H
that can significantly
contribute to the H![]() line profile. Even if any lines are
present their intensity is probably negligible. It has been shown
(e.g. Lípari et al. 1993; Halpern & Oke 1987) that AGNs with strong iron emission in
the H
line profile. Even if any lines are
present their intensity is probably negligible. It has been shown
(e.g. Lípari et al. 1993; Halpern & Oke 1987) that AGNs with strong iron emission in
the H![]() wavelength region have a weak emission of Fe II in
the H
wavelength region have a weak emission of Fe II in
the H![]() band (see e.g. Figs. 1 and 2 in Halpern & Oke 1987). By
inspection of the NIST
database
band (see e.g. Figs. 1 and 2 in Halpern & Oke 1987). By
inspection of the NIST
database![]() in the H
in the H![]() region we found that a possible Fe II
contribution may come from the permitted lines
region we found that a possible Fe II
contribution may come from the permitted lines
![]() (Fe II lines 6700.64 Å and 6873.84 Å) and
(Fe II lines 6700.64 Å and 6873.84 Å) and
![]() (lines 6746.53 Å, 6689.41 Å and 6404.615 Å) as well as from FeII
(lines 6746.53 Å, 6689.41 Å and 6404.615 Å) as well as from FeII![]() 6456.387. In
the fitting procedure we included these lines assuming that they
originate from the same region, i.e. that they have the same width
and redshift. As one can see from Fig. 5 (broad dashed lines),
these lines, as well as the He I and SiII lines, make a negligible
contribution to the H
6456.387. In
the fitting procedure we included these lines assuming that they
originate from the same region, i.e. that they have the same width
and redshift. As one can see from Fig. 5 (broad dashed lines),
these lines, as well as the He I and SiII lines, make a negligible
contribution to the H![]() line profile, i.e. a satisfactory
fit can be obtained without them.
line profile, i.e. a satisfactory
fit can be obtained without them.
In Fig. 6 we present the Gaussian widths of the different broad components versus their centroid velocities (relative to the systemic one). The different components appear relatively well separated in this diagram, showing the consistency of the multi-Gaussian decomposition. By inspection of Figs. 2, 4 and 5 as well as of the diagrams in Figs. 6 and 7, we can derive a number of conclusions concerning the broad line and the narrow line components, consequently concerning the BLR and the NLR.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0431f9.ps} \end{figure}](/articles/aa/full/2004/33/aa0431-03/Timg52.gif) |
Figure 6:
The widths (w) as a function of the inner shifts of the broad
Gaussian components obtained for the H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0431f10.ps}\end{figure}](/articles/aa/full/2004/33/aa0431-03/Timg53.gif) |
Figure 7:
The Gaussian width of the Fe II template (
|
| Open with DEXTER | |
Considering only the broad line Gaussian components we can conclude:
The NLRs of the AGNs considered also show a complex structure, and we can clearly see at least two NLR regions:
The difference in shifts and widths of
[OIII]
![]() between these two NLRs indicate
different kinematical and physical properties.
Here we note that the parameters for the NLR1 of 3C 273 and PG 1116+215
given
in Table 2 should be taken with caution because of the low
intensity of the [OIII] lines. We excluded these data in the discussion
above.
between these two NLRs indicate
different kinematical and physical properties.
Here we note that the parameters for the NLR1 of 3C 273 and PG 1116+215
given
in Table 2 should be taken with caution because of the low
intensity of the [OIII] lines. We excluded these data in the discussion
above.
The clear tendency of the NLR1 to have a blue-shifted systemic
velocity (though in the case of Mrk 110 and Mrk 841 the blue-shift
is marginal and very close to the cosmological redshift) supports
the idea of a jet geometry of the NLR (see e.g. Dopita et
al. 2003). In this case the receding jet component in the [OIII] lines might
be obscured or absorbed by the host galaxy, so one sees only the
outflowing gas from the closer part of the jet.
Many papers have been
devoted to the radial velocity difference between narrow and
broad lines (starting e.g. from Gaskell 1982), especially the
velocity difference between the [OIII] lines and H![]() that
indicates a jet geometry of the NLR or of part of the NLR (see
e.g. Bennert 2002; Zamanov 2002). On the other hand, 2D
spectroscopy
clearly shows that AGN NLRs have a complex structure (see e.g.
Arribas 1997).
The tendency for the [OIII] lines to be blue-shifted
relative to the H
that
indicates a jet geometry of the NLR or of part of the NLR (see
e.g. Bennert 2002; Zamanov 2002). On the other hand, 2D
spectroscopy
clearly shows that AGN NLRs have a complex structure (see e.g.
Arribas 1997).
The tendency for the [OIII] lines to be blue-shifted
relative to the H![]() suggests that they are associated
with a
high-ionization outflow originating in these highly accreting sources
(see e.g. Zamanov 2002).
suggests that they are associated
with a
high-ionization outflow originating in these highly accreting sources
(see e.g. Zamanov 2002).
Here we apply the two-component model in modeling the broad line
shapes of 12 AGNs, where one component is the disk or disk-like
region.
We start from the paper of
Corbin & Boroson (1996), who investigated the combined ultraviolet and optical
spectra of 48 QSOs and Seyfert 1 galaxies in the redshift range
0.034-0.774. They found a statistically significant difference
between the FWZI distributions of the Ly![]() and H
and H![]() lines. The difference between the Ly
lines. The difference between the Ly![]() and H
and H![]() FWZI
values provides additional evidence for an optically thin VBLR
(which might be a disk or disk-like region) which contributes to
the line wings. It is located inside an ILR which produces the
profile cores. Also, they found relative weakness of the
correlations between the UV profile asymmetries and widths and
those of H
FWZI
values provides additional evidence for an optically thin VBLR
(which might be a disk or disk-like region) which contributes to
the line wings. It is located inside an ILR which produces the
profile cores. Also, they found relative weakness of the
correlations between the UV profile asymmetries and widths and
those of H![]() line. This suggests a stratified structure of
the BLR, consistent with the variability studies of Seyfert 1 galaxies (see e.g. Kollatschny 2003). The smaller average FWHM
values
of the UV lines compared to H
line. This suggests a stratified structure of
the BLR, consistent with the variability studies of Seyfert 1 galaxies (see e.g. Kollatschny 2003). The smaller average FWHM
values
of the UV lines compared to H![]() indicate that the ILR emission make a
higher contribution to the UV lines,
whereas in the Balmer lines the VBLR component is more dominant. This is
also the case
in well known AGNs with double-peaked Balmer lines, which usually
show a single-peaked Ly
indicate that the ILR emission make a
higher contribution to the UV lines,
whereas in the Balmer lines the VBLR component is more dominant. This is
also the case
in well known AGNs with double-peaked Balmer lines, which usually
show a single-peaked Ly![]() line (see e.g. the case of Arp 102B, Halpern et al. 1996).
line (see e.g. the case of Arp 102B, Halpern et al. 1996).
The wings of the broad H![]() emission line in the spectra of a
large sample of AGNs (around 100 spectra) were investigated by
Romano et al. (1996). They found an indication of multiple BLR emission.
Moreover, recently Popovic (2003) investigated the physical
conditions in BLRs finding an indication that BLRs are
complex and that
physical conditions of the regions which contribute to the line core and
the line wings are different.
emission line in the spectra of a
large sample of AGNs (around 100 spectra) were investigated by
Romano et al. (1996). They found an indication of multiple BLR emission.
Moreover, recently Popovic (2003) investigated the physical
conditions in BLRs finding an indication that BLRs are
complex and that
physical conditions of the regions which contribute to the line core and
the line wings are different.
Though a two-component model can probably also be represented by other geometries, we choose the one with: a disk giving the wings of the lines, and a spherical component giving the core of the lines.
For the disk we use the Keplerian relativistic model of
Chen
& Halpern (1989). The emissivity of the disk as a function of radius,
R, is given by
![]() Generally, when trying to
fit the double-peaked line profiles by disk emission one should leave
this index as a free parameter. However, we have to take into
account two facts: (1) we have here single-peaked lines, i.e. the
profile coming from the disk is not a priori well defined;
(2) we will be using a two-component model which includes more
parameters than a disk-only model. We should therefore include
some constraints. Since the illumination is due to a point
source radiating isotropically, located at the center of the disk,
the flux in the outer disk at different radii should vary as
r-3 (Eracleous & Halpern 1994). We note here that this is indeed the way
the incident flux varies, but not necessarily the way in which
the lines respond to it (Eracleous & Halpern 2003; Dumont & Collin-Souffrin 1990; Rokaki & Boisson 1999).
However,
the power index
Generally, when trying to
fit the double-peaked line profiles by disk emission one should leave
this index as a free parameter. However, we have to take into
account two facts: (1) we have here single-peaked lines, i.e. the
profile coming from the disk is not a priori well defined;
(2) we will be using a two-component model which includes more
parameters than a disk-only model. We should therefore include
some constraints. Since the illumination is due to a point
source radiating isotropically, located at the center of the disk,
the flux in the outer disk at different radii should vary as
r-3 (Eracleous & Halpern 1994). We note here that this is indeed the way
the incident flux varies, but not necessarily the way in which
the lines respond to it (Eracleous & Halpern 2003; Dumont & Collin-Souffrin 1990; Rokaki & Boisson 1999).
However,
the power index
![]() can be adopted as a reasonable
prescription at least for H
can be adopted as a reasonable
prescription at least for H![]() (Eracleous & Halpern 2003). In our case, as
one can see in Fig. 8, the shapes of H
(Eracleous & Halpern 2003). In our case, as
one can see in Fig. 8, the shapes of H![]() and H
and H![]() in
our sample are practically the same, so we can fit an averaged
profile (see Sect. 4.2). Therefore we will start our fitting
procedure by imposing the constraint p = 3,
but later we will change this parameter and use
other constraints (see Sect. 4.2).
in
our sample are practically the same, so we can fit an averaged
profile (see Sect. 4.2). Therefore we will start our fitting
procedure by imposing the constraint p = 3,
but later we will change this parameter and use
other constraints (see Sect. 4.2).
We express the disk dimension
in gravitational radii (
![]() ,
G being the gravitational
constant,
M the mass of the central black hole, and c the velocity of light).
The local broadening parameter (
,
G being the gravitational
constant,
M the mass of the central black hole, and c the velocity of light).
The local broadening parameter (![]() )
and shift (
)
and shift (![]() )
within the
disk
have been taken into account as in Chen & Halpern (1989), i.e.
the
)
within the
disk
have been taken into account as in Chen & Halpern (1989), i.e.
the ![]() function has been replaced by a Gaussian function:
function has been replaced by a Gaussian function:
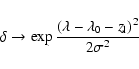
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{0431f11.ps} \end{figure}](/articles/aa/full/2004/33/aa0431-03/Timg62.gif) |
Figure 8:
The comparison of H |
| Open with DEXTER | |
On the other hand, we assume that the kinematics of the additional
emission
region can be described as the emission of a spherical region
with
an isotropic velocity distribution, i.e. with
a local broadening ![]() and shift
and shift ![]() .
Consequently, the emission
line
profile
can be described by a Gaussian function.
The whole line profile can be described by the relation:
.
Consequently, the emission
line
profile
can be described by a Gaussian function.
The whole line profile can be described by the relation:
Before performing the fitting we "cleaned'' the spectra by
subtracting (i) from H![]() the narrow H
the narrow H![]() line, the narrow
[OIII] lines, the He I lines, and the Fe II template; (ii) from
H
line, the narrow
[OIII] lines, the He I lines, and the Fe II template; (ii) from
H![]() the narrow H
the narrow H![]() and [NII] lines. Furthermore, we
normalized the intensities of H
and [NII] lines. Furthermore, we
normalized the intensities of H![]() and H
and H![]() to unity and
converted the wavelength into a velocity scale:
to unity and
converted the wavelength into a velocity scale:
![]() .
These conversions allowed us to
compare the H
.
These conversions allowed us to
compare the H![]() and H
and H![]() high resolution profile. We
found that in the AGNs of the sample the H
high resolution profile. We
found that in the AGNs of the sample the H![]() and H
and H![]() have similar profiles (see Fig. 8). That concept supports the case
that both lines are formed in the same emission region. First we
found an averaged line profile from the H
have similar profiles (see Fig. 8). That concept supports the case
that both lines are formed in the same emission region. First we
found an averaged line profile from the H![]() and H
and H![]() lines from each AGN (here we should note that for 3C 273 only the
high resolution H
lines from each AGN (here we should note that for 3C 273 only the
high resolution H![]() ,
and for Mrk 493 and Mrk 141 only
H
,
and for Mrk 493 and Mrk 141 only
H![]() were used). The averaged profile for each AGN was fitted
with the above described two-component model.
were used). The averaged profile for each AGN was fitted
with the above described two-component model.
When a chi-square minimization including all the parameters was
attempted, it was found that the results are very dependent on the
initial values given to the parameters. As mentioned above, the
reason for this is that we apply a two-component model to
single-peaked lines, so
the number of free parameters is
too large.
To overcome this problem we have to use the additional constraint that
the disc component fits the line wings, and the spherical
component the line core. With this aim,
we tried several values for the
inclination. The starting point for the inclination can be the
relative displacement of red- and blue-shifted Gaussians, ![]() .
We use the empirical relation given by Smak (1981) (see
also Popovic et al. 2002, 2003). If we assume that a disk (or a
disk-like) region exists, we can roughly estimate the parameters
of the disk using the results of Gaussian analysis and the
relationship (see Popovic et al. 2002 for more details)
.
We use the empirical relation given by Smak (1981) (see
also Popovic et al. 2002, 2003). If we assume that a disk (or a
disk-like) region exists, we can roughly estimate the parameters
of the disk using the results of Gaussian analysis and the
relationship (see Popovic et al. 2002 for more details)
![]() where i is the inclination
of the disk, and
where i is the inclination
of the disk, and
![]() is the outer radius given in
gravitational radii. Taking into account that
is the outer radius given in
gravitational radii. Taking into account that
![]() ,
we
can estimate the maximal outer radius. From Fig. 6 one can
estimate that
,
we
can estimate the maximal outer radius. From Fig. 6 one can
estimate that
![]() 0.00033 (
0.00033 (![]() 1000 km s-1)
1000 km s-1)
![]() 0.013 (
0.013 (![]() 4000 km s-1), thus the maximal outer radius may be in the interval
4000 km s-1), thus the maximal outer radius may be in the interval ![]() a few
a few
![]() to
to ![]() a few
a few
![]() for the highest
inclination. On the other hand, from previous investigations
(Chen et al. 1989; Eracleous & Halpern 1994; Eracleous 2003) it was found that the outer radius of
the disk has typical dimensions of
for the highest
inclination. On the other hand, from previous investigations
(Chen et al. 1989; Eracleous & Halpern 1994; Eracleous 2003) it was found that the outer radius of
the disk has typical dimensions of
![]() a few
a few
![]() ;
in that case, the inclination for the
sample is in the interval
;
in that case, the inclination for the
sample is in the interval
![]() .
.
![\begin{figure}
\par\includegraphics[width=4.1cm,clip]{0431f12.ps}\hspace*{3mm}
\includegraphics[width=4.1cm,clip]{0431f13.ps} \end{figure}](/articles/aa/full/2004/33/aa0431-03/Timg77.gif) |
Figure 9:
Two fits of 3C 273 with the two-component model.
The disk parameters are: a)
|
| Open with DEXTER | |
As we noted in Sect. 4.1, first we fixed p=3, and chose
different values of the inclination.
Then we found the best fit by eye and after that we used a "fixed''
inclination such that other parameters can change more (with
greater step) than the inclination![]() . After that we performed a chi-square fitting of
the parameters starting from suitable initial values. Note that
this is not an "orthodox'' chi-square fitting procedure, but in
this case the main point is not only to find the best fit, as we
did with the Gaussian fitting procedure, but also to try to
explain the line profile with our two-component model.
Consequently, we found that
the fit of the wings of the BELs strongly restricts the value of the inner
radius and the "local''
broadening, i.e. the random velocity of emission gas in the disk.
We found that the inclinations of the disk are relatively small,
between
. After that we performed a chi-square fitting of
the parameters starting from suitable initial values. Note that
this is not an "orthodox'' chi-square fitting procedure, but in
this case the main point is not only to find the best fit, as we
did with the Gaussian fitting procedure, but also to try to
explain the line profile with our two-component model.
Consequently, we found that
the fit of the wings of the BELs strongly restricts the value of the inner
radius and the "local''
broadening, i.e. the random velocity of emission gas in the disk.
We found that the inclinations of the disk are relatively small,
between ![]() and
and ![]() .
One should have expected higher
inclinations in the sample (e.g. on average 30
.
One should have expected higher
inclinations in the sample (e.g. on average 30![]() ).
).
Table 3:
The parameters of the disk: ![]() is the
shift and
is the
shift and
![]() is the Gaussian broadening term
from the disk which is a measure of the random velocity in the
disk,
is the Gaussian broadening term
from the disk which is a measure of the random velocity in the
disk,
![]() is the inner radius,
is the inner radius,
![]() is the
outer radius.
is the
outer radius. ![]() and
and ![]() represent the parameters
of the Gaussian component.
represent the parameters
of the Gaussian component.
Therefore we decided to choose the inclination in the range
![]() ,
leaving p as a free parameter, and looking for the
maximal inclinations. We obtained
reasonably good fits for the lines of more than half of the sample,
for p< 3 and higher values of the inner and outer accretion disk
radii (see Figs. 9a,b). Note that low values of the emissivity
index, p, were obtained also by
Eracleous & Halpern (1994) and Eracleous (2003) when fitting double peaked
lines. Consequently, we did fitting tests for different fixed
values of p in the range from 1.0 to 3.0. Also, in this case we
can find acceptable fit for some AGNs.
As an example, in Fig. 9 one can see two fits of the 3C 273
line with different parameters. The best fit corresponds to Fig. 9a, but
the fit in Fig. 9b is
also reasonable.
From these fitting tests (without any constraints
for the disk parameters) we are able only to give rough estimates
of the disk parameters (see Table 3). We should mention here that
for lines with the smallest asymmetry it was more difficult to
estimate the parameters. Consequently, the estimated range of the
parameters is higher (see Table 3, e.g. Mrk 110).
,
leaving p as a free parameter, and looking for the
maximal inclinations. We obtained
reasonably good fits for the lines of more than half of the sample,
for p< 3 and higher values of the inner and outer accretion disk
radii (see Figs. 9a,b). Note that low values of the emissivity
index, p, were obtained also by
Eracleous & Halpern (1994) and Eracleous (2003) when fitting double peaked
lines. Consequently, we did fitting tests for different fixed
values of p in the range from 1.0 to 3.0. Also, in this case we
can find acceptable fit for some AGNs.
As an example, in Fig. 9 one can see two fits of the 3C 273
line with different parameters. The best fit corresponds to Fig. 9a, but
the fit in Fig. 9b is
also reasonable.
From these fitting tests (without any constraints
for the disk parameters) we are able only to give rough estimates
of the disk parameters (see Table 3). We should mention here that
for lines with the smallest asymmetry it was more difficult to
estimate the parameters. Consequently, the estimated range of the
parameters is higher (see Table 3, e.g. Mrk 110).
As one can see from Fig. 9, the line profiles can be well fitted
with the two-component model, but some of the parameters (e.g. the
emissivity index, the inclination, the inner and outer radii) are
not constrained. It is therefore not possible to find a unique
solution for the model. For this,
one should arbitrarily constrain at least
one of the disk parameters![]() . However, it is obvious that in the AGNs of the
sample, the shape of the line wings indicates radial motion,
which may be caused by a disk-like geometry. In any case, the
fitting tests described above allow us to obtain rough estimates
of the kinematical parameters of the two-component model (Table 3). In Table 3 we present the estimated range of inclinations (i)
and the minimal emissivity index (
. However, it is obvious that in the AGNs of the
sample, the shape of the line wings indicates radial motion,
which may be caused by a disk-like geometry. In any case, the
fitting tests described above allow us to obtain rough estimates
of the kinematical parameters of the two-component model (Table 3). In Table 3 we present the estimated range of inclinations (i)
and the minimal emissivity index (
![]() ), minimal and
maximal value for shifts and widths of the Gaussian broadening
term from the disk (
), minimal and
maximal value for shifts and widths of the Gaussian broadening
term from the disk (
![]() ,
,
![]() ),
the shifts and widths of the Gaussian component (
),
the shifts and widths of the Gaussian component (![]() ,
,
![]() ), and
estimates for the minimal inner radius (
), and
estimates for the minimal inner radius (
![]() )
and maximal outer radius (
)
and maximal outer radius (
![]() ).
).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0431f14.ps} \end{figure}](/articles/aa/full/2004/33/aa0431-03/Timg89.gif) |
Figure 10:
The random velocities of a spherical region (ILR) as
a function of the local random disk velocities. The dashed line
represents the function
|
| Open with DEXTER | |
Concerning the disk we can point out the following:
(i) the maximal outer radius is in the range 104 to
![]() .
(ii) The local random velocities in the disk are different
from object to object and they are in the broad range from
.
(ii) The local random velocities in the disk are different
from object to object and they are in the broad range from ![]() 300 km s-1 to 1700 km s-1; so are the local redshifts (
300 km s-1 to 1700 km s-1; so are the local redshifts (
![]() to +450 km s-1). (iii) The minimal inner radius of the
emitting disk is in the range from
to +450 km s-1). (iii) The minimal inner radius of the
emitting disk is in the range from ![]() 100 to 600
100 to 600 ![]() .
(iv)
The inclinations are
.
(iv)
The inclinations are
![]() ,
and in about
half
of the AGNs
,
and in about
half
of the AGNs
![]() .
Such values of the inclinations support
the idea that we
more frequently
observe the Sy 1 type of AGNs at face-on
inclinations (Rokaki & Boisson 1999).
.
Such values of the inclinations support
the idea that we
more frequently
observe the Sy 1 type of AGNs at face-on
inclinations (Rokaki & Boisson 1999).
Concerning the spherical emission region we can point out that: i)
the redshifts are within 300 km s-1 of the cosmological value;
(ii) the random velocities in this
region are also different for different objects, they are in the
range from ![]() 400 to 1600 km s-1.
400 to 1600 km s-1.
Particularly, it is interesting to see the correlation between local broadening in the two regions presented in Fig. 10. The local random velocities in the disk (averaged value from Table 3) are well correlated with those of the spherical region. This can be explained if this region originates from an accretion disk wind, which is created through several disturbances in the disk capable of producing shocks (e.g. Bondi-Hoyl flow, stellar wind-wind collision, and turbulences). Recently, Fromerth & Melia (2001) described a scenario for the formation of a part of the BLR caused by shocks in the accretion disk; this may also create an ILR.
We should mention that besides a disk (or a disk-like region) or spiral shock waves within a disk (Chen et al. 1989; Chen & Halpern 1989), other geometries may cause the same kinds of substructure in the line profiles: i) emission from the oppositely-directed sides of a bipolar outflow (Zheng et al. 1991,1990); ii) emission from a spherical system of clouds in randomly inclined Keplerian orbits illuminated anisotropically from the center (Goad & Wanders 1996); and iii) emission from a binary black hole system (Gaskell 1996,1983). In any case one should consider a two-component model with an ILR contributing to the broad line cores and one additional emitting region contributing to the broad line wings. Recent investigations (see e.g. Wang et al. 2003; Eracleous & Halpern 2003) have shown that the disk geometry for VBLR may be accepted as a reality. Moreover, Eracleous & Halpern (2003) found that the disk emission is more successful not only in explaining double-peaked line profiles but also in interpreting the other spectroscopic properties of AGNs presenting these double-peaked Balmer lines.
We observed 12 AGNs with INT in order to obtain high-resolution
spectra of the H![]() and H
and H![]() lines that can be used for
modeling BLRs. First we applied Gaussian analysis to the complex
H
lines that can be used for
modeling BLRs. First we applied Gaussian analysis to the complex
H![]() and H
and H![]() lines, from which we can conclude: (i) both
the BLR and the NLR are complex; (ii) the [OIII] narrow lines can
be fitted satisfactory only with two Gaussians, one shifted toward
blue, which may indicate the existence of an outflow; (iii) the different parameters of
these two Gaussians indicate that they originate in two NLR regions
having different physical properties, (iv) the broad lines also
show a complex structure, and they can be decomposed into three
broad Gaussians - one red-, one blue-shifted and one at the
systemic redshift.
lines, from which we can conclude: (i) both
the BLR and the NLR are complex; (ii) the [OIII] narrow lines can
be fitted satisfactory only with two Gaussians, one shifted toward
blue, which may indicate the existence of an outflow; (iii) the different parameters of
these two Gaussians indicate that they originate in two NLR regions
having different physical properties, (iv) the broad lines also
show a complex structure, and they can be decomposed into three
broad Gaussians - one red-, one blue-shifted and one at the
systemic redshift.
We adopt a two-component model, which comprises a VBLR and an ILR. We identify the VBLR with an accretion disk which contributes to the line wings. The cores of the lines originate in the ILR which is assumed to have a spherical geometry. This two-component model has been applied to the observed line profiles and we can conclude that: (i) the model can very well fit the observed line profiles, but it is very hard to obtain the disk parameters without imposing at least one constraint because of the large number of parameters and the lack of two peaks in the line profiles. They can be only roughly estimated using fitting tests (see Table 3). (ii) The random velocities in the spherical emission region and the random velocities in the disk are similar. This indicates that these two regions are linked through a common process, such as a wind produced by the disk.
To find constraints for the model parameters further investigations are needed.
Acknowledgements
The work was supported by the Ministry of Science, Technologies and Development of Serbia through the project "Astrophysical Spectroscopy of Extragalactic Objects'' (L.C.P., E.B., and D.I.), the IAC through the project P6/88 "Relativistic and Theoretical Astrophysics'' (E.M. and L.C.P.) and the Alexander von Humboldt Foundation through the program for foreign scholars (L.C.P.). L.C.P. & E.B. thank to Institute for Astrophysics Canarias for the hospitality before and after observations. Also, we would like to thank the anonymous referee for very useful comments.
Table 1: The observed AGNs with the coordinates, redshift, central wavelength and exposition.