A&A 423, 821-831 (2004)
DOI: 10.1051/0004-6361:20040337
A hint of Poincaré dodecahedral topology in the WMAP first year sky map
B. F. Roukema1 -
B. Lew1 -
M. Cechowska1 -
A. Marecki1 -
S. Bajtlik2
1 - Torun Centre for Astronomy, N. Copernicus University,
ul. Gagarina 11, 87-100 Torun, Poland
2 -
Nicolas Copernicus Astronomy Centre,
ul. Bartycka 18, 00-716 Warsaw, Poland
Received 25 February 2004 / Accepted 26 May 2004
Abstract
It has recently been suggested
by Luminet et al. (2003) that the WMAP data are better
matched by a geometry in which the topology is that of
a Poincaré dodecahedral model and the curvature is "slightly'' spherical,
rather than by an (effectively) infinite flat model. A general back-to-back
matched circles analysis by Cornish et al. (2004)
for angular radii in the range
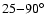 ,
using a correlation statistic
for signal detection, failed to support this. In this paper, a matched circles
analysis specifically designed to detect dodecahedral patterns of matched
circles is performed over angular radii in the range
,
using a correlation statistic
for signal detection, failed to support this. In this paper, a matched circles
analysis specifically designed to detect dodecahedral patterns of matched
circles is performed over angular radii in the range
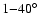 on the one-year WMAP data. Signal detection is attempted via a
correlation statistic and an rms difference statistic.
Extreme value distributions of these statistics are calculated for
one orientation of the 36
on the one-year WMAP data. Signal detection is attempted via a
correlation statistic and an rms difference statistic.
Extreme value distributions of these statistics are calculated for
one orientation of the 36
 "screw motion'' (Clifford translation)
when matching circles, for the opposite screw motion, and for a zero (unphysical) rotation.
The most correlated circles appear for circle
radii of
"screw motion'' (Clifford translation)
when matching circles, for the opposite screw motion, and for a zero (unphysical) rotation.
The most correlated circles appear for circle
radii of
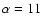
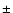
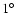 ,
for the left-handed screw motion, but not for the right-handed one, nor for the zero rotation. The favoured six dodecahedral face centres
in galactic coordinates are
,
for the left-handed screw motion, but not for the right-handed one, nor for the zero rotation. The favoured six dodecahedral face centres
in galactic coordinates are
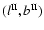
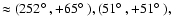
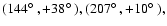
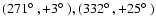 and their opposites. The six pairs of circles independently each
favour a circle angular radius of 11
and their opposites. The six pairs of circles independently each
favour a circle angular radius of 11 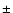
 .
The temperature fluctuations along the matched circles are plotted
and are clearly highly correlated.
Whether or not these six circle pairs centred on dodecahedral faces
match via a
.
The temperature fluctuations along the matched circles are plotted
and are clearly highly correlated.
Whether or not these six circle pairs centred on dodecahedral faces
match via a
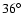 rotation only due to unexpected statistical
properties of the WMAP ILC map, or whether they match due to global
geometry, it is clear that the WMAP ILC map has some unusual statistical
properties which mimic a potentially interesting cosmological signal.
rotation only due to unexpected statistical
properties of the WMAP ILC map, or whether they match due to global
geometry, it is clear that the WMAP ILC map has some unusual statistical
properties which mimic a potentially interesting cosmological signal.
Key words: cosmology: observations - cosmology: cosmic microwave background - reference systems
In the past twelve months, several authors have analysed the possibility that
the primordial temperature fluctuations in the cosmic microwave
background, as measured in the first-year data of WMAP (Wilkinson
Microwave Anisotropy Probe) satellite
(Spergel et al. 2003, and accompanying papers), could be better matched by a
perturbed Friedmann-Lemaître-Robertson-Walker (FLRW) model in which the global
geometry is multiply connected rather than simply connected.
The possibility of the Universe being multiply connected is first
known to have been suggested by Schwarzschild (1900, 1998).
For recent reviews on cosmic topology, see
Lachièze-Rey & Luminet (1995), Luminet (1998), Starkman (1998) and Luminet & Roukema (1999).
For workshop proceedings on the subject, see Starkman (1998) and following articles, and Blanl il & Roukema (2000). Detection strategies include both two-dimensional methods (based on temperature fluctuations in the surface of last
scattering) and three-dimensional methods (based on distributions
of gravitationally collapsed objects distributed in three-dimensional
comoving space). For a list and discussion of both two-dimensional and
three-dimensional methods,
see Table 2 of Luminet & Roukema (1999) and the accompanying discussion.
il & Roukema (2000). Detection strategies include both two-dimensional methods (based on temperature fluctuations in the surface of last
scattering) and three-dimensional methods (based on distributions
of gravitationally collapsed objects distributed in three-dimensional
comoving space). For a list and discussion of both two-dimensional and
three-dimensional methods,
see Table 2 of Luminet & Roukema (1999) and the accompanying discussion.
The WMAP data has motivated many two-dimensional analyses.
Some of the authors mentioning either multiply connected models consistent with
the WMAP data, or indirect hints of multiple connectedness, include
Spergel et al. (2003); Tegmark et al. (2003); Chiang et al. (2003); Copi et al. (2003), - finding low values of low l multipoles or applying a multipole vector analysis.
However, other authors (e.g., Feng & Zhang 2003; Cline et al. 2003; Contaldi et al. 2003; Efstathiou 2003a)
have suggested various non-topological explanations for the
low multipole WMAP 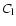 spectrum, such as double inflation or
other phenomena from early universe physics, or positive curvature.
spectrum, such as double inflation or
other phenomena from early universe physics, or positive curvature.
Yet others (Naselsky et al. 2003, 2004) point out that at least the "internal linear combination'' (ILC) map of the WMAP data contains
non-Poissonian signal, due to foreground residues on large scales.
On smaller scales, Giommi & Colafrancesco (2004) find that somewhere between 20-100% of the signal at spherical harmonic l values in the range
500 < l < 800 may be due to blazars.
Attempts to exclude classes of global geometry models using the WMAP data include the calculations of de Oliveira-Costa et al. (2004) and of Cornish et al. (2004). The latter performed a general back-to-back
matched circles analysis for angular radii in the range
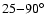 ,
using a correlation statistic for signal detection. They failed to find matched circles
for a wide class of models, including the torus models, up to a scale
of 16.8 h-1 Gpc, which Cornish et al. (2004) state as 24 Gpc, since they
adopt H0= 70 km s-1 Mpc-1
,
using a correlation statistic for signal detection. They failed to find matched circles
for a wide class of models, including the torus models, up to a scale
of 16.8 h-1 Gpc, which Cornish et al. (2004) state as 24 Gpc, since they
adopt H0= 70 km s-1 Mpc-1![[*]](/icons/foot_motif.gif) .
.
Disagreement also exists on whether or not the low quadrupole is
really significant in rejecting the infinite flat "concordance'' model
(Efstathiou 2003b, 2004).
Possibly one of the strongest claims in favour of a possible detection
is that by Luminet et al. (2003), who point out that given
standard assumptions on the statistics of the fluctuations,
the Poincaré dodecahedral model implies a quadrupole and an octupole
very close to those calculated from the WMAP data, for the same
value of the total density parameter,
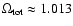
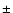 0.02.
0.02.
In principle, this is excluded by the Cornish et al. (2004) analysis.
The Poincaré dodecahedral model requires positive (spherical)
curvature. Luminet et al. (2003) favour a total density parameter of
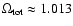
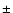 0.002 based on the spherical harmonic statistical
analyses of the WMAP data, with non-relativistic matter density parameter,
0.002 based on the spherical harmonic statistical
analyses of the WMAP data, with non-relativistic matter density parameter,
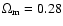 and cosmological constant
and cosmological constant
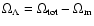 .
This implies that points on the surface of last scattering
which are multiple topological images of single physical points in space-time
should correspond to matched circles (Cornish et al. 1996, 1998) which subtend angular radii at the observer of "about
.
This implies that points on the surface of last scattering
which are multiple topological images of single physical points in space-time
should correspond to matched circles (Cornish et al. 1996, 1998) which subtend angular radii at the observer of "about
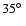 '' (Luminet et al. 2003).
'' (Luminet et al. 2003).
Since the angular relations between face centres are identical for
Euclidean and spherical dodecahedra, Euclidean calculations of the
relative positions of circles are sufficient for testing the Poincaré
dodecahedral hypothesis. For example, the Euclidean half-angle of
about
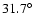 is valid for angular separations of adjacent face
centres in the spherical dodecahedron. Since the adjacent circles
expected by Luminet et al. (2003) have larger angular radii (subtended at the observer), this implies that they intersect with the face edges.
is valid for angular separations of adjacent face
centres in the spherical dodecahedron. Since the adjacent circles
expected by Luminet et al. (2003) have larger angular radii (subtended at the observer), this implies that they intersect with the face edges.
However, as is shown in Sect. 3.2, this angular
radius is extremely sensitive to the value of
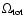 .
For example,
keeping
.
For example,
keeping
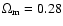 fixed, it is sufficient to decrease
fixed, it is sufficient to decrease
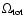 to
to
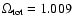 to bring the angular radius to nearly zero.
to bring the angular radius to nearly zero.
This implies that a Poincaré dodecahedral signal may have been
missed by Cornish et al. (2004) because they did not explore the part of
parameter space for small matched circles.
In this paper, the missing part of parameter space is investigated. A
matched circles analysis specifically designed to detect dodecahedral
patterns of matched circles is performed over angular radii in the
range
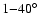 on Internal Linear Combination map (ILC) of
the one-year WMAP data. The WMAP data are briefly discussed in Sect. 2.
While the ILC is unlikely to be ideal for the studies of
on Internal Linear Combination map (ILC) of
the one-year WMAP data. The WMAP data are briefly discussed in Sect. 2.
While the ILC is unlikely to be ideal for the studies of 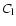 statistics, and some authors (cited above) claim correlations with foregrounds, it is hard to see how any signal mimicking matched circles oriented in a dodecahedral pattern could be imposed, either by
the construction method of the ILC or by foregrounds.
statistics, and some authors (cited above) claim correlations with foregrounds, it is hard to see how any signal mimicking matched circles oriented in a dodecahedral pattern could be imposed, either by
the construction method of the ILC or by foregrounds.
Signal detection is attempted via a correlation statistic and
an rms difference statistic, similarly to Roukema (2000a,b).
Extreme value distributions of these statistics between
a right-handed rotation when matching circles,
a left-handed rotation, and a zero rotation. A genuine signal should appear
for either the right-handed or left-handed rotation, but not both, and
should not appear for the zero rotation.
The relation between circle angular radius (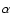 )
and local cosmological
parameters (
)
and local cosmological
parameters (
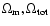 )
and the statistics used are presented in
Sect. 3.
)
and the statistics used are presented in
Sect. 3.
The tentative detection of dodecahedrally distributed matched circles
with
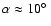 and analysis of their statistical significance
are presented in Sect. 4. Further discussions and conclusions are made in
Sect. 5.
and analysis of their statistical significance
are presented in Sect. 4. Further discussions and conclusions are made in
Sect. 5.
For reviews on cosmological topology, see Lachièze-Rey & Luminet (1995), Luminet (1998), Starkman (1998) and Luminet & Roukema (1999). For workshop proceedings on the subject, see Starkman (1998) and the following articles, and Blanl il & Roukema (2000). For a list and discussion of both two-dimensional and three-dimensional methods, see Table 2 of Luminet & Roukema (1999) and the accompanying discussion. The reader should be reminded that while microwave background data is still the most popular for topology analyses, considerable work in three-dimensional methods has been carried out, including, e.g.,
Lehoucq et al. (1996); Roukema (1996); Fagundes & Gausmann (1998b); Roukema & Edge (1997); Roukema & Blanl
il & Roukema (2000). For a list and discussion of both two-dimensional and three-dimensional methods, see Table 2 of Luminet & Roukema (1999) and the accompanying discussion. The reader should be reminded that while microwave background data is still the most popular for topology analyses, considerable work in three-dimensional methods has been carried out, including, e.g.,
Lehoucq et al. (1996); Roukema (1996); Fagundes & Gausmann (1998b); Roukema & Edge (1997); Roukema & Blanl il (1998); Gomero et al. (2002); Lehoucq et al. (1999); Fagundes & Gausmann (1998a); Uzan et al. (1999); Fagundes & Gausmann (1999); Gomero et al. (2000, 2001).
il (1998); Gomero et al. (2002); Lehoucq et al. (1999); Fagundes & Gausmann (1998a); Uzan et al. (1999); Fagundes & Gausmann (1999); Gomero et al. (2000, 2001).
For background on spherical multiply connected spaces, apart from the
recent analysis by Luminet et al. (2003), see Gausmann et al. (2001); Lehoucq et al. (2002); Riazuelo et al. (2003) for extremely thorough, in-depth mathematical background directly related to the cosmological context.
For a general background on geometry and topology, see e.g. Weeks (2001).
Comoving coordinates are used when discussing distances
(i.e. "proper distances'', Weinberg 1972, equivalent to "conformal time''
if c=1).
2 Observations
See Spergel et al. (2003) and accompanying papers for an introduction
to the WMAP data.
While some authors make their own combinations of the WMAP maps in
individual frequencies, it is hard to see how any signal mimicking
matched circles oriented in a dodecahedral pattern could be imposed,
by the method according to which the Internal Linear Combination (ILC) map is constructed. So this is the data set used here.
However, in order to obtain conservative results, all points
within
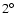 of the galactic plane or
of the galactic plane or
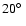 of the galactic
centre are removed from the analysis.
of the galactic
centre are removed from the analysis.
Moreover, a smoothing of
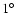 HWHM is applied for the main
calculation, since if a signal
is present, it should be present both on super-degree scales and on
sub-degree scales, but should be easier to detect on the larger scales,
because the search calculations can be made much faster, because the
naïve Sachs-Wolfe dominates over the Doppler effect on larger scales,
and because there is likely to be less influence from subtle effects
which need to be taken into account as correction factors, e.g. the
special relativistic correction for the observer's motion with respect
to the microwave background, Barrow & Levin (2001); Uzan et al. (2002).
HWHM is applied for the main
calculation, since if a signal
is present, it should be present both on super-degree scales and on
sub-degree scales, but should be easier to detect on the larger scales,
because the search calculations can be made much faster, because the
naïve Sachs-Wolfe dominates over the Doppler effect on larger scales,
and because there is likely to be less influence from subtle effects
which need to be taken into account as correction factors, e.g. the
special relativistic correction for the observer's motion with respect
to the microwave background, Barrow & Levin (2001); Uzan et al. (2002).
3 Method
3.1 The identified circles principle
The identified circles principle was first published by
Cornish et al. (1996, 1998). This defines the set of multiply topologically imaged points for a given manifold.
This set can be generated by considering copies of the observer in the covering space
placed at distances less than the horizon diameter from the observer. The
intersection of the two surfaces of last scattering (spheres) of the observer and a copy of the observer is a circle. Since the copy of the observer is physically identical to the observer,
what appears to be two observers looking at one circle
is equivalent to one observer looking at two circles.
Hence, each pair of virtual copies of the observer in the covering
space (separated by less than the diameter of the surface of last
scattering) implies a pair of circles on the surface of last scattering
which correspond to identical points in space-time.
3.2 Relating circle angular radius 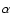 to
to
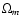 ,
,
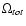
As mentioned above, Euclidean geometry is sufficient for calculating
the positions of matched circles for the Poincaré dodecahedral
hypothesis of Luminet et al. (2003), even though the model is for positive curvature. Errors would occur only if, for example, the angular radius of a circle, 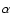 ,
is converted into a comoving distance in megaparsecs, or if the ratio of
the inverse cosine of the ratio of the in-radius, r-, to
the distance to the surface of last scattering,
,
is converted into a comoving distance in megaparsecs, or if the ratio of
the inverse cosine of the ratio of the in-radius, r-, to
the distance to the surface of last scattering,
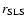 ,
is used
to infer the angular radius of a matched circle, i.e.
,
is used
to infer the angular radius of a matched circle, i.e.
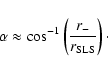 |
(1) |
Since the values of
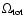 of interest are very close to unity,
either of these calculations should only lead to small errors.
of interest are very close to unity,
either of these calculations should only lead to small errors.
In fact, a much bigger uncertainty is due to the sensitivity of 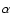 to the values of
to the values of
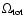 and
and
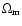 .
.
The curvature radius can be defined in a strict sense, without taking an
absolute value of the curvature, as
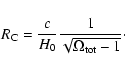 |
(2) |
This has the advantage of showing that the transition from "slightly''
hyperbolic space to flat space to spherical space, i.e. from
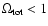 to
to
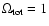 to
to
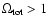 starts from imaginary
values of the curvature radius, increases to larger and larger imaginary
curvature radii without bounds, goes through a singularity, and decreases
from unbounded large, real values to smaller and smaller real values
as
starts from imaginary
values of the curvature radius, increases to larger and larger imaginary
curvature radii without bounds, goes through a singularity, and decreases
from unbounded large, real values to smaller and smaller real values
as
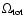 increases through positive values.
increases through positive values.
It is therefore unsurprising that other physical quantities related to
the curvature radius may show rapid changes near the flatness limit.
To illustrate the relation between 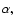
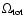 and
and
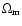 ,
the value of r-, the in-radius of the fundamental domain of the Poincaré dodecahedron, expressed as
,
the value of r-, the in-radius of the fundamental domain of the Poincaré dodecahedron, expressed as
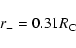 |
(3) |
is used, along with Eq. (1) and the comoving
distance to the surface of last scattering
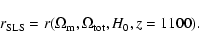 |
(4) |
Figure 1 shows how a few tenths of a percent drop in
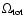 are sufficient to increase the curvature radius so that
the in-radius of the fundamental dodecahedron becomes as large as the
surface of last scattering, reducing the circle size from
are sufficient to increase the curvature radius so that
the in-radius of the fundamental dodecahedron becomes as large as the
surface of last scattering, reducing the circle size from 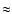
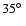 to zero.
to zero.
So, while Luminet et al. (2003)'s statistical estimates of 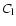 values do suggest that
values do suggest that
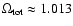 and
and
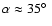 ,
it
is clear that smaller
,
it
is clear that smaller
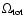 values and circle sizes should be
investigated.
values and circle sizes should be
investigated.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0337fg01.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg63.gif) |
Figure 1:
Dependence of the angular size 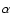 of matched circle radii on
the total density parameter
of matched circle radii on
the total density parameter
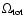 and the non-relativistic matter density
parameter
and the non-relativistic matter density
parameter
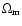 for the Poincaré dodecahedral hypothesis.
Clearly only slight changes in
for the Poincaré dodecahedral hypothesis.
Clearly only slight changes in
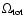 are needed for the circle
radius to change significantly. The values
are needed for the circle
radius to change significantly. The values
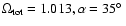 expected by Luminet et al. (2003) are shown by a star.
The word "approx'' is used in the label to remind the reader that this
is not an exact calculation, since Euclidean geometry is assumed. expected by Luminet et al. (2003) are shown by a star.
The word "approx'' is used in the label to remind the reader that this
is not an exact calculation, since Euclidean geometry is assumed. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0337fg02.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg66.gif) |
Figure 2:
An inversion of Fig. 1, focussing on the angles
found to be of interest in the WMAP ILC map. Independently of
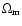 ,
the
slope in the range ,
the
slope in the range
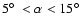 is
is
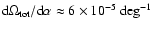 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0337fg03.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg68.gif) |
Figure 3:
Dependence of
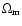 on
on 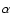 ,
similarly to
Fig. 2. The slope in the range ,
similarly to
Fig. 2. The slope in the range
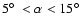 is
is
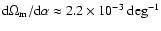 ,
with only weak dependence on ,
with only weak dependence on
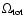 over this interval.
over this interval. |
| Open with DEXTER |
In Figs. 2 and 3, the dependence of
 and
and
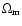 on
on 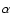 in the angular range found to be of interest in the
WMAP data is illustrated. Given the fact that the Universe is
anisotropic (we clearly do not live in a true FLRW universe;
we live in a perturbed FLRW universe) some variation in the size of circles
could be expected due to perturbations in the values of
in the angular range found to be of interest in the
WMAP data is illustrated. Given the fact that the Universe is
anisotropic (we clearly do not live in a true FLRW universe;
we live in a perturbed FLRW universe) some variation in the size of circles
could be expected due to perturbations in the values of
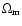 and
and
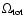 .
.
The variation shown in Fig. 3,
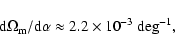 |
(5) |
is clearly much larger than temperature fluctuations on scales of
about a radian (
 ).
).
However, the variation in
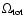 ,
,
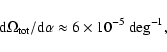 |
(6) |
is only slightly larger than that indicated by temperature fluctuations.
Moreover, the unknown physics of the cosmological constant (or
quintessence) makes it hard to a priori exclude any fluctuations
in
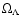 ,
especially with an amplitude so close to that of
matter fluctuations.
,
especially with an amplitude so close to that of
matter fluctuations.
Hence, a variation in circle size of about one degree would be consistent
with fluctuations in
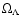 on scales of about a radian of
amplitude about
on scales of about a radian of
amplitude about
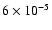 .
.
Along with restrictions in practical computing power, this motivates
a search strategy and smoothing on a scale of about one degree.
3.3 Parameter space
The space of possible orientations of a dodecahedron (centred on the
observer) and possible circle matches is defined by five parameters:
three for the orientation of the dodecahedron, one for the
mapping between faces, and one for the circle radius.
The orientation of the dodecahedron depends on
three continuous free parameters. The definition used
here includes the
galactic longitude and latitude
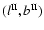 of one face centre, and
a third parameter allowing a rotation of up to
of one face centre, and
a third parameter allowing a rotation of up to
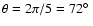 around the axis defined by the first centre and its opposite.
The zero point of the rotation
around the axis defined by the first centre and its opposite.
The zero point of the rotation 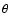 is arbitrary.
is arbitrary.
A given triple
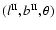 can equivalently be written
as a quadruple
can equivalently be written
as a quadruple
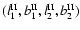 representing two
non-opposite face centres, which uniquely define
the same orientation.
representing two
non-opposite face centres, which uniquely define
the same orientation.
The mapping of one copy of the fundamental domain to
the next, or what is most interesting in the present case,
the matching of one face of the dodecahedron to its matching face,
has one free binary parameter, 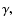 the handed-ness of the screw motion of the
mapping (which is a Clifford translation).
For a given triple
the handed-ness of the screw motion of the
mapping (which is a Clifford translation).
For a given triple
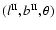 ,
the screw motion
can either be left-handed or right-handed. The amplitude of the
screw motion is
,
the screw motion
can either be left-handed or right-handed. The amplitude of the
screw motion is
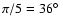 ,
equal to the in-diameter of
the fundamental domain in units of the curvature radius.
,
equal to the in-diameter of
the fundamental domain in units of the curvature radius.
For a rotation of
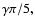 the only physically valid values
are
the only physically valid values
are
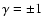 .
.
The remaining parameter is that discussed above, the angular radius
of a circle, 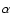 .
.
Putting these together, these can be written as five-dimensional parameter
space:
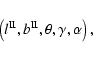 |
(7) |
where four parameters are continuous variables and
one of the parameters, 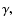 has only two
physically possible values,
has only two
physically possible values, 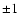 .
.
The binary parameter provides an easy method for providing a control
test which should demonstrate the likely distribution of values of
statistical measures of circle identity for false matches.
By setting the Clifford translation as a translation plus a zero
rotation, i.e. setting 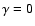 ,
rather than a translation plus a
,
rather than a translation plus a 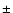
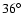 rotation,
an extra 4-plane in parameter space, in which there is sure to be no
genuine signal, is provided.
rotation,
an extra 4-plane in parameter space, in which there is sure to be no
genuine signal, is provided.
So, this extra 4-plane is tested here.
Strictly speaking, values of
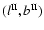 only need to be searched
over one-twelth of the sphere, since outside of one spherical pentagon
of the spherical dodecahedron, redundant points would be searched.
For simplicity, the search is made for
only need to be searched
over one-twelth of the sphere, since outside of one spherical pentagon
of the spherical dodecahedron, redundant points would be searched.
For simplicity, the search is made for
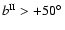 ,
so that
some redundant points are expected.
,
so that
some redundant points are expected.
The full parameter search space is:
where the zero screw motion is a control experiment which can only
give false detections.
For a given triple
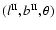 ,
,
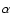 ,
and the handed-ness
of the screw motion, there are six pairs of circles which should have
identical temperature fluctuations if there were only the naïve
Sachs-Wolfe effect, no foregrounds and no other statistical or systematic
sources of noise.
,
and the handed-ness
of the screw motion, there are six pairs of circles which should have
identical temperature fluctuations if there were only the naïve
Sachs-Wolfe effect, no foregrounds and no other statistical or systematic
sources of noise.
Here, the statistic of Cornish et al. (1998) is used as the correlator,
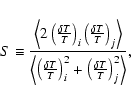 |
(9) |
where i and j are the hypothetically multiply imaged locations
in space-time. The mean is calculated using linearly interpolated
temperature fluctuations in the ILC at intervals of 0.5 great circle degrees.
This is essentially a two-point autocorrelation function normalised by the variance.
The other statistic used is an rms difference statistic:
![\begin{displaymath}%
\sigma^2 \equiv { \left<
{ \left[ \left({\delta T \over T}...
...i -
\left({\delta T \over T}\right)_j \right]^2 }
\right>, }
\end{displaymath}](/articles/aa/full/2004/33/aa0337-04/img91.gif) |
(10) |
using the same notation.
Both statistics are means for all six circle pairs for the given
point in parameter space
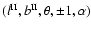 .
.
For genuine matched circles, S should be larger than for surrounding
regions in parameter space, while 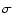 should be smaller than
for surrounding regions.
should be smaller than
for surrounding regions.
4 Results
The full parameter space (Eq. (8)) is searched
with a resolution of
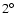 .
Since the parameter space is large,
not all values of S and
.
Since the parameter space is large,
not all values of S and 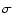 are stored. Instead, over
the
are stored. Instead, over
the 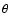 dimension, values of S and
dimension, values of S and 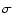 are stored for the
two values of
are stored for the
two values of 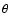 which maximise S and minimise
which maximise S and minimise 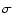 respectively. These two values of
respectively. These two values of 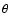 may be, but are not
necessarily, identical. Cornish et al. (2004) write
may be, but are not
necessarily, identical. Cornish et al. (2004) write
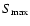 to indicate that S is a maximum value, not a mean value, but this is not strictly identical to the value used here, since values of both S and
to indicate that S is a maximum value, not a mean value, but this is not strictly identical to the value used here, since values of both S and 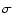 are stored for both the cases of maximum S and minimum
are stored for both the cases of maximum S and minimum 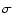 .
.
Taking the same approach as Cornish et al. (2004), the values of S and 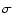 are plotted as a function of
are plotted as a function of 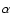 ,
for the Clifford translations of both orientations, i.e. rotations of
,
for the Clifford translations of both orientations, i.e. rotations of 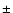
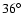 and for a zero rotation.
and for a zero rotation.
These values are shown in Figs. 4-9.
There is clearly a cluster of points at 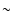
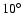 which show
excessively high values of S (Fig. 4) and excessively low
values of
which show
excessively high values of S (Fig. 4) and excessively low
values of 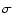 (Fig. 7) for the left-handed
rotation, in contrast to the general distributions of these
statistics in the right-handed and zero (unphysical) cases.
(Fig. 7) for the left-handed
rotation, in contrast to the general distributions of these
statistics in the right-handed and zero (unphysical) cases.
The general increase in the value of S as 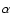 decreases is similar to its behaviour in the figures of Cornish et al. (2004), and consistently, there is
a corresponding decrease in
decreases is similar to its behaviour in the figures of Cornish et al. (2004), and consistently, there is
a corresponding decrease in 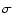 values as
values as 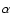 decreases.
decreases.
Could this cluster of points indicate a real signal?
If they correspond to a real signal, spread out over about a degree
due to smoothing of the ILC map, to origin of the signal from
the naïve Sachs-Wolfe effect at super-degree
scales, and possibly due to intrisic variations in
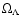 of
of
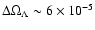 (Eq. (6)), then
(Eq. (6)), then
-
- (i)
- they should represent adjacent points in parameter space
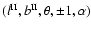 ,
and
,
and
- (ii)
- each of the six individual circle pairs should show excess correlations and low differences near the optimal point.
The twenty points with the highest values of S in the range
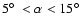 all lie in one of the two ranges
all lie in one of the two ranges
or
These two triples
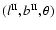 correspond to the
same orientation of the dodecahedron - they are two face centres
for a single orientation. As mentioned above, the full parameter space is covered a little more
than once, in order to be sure that all orientations are tested.
correspond to the
same orientation of the dodecahedron - they are two face centres
for a single orientation. As mentioned above, the full parameter space is covered a little more
than once, in order to be sure that all orientations are tested.
The difference statistic 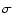 varies more rapidly with
varies more rapidly with 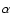 ,
so a narrower range around
,
so a narrower range around 
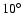 is required to see if
is required to see if 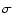 isolates similar points to S.
isolates similar points to S.
Of the twenty points with the lowest values of 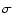 in the range
in the range
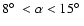 ,
all but four lie in the ranges of Eqs. (11) and (12), except for four points with
,
all but four lie in the ranges of Eqs. (11) and (12), except for four points with
However, the four points of Eq. (13) have correlations
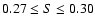 ,
much lower than for the other sixteen points,
which have
,
much lower than for the other sixteen points,
which have
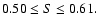 This solution is not a face centre
of the same dodecahedron as Eqs. (11) and (12).
This solution is not a face centre
of the same dodecahedron as Eqs. (11) and (12).
Clearly, only the solution (11) and (12) is simultaneously indicated by both statistics.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0337fg04.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg111.gif) |
Figure 4:
Values of the correlation statistic S(Eq. (9)) as a function of matched circle angular
radius 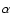 for each pair of six matched circles implied by an
orientation of the fundamental dodecahedron, where the rotation of
the Clifford translation (screw motion) mapping from a circle to its
image is
for each pair of six matched circles implied by an
orientation of the fundamental dodecahedron, where the rotation of
the Clifford translation (screw motion) mapping from a circle to its
image is
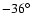 (left-handed).
The values of
(left-handed).
The values of 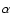 are discrete, but a small random offset in
are discrete, but a small random offset in 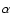 filling the
filling the
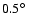 interval between discrete values is used for to better display
individual points. The intervals in interval between discrete values is used for to better display
individual points. The intervals in
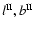 and
and 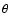 are
are
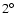 .
Points with excess correlation appear at .
Points with excess correlation appear at 
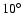 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0337fg05.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg112.gif) |
Figure 5:
As for Fig. 4, for a right-handed rotation.
If a signal is present, it should be present for a left-handed
rotation or a right-handed rotation, but not for both. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0337fg06.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg113.gif) |
Figure 6:
As for Fig. 4, for a zero rotation. This is
unphysical, so only noise signals should be present. |
| Open with DEXTER |
4.3 (ii) individual circle pairs
If the 
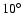 signal is really due to the Poincaré
dodecahedral topology, then it should appear independently in each of
the six circle pairs. If it is due to non-Gaussian and/or non-Poissonian
properties of the ILC, it is unlikely to appear in all six pairs.
signal is really due to the Poincaré
dodecahedral topology, then it should appear independently in each of
the six circle pairs. If it is due to non-Gaussian and/or non-Poissonian
properties of the ILC, it is unlikely to appear in all six pairs.
To test this, the correlation statistic S is calculated separately
for each of the six individual pairs within the range
with a
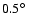 resolution.
resolution.
Since the domain in most parameters is small, the mode for any given 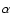 value is plotted rather than a scatter plot of the individual values.
value is plotted rather than a scatter plot of the individual values.
Figures 10-12 clearly show that the peak correlation at around
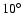 is present in all six circle pairs for the left-handed screw motion.
is present in all six circle pairs for the left-handed screw motion.
Correlations for a few individual peaks reach similar values for the right-handed and zero (unphysical) screw motions, but not for all six pairs simultaneously.
The maximum of the individual curves in Fig. 10 is used
to estimate the circle radius.
As shown in Table 1, these radii all agree to within
one degree, i.e.
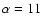
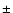
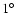 .
.
![\begin{figure}
\includegraphics[width=8cm,clip]{0337fg07.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg117.gif) |
Figure 7:
As for Fig. 4, showing values of the difference statistic 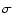 (Eq. (10)) as a function of matched circle angular
radius (Eq. (10)) as a function of matched circle angular
radius 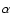 for each pair of six matched circles implied by an
orientation of the fundamental dodecahedron, again for a left-handed
rotation. A cluster of points with smaller differences
for each pair of six matched circles implied by an
orientation of the fundamental dodecahedron, again for a left-handed
rotation. A cluster of points with smaller differences 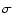 than
the general distribution is visible at
than
the general distribution is visible at 
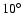 . . |
| Open with DEXTER |
Table 1:
Sky positions of the six face centres for the dodecahedron
which shows excess values of the correlation statistic S.
A face number i, galactic
longitude, latitude and estimated circle radius 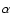 (all in degrees)
are listed. The other 6 faces are directly opposite.
The orientation of the
(all in degrees)
are listed. The other 6 faces are directly opposite.
The orientation of the
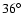 screw motion between faces is left-handed.
screw motion between faces is left-handed.
What are the actual values of the temperature fluctuations along the
identified circles? The identified circles for the central values
listed in Eq. (16) are shown in
Figs. 13-18.
These clearly show that temperature values around these circles
are highly correlated.
4.5 Point source catalogue
If the matched circles are due to topology, then any foreground
point sources close to them in celestial position should be present in
one circle but not the other.
Of the 208 point sources listed in the WMAP point source catalogue
(Bennett et al. 2003), only one is within
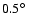 of the matched circle solution. This source is GB6 J1635+3808 at
of the matched circle solution. This source is GB6 J1635+3808 at
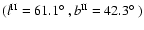 and is located within
and is located within
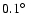 of the circle shown by the solid curve in Fig. 14.
of the circle shown by the solid curve in Fig. 14.
The point source appears to be present in the curve (at position
along the circle of about 1000 h-1 Mpc, shown by a pair of overlapping circles).
A removal of flux in order to correct for the presence of this point
source would improve the match between the circles.
5 Discussion and conclusions
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0337fg10.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg124.gif) |
Figure 10:
Values of the correlation statistic S calculated for the
six individual pairs of circles for dodecahedrons with orientations
in the apparently favoured range (Eq. (16)), shown
as the mode at each circle radius 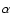 .
This is for a left-handed
screw motion. All six pairs have high correlations at around .
This is for a left-handed
screw motion. All six pairs have high correlations at around 
 . .
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0337fg11.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg125.gif) |
Figure 11:
As for Fig. 10, for a right-handed
screw motion. Although correlations of some circle pairs are high,
there is no case where all six are high. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0337fg12.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg126.gif) |
Figure 12:
As for Fig. 10, for a zero (unphysical)
screw motion. Although correlations of some circle pairs are high,
there is no case where all six are high. |
| Open with DEXTER |
It is clearly premature to claim a highly significant detection of the topology of
the Universe based on just one simple analysis of the first year WMAP ILC cosmic microwave background map.
However, the plots are striking and it seems prudent to release
them to the scientific community while a companion paper is prepared
with formal statistical analyses.
Whether or not the matched circles found are just coincidence or due
to global geometry, it is clear that temperature fluctuations around
12 dodecahedrally spaced circles of radius 11 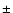
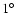 in the WMAP ILC map correlate unusually well in their respective pairs when a phase shift of
in the WMAP ILC map correlate unusually well in their respective pairs when a phase shift of
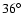 ,
corresponding to a left-handed screw motion, is applied.
,
corresponding to a left-handed screw motion, is applied.
If simulations can show that this is a fairly likely occurrence due
to Gaussian fluctuations in an infinite flat universe, then this would
show that genuine matched circles will be even harder to distinguish
from spurious detections than was previously thought.
However, Vielva et al. (2004) have found non-Gaussian fluctuations at
about
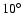 - extremely close to radius of the matched circle radius. While it is not obvious how this non-Gaussianity detection should relate to the radius of matched circles, since correlations are between circles, not along individual circles, this would also
complicate simulations, since they would need to be consistent with
observational analyses like this one.
- extremely close to radius of the matched circle radius. While it is not obvious how this non-Gaussianity detection should relate to the radius of matched circles, since correlations are between circles, not along individual circles, this would also
complicate simulations, since they would need to be consistent with
observational analyses like this one.
Cornish et al. (2004) avoided circles of radii smaller than
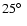 because of the risk of false positives, and carried out extensive simulations of what signal would be expected from a genuinely multiply connected universe.
because of the risk of false positives, and carried out extensive simulations of what signal would be expected from a genuinely multiply connected universe.
However, these simulations risk the problem of cosmic variance
and logical circularity. If the Universe really is detectably multiply
connected, then it would be fairly reasonable that the density perturbations
(eigenmodes) on the largest scales are somewhat affected by the global
physics of the Universe, so that modelling them on the basis of
Gaussianity and random phases may lead to statistical statements which
are incorrect, because they talk about an ensemble of likely universes
with different statistical properties to the real Universe.
The cosmic variance problem is that our actual Universe is just one
realisation - the number of perturbations on large scales are too small
for the large number theorem to make statistics of ensembles valid.
An apparently strong heuristic argument against these matches being
physical is the need for extreme fine-tuning. If the claimed matched
circles are due to topology, then the in-radius of the Universe
happens by chance to be about
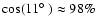 of the
distance to the surface of last scattering. Intuitively, this is
difficult to accept.
of the
distance to the surface of last scattering. Intuitively, this is
difficult to accept.
However, as pointed out by Luminet et al. (2003), in the case of a
positively curved Universe, especially if
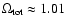 ,
there
is necessarily a fine-tuning, since the curvature scale is only about
three times the matter-dominated horizon size.
,
there
is necessarily a fine-tuning, since the curvature scale is only about
three times the matter-dominated horizon size.
![\begin{figure}
\par\includegraphics[angle=360,width=12.6cm,clip]{0337fg13.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg132.gif) |
Figure 13:
Temperature fluctuations in the WMAP ILC data around an
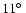 radius
circle centred at position i=1 in Table 1
(continuous curve) and its opposite circle (dot-dashed circle),
matched by a screw motion with a left-handed
rotation of radius
circle centred at position i=1 in Table 1
(continuous curve) and its opposite circle (dot-dashed circle),
matched by a screw motion with a left-handed
rotation of
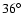 shown against the distance
around each circle for
shown against the distance
around each circle for
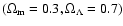 .
These distances are a slight underestimate of the true distances for
the hypothesis, since Euclidean calculation is used for a "slightly''
positively curved space. The two curves shown are .
These distances are a slight underestimate of the true distances for
the hypothesis, since Euclidean calculation is used for a "slightly''
positively curved space. The two curves shown are
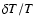 In the general analysis in this paper and
in this and following plots, point pairs where either point
lies at a galactic latitudes with
In the general analysis in this paper and
in this and following plots, point pairs where either point
lies at a galactic latitudes with
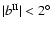 and or within
and or within
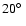 of
the galactic centre are excluded.
of
the galactic centre are excluded. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=360,width=12.6cm,clip]{0337fg14.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg133.gif) |
Figure 14:
As for Fig. 13, for position i=2 in Table 1.
This is the only one of the six circle pairs for which one of the Bennett et al. (2003) point sources lies
within
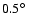 .
This source is GB6 J1635+3808 at .
This source is GB6 J1635+3808 at
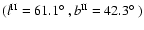 and is shown by a pair of overlapping circles at (arbitrarily)
and is shown by a pair of overlapping circles at (arbitrarily)
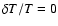 .
Its sky position is within .
Its sky position is within
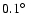 of the
circle shown by the solid curve, suggesting that it is a contaminant
present in the solid curve (Sect. 4.5).
of the
circle shown by the solid curve, suggesting that it is a contaminant
present in the solid curve (Sect. 4.5). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=360,width=12.6cm,clip]{0337fg16.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg135.gif) |
Figure 16:
As for Fig. 13, for position i=2 in Table 1. The exclusion due to the Galaxy mentioned in Fig. 13 excludes many
points in this plot. |
| Open with DEXTER |
Moreover, the non-zero cosmological constant,
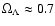 ,
is well established observationally (though see
Blanchard et al. 2003; Vauclair et al. 2003, for a minority viewpoint) and definitely requires fine-tuning of some sort.
,
is well established observationally (though see
Blanchard et al. 2003; Vauclair et al. 2003, for a minority viewpoint) and definitely requires fine-tuning of some sort.
Attempts have been made to link a non-zero cosmological constant with
detectable cosmic topology, but so far no obvious successes have been
found.
Independently of theoretical arguments, the results presented in this
paper are testable by several observationally based
methods which do not require assumptions
on hypothetical statistical ensembles of universes, and each
should potentially be able to
improve the signal if it is cosmological in origin:
-
- (i)
- an attempt to separate out the naïve Sachs-Wolfe effect,
the doppler component, and the integrated Sachs-Wolfe effect, and
analysis at higher resolution;
- (ii)
- improved removal of foregrounds, either independently of the
hypothesis, or using the matched circles hypothesis to predict
foregrounds which intervene in one circle but not the other
(cf. Sect. 4.5);
- (iii)
- polarisation data from Planck.
Similarly to the prediction by Luminet et al. (2003)
that "
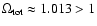 '', Fig. 1 shows
that for
'', Fig. 1 shows
that for
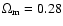
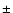 0.02, the total density parameter must be
0.02, the total density parameter must be
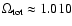
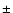 0.001 for these matched circles of
radius 11
0.001 for these matched circles of
radius 11 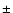
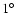 to be cosmological in origin. A larger uncertainty in
to be cosmological in origin. A larger uncertainty in
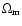 would
correspondingly increase the uncertainty in
would
correspondingly increase the uncertainty in
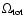 ,
but the prediction that
,
but the prediction that
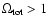 remains: the fundamental dodecahedron of the Poincaré dodecahedral manifold is that of a manifold of positive curvature.
remains: the fundamental dodecahedron of the Poincaré dodecahedral manifold is that of a manifold of positive curvature.
Acknowledgements
B.F.R. is extremely grateful to Roman Juszkiewicz, Marek Demianski,
Bronek Rudak and Andrzej Kus, who enabled him to continue doing
cosmology research.
Use was made of the WMAP data
http://lambda.gsfc.nasa.gov/product/ and of the
Centre de Données astronomiques de Strasbourg
http://cdsads.u-strasbg.fr.
Some of the results in this paper have been derived using the
HEALPix
(Górski et al. 1999)![[*]](/icons/foot_motif.gif) .
S.B. acknowledges support from KBN Grant 1P03D 012 26.
.
S.B. acknowledges support from KBN Grant 1P03D 012 26.
- Barrow, J.
D., & Levin, J. 2001, Phys. Rev. A, 63, 044104 [NASA ADS] [CrossRef] (In the text)
-
Bennett, C. L., Hill, R. S., Hinshaw, G., et al. 2003, ApJS, 148,
97 [NASA ADS] [CrossRef] (In the text)
-
Blanchard, A., Douspis, M., Rowan-Robinson, M., & Sarkar, S.
2003, A&A, 412, 35 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Blanloeil, V., &
Roukema, B. F. 2000, Cosmological Topology in Paris 1998, Paris
[arXiv:astro-ph/0010170]
(In the text)
- Chiang, L.,
Naselsky, P. D., Verkhodanov, O. V., & Way, M. J. 2003, ApJ,
590, L65 [NASA ADS] [CrossRef] (In the text)
- Cline, J. M., Crotty,
P., & Lesgourgues, J. 2003, JCAP, 0309, 010 [NASA ADS] (In the text)
- Contaldi, C.
R., Peloso, M., Kofman, L., & Linde, A. 2003, J. Cosm.
Astro-Part. Phys., 7, 2 [NASA ADS] (In the text)
- Copi, C.
J., Huterer, D., & Starkman, G. D. 2003
[arXiv:astro-ph/0310511]
(In the text)
- Cornish, N. J.,
Spergel, D. N., & Starkman, G. D. 1996
[arXiv:gr-qc/9602039]
(In the text)
- Cornish, N. J.,
Spergel, D. N., & Starkman, G. D. 1998, Class. Quant. Grav.,
15, 2657 [NASA ADS] [MathSciNet] (In the text)
- Cornish, N. J.,
Spergel, D. N., Starkman, G. D., & Komatsu, E. 2004, Phys. Rev.
Lett., 92, 201302 [NASA ADS] [CrossRef] (In the text)
-
de Oliveira-Costa, A., Tegmark, M., Zaldarriaga, M., &
Hamilton, A. 2004, Phys. Rev. D, 69, 063516 [NASA ADS] [CrossRef] (In the text)
- Efstathiou, G.
2003a, MNRAS, 343, L95 [NASA ADS] [CrossRef] (In the text)
-
Efstathiou, G. 2003b, MNRAS, 346, L26 [NASA ADS] [CrossRef] (In the text)
-
Efstathiou, G. 2004, MNRAS, 348, 885 [NASA ADS] [CrossRef] (In the text)
- Fagundes, H. V.,
& Gausmann, E. 1998a
(In the text)
- Fagundes, H. V., &
Gausmann, E. 1998b, Phys. Lett. A, 238, 235 [NASA ADS] [CrossRef] (In the text)
- Fagundes, H. V.,
& Gausmann, E. 1999, Phys. Lett. A, 261, 235 [NASA ADS] [CrossRef] (In the text)
- Feng, B.,
& Zhang, X. 2003, Phys. Lett. B, 570, 145 [NASA ADS] [CrossRef] (In the text)
- Gausmann, E.,
Lehoucq, R., Luminet, J.-P., Uzan, J.-P., & Weeks, J. 2001,
Classical and Quantum Gravity, 18, 5155 [NASA ADS] [CrossRef] [MathSciNet] (In the text)
- Giommi, P., &
Colafrancesco, S. 2004, A&A, 414, 7 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Gomero, G. I.,
Reboucas, M. J., & Teixeira, A. F. F. 2000, Phys. Lett A, 275,
355 [NASA ADS] [CrossRef] [MathSciNet] (In the text)
- Gomero, G. I.,
Reboucas, M. J., & Teixeira, A. F. F. 2001, Class. Quant.
Grav., 18, 1885 [NASA ADS] [MathSciNet] (In the text)
- Gomero, G. I.,
Reboucas, M. J., & Teixeira, A. F. F. 2002, Int. J. Mod. Phys.,
11, 869 [NASA ADS] [MathSciNet] (In the text)
- Górski, K.
M., Hivon, E., & Wandelt, B. D. 1999, in Proc. of the MPA/ESO
Cosmology Conf., Evolution of Large-Scale Structure, ed. A. J.
Banday, R. S. Sheth, & L. Da Costa, PrintPartners Ipskamp, NL,
37 [arXiv:astro-ph/9812350]
(In the text)
- Lachièze-Rey, M.,
& Luminet, J. 1995, Phys. Rep., 254, 135 [NASA ADS] [MathSciNet] (In the text)
- Lehoucq, R.,
Lachièze-Rey, M., & Luminet, J.-P. 1996, A&A, 313,
339 [NASA ADS] (In the text)
- Lehoucq, R., Luminet,
J.-P., & Uzan, J.-P. 1999, A&A, 344, 735 [NASA ADS] (In the text)
- Lehoucq, R., Weeks,
J., Uzan, J.-P., Gausmann, E., & Luminet, J.-P. 2002, Classical
and Quantum Gravity, 19, 4683 [NASA ADS] [CrossRef] [MathSciNet] (In the text)
- Luminet, J., & Roukema,
B. F. 1999, in NATO ASIC Proc. 541, Theor. Obs. Cosm., 117
(In the text)
- Luminet, J., Weeks,
J. R., Riazuelo, A., Lehoucq, R., & Uzan, J. 2003, Nature, 425,
593 [NASA ADS] [CrossRef] (In the text)
- Luminet, J.-P. 1998, Acta
Cosmol., XXIV-1, 105
(In the text)
- Naselsky, P.
D., Doroshkevich, A. G., & Verkhodanov, O. V. 2003, ApJ, 599,
L53 [NASA ADS] [CrossRef] (In the text)
- Naselsky, P.
D., Doroshkevich, A. G., & Verkhodanov, O. V. 2004, MNRAS, 349,
695 [NASA ADS] (In the text)
- Riazuelo, A.,
Weeks, J., Uzan, J.-P., Lehoucq, R., & Luminet, J. 2004, Phys.
Rev. D, 69, 103518 [NASA ADS] [CrossRef] (In the text)
- Roukema, B. F. 1996,
MNRAS, 283, 1147 [NASA ADS] (In the text)
- Roukema, B. F. 2000a,
Class. Quant. Grav., 17, 3951 [NASA ADS] (In the text)
- Roukema, B. F. 2000b,
MNRAS, 312, 712 [NASA ADS] [CrossRef]
- Roukema, B. F., &
Blanloeil, V. 1998, Class. Quant. Grav., 15, 2645 [NASA ADS] [MathSciNet] (In the text)
- Roukema, B. F., & Edge,
A. C. 1997, MNRAS, 292, 105 [NASA ADS] (In the text)
- Schwarzschild, K. 1900,
Vier. d. Astr. Gess, 35, 337 [NASA ADS] (In the text)
- Schwarzschild, K. 1998,
Class. Quant. Grav., 15, 2539 [NASA ADS] [MathSciNet] (In the text)
- Spergel, D.
N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] (In the text)
- Starkman, G. D. 1998,
Class. Quant. Grav., 15, 2529 [NASA ADS] [MathSciNet] (In the text)
-
Tegmark, M., de Oliveira-Costa, A., & Hamilton, A. 2003, Phys.
Rev. D, 68, 123 [NASA ADS] 523
(In the text)
- Uzan, J.-P., Lehoucq,
R., & Luminet, J.-P. 1999, A&A, 351, 766 [NASA ADS] (In the text)
- Uzan, J.-P.,
Luminet, J.-P., Lehoucq, R., & Peter, P. 2002, Eur. J. Phys.,
23, 277 [NASA ADS] [CrossRef] [MathSciNet] (In the text)
- Vauclair,
S. C., Blanchard, A., Sadat, R., et al. 2003, A&A, 412,
L37 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Vielva, P.,
Martinez-González, E., Barreiro, R. B., Sanz, J. L., &
Cayón, L. 2004, ApJ, 609, 22 [NASA ADS] [CrossRef] (In the text)
- Weeks, J. 2001,
The Shape of Space, 2nd edition (Manhattan: Marcel Dekker)
(In the text)
- Weinberg, S. 1972,
Gravitation and cosmology: Principles and applications of the
general theory of relativity (New York: Wiley)
(In the text)
Copyright ESO 2004
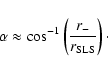
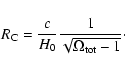
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0337fg01.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg63.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0337fg02.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg66.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0337fg03.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg68.gif)
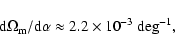
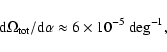
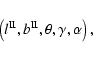
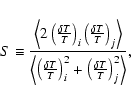
![\begin{displaymath}%
\sigma^2 \equiv { \left<
{ \left[ \left({\delta T \over T}...
...i -
\left({\delta T \over T}\right)_j \right]^2 }
\right>, }
\end{displaymath}](/articles/aa/full/2004/33/aa0337-04/img91.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0337fg04.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg111.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0337fg05.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg112.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0337fg06.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg113.gif)
![\begin{figure}
\includegraphics[width=8cm,clip]{0337fg07.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg117.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0337fg08.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg118.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0337fg09.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg121.gif)
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0337fg10.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg124.gif)
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0337fg11.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg125.gif)
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0337fg12.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg126.gif)
![\begin{figure}
\par\includegraphics[angle=360,width=12.6cm,clip]{0337fg13.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg132.gif)
![\begin{figure}
\par\includegraphics[angle=360,width=12.6cm,clip]{0337fg14.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg133.gif)
![\begin{figure}
\par\includegraphics[angle=360,width=12.6cm,clip]{0337fg15.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg134.gif)
![\begin{figure}
\par\includegraphics[angle=360,width=12.6cm,clip]{0337fg16.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg135.gif)
![\begin{figure}
\par\includegraphics[angle=360,width=12.6cm,clip]{0337fg17.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg136.gif)
![\begin{figure}
\par\includegraphics[angle=360,width=12.6cm,clip]{0337fg18.ps}\end{figure}](/articles/aa/full/2004/33/aa0337-04/Timg137.gif)