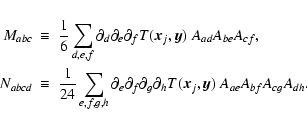A&A 423, 787-792 (2004)
DOI: 10.1051/0004-6361:20040212
R. Takahashi
Division of Theoretical Astrophysics, National Astronomical Observatory, Mitaka, Tokyo 181-8588, Japan
Received 6 February 2004 / Accepted 28 April 2004
Abstract
The gravitational lensing of gravitational waves should
be treated in wave optics instead of geometrical optics
when the wave length ![]() of the gravitational waves
is larger than the Schwarzschild radius of the lens mass M.
Wave optics is based on the diffraction integral which represents
the amplification of the wave amplitude by lensing.
We study the asymptotic expansion of the diffraction integral in
the powers of the wave length
of the gravitational waves
is larger than the Schwarzschild radius of the lens mass M.
Wave optics is based on the diffraction integral which represents
the amplification of the wave amplitude by lensing.
We study the asymptotic expansion of the diffraction integral in
the powers of the wave length ![]() .
The first term, arising from the short wavelength limit
.
The first term, arising from the short wavelength limit
![]() ,
corresponds to the geometrical optics limit.
The second term, being of the order of
,
corresponds to the geometrical optics limit.
The second term, being of the order of ![]() ,
is the leading
correction term arising from the diffraction effect.
Analysing this correction term, we find that (1) the lensing
magnification
,
is the leading
correction term arising from the diffraction effect.
Analysing this correction term, we find that (1) the lensing
magnification ![]() is modified to
is modified to
![]() ,
where
,
where ![]() is of the order of
is of the order of
![]() ,
and (2) if the lens has a cuspy
(or singular) density profile at center
,
and (2) if the lens has a cuspy
(or singular) density profile at center
![]() (
(
![]() ), the diffracted image is formed
at the lens center with magnification
), the diffracted image is formed
at the lens center with magnification
![]() .
.
Key words: gravitational lensing - gravitational waves
The gravitational lensing of light is usually treated in the geometrical
optics approximation, which is valid in almost all observational
situations since the wavelength of light is much
smaller than typical scales of astrophysical lens objects.
However, for the gravitational lensing of gravitational waves
the wavelength is long so that the geometrical optics approximation is
not valid in some cases.
As shown by several authors (Ohanian 1983; Bliokh & Minakov 1975;
Bontz & Haugan 1981; Thorne 1983; Deguchi & Watson 1986),
if the wavelength ![]() is larger than the Schwarzschild radius
of the lens mass M, the diffraction effect becomes important.
Thus, the diffraction effect is important for a lens mass smaller
than
is larger than the Schwarzschild radius
of the lens mass M, the diffraction effect becomes important.
Thus, the diffraction effect is important for a lens mass smaller
than
![]() ,
where 1 AU is the wavelength for the planned laser interferometer space antenna
(LISA: Bender et al. 2000).
,
where 1 AU is the wavelength for the planned laser interferometer space antenna
(LISA: Bender et al. 2000).
From the above discussion, for
![]() the diffraction effect
is important and the magnification is small (the wavelength is so long
that the wave does not feel the existence of the lens), and
for
the diffraction effect
is important and the magnification is small (the wavelength is so long
that the wave does not feel the existence of the lens), and
for
![]() the geometrical optics approximation is valid.
In this paper, we consider the case for
the geometrical optics approximation is valid.
In this paper, we consider the case for
![]() ,
i.e.
the quasi-geometrical optics approximation which is
geometrical optics including corrections
arising from the effects of the finite wavelength.
We can obtain these correction terms by an asymptotic expansion of
the diffraction integral in powers of the wavelength
,
i.e.
the quasi-geometrical optics approximation which is
geometrical optics including corrections
arising from the effects of the finite wavelength.
We can obtain these correction terms by an asymptotic expansion of
the diffraction integral in powers of the wavelength ![]()
![]() .
The diffraction integral represents the amplification of the
wave amplitude by lensing in wave optics.
It is important to derive the correction terms
for the following two reasons:
(1) the calculations in wave optics are based on the diffraction
integral, but it is time-consuming to numerically calculate this
integral, especially for high frequency
(see e.g., Ulmer & Goodman 1995).
Hence, it is a great saving of computing time to use the analytical
expressions.
(2) We can understand clearly the difference between
wave optics and geometrical optics (i.e. the diffraction effect).
.
The diffraction integral represents the amplification of the
wave amplitude by lensing in wave optics.
It is important to derive the correction terms
for the following two reasons:
(1) the calculations in wave optics are based on the diffraction
integral, but it is time-consuming to numerically calculate this
integral, especially for high frequency
(see e.g., Ulmer & Goodman 1995).
Hence, it is a great saving of computing time to use the analytical
expressions.
(2) We can understand clearly the difference between
wave optics and geometrical optics (i.e. the diffraction effect).
This paper is organized as follows:
in Sect. 2 we briefly discuss wave optics in gravitational lensing of
gravitational waves. In Sect. 3 we show that in the short wavelength limit
![]() ,
wave optics is reduced to the geometrical optics limit.
In Sect. 4 we expand the diffraction integral in powers of the
wavelength
,
wave optics is reduced to the geometrical optics limit.
In Sect. 4 we expand the diffraction integral in powers of the
wavelength ![]() ,
and derive the leading correction terms arising
from the effect of finite wavelength.
In Sect. 5 we apply the quasi-geometrical optics approximation to
simple lens models (the point mass lens, SIS lens, isothermal
sphere with a finite core lens, and the NFW lens).
Section 6 is devoted to a summary and discussions.
We use units of c=G=1.
,
and derive the leading correction terms arising
from the effect of finite wavelength.
In Sect. 5 we apply the quasi-geometrical optics approximation to
simple lens models (the point mass lens, SIS lens, isothermal
sphere with a finite core lens, and the NFW lens).
Section 6 is devoted to a summary and discussions.
We use units of c=G=1.
We consider gravitational waves propagating near a lens object
under the thin lens approximation in which the gravitational wave
is scattered only on the thin lens plane.
The gravitational wave amplitude is magnified by an amplification
factor F which is given by the diffraction integral as
(Schneider et al. 1992)
It is useful to rewrite the amplification factor F in terms of
dimensionless quantities.
We introduce ![]() as the normalization constant
of the length in the lens plane.
The impact parameter
as the normalization constant
of the length in the lens plane.
The impact parameter
![]() ,
the source position
,
the source position
![]() ,
the frequency
,
the frequency ![]() ,
and the time delay
,
and the time delay ![]() are rewritten
in dimensionless form,
are rewritten
in dimensionless form,
In the geometrical optics limit (![]() ), the stationary
points of
), the stationary
points of
![]() contribute to the integral of Eq. (5) so that the image
positions
contribute to the integral of Eq. (5) so that the image
positions ![]() are determined by the lens equation,
are determined by the lens equation,
![]() or
or
![]() .
This is just Fermat's principle.
We expand
.
This is just Fermat's principle.
We expand
![]() around the jth image position
around the jth image position ![]() as
as
We expand the amplification factor
![]() in powers of
in powers of
![]() and discuss the behavior of the term of
the order of 1/w.
Here, we only consider axially symmetric lens models because
the basic formulae are relatively simple,
while the case of the non-axially symmetric lens models is discussed
in Appendix B.
We expand
and discuss the behavior of the term of
the order of 1/w.
Here, we only consider axially symmetric lens models because
the basic formulae are relatively simple,
while the case of the non-axially symmetric lens models is discussed
in Appendix B.
We expand
![]() in Eq. (7) up to
the fourth order of
in Eq. (7) up to
the fourth order of ![]() as
as
![\begin{displaymath}%
\Delta_j = \frac{1}{16} \left[ \frac{1}{2 \alpha_j^2} \psi_...
...beta_j}{\alpha_j
\beta_j} \frac{1}{\vert x_j\vert^2} \right],
\end{displaymath}](/articles/aa/full/2004/33/aa0212-04/img75.gif) |
(13) |
In the previous section, we showed that the contributions to the
diffraction integral F arise
from the stationary points (or image positions).
In this section, we discuss the contributions from the non-stationary
points. We denote
![]() as the non-stationary point,
at which the condition
as the non-stationary point,
at which the condition
![]() is satisfied.
If
is satisfied.
If
![]() can be expanded at
can be expanded at
![]() ,
we obtain the series of T similar to Eq. (7) as
,
we obtain the series of T similar to Eq. (7) as
Inserting Eq. (15) into Eq. (5) and expanding the
integrand in powers of 1/w, we obtain
In the above discussion, we assume that
![]() has derivatives at the non-stationary point
has derivatives at the non-stationary point
![]() in Eq. (15).
But, if the derivatives of T are not defined at
in Eq. (15).
But, if the derivatives of T are not defined at
![]() ,
the result in Eq. (16) should be reconsidered.
If the lens has a cuspy (or singular) density profile at the center,
the derivatives of T are not defined at the lens center.
We will discuss this case in the next section.
,
the result in Eq. (16) should be reconsidered.
If the lens has a cuspy (or singular) density profile at the center,
the derivatives of T are not defined at the lens center.
We will discuss this case in the next section.
We consider the correction terms in the amplification
factor F arising at the central cusp of the lens.
For the inner density profile of the lens
![]() (
(
![]() )
)![]() , the surface density and the deflection potential at small radius
are given by
, the surface density and the deflection potential at small radius
are given by
| |
|||
| (17) |
If the inner density profile is
![]() (e.g. singular
isothermal sphere model), the deflection potential is given by
(e.g. singular
isothermal sphere model), the deflection potential is given by
![]() (
(![]() is a constant) from
Eq. (18).
Inserting this potential
is a constant) from
Eq. (18).
Inserting this potential ![]() into Eq. (5), we obtain
into Eq. (5), we obtain
If the inner density profile is
![]() (e.g. the Navarro
Frenk White model), the deflection potential is given by
(e.g. the Navarro
Frenk White model), the deflection potential is given by
![]() (
(![]() is a constant) from
Eq. (18).
Inserting this
is a constant) from
Eq. (18).
Inserting this ![]() into Eq. (6), we have
into Eq. (6), we have
![\begin{displaymath}%
{\rm d}F_{\rm c}(w,y) = \frac{-4 \psi_0}{\left(w y^2\right)^2} ~{\rm e}^{{\rm i} w \left[y^2 / 2+\phi_{\rm m}(y)\right]}.
\end{displaymath}](/articles/aa/full/2004/33/aa0212-04/img129.gif) |
(23) |
The deflection potential is
![]() (
(![]() is a constant) from Eq. (18).
Inserting
is a constant) from Eq. (18).
Inserting ![]() into Eq. (6),
we obtain
into Eq. (6),
we obtain
![]() as
as
From the above discussion for the three cases, the diffracted image is always
formed at the lens center for an inner density profile
![]() (
(
![]() ).
The magnification of this central image is roughly given by
).
The magnification of this central image is roughly given by
![]() .
.
We apply the quasi-geometrical optics approximation to
simple lens models.
We consider the following axially symmetric lens models:
point mass lens, singular isothermal sphere (SIS) lens,
isothermal sphere lens with a finite core,
and Navarro Frenk White (NFW) lens.
We derive the amplification factor F, that in the geometrical optics
limit
![]() ,
and its correction terms
,
and its correction terms
![]() (in Sect. 4.1) and
(in Sect. 4.1) and
![]() (in Sect. 4.3) for the above lens models.
We define
(in Sect. 4.3) for the above lens models.
We define ![]() for convenience as the sum of
for convenience as the sum of
![]() and
and
![]() :
:
![]() .
.
The surface mass density is expressed as
![]() ,
where M is the lens mass,
and the deflection potential is
,
where M is the lens mass,
and the deflection potential is
![]() .
This lens model is most frequently used in wave optics in
gravitational lensing of gravitational waves (Nakamura 1998;
Ruffa 1999; De Paolis et al. 2001, 2002;
Zakharov & Baryshev 2002; Takahashi & Nakamura 2003;
Yamamoto 2003; Varvella et al. 2003; Seto 2004).
The amplification factor F of Eq. (6) is
analytically integrated as (Peters 1974;
Deguchi & Watson 1986)
.
This lens model is most frequently used in wave optics in
gravitational lensing of gravitational waves (Nakamura 1998;
Ruffa 1999; De Paolis et al. 2001, 2002;
Zakharov & Baryshev 2002; Takahashi & Nakamura 2003;
Yamamoto 2003; Varvella et al. 2003; Seto 2004).
The amplification factor F of Eq. (6) is
analytically integrated as (Peters 1974;
Deguchi & Watson 1986)
![\begin{figure}
\par\hspace*{5.7mm}\includegraphics[width=7.15cm,clip]{0212fig1.eps}\par\vspace*{1cm}
\includegraphics[width=7.8cm,clip]{0212fig2.eps}\end{figure}](/articles/aa/full/2004/33/aa0212-04/Timg149.gif) |
Figure 1:
a) The amplification factor |F(w,y)| for a point mass lens
as a function of w with a fixed source position y=0.3.
The solid line is the full result F; the dotted line
is the geometrical optics approximation
|
| Open with DEXTER | |
In Fig. 1a, the amplification factor |F| is shown
as a function of w with a fixed source position y=0.3.
The solid line is the result F in Eq. (25); the dotted line
is the geometrical optics approximation
![]() in Eq. (26);
the dashed line is the quasi-geometrical optics approximation
in Eq. (26);
the dashed line is the quasi-geometrical optics approximation
![]() in Eqs. (26) and (27).
For the high frequency limit
in Eqs. (26) and (27).
For the high frequency limit ![]() ,
|F| converge to the
geometrical optics limit in Eq. (26),
,
|F| converge to the
geometrical optics limit in Eq. (26),
In Fig. 1b, the differences between F,
![]() and
and
![]() are shown as a function of w with y=0.3.
The thin solid line is
are shown as a function of w with y=0.3.
The thin solid line is
![]() ,
and the thin dashed line
is
,
and the thin dashed line
is
![]() .
The thick solid (dashed) line is the power of
w-1 (w-2).
From this figure, for larger w (
.
The thick solid (dashed) line is the power of
w-1 (w-2).
From this figure, for larger w (![]() 1) F converges to
1) F converges to
![]() with an error of
with an error of
![]() ,
and
converges to
,
and
converges to
![]() with an error of
with an error of
![]() .
These results are consistent with the analytical calculations in Sects. 3 and 4.
.
These results are consistent with the analytical calculations in Sects. 3 and 4.
The surface density of the SIS (Singular Isothermal Sphere) is characterized
by the velocity dispersion v as
![]() .
and the deflection potential is
.
and the deflection potential is
![]() .
The SIS model is used for more realistic lens objects than the point
mass lens, such as galaxies, star clusters and dark halos
(Takahashi & Nakamura 2003).
In this model F is numerically computed in Eq. (6).
In the geometrical optics limit
.
The SIS model is used for more realistic lens objects than the point
mass lens, such as galaxies, star clusters and dark halos
(Takahashi & Nakamura 2003).
In this model F is numerically computed in Eq. (6).
In the geometrical optics limit ![]() ,
,
![]() is given by
is given by
![\begin{figure}
\par\hspace*{5.5mm}\includegraphics[width=7.15cm,clip]{0212fig3.eps}\par\vspace*{1cm}
\includegraphics[width=7.8cm,clip]{0212fig4.eps}\end{figure}](/articles/aa/full/2004/33/aa0212-04/Timg170.gif) |
Figure 2: Same as Fig. 1, but for SIS lens with a source position y=0.3. |
| Open with DEXTER | |
Figure 2 is the same as Fig. 1, but for a SIS lens
with a source position y=0.3.
In Fig. 2a, the behavior is similar to that in the point mass
lens (in Fig. 1a).
The oscillation of
![]() is due to the interference between the
double images, while the oscillation of
is due to the interference between the
double images, while the oscillation of
![]() is due to
the interference among the three images.
As shown in Fig. 2b, the errors decrease as w increases, and
the results are consistent with the analytical calculations.
is due to
the interference among the three images.
As shown in Fig. 2b, the errors decrease as w increases, and
the results are consistent with the analytical calculations.
We investigate the effect of a finite core in the lens center on the
amplification factor.
We consider an isothermal sphere having a finite core.
The deflection potential is
![]() where
where ![]() is
the dimensionless core radius.
In this model, the central core of the lens contributes the integral of F in Eq. (5).
Denoting
is
the dimensionless core radius.
In this model, the central core of the lens contributes the integral of F in Eq. (5).
Denoting
![]() as
the contribution of F at the lens center, we obtain,
as
the contribution of F at the lens center, we obtain,
The NFW profile was proposed from numerical simulations of cold dark
matter (CDM) halos by Navarro, Frenk & White (1997).
They showed that the density profile of dark halos has the
"universal'' form,
![]() ,
where
,
where ![]() is a scale length and
is a scale length and
![]() is a characteristic density.
The NFW lens is used for lensing by galactic halos and clusters of
galaxies. The deflection potential is written as (Bartelmann 1996),
is a characteristic density.
The NFW lens is used for lensing by galactic halos and clusters of
galaxies. The deflection potential is written as (Bartelmann 1996),
We studied gravitational lensing in the quasi-geometrical optics
approximation which is geometrical optics including the corrections
arising from the effect of a finite wavelength.
These correction terms can be obtained analytically by asymptotic
expansion of the diffraction integral in powers of the wavelength ![]() .
The first term, arising from the short wavelength limit
.
The first term, arising from the short wavelength limit
![]() ,
corresponds to the geometrical optics limit.
The second term, being of the order of
,
corresponds to the geometrical optics limit.
The second term, being of the order of ![]() (M is the
Schwarzschild radius of the lens), is the first correction term
arising from the diffraction effect.
By analyzing this correction term, we obtain the following results:
(1) the lensing magnification
(M is the
Schwarzschild radius of the lens), is the first correction term
arising from the diffraction effect.
By analyzing this correction term, we obtain the following results:
(1) the lensing magnification ![]() is modified to
is modified to
![]() ,
where
,
where ![]() is of the order of
is of the order of
![]() .
(2) If the lens has a cuspy (or singular) density profile at the center
.
(2) If the lens has a cuspy (or singular) density profile at the center
![]() (
(
![]() )
the diffracted image
is formed at the lens center with magnification
)
the diffracted image
is formed at the lens center with magnification
![]() .
Thus if we observe this diffracted image in various wavelengths,
the slope
.
Thus if we observe this diffracted image in various wavelengths,
the slope ![]() can be determined.
can be determined.
Acknowledgements
i would like to thank Takashi Nakamura, Takeshi Chiba, and Kazuhiro Yamamoto for useful comments and discussions.
We present the method for the numerical integration of F discussed
in Sect. 2. F in Eq. (5) is rewritten as
Especially for an axially symmetric lens, the function f in Eq. (A.3) is reduced to the simple form as
![\begin{displaymath}%
f(z:w,y)=-{\rm i}w {\rm e}^{{\rm i}w \left[y^2/2+\phi_{\rm ...
...)\right]} J_0 \left(wy \sqrt{2z}\right)
~{\rm e}^{{\rm i}wz}.
\end{displaymath}](/articles/aa/full/2004/33/aa0212-04/img200.gif) |
(A.5) |
We consider the expansion of F in powers of 1/w for the non-axially symmetric lens model.
In this case, the expansion of
![]() around the
jth image position
around the
jth image position ![]() in Eq. (9) is rewritten as
in Eq. (9) is rewritten as