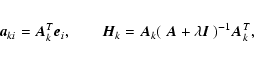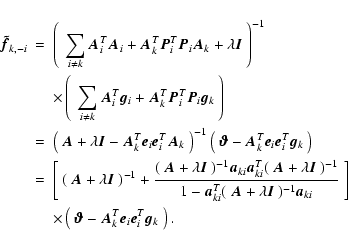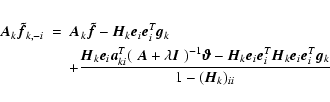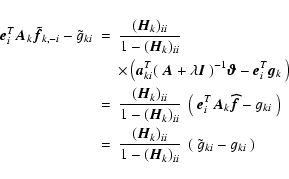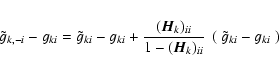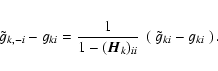A&A 423, 1179-1186 (2004)
DOI: 10.1051/0004-6361:20047113
Estimation of regularization parameters in multiple-image deblurring
R. Vio1 -
P. Ma2 -
W. Zhong3 -
J. Nagy4 -
L. Tenorio5 -
W. Wamsteker6
1 - Chip Computers Consulting s.r.l., Viale Don L. Sturzo 82,
S. Liberale di Marcon, 30020 Venice, Italy
ESA-VILSPA, Apartado 50727, 28080 Madrid, Spain
2 -
Department of Statistics, Harvard University, Cambridge, MA 02138, USA
3 -
Department of Statistics, Purdue University, West Lafayette, IN 47907, USA
4 -
Department of Mathematics and Computer Science, Emory University, Atlanta, GA 30322, USA
5 -
Department of Mathematical and Computer Sciences, Colorado School of Mines, Golden CO 80401, USA
6 -
ESA-VILSPA, Apartado 50727, 28080 Madrid, Spain
Received 21 January 2004 / Accepted 25 May 2004
Abstract
We consider the estimation of the regularization parameter for the simultaneous
deblurring of multiple noisy images via Tikhonov regularization. We approach the problem in three ways. We first reduce the problem to a single-image deblurring for which the regularization parameter can be estimated through a classic generalized cross-validation ( ) method. A modification of this function is used for correcting the undersmoothing typical of the original technique. With a second method, we minimize an average least-squares fit to the images and define a new
) method. A modification of this function is used for correcting the undersmoothing typical of the original technique. With a second method, we minimize an average least-squares fit to the images and define a new  function. In the last approach, we use the classical
function. In the last approach, we use the classical  on a single higher-dimensional image obtained by concatenating all the images into a single vector.
With a reliable estimator of the regularization parameter, one can fully exploit the
excellent computational characteristics typical of direct deblurring methods, which, especially for
large images, makes them competitive with the more flexible but much slower iterative
algorithms. The performance of the techniques is analyzed through numerical experiments.
We find that under the independent homoscedastic and Gaussian assumptions made on the noise,
the three approaches provide almost identical results
with the first single image providing the practical advantage that no new software is required and the same image can be used with other deblurring algorithms.
on a single higher-dimensional image obtained by concatenating all the images into a single vector.
With a reliable estimator of the regularization parameter, one can fully exploit the
excellent computational characteristics typical of direct deblurring methods, which, especially for
large images, makes them competitive with the more flexible but much slower iterative
algorithms. The performance of the techniques is analyzed through numerical experiments.
We find that under the independent homoscedastic and Gaussian assumptions made on the noise,
the three approaches provide almost identical results
with the first single image providing the practical advantage that no new software is required and the same image can be used with other deblurring algorithms.
Key words: methods: data analysis - methods: statistical - techniques: image processing
An important problem in image processing is the simultaneous deblurring of a set of observed images (of a fixed object), each of which is degraded by a different point spread function (PSF).
Consider, for example, images obtained by the Large Binocular Telescope (LBT). This instrument consists of two
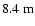 mirrors on a common mount with a spacing of
mirrors on a common mount with a spacing of
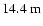 between the centers (Angel et al. 1998). For a given orientation of the telescope, the diffraction-limited resolution along the center-to-center baseline is equivalent to that of a
between the centers (Angel et al. 1998). For a given orientation of the telescope, the diffraction-limited resolution along the center-to-center baseline is equivalent to that of a
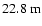 mirror, while the resolution along the perpendicular direction is that of a single
mirror, while the resolution along the perpendicular direction is that of a single 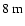 mirror. One way to obtain an image with improved and uniform spatial resolution is to simultaneously
deconvolve the images taken with different orientations of the telescope.
mirror. One way to obtain an image with improved and uniform spatial resolution is to simultaneously
deconvolve the images taken with different orientations of the telescope.
In a recent paper, Vio et al. (2004) presented an efficient solution based on a single image
that improves the performance of iterative algorithms developed in the context of a
least-squares approach (Bertero & Boccacci 2000). An important advantage of iterative algorithms is the
ease with which constraints such as nonnegativity of the solution can be implemented.
However, this incurs a high computational cost (especially in case of slow
convergence). In addition, there is a lack of a reliable stopping criteria. Although these issues
may not be critical for images of moderate size, they are critical for large images ( 107-108 pixels) or studies that require the deblurring of a large number of images. In this respect, direct methods are potentially more useful. For example, with a fixed regularization parameter, Tikhonov deblurring requires only two two-dimensional discrete Fourier transforms.
107-108 pixels) or studies that require the deblurring of a large number of images. In this respect, direct methods are potentially more useful. For example, with a fixed regularization parameter, Tikhonov deblurring requires only two two-dimensional discrete Fourier transforms.
A limitation of any regularization method, and in particular of Tikhonov's approach, is the need to get a computationally efficient and reliable estimate of the regularization parameter.
We present three different methods for such a task in the case of multiple spatially invariant PSFs and additive Gaussian noise. In Sect. 2, we formalize the problem and propose three solutions in Sect. 3. Their performance is studied through numerical experiments in Sect. 4. Section 5 closes with final comments.
2 Formalization of the problem
The image restoration problem is to find an estimate f(x,y) of a fixed two-dimensional object f0(x,y) given p observed images gj(x,y) (
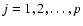 )
each of which is degraded by a different spatially invariant blurring operator; that is,
)
each of which is degraded by a different spatially invariant blurring operator; that is,
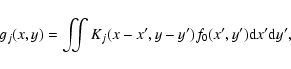 |
(1) |
where each Kj(x,y) is a known space invariant PSF.
In practice, the observed images are discrete N 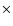 N arrays of pixels
(images are assumed square for simplicity) contaminated by noise. Therefore, model (1)
has to be recast in the form
N arrays of pixels
(images are assumed square for simplicity) contaminated by noise. Therefore, model (1)
has to be recast in the form
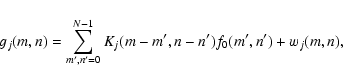 |
(2) |
where wj(m,n) will be assumed to be Gaussian white noise with standard deviation
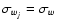 .
Note however that the methods in Sect. 3 may be used when the noise is not white but has a correlation structure that is known up to a constant factor.
.
Note however that the methods in Sect. 3 may be used when the noise is not white but has a correlation structure that is known up to a constant factor.
If the central peak (i.e., support) of each PSF is much smaller than the image and
the object does not have structures near the image boundaries, then the convolution
product in Eq. (2) can be well approximated by cyclic convolution, which
leads to
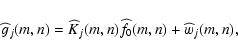 |
(3) |
where the symbol "
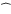 '' denotes the discrete Fourier transform (DFT).
'' denotes the discrete Fourier transform (DFT).
In order to estimate f0 using Tikhonov regularization, it is helpful to use matrix-vector notation. Rewrite Eq. (2) as
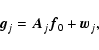 |
(4) |
where the arrays 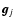 ,
,
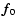 and
and 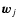 are obtained by column stacking gj(m,n),
f0(m,n), and wj(m,n), respectively. The matrix
are obtained by column stacking gj(m,n),
f0(m,n), and wj(m,n), respectively. The matrix 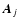 is block-circulant and defined
by cyclic convolution with the jth PSF.
is block-circulant and defined
by cyclic convolution with the jth PSF.
Bertero & Boccacci (2000) estimate 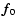 by Tikhonov regularization where the estimate
by Tikhonov regularization where the estimate
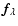 minimizes an average fit to the images subject to a smoothness constraint:
minimizes an average fit to the images subject to a smoothness constraint:
where the global imaging matrix and global image are defined, respectively, as
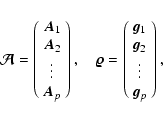 |
(7) |
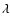 is the regularization parameter and
is the regularization parameter and 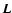 is, usually, the identity matrix (for energy bound) or a discrete Laplacian operator (for smoothness constraint) (Wahba 1990).
The solution
is, usually, the identity matrix (for energy bound) or a discrete Laplacian operator (for smoothness constraint) (Wahba 1990).
The solution
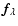 satisfies the normal equations
satisfies the normal equations
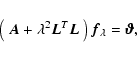 |
(8) |
where
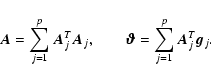 |
(9) |
For a fixed value of 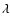 ,
its explicit solution is given by:
,
its explicit solution is given by:
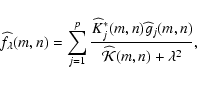 |
(10) |
where
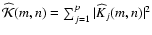 .
.
In the rest of the paper we consider the selection of the regularization parameter 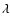 for
three different methods whose normal equations reduce in each case to Eq. (8).
for
three different methods whose normal equations reduce in each case to Eq. (8).
3 Estimating the regularization parameter
The Tikhonov regularization (5) is transformed into a single-image problem (6) through the
use of the higher dimensional global image
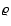 .
We now define an alternative single-image
approach whose dimensionality is the same as that of the original images.
.
We now define an alternative single-image
approach whose dimensionality is the same as that of the original images.
The solution of the normal Eq. (8) depends on the original data
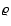 only through
only through
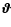 .
In fact, in the case of homoscedastic uncorrelated Gaussian noise,
.
In fact, in the case of homoscedastic uncorrelated Gaussian noise,
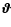 and
and
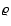 contain the same information about
contain the same information about 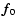 .
This can be justified with a sufficiency argument on
.
This can be justified with a sufficiency argument on
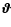 (Lehmann & Casella 1998). It thus seems natural to pose the problem directly through
(Lehmann & Casella 1998). It thus seems natural to pose the problem directly through
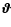 :
since the expected value of
:
since the expected value of
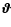 is
is
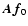 ,
we propose to estimate
,
we propose to estimate 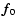 by regularizing the misfit
by regularizing the misfit
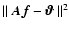 .
But one problem with
.
But one problem with
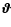 is that its covariance matrix is
is that its covariance matrix is
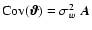 ,
which is no longer proportional to the identity and therefore the classical generalized cross-validation (
,
which is no longer proportional to the identity and therefore the classical generalized cross-validation ( )
is not expected to work well.
In fact, our simulations show that
)
is not expected to work well.
In fact, our simulations show that  consistently underestimates
consistently underestimates 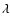 when used with
when used with
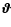 .
However, since
.
However, since 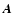 is known, one can easily
correct for this correlation using a square-root of the symmetric matrix
is known, one can easily
correct for this correlation using a square-root of the symmetric matrix 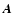 :
the image
:
the image
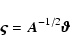 |
(11) |
has mean
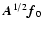 and covariance matrix
and covariance matrix
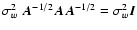 .
Hence, we define the Tikhonov functional
.
Hence, we define the Tikhonov functional
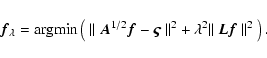 |
(12) |
It can be easily shown that the normal equations for Eq. (12) are given by Eq. (8). This result indicates that the functional (5) can be expressed in terms of a single-image
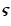 with PSF
with PSF
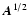 ,
whose
Fourier domain representation is
,
whose
Fourier domain representation is
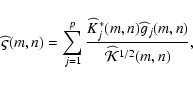 |
(13) |
and
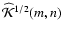 ,
respectively. Through
,
respectively. Through
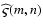 ,
the solution (10) for
,
the solution (10) for
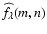 can be expressed in the form
can be expressed in the form
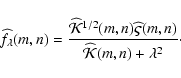 |
(14) |
Since the covariance matrix of
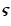 is proportional
to the identity, we can make
use of the classical generalized cross-validation (
is proportional
to the identity, we can make
use of the classical generalized cross-validation ( ) function
to estimate
) function
to estimate 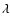 (e.g., Wahba 1990; Vio et al. 2003):
(e.g., Wahba 1990; Vio et al. 2003):
![\begin{displaymath}%
{\rm GCV}^{(\vec{\varsigma})}(\lambda) = \frac{1}{N^2}\frac...
...rm Tr}\left[\vec{H}^{(\vec{\varsigma})}\right]/N^2~\right)^2},
\end{displaymath}](/articles/aa/full/2004/33/aa0113-04/img58.gif) |
(15) |
where
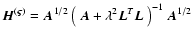 ,
with frequency domain representation
,
with frequency domain representation
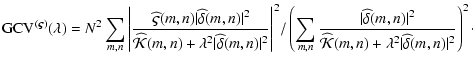 |
|
|
(16) |
Here,
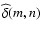 provides the two-dimensional DFT of matrix
provides the two-dimensional DFT of matrix 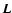 .
However, despite its theoretical justification and adequate practical performance,
.
However, despite its theoretical justification and adequate practical performance,  tends to underestimate the regularization parameter (too small a
tends to underestimate the regularization parameter (too small a 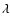 )
in about
)
in about 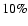 of the cases. A corrected
of the cases. A corrected  can be used
to control this without sacrificing its generally good performance. The corrected weighted
can be used
to control this without sacrificing its generally good performance. The corrected weighted  is:
is:
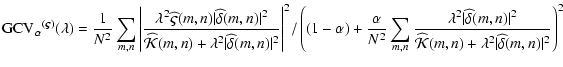 |
|
|
(17) |
where
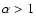 .
It reduces to Eq. (16) when
.
It reduces to Eq. (16) when
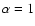 and yields
smoother estimates as
and yields
smoother estimates as 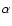 increases.
increases.
Empirical studies suggest good values of 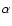 for practical use in the range of 1.2 and 1.4.
Modifications of this sort have been suggested by various researchers (e.g., Nychka et al. 1998). However, only recently (Cummins et al. 2001; Kim & Gu 2004) have systematic simulation studies been conducted to evaluate the performance of the corrected
for practical use in the range of 1.2 and 1.4.
Modifications of this sort have been suggested by various researchers (e.g., Nychka et al. 1998). However, only recently (Cummins et al. 2001; Kim & Gu 2004) have systematic simulation studies been conducted to evaluate the performance of the corrected  in the context of statistical nonparametric modeling. The optimality of the corrected
in the context of statistical nonparametric modeling. The optimality of the corrected  (17) can be
interpreted in a way similar to that of
(17) can be
interpreted in a way similar to that of  (16).
Instead of estimating a relative loss function, Eq. (17) estimates a weighted combination of the average squared bias and the average variance (Cummins et al. 2001). It should also be noted that
(16).
Instead of estimating a relative loss function, Eq. (17) estimates a weighted combination of the average squared bias and the average variance (Cummins et al. 2001). It should also be noted that  is a function of both
is a function of both 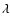 and
and 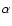 ,
but it is difficult to decide whether
,
but it is difficult to decide whether  should be minimized over
should be minimized over 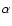 .
Current research efforts are still trying to resolve this issue.
.
Current research efforts are still trying to resolve this issue.
It is important to emphasize that the problem of underestimation is not unique to  ,
it is common to virtually all regularization parameter selection techniques. For example, the generalized maximum likelihood (GML) estimate of
,
it is common to virtually all regularization parameter selection techniques. For example, the generalized maximum likelihood (GML) estimate of 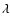 (Wahba 1985) asymptotically tends to deliver slightly smaller estimates than
(Wahba 1985) asymptotically tends to deliver slightly smaller estimates than  .
An attractive feature of our simple correction is that it is not restricted to
.
An attractive feature of our simple correction is that it is not restricted to  ,
and sheds a fresh light on
underestimation corrections for GML and other approaches.
,
and sheds a fresh light on
underestimation corrections for GML and other approaches.
The minimization of the  function cannot be done analytically, some numerical
iteration method has to be used. In our simulation we use the Newton-Raphson algorithm.
function cannot be done analytically, some numerical
iteration method has to be used. In our simulation we use the Newton-Raphson algorithm.
Although the single-image
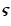 is adequate
for applications where the most important information is preserved in the single image,
here we define
is adequate
for applications where the most important information is preserved in the single image,
here we define  for functions (5) and (6), and
compare their performances with that obtained with the single-image
for functions (5) and (6), and
compare their performances with that obtained with the single-image
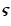 .
.
We start by defining a multiple-image ordinary
cross validation (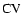 ) function. One such function can be obtained
by estimating the prediction error of each image
using a leave-one-out estimate
) function. One such function can be obtained
by estimating the prediction error of each image
using a leave-one-out estimate
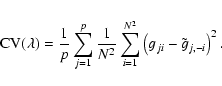 |
(18) |
Here,
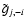 is the prediction based on the estimate of
is the prediction based on the estimate of 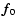 that uses
all the data except the ith entry in
that uses
all the data except the ith entry in 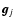 .
Simple algebra leads to an equation for
.
Simple algebra leads to an equation for
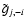 in terms of
in terms of
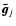 (see Appendix A)
(see Appendix A)
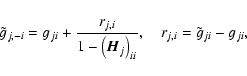 |
(19) |
where,
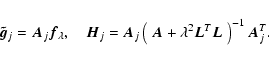 |
(20) |
The multiple-image 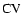 function can then be written as
function can then be written as
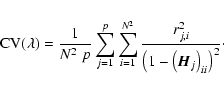 |
(21) |
The multiple-image  is obtained by modifying Eq. (18) to be rotationaly invariant. That is, the value of the GCV function should
remain unchanged if each
is obtained by modifying Eq. (18) to be rotationaly invariant. That is, the value of the GCV function should
remain unchanged if each 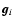 is rotated. There is no unique way to achieve such rotational invariance but one method is to substitute the average diagonal value
is rotated. There is no unique way to achieve such rotational invariance but one method is to substitute the average diagonal value
![${\rm Tr}~[\vec{H}_j]/N^2$](/articles/aa/full/2004/33/aa0113-04/img74.gif) for
for
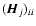
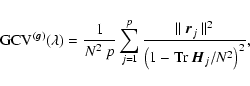 |
(22) |
where
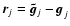 .
Note that Eq. (22) reduces to the classical
.
Note that Eq. (22) reduces to the classical  when p=1.
when p=1.
The implementation of Eq. (22) is done in the frequency domain. It can be rewritten as
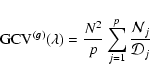 |
(23) |
where
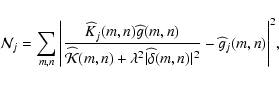 |
(24) |
with
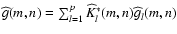 ,
and
,
and
![\begin{displaymath}%
{\cal D}_j= \left[ \sum_{m,n} \left(1- \frac{\vert\Kh_j(m,n...
...mbda^2 \vert\widehat{\delta}(m,n)\vert^2}\right)\right]^2\cdot
\end{displaymath}](/articles/aa/full/2004/33/aa0113-04/img81.gif) |
(25) |
To avoid underestimating the regularization parameter, the corrected  for Eq. (22) can be derived as
for Eq. (22) can be derived as
![\begin{displaymath}%
{\rm GCV}_{\alpha}^{(\vec{g})}(\lambda)=\frac{1}{N^2~p}\sum...
...eft(1-\alpha~{\rm Tr}\left[\vec{H}_j\right]/N^2\right)^2}\cdot
\end{displaymath}](/articles/aa/full/2004/33/aa0113-04/img82.gif) |
(26) |
Its form in the frequency domain is given by Eqs. (23)-(24), and
![\begin{displaymath}%
{\cal D}_j= \left[ \sum_{m,n}\left( 1- \frac{\alpha \vert\K...
...mbda^2 \vert\widehat{\delta}(m,n)\vert^2}\right)\right]^2\cdot
\end{displaymath}](/articles/aa/full/2004/33/aa0113-04/img83.gif) |
(27) |
An alternative form for the  functional (22)
can be obtained by applying the standard
functional (22)
can be obtained by applying the standard  directly to Eq. (6)
directly to Eq. (6)![[*]](/icons/foot_motif.gif) based on the single global-image
based on the single global-image
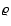 .
In this case the rotation invariance is enforced in a higher dimensional space of concatenated images which leads to
.
In this case the rotation invariance is enforced in a higher dimensional space of concatenated images which leads to
where
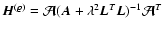 .
.
Following the usual interpretation of the denominator in the  function (Wahba 1990), we see that
function (Wahba 1990), we see that
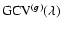 and
and
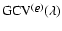 differ in that the former weights each residual error by the noise degrees of freedom of each image; images with a larger trace of
differ in that the former weights each residual error by the noise degrees of freedom of each image; images with a larger trace of 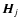 receive a higher weight.
In our case the two
receive a higher weight.
In our case the two  functions provide identical results (see below).
functions provide identical results (see below).
It can also be shown that even though
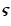 and
and
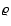 lead to the same normal equations,
their solutions may differ because their
lead to the same normal equations,
their solutions may differ because their  may give different answers. In fact, one can check that
may give different answers. In fact, one can check that
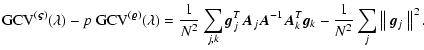 |
|
|
(29) |
4 Some numerical experiments
We present the results of numerical simulations to test the
reliability of the regularization parameter estimated through the  functions defined in
Sect. 3.
functions defined in
Sect. 3.
Figures 1-6 compare the deblurring of
an extended object with a sharp outline and a set of point-like objects.
We have chosen these particular examples because their restoration is a difficult problem.
Eight images are available for each object. In each case the PSF is a bidimensional Gaussian with
dispersion along the major axis set
to twelve pixels, and to four pixels along the minor axis. Their inclinations take equispaced
values in the range
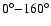 .
Gaussian white noise is added with two different
levels of noise by setting the standard deviations to
.
Gaussian white noise is added with two different
levels of noise by setting the standard deviations to 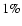 and
and 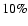 ,
respectively, of the maximum value of the blurred images.
Three deblurring methods have been used: (I) single-image Tikhonov based on the functional (12)
and the
,
respectively, of the maximum value of the blurred images.
Three deblurring methods have been used: (I) single-image Tikhonov based on the functional (12)
and the
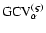 function (17) (
function (17) (
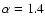 );
(II) Tikhonov based on the functional (5) and
);
(II) Tikhonov based on the functional (5) and
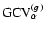 function (26)
(
function (26)
(
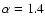 ); (III) a classic iterative Projected Landweber Method
applied to the single-image images for the iterative methods obtained as explained in Vio et al. (2004),
that can be used to enforce nonnegativity of the solution (a maximum number
of 2000 iterations has been adopted, that is sufficient to provide results that do not
show further appreciable visual changes).
); (III) a classic iterative Projected Landweber Method
applied to the single-image images for the iterative methods obtained as explained in Vio et al. (2004),
that can be used to enforce nonnegativity of the solution (a maximum number
of 2000 iterations has been adopted, that is sufficient to provide results that do not
show further appreciable visual changes).
There is no need to test the  functional (28) because in our case
it is identical to (26). The reason is that the shape of all
the selected PSFs is the same, they only differ in their orientation, and since orientation
information is lost through the trace, the denominator
functional (28) because in our case
it is identical to (26). The reason is that the shape of all
the selected PSFs is the same, they only differ in their orientation, and since orientation
information is lost through the trace, the denominator
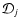 does not depend
on the image index j. That is, all the images share the same effective degrees of freedom.
does not depend
on the image index j. That is, all the images share the same effective degrees of freedom.
Since the Tikhonov technique does not enforce the nonnegativity constraint, the deblurred images obtained with the single-image approach are also shown with their negative values set to zero.
Finally, for each of the experiments, the true "optimal'' value (in the sense of the minimization of the rms of the true residuals) for the regularization parameter provided by the  function (17) has been determined, with an accuracy of two significant digits, by a simple grid search. In all cases, the "true'' and the estimated regularization parameter have been almost identical. In particular, the relative difference between the rms of the true residuals
of the corresponding solutions was always less than
function (17) has been determined, with an accuracy of two significant digits, by a simple grid search. In all cases, the "true'' and the estimated regularization parameter have been almost identical. In particular, the relative difference between the rms of the true residuals
of the corresponding solutions was always less than 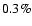 .
.
As shown by the figures, the multiple and single-image approaches lead to very similar, if not identical, residual rms values.
As expected, Projected Landweber provides the best results in terms of visual appearance and residual rms. In fact, as is well known, the nonnegativity constraint limits the ringing effect
around the sharp structures in the image. However, in these experiments the difference seems important only for point-like objects. In any case, these results are obtained at a very high
computational cost (each iteration requires the computation of two two-dimensional DFTs).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0113fig1.eps}\end{figure}](/articles/aa/full/2004/33/aa0113-04/Timg97.gif) |
Figure 1:
Original image, blurred version and blurred + noise version of the first image in the set (see text) and corresponding PSF. The images are
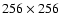 pixels, and the standard deviation of the noise is pixels, and the standard deviation of the noise is 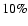 of the maximum value of the blurred image.
of the maximum value of the blurred image. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0113fig2.eps}\end{figure}](/articles/aa/full/2004/33/aa0113-04/Timg101.gif) |
Figure 2:
Deblurring of the image in Fig. 1 with the methods decribed in the text: (I) single-image Tikhonov (12) and
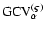 (17); its version with the negative elements zeroed;
(II) Tikhonov (5) and (17); its version with the negative elements zeroed;
(II) Tikhonov (5) and
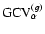 (26);
(III) a classic iterative Projected Landweber Method (convergence after 61 iterations).
Tikhonov has been used with (26);
(III) a classic iterative Projected Landweber Method (convergence after 61 iterations).
Tikhonov has been used with
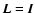 and
and
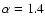 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0113fig3.eps}\end{figure}](/articles/aa/full/2004/33/aa0113-04/Timg102.gif) |
Figure 3:
The same as Fig. 2 but obtained from an image contaminated
with noise whose standard deviation is 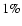 of the maximum value of the blurred image.
For the Projected Landweber algorithm 2000 iterations have been carried out.
of the maximum value of the blurred image.
For the Projected Landweber algorithm 2000 iterations have been carried out. |
| Open with DEXTER |
Apart from the nonnegativity constraint, the worst performance of the Tikhonov method is due to
the functional 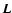 that tends to smooth out structures with sharp features.
This characteristic makes Tikhonov more suited for the restoration of images of diffuse objects.
In fact, Figs. 7-9 show that for diffuse objects,
single-image Tikhonov provides competitive restoration quality (see also Bertero & Boccacci 1998). Because of the presence of features close to the borders of the images, calculations for the image
that tends to smooth out structures with sharp features.
This characteristic makes Tikhonov more suited for the restoration of images of diffuse objects.
In fact, Figs. 7-9 show that for diffuse objects,
single-image Tikhonov provides competitive restoration quality (see also Bertero & Boccacci 1998). Because of the presence of features close to the borders of the images, calculations for the image
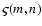 and the deblurring operation have been implemented with the windowing procedure as explained in Vio et al. (2004). This has required the removal of a border 50 pixels thick from the image and has only been done with the single-image Tikhonov approach because, given the necessity of windowing each single image, it would be tortuous to implement the other version of the algorithm.
and the deblurring operation have been implemented with the windowing procedure as explained in Vio et al. (2004). This has required the removal of a border 50 pixels thick from the image and has only been done with the single-image Tikhonov approach because, given the necessity of windowing each single image, it would be tortuous to implement the other version of the algorithm.
In order to test the stability of the 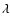 estimates, for each experiment 100 realizations of the corresponding noise process are generated and added to the image. In general, the estimates of this parameter appear quite stable; as measured by the rms of the estimated values divided by their median, they fall in the range
estimates, for each experiment 100 realizations of the corresponding noise process are generated and added to the image. In general, the estimates of this parameter appear quite stable; as measured by the rms of the estimated values divided by their median, they fall in the range 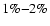 .
Figure 10 shows the histogram of the values of
.
Figure 10 shows the histogram of the values of 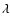 obtained with the single-image Tikhonov approach in the experiments with the worst relative variation.
obtained with the single-image Tikhonov approach in the experiments with the worst relative variation.
5 Concluding remarks
We have considered the estimation of the regularization parameter for the simultaneous Tikhonov deblurring of multiple noisy images using three types of  functions based on different data transformations. The first approach reduces the multiple-image problem to single-image deblurring that allows the use of the classical
functions based on different data transformations. The first approach reduces the multiple-image problem to single-image deblurring that allows the use of the classical  ,
but we use a corrected
,
but we use a corrected  that reduces its tendency to undersmooth the final solution. A second approach is perhaps the most natural as it is a straightforward extension of a classical single-image
approach. It aims to achieve a balance between the smoothness of the unknown image and its average goodness of fit to the observed images. The regularization parameter is estimated through a multiple-image extension of the traditional
that reduces its tendency to undersmooth the final solution. A second approach is perhaps the most natural as it is a straightforward extension of a classical single-image
approach. It aims to achieve a balance between the smoothness of the unknown image and its average goodness of fit to the observed images. The regularization parameter is estimated through a multiple-image extension of the traditional  function. The third approach is based on a higher dimensional single image defined by concatenating all the images into a single vector and then using the classical
function. The third approach is based on a higher dimensional single image defined by concatenating all the images into a single vector and then using the classical  .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0113fig4.eps}\end{figure}](/articles/aa/full/2004/33/aa0113-04/Timg104.gif) |
Figure 4:
Original image, blurred version and blurred + noise version of the first image in the set (see text) and corresponding PSF. The images are
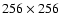 pixels, and the standard deviation of the noise is pixels, and the standard deviation of the noise is 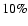 of the maximum value of the blurred image.
of the maximum value of the blurred image. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0113fig5.eps}\end{figure}](/articles/aa/full/2004/33/aa0113-04/Timg105.gif) |
Figure 5:
Deblurring of the image in Fig. 4 with the methods described in the text: (I) single-image Tikhonov (12) and
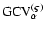 (17); its version with the negative elements zeroed;
(II) Tikhonov (5) and (17); its version with the negative elements zeroed;
(II) Tikhonov (5) and
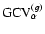 (26);
(III) a classic iterative Projected Landweber Method (2000 iterations).
Tikhonov has been used with (26);
(III) a classic iterative Projected Landweber Method (2000 iterations).
Tikhonov has been used with
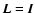 and
and
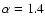 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0113fig6.eps}\end{figure}](/articles/aa/full/2004/33/aa0113-04/Timg106.gif) |
Figure 6:
The same as Fig. 5 but obtained from an image contaminated
with noise whose standard deviation is 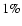 of the maximum value of the blurred image.
of the maximum value of the blurred image. |
| Open with DEXTER |
Our numerical experiments indicate that the three approaches provide very similar
results, with the lower-dimensional single image providing
the practical advantage that no new software is required and the same image can
be used with other deblurring algorithms.
We have assumed that the noise in all the images is independent Gaussian and of constant variance.
Combinations of the methods we propose can be used when some of these assumptions are not met.
For example, if there are k groups of images with different variances,
a weighted Tikhonov regularization method can be applied to a
multiple-image deblurring of k single images. In additon, the multiple-image
approach can be used if the noise in the original image is correlated but the covariance
matrix is known up to a constant (e.g., Gu 2002).
The extreme computational efficiency, coupled with the stability and reliabilty of the estimated regularization parameters, make Tikhonov's method competitive with the more flexible,
but much slower, iterative algorithms. In fact, and especially for very large images,
even in situations where these algorithms are expected to provide better results (e.g., when the
nonnegativity constraint can be exploited), the Tikhonov approach is still a valuable resource
(see also Bertero & Boccacci 2000). For example, it can be used to obtain initial solutions for
iterative algorithms that may speed up the convergence. Figure 11 shows the residual
rms as a function of iteration number for the Projected Landweber algorithm started at
a Tikhonov solution and at the uniform image traditionally used. The figure shows that
the saving in computation time can be considerable (here it is more than a factor of 10).
Acknowledgements
We thank Prof. M. Bertero for a careful reading of the manuscript and his useful suggestions.
Appendix A: Derivation of Eq. (19)
Let 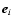 be the vector with 1 in the ith entry and zero everywhere else, and
be the vector with 1 in the ith entry and zero everywhere else, and
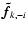 the estimate of
the estimate of 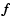 that does not use the ith entry of
that does not use the ith entry of 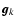 .
We can write
.
We can write
Let 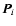 be the projection that deletes the ith entry:
be the projection that deletes the ith entry:
so that
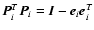 .
Let
.
Let
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{0113fig7.eps}\end{figure}](/articles/aa/full/2004/33/aa0113-04/Timg115.gif) |
Figure 7:
Original image, blurred version and blurred + noise version of the first image in the set (see text) and corresponding PSF. The original images was
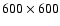 pixels, but only the central pixels, but only the central
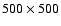 pixels are displayed (see text). The standard deviation of the noise is pixels are displayed (see text). The standard deviation of the noise is 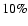 of the standard deviation of the blurred image.
of the standard deviation of the blurred image. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{0113fig8.eps}\end{figure}](/articles/aa/full/2004/33/aa0113-04/Timg117.gif) |
Figure 8:
Image
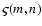 for the image shown in Fig. 4, single-image Tikhonov deblurring (
for the image shown in Fig. 4, single-image Tikhonov deblurring (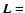 discrete Laplacian), its version with the negative elements zeroed, and the iterative Projected Landweber deblurring (convergence after 24 iterations).
discrete Laplacian), its version with the negative elements zeroed, and the iterative Projected Landweber deblurring (convergence after 24 iterations). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{0113fig9.eps}\end{figure}](/articles/aa/full/2004/33/aa0113-04/Timg118.gif) |
Figure 9:
The same as Fig. 8 but obtained from an image contaminated
with noise whose standard deviation is 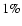 of the standard deviation of the blurred image.
Tikhonov has been used with
of the standard deviation of the blurred image.
Tikhonov has been used with
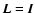 .
For the Projected Landweber algorithm 2000 iterations have been carried out. .
For the Projected Landweber algorithm 2000 iterations have been carried out. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{0113fig10.eps}\end{figure}](/articles/aa/full/2004/33/aa0113-04/Timg119.gif) |
Figure 10:
Histogram of the values of the estimated parameter 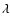 for the 100 experiments based in Fig. 6.
for the 100 experiments based in Fig. 6. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{0113fig11.eps}\end{figure}](/articles/aa/full/2004/33/aa0113-04/Timg120.gif) |
Figure 11:
Convergence rates for the Projected Landweber algorithm in the numerical experiment corresponding to Fig. 3. Two starting guesses are used:
the uniform image typical of the classic implementation of the algorithm, and the nonnegative
single-image Tikhonov shown in Fig. 3. |
| Open with DEXTER |
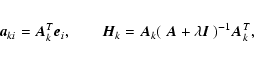
then, by definition,
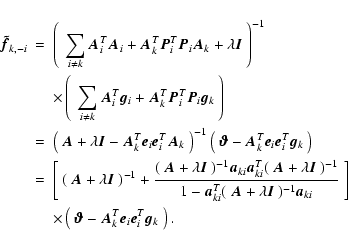
It follows that
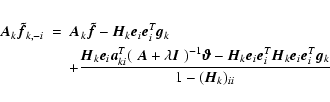
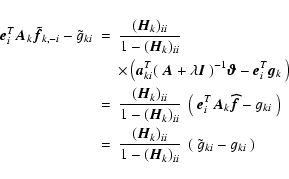
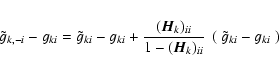
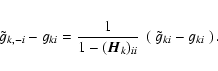
- Angel, J. R. P., Hill, J.
M., Strittmatter, P. A., Salinari, P., & Weigelt, G. 1998, in
Astronomical Interferometry, ed. R. D. Reasenberg, Proc.
SPIE, 3352, 881
(In the text)
- Bertero, M., &
Boccacci, P. 1998, Introduction to Inverse Problems in Imaging
(Bristol: IOP Publishing)
(In the text)
- Bertero, M., &
Boccacci, P. 2000, A&A, 147, 323 [NASA ADS] (In the text)
- Gu, C. 2002, Smoothing
Spline ANOVA Models (New York: Springer-Verlag)
(In the text)
- Cummins, D. J., Filloon,
T. G., & Nychka, D. 2001, J. Am. Stat. Assoc., 96, 233 [NASA ADS] [CrossRef] [MathSciNet]
- Kim, Y. J., & Gu, C.
2004, J. Roy. Stat. Soc. B, 66, 337 [NASA ADS] [MathSciNet]
- Lehmann, E. L., &
Casella, G. 1998, Theory of Point Estimation (New York:
Springer-Verlag)
(In the text)
- Nychka, D.,
Haaland, P. D., O'Connell, M. A., & Ellner, S. 1998, Case
Studies in Environmental Statistics, ed. Nychka et al.
(New York: Springer-Verlag)
(In the text)
- Vio, R., Nagy, J.,
Tenorio, L., et al. 2003, A&A, 401, 389 [EDP Sciences] [NASA ADS]
- Vio, R., Nagy, J.,
Tenorio, L., & Wamsteker 2004, A&A, 416, 403 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Wahba, G. 1985, Ann.
Stat., 13, 1378 [NASA ADS] [MathSciNet] (In the text)
- Wahba, G. 1990,
Spline Models for Observational Data (Philadelphia: SIAM)
(In the text)
Copyright ESO 2004
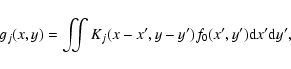
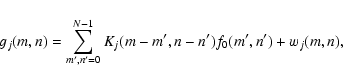
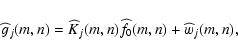
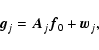
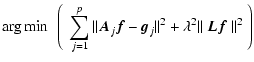
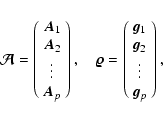
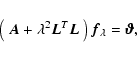
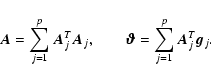
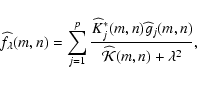
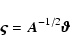
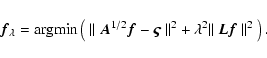
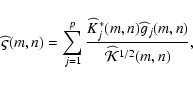
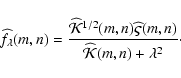
![\begin{displaymath}%
{\rm GCV}^{(\vec{\varsigma})}(\lambda) = \frac{1}{N^2}\frac...
...rm Tr}\left[\vec{H}^{(\vec{\varsigma})}\right]/N^2~\right)^2},
\end{displaymath}](/articles/aa/full/2004/33/aa0113-04/img58.gif)
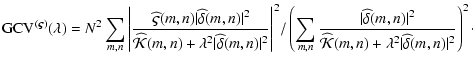
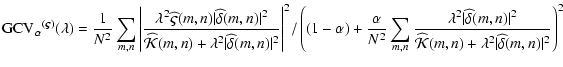
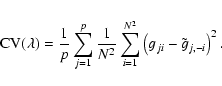
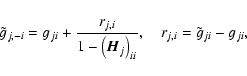
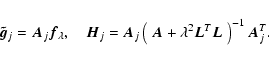
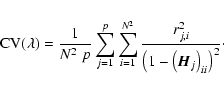
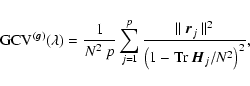
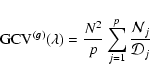
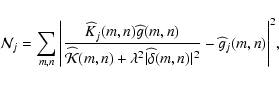
![\begin{displaymath}%
{\cal D}_j= \left[ \sum_{m,n} \left(1- \frac{\vert\Kh_j(m,n...
...mbda^2 \vert\widehat{\delta}(m,n)\vert^2}\right)\right]^2\cdot
\end{displaymath}](/articles/aa/full/2004/33/aa0113-04/img81.gif)
![\begin{displaymath}%
{\rm GCV}_{\alpha}^{(\vec{g})}(\lambda)=\frac{1}{N^2~p}\sum...
...eft(1-\alpha~{\rm Tr}\left[\vec{H}_j\right]/N^2\right)^2}\cdot
\end{displaymath}](/articles/aa/full/2004/33/aa0113-04/img82.gif)
![\begin{displaymath}%
{\cal D}_j= \left[ \sum_{m,n}\left( 1- \frac{\alpha \vert\K...
...mbda^2 \vert\widehat{\delta}(m,n)\vert^2}\right)\right]^2\cdot
\end{displaymath}](/articles/aa/full/2004/33/aa0113-04/img83.gif)
![$\displaystyle \frac{1}{p N^2} \frac{\sum_j \Vert ~\vec{r}_j~\Vert^2}
{\left(~1-...
...a ~{\rm Tr}\left[\vec{H}^{(\vec{\varrho})}\right]/\left(p N^2\right)~\right)^2}$](/articles/aa/full/2004/33/aa0113-04/img85.gif)
![$\displaystyle \frac{1}{p N^2} \frac{\sum_j \Vert ~\vec{r}_j~\Vert^2}{\left(~1-
\alpha ~\sum_j {\rm Tr}\left[\vec{H}_j\right]/\left(p N^2\right)~\right)^2},$](/articles/aa/full/2004/33/aa0113-04/img86.gif)
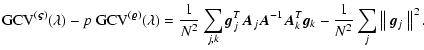
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0113fig1.eps}\end{figure}](/articles/aa/full/2004/33/aa0113-04/Timg97.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0113fig2.eps}\end{figure}](/articles/aa/full/2004/33/aa0113-04/Timg101.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0113fig3.eps}\end{figure}](/articles/aa/full/2004/33/aa0113-04/Timg102.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0113fig4.eps}\end{figure}](/articles/aa/full/2004/33/aa0113-04/Timg104.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0113fig5.eps}\end{figure}](/articles/aa/full/2004/33/aa0113-04/Timg105.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0113fig6.eps}\end{figure}](/articles/aa/full/2004/33/aa0113-04/Timg106.gif)
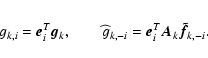
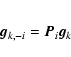
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{0113fig7.eps}\end{figure}](/articles/aa/full/2004/33/aa0113-04/Timg115.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{0113fig8.eps}\end{figure}](/articles/aa/full/2004/33/aa0113-04/Timg117.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{0113fig9.eps}\end{figure}](/articles/aa/full/2004/33/aa0113-04/Timg118.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{0113fig10.eps}\end{figure}](/articles/aa/full/2004/33/aa0113-04/Timg119.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{0113fig11.eps}\end{figure}](/articles/aa/full/2004/33/aa0113-04/Timg120.gif)