A&A 423, 975-982 (2004)
DOI: 10.1051/0004-6361:20047087
K. Lehtinen1 - D. Russeil1,2 - M. Juvela1 - K. Mattila1 - D. Lemke3
1 - Observatory, Tähtitorninmäki, PO Box 14, University of Helsinki, 00014 Helsinki, Finland
2 - Laboratoire d'Astrophysique de Marseille, 2 place Le Verrier,
13004 Marseille, France
3 - Max-Planck-Institut für Astronomie, Königstuhl 17, 69117
Heidelberg, Germany
Received 16 January 2004 / Accepted 28 April 2004
Abstract
We have performed a large-scale mapping of the high-latitude,
moderate extinction dark cloud L 1642 with ISO (Infrared Space
Observatory) at 200 ![]() m to study the properties of dust,
the virial equilibrium condition of the cloud, and their relation to
star formation. The cloud consists of three denser regions which are
connected by diffuse material. Only one of the regions, the
one most massive and with the greatest optical depth, is related to a
temperature mimimum. The pre-main sequence binary stars
IRAS 04325-1419 and IRAS 04327-1419, probably born within the cloud,
are located close to this temperature mimimum coinciding with the
column density maximum. The minimum dust temperature is
m to study the properties of dust,
the virial equilibrium condition of the cloud, and their relation to
star formation. The cloud consists of three denser regions which are
connected by diffuse material. Only one of the regions, the
one most massive and with the greatest optical depth, is related to a
temperature mimimum. The pre-main sequence binary stars
IRAS 04325-1419 and IRAS 04327-1419, probably born within the cloud,
are located close to this temperature mimimum coinciding with the
column density maximum. The minimum dust temperature is ![]() 13.8 K. The ratio
13.8 K. The ratio
![]() /
/
![]() for
the star-forming region is about 1.2, and thus it is close to being
gravitationally bound. However, the other regions are not
gravitationally bound. On a 1
for
the star-forming region is about 1.2, and thus it is close to being
gravitationally bound. However, the other regions are not
gravitationally bound. On a 1![]() -10
-10![]() spatial scale the
radial density distributions, derived from far-infared optical depth
maps, are similar between the star-forming and non star-forming
regions. The differences that distinguish the star-forming core appear
to be its higher density and lower dust temperature.
spatial scale the
radial density distributions, derived from far-infared optical depth
maps, are similar between the star-forming and non star-forming
regions. The differences that distinguish the star-forming core appear
to be its higher density and lower dust temperature.
Key words: infrared: ISM - ISM: individual objects: Lynds 1642 - ISM: individual objects: IRAS 04325-1419 - ISM: individual objects: IRAS 04327-1419 - ISM: clouds - ISM: dust, extinction
Translucent high latitude molecular clouds have properties intermediate between diffuse high latitude clouds and dark molecular clouds. Only in rare cases do these clouds have any star formation. Thus the study of such clouds may constrain the physical mechanisms responsible for triggering low mass star formation.
Lynds 1642 is a well-known high galactic latitude
(b=-36.7![]() )
translucent/dark cloud, also listed as MBM 20 in
Magnani et al. (1985). For a review of the cloud see
Liljeström (1991). Hearty et al. (2000) determined a distance of 112-160 pc for
L 1642. In this paper we adopt a distance of 140 pc. The
maximum optical extinction at the centre has been estimated to be
)
translucent/dark cloud, also listed as MBM 20 in
Magnani et al. (1985). For a review of the cloud see
Liljeström (1991). Hearty et al. (2000) determined a distance of 112-160 pc for
L 1642. In this paper we adopt a distance of 140 pc. The
maximum optical extinction at the centre has been estimated to be
![]() mag (Lehtinen et al. 2004) based on near-IR color excesses derived from
2MASS data. An extended lower extinction halo is seen around the
central core, visible in extinction, optical scattered light and
far-IR 100
mag (Lehtinen et al. 2004) based on near-IR color excesses derived from
2MASS data. An extended lower extinction halo is seen around the
central core, visible in extinction, optical scattered light and
far-IR 100 ![]() m IRAS maps.
m IRAS maps.
Taylor et al. (1982) made HI observations of a region adjacent to and including L 1642. They suggested that L 1642 is a result of hydrodynamic instability within a larger cometary cloud.
The optical and infrared properties of L 1642 have been studied
by Laureijs et al. (1987). Using 60 ![]() m
and 100
m
and 100 ![]() m IRAS data they derived for the region of maximum
extinction a temperature of
m IRAS data they derived for the region of maximum
extinction a temperature of ![]() 21 K for a
21 K for a
![]() emissivity law. However, it is now known that at 60
emissivity law. However, it is now known that at 60 ![]() m much
of the emission comes from small grains and thus the ratio I(60
m much
of the emission comes from small grains and thus the ratio I(60 ![]() m)/I(100
m)/I(100 ![]() m) cannot be used to derive a
temperature for the dust grains. Laureijs et al. (1987) showed that the radial density
distribution
m) cannot be used to derive a
temperature for the dust grains. Laureijs et al. (1987) showed that the radial density
distribution ![]() follows the
follows the
![]() profile in the outer parts, and a flatter profile in the inner
parts. A similar conclusion was drawn by Liljeström
(1991) and Russeil et al. (2003) from
CO data. However, all these studies treated the cloud as a single
unit, although it consists of several components. Liljeström
(1991) studied the dynamical state of the
cloud and found that within the region of 13CO emission the
cloud is in virial equilibrium.
profile in the outer parts, and a flatter profile in the inner
parts. A similar conclusion was drawn by Liljeström
(1991) and Russeil et al. (2003) from
CO data. However, all these studies treated the cloud as a single
unit, although it consists of several components. Liljeström
(1991) studied the dynamical state of the
cloud and found that within the region of 13CO emission the
cloud is in virial equilibrium.
Despite the modest opacity of the cloud, two low-luminosity young stellar objects have been detected by IRAS in the core of L 1642; IRAS 04325-1419 and IRAS 04327-1419. Both objects are nebulous low-luminosity pre-main sequence binary stars (Sandell et al. 1990; Reipurth & Heathcote 1990). L 1642 is one of the two high-latitude (|b|>30 deg) clouds known to have star formation; the other one is MBM 12 (Luhman 2001 and references therein).
In addition, there are four other IRAS Point Source Catalog
objects within the boundaries of our 200 ![]() m map;
04336-1412, 04347-1415, 04342-1444 and 04349-1436, which are
detected only at 60
m map;
04336-1412, 04347-1415, 04342-1444 and 04349-1436, which are
detected only at 60 ![]() m, 100
m, 100 ![]() m, 12
m, 12 ![]() m and
100
m and
100 ![]() m, respectively. The 100
m, respectively. The 100 ![]() m-only detections
are probably artefacts caused by cirrus structures. The
12
m-only detections
are probably artefacts caused by cirrus structures. The
12 ![]() m-only detection is probably a field star. There is a
non-stellar object on the digitized SERC-J survey image at the
position of the 60
m-only detection is probably a field star. There is a
non-stellar object on the digitized SERC-J survey image at the
position of the 60 ![]() m-only detection, and thus it is
probably a galaxy.
m-only detection, and thus it is
probably a galaxy.
The objective of the present paper is to make a detailed study of dust
in a translucent high galactic latitude dark cloud. The 200 ![]() m
ISO observations, combined with 100
m
ISO observations, combined with 100 ![]() m IRAS/ISSA data, will
provide accurate estimates of dust temperature, column density and
mass. The 200
m IRAS/ISSA data, will
provide accurate estimates of dust temperature, column density and
mass. The 200 ![]() m map provides an opportunity to trace by their
IR emission the "classical large'' dust grains which make up most of
the dust mass and are responsible for most of the interstellar
extinction in the optical. Far-infrared dust emission is optically
thin, and less dependent on effects such as chemical evolution which
hamper the analysis of molecular emission line data. The dynamic range
of far-IR emission is large, enabling us to study both the low density
outer regions of the cloud and the high density central regions.
m map provides an opportunity to trace by their
IR emission the "classical large'' dust grains which make up most of
the dust mass and are responsible for most of the interstellar
extinction in the optical. Far-infrared dust emission is optically
thin, and less dependent on effects such as chemical evolution which
hamper the analysis of molecular emission line data. The dynamic range
of far-IR emission is large, enabling us to study both the low density
outer regions of the cloud and the high density central regions.
In this paper we describe the basic properties of the cloud, such as dust temperature, mass, and virial equilibrium. In forthcoming articles we shall combine the far-IR data with visual star-count data, near-IR extinction data, mid-IR ISO and IRAS data, and CO emission line data in order to study the properties of different dust populations and their relationship to molecular gas.
The observations were made with the ISOPHOT instrument aboard the
Infrared Space Observatory (ISO) (Kessler et al. 1996)
satellite, using the C200 detector (Lemke et al. 1996).
All observations were made using the observing template PHT22 in
raster mode. Basic parameters of the observations are given in
Table 1. The data analysis was done using
PIA![]() (ISOPHOT Interactive Analysis) V 8.1 (Gabriel et al. 1997). At the first processing level, the detector
ramps were corrected for non-linearity of the detector response,
glitches in ramps were removed by using the two-threshold glitch
recognition method, and the ramps were fitted with first-order
polynomials. At subsequent levels the signals were deglitched, reset
interval correction was applied, signals were linearized for the
dependence of detector response on illumination, and orbital
position-dependent dark currents were subtracted.
(ISOPHOT Interactive Analysis) V 8.1 (Gabriel et al. 1997). At the first processing level, the detector
ramps were corrected for non-linearity of the detector response,
glitches in ramps were removed by using the two-threshold glitch
recognition method, and the ramps were fitted with first-order
polynomials. At subsequent levels the signals were deglitched, reset
interval correction was applied, signals were linearized for the
dependence of detector response on illumination, and orbital
position-dependent dark currents were subtracted.
There are 8 maps with a size of
![]() each, which
have been calibrated individually by using the FCS (fine calibration
source) measurements bracketing the actual measurement. The typical
statistical uncertainty of a map pixel is 0.2 MJy sr-1.
The calibration differences between individual maps in the final mosaic
have been minimized by simultaneously minimizing the surface brightness
differences at each border between maps. The applied relative scaling of
individual maps is typically 12%.
each, which
have been calibrated individually by using the FCS (fine calibration
source) measurements bracketing the actual measurement. The typical
statistical uncertainty of a map pixel is 0.2 MJy sr-1.
The calibration differences between individual maps in the final mosaic
have been minimized by simultaneously minimizing the surface brightness
differences at each border between maps. The applied relative scaling of
individual maps is typically 12%.
To derive the dust temperature we combine our ISO data with
IRAS ISSA 100 ![]() m data. Because the surface brightness of DIRBE data is more accurately calibrated than that of IRAS, we have scaled
the IRAS data to the DIRBE calibration with a relation I(DIRBE
m data. Because the surface brightness of DIRBE data is more accurately calibrated than that of IRAS, we have scaled
the IRAS data to the DIRBE calibration with a relation I(DIRBE
![]() IRAS)+1.34 MJy sr-1 (for the method see Lehtinen
et al. 2003a). This relation is derived from a 6
IRAS)+1.34 MJy sr-1 (for the method see Lehtinen
et al. 2003a). This relation is derived from a 6![]() diameter circular region around L 1642.
diameter circular region around L 1642.
Table 1: The parameters of the individual maps. TDT is the Target Dedicated Time number of the observation, PA is the position angle measured from North to East. Observations were made on March 26th 1998.
The values of the 200 ![]() m surface brightness map have been compared
with the DIRBE data. There are 11 DIRBE pixels within the 200
m surface brightness map have been compared
with the DIRBE data. There are 11 DIRBE pixels within the 200 ![]() m
map. The DIRBE surface brightness values at 100
m
map. The DIRBE surface brightness values at 100 ![]() m, 140
m, 140 ![]() m
and 240
m
and 240 ![]() m have been fitted with a modified blackbody function
with
m have been fitted with a modified blackbody function
with
![]() emissivity law to get values at 200
emissivity law to get values at 200 ![]() m. The 200
m. The 200 ![]() m ISO map has been convolved with the DIRBE beam and color corrected using the temperatures derived from fitting
the DIRBE values. The relation between ISO- and DIRBE-based intensities
at 200
m ISO map has been convolved with the DIRBE beam and color corrected using the temperatures derived from fitting
the DIRBE values. The relation between ISO- and DIRBE-based intensities
at 200 ![]() m is shown in Fig. 1. A linear fit forced to go
through the origin gives I(ISO)=0.82I(DIRBE), which is within the
uncertainties of each dataset. Therefore, we prefer to keep the FCS based calibration for the 200
m is shown in Fig. 1. A linear fit forced to go
through the origin gives I(ISO)=0.82I(DIRBE), which is within the
uncertainties of each dataset. Therefore, we prefer to keep the FCS based calibration for the 200 ![]() m ISO data.
m ISO data.
The angular resolution of the 100 ![]() m ISSA map near L 1642 has
been determined by fitting some point sources with Gaussians, giving a
FWHM resolution
m ISSA map near L 1642 has
been determined by fitting some point sources with Gaussians, giving a
FWHM resolution ![]() 4.5
4.5![]() .
When combining the ISO and IRAS maps we thus convolve the ISO data with a Gaussian function having
.
When combining the ISO and IRAS maps we thus convolve the ISO data with a Gaussian function having
![]()
![]() .
The maps shown in this paper all have the original
.
The maps shown in this paper all have the original
![]() pixel size of the ISOPHOT C200 camera.
pixel size of the ISOPHOT C200 camera.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0087fig1.eps}
\end{figure}](/articles/aa/full/2004/33/aa0087-04/Timg36.gif) |
Figure 1:
Relation between 200 |
| Open with DEXTER | |
The 200 ![]() m surface brightness map is shown in Fig. 2.
The cloud consists of three separate denser regions which are seen in
brightness and optical depth maps, and which we have named region A,
B, and C. These regions are interlaced by diffuse dust which extends
all the way to the map borders. Region A consists of two maxima separated
by 5.3
m surface brightness map is shown in Fig. 2.
The cloud consists of three separate denser regions which are seen in
brightness and optical depth maps, and which we have named region A,
B, and C. These regions are interlaced by diffuse dust which extends
all the way to the map borders. Region A consists of two maxima separated
by 5.3![]() ,
which we call clump A1 and A2. We have used the
200
,
which we call clump A1 and A2. We have used the
200 ![]() m optical depth map to derive the physical dimensions of the
regions. Regions B and C have been fitted with two-axial Gaussian
surfaces, while the clumps A1 and A2 have been fitted with one-axial
Gaussian surfaces. The positions and FWHM sizes of the fitted
Gaussians are given in Table 2, and are plotted in
Figs. 2, 3, 5 and 6. The
properties of these condensations are discussed in more detail in
Sect. 3.4.
m optical depth map to derive the physical dimensions of the
regions. Regions B and C have been fitted with two-axial Gaussian
surfaces, while the clumps A1 and A2 have been fitted with one-axial
Gaussian surfaces. The positions and FWHM sizes of the fitted
Gaussians are given in Table 2, and are plotted in
Figs. 2, 3, 5 and 6. The
properties of these condensations are discussed in more detail in
Sect. 3.4.
There are two filaments of dust extending to the North-East and East
from the main cloud. None of the six IRAS sources within our map is
detected at 200 ![]() m, nor any new point source candidates.
m, nor any new point source candidates.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0087fig2.eps}
\end{figure}](/articles/aa/full/2004/33/aa0087-04/Timg37.gif) |
Figure 2:
An image of 200 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0087fig3.eps}
\end{figure}](/articles/aa/full/2004/33/aa0087-04/Timg38.gif) |
Figure 3:
A temperature map derived from 200 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0087fig4.eps}
\end{figure}](/articles/aa/full/2004/33/aa0087-04/Timg39.gif) |
Figure 4:
Relation between 200 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0087fig5.eps}
\end{figure}](/articles/aa/full/2004/33/aa0087-04/Timg40.gif) |
Figure 5:
Optical depth map at 200 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0087fig6.eps}
\end{figure}](/articles/aa/full/2004/33/aa0087-04/Timg41.gif) |
Figure 6:
A combined grayscale and contour image of 200 |
| Open with DEXTER | |
The temperature of the dust has been derived, pixel by pixel, from the
200 ![]() m ISO map and 100
m ISO map and 100 ![]() m IRAS ISSA map by using a modified
blackbody function
m IRAS ISSA map by using a modified
blackbody function
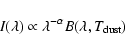 |
(1) |
The dust temperature map is shown in Fig. 3. The minimum
temperature is ![]() 13.8 K. The position of the minimum temperature
corresponds well to the position of the optical depth maximum of the
region B (see Fig. 5). Region B is the only region in L 1642
which is related to a temperature minimum. The IRAS sources
04325-1419 and 04327-1419 are located close to the temperature
minimum.
13.8 K. The position of the minimum temperature
corresponds well to the position of the optical depth maximum of the
region B (see Fig. 5). Region B is the only region in L 1642
which is related to a temperature minimum. The IRAS sources
04325-1419 and 04327-1419 are located close to the temperature
minimum.
The relation between 200 ![]() m ISO and 100
m ISO and 100 ![]() m IRAS surface
brightness is shown in Fig. 4. The relation diverges into
two sections, and shows that regions with brightest 200
m IRAS surface
brightness is shown in Fig. 4. The relation diverges into
two sections, and shows that regions with brightest 200 ![]() m
emission are also the coldest. The range of temperatures within the
cloud is strictly limited by the outer envelope of the distribution.
The solid lines show the surface brightness ratio at the indicated
temperatures. Most of the data points with I(200
m
emission are also the coldest. The range of temperatures within the
cloud is strictly limited by the outer envelope of the distribution.
The solid lines show the surface brightness ratio at the indicated
temperatures. Most of the data points with I(200 ![]() m
m![]() MJy sr-1 belong to region B, where the temperature is
limited to
MJy sr-1 belong to region B, where the temperature is
limited to ![]() 13.8-14.7 K. Elsewhere, the temperature has
a maximum value of about 19.0 K.
13.8-14.7 K. Elsewhere, the temperature has
a maximum value of about 19.0 K.
Table 2:
Properties of the regions, derived under their FWHM areas.
![]() is the mean dust temperature,
is the mean dust temperature,
![]() is the mean visual extinction,
is the mean visual extinction,
![]() is the total mass derived from far-IR data,
M(13CO) is the total mass derived from 13CO data of Russeil
et al. (2003),
is the total mass derived from far-IR data,
M(13CO) is the total mass derived from 13CO data of Russeil
et al. (2003),
![]() is the virial mass,
n(H2) is the mean density assuming constant density inside the
regions.
is the virial mass,
n(H2) is the mean density assuming constant density inside the
regions.
![]() ,
,
![]() and
and
![]() are thermal, turbulent and potential energies. The
ratio of kinetic to potential energies,
are thermal, turbulent and potential energies. The
ratio of kinetic to potential energies,
![]() /
/
![]() ,
is unity in the case of
virial equilibrium.
,
is unity in the case of
virial equilibrium.
The optical depth at 200 ![]() m has been calculated with the formula
m has been calculated with the formula
| (2) |
The total masses (gas plus dust) of the regions have been calculated
by using the formula
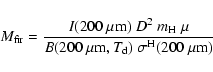 |
(3) |
For comparison, we give in Table 2 the total masses of regions B and C derived from 13CO data (Russeil et al. 2003). We have assumed for 13CO a fractional abundance of 10-6 relative to molecular hydrogen. The two mass estimates are in excellent agreement in the case of region B, while for region C we derive a factor of 1.3 times higher mass from far-IR data. This may imply a lower dust-to-gas ratio, or lower abundance of 13CO in region C compared to region B, to be discussed in more detail in our forthcoming papers.
Assuming a constant density within the regions, we derive densities of
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() cm-3 for
the regions A1, A2, B and C, respectively.
cm-3 for
the regions A1, A2, B and C, respectively.
We have studied the virial equilibrium condition of regions B and C
and the clumps A1 and A2 by including kinetic and gravitational
energies. For the kinetic energy we have included the thermal and the
turbulent motions. The thermal energy of molecules is
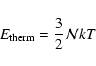 |
(4) |
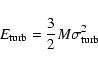 |
(5) |
The value of potential energy has been derived for a centrally condensed
sphere with the formula
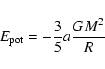 |
(6) |
The values of thermal, turbulent and potential energies, together with
the value of the ratio
![]() /
/
![]() (equal to unity in the case of virial equilibrium), are given in
Table 2. For region B the ratio
(equal to unity in the case of virial equilibrium), are given in
Table 2. For region B the ratio
![]() /
/
![]() is about 1.2. Taking into
count the relatively large uncertainties related to the values of D and
is about 1.2. Taking into
count the relatively large uncertainties related to the values of D and
![]() ,
and with the background subtraction in
the maps, we can say that region B is close to being gravitationally
bound. On the other hand, for region C and clumps A1 and A2 the ratio
,
and with the background subtraction in
the maps, we can say that region B is close to being gravitationally
bound. On the other hand, for region C and clumps A1 and A2 the ratio
![]() /
/
![]() is greater than unity by a
factor of much more than two, which indicates that they are not
gravitationally bound.
is greater than unity by a
factor of much more than two, which indicates that they are not
gravitationally bound.
Table 2 includes the virial mass
![]() ,
derived
with the formula
,
derived
with the formula
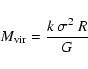 |
(7) |
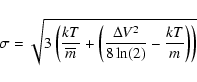 |
(8) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0087fig7.eps}
\end{figure}](/articles/aa/full/2004/33/aa0087-04/Timg90.gif) |
Figure 7:
The observed 200 |
| Open with DEXTER | |
Dust emission from L 1642 at 200 ![]() m is optically thin, and traces
all the dust along a line of sight. The optical depth through the
cloud is so low,
m is optically thin, and traces
all the dust along a line of sight. The optical depth through the
cloud is so low,
![]() ,
that dust
at the centre of the cloud cannot be hidden by absorption at the
wavelength of our observations. Thus, we can use the optical depth
map to derive the radial dust density distribution, in analogy to the
method of Yun & Clemens (1991). This method assumes
that the volume density follows a single power law function of the
form
,
that dust
at the centre of the cloud cannot be hidden by absorption at the
wavelength of our observations. Thus, we can use the optical depth
map to derive the radial dust density distribution, in analogy to the
method of Yun & Clemens (1991). This method assumes
that the volume density follows a single power law function of the
form
![]() ,
and that the dust is isothermal.
Then, the optical depth
,
and that the dust is isothermal.
Then, the optical depth ![]() as a function of impact parameter phas the form
as a function of impact parameter phas the form
![]() .
.
In order to derive optical depth ![]() as a function of the impact
parameter p we have used the method where one draws contours on the
optical depth map and derives the
as a function of the impact
parameter p we have used the method where one draws contours on the
optical depth map and derives the
![]() relation from the contours. We have drawn
the contours at the 35%-95% level of the optical depth maximum, in
steps of 10%. The derived radial optical depth profiles of regions B
and C, shown in Fig. 7, are similar. In the outer parts the
column density profiles steepen, which is partly due to the finite
cloud radius (Yun & Clemens 1991), and partly due to a
real change in the value of
relation from the contours. We have drawn
the contours at the 35%-95% level of the optical depth maximum, in
steps of 10%. The derived radial optical depth profiles of regions B
and C, shown in Fig. 7, are similar. In the outer parts the
column density profiles steepen, which is partly due to the finite
cloud radius (Yun & Clemens 1991), and partly due to a
real change in the value of ![]() .
Separation of these two effects
requires modelling of the cloud, and will be discussed in a
forthcoming paper.
.
Separation of these two effects
requires modelling of the cloud, and will be discussed in a
forthcoming paper.
In order to derive the value of ![]() we use the three innermost
data points, where the effects of finite cloud radius are smallest.
For both region B and region C we derive the same value,
we use the three innermost
data points, where the effects of finite cloud radius are smallest.
For both region B and region C we derive the same value,
![]() (see Fig. 7). The derived value of
(see Fig. 7). The derived value of ![]() then corresponds
to a radial power law exponent
then corresponds
to a radial power law exponent
![]() for both regions.
for both regions.
The effect of finite cloud radius on the determination of the value of ![]() is discussed by Yun & Clemens (1991). The
effect is such that the value of
is discussed by Yun & Clemens (1991). The
effect is such that the value of ![]() derived from observations
is always an upper limit to the actual value of
derived from observations
is always an upper limit to the actual value of ![]() .
The three
innermost datapoints sample the cloud up to about 0.25 times the cloud
radius. From Fig. 7 of Yun & Clemens we then estimate a correction
factor for
.
The three
innermost datapoints sample the cloud up to about 0.25 times the cloud
radius. From Fig. 7 of Yun & Clemens we then estimate a correction
factor for ![]() of about -0.4. Thus the true value of
of about -0.4. Thus the true value of ![]() is
is
![]() for regions B and C.
for regions B and C.
High latitude molecular clouds can be divided into three groups
depending on their visual extinction; diffuse (
![]() mag),
translucent (
mag),
translucent (
![]() mag) and dark clouds (
mag) and dark clouds (
![]() mag)
(van Dishoeck & Black 1988). The maximum visual
extinctions of regions A, B and C are about 3 mag, 8 mag and 2 mag, respectively (Lehtinen et al. 2004), when
mapping the extinction with a
mag)
(van Dishoeck & Black 1988). The maximum visual
extinctions of regions A, B and C are about 3 mag, 8 mag and 2 mag, respectively (Lehtinen et al. 2004), when
mapping the extinction with a
![]()
![]() Gaussian beam. Thus
region B can be considered as a dark cloud, while the other two
regions are translucent.
Gaussian beam. Thus
region B can be considered as a dark cloud, while the other two
regions are translucent.
In the past, it has been attempted to estimate the equilibrium
temperature of "classical large'' dust grains by using the IRAS 60 ![]() m and 100
m and 100 ![]() m data (Laureijs et al. 1987). The minimum temperature derived by us from 100
m data (Laureijs et al. 1987). The minimum temperature derived by us from 100 ![]() m and 200
m and 200 ![]() m data,
m data, ![]() 16 K for a
16 K for a
![]() emissivity law, is considerably lower than that derived from 60
emissivity law, is considerably lower than that derived from 60 ![]() m and 100
m and 100 ![]() m data,
m data, ![]() 21 K. The difference is
caused by the fact that most of the 60
21 K. The difference is
caused by the fact that most of the 60 ![]() m emission is due to
another grain population, the "very small grains'', VSGs
(Draine & Li 2001 and references therein).
m emission is due to
another grain population, the "very small grains'', VSGs
(Draine & Li 2001 and references therein).
It is notable that although there is a local column density maximum towards regions A1/2 and C, there is no temperature minimum towards these column density maxima, but instead there is a temperature gradient towards the center of region B, where the global temperature minimum of the cloud is located. We have used the Monte Carlo method of Juvela & Padoan (2003) to estimate the expected temperature change and to study whether the temperature differences between the regions can be explained solely due to attenuation of the general interstellar radiation field (ISRF). The model consists of a spherical cloud which has a constant density over 10% of the radius, and a density proportional to r-1.5 outside of that. The properties of dust particles are those of the Li & Draine (2001) model, and the ISRF is the Solar neighbourhood ISRF according to Mezger et al. (1983) and Mathis et al. (1983). A model applied for region A2, with 3 mag of maximum extinction, gives a theoretical temperature drop of about 0.6 K towards the cloud centre. Such a temperature drop should be discernible in our temperature map. The observed extinction difference between the centers of regions B and C is about 6 mag, and the observed temperature difference is about 2.6 K. According to radiative transfer calculations a 6 mag difference corresponds to about 1 K temperature difference. Furthermore, any clumping present in the cloud further reduces the temperature difference. Thus the observed temperature minimum towards region B cannot be explained by extinction only, but a change in the properties of dust particles is required. We conclude that there is a gradual change of dust properties towards the temperature minimum, possibly due to grain coagulation at higher densities.
The derived radial density distributions at the centers of regions B
and C are not consistent with an infinite isothermal sphere in
equilibrium wich has a
![]() density distribution,
neither with the dynamical inside-out free-fall collapse, which has a
density distribution,
neither with the dynamical inside-out free-fall collapse, which has a
![]() distribution Shu (1977). Instead,
they are more compatible with density distributions of Bonnor-Ebert
spheres (Ebert 1955; Bonnor 1956) or of clouds
evolved under the influence of ambipolar diffusion (Ciolek &
Mouschovias 1994, 1995; Basu & Mouschovias
1994, 1995a, 1995b), which have a flatter
density distribution at the core.
distribution Shu (1977). Instead,
they are more compatible with density distributions of Bonnor-Ebert
spheres (Ebert 1955; Bonnor 1956) or of clouds
evolved under the influence of ambipolar diffusion (Ciolek &
Mouschovias 1994, 1995; Basu & Mouschovias
1994, 1995a, 1995b), which have a flatter
density distribution at the core.
In general, high latitude molecular clouds are considered to be
young and transient. By comparing the observed velocity
dispersion of 13CO emission with the expected dispersion for
a cloud in virial equilibrium, Liljeström (1991)
concluded that L 1642 as a whole is in virial
equilibrium. However, the 13CO map of Liljeström covers an
area of about
![]() around core B, but not
the regions A1/2 or C. Russeil et al. (2003) have
estimated the mass of the cloud based on three-dimensional
non-LTE modelling of 13CO emission. Although they derived
total masses similar to those of Liljeström
(1991), they concluded that the mass estimates are
uncertain by a factor of about two, due to the unknown density
and kinetic temperature distributions. We find that the ratio
between virialized and observed mass is about 1.2 for region B,
while for other regions it is about 10. We believe that within
uncertainties only region B can be gravitationally bound, while
the other regions of L 1642 are transient.
around core B, but not
the regions A1/2 or C. Russeil et al. (2003) have
estimated the mass of the cloud based on three-dimensional
non-LTE modelling of 13CO emission. Although they derived
total masses similar to those of Liljeström
(1991), they concluded that the mass estimates are
uncertain by a factor of about two, due to the unknown density
and kinetic temperature distributions. We find that the ratio
between virialized and observed mass is about 1.2 for region B,
while for other regions it is about 10. We believe that within
uncertainties only region B can be gravitationally bound, while
the other regions of L 1642 are transient.
Comparison between star forming region B and a non-star forming region C may elucidate the conditions necessary for onset of low-mass star formation. The regions B and C have the following properties:
Based on the above facts, the main reason for star formation in region B is its much higher volume density, which makes region B gravitationally bound.
To study the properties of dust in the high latitude cloud
Lynds 1642, we have made a wide field 200 ![]() m ISOPHOT mapping. By
combining our data with 100
m ISOPHOT mapping. By
combining our data with 100 ![]() m IRAS/ISSA data we have derived
maps of dust column density, temperature and mass. We have studied
the virial equilibrium condition of the star-forming and non
star-forming regions of the cloud. Our main conclusions are:
m IRAS/ISSA data we have derived
maps of dust column density, temperature and mass. We have studied
the virial equilibrium condition of the star-forming and non
star-forming regions of the cloud. Our main conclusions are:
Acknowledgements
The work of K.L., M.J. and K.M. has been supported by the Finnish Academy through grants Nos. 17854 and 176071, which is gratefully acknowledged.Based on photographic data obtained using The UK Schmidt Telescope. The UK Schmidt Telescope was operated by the Royal Observatory Edinburgh, with funding from the UK Science and Engineering Research Council, until June 1988, and thereafter by the Anglo-Australian Observatory. Original plate material is copyright © the Royal Observatory Edinburgh and the Anglo-Australian Observatory. The plates were processed into the present compressed digital form with their permission. The Digitized Sky Survey was produced at the Space Telescope Science Institute under US Government grant NAG W-2166.
We wish to thank the anonymous referee whose comments improved the paper.