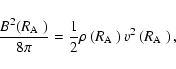A&A 423, 401-404 (2004)
DOI: 10.1051/0004-6361:20035808
The MHD Alfven wave oscillation model of kHz Quasi Periodic Oscillations of Accreting X-ray binaries
C. Zhang
1 - National Astronomical Observatories,
Chinese Academy of Sciences,
Beijing 100012, PR China
2 -
Research Center for Theoretical Astrophysics,
School of Physics, The University of Sydney,
NSW 2006, Australia
Received 4 December 2003 / Accepted 19 April 2004
Abstract
We ascribe the interpretation of the twin kilohertz
Quasi Periodic Oscillations (kHz QPOs) of X-ray spectra of Low
Mass X-Ray Binaries (LMXBs) to MHD Alfvén wave oscillations in
the different mass density regions of the accreted matter at the
preferred radius, and the upper kHz QPO frequency
coincides with the Keplerian frequency. The proposed model
concludes that the kHz QPO frequencies depend inversely on the
preferred radius,
and that theoretical relation between the upper frequency (
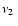 )
and
the lower frequency (
)
and
the lower frequency (
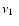 )
is
)
is
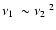 ,
which is similar
to the measured empirical relation. The separation between the
twin frequencies decreases (increases) with increasing kHz QPO
frequency if the lower kHz QPO frequency is more (less) than
,
which is similar
to the measured empirical relation. The separation between the
twin frequencies decreases (increases) with increasing kHz QPO
frequency if the lower kHz QPO frequency is more (less) than 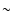 400 Hz.
400 Hz.
Key words: stars: neutron - X-rays: stars
The launch of the X-ray timing satellite, Rossi X-ray Timing Explorer (RXTE),
led to the discovery of Quasi
Periodic Oscillations (QPOs) of LMXBs in their X-ray brightness, with frequencies
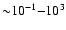 Hz (see van der Klis 2000, for a recent review).
Thereafter, much attention has been paid to the kHz QPO mechanism of LMXB;
however the proposed
models are still far from explaining all detected data. The Z sources (Atoll sources), which are high (less) luminous neutron star (NS) LMXBs
(Hasinger & van der Klis 1989), typically show four distinct
types of QPOs (van der Klis 2000). At present, these are the
normal branch oscillation (NBO)
Hz (see van der Klis 2000, for a recent review).
Thereafter, much attention has been paid to the kHz QPO mechanism of LMXB;
however the proposed
models are still far from explaining all detected data. The Z sources (Atoll sources), which are high (less) luminous neutron star (NS) LMXBs
(Hasinger & van der Klis 1989), typically show four distinct
types of QPOs (van der Klis 2000). At present, these are the
normal branch oscillation (NBO)
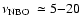 Hz, the horizontal
branch oscillation (HBO)
Hz, the horizontal
branch oscillation (HBO)
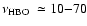 Hz, and the kHz QPOs
Hz, and the kHz QPOs
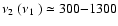 Hz that typically occur in pairs in
more than 20 sources, with upper frequency
Hz that typically occur in pairs in
more than 20 sources, with upper frequency
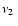 and lower frequency
and lower frequency
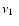 .
In
11 sources, nearly coherent burst oscillations
.
In
11 sources, nearly coherent burst oscillations
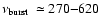 Hz
have also
been detected during thermonuclear type I X-ray bursts; these are
considered to be the NS spin frequencies
Hz
have also
been detected during thermonuclear type I X-ray bursts; these are
considered to be the NS spin frequencies
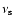 or their first overtone (see,
e.g., Strohmayer &
Bildsten 2003). Moreover, the existence of a third kHz QPO
has also been reported
in three low-luminosity sources (Jonker et al. 2000).
All of these QPOs but the burst oscillations have
centroid frequencies that increase with the inferred mass
accretion rate
or their first overtone (see,
e.g., Strohmayer &
Bildsten 2003). Moreover, the existence of a third kHz QPO
has also been reported
in three low-luminosity sources (Jonker et al. 2000).
All of these QPOs but the burst oscillations have
centroid frequencies that increase with the inferred mass
accretion rate 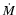 .
Furthermore, the frequencies
.
Furthermore, the frequencies
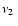 and
and
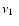 ,
as well as the frequencies
,
as well as the frequencies
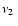 and
and
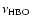 ,
follow very
similar relations in five Z sources, and the QPO frequencies of
LMXBs and black hole candidates (BHC) have a tight and
systematical correlation over three orders of magnitude in
frequency (Psaltis et al. 1998, 1999; Belloni et al. 2002).
,
follow very
similar relations in five Z sources, and the QPO frequencies of
LMXBs and black hole candidates (BHC) have a tight and
systematical correlation over three orders of magnitude in
frequency (Psaltis et al. 1998, 1999; Belloni et al. 2002).
Various theoretical models have been proposed to account for
the QPO phenomenon in X-ray binaries (for a review see, e.g., Psaltis
2000). In the early detection of RXTE, the upper kHz QPO (
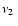 )
was
simply considered to originate
from the Keplerian orbital frequency at the preferred radius,
and the lower kHz QPO
(
)
was
simply considered to originate
from the Keplerian orbital frequency at the preferred radius,
and the lower kHz QPO
(
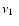 )
is attributed to
the beat of this frequency with the stellar spin frequency
)
is attributed to
the beat of this frequency with the stellar spin frequency
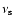 (Strohmayer et al. 1996; Miller et al. 1998). However, this beat
model is inadequate, for the detected frequency separation
(
(Strohmayer et al. 1996; Miller et al. 1998). However, this beat
model is inadequate, for the detected frequency separation
(
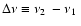 )
decreased systematically
with instantaneous
)
decreased systematically
with instantaneous 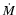 (see, e.g., van der Klis 2000).
Later on, general
relativistic effects were invoked to account for kHz QPOs (Stella
& Vietri 1999; Stella et al. 1999; Psaltis &
Norman 2000), which can satisfactorily explain the variation in kHz QPO
separation
(see, e.g., van der Klis 2000).
Later on, general
relativistic effects were invoked to account for kHz QPOs (Stella
& Vietri 1999; Stella et al. 1999; Psaltis &
Norman 2000), which can satisfactorily explain the variation in kHz QPO
separation 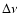 .
Moreover, the theory of epicyclic parametric resonance
in relativistic accretion disks
was proposed (Abramowicz et al. 2003), where the twin kHz QPOs occur
at the frequency of meridional
oscillation and the radial epicyclic frequency in the same orbit,
which can explain
the frequency ratio 3:2 detected
in black hole candidates.
Although many other feasible ideas have also proposed, such as
the disk seismic model (Wagoner 1999), a two-oscillator model
(Osherovich & Titarchuk) and the
photon bubble model (Klein et al. 1996),
no model has yet explained satisfactorily
all observed QPO phenomena of LMXBs until now.
.
Moreover, the theory of epicyclic parametric resonance
in relativistic accretion disks
was proposed (Abramowicz et al. 2003), where the twin kHz QPOs occur
at the frequency of meridional
oscillation and the radial epicyclic frequency in the same orbit,
which can explain
the frequency ratio 3:2 detected
in black hole candidates.
Although many other feasible ideas have also proposed, such as
the disk seismic model (Wagoner 1999), a two-oscillator model
(Osherovich & Titarchuk) and the
photon bubble model (Klein et al. 1996),
no model has yet explained satisfactorily
all observed QPO phenomena of LMXBs until now.
In this paper, the MHD Alfvén wave oscillation model is proposed,
and its predictions and comparisons with the
well detected
sample sources are shown in the figures.
The model's idea is traced to the
analogies with magnetic waves in coronal oscillations in solar physics,
where the MHD turbulence
driven by Alfvén wave oscillations
occurs in the magnetic loops of the Sun's coronal atmosphere (Roberts 2000).
While the dynamical details of the mechanisms
responsible for the kHz QPOs in LMXBs are still uncertain,
it is convenient to imagine that the MHD Alfvén wave
oscillations occur at a certain preferred radius, where a MHD tube
loop may be formed to conduct
the accreted matter to the polar cap of star. Nevertheless,
it is assumed that this preferred radius is a critical or a transitional
radius where the spherical accretion matter with low mass density
is transferred into polar channel accretion with
high mass density that follows the loop and accretes onto
NS polar cap. Possibly,
this critical transition may give rise to MHD
turbulence so that much more energy is liberated than at other positions.
As a phenomenological prescription, we associate the twin
kHz QPO frequencies
with the Alfvén wave oscillation frequencies (AWOFs)
at a preferred radius described in the appendix, where
the AWOF
with the spherical accretion mass density coincides with
the Keplerian orbital frequency
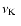 and the AWOF with the polar accretion mass density
corresponds to a
lower frequency. As a preliminary investigation,
we are not concerned with the
actual mechanisms of producing the kHz QPOs in the X-ray fluxes of
LMXBs (see, e.g., Miller et al. 1998;
Psaltis 2000). Rather, our main purpose is to
stress the consistence between the model and the measured kHz QPO data,
and leave the arguments concerning the possibility of the mechanism to a later paper.
and the AWOF with the polar accretion mass density
corresponds to a
lower frequency. As a preliminary investigation,
we are not concerned with the
actual mechanisms of producing the kHz QPOs in the X-ray fluxes of
LMXBs (see, e.g., Miller et al. 1998;
Psaltis 2000). Rather, our main purpose is to
stress the consistence between the model and the measured kHz QPO data,
and leave the arguments concerning the possibility of the mechanism to a later paper.
At the preferred radius r, the Alfvén
velocity is,
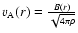 ,
where
,
where
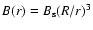 and
and 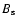 are the
dipole magnetic field strengths at radius r and at the surface
of star with radius R, respectively. Therefore,
the AWOF
are the
dipole magnetic field strengths at radius r and at the surface
of star with radius R, respectively. Therefore,
the AWOF
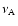 is
is
 |
(1) |
where the mass density of
the accreted matter,
![$\rho=\mbox{$\dot M$ }/[S\mbox{$v_{\rm ff}$ }]$](/articles/aa/full/2004/32/aa0808/img25.gif) (Shapiro & Teukolsky
1983) is
applied with the free fall
velocity
(Shapiro & Teukolsky
1983) is
applied with the free fall
velocity
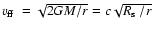 ,
where
,
where
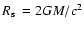 is the Schwarzschild radius and can be expressed as
is the Schwarzschild radius and can be expressed as
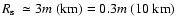 with
with
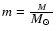 ,
the NS mass in units of solar mass, and
the area S representing the spherical area
,
the NS mass in units of solar mass, and
the area S representing the spherical area
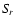 or the polar cap area
or the polar cap area
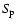 ,
respectively,
,
respectively,
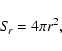 |
(2) |
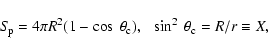 |
(3) |
where
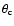 is the
open angle of the last field line to close at radius r. As an
approximation, the polar cap area is usually written as
is the
open angle of the last field line to close at radius r. As an
approximation, the polar cap area is usually written as
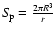 if
if 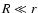 (Shapiro & Teukolsky 1983).
For simplicity, it is
convenient to write the two areas by means of the scaled radius
parameter
(Shapiro & Teukolsky 1983).
For simplicity, it is
convenient to write the two areas by means of the scaled radius
parameter
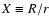 ,
so we have,
,
so we have,
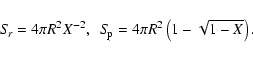 |
(4) |
It is assumed that
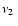 and
and
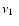 are from the MHD Alfvén wave oscillations with the different accreted
material mass densities, corresponding to the different areas
are from the MHD Alfvén wave oscillations with the different accreted
material mass densities, corresponding to the different areas
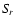 and
and
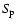 respectively, and
respectively, and
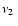 coincides with the
Keplerian frequency at the preferred radius (see Appendix),
therefore,
coincides with the
Keplerian frequency at the preferred radius (see Appendix),
therefore,
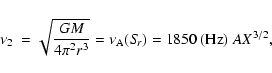 |
(5) |
with the parameter A defined
as
A = (m/R63)1/2 and
R6=R/106 cm.
The physical meaning of A is clear in that A2 represents the
NS averaged mass density. So, by
means of Eq. (1) with the correlation
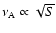 ,
we obtain the lower kHz QPO frequency,
,
we obtain the lower kHz QPO frequency,
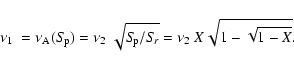 |
(6) |
The twin kHz QPO frequencies only
depend on two variables, the parameter A and the scaled
radius X, so these two variables are implied if the
twin kHz QPO frequencies are detected simultaneously. Therefore,
the ratio of the twin frequencies is obtained easily, by setting
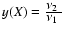 ,
,
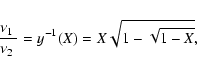 |
(7) |
which is independent
of the parameter A and is only related to the
parameter X. Furthermore, the twin frequency separation is
given as follows,
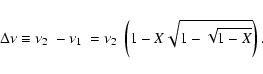 |
(8) |
The comparisons of the model's conclusions to the four detected
sample sources, Sco X-1 (van der Klis et al. 1997), 4U1608-52
(Méndez et al. 1998a,b), 4U1735-44 (Ford et al. 1998)
and 4U1728-34 (Méndez & van der Klis 1999), are shown in the figures.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0808fig1.eps}\end{figure}](/articles/aa/full/2004/32/aa0808/Timg44.gif) |
Figure 1:
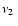 versus
versus
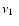 plot.
The horizontal axis is the lower kHz QPO frequency
plot.
The horizontal axis is the lower kHz QPO frequency
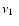 and the vertical axis is the upper kHz QPO frequency and the vertical axis is the upper kHz QPO frequency
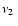 .
The kHz QPO data of four detected sample sources are plotted. The model
presents a good consistence with the measured data for the NS averaged mass density
parameters A=0.6, 0.7 and 0.8, which are shown in the three theoretical curves
from bottom to top. .
The kHz QPO data of four detected sample sources are plotted. The model
presents a good consistence with the measured data for the NS averaged mass density
parameters A=0.6, 0.7 and 0.8, which are shown in the three theoretical curves
from bottom to top. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0808fig2.eps}\end{figure}](/articles/aa/full/2004/32/aa0808/Timg45.gif) |
Figure 2:
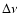 versus
versus
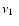 plot.
The horizontal axis is the lower kHz QPO frequency
plot.
The horizontal axis is the lower kHz QPO frequency
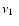 and the vertical axis is the twin kHz QPO frequency separation and the vertical axis is the twin kHz QPO frequency separation 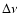 .
The kHz QPO data of four detected sample sources are plotted.
The model
presents a good consistence with the measured data for the NS averaged mass density
parameters A=0.6, 0.7 and 0.8, which are shown in the three theoretical curves
from bottom to top. .
The kHz QPO data of four detected sample sources are plotted.
The model
presents a good consistence with the measured data for the NS averaged mass density
parameters A=0.6, 0.7 and 0.8, which are shown in the three theoretical curves
from bottom to top. |
| Open with DEXTER |
The relations
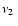 versus
versus
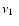 and
and 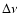 versus
versus
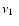 are plotted in
Figs. 1 and 2, respectively, and they show that the agreement between the model
and the observed QPO data is quite good for the selected
ranges of NS parameters A=0.6, 0.7 and 0.8. In Fig. 2, we find
that
are plotted in
Figs. 1 and 2, respectively, and they show that the agreement between the model
and the observed QPO data is quite good for the selected
ranges of NS parameters A=0.6, 0.7 and 0.8. In Fig. 2, we find
that 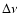 increases with increasing
increases with increasing
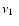 if
if
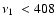 (A/0.7) Hz and
(A/0.7) Hz and 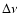 decreases with increasing
decreases with increasing
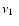 if
if
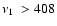 (A/0.7) Hz.
The theoretical relation between the twin frequencies is derived from
Eqs. (5) and (6),
(A/0.7) Hz.
The theoretical relation between the twin frequencies is derived from
Eqs. (5) and (6),
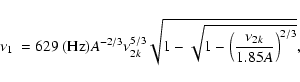 |
(9) |
where
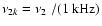 .
If
.
If
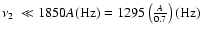 ,
then we obtain the
approximated theoretical relation between the twin kHz QPO frequencies,
,
then we obtain the
approximated theoretical relation between the twin kHz QPO frequencies,
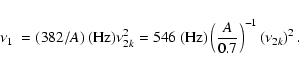 |
(10) |
A similar
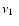 -
-
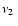 empirical correlation has also been
found for the measured kHz QPO sources (see, e.g., Stella et al.
1999; Psaltis et al. 1998; Psaltis 2000; Psaltis & Norman 2000).
In Fig. 3, we plot the
empirical correlation has also been
found for the measured kHz QPO sources (see, e.g., Stella et al.
1999; Psaltis et al. 1998; Psaltis 2000; Psaltis & Norman 2000).
In Fig. 3, we plot the
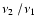 versus
versus
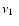 diagram, and it is found that
the ratio
diagram, and it is found that
the ratio
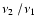 decreases with increasing
decreases with increasing
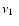 .
The averaged frequency
ratio for the four sample sources is about
.
The averaged frequency
ratio for the four sample sources is about
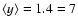 :5,
corresponding to the averaged X,
:5,
corresponding to the averaged X,
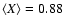 .
In Fig. 4, we plot
.
In Fig. 4, we plot
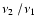 versus X, and find that
the theoretical curve is independent of the parameter A, which
reflects the pure
geometrical scaling relation between the twin frequency
ratio and the parameter X=R/r. The X distributions for the four
examples are very similar (from X=0.8 to X=0.93),
which implies that the dynamic mechanism
that accounts for kHz QPO is intimately related to the scaled radius X and has no direct relation with the other physical quantities.
versus X, and find that
the theoretical curve is independent of the parameter A, which
reflects the pure
geometrical scaling relation between the twin frequency
ratio and the parameter X=R/r. The X distributions for the four
examples are very similar (from X=0.8 to X=0.93),
which implies that the dynamic mechanism
that accounts for kHz QPO is intimately related to the scaled radius X and has no direct relation with the other physical quantities.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{0808fig3.eps}\end{figure}](/articles/aa/full/2004/32/aa0808/Timg55.gif) |
Figure 3:
The ratio between the twin kHz QPO frequencies versus the
lower kHz QPO frequency. The three
theoretical curves represent the NS mass density parameter conditions
with A=0.6, 0.7 and 0.8 from bottom to top.
The data of four sample sources are plotted. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{0808fig4.eps}\end{figure}](/articles/aa/full/2004/32/aa0808/Timg57.gif) |
Figure 4:
The ratio between the twin kHz QPO frequencies
versus the parameter
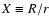 .
The horizontal axis is Xand the vertical axis is the ratio .
The horizontal axis is Xand the vertical axis is the ratio
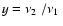 .
It is found that the theoretical curve is independent of the NS
mass density parameter A.
The two horizontal lines represent y=5:4 and y=5:3,
from bottom to top, respectively,
which cover the ratios of the
detected kHz QPO data of the four samples. .
It is found that the theoretical curve is independent of the NS
mass density parameter A.
The two horizontal lines represent y=5:4 and y=5:3,
from bottom to top, respectively,
which cover the ratios of the
detected kHz QPO data of the four samples.
|
| Open with DEXTER |
In conclusion, the consistence between the model and the detections is robust, and
the main results are summaried as follows:
(1) the twin QPOs are inversely (proportionally) related to the radii
(the accretion rate); (2) the theoretical relation between the twin frequencies is
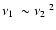 ;
(3) the separation between the
twin frequencies decreases (increases) with increasing the kHz QPO
frequency if the lower kHz frequency is more (less) than
;
(3) the separation between the
twin frequencies decreases (increases) with increasing the kHz QPO
frequency if the lower kHz frequency is more (less) than 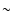 400 Hz; (4) the ratio between the twin frequencies is only related to the scaled
radius parameter X, and the homogenous kHz QPO frequency distributions of
four detected sources indicate that these frequencies are from regions
close to the surface of the NS, approximately, from 1.08R to 1.25R.
With regard to conclusion (3), for the theoretical
400 Hz; (4) the ratio between the twin frequencies is only related to the scaled
radius parameter X, and the homogenous kHz QPO frequency distributions of
four detected sources indicate that these frequencies are from regions
close to the surface of the NS, approximately, from 1.08R to 1.25R.
With regard to conclusion (3), for the theoretical 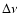 -
-
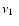 relation with
relation with
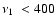 Hz future detection is needed to confirm this prediction.
Hz future detection is needed to confirm this prediction.
Acknowledgements
Thanks are due to T. Belloni, M. Méndez, and D. Psaltis for providing
the data files, and discussion with T. P. Li is highly appreciated.
The Alfvén radius
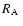 is determined by the condition that
the magnetic ram pressure
should match the plasma momentum energy density (Shapiro & Teukolsky 1983),
where
is determined by the condition that
the magnetic ram pressure
should match the plasma momentum energy density (Shapiro & Teukolsky 1983),
where
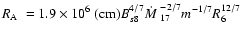 ,
and
,
and
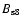 the surface field in unit of 108 Gauss,
the surface field in unit of 108 Gauss,
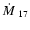 the accretion rate in unit of 1017 g/s,
the accretion rate in unit of 1017 g/s,
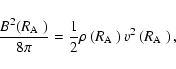 |
(11) |
or equivalently,
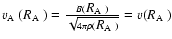 ,
where
,
where
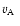 and v represent the Alfvén velocity and the free fall velocity,
and v represent the Alfvén velocity and the free fall velocity,
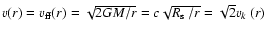 and
and
![$\rho(r)=\rho_{\rm ff}(r)=\mbox{$\dot M$ }/[S\mbox{$v_{\rm ff}$ }(r)]$](/articles/aa/full/2004/32/aa0808/img67.gif) with the
area factor
with the
area factor
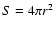 .
In other
words, the Alfvén velocity equals the free fall
velocity at the Alfvén radius.
If the area factor S decreases
(the polar cap area for instance), the mass density
.
In other
words, the Alfvén velocity equals the free fall
velocity at the Alfvén radius.
If the area factor S decreases
(the polar cap area for instance), the mass density 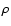 will increase and
the Alfvén velocity will decrease.
If we set
will increase and
the Alfvén velocity will decrease.
If we set
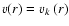 and
and 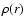 =
=
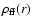 ,
then we will obtain a preferred radius where the Alfvén velocity
matches the Keplerian flow velocity,
,
then we will obtain a preferred radius where the Alfvén velocity
matches the Keplerian flow velocity,
 |
(12) |
So, the radius
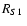 can be obtained to be
can be obtained to be
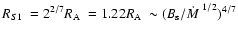 ,
where the Alfvén wave oscillation frequency matches the Keplerian
frequency,
,
where the Alfvén wave oscillation frequency matches the Keplerian
frequency,
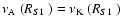 ;
we prefer to call it
the quasi sonic-point radius as a distinction
of the sonic-point radius by Miller et al. (1998) and Lai (1998).
;
we prefer to call it
the quasi sonic-point radius as a distinction
of the sonic-point radius by Miller et al. (1998) and Lai (1998).
- Abramowicz,
M. A., Bulik, T., Bursa, M., & Kluzniak, W. 2003, A&A, 404,
L21 [EDP Sciences] [NASA ADS] (In the text)
- Belloni, T.,
Psaltis, D., & van der Klis, M. 2002, ApJ, 572, 392 [NASA ADS] (In the text)
- Ford, E. C., van der
Klis, M., van Paradijs, J., et al. 1998, ApJ, 508, L155 [NASA ADS] (In the text)
- Hasinger, G.,
& van der Klis, M. 1989, A&A, 225, 79 [NASA ADS] (In the text)
- Jonker, P. G.,
Méndez, M., & van der Klis, M. 2000, ApJ, 540, L29 [NASA ADS] (In the text)
- Klein, R. L.,
Jernigan, G. J., Arons, J., Morgan, E. H., & Zhang, W. 1996,
ApJ, 469, L119 [NASA ADS] (In the text)
- Lai, D. 1998, ApJ, 502,
721 [NASA ADS] (In the text)
- Méndez, M.,
& van der Klis, M. 1999, ApJ, 517, L51 [NASA ADS] (In the text)
- Méndez, M.,
van der Klis, M., van Paradijs, J., Lewin, W. H. G., & Vaughan,
B. A. 1998a, ApJ, 494, L65 [NASA ADS] (In the text)
- Méndez, M.,
van der Klis, M., Wijnands, R., et al. 1998b, ApJ, 505, L23 [NASA ADS]
- Miller, M. C.,
Lamb, F. K., & Psaltis, D. 1998, ApJ, 508, 791 [NASA ADS] (In the text)
- Osherovich,
V., & Titarchuk, L. 1999, ApJ, 522, L113 [NASA ADS]
- Psaltis, D. 2000,
Adv. Space Res., 481, 281 [NASA ADS] [arXiv:astro-ph/0012251]
(In the text)
- Psaltis, D.,
& Norman, C. 2000 [arXiv:astro-ph/0001391]
(In the text)
- Psaltis, D.,
Belloni, T., & van der Klis, M. 1999, ApJ, 520, 262 [NASA ADS]
[arXiv:astro-ph/9902130]
(In the text)
- Psaltis, D.,
Méndez, M., Wijnands, R., et al. 1998, ApJ, 501, L95 [NASA ADS] (In the text)
- Roberts, B. 2000,
Sol. Phys., 193, 139 [NASA ADS] (In the text)
- Shapiro, S. L.,
& Teukolsky, S. A. 1983, Black holes, white dwarfs and neutron
stars (New York: Wiley)
(In the text)
- Stella, L., &
Vietri, M. 1999, Phys. Rev. Lett., 82, 17 [NASA ADS] (In the text)
- Stella, L., Vietri,
M., & Morsink, S. 1999, ApJ, 524, L63 [NASA ADS] (In the text)
- Strohmayer,
T., & Bildsten, L. 2003, in Compact stellar X-ray sources, ed.
W. H. G. Lewin, & M. van der Klis (Cambridge University Press)
[arXiv:astro-ph/0301544]
(In the text)
- Strohmayer,
T., Zhang, W., Smale, A., et al. 1996, ApJ, 469, L9 [NASA ADS] (In the text)
- van der Klis, M. 2000,
ARA&A, 38, 717 [NASA ADS] [arXiv:astro-ph/0001167]
(In the text)
- van der Klis, M.,
Wijnands, A. D., Horne, K., & Chen, W. 1997, ApJ, 481, L97 [NASA ADS] (In the text)
- Wagoner, R. W.
1999, Phys. Rep., 311, 259 [NASA ADS] (In the text)
- Zhang, W., Smale, A.
P., Strohmayer, T. E., & Swank, J. H. 1998, ApJ, 500, L171 [NASA ADS]
- Zhang, W.,
Strohmayer, T. E., & Swank, J. H. 1997, ApJ, 482, L167 [NASA ADS]
Copyright ESO 2004

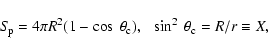
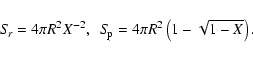
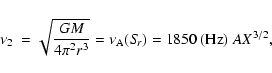
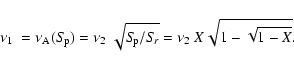
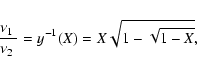
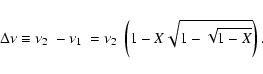
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0808fig1.eps}\end{figure}](/articles/aa/full/2004/32/aa0808/Timg44.gif)
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0808fig2.eps}\end{figure}](/articles/aa/full/2004/32/aa0808/Timg45.gif)
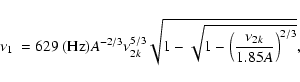
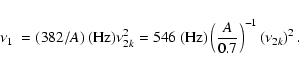
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{0808fig3.eps}\end{figure}](/articles/aa/full/2004/32/aa0808/Timg55.gif)
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{0808fig4.eps}\end{figure}](/articles/aa/full/2004/32/aa0808/Timg57.gif)