B. Vrsnak 1 - D. Ruzdjak 1 - D. Sudar 1 - N. Gopalswamy 2
1 - Hvar Observatory, Faculty of Geodesy, Kaciceva 26, 10000 Zagreb, Croatia
2 -
NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA
Received 30 January 2004 / Accepted 21 April 2004
Abstract
Kinematics of more than 5000 coronal mass ejections (CMEs) measured in the distance
range 2-30 solar radii is investigated. A distinct anticorrelation between the acceleration, a,
and the velocity, v, is found. In the linear form, it can be represented as
a=-k1(v-v0),
where v0=400 km s-1, i.e., most of CMEs faster than 400 km s-1 decelerate, whereas
slower ones generally accelerate.
After grouping CMEs into the width and mean-distance bins, it was found that
the slope k1 depends on these two parameters: k1 is smaller for CMEs of larger width and
mean-distance. Furthermore, the obtained CME subsets show distinct quadratic-form correlations, of
the form
![]() .
The value of k2 decreases with increasing distance
and width, whereas v0 increases with the distance and is systematically larger than the slow
solar wind speed by 100-200 km s-1.
.
The value of k2 decreases with increasing distance
and width, whereas v0 increases with the distance and is systematically larger than the slow
solar wind speed by 100-200 km s-1.
The acceleration-velocity relationship is interpreted as a consequence of the aerodynamic drag.
The excess of v0 over the solar wind speed is explained assuming that in a certain fraction of
events the propelling force is still acting in the considered distance range. In most events the
inferred propelling force acceleration at 10 solar radii ranges between
![]() and 10 m s-2,
being on average smaller at larger distances. However, there are also events that show
and 10 m s-2,
being on average smaller at larger distances. However, there are also events that show
![]() m s-2, as well as events indicating
m s-2, as well as events indicating
![]() .
Implications for the interplanetary
motion of CMEs are discussed, emphasizing the prediction of the 1 a.u. arrival time.
.
Implications for the interplanetary
motion of CMEs are discussed, emphasizing the prediction of the 1 a.u. arrival time.
Key words: magnetohydrodynamics (MHD) - Sun: corona - Sun: coronal mass ejections (CMEs) - Sun: solar-terrestrial relations - Sun: solar wind - interplanetary medium
Coronal mass ejection (CME) is a process in which the free energy contained in the coronal non-potential magnetic field is released in the form of kinetic and potential energy of ejected plasma (Forbes 2000). In large eruptions the magnetic flux of some 1023 Wb is expelled into the interplanetary space at velocities of the order of 1000 km s-1, carrying along 1013 kg of coronal plasma (Gosling 1990; Webb et al. 1994).
The non-potential field of the erupting structure carries the electric current, I, providing the Lorentz force that drives the eruption. The free energy of any current-carrying system can most generally be expressed as W=LI2, where L is the inductance of the structure (Jackson 1975; Landau et al. 1984; for a detailed discussion of the MHD aspect see Chen & Krall 2002).
The inductance depends on the size of the current-carrying structure, implying that during the
eruption L increases (see, e.g., Anzer 1978; Vrsnak 1990; Chen 1996,
and references therein). On the other hand, L is related to the magnetic flux ![]() associated
with the current,
associated
with the current, ![]() .
Since it can be taken approximately that the erupting magnetic flux
.
Since it can be taken approximately that the erupting magnetic flux ![]() does not change much, this implies that the current has to decrease as the erupting
structure enlarges,
does not change much, this implies that the current has to decrease as the erupting
structure enlarges,
![]() .
Because of the decreasing current, the Lorentz force
weakens, eventually ceasing at large heliocentric distances.
.
Because of the decreasing current, the Lorentz force
weakens, eventually ceasing at large heliocentric distances.
Note that the condition
![]() could be violated in a limited time interval due to reconnection below the erupting flux tube (e.g., Vrsank 1990; Lin & Forbes 2000; see also Wang et al. 2003), or by an injection of the poloidal flux from the
subphotospheric layers (e.g., Chen 1996). The supply of the poloidal flux prolongs the
acceleration phase of the eruption.
could be violated in a limited time interval due to reconnection below the erupting flux tube (e.g., Vrsank 1990; Lin & Forbes 2000; see also Wang et al. 2003), or by an injection of the poloidal flux from the
subphotospheric layers (e.g., Chen 1996). The supply of the poloidal flux prolongs the
acceleration phase of the eruption.
The free energy of the system
![]() decreases, and if only the Lorentz
force and
gravity are considered, it should be directly
transformed into kinetic and potential energy.
However, CMEs travel through the ambient coronal/interplanetary (C/IP) plasma, causing the emission
of MHD waves and appearance of the "aerodynamic'' drag. The drag can have complex characteristics
depending on the orientation of the ambient magnetic field (Vandas et al. 1995,
1996; Cargill et al. 1996; Cargill & Schmidt 2002), but still can be
expressed as:
decreases, and if only the Lorentz
force and
gravity are considered, it should be directly
transformed into kinetic and potential energy.
However, CMEs travel through the ambient coronal/interplanetary (C/IP) plasma, causing the emission
of MHD waves and appearance of the "aerodynamic'' drag. The drag can have complex characteristics
depending on the orientation of the ambient magnetic field (Vandas et al. 1995,
1996; Cargill et al. 1996; Cargill & Schmidt 2002), but still can be
expressed as:
The interaction of CMEs and the solar wind plasma is under favourable conditions "visualized'' by the dekameter-to-kilometer wavelength type II radio bursts. Such bursts are excited at the C/IP shocks that are driven by CMEs (e.g., Gopalswamy et al. 2001a).
As the Lorentz force and gravity decrease, the drag could become a dominant force. Indeed,
Gopalswamy et al. (2000) inferred that in the IP space the CMEs that are faster than the
solar wind decelerate, whereas the slower ones are additionally accelerated by the wind. The net
acceleration was found to be anticorrelated with the CME speed; the issue was elaborated in a
subsequent paper (Goplaswamy et al. 2001b) where the projection effects were partly
eliminated and different distances from the Sun were considered. On the other hand, Gopalswamy et al. (2001a) analysed the relationship between acceleration and speed for fast
(v > 900 km s-1) and wide (![]() > 60
> 60![]() )
CMEs associated with type II
bursts, and found that in the upper corona faster CMEs show stronger deceleration. A similar result
was obtained by Vrsnak (2001a) who in addition showed that the deceleration rate
statistically depends not only on the speed of ejecta, but also on the height. An empirical scaling
law was established, describing the decrease of the average drag with increasing radial distance,
which provides a better prediction of the Sun-Earth transit time (Vrsnak & Gopalswamy 2002).
)
CMEs associated with type II
bursts, and found that in the upper corona faster CMEs show stronger deceleration. A similar result
was obtained by Vrsnak (2001a) who in addition showed that the deceleration rate
statistically depends not only on the speed of ejecta, but also on the height. An empirical scaling
law was established, describing the decrease of the average drag with increasing radial distance,
which provides a better prediction of the Sun-Earth transit time (Vrsnak & Gopalswamy 2002).
In the papers by Vrsnak (2001a) and Gopalswamy et al. (2001b) the acceleration/speed relationship (hereinafter a-v relationship) was studied on relatively small samples of events of specific characteristics. The former one embraced only fast events showing an exponential-like decay of speed, whereas the second one included only fast and wide CMEs associated with type II bursts. For this reason, Vrsnak et al. (2003) and Ruzdjak et al. (2004) extended the investigation of the a-v relationship to a large sample of more than 5000 CMEs observed by the Large Angle and Spectrometric Coronagraph (LASCO) aboard the Solar and Heliospheric Observatory (Brueckner et al. 1995) in the period 1996-2001. Again, the data showed a distinct a-v anticorrelation.
In this paper we perform a detailed analysis of the a-v relationship utilizing the same data set as in the preliminary reports by Vrsnak et al. (2003) and Ruzdjak et al. (2004). The aim of the paper is two-fold. Firstly, it is an extension of previous statistical analyses of kinematics of large samples of CMEs (e.g. Hundhausen 1993; Hundhausen et al. 1994; Harrison 1995; St. Cyr et al. 1999, 2000; Moon et al. 2002; Gopalswamy et al. 2003, and references therein). Secondly, the obtained empirical relationships are used as an insight into the physical background of CME dynamics in the near-Sun IP space. Both of these aspects could be essential in advancing the prediction of the CME arrival time at the Earth (Gopalswamy 2002).
The paper is organized as follows: the data set, the data sampling, and the parameters used are described in Sect. 2. Supplementary information concerning the statistical properties of the data set are shown in Appendix A. In Sects. 3 and 4 we present the empirical results, leaving explanations regarding the procedure for Appendix B. The results are discussed and interpreted in Sect. 5 and summarized in Sect. 6.
The following analysis is based on the CME distance-time measurements, R(t), where
![]() is the plane-of-sky heliocentric distance r normalized with respect to the solar
radius
is the plane-of-sky heliocentric distance r normalized with respect to the solar
radius ![]() .
The measurements are provided in the LASCO CME catalogue (Yashiro and Michalek,
http://cdaw.gsfc.nasa.gov/CME_list/). We utilize the data from 5012 events recorded in the
2<R<30 range from 1996 to 2001. From this sample we extracted two subsamples: one consists of
events which had been measured in
.
The measurements are provided in the LASCO CME catalogue (Yashiro and Michalek,
http://cdaw.gsfc.nasa.gov/CME_list/). We utilize the data from 5012 events recorded in the
2<R<30 range from 1996 to 2001. From this sample we extracted two subsamples: one consists of
events which had been measured in ![]() instants, and the other with
instants, and the other with ![]() (hereinafter
n4-set and n6-set, containing 4609 and 3697 events, respectively). Such a sampling was applied to
check how the accuracy of the acceleration and velocity estimates affects the results. Demanding a
still larger n would certainly improve the accuracy of individual kinematic data, but it would
lead to a systematic exclusion of the fastest CMEs due to the limited image acquisition rate of the
LASCO instruments.
(hereinafter
n4-set and n6-set, containing 4609 and 3697 events, respectively). Such a sampling was applied to
check how the accuracy of the acceleration and velocity estimates affects the results. Demanding a
still larger n would certainly improve the accuracy of individual kinematic data, but it would
lead to a systematic exclusion of the fastest CMEs due to the limited image acquisition rate of the
LASCO instruments.
The basic parameters treated in the following are:
In the preliminary reports by Vrsnak et al. (2003) and Ruzdjak et al. (2004) it
was shown that CME accelerations and velocities are anticorrelated, indicating that the aerodynamic
drag plays an important role in the CME dynamics. Since the drag acceleration depends on the
ambient solar wind speed and density, as well as on the CME dimensions and density, it would be
ideal if all events were recorded in the same range of heights. However, mean distances are found
in the range from
![]() to 20 (see Fig. 10 in Appendix A). Therefore, it is instructive to
consider the velocity "normalized'' to a particular height so that the ambient wind speed and
density are the same for all events. Since a vast majority of events were measured from
to 20 (see Fig. 10 in Appendix A). Therefore, it is instructive to
consider the velocity "normalized'' to a particular height so that the ambient wind speed and
density are the same for all events. Since a vast majority of events were measured from
![]() ,
we included in the analysis the velocity v3 as a kind of "initial velocity'' at a fixed (plane-of-sky) height. Other reasons for using v3 are explained in more detail and discussed in Sect. 5.1 and Appendix B.
,
we included in the analysis the velocity v3 as a kind of "initial velocity'' at a fixed (plane-of-sky) height. Other reasons for using v3 are explained in more detail and discussed in Sect. 5.1 and Appendix B.
The velocity v5 represents (statistically) the velocity at R somewhere in between the
"initial distance'' R=3 and the average value of mean-distances,
![]() ,
which amounts to
,
which amounts to
![]() (see Appendix A). We also considered
(see Appendix A). We also considered
![]() obtained from the 2nd degree polynomial fit, but since
obtained from the 2nd degree polynomial fit, but since
![]() the difference in the outcome for
the difference in the outcome for
![]() and
and ![]() turned out to be statistically insignificant. Hereafter, v3, v5,
turned out to be statistically insignificant. Hereafter, v3, v5, ![]() ,
and
,
and
![]() are denoted as "velocity options''.
are denoted as "velocity options''.
An important consequence of employing v3 is that the events with
![]() for which the fitted R(t) parabolas do not have an intercept with the R=3 level dropped out from the analysed
sample. Similarly, considering v5 one excludes the events that show a large deceleration and are
observed only across a relatively small range of heights, so that the fitted R(t) parabola has no
intercept with R=5. Such a "silent elimination'' additionally filters out unreliable/odd data. In
this way we got four subsamples which we denote n4v3-subset, n6v3-subset, n4v5-subset, and
n6v5-subset, containing 4463, 3581, 4570, and 3681 events, respectively.
for which the fitted R(t) parabolas do not have an intercept with the R=3 level dropped out from the analysed
sample. Similarly, considering v5 one excludes the events that show a large deceleration and are
observed only across a relatively small range of heights, so that the fitted R(t) parabola has no
intercept with R=5. Such a "silent elimination'' additionally filters out unreliable/odd data. In
this way we got four subsamples which we denote n4v3-subset, n6v3-subset, n4v5-subset, and
n6v5-subset, containing 4463, 3581, 4570, and 3681 events, respectively.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{0169f1.eps}
\end{figure}](/articles/aa/full/2004/32/aa0169-04/Timg92.gif) |
Figure 1:
The acceleration-speed correlation:
a) 2D distribution of events in a-v space for n4vm-subset. N is the number of events in the [ |
| Open with DEXTER | |
In Fig. 1 we present the general relationship between CME accelerations and velocities. The four presented graphs are chosen to show basic characteristics of the a-v correlation, and various statistical aspects of the relationship. Different subsets are chosen to illustrate that the general outcome is qualitatively the same, whatever sampling and velocity options are employed.
Since it is impossible to transparently present several thousands of data points in a single graph,
we first present in Fig. 1a the dependence
![]() by showing a 2-dimensional
distribution of data. An example of the "all-data''
by showing a 2-dimensional
distribution of data. An example of the "all-data''
![]() graph, analogous to the
graph, analogous to the
![]() graph that is shown in Fig. 1b, can be found in the paper by Moon et al. (2002), or Ruzdjak et al. (2004).
graph that is shown in Fig. 1b, can be found in the paper by Moon et al. (2002), or Ruzdjak et al. (2004).
The complete n4v3-subset data are shown in the
![]() graph in Fig. 1b, and in
Fig. 1c we show the corresponding bin-averaged values with the standard deviations (for
mean errors
graph in Fig. 1b, and in
Fig. 1c we show the corresponding bin-averaged values with the standard deviations (for
mean errors
![]() see Vrsnak et al. 2003). The fit in Fig. 1c is
obtained by attributing equal weights to all bin-averaged values in order to eliminate the effect
of data grouping. The quadratic fit of the form
see Vrsnak et al. 2003). The fit in Fig. 1c is
obtained by attributing equal weights to all bin-averaged values in order to eliminate the effect
of data grouping. The quadratic fit of the form
![]() is illustrated in Fig. 1d, where the n6v3-subset is used.
is illustrated in Fig. 1d, where the n6v3-subset is used.
Note that the a(v) graphs are presented in the most convenient form, where the acceleration is
expressed in m s-2 and the velocity in km s-1. So, the slope k1 of the linear
regression line in such a presentation has the unit
[km-1 m s-1] = [10-3 s-1], thus the units-adjusted slope has the value
![]() .
Analogously, the parameter k2, which appears in the quadratic fit and has
the unit [m km-2] = [10-3 km-1], is related to the unit adjusted slope as
.
Analogously, the parameter k2, which appears in the quadratic fit and has
the unit [m km-2] = [10-3 km-1], is related to the unit adjusted slope as
![]() ,
where
,
where ![]() is expressed in km-1.
is expressed in km-1.
The same regression analysis as the one shown in Fig. 1 is performed for all other velocity
options and data-subsets. The results are summarized in the upper part of Table 1, where
in the first two columns the velocity option and the data-subset label are indicated. In the 3rd,
and 4th column we present the unit-adjusted slope,
![]() s-1, and the x-axis intercept,
s-1, and the x-axis intercept,
![]() ,
of the linear least squares fit,
,
of the linear least squares fit,
![]() .
In
the last column the correlation coefficients C are presented. According to the F-test the
statistical significance
.
In
the last column the correlation coefficients C are presented. According to the F-test the
statistical significance ![]() is larger than 99% for all correlations listed in Table 1
(
is larger than 99% for all correlations listed in Table 1
(
![]() gives the probability for C=0).
gives the probability for C=0).
Table 1:
Summary of linear fits
![]() .
.
In order to check how much the accuracy of measurements influences the obtained results, we successively excluded the events with the acceleration-error Ma larger than 30, 20, 10 m s-2. It was found that the results do not depend significantly on such a subsampling.
In the lower part of Table 1 we show the results obtained using the bin-averaged values of
![]() and
and
![]() (Fig. 1c). The linear least squares fits presented in
Table 1 exclude the highest velocity bins,
1500<v<2000 km s-1 and
2000<v<2500 km s-1, where only a small number of events is found (e.g., in the n6v3-subset these two bins contain only 21 and 1 event, respectively).
(Fig. 1c). The linear least squares fits presented in
Table 1 exclude the highest velocity bins,
1500<v<2000 km s-1 and
2000<v<2500 km s-1, where only a small number of events is found (e.g., in the n6v3-subset these two bins contain only 21 and 1 event, respectively).
Figure 1 and Table 1 reveal a distinct anticorrelation of accelerations and speeds. The largest correlation coefficients are found for the n6v3-subset and n4v3-subset, which will be addressed in Sect. 5.1 and Appendix B.
Inspecting Table 1, one finds that the slopes are scattered in the range
![]() -0.03
-0.03 ![]() 10-3 s-1. The acceleration
10-3 s-1. The acceleration
![]() is found between
is found between
![]() 350 and
450 km s-1 in most of the data subsets considered. The bin-averaged data give systematically
lower values of v0 than the complete data sets (
350 and
450 km s-1 in most of the data subsets considered. The bin-averaged data give systematically
lower values of v0 than the complete data sets (
![]() and
and
![]()
![]() 20 km s-1, respectively).
20 km s-1, respectively).
The results shown in Table 1 can be summarized in general terms as:
![\begin{displaymath}%
a_{\rm\left[m~s^{-2}\right]}=-k_1(v-v_0)_{\rm\left[km~s^{-1}\right]}= -0.02_{\pm 0.01} \left(v-400_{\pm 50}\right),
\end{displaymath}](/articles/aa/full/2004/32/aa0169-04/img140.gif) |
(2) |
Finally, we emphasize that Figs. 1a, b, and d expose a void of data-points in the range v<150 km s-1, a<0, revealing that there are practically no slow events that decelerate.
Results presented by Gopalswamy et al. (2001b) and Vrsnak (2001a) indicate that
the a-v relationship might be better approximated by the quadratic dependence of the form
defined by Eq. (1)![]() . The
quadratic fit parameters, given in Table 2, show a much larger scatter than the linear-fit
ones (to be discussed in Sect. 5.3). Statistically, the most reliable quadratic fit is
obtained for the n6v3-subset which is shown in Fig. 1d. For this sample the least squares
fit gives
. The
quadratic fit parameters, given in Table 2, show a much larger scatter than the linear-fit
ones (to be discussed in Sect. 5.3). Statistically, the most reliable quadratic fit is
obtained for the n6v3-subset which is shown in Fig. 1d. For this sample the least squares
fit gives
![]()
![]() 10-6 km-1 and v0=500 km s-1. The values averaged over all considered data sets are
10-6 km-1 and v0=500 km s-1. The values averaged over all considered data sets are
![]()
![]() 0.012
0.012 ![]() 10-6 km-1 and
10-6 km-1 and
![]()
![]() 170 km s-1. A more detailed treatment of quadratic fits is presented in Sect. 4.2, where it will be shown that they become statistically relevant after the data are sorted into the width and mean-distance bins.
170 km s-1. A more detailed treatment of quadratic fits is presented in Sect. 4.2, where it will be shown that they become statistically relevant after the data are sorted into the width and mean-distance bins.
Table 2:
Summary of quadratic fits
![]() .
.
The a-v anticorrelation indicates that the motion of CMEs in the R=2-30 range is strongly
influenced by the aerodynamic drag. If so, it can be expected that the CME width ![]() is an
important parameter since the drag acceleration depends on the dimensions of the moving body. On
the other hand, the drag depends on the external density and flow speed, so one can suspect that
another relevant parameter is the height range in which a particular CME is measured. To
investigate the role of the parameters
is an
important parameter since the drag acceleration depends on the dimensions of the moving body. On
the other hand, the drag depends on the external density and flow speed, so one can suspect that
another relevant parameter is the height range in which a particular CME is measured. To
investigate the role of the parameters ![]() and
and ![]() we rely mainly on the n4-set, which is
large enough to provide a further sub-grouping of the data into a number of
we rely mainly on the n4-set, which is
large enough to provide a further sub-grouping of the data into a number of ![]() and
and ![]() bins. Furthermore, we limit the analysis only to
bins. Furthermore, we limit the analysis only to
![]() ,
to exclude halo CMEs, being
predominantly Earth- or anti-Earth- directed, i.e., to exclude events where projection effects are
large.
,
to exclude halo CMEs, being
predominantly Earth- or anti-Earth- directed, i.e., to exclude events where projection effects are
large.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0169f2.eps}
\end{figure}](/articles/aa/full/2004/32/aa0169-04/Timg147.gif) |
Figure 2:
Slopes
|
| Open with DEXTER | |
In the first step we tried to sort the data into the
![]() bins, and for each
bin we have drawn the a(v) graphs independently to check if, and how, the slopes
bins, and for each
bin we have drawn the a(v) graphs independently to check if, and how, the slopes ![]() depend on
depend on ![]() .
The procedure was applied to all velocity options and it turned out that the
.
The procedure was applied to all velocity options and it turned out that the
![]() bins are generally too narrow, giving a clear
bins are generally too narrow, giving a clear
![]() relationship only in the case of the n4v3-subset. The outcome is shown in Fig. 2a, where
the
relationship only in the case of the n4v3-subset. The outcome is shown in Fig. 2a, where
the
![]() and
and
![]() data are merged, since for
data are merged, since for
![]() the
the
![]() bins are not abundant enough (see Fig. 10d
in Appendix A) to provide statistically significant a-v correlations.
bins are not abundant enough (see Fig. 10d
in Appendix A) to provide statistically significant a-v correlations.
Figure 2a shows that the parameter ![]() is smaller for broader CMEs, exposing a
distinct power-law-like dependence. On the other hand, as the bin-averaged values
is smaller for broader CMEs, exposing a
distinct power-law-like dependence. On the other hand, as the bin-averaged values
![]() increase, the bin-averaged distances
increase, the bin-averaged distances
![]() also increase because wider CMEs are usually traced to larger heights, i.e.,
also increase because wider CMEs are usually traced to larger heights, i.e., ![]() and
and ![]() are correlated (see Fig. 11c in Appendix A). Consequently, one finds also a distinct
are correlated (see Fig. 11c in Appendix A). Consequently, one finds also a distinct
![]() power-law-like dependence which is shown in Fig. 2b.
power-law-like dependence which is shown in Fig. 2b.
The decreasing trend of
![]() and
and
![]() can be recognized also when other
velocity options and data-subsets are utilized. However, statistically significant results
(P>95% confidence level) are achieved only if the bins are broadened to
can be recognized also when other
velocity options and data-subsets are utilized. However, statistically significant results
(P>95% confidence level) are achieved only if the bins are broadened to
![]() bins. In the insets in Fig. 2 we show the outcome for n4v3, n4v5, and n4vm subsets, split into the
bins. In the insets in Fig. 2 we show the outcome for n4v3, n4v5, and n4vm subsets, split into the
![]() bins. The power-law fit parameters are summarized in Table 3.
bins. The power-law fit parameters are summarized in Table 3.
Table 3 and the insets in Fig. 2 illustrate that the fit parameters depend
considerably on the velocity option - the errors of individual fit parameters are far smaller than
the difference between different subsets. The power-law exponents ![]() received from the
received from the
![]() fit vary from
fit vary from
![]() to 3.1, whereas the exponents of
the
to 3.1, whereas the exponents of
the
![]() fit vary from
fit vary from
![]() to 0.69.
to 0.69.
Table 3:
Summary of power-law fit parameters (
![]() ,
,
![]() )
for
)
for
![]() -bin sampling.
-bin sampling.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0169f3.eps}
\end{figure}](/articles/aa/full/2004/32/aa0169-04/Timg175.gif) |
Figure 3:
The a-v correlations shown for three |
| Open with DEXTER | |
Due to the crosstalk of ![]() and
and ![]() ,
the presented simple-bin analysis does not really specify how
,
the presented simple-bin analysis does not really specify how ![]() depends on
depends on ![]() at a given height, and vice versa, how
at a given height, and vice versa, how ![]() depends on
depends on ![]() for CMEs of a given width class. So, in the next step we try to decouple the
for CMEs of a given width class. So, in the next step we try to decouple the
![]() dependence. The straightforward procedure would be to select the data within a narrow
interval of
dependence. The straightforward procedure would be to select the data within a narrow
interval of ![]() ,
and then to divide the data into a number of
,
and then to divide the data into a number of ![]() -bins. Analogously, one could try to select CMEs having widths within a certain interval, and then to separate the data into
-bins. Analogously, one could try to select CMEs having widths within a certain interval, and then to separate the data into
![]() -bins. However, in the former case the results turned out to be statistically significant only if the
-bins. However, in the former case the results turned out to be statistically significant only if the ![]() -interval includes at least
-interval includes at least
![]() ,
and analogously in the later case, if the width-interval embraces
,
and analogously in the later case, if the width-interval embraces
![]() .
Thus, although in this way the
.
Thus, although in this way the
![]() -
- ![]() crosstalk is reduced to a certain degree, the effect of the
crosstalk is reduced to a certain degree, the effect of the
![]() dependence is still present because of too wide
dependence is still present because of too wide
![]() ,
or
,
or
![]() intervals used.
intervals used.
So we apply another, less stringent procedure, where we start by creating
![]() bins, and then proceed by eliminating in each bin CMEs with largest (smallest) values of
bins, and then proceed by eliminating in each bin CMEs with largest (smallest) values of ![]() ,
until
,
until
![]() in all
in all ![]() -bins attains a previously chosen value. This provides an insight into the
-bins attains a previously chosen value. This provides an insight into the
![]() dependence at a given height. Analogously, we group the data into
dependence at a given height. Analogously, we group the data into
![]() bins, and then successively eliminate wide (narrow) CMEs until all
bins, and then successively eliminate wide (narrow) CMEs until all ![]() -bins show the same mean width
-bins show the same mean width
![]() .
This provides an insight into the
.
This provides an insight into the ![]() dependence for a chosen mean CME width.
dependence for a chosen mean CME width.
Figure 3 illustrates how the a-v relationship changes with increasing
![]() .
We show the n4v3-subset data in three different
.
We show the n4v3-subset data in three different
![]() bins, with the average width adjusted to the value
bins, with the average width adjusted to the value
![]() in each bin. The data are fitted by the linear and quadratic dependencies, and it turned out that the quadratic fits show a much larger
statistical significance than in the case of complete data sets (Sect. 3) and the
in each bin. The data are fitted by the linear and quadratic dependencies, and it turned out that the quadratic fits show a much larger
statistical significance than in the case of complete data sets (Sect. 3) and the ![]() -
- ![]() coupled data (Sect. 4.1). Note that the linear, as well as the quadratic fits, become succesively less steep, whereas the x-axis intercepts v0 shift to larger velocities. A similar behaviour can be recognized if one focuses on the lower boundary of the data (the "void'' mentioned in Sect. 3)
coupled data (Sect. 4.1). Note that the linear, as well as the quadratic fits, become succesively less steep, whereas the x-axis intercepts v0 shift to larger velocities. A similar behaviour can be recognized if one focuses on the lower boundary of the data (the "void'' mentioned in Sect. 3)
In Fig. 4 the outcome for n4v3-subset is summarized. The dependencies
![]() and
and
![]() are shown in Fig. 4a, where the
are shown in Fig. 4a, where the ![]() -bin averaged value of
-bin averaged value of ![]() is
adjusted to the value
is
adjusted to the value
![]() .
The top panel depicts the linear-fit results,
.
The top panel depicts the linear-fit results,
![]() ,
whereas in the bottom panel we present the quadratic-fit outcome,
,
whereas in the bottom panel we present the quadratic-fit outcome,
![]() .
Similar results are obtained for
.
Similar results are obtained for
![]() .
For
.
For
![]() and
and
![]() the statistical significances of a(v) fits in some
the statistical significances of a(v) fits in some ![]() -bins become lower than P<95% due to a small number of data, so the
-bins become lower than P<95% due to a small number of data, so the
![]() dependencies become unreliable.
dependencies become unreliable.
In Fig. 4b we show the
![]() dependence for
dependence for
![]() and
and
![]() .
For
.
For
![]() and
and
![]() the
results become unreliable due to the same reason as in the
the
results become unreliable due to the same reason as in the
![]() and
and
![]() case.
case.
In Fig. 4c we show the x-axis intercept v0 as a function of
![]() ,
for
,
for
![]() and
and
![]() ,
as found from the linear-fitting (top)
and the quadratic-fitting (bottom). The values of v0 show a distinct increase with the radial
distance. The obtained velocities are compared with the empirical solar wind model by Sheeley et al. (1997):
,
as found from the linear-fitting (top)
and the quadratic-fitting (bottom). The values of v0 show a distinct increase with the radial
distance. The obtained velocities are compared with the empirical solar wind model by Sheeley et al. (1997):
The outcome for the n4vm-subset and the n4v5-subset is statistically less reliable than for the
n4v3-subset. These options show a lower significance of a-v correlations, and consequently
larger errors of power-law fit coefficients for the
![]() and
and
![]() dependencies. Yet, the overall decreasing trend of
dependencies. Yet, the overall decreasing trend of
![]() and
and
![]() is well
recognizable, although not as clear as in the
is well
recognizable, although not as clear as in the ![]() -
- ![]() coupled case (insets in Fig. 2).
coupled case (insets in Fig. 2).
![\begin{figure}
\par\includegraphics[width=17.15cm,clip]{0169f4.eps}
\end{figure}](/articles/aa/full/2004/32/aa0169-04/Timg195.gif) |
Figure 4:
Summary of the a-v correlation parameters obtained for the n4v3-subset.
a) Slopes |
| Open with DEXTER | |
The acceleration-velocity relationship analysed in Sects. 3 and 4 indicates that the aerodynamic drag plays an important role in the dynamics of CMEs in the upper corona and the near-Sun interplanetary space. In this section we interpret the obtained empirical relationships, relying on basic physical characteristics of the drag.
However, first we have to clarify some important issues considering the a-v correlation as a statistical superposition of extracted kinematical parameters of different-width CMEs measured at different mean heights. Then we proceed by discussing the qualitative aspects of results that do not depend on the procedure and the velocity option. Eventually, we compare the results with some previous studies, and discuss the motion beyond R=30.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0169f5.eps}
\end{figure}](/articles/aa/full/2004/32/aa0169-04/Timg197.gif) |
Figure 5:
a) A sketch showing three
|
| Open with DEXTER | |
When the dynamics of an individual CME is considered, Eq. (1) relates the instantaneous acceleration with the instantaneous velocity, whereas actual CME measurements
provide only the mean acceleration estimated over a wide distance range. Furthermore, CMEs have
different widths ![]() ,
and are measured at different
,
and are measured at different ![]() ,
across different
,
across different ![]() .
This means that the interaction of CMEs with the solar wind is (quantitatively) different for various "categories'' of CMEs, as demonstrated in Sect. 4. For this reason it is instructive to pay
attention to the meaning of the statistical outcome, taking into account the nature of individual
measurements. Furthermore, one should bear in mind that CMEs move in various directions (different
projection effects), the solar wind is highly inhomogeneous (different ambient densities and flow
velocities for different CMEs), and the relative contribution of other forces might be different.
.
This means that the interaction of CMEs with the solar wind is (quantitatively) different for various "categories'' of CMEs, as demonstrated in Sect. 4. For this reason it is instructive to pay
attention to the meaning of the statistical outcome, taking into account the nature of individual
measurements. Furthermore, one should bear in mind that CMEs move in various directions (different
projection effects), the solar wind is highly inhomogeneous (different ambient densities and flow
velocities for different CMEs), and the relative contribution of other forces might be different.
In Fig. 5a we present schematically the physical background of the statistical relationship
between the mean accelerations and velocities for an imaginary set of CMEs whose motion is
dominated by the drag. We have drawn three
![]() curves,
hereinafter abbreviated as a(v)-trajectories. The curves are characterized by a successively larger w and smaller
curves,
hereinafter abbreviated as a(v)-trajectories. The curves are characterized by a successively larger w and smaller ![]() ,
representing the drag acceleration at different heights. Note
that at a given ambient flow speed w, CMEs of different widths
,
representing the drag acceleration at different heights. Note
that at a given ambient flow speed w, CMEs of different widths ![]() have different
have different ![]() ,
which should be represented by a fan of curves crossing the x-axis at the given w. Furthermore,
the presence of other forces shifts the curves up or down (see Sect. 5.3).
,
which should be represented by a fan of curves crossing the x-axis at the given w. Furthermore,
the presence of other forces shifts the curves up or down (see Sect. 5.3).
On the three depicted quadratic curves we have drawn the "real'' a(v)-trajectories (bold segments
of the curves) of several CMEs traveling at various velocities in different solar wind
environments. CMEs that are faster than the solar wind (
![]() )
move in the
left-up direction, whereas those with v<w, i.e.,
)
move in the
left-up direction, whereas those with v<w, i.e.,
![]() ,
move right-down. Note that the
instantaneous acceleration of CMEs is changing. The measured mean acceleration and velocity
are indicated by circles, whereas the change of the velocity is indicated by thin horizontal bars.
,
move right-down. Note that the
instantaneous acceleration of CMEs is changing. The measured mean acceleration and velocity
are indicated by circles, whereas the change of the velocity is indicated by thin horizontal bars.
Figure 5a explains several aspects of the statistical results obtained in Sects. 3 and 4. First of all, it clarifies why the quadratic fits turned out to be worse than linear ones when the complete data set is considered. Measuring CMEs of different dimensions and at different heights smears out the basic a(v) form into an inclined "cloud'' of data points which is naturally better fitted by the straight line.
On the other hand, the analysed CMEs were measured only above the occulting disc of the LASCO-C2
coronagraph. So, the smearing effect is reduced below some a(v)-curve that is defined by the
solar wind speed w and ![]() appropriate for
appropriate for ![]() of CMEs measured at low heights across relatively short distance interval. Indeed, one finds a sharp-edged void at a<0,
v<150 km s-1 (see Fig. 1) for any of the subsets and velocity options used. In
Fig. 5b we show this part of the n4v3-subset a-v graph enlarged, where two
(provisionally chosen) quadratic a(v)-curves are inserted to depict roughly the limits within
which lies the border of the void (pluses and crosses represent
of CMEs measured at low heights across relatively short distance interval. Indeed, one finds a sharp-edged void at a<0,
v<150 km s-1 (see Fig. 1) for any of the subsets and velocity options used. In
Fig. 5b we show this part of the n4v3-subset a-v graph enlarged, where two
(provisionally chosen) quadratic a(v)-curves are inserted to depict roughly the limits within
which lies the border of the void (pluses and crosses represent
![]() and
3
and
3 ![]() 10-6 km-1, respectively; in both cases w=100 km s-1). Going back to
Fig. 3 one finds that as
10-6 km-1, respectively; in both cases w=100 km s-1). Going back to
Fig. 3 one finds that as ![]() increases, the edge of the void successively expands towards higher velocities and becomes less steep.
increases, the edge of the void successively expands towards higher velocities and becomes less steep.
Let us now focus on the results that qualitatively do not depend on the procedure (the velocity option or sampling):
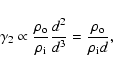 |
(5) |
Here we have implicitly assumed that at a given height there is no statistical correlation between
the CME density
![]() and d. However, wider CMEs seem to be denser: they can be traced to
larger distances (see Fig. 11c in Appendix A), implying that they are brighter, meaning also
denser. This effect tends to steepen the slope of the
and d. However, wider CMEs seem to be denser: they can be traced to
larger distances (see Fig. 11c in Appendix A), implying that they are brighter, meaning also
denser. This effect tends to steepen the slope of the
![]() dependence.
dependence.
Equation (4) can be rewritten also as
![]() .
Let us assume that
.
Let us assume that
![]() ,
i.e., that the mass loss from the prominence body and the mass pile-up at the leading edge of CME, at least partly compensate each other. Furthermore, utilizing
,
i.e., that the mass loss from the prominence body and the mass pile-up at the leading edge of CME, at least partly compensate each other. Furthermore, utilizing
![]() ,
and taking into account that in the considered distance range the ambient density decreases with the height as, say,
,
and taking into account that in the considered distance range the ambient density decreases with the height as, say,
![]() (see, e.g. Leblanc et al. 1998, or Vrsnak et al. 2003) one finds roughly
(see, e.g. Leblanc et al. 1998, or Vrsnak et al. 2003) one finds roughly
![]() .
In other words,
.
In other words, ![]() has to decrease with the distance, consistent with Fig. 4b. At larger distances, where
has to decrease with the distance, consistent with Fig. 4b. At larger distances, where
![]() ,
it should become approximately constant, except for the mass pile-up effect (for details see Cargill 2004).
,
it should become approximately constant, except for the mass pile-up effect (for details see Cargill 2004).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0169f6.eps}
\end{figure}](/articles/aa/full/2004/32/aa0169-04/Timg215.gif) |
Figure 6:
a) The parameter
|
| Open with DEXTER | |
The slopes of the empirical
![]() and
and
![]() dependencies obtained in
Sects. 3 and 4 are quite sensitive on the sampling and velocity option. In such a situation a
reliable quantitative comparison with a more detailed theoretical consideration would be
exaggerated. On the other hand, the x-axis intercept v0 in the a-v correlation shows a
much more coherent behaviour, so in the following we focus on this parameter.
dependencies obtained in
Sects. 3 and 4 are quite sensitive on the sampling and velocity option. In such a situation a
reliable quantitative comparison with a more detailed theoretical consideration would be
exaggerated. On the other hand, the x-axis intercept v0 in the a-v correlation shows a
much more coherent behaviour, so in the following we focus on this parameter.
In the absence of other forces the CME acceleration would be governed by Eq. (1), or in
linear approximation by
![]() .
Consequently, CMEs of a given
.
Consequently, CMEs of a given
![]() would form the a-v correlation that crosses the x-axis around
would form the a-v correlation that crosses the x-axis around
![]() .
Here we find a distinct quantitative discrepancy: Fig. 4c shows that the x-axis intercepts v0(R) are systematically higher than the corresponding solar wind speeds w(R).
.
Here we find a distinct quantitative discrepancy: Fig. 4c shows that the x-axis intercepts v0(R) are systematically higher than the corresponding solar wind speeds w(R).
To check this issue in more detail, in Fig. 6a we compare the v0(R) dependencies
obtained from different data sets and velocity options, with the model values evaluated by Eq. (3).
One finds out that velocities v0 closely follow the solar wind model for the asymptotic speed of
![]() km s-1, which is considerably higher than the widely accepted value
km s-1, which is considerably higher than the widely accepted value
![]() km s-1. Going back to Table 1 and comparing the listed values with
km s-1. Going back to Table 1 and comparing the listed values with
![]() km s-1 evaluated from Eq. (3) for
km s-1 evaluated from Eq. (3) for
![]() ,
one finds again that the values in Table 1 are larger for
,
one finds again that the values in Table 1 are larger for ![]() 150 km s-1.
150 km s-1.
| |
Figure 7: Schematic presentation showing how the a-v correlation (bold line) is shifted in the presence of a force which gives rise to the acceleration ax. The resulting dependence (gray-dashed line) intercepts x-axis at v0>w if ax>0, and at v0<w if ax<0. |
| Open with DEXTER | |
Such an excess can be interpreted in terms of a non-negligible propelling force![]() . In Fig. 7 we schematically draw how the
a-v correlation is modified if the drag is not the only force acting on CMEs in the studied
distance range. We consider only the simplest situation where the force (or several forces), giving
rise to an acceleration ax, does not statistically depend on v. Such a force does not
affect the slope of the a-v correlation - it only changes the x-axis intercept to
. In Fig. 7 we schematically draw how the
a-v correlation is modified if the drag is not the only force acting on CMEs in the studied
distance range. We consider only the simplest situation where the force (or several forces), giving
rise to an acceleration ax, does not statistically depend on v. Such a force does not
affect the slope of the a-v correlation - it only changes the x-axis intercept to ![]() .
If ax<0 (like gravity), the intercept value decreases (v0<w), and if ax>0the intercept value increases to v0>w. The acceleration ax can be determined from the
difference
.
If ax<0 (like gravity), the intercept value decreases (v0<w), and if ax>0the intercept value increases to v0>w. The acceleration ax can be determined from the
difference
![]() as
as
![]() (Fig. 7).
(Fig. 7).
In the following we consider the influence of gravity and the propelling (presumably Lorentz)
force, giving rise to accelerations g and ![]() .
The total acceleration (force per unit mass) can be written as
.
The total acceleration (force per unit mass) can be written as
![]() ,
where
,
where ![]() represents the drag acceleration. So, the additional net acceleration
represents the drag acceleration. So, the additional net acceleration
![]() can be estimated as
can be estimated as
![]() .
Since the values
.
Since the values
![]() are known from observations (e.g., Fig. 4b) and
are known from observations (e.g., Fig. 4b) and
![]() can be estimated using some solar wind model (e.g., Eq. (3)), the Lorentz force acceleration can be evaluated as
can be estimated using some solar wind model (e.g., Eq. (3)), the Lorentz force acceleration can be evaluated as
![]() ,
where
g(R)=274/R2.
,
where
g(R)=274/R2.
Note that by using
g(R)=274/R2 we neglect the buoyancy - assuming
![]() one gets for the net acceleration of gravity
one gets for the net acceleration of gravity
![]() .
The value of
.
The value of ![]() inferred by using g can be considered as an upper limit. Another drawback of the procedure lies in the fact that faster CMEs have on average larger
inferred by using g can be considered as an upper limit. Another drawback of the procedure lies in the fact that faster CMEs have on average larger ![]() .
So, the slope of the a-v correlation would be altered since g(R) decreases: the influence of g is, statistically, smaller at larger velocities and the a-v correlation becomes less steep (
.
So, the slope of the a-v correlation would be altered since g(R) decreases: the influence of g is, statistically, smaller at larger velocities and the a-v correlation becomes less steep (![]() decreases). Analogously if
decreases). Analogously if
![]() decreases, the a-v correlation becomes steeper. In principle, it would be possible to perform an iterative procedure to estimate more precisely
decreases, the a-v correlation becomes steeper. In principle, it would be possible to perform an iterative procedure to estimate more precisely
![]() ,
but bearing in mind the accuracy of the observational input and other drawbacks of the applied procedure (see Appendix B), such a treatment would be exaggerated.
,
but bearing in mind the accuracy of the observational input and other drawbacks of the applied procedure (see Appendix B), such a treatment would be exaggerated.
For the matter of illustration, let us first take
![]()
![]() 10-3 s-1 and v0=350-400 km s-1 ("average'' values from Table 1). Using
10-3 s-1 and v0=350-400 km s-1 ("average'' values from Table 1). Using
![]() km s-1 at
km s-1 at
![]() as obtained from Eq. (3), one finds
as obtained from Eq. (3), one finds
![]() -150 km s-1. Utilizing these values one receives
-150 km s-1. Utilizing these values one receives
![]() -3 m s-2, i.e.,
-3 m s-2, i.e.,
![]() m s-2, since
gR=9=3.4 m s-2.
m s-2, since
gR=9=3.4 m s-2.
Let us now evaluate
![]() using the differences
using the differences
![]() and slopes
and slopes
![]() for all individual R-bins considered in Sects. 3. and 4.
for all individual R-bins considered in Sects. 3. and 4.
The outcome is shown in Fig. 6b for all subsets that are utilized in
Fig. 6a. Bearing in mind all drawbacks of the procedure, one can say that the
propelling-force acceleration, i.e., the propelling force per unit mass, at
![]() amounts
to
amounts
to
![]() 5-10 m s
5-10 m s
![]() -10 N kg-1. The data show a decreasing trend which can be roughly expressed as
-10 N kg-1. The data show a decreasing trend which can be roughly expressed as ![]() R-1. The values based on the velocity v3 are larger than those obtained by using
R-1. The values based on the velocity v3 are larger than those obtained by using ![]() .
This is primarily a result of the steeper slope
.
This is primarily a result of the steeper slope ![]() and somewhat larger v0 of the a-v3 correlation (Sect. 5.1).
and somewhat larger v0 of the a-v3 correlation (Sect. 5.1).
Let us note that using the isothermal (T=106 K) solar wind model by Parker (1958; see
also Mann et al. 2003) instead of Eq. (3), one gets a 30-50% larger ax(resulting in 10-30% larger ![]() ), but the slope of ax(R) remains approximately R-1.
), but the slope of ax(R) remains approximately R-1.
We emphasize the statistical nature of Fig. 6b, i.e., it does not represent an
average behaviour of the propelling force
![]() in a "typical'' CME. It rather shows that the propelling force is on average weaker at larger distances, being consistent with the anticipated
behaviour of the Lorentz force (Sect. 1).
in a "typical'' CME. It rather shows that the propelling force is on average weaker at larger distances, being consistent with the anticipated
behaviour of the Lorentz force (Sect. 1).
There is also another way to estimate the quantity
![]() .
The drag acceleration for a given CME can be evaluated from
.
The drag acceleration for a given CME can be evaluated from
![]() by substituting the velocity
by substituting the velocity
![]() ,
v3, or v5, and the model-value
,
v3, or v5, and the model-value
![]() .
For estimating
.
For estimating ![]() one can take the empirical scaling law
one can take the empirical scaling law
![]() s-1 found by a different procedure by Vrsnak (2001a). Finally, using the measured values
s-1 found by a different procedure by Vrsnak (2001a). Finally, using the measured values ![]() and
and
![]() one can estimate
one can estimate ![]() for each event individually.
for each event individually.
The calculated values ![]() are shown in Fig. 8a as a function
of v3 (a similar outcome is also found using
are shown in Fig. 8a as a function
of v3 (a similar outcome is also found using ![]() or v5).
The overall anticorrelation pattern in Fig. 8a is similar to that exposed
by Fig. 1, justifying the proposed interpretation in terms of the
drag force, and on the other hand confirming reliability of the empirical scaling law
or v5).
The overall anticorrelation pattern in Fig. 8a is similar to that exposed
by Fig. 1, justifying the proposed interpretation in terms of the
drag force, and on the other hand confirming reliability of the empirical scaling law
![]() obtained by Vrsnak (2001a). The slopes of the linear fits in Figs. 8a and 1 are similar, whereas there is a difference in the x-axis intercept v0. The
linear fit in Fig. 8a crosses the x-axis at
obtained by Vrsnak (2001a). The slopes of the linear fits in Figs. 8a and 1 are similar, whereas there is a difference in the x-axis intercept v0. The
linear fit in Fig. 8a crosses the x-axis at
![]() km s-1, i.e., it is
lower for
km s-1, i.e., it is
lower for
![]() km s-1. Again, this can be attributed to the existence of
ax>0. Taking for the slope of the
km s-1. Again, this can be attributed to the existence of
ax>0. Taking for the slope of the
![]() correlation
correlation
![]()
![]() 10-3 s-1 (see the fit in Fig. 8a) one finds
10-3 s-1 (see the fit in Fig. 8a) one finds
![]() m s-2, and assuming
m s-2, and assuming
![]() one receives
one receives
![]() m s-2, consistent with the previous estimates.
m s-2, consistent with the previous estimates.
Another difference found in Figs. 1 and 8a is a considerably larger scatter of the
data in Fig. 1. Firstly, this can be attributed to a variety of the propelling force
strengths. Furthermore, the differences in CME widths are not included in the evaluation of ![]() since the used scaling law by Vrsnak (2001a) does not provide that. Finally, note that in the low-velocity regime, v<150 km s-1, the accelerations appear in Fig. 8a down to
since the used scaling law by Vrsnak (2001a) does not provide that. Finally, note that in the low-velocity regime, v<150 km s-1, the accelerations appear in Fig. 8a down to
![]() m s-2, whereas in Fig. 1 (see also Fig. 5) the upper edge of the void is at a=0. Such a difference is also consistent with the previous estimates of the propelling force.
m s-2, whereas in Fig. 1 (see also Fig. 5) the upper edge of the void is at a=0. Such a difference is also consistent with the previous estimates of the propelling force.
In Fig. 8b we compare the distributions
![]() and
and
![]() for the n6v3-subset (see also the the distribution of measured accelerations,
for the n6v3-subset (see also the the distribution of measured accelerations,
![]() shown in Fig. 10f in Appendix A). In addition, we present in the inset the distribution N(g), where
shown in Fig. 10f in Appendix A). In addition, we present in the inset the distribution N(g), where
![]() .
Mean values are:
.
Mean values are:
![]()
![]() 9.7 m s-2,
9.7 m s-2,
![]()
![]() 13.9 m s-2, and
13.9 m s-2, and
![]()
![]() 4.6 m s-2, which explains why CMEs
in the upper corona and near-Sun interplanetary space show on average
4.6 m s-2, which explains why CMEs
in the upper corona and near-Sun interplanetary space show on average
![]() (Appendix A). We emphasize that very similar distributions are obtained utilizing any other subset
or velocity option. The drag acceleration is dominantly negative, i.e., most events are faster than
the solar wind. On the other hand, in the majority of events,
(Appendix A). We emphasize that very similar distributions are obtained utilizing any other subset
or velocity option. The drag acceleration is dominantly negative, i.e., most events are faster than
the solar wind. On the other hand, in the majority of events, ![]() lies between 0 and 20 m s-2, consistent with Fig. 6b. The distribution indicates that there is a
considerable fraction (18%) of events where
lies between 0 and 20 m s-2, consistent with Fig. 6b. The distribution indicates that there is a
considerable fraction (18%) of events where ![]() appears to be larger than 20 m s-2 (see also Vrsnak 2001b). In extreme cases (2%)
appears to be larger than 20 m s-2 (see also Vrsnak 2001b). In extreme cases (2%) ![]() is larger than 50 m s-2 (to be studied in detail in a separate paper). In 17% of events the inferred values of
is larger than 50 m s-2 (to be studied in detail in a separate paper). In 17% of events the inferred values of ![]() are negative, with 5% showing
are negative, with 5% showing
![]() m s-2. Note that the
m s-2. Note that the
![]() regime is revealed by the "fall-back'' events described by Wang & Sheeley (2002) and by the existence of an upper equilibrium observed in some events (Vrsnak et al. 1990; Vrsnak 2001b). Such a behaviour is anticipated in the flux rope model by Vrsnak (1990).
regime is revealed by the "fall-back'' events described by Wang & Sheeley (2002) and by the existence of an upper equilibrium observed in some events (Vrsnak et al. 1990; Vrsnak 2001b). Such a behaviour is anticipated in the flux rope model by Vrsnak (1990).
Finally, let us emphasize one potentially important side-result of the presented analysis. None of the presented graphs (including those in Appendix A) shows any kind of grouping of CMEs that would confirm the existence of two (or more) distinct classes of events regarding the velocity and/or acceleration behaviour, as proposed by some authors who studied small samples of preferentially large CMEs (see, e.g., MacQueen & Fisher 1983, or Andrews & Howard 2001). Rather, the distribution of CMEs in the a-v space indicates that there is a continuum of events over the actual acceleration and velocity range.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0169f8.eps}
\end{figure}](/articles/aa/full/2004/32/aa0169-04/Timg265.gif) |
Figure 8:
a) Drag accelerations estimated using |
| Open with DEXTER | |
Values of the exponent ![]() in the
in the
![]() scaling received in
Sect. 4.1, can be directly compared with the result by Vrsnak (2001a) since the
scaling received in
Sect. 4.1, can be directly compared with the result by Vrsnak (2001a) since the
![]() -
- ![]() crosstalk was implicitly present therein too. The obtained values
crosstalk was implicitly present therein too. The obtained values
![]() -3.1 are larger than
-3.1 are larger than
![]() found by Vrsnak (2001a), indicating a
considerably steeper decrease of
found by Vrsnak (2001a), indicating a
considerably steeper decrease of ![]() .
However, it should be noted that the results by Vrsnak (2001a) were based on a limited set of only 12 events, all of which showed an
exponential-like decay of velocity, indicating that the drag is a dominant force. Furthermore,
seven of these events were measured at low heights by tracing H
.
However, it should be noted that the results by Vrsnak (2001a) were based on a limited set of only 12 events, all of which showed an
exponential-like decay of velocity, indicating that the drag is a dominant force. Furthermore,
seven of these events were measured at low heights by tracing H![]() features, i.e., the
deceleration rates could be higher for leading edges of CMEs.
features, i.e., the
deceleration rates could be higher for leading edges of CMEs.
In Fig. 9 we compare the slopes of the a-v correlations obtained herein with the
scaling law
![]() established by Vrsnak (2001a), and with the results for the
interplanetary space obtained by Gopalswamy et al. (2000) and Gopalswamy et al.
(2001b). The values for the complete n4v3-subset and n6v3-subset are positioned at
established by Vrsnak (2001a), and with the results for the
interplanetary space obtained by Gopalswamy et al. (2000) and Gopalswamy et al.
(2001b). The values for the complete n4v3-subset and n6v3-subset are positioned at
![]() and overlap each other. The slopes from Gopalswamy et al. (2000) and Gopalswamy et al. (2001b) are drawn at R=40 and R=46, respectively, corresponding to
the geometrical mean (see the argumentation in Vrsnak 2001a) of the considered distance
ranges (0.76 and 1 au, respectively). The fit through the presented data-points matches quite
closely to the scaling
k1 = 2 R-1.5 that was inferred by Vrsnak & Gopalswamy
(2002) from the Sun-Earth transit times.
and overlap each other. The slopes from Gopalswamy et al. (2000) and Gopalswamy et al. (2001b) are drawn at R=40 and R=46, respectively, corresponding to
the geometrical mean (see the argumentation in Vrsnak 2001a) of the considered distance
ranges (0.76 and 1 au, respectively). The fit through the presented data-points matches quite
closely to the scaling
k1 = 2 R-1.5 that was inferred by Vrsnak & Gopalswamy
(2002) from the Sun-Earth transit times.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{0169f9.eps}
\end{figure}](/articles/aa/full/2004/32/aa0169-04/Timg270.gif) |
Figure 9:
The slopes
|
| Open with DEXTER | |
Figure 8b indicates that in the R=2-30 range the majority of events has already more or
less adjusted to the solar wind speed since the
![]() distribution (Fig. 8) is sharply peaked at
distribution (Fig. 8) is sharply peaked at
![]() .
A similar conclusion can be drawn from Fig. 1a, since most events are grouped around a=0,
.
A similar conclusion can be drawn from Fig. 1a, since most events are grouped around a=0,
![]() km s-1.
km s-1.
Let us now inspect the distribution of speeds ![]() estimated at the time of last measurement (see Sect. 2) for the events that were traced to
estimated at the time of last measurement (see Sect. 2) for the events that were traced to
![]() .
We find that only 374 out of 4463 n4v3-events (8%) had
.
We find that only 374 out of 4463 n4v3-events (8%) had
![]() km s-1. The number of events with velocities above some referent value,
km s-1. The number of events with velocities above some referent value,
![]() ,
decreases as we increase the limit v*. The events with
,
decreases as we increase the limit v*. The events with
![]() are on average much broader than the rest of the sample. Furthermore, they show a positive mean acceleration, being statistically larger for faster (and broader) CMEs. The n4v3-subset statistics is summarized in Table 4 for different values of v*. The number (N) and the percentage (%) of the v>v* events is presented in the 2nd and 3rd column. The values in brackets provide the number (and relative percentage) of
are on average much broader than the rest of the sample. Furthermore, they show a positive mean acceleration, being statistically larger for faster (and broader) CMEs. The n4v3-subset statistics is summarized in Table 4 for different values of v*. The number (N) and the percentage (%) of the v>v* events is presented in the 2nd and 3rd column. The values in brackets provide the number (and relative percentage) of
![]() events. The average values of widths and accelerations are given in the last two columns. Note that more than half of the
events. The average values of widths and accelerations are given in the last two columns. Note that more than half of the
![]() events are characterized by
events are characterized by
![]() .
In some cases it is larger than
.
In some cases it is larger than
![]() m s-2.
m s-2.
Table 4:
Statistics of CMEs faster than solar wind at ![]() .
.
Such a behaviour has important implications for the prediction of the 1 au transit. In most CMEs
the propelling force ceases, and the velocity becomes adjusted to the solar wind speed, already
below R=30. The arrival of these events to the Earth (if they preserve their integrity) can be
estimated to a sufficient accuracy utilizing the
![]() km s-1 approximation.
However, for very fast/wide CMEs, which in fact are the most geo-effective events (Zhang et al. 2003), the prediction based on LASCO observations is more difficult since the action of
the propelling force is prolonged in such events. To be successful in predicting the 1 au
transit, a higher degree polynomial fit to the R(t) LASCO-data should be tried, to estimate if
possible, how the acceleration changes. This might give a clue whether the event had entered the
drag-dominated regime or not. If yes, the interplanetary motion of the CME should be calculated
using the velocity at R=30 as the initial velocity and utilizing the scaling
km s-1 approximation.
However, for very fast/wide CMEs, which in fact are the most geo-effective events (Zhang et al. 2003), the prediction based on LASCO observations is more difficult since the action of
the propelling force is prolonged in such events. To be successful in predicting the 1 au
transit, a higher degree polynomial fit to the R(t) LASCO-data should be tried, to estimate if
possible, how the acceleration changes. This might give a clue whether the event had entered the
drag-dominated regime or not. If yes, the interplanetary motion of the CME should be calculated
using the velocity at R=30 as the initial velocity and utilizing the scaling
![]() for
the corresponding
for
the corresponding ![]() -bin. Then, the equation of motion given by Eq. (1) should be
solved numerically, in the manner demonstrated by Vrsnak & Gopalswamy (2002). Note
that events of this kind should have the smallest deceleration rates since they are broad, which
implies a relatively small
-bin. Then, the equation of motion given by Eq. (1) should be
solved numerically, in the manner demonstrated by Vrsnak & Gopalswamy (2002). Note
that events of this kind should have the smallest deceleration rates since they are broad, which
implies a relatively small ![]() .
.
The prolonged action of the propelling force in fast/wide CMEs is consistent with the observations
based on the interplanetary scintillation (IPS). For example, Manoharan et al. (2001) have
analysed the IP propagation of the CME associated with the large flare of 14 July 2000. Until
![]() the speed of ejection was almost constant (
the speed of ejection was almost constant (
![]() ), and only beyond
this distance it started decelerating more rapidly, as
), and only beyond
this distance it started decelerating more rapidly, as
![]() .
In such cases, the
Thompson scattering measurements by the Solar Mass Ejection Imager (SMEI) combined with IPS observations (Jackson et al. 2003; Eyles et al. 2003) could be essential for the understanding of the IP propagation of CMEs and a successful prediction of 1 au transit time.
.
In such cases, the
Thompson scattering measurements by the Solar Mass Ejection Imager (SMEI) combined with IPS observations (Jackson et al. 2003; Eyles et al. 2003) could be essential for the understanding of the IP propagation of CMEs and a successful prediction of 1 au transit time.
We have shown that there is a well defined anticorrelation between the acceleration and velocity of CMEs measured in the range 2<R<30. The relationship can be comprehended as the statistical outcome for a sample of CMEs whose motion is significantly influenced by the aerodynamic drag: Only 14% of fast (v3>1000 km s-1) CMEs are still speeding up, and 7% of slow CMEs (v3<150 km s-1) show (only a weak) deceleration.
However, the existence of fast events whose velocity is still increasing suggests that in a certain
fraction of events the propelling force is not negligible. On the other hand, the deceleration of
slow events, and existence of the
![]() events in the
events in the
![]() distribution (Fig. 8b)
indicates that the deceleration in these events could be caused not only by the gravity, but also
by the Lorentz force (see also Wang & Sheeley 2002), which under special conditions might
change its sign after passing an upper equilibrium point (Vrsnak 1990).
distribution (Fig. 8b)
indicates that the deceleration in these events could be caused not only by the gravity, but also
by the Lorentz force (see also Wang & Sheeley 2002), which under special conditions might
change its sign after passing an upper equilibrium point (Vrsnak 1990).
The overall behaviour of the parameter ![]() ,
decreasing with the distance and being of the
order of 0.1
,
decreasing with the distance and being of the
order of 0.1 ![]() 10-6 km-1 at
10-6 km-1 at
![]() ,
is very similar to that obtained by Vrsnak (2001a). In addition, we found herein that the value of
,
is very similar to that obtained by Vrsnak (2001a). In addition, we found herein that the value of ![]() is smaller for broader CMEs when measured at the same
is smaller for broader CMEs when measured at the same ![]() .
On the other hand, the slope of the linear a-v correlation at
.
On the other hand, the slope of the linear a-v correlation at
![]() ranges between
ranges between
![]() -0.03
-0.03 ![]() 10-3 s-1, which is smaller by roughly a factor of two than found by Vrsnak (2001a).
10-3 s-1, which is smaller by roughly a factor of two than found by Vrsnak (2001a).
The results indicate that in the majority of events the
![]() regime is achieved already in
the LASCO field-of-view, i.e., below R<30. Only CMEs with prolonged action of the propelling
force come into the
regime is achieved already in
the LASCO field-of-view, i.e., below R<30. Only CMEs with prolonged action of the propelling
force come into the
![]() regime beyond R>30, but the events with, e.g.,
v>500 km s-1 at R>25 represent less than 10% of the CME population.
regime beyond R>30, but the events with, e.g.,
v>500 km s-1 at R>25 represent less than 10% of the CME population.
Acknowledgements
We are grateful to the LASCO-SOHO team for operating the instruments and performing the basic data reduction, and especially, for the open data policy.
![\begin{figure}
\par\includegraphics[width=11.25cm,clip]{0169f10.eps}
\end{figure}](/articles/aa/full/2004/32/aa0169-04/Timg285.gif) |
Figure 10:
Distribution of CME parameters in the n4v3-subset:
a) initial radial distances |
| Open with DEXTER | |
The events which were measured at ![]() instants, show the distribution centered at
instants, show the distribution centered at
![]() ,
with the standard deviation
,
with the standard deviation
![]() m s-2. The average initial, mean, and final distances amount to
m s-2. The average initial, mean, and final distances amount to
![]()
![]() 1.0,
1.0,
![]()
![]() 4, and
4, and
![]()
![]() 7, respectively.
7, respectively.
In Fig. 10 we present the distribution of initial radial distances ![]() ,
the distance range
,
the distance range
![]() ,
mean radial distances
,
mean radial distances ![]() ,
widths
,
widths ![]() ,
mean velocities
,
mean velocities ![]() ,
and mean accelerations
,
and mean accelerations ![]() ,
for the n4v3-subset. Note that most often the events start at
,
for the n4v3-subset. Note that most often the events start at ![]() .
The n4v3-subset contains 280 CME events (6%) of the angular width larger than
.
The n4v3-subset contains 280 CME events (6%) of the angular width larger than
![]() ,
out of which 184 were classified as
,
out of which 184 were classified as
![]() -halo CMEs (4%). The basic statistical parameters of the distributions are given in Table 5.
-halo CMEs (4%). The basic statistical parameters of the distributions are given in Table 5.
The average error of the accelerations obtained from the 2nd degree polynomial fits is
![]() m s-2 in the n4-set, and it drops to 4.7 m s-2 in the n6-set. The fraction of events with errors
m s-2 in the n4-set, and it drops to 4.7 m s-2 in the n6-set. The fraction of events with errors
![]() m s-2 is 18% and 10% for the two data-sets, respectively.
m s-2 is 18% and 10% for the two data-sets, respectively.
The parameters ![]() ,
,
![]() ,
and
,
and ![]() are mutually correlated (see also, e.g., Hundhausen et al. 1994), which is shown in Fig. 11, where the data are presented together with the linear least squares fits and corresponding correlation coefficients (C). We emphasize that the
are mutually correlated (see also, e.g., Hundhausen et al. 1994), which is shown in Fig. 11, where the data are presented together with the linear least squares fits and corresponding correlation coefficients (C). We emphasize that the
![]() correlation does not represent the broadening of CMEs with the height, but rather demonstrates that larger CMEs can be traced to larger distances, i.e., that broader CMEs are generally brighter. Similar holds also for the
correlation does not represent the broadening of CMEs with the height, but rather demonstrates that larger CMEs can be traced to larger distances, i.e., that broader CMEs are generally brighter. Similar holds also for the
![]() relationship - faster CMEs are on average brighter and can be followed to larger heights. No statistically significant correlation between
relationship - faster CMEs are on average brighter and can be followed to larger heights. No statistically significant correlation between ![]() and
and ![]() ,
or
,
or ![]() is found (C<0.01).
is found (C<0.01).
The basic characteristics shown in Figs. 10 and 11 are very similar for all of the considered subsets and velocity options.
The main problem included implicitly in the performed analysis is that Eq. (1) relates the
instantaneous acceleration, a, with the instantaneous velocity, v, whereas the
measurements provide only the mean acceleration ![]() estimated over a wide distance range,
estimated over a wide distance range, ![]() .
Consequently, it would be erroneous to expect ad hoc that the measured mean acceleration
is simply related to the mean speed, even if the drag is the dominant force in the considered
distance range. Since this issue can cause a systematic error, we have to clarify its influence.
.
Consequently, it would be erroneous to expect ad hoc that the measured mean acceleration
is simply related to the mean speed, even if the drag is the dominant force in the considered
distance range. Since this issue can cause a systematic error, we have to clarify its influence.
In Fig. 12a the drag-dominated a(v)-trajectory of one a<0 event is sketched in details.
The velocity of CME at the beginning of measurement is denoted at the x-axis by "b'' and at the
end by "e''. The mean velocity ![]() ,
defined in the
,
defined in the
![]() approximation as
approximation as
![]() ,
is marked by "m''. The mean acceleration, in the
,
is marked by "m''. The mean acceleration, in the
![]() approximation equivalent to
approximation equivalent to
![]() ,
is depicted by the horizontal dashed line. If the solar wind speed and
the parameter
,
is depicted by the horizontal dashed line. If the solar wind speed and
the parameter ![]() are taken in the first approximation to be constant, the CME-trajectory
(bold-dotted arrow) would follow the a(v) line defined by
are taken in the first approximation to be constant, the CME-trajectory
(bold-dotted arrow) would follow the a(v) line defined by ![]() and
and
![]() .
However, as the CME advances, the ambient solar wind speed increases whereas
.
However, as the CME advances, the ambient solar wind speed increases whereas ![]() decreases (Vrsnak
2001; see also Sects. 4.2 and 5.2). Consequently, the CME "slides'' across a(v)-curves,
ending at the one defined by
decreases (Vrsnak
2001; see also Sects. 4.2 and 5.2). Consequently, the CME "slides'' across a(v)-curves,
ending at the one defined by ![]() and
and
![]() ,
as sketched by the bold arrow. Note that the line depicting the mean acceleration intersects the bold arrow at the velocity v different from
,
as sketched by the bold arrow. Note that the line depicting the mean acceleration intersects the bold arrow at the velocity v different from ![]() .
Furthermore, note that the intercept of the
.
Furthermore, note that the intercept of the ![]() and
and ![]() line is below both depicted a(v)-curves, i.e., it lies on a curve of too large
line is below both depicted a(v)-curves, i.e., it lies on a curve of too large ![]() ,
corresponding to some distance smaller than
,
corresponding to some distance smaller than ![]() .
On the other hand, the intercept of the
.
On the other hand, the intercept of the ![]() line with
line with ![]() is located between the "initial'' and "final'' a(v)-curve, i.e., it is associated with
is located between the "initial'' and "final'' a(v)-curve, i.e., it is associated with ![]() corresponding to some distance between
corresponding to some distance between ![]() and
and ![]() ,
presumably close to
,
presumably close to ![]() .
.
Table 5: Statistical characteristics of the n4v3-subset and (n6v3-subset).
If we want to inspect quantitatively the effect sketched in Fig. 12a, it is instructive to
consider firstly what mean acceleration would be measured if an object would move according to
Eq. (1) in a homogeneous medium (
![]() ,
,
![]() ;
depicted by the
bold-dashed arrow in Fig. 12a). The mean acceleration of the object, evaluated from the 2nd order polynomial fit to the distance-time data can be expressed, by definition, as:
;
depicted by the
bold-dashed arrow in Fig. 12a). The mean acceleration of the object, evaluated from the 2nd order polynomial fit to the distance-time data can be expressed, by definition, as:
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0169f11.eps}
\end{figure}](/articles/aa/full/2004/32/aa0169-04/Timg309.gif) |
Figure 11:
Relation between different CME parameters in the n4v3-subset:
a)
|
| Open with DEXTER | |
The solution of Eq. (1) in the case
![]() reads:
reads:
Actually, if ![]() increases,
increases,
![]() increases too, which means that
increases too, which means that ![]() decreases (Sect. 4). Thus, the two effects partly compensate each other. In Fig. 12b we show the deviation X as a function of
decreases (Sect. 4). Thus, the two effects partly compensate each other. In Fig. 12b we show the deviation X as a function of ![]() .
In evaluating
.
In evaluating
![]() we have used
we have used
![]() as given by Eq. (3), and
as given by Eq. (3), and
![]() estimated utilizing the two scalings displayed in the bottom panel of Fig. 4b (
estimated utilizing the two scalings displayed in the bottom panel of Fig. 4b (
![]()
![]() 10-6R-2 and
10-6R-2 and
![]()
![]() 10-6R-0.98).
10-6R-0.98).
Note that in the considered approximation, in most of events (
![]() ;
see Appendix A) the value of
;
see Appendix A) the value of
![]() is underestimated for not more than 50% with respect to
is underestimated for not more than 50% with respect to ![]() .
.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0169f12.eps}
\end{figure}](/articles/aa/full/2004/32/aa0169-04/Timg330.gif) |
Figure 12:
a) Comparison of the a(v)-trajectory of an event moving in the
|
| Open with DEXTER | |
Let us now consider the more realistic situation, where the wind speed and density, as well as the
dimensions and density of CME, depend on the radial distance, so w and ![]() are functions
of R. We presume that w(R) increases, whereas
are functions
of R. We presume that w(R) increases, whereas
![]() decreases.
decreases.
We performed a series of numerical simulations from which we estimated ![]() to determine how much the approximate value
to determine how much the approximate value
![]() differs from the true
differs from the true
![]() .
Again we used the two
.
Again we used the two
![]() scalings from the bottom panel of Fig. 4b, combined with the solar wind model given by Eq. (3). The results are illustrated by Fig. 12c, revealing a complex situation. The deviation X is generally X<1, but it can also be X>1, i.e.,
scalings from the bottom panel of Fig. 4b, combined with the solar wind model given by Eq. (3). The results are illustrated by Fig. 12c, revealing a complex situation. The deviation X is generally X<1, but it can also be X>1, i.e.,
![]() can be overestimated (see also the explanation of
Fig. 12a). The later case is more pronounced for larger values of the exponent
can be overestimated (see also the explanation of
Fig. 12a). The later case is more pronounced for larger values of the exponent ![]() in
the
in
the
![]() scaling. When
scaling. When ![]() is considered instead of
is considered instead of ![]() ,
the value of
,
the value of
![]() is always overestimated. For this reason in the previous analysis (Sects. 3 and 4) we relied more on the velocity v3 than on
is always overestimated. For this reason in the previous analysis (Sects. 3 and 4) we relied more on the velocity v3 than on ![]() .
Note that weak-acceleration events are not affected much by the choice of v3 or
.
Note that weak-acceleration events are not affected much by the choice of v3 or ![]() .
.
Finally, we stress another important aspect of employing the velocity v3. Considering what
happens in the a-v graph when the
![]() data are replaced by
data are replaced by
![]() ,
one finds that the usage of v3 shifts the
,
one finds that the usage of v3 shifts the
![]() events to lower velocities (to the left in the graph), and
events to lower velocities (to the left in the graph), and
![]() events to higher velocities (to the right). This would tend to decrease the slope of the a-v correlation if only the drag force dominated events would be present (see the explanation of Fig. 12a). However, a compensating effect appears at large velocities where we find also the events with large
events to higher velocities (to the right). This would tend to decrease the slope of the a-v correlation if only the drag force dominated events would be present (see the explanation of Fig. 12a). However, a compensating effect appears at large velocities where we find also the events with large
![]() (presumably those whose motion is still governed by the propelling force). These events, which tend to smear the correlation and decrease
(presumably those whose motion is still governed by the propelling force). These events, which tend to smear the correlation and decrease
![]() ,
are shifted to the left towards v0, which reduces their influence in the a(v) fitting. This is a reason reason why the
,
are shifted to the left towards v0, which reduces their influence in the a(v) fitting. This is a reason reason why the
![]() relationship shows higher correlation coefficients than
relationship shows higher correlation coefficients than
![]() relationship and a steeper slope
relationship and a steeper slope ![]() .
.
| |
Figure 13:
The fitted
|
| Open with DEXTER | |
In conclusion, let us note that Eq. (10) provides another possibility to estimate
![]() scaling, different from that performed in Sect. 4. Combining the observed values
scaling, different from that performed in Sect. 4. Combining the observed values ![]() ,
,
![]() ,
and
,
and ![]() ,
with the model values for the solar wind speed
,
with the model values for the solar wind speed
![]() and
and
![]() as given by Eq. (3), one can estimate:
as given by Eq. (3), one can estimate: