A&A 423, 33-47 (2004)
DOI: 10.1051/0004-6361:20035856

XMM-Newton observation of the relaxed cluster A478: Gas and dark matter distribution from 0.01R200 to 0.5R200

E. Pointecouteau 1 - M. Arnaud 1 - J. Kaastra 2 - J. de Plaa 2


1 - Service d'Astrophysique du CEA, L'Orme des Merisiers, Bât. 709, 91191 Gif-sur-Yvette, France
2 - SRON, Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands

Received 12 December 2003 / Accepted 5 March 2004

Abstract
We present an XMM-Newton mosaic observation of the hot ($kT\sim6.5$ keV) and nearby (z=0.0881) relaxed cluster of galaxies A478. We derive precise gas density, gas temperature, gas mass and total mass profiles up to  $12\hbox{$^\prime$ }$ (about half of the virial radius R200). The gas density profile is highly peaked towards the center and the surface brightness profile is well fitted by a sum of three $\beta$-models. The derived gas density profile is in excellent agreement, both in shape and in normalization, with the published Chandra density profile (measured within  $5\hbox{$^\prime$ }$ of the center). Projection and PSF effects on the temperature profile determination are thoroughly investigated. The derived radial temperature structure is as expected for a cluster hosting a cooling core, with a strong negative gradient at the cluster center. The temperature rises from $\sim$2 keV up to a plateau of $\sim$6.5 keV beyond  $2\hbox{$^\prime$ }$ (i.e. $r>208~{\rm kpc}=0.1~R_{200}$,  R200=2.08 Mpc being the virial radius). From the temperature profile and the density profile and on the hypothesis of hydrostatic equilibrium, we derived the total mass profile of A478 down to 0.01 and up to 0.5 times the virial radius. We tested different dark matter models against the observed mass profile. The Navarro et al. (1997) model is significantly preferred to other models. It leads to a total mass of  $M_{200}=1.1\times 10^{15}~M_\odot$ for a concentration parameter of  $c=4.2\pm0.4$. The gas mass fraction increases slightly with radius. The gas mass fraction at a density contrast of  $\delta=2500$ is  $f_{\rm gas}=0.13\pm0.02$, consistent with previous results on similar hot and massive clusters. We confirm the excess of absorption in the direction of A478. The derived absorbing column density exceeds the 21 cm measurement by a factor of $\sim$2, this excess extending well beyond the cool core region. Through the study of this absorbing component and a cross correlation with infrared data, we argue that the absorption excess is of Galactic origin, rather than intrinsic to the cluster.

Key words: galaxies: clusters: individual: A478 - galaxies: intergalacic medium - cosmology: observations - cosmology: dark matter - X-rays: galaxies: clusters

1 Introduction

As nodes of large scale structure and thus places of dark matter concentration, galaxy clusters can be used as powerful tools to test theories of structure formation. The basic hierarchical scenarios based on gravitation make the population of galaxy clusters a homologous population of sources. Their physical properties follow scaling laws depending only on their redshift and mass, and their internal structures are similar.

The exceptional capabilities of XMM-Newton in terms of sensitivity and of Chandra in term of spatial resolution allow us to characterize the gas density and temperature profiles with unprecedented accuracy. For a relaxed cluster, the hydrostatic equations can be used to derive the underlying dark matter distribution, from the very central part of clusters up to nearly the virial radius (David et al. 2001; Allen et al. 2001b; Arabadjis et al. 2002; Allen et al. 2002a; Pratt & Arnaud 2002, 2003; Lewis et al. 2003; Buote & Lewis 2003). The observed clusters seem to have a cusped dark matter profile as predicted by numerical simulations (Navarro et al. 1997, hereafter NFW; Moore et al. 1999, hereafter MQGSL). However, the central slope of the dark matter profile and the possible dispersion of the concentration parameter remain open issues. Larger samples of high quality mass profiles are needed to further assess these points.

In this paper we present the XMM-Newton spectro-imaging observation of A478, a massive, relaxed nearby cluster (z=0.0881 - Struble & Rood 1999). Detected in surveys (UHURU, HEAO-1, Ariel-V), this cluster is well known in X-rays and its physical properties have been carefully studied with previous X-ray observatories: EXOSAT (Edge & Stewart 1991), Einstein and Ginga (Johnstone et al. 1992), ROSAT (Allen et al. 1993; White et al. 1994) and ASCA (Markevitch 1998; White et al.  2000). All those previous studies converge for what concerns the overall temperature of the cluster,  $kT \sim 6.8$ keV. Recently, Sun et al. (2003) performed a high angular resolution study of the central part of the cluster with Chandra. They pointed out the presence of an X-ray cavity in the very central part of the cluster which is anti-correlated with the radio lobes.

Here we focus on the characterization of the gas and dark matter distribution of A478. In a companion paper de Plaa et al. (2004) present a detailed spectroscopic study of the metal abundances and their distribution within A478's core based on EPIC and RGS data. We present the observation and the different data processing steps in Sect. 2. In Sect. 3 we briefly discuss the cluster morphology. In Sect. 4 we analyze the surface brightness profile and derive the gas density profile. Spatially resolved spectroscopic analysis is presented in Sect. 5, where we also discuss the temperature and absorption profiles. In Sect. 6, we present the resulting total mass and gas mass fraction profiles of A478 and we discuss the shape of the dark matter profile according to our observational results.

Throughout this paper, we use H0=70 km Mpc-1 s-1, $\Omega_{\rm m}=0.3$ and  $\Omega_{\Lambda}=0.7$. In such a cosmological framework, at the cluster redshift (z=0.0881)  $1\hbox{$^\prime$ }=99$ kpc.

   
2 XMM-Newton observations and data processing

2.1 Observations

A478 was observed with XMM-Newton during revolution 401 for a total exposure time of 126 ks with the EMOS camera and 122 ks with the EPN camera. For the first 70 ks two CCDs ($CCD \char93 4$ and $\char93 7$) of the EMOS1 camera were not operating. An offset observation, centered at $\alpha=$ 04$^{\rm h}$12$^{\rm m}$35$^{\rm s}$, $\delta=$ 10$^\circ$15'45'',  $17\hbox{$^\prime$ }$ South West of the cluster center, was performed in revolution 401 for 38 ks (EMOS camera) and 34 ks (EPN camera). All observations were performed in EXTENDED FULL FRAME mode and using the THIN1 filter. We used the calibrated events list produced by the XMM-Newton SOC pipeline and processed them with the SAS (v5.4.1). We also used the blank-sky event files accumulated by Lumb et al. (2002).

2.2 Event list screening

In this work, we only kept events with pattern 0 to 12 from EMOS data, pattern 0 from EPN data and flag equal 0 for both detectors.

First the event list for each camera and each observation was filtered for periods of high background due to soft proton flares. Visual inspection of the light curve in a source-free energy band ( $[10{-}12]~\rm keV$ for EMOS and  $[12{-}14]~\rm keV$ for EPN) revealed long periods of high background. These were excluded. We then fine-tuned the flare cleaning by using a "3$\sigma $ clipping'' selection of good time intervals as described in Pratt & Arnaud (2003). The Poisson fit of the light curve histogram provides a 3$\sigma $ threshold above which corresponding frames are discarded. To excise all flaring periods, this clipping method was applied in different energy bands:  $[2{-}5]~\rm keV$,  $[5{-}8]~\rm keV$ $[8{-}10]~\rm keV$ and  $[10{-}12]~\rm keV$ for EMOS;  $[5{-}8]~\rm keV$, $[8{-}10]~\rm keV$,  $[10{-}12]~\rm keV$ and  $[12{-}14]~\rm keV$ for EPN. This quite conservative choice was made to avoid any low energy flares that are present in some observations (Pratt & Arnaud 2002).

The remaining exposure times after cleaning are 48.0 ks, 40.9 ks and 37.3 ks for the central pointing and the EMOS1, EMOS2 and EPN camera respectively. The corresponding times for the offset pointing are 13.1 ks for the EMOS camera and 11.0 ks for the EPN camera.


  \begin{figure} \par\includegraphics[width=17.5cm,clip]{fig1.eps} \end{figure} Figure 1: Left panel: total (EMOS+EPN) XMM-Newton mosaic image of A478 in the  $[0.3{-}7]~\rm{keV}$ energy band. The image is corrected for vignetting and exposure, and background subtracted using blank field data. Right panel: hardness ratio map (ratio of the count rates in the  $[1.7{-}7]~\rm keV$ and in the  $[0.3{-}1.7]~\rm keV$ energy bands). The smoothed contours of the mosaic image have been overlaid.
Open with DEXTER

2.3 Extraction of imaging data and spectra

For each camera, we merged the cleaned event lists of the two observations into a single event list. We only selected events falling within a  $15\hbox{$^\prime$ }$ circular region centered on the detector optical axis. The sky pixel coordinates of each event of the offset pointing were re-projected onto the sky pixel grid of the central pointing.

Scientific products (spectra, images, surface brightness profiles) can thus be extracted in a single step from the merged events list, simplifying the analysis. However, the exposure time can vary strongly in a given extraction region and this has to be taken into account in estimating count rates. The extraction method we used is fully described in Appendix A. All the products are corrected for vignetting in this extraction process. The vignetting correction is based on the photon weighting method described in Arnaud et al. (2001), the weight coefficients being tabulated in the event list with the SAS task EVIGWEIGHT.

   
2.4 Background subtraction

For each camera, a clean background event list was extracted from the corresponding blank-field data using the same filtering criteria (pattern and flag selection, 3$\sigma $ flare clipping) as for the observations. Cast-background files were then generated for each pointing by applying the aspect solution of the observation to the background dataset. The correct exposure time was computed for each blank field event list.

To estimate the difference of particle background level between each observation and the corresponding blank field data, we computed the ratio of the total count rates in the high energy band ( $[10{-}12]~\rm keV$ and  $[12{-}14]~\rm keV$ respectively for EMOS and EPN data). As the expected average temperature of this bright cluster is quite high ($\sim$ $6.8~\rm keV$) we excluded a circular central region $(\theta<6\hbox{$^\prime$ })$ to avoid any contamination due to the cluster.

Blank field products have to be normalized by this ratio, when used as a background for the corresponding observation products. The normalizations are slightly different from one pointing to the other. To take that normalization into account, we multiplied the weight coefficients in each cast background file by the corresponding normalization factor. Vignetting-corrected blank field counts are then automatically "normalized''. These cast background files of the two pointings are then merged as for the observations. Product extraction is then the same (see Appendix A).

For the EPN data, we generated a list of out-of-time events (OoT hereafter) to be treated as an additional background component. An OoT event occurs when a photon is detected during the read-out process. The current observing mode (Extended Full Frame) minimizes the effect of OoT to 2.3%. The OoT event list was processed similarly to the observation EPN event files.

The background subtraction (for spectra and surface brightness profiles) is performed as described in full detail in Arnaud et al. (2002). It is a two-step procedure, which insures a correct cosmic X-ray background (CXRB) subtraction, even when the local CRXB is different from the average CRXB in blank field data. In a first step, for each product extracted from the merged observation event list, an equivalent product is extracted from the corresponding merged blank-field file and subtracted from it. For EPN the OoT data are also subtracted. This first step allows us to remove the particle background. However, it may over (under) subtract the CRXB if the CRXB in the observation region is smaller (larger) than the average value in the blank field observation. The residual CXRB (i.e. the difference between the CXRB in the A478 field and in the blank field) is then estimated by using blank field subtracted data in the region free of cluster emission ( $\theta>16\hbox{$^\prime$ }$ from the cluster center - the cluster is significantly detected in the background subtracted surface brightness profile up to 12-13$^\prime$). This residual CRXB is subtracted in a second step from each EMOS and EPN product. In our case the residual is negative in the  $[0.3{-}3]~\rm keV$ energy band. The residual count rate summed over the three detectors is -0.68 counts/s/arcmin2, which represents 23% of the total background count rate in this energy band. Beyond 3 keV the residual background ( $r>16\hbox{$^\prime$ }$) spectrum is consistent with zero. Therefore the double subtraction beyond 3 keV will only contribute increasing the noise level in each channel. To minimize errors, the double subtraction is thus applied only to data in the energy band $[0.3{-}3]~\rm keV$. We nevertheless check (on the global spectrum) that the best fit values remain the same if a full double subtraction is applied.

2.5 Point source exclusion

Starting from the output of the SAS detection source task, we made a visual selection on a wide energy band EMOS & EPN image (extracted from the merged event lists) of point sources in the FOV. Events from these regions were excluded directly from each merged event list. We generated corresponding mask mosaic images, which were then used to compute the surface of each extraction region.

   
3 Cluster morphology

The mosaic count rate image (EMOS+EPN) in the  $[0.3{-}7]~\rm{keV}$ energy band is presented in Fig. 1, together with the hardness ratio map computed from the ratio of the images in the  $[1.7{-}7]~\rm keV$ and  $[0.3{-}1.7]~\rm keV$ energy bands. The images in various energy bands are vignetting corrected and background subtracted using the corresponding blank field image and the OoT image in case of EPN. To generate the hardness ratio map, the hard band image was first adaptively smoothed (with the task ASMOOTH). The soft band image was then smoothed using the same smoothing template as was created for the hard band image. The cluster morphology is regular and the hardness ratio map does not exhibit any peculiar feature, reinforcing the assessment that A478 is a very relaxed cluster.

A478 has an elliptical shape. From optical and ROSAT/PSPC and HRI data White et al. (1994), derived an ellipticity $\epsilon$varying between 1.2 and 1.4 within the central  $(\theta < 100\hbox{$^{\prime\prime}$ })$region. We fitted a 2D $\beta$-model to the EMOS1+EMOS2 image in the $[0.3{-}2]~\rm keV$energy band, within the  $\theta < 10\hbox{$^\prime$ }$ region. We derived a consistent value of the ellipticity,  $\epsilon=1.22$. The quality of the fit is poor, however: the residual image shows a strong excess at the cluster center position, as expected for a strong cooling flow cluster.

Despite its slightly elliptical shape, in the remainder of this work we assume spherical symmetry and use circular annuli to extract the surface brightness profile and spectra. Pratt & Arnaud (2002) showed in the case of A1413, a cluster of a higher ellipticity of  $\epsilon=1.4$, that this has negligible impact on the derived temperature and mass profiles.

   
4 Gas density radial profile

    
4.1 Surface brightness profile

We computed a background-subtracted vignetting-corrected radial surface brightness profile for each detector in the  $[0.3{-}2]~\rm keV$energy band. The width of the radial bins was  $3.3\hbox{$^{\prime\prime}$ }$. The profiles for the three detectors were added into a single profile, which was rebinned to reach a significance level of at least 3$\sigma $in each radial bin. The cluster emission is detected up to  $13\hbox{$^\prime$ }$.

The emissivity in the considered energy band varies slightly with radius, due to the radial gradients in the hydrogen column density along the line of sight ( ${N_{\rm H}}$), temperature (${\it kT}$) and metallicity (Z) (see Sect. 5.2). The  ${N_{\rm H}}$, ${\it kT}$ and Z values were extrapolated at each radius of the surface brightness profile by fitting the observed  ${N_{\rm H}}$, ${\it kT}$ and Z profiles (see Sect. 5.2) with a 3 degree polynomial, an empirical temperature profile as described in Allen et al. (2001b) and a lognorm law respectively. The corresponding emissivity profile (with errors) was estimated using an absorbed redshifted MEKAL model, convolved with the instrument response. Its radial variation is mainly dominated by the variations of  ${N_{\rm H}}$. The surface brightness profile was then divided by the emissivity profile normalized to its value at large radii. The errors on the emissivity were propagated to the corrected surface brightness profile.

   
4.2 Gas density profile modeling


  \begin{figure} \par\includegraphics[width=7.7cm,clip]{aa0856f2.eps} \end{figure} Figure 2: A478 XMM-Newton (EMOS+EPN) surface brightness profile in the  $[0.3{-}2.0]~\rm keV$ band. The profile is background subtracted, corrected for vignetting and for the radial variations of the emissivity factor (see text). The best fit KBB gas density model (Eq. (1)), fitted over the  $\theta > 0.33\hbox {$^\prime $ }$ region is over-plotted as a solid line. The dotted line is the extrapolation of this model in the central region. Bottom panel: ratio between the data and the model. The dotted lines indicate the $\pm $5% level.
Open with DEXTER

The corrected surface brightness profile (presented in Fig. 2) is proportional to the emission measure profile, EM(r), and can be fitted directly using various parametric models of the gas density profile,  ${n_{\rm e}}(r)$. The corresponding emission measure models were convoluted with the XMM-Newton PSF (Ghizzardi et al. 2001, 2002) and binned in the same way as the observed profile.

As expected, a standard $\beta$-model provides an unacceptable fit, the data showing a strong excess in the center compared to the model. Progressively cutting the central region decreases the reduced $\chi ^{2}$. The fit becomes acceptable ( $\chi_{\rm red}^2\sim 1$) for a cut-out radius of  $\theta_{\rm cut} \sim 2.4\hbox{$^\prime$ }$ with a best fit $\beta$ value of  $0.79\pm0.01$ ($1\sigma $ errors). The reduced $\chi ^{2}$ keeps decreasing with increasing $\theta_{\rm cut}$ until it stabilizes to a value of  $\chi_{\rm red}^2\sim 0.7$ for $\theta_{\rm cut} > 3\hbox{$^\prime$ }$. There is an indication that $\beta$increases with increasing  $\theta_{\rm cut}$, but the effect is marginally significant: for instance we obtained  $\beta = 0.85\pm0.05$for  $\theta_{\rm cut}= 3.9 \hbox{$^\prime$ }$.

We then considered the alternative parametrisations of the gas density profile proposed by Pratt & Arnaud (2002) for cases where a central excess is seen. We fitted the entire profile with a cusped model, similar to the NFW profile (their AB model) and a double isothermal $\beta$-model (their BB model). Both models fail to account for the data, although formally the latter provides a better fit than the former: the reduced $\chi ^{2}$ are respectively 5.5 and 4.2. We then tried a generalized double $\beta$-model (their KBB model). This model allows a more centrally peaked gas density profile in the core than the BB model and is defined by:

 \begin{displaymath}\begin{array}{llllll} r < R_{\rm cut}&~~~&{n_{\rm e}}(r)& = &... ...{\rm c}}}\right)^2 \right]^{-\frac{3 \beta}{2}}\\ \end{array}\end{displaymath} (1)

where $\xi$,  $r_{\rm ci}$,  $R_{\rm cut}$,  ${r_{\rm c}}$ and $\beta$ are free parameters, the parameters N and  $\beta_{\rm i}$ being related to them so that both the density distribution and its gradient are continuous across  $R_{\rm cut}$.

This model provides an excellent fit to the data, but only if the very central part is excluded from the fit (see Fig. 2). Fitting the  $(\theta > 0.33\hbox{$^\prime$ }\sim 32~{\rm kpc})$ region gives a reduced $\chi ^{2}$ of  $\chi_{\rm red}^2\sim 0.92$ for  $\xi = 0.42$, $r_{\rm ci}=0.99\hbox{$^\prime$ }$,  $R_{\rm cut}=4.5\hbox{$^\prime$ }$,  ${r_{\rm c}}=2.5\hbox{$^\prime$ }$ and $\beta=0.81$. A clear excess is observed when extrapolating this model in the central part (see Fig. 2).

  \begin{figure} \par\includegraphics[width=8cm,clip]{aa0856f3.eps} \end{figure} Figure 3: Same as Fig. 2 with the best fit BBB model (Eq. (2)) fitted over the full radial range.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{aa0856f4.eps} \end{figure} Figure 4: Comparison between the Chandra gas density profile derived by Sun et al. (2003) and the XMM-Newton best fit BBB gas density model (as plotted in Fig. 3). Bottom panel: ratio between the Chandra data and this model.
Open with DEXTER

We then tried a 3 component model. We went back to direct parametrisation of the emission measure profile (rather than the density profile) for simplicity. We considered the sum of three $\beta$-models (hereafter BBB model).

 \begin{displaymath}\begin{array}{lll} EM(r) &=& EM_{1}(r) + EM_{2}(r) + EM_{3}(... ..._{\rm c}}_{i}}\right)^2 \right]^{-3 \beta+1/2}\cdot \end{array}\end{displaymath} (2)

A common $\beta$ value is assumed to insure a smooth (single power law) behavior at high radii. The model has thus 7 free parameters. The corresponding density profile is:

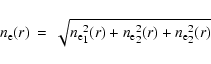\begin{displaymath}\begin{array}{lll} {n_{\rm e}}(r)& =& \sqrt{{n_{\rm e}}_{1}^... ... + {n_{\rm e}}_{2}^{2}(r) + {n_{\rm e}}_{2}^{2}(r)} \end{array}\end{displaymath} (3)

where each  ${n_{\rm e}}_{i}(r)$ profile is the density $\beta$-model profile corresponding to the emission measure profile EMi(r).

This BBB model provides an excellent fit to the data over the whole radial range: the reduced $\chi ^{2}$ is  $\chi_{\rm red}^2\sim 0.90$ for 56 d.o.f. This best fit model is plotted in Fig. 3, together with the ratio between data and model. The best fit parameters are  $\beta=0.84^{+0.04}_{-0.03}$,  ${r_{\rm c}}_{1} = 0.25\hbox{$^\prime$ }\pm0.02\hbox{$^\prime$ }$,  ${r_{\rm c}}_{2} = 1.12\hbox{$^\prime$ }\pm0.07\hbox{$^\prime$ }$,  ${r_{\rm c}}_{3} = 3.3\hbox{$^\prime$ }\pm0.3\hbox{$^\prime$ }$ ($90\%$ errors). The best fit central density is  ${n_{\rm e}}(0) =0.109~{\rm cm^{-3}}$, with a relative normalization of the second and third components of  $({n_{\rm e}}_{2}(0)/{n_{\rm e}}(0))^{2} = 5.40\times 10^{-2}$ and  $({n_{\rm e}}_{2}(0)/{n_{\rm e}}(0))^{2}=1.32\times 10^{-3}$, respectively.

We further compared this best fit density profile with the profile obtained by Sun et al. (2003) from a deprojection of the Chandra ACIS-S3 surface brightness (see Fig. 4). The Chandra profile is determined out to $\sim$ $5\hbox{$^\prime$ }$. There is a good agreement between the two profiles, both in shape and in normalization. Simply adjusting the overall normalization of the XMM-Newton best fit model to the Chandra data gives already a reduced $\chi ^{2}$of 1.3 with residuals between model and data less than $5\%$. The normalization is $2\%$ lower than the XMM-Newton value, corresponding to $\sim$$4\%$ discrepancy in X-ray flux, well within the discrepancy of $\sim$$\pm $$5\%$ between the two instruments found by Snowden (2002). Although the best fit XMM model does not fit perfectly the Chandra profile shape, slightly adjusting the parameters provides an acceptable fit. We kept the $\beta$ and outer core radius values to their best fit XMM values, as the external shape of the density profile is not well constrained by Chandra data. We obtained a reduced $\chi ^{2}$ of 1.0 for ${r_{\rm c}}_{1} = 0.26\hbox{$^\prime$ }$ and  ${r_{\rm c}}_{2} = 1.18\hbox{$^\prime$ }$, consistent with the XMM $90\%$ confidence range. The relative normalizations of the three components are marginally inconsistent. Nevertheless, taking into account that the effect of the Chandra PSF is negligible, the good agreement between XMM and Chandra central core radius indicates that the PSF modeling we have used to fit the XMM-Newton data is basically correct.

The XMM best fit BBB model is thus used in the following to estimate the cluster gas and total mass profiles and to correct the temperature profile for PSF and projection effects. The total mass profile depends on the logarithmic slope of the density profile. To estimate the systematic uncertainties in the mass estimates we will also consider the density logarithmic slopes derived from the BBB model best fitting the Chandra profile. The differences are small however, in the range  $0.2{-}4.5\%$. Finally we would like to emphasize that the BBB model functional form must only be viewed as a convenient parametric representation of the gas density profile. It has no particular physical ground and must not be over-interpreted (e.g. in terms of three distinct gravitational systems in the cluster).

   
5 Temperature and absorption profiles

Throughout the analysis, the spectra are binned to reach a significance level of at least 3$\sigma $ in each bin. We used XSPEC to fit the data with an absorbed redshifted thermal model ( WABS ( MEKAL)). Due to larger calibration uncertainties in the instrument response below the O edge we only fitted the spectra above $E =0.6~\rm keV$. We used the following response matrices: m1_thin1v9q20t5r6_all_15.rsp (EMOS1), m2_thin1v9q20t5r6_all_15.rsp (EMOS2) and epn_ef20_sY9_thin.rsp (EPN, created in December 2002). Unless otherwise stated, the relative normalizations of the EPN and EMOS spectra were left free when fitted simultaneously.

   
5.1 Global spectrum analysis

We first extracted the cluster EMOS1, EMOS2 and EPN spectra within a circular region of  $10\hbox{$^\prime$ }$. Fitting simultaneously the EMOS and EPN spectra, we obtained a redshift of  $z=0.0868\pm 0.0004$. This value is significantly smaller than the optical value ( $z=0.0881\pm0.0009$). An investigation of the variation of $\chi ^{2}$ with z revealed two local minima, one at the optical redshift location and one at z= 0.079. Independent spectral fits of EMOS and EPN spectra clarify the issue. The EMOS best fit value is $z=0.0889\pm 0.0010$, perfectly consistent with the optical value. On the other hand, the EPN best fit redshift is $z=0.0793\pm 0.0007$ and corresponds to the second minimum. The redshift difference from the optical value corresponds to an energy shift of  $\Delta E = +50\pm4~{\rm eV}$ with respect to the expected iron line position.

We thus checked for a possible gain problem in the EPN data. The non-background subtracted spectrum shows strong Al-K, Ni-K and Cu-K fluorescence lines, which can be used for this purpose. We fitted the spectrum extracted in the  $6\hbox{$^\prime$ }< \theta < 12\hbox{$^\prime$ }$ region in a restricted energy range around these lines with a power law plus Gaussian line(s). The fitted Ni-K and Cu-K line energies are significantly higher than expected:  $E=7517\pm6~{\rm eV}$ and  $E=8081\pm1.5~{\rm eV}$ respectively, to be compared to the expected values of  $7477~{\rm eV}$ and  $8047~{\rm eV}$. However, the discrepancies,  $\Delta E = 40\pm6~{\rm eV}$ and  $\Delta E=34\pm2~{\rm eV}$ respectively, are smaller than observed for the cluster iron line. Furthermore we cannot simply add a constant offset to the energy scale: the centroid energy of Al-K, $E=1489^{+4}_{-3}~{\rm eV}$, is consistent with the expected value of  $1487~{\rm eV}$. Any linear gain correction based on the position of these fluorescence lines would thus be insufficient to bring the EPN redshift determination into agreement with the optical value.

We thus did not try to define and apply a gain correction In principle, the EPN gain uncertainty could affect our results. To assess this point, we fitted the EPN spectrum both fixing the redshift at the optical value and letting this parameter free. The derived  ${N_{\rm H}}$ values are the same, the best fit temperatures differ by  $0.10~\rm keV$, similar to the statistical uncertainty. As expected the main impact is on the derived abundance: for a free redshift  $Z=0.34\pm0.02~{Z_{\odot}}$, only marginally consistent with the value, $Z=0.30\pm0.02~{Z_{\odot}}$, obtained fixing the redshift at the optical value. When the EPN spectrum is fitted simultaneously with the EMOS spectrum, these discrepancies are even smaller. The abundance difference is two times less and the temperature is the same.

As we are mostly interested in the temperature information, we can neglect the gain uncertainty and choose to fix the redshift to the optical value, in all the following analysis. The overall cluster parameters are: ${N_{\rm H}}=2.66_{-0.03}^{+0.02}\times 10^{21}$ cm-2, ${\it kT}=6.17_{-0.06}^{+0.12}$ keV and  $Z=0.32\pm 0.013$ $Z_{\odot}$( $\chi_{\rm red}^2 = 1.02{-}90\%$ confidence level).

   
5.2 Annular spectra analysis

We extracted background-subtracted, vignetting-corrected spectra in 13 concentric annuli centered at the peak of the X-ray emission. The annuli were defined to have about the same number of counts per bins (except the outermost annulus).

The EMOS1, EMOS2 and EPN spectra of each annulus were simultaneously fitted with a WABS ( MEKAL) model. The resulting  ${N_{\rm H}}$, ${\it kT}$, and abundance profiles are plotted in Fig. 5. The definition of the annuli and the best fit parameters are gathered in Table 2. We also checked that the temperature profiles obtained by fitting the EMOS and EPN spectra independently are consistent within the error bars.

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{0856fig5.eps} \end{figure} Figure 5: Result of the radial spectral fitting. From top to bottom the temperature (kT), Galactic absorption ( ${N_{\rm H}}$), metallicity (Z) and reduced $\chi ^{2}$ for the best fit model. Errors are $1\sigma $. For the temperature profile the best fit model using Eq. (4) is over-plotted as a dashed line.
Open with DEXTER

Table 1: A478 global properties from previous studies.

The temperature profile shows a clear drop towards the center. It is well fitted by the analytical formula proposed by Allen et al.  (2001b):

 \begin{displaymath}T(r)=T_0+T_1\left[\frac{(r/{r_{\rm c}})^\eta}{1+(r/{r_{\rm c}})^\eta}\right] \end{displaymath} (4)

with  $T_{\rm0}= 3.26~\rm keV$ and  $T_{\rm 1}=3.52~\rm keV$,  ${r_{\rm c}}= 0.396\hbox{$^\prime$ }~$ and $\eta=1.52$ ( $\chi^{2}=12.7$ for 13 degrees of freedom). The best fit model is plotted in Fig. 5. To fit the observed profile with such a formula, we had to assign a radius to each annulus temperature. Following the prescription of Lewis et al.  (2003), we used the weighted effective radius of each annulus, defined as:

 \begin{displaymath}r_{\rm i} = \left[\left(r_{\rm out_{i}}^{3/2} + r_{\rm in_{i}}^{3/2}\right)/2 \right]^{2/3} \end{displaymath} (5)

rather than the mean radius. We checked that the best fit temperature profile then becomes insensitive to the binning choice. We regrouped the first two annuli and then the next two annuli and re-ran an isothermal fit to the spectra of those new larger annuli. The resulting profiles were fitted again with Eq. (4), using the weighted effective radii. We obtained the same best fit profile as with the original binning. This is not the case if we use instead the mean radius of each annulus.

The temperature profile shows a strong gradient towards the center, whereas we recall that the surface brightness profile is very peaked. This temperature profile is thus likely to be affected by both PSF and projection effects. These effects will be analyzed in Sect. 5.5. However, the overall  ${N_{\rm H}}$ value is significantly higher than the 21 cm value and its radial profile is not flat. As the  ${N_{\rm H}}$ and ${\it kT}$ determination are not independent, we will first discuss our absorption results.

   
5.3 The absorption profile

Our best fit overall value for the Galactic absorption, ${N_{\rm H}}=2.66_{-0.03}^{+0.02}\times 10^{21}$ cm-2, is nearly two times the 21 cm value of  ${N_{\rm H}}=1.53\times 10^{21}$ cm-2 (Dickey & Lockman 1990). Such an excess absorption was found in all previous X-rays studies of A478 and our derived value is only marginally higher than the value derived from ROSAT/Ginga and Chandra data (see Table 1).

The radial  ${N_{\rm H}}$ profile that we obtained exhibits a clear gradient ranging from  $3\times 10^{21}$ cm-2 in the central regions to  $1.7\times 10^{21}$ cm-2 at  $12\hbox{$^\prime$ }$. This gradient is consistent with the Chandra gradient measured by Sun et al. (2003): from a central value of  $2.9~\pm ~0.1 \times 10^{21}$ cm-2 down to $2.4~\pm ~0.1 \times 10^{21}$ cm-2 for the last bin at $\sim$ $5\hbox{$^\prime$ }$ (perfectly consistent with the XMM-Newton value, see Table 2).

Table 2: Radial spectral fitting - best fit values and associated error bars (90% confidence level).

This excess of absorption seen in A478 and other cooling flow clusters was interpreted in previous studies (e.g., Allen et al. 1993, 2001a) in terms of intrinsic absorption by very cold gas related to the strong cooling flow. However our vision of cool cluster cores has dramatically changed due to XMM-Newton observations. The standard cooling flow model predicts low energy emission lines which are simply not seen in the RGS spectra (Peterson et al. 2001, 2003). This standard model is also inconsistent with EPIC data (e.g., Molendi & Pizzolato 2001; Matsushita et al. 2002; Böhringer et al. 2002; Kaastra et al. 2003). No evidence of intrinsic absorption was found with XMM-Newton in the center of the cooling flow regions in M 87 and the Perseus cluster, and Böhringer et al.  (2002) argued that the excess absorption measured by previous missions is an artifact of fitting standard cooling flow models. The low energy emission over-predicted by this model can be artificially suppressed by adding an extra absorption component when fitting spectra obtained with instruments like ASCA, which have relatively low sensitivity at low energies.

Although the absorption excess in A478 is confirmed by XMM-Newton data, it is more likely, in view of our current knowledge of cooling cores in clusters, that all the absorption is of Galactic origin. This hypothesis is reinforced by the spatial distribution of the excess absorption: the excess extends well beyond the cool core region. We also note that if cold gas has indeed now been detected in the core of clusters, like A478, through CO measurements (Edge 2001), there is still a large mismatch, by an order of magnitude, between the inferred column densities and the absorption excess (see Edge 2001, for full discussion). Finally the local CXRB that we measure with XMM-Newton is lower than the average blank field value (see Sect. 2.4). The Rosat All Sky Survey (RASS)  $3/4~\rm keV$ maps (see Snowden 1997) also clearly show a deficit of CXRB in that region. This again points towards a high Galactic absorption.

To further test the origin of the absorption and the robustness of our  ${N_{\rm H}}$ estimates, we considered other indicators of the Galactic gas column density. We recall that the column density derived from X-ray data is actually the total hydrogen column density (assuming standard abundances). We considered the IRAS 100 $\mu $m cleaned map of Schlegel et al. (1998). The Galactic hydrogen is correlated with the Galactic dust responsible for the IR emission, as shown by Boulanger et al. (1996) and Schlegel et al.  (1998), who correlated COBE/DIRBE and IRAS data with the Leiden/Dwingeloo survey (Hartmann & Burton 1997). The correlation between the IR emission and the atomic hydrogen column density is determined from low  ${N_{\rm H}}$ data ( ${N_{\rm H}}< 4.6 \times 10^{20}$ cm-2). Above this threshold an increasing dispersion is observed with higher IR/HI ratio on average. Boulanger et al. (1996) argued that this excess IR emission is due to dust associated with molecular hydrogen. The IR emission could thus actually be a tracer of the total hydrogen content. Assuming that the correlation determined at low  ${N_{\rm H}}$ values (where the H2 fraction is expected to be small) is representative of this IR - total  ${N_{\rm H}}$ correlation, we converted the IR brightness map into a total  ${N_{\rm H}}$ map. We used both the Boulanger et al. (1996) and Schlegel et al. (1998) results, these two groups having derived slightly different correlation coefficients. We then derived radial profiles which are compared with the XMM-Newton derived  ${N_{\rm H}}$ profile in Fig. 7. Interestingly, the IR and X-ray derived  ${N_{\rm H}}$ profiles are indeed found to be consistent up to about  $5\hbox{$^\prime$ }$.

Beyond that radius the XMM-Newton   ${N_{\rm H}}$ profile starts to become significantly lower than the expected values from the IR emission. However, the IR emission shows a strong gradient over the cluster area in the north-east/south-west direction (see Fig. 6). There is a drop by a factor of two between the north-east sector of our mosaic and the south-east sector. Obviously the azimuthal average tends to smooth the gradient effects. Keeping the previous definition of annuli, we then divided each annulus in four sectors separated by a North-South and an East-West axis (see Fig. 6). In each sector, we ran a spectral fit for each annulus. The resulting  ${N_{\rm H}}$ profiles are presented in Fig. 7. All four profiles are compatible with the azimuthally averaged profile within a 3$\sigma $ limit. One can notice, however, that the South-East measurements are systematically lower than the azimuthal values whereas the North-West values are systematically larger.

In summary, both X-ray and IR data indicate a higher Galactic hydrogen column density than the 21 cm value. Both X-ray and IR  ${N_{\rm H}}$estimates agree remarkably well in the cluster center, suggesting that the excess absorption is indeed of Galactic origin. Moreover, FIR observations from the ISO satellite at 90 and 180 $\mu $m show a color ratio favoring a cold temperature structure (Pointecouteau & Giard, in preparation), which is more likely to be due to a Galactic structure than to an intracluster dust component. Indeed, the expected temperatures for the intracluster dust according to the current models are >20 K (Montier & Giard 2003). However, the radial variations of the X-ray and IR derived hydrogen column density differ. This could be due to variations in gas to dust ratio and/or metallicity for instance. To probe the foreground structure on the cluster scale toward A478, FIR observations with a higher spatial resolution would be extremely useful. For instance, soon the ASTRO-F mission (Shibai 2002) will survey the whole sky at FIR wavelengths and will provide observations up to 200$~\mu$m that will reveal the galactic cold component structure. These upcoming observations on the whole cluster scale will certainly help to clarify this issue.


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{fig6.eps} \end{figure} Figure 6: IRAS 100 $\mu $m (Schlegel et al. 1998) in A478 direction. The overplotted contours show the X-ray emission as well as the area covered by our XMM-Newton observation. The vertical and horizontal lines defined the sectors used to cross-check the  ${N_{\rm H}}$ profiles (see text).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.3cm,clip]{0856fig7.eps} \end{figure} Figure 7: ${N_{\rm H}}$ profiles derived from XMM-Newton data in the North-East (diamonds), North-West (triangles), South-West (squares) and South-East (crosses) quadrant compared to the azimuthal profile (smoothed - solid line). The two dashed lines are the 3$\sigma $ error bars (smoothed) associated to the azimuthal profile. The two dotted-dashed lines correspond to the  ${N_{\rm H}}$ value estimated from the 100 $\mu $m IRAS map according to Boulanger et al. (upper line - 1996) and Schlegel et al. (lower line - 1998).
Open with DEXTER

In view of the discrepancy between the IR and X-ray derived  ${N_{\rm H}}$values beyond  $\theta \sim 5\hbox{$^\prime$ }$, we further checked the robustness of our  ${N_{\rm H}}$ and thus ${\it kT}$ measurements in that region (two outer annuli). We ran again the individual spectral fit on the annuli, fixing the value of the Galactic absorption to  $2.5~\times 10^{21}$ cm-2. The derived temperature drops from $\sim$$7~\rm keV$down to $\sim$$5~\rm keV$. However, the fit is significantly worse. Indeed, the F-test probability, given the $\chi ^{2}$ value and the one obtained previously by letting free the  ${N_{\rm H}}$, is 10-8. Furthermore, if we still fix the ${N_{\rm H}}$ value to  $2.5~\times 10^{21}$ cm-2, but fit the spectra for E>1.5 keV, avoiding the low energy band that is sensitive to the Galactic absorption, the derived temperature profile is fully compatible with the nominal one. Therefore, we can be reasonably confident that the derived radial column density and temperature profiles are real.

5.4 Comparison with previous results

The best fit values we derived for the overall physical properties of A478 are in agreement with the previous results for the Galactic absorption and the metallicity (see Table 1). Moreover, their radial profiles match closely those derived by Sun et al. (2003) using the Chandra data. However, our overall temperature value is marginally compatible with the temperature values from ROSAT/Ginga and ASCA. A478 does not exhibit an overall isothermal plasma (presence of a cool core). The temperature derived from an isothermal fit is actually an emission weighted temperature, which depends on the instrument response. Due to its higher sensitivity at low energies, XMM is more sensitive to the presence of a cool component. This would explain the slightly lower temperature derived from our data with respect to Ginga and ASCA results. To further check this point, we fixed the absorption value to $2.5\times 10^{21}$ cm-2 (the value derived from the ROSAT/Ginga analysis) and we fitted the overall spectrum over the [1-10] keV energy band. The best fit temperature value is then   $kT=6.42\pm 0.06~\rm keV$, a value compatible with ROSAT/Ginga value, as well as ASCA value.

Despite this agreement, some important discrepancies appear between the temperature profiles obtained from XMM-Newton and Chandra. If we focus on the average value of the temperature excluding the cool core region, the Chandra value ($\sim$ $8.5~\rm keV$) is significantly higher than the XMM-Newton value ($\sim$ $6.5~\rm keV$). Similar discrepancies appear for the luminous X-ray cluster PKS 0745-191. Indeed, the temperature derived from the Chandra analysis (Hicks et al. 2002) outside the cool core ( 1.5'<r<2.3'), $\sim$ $10.5~\rm keV$, is significantly higher than the value derived from XMM-Newton data (Chen et al. 2003) in the same region, $\sim$ $7.5~\rm keV$. In this case, the XMM-Newton result compares better with the value of $\sim$$8~\rm keV$ by BeppoSAX (De Grandi & Molendi 1999). However, it must be noted that the BeppoSAX temperature measurement includes the cold core region which is likely to induce a bias toward lower temperatures.

We have failed to explain the discrepancy between XMM-Newton and Chandra. Apart from calibration related problems, we thought that it could be due to background subtraction problems. For both PKS 0745-191 and A478, the CXRB was found with XMM-Newton to be different from the CXRB of a typical blank field. The higher  ${N_{\rm H}}$ observed in the direction of the A478 cluster certainly contributes to this difference for this cluster, but we cannot exclude a contribution from some intrinsic spatial variation in the soft X-ray Galactic emission. This difference was taken into account in the XMM-Newton background subtraction procedure (in the second subtraction step - see Sect. 2.4). On the other hand, Chandra analysis had to rely on a simple blank field background subtraction, by lack of data at large radii. In the Chandra analysis of A478, the CRXB is a priori oversubtracted and this could bias the temperature determination, especially in the outer cluster region where the CXRB count rate is no longer negligible with respect to the cluster count rate. To test this hypothesis for A478, we perform a single blank field subtraction for each XMM annular spectrum and re-ran the spectral isothermal fit. The resulting absorption and temperature profiles become significantly different beyond  $5\hbox{$^\prime$ }$(the upper limit of the Chandra profile). However, below $\sim$ $5\hbox{$^\prime$ }$, the profiles are not significantly affected and remain inconsistent with Chandra values[*]. Although the Chandra blank field observations are not the same as those of XMM-Newton, it is thus unlikely that the background subtraction issue is an explanation of the discrepancies. Furthermore the agreement between the XMM-Newton and Chandra profiles for the Galactic absorption would be puzzling if that was the explanation, since the  ${N_{\rm H}}$ determination is particularly sensitive to the subtraction of the residual CXRB, which affects the low energy part of the spectrum most.

   
5.5 The cluster temperature profile: Correction of PSF and projection effects


  \begin{figure} \par\includegraphics[width=18cm,clip]{aa0856f8.eps} \end{figure} Figure 8: Temperature profiles corrected for the PSF effect ( left panel), deprojected ( middle panel), PSF corrected and deprojected ( right panel). The data points are the temperatures derived from simultaneous fitting of the annular spectra. The open points are the temperatures obtained by fitting each annular spectrum individually with an isothermal model (Same as in Fig. 5). The dotted line is the analytical model fitted to these data (Eq. (4)). The full lines are the PSF corrected model ( left panel), the deprojected model ( middle panel) and the PSF corrected deprojected model (see Sect. 5.5.3 for details).
Open with DEXTER

The central drop in the temperature profile emphasizes the need to perform a deprojection analysis and to take into account the PSF effect. For such a highly peaked cooling flow cluster, PSF effects are important in the center where we have chosen narrow bins for the temperature computation to recover the best temperature profile.

5.5.1 PSF and projection effect modeling

The incident emission of each annulus, i, is the projected sum of the emission from various shells, $j \geq i$. This emission is then redistributed among various annuli due to the finite PSF. In principle, we should apply an absorption model to each incident annular spectrum (i.e. after the projection and before the PSF convolution). However the  ${N_{\rm H}}$ profile derived from the annular spectra fit does not show strong gradients in the central region (where the PSF effect is significant). We thus used a single absorption model for each observed annular spectrum, fixing the  ${N_{\rm H}}$ value to the best fit value obtained from individual annular fits (see Table 2).

We thus model the observed annular spectra,  $S_{\rm i}^{\rm O}(E)$, with a linear combination of isothermal MEKAL models (normalized to the unit emission measure), multiplied by a WABS model:

 \begin{displaymath}S_{\rm i}^{\rm O}(E) = \hbox{\sc wabs}({N_{\rm H}}_{i}) \sum_{j=1}^{n} a_{i,j} \hbox{\sc mekal} (T_{j}, Z_{j}). \end{displaymath} (6)

We first considered pure PSF effects. In that case, each ai,j coefficient is the emission measure contribution of the ring j to the ring i. The fitted temperatures Tj can be considered as "PSF corrected'' projected temperatures. The ai,j factors were derived from our best fit gas density profile (BBB model), converted to an emission measure profile and convolved with the XMM-Newton PSF estimated at $1~\rm keV$. To crudely validate our absorption modeling, we ran this PSF correction fit leaving the  ${N_{\rm H}}$ as a free parameter. We found completely consistent values with the best fit value of the annular spectral fit.

Similarly we assess the projection effects, neglecting the PSF blurring. We used the same formula with the ai,j redistribution factors being now the emission measure contribution of the shell jto the ring i and Tj the temperature of the shell j (assumed to be isothermal).

Finally we took into account both effects, using as ai,j the emission measure contribution of the shell j to the ring i after convolution with the PSF.

5.5.2 Simultaneous fits of annular spectra

The fitting was done with XSPEC. We have to take into account that XSPEC can only handle 1000 parameters (even if most of them are frozen). The EMOS1, EMOS2 and EPN spectrum of each annulus was loaded into XSPEC as a data group. The same model parameters are applied to each spectrum of a given group. Therefore, EMOS and EPN spectra have to be normalized in order to be fitted with the same normalization. Furthermore the ai,j coefficients are computed without taking into account flux loss due CCD gaps, bright pixels, etc. We therefore first renormalized each spectrum by the ratio of the annular geometrical area to the actual extraction region surface ( BACKSCALE value). After this correction, the ratio of the EMOS and EPN normalizations obtained from the annular fits (Sect. 5.2) were found to be consistent with the ratio obtained by fitting the overall EMOS and EPN spectra:  $N_{\rm EMOS/EPN} = 1.11$. We thus applied this factor to all EPN spectra. Finally, we checked that the annular fit results indeed remain the same: the differences in derived kT are negligible compared to the statistical errors.

Fitting simultaneously n annular spectra with a sum of n MEKAL models, multiplied by a WABS model, gives a total number of parameters of (6n + 1)n. We thus have to limit n to 12. To overcome this problem, we have used two different sets of 12 annular spectra. The first set is obtained by grouping the last two annuli into a single annulus and the second set by grouping the first two annuli. We then combined the first set results for annuli $\char93 1$ to $\char93 9$ with the second set results for annuli $\char93 10$ to $\char93 13$.

For each set, the free parameters are the 12 temperatures, 12 normalizations, one per data group (annulus), the other normalizations being linked according to Eq. (6). In practice we ignore all contributions less than 1%. We have frozen the abundance of each MEKAL model to the annular best fit value, except for the 4 innermost components corresponding to the r <1' region. Beyond that region the annular abundance profile is flat. PSF and projections effects are unlikely to affect the abundance determination in such a way that it has a significant impact on the temperature determination. To further check this point, we also fixed all the abundances to the best fit annular value. Only the central temperature is changed significantly.

The resulting corrected temperatures are plotted versus effective radius (defined in Eq. (5)) in Fig. 8. These data are compared to the temperature profile derived in Sect. 5.2 (hereafter the raw temperature profile).

   
5.5.3 Correction of the temperature profile model

We also considered the best fit model (Eq. (4)) of the raw temperature profile (dotted line in Fig. 8). It can also be corrected for PSF and/or projection effects, assuming that the annular temperatures  $T_{\rm i}^{\rm M}$ are emission-weighted temperatures:

 \begin{displaymath}T_{\rm i}^{\rm M} = \sum_{j=1}^{n} \frac{a_{i,j}}{\sum_{j=1}^{n} a_{i,j}} T_{j}. \end{displaymath} (7)

The factors ai,j are the same as computed above. The PSF-corrected model, the deprojected model and the PSF-corrected deprojected model are plotted in Fig. 8 (full lines).

   
5.5.4 Results

First, it is instructive to consider the PSF correction (Fig. 8, left panel) and the deprojection (Fig. 8, middle panel) separately. In both cases, the corrected model fits reasonably well the corresponding corrected temperature profile derived from the spectral fit. However, while the former remains a smooth function of radius, the later is more noisy. A comparison of the observed and model profiles before and after correction shows that the correction process amplifies any variation of the raw temperature profile compared to the smooth model (see in particular the temperatures of annuli # 3, #10 #11 and #12). This is probably linked to the well known problem of noise amplification when deconvolving or deprojecting noisy data (see also Kaastra et al. (2003) for a discussion on PSF/projection effects).

The PSF-corrected projected temperatures and the deprojected temperatures are consistent, within the error bars, with the raw temperatures in the external part of the cluster (nearly isothermal region, R > 100 kpc). Significant deviations are seen for the first four annuli. The general effect of the PSF blurring and of the projection are best seen by comparing the corrected and uncorrected models. The PSF affects mostly the central bin (the temperature of which is increased due to contamination by the higher temperatures of the external bins). In turn the other bins are contaminated by the low temperature central bin, and their observed raw temperatures are slightly lower than the incident ones. The effect is small however and consistently tends to zero with increasing radius. The main effect is the projection effect. As expected it damps down the gradient in the central region. The deprojected temperatures are always smaller than the projected ones, the effect increasing with decreasing radius.

The PSF-corrected deprojected temperature profile is shown in Fig. 8 (right panel). When both PSF and projection effects are taken into account the noise amplification is dramatic. The temperature profile derived from the spectral fit shows strong discontinuities (e.g. bins #3, 4, 5, bin #10). On the other hand, the corrected model remains smooth. Although the corrected temperatures derived from the spectral fit are not consistent with the corrected model within the statistical errors, they are distributed around it. The largest deviations correspond to the discontinuities mentioned above and are again clearly located around the bins which originally deviate most from the smooth model profile. These discontinuities are thus very likely non-physical and the corrected model is probably a better representation of the true cluster temperature profile than the profile derived from the spectral fit. As discussed in Sect. 6, we will use this corrected model as a reference in our computation of the mass profile.

The PSF-corrected deprojected model profile is consistently intermediate between the PSF-corrected model profile and the deprojected model profile for bins $\char93 2$ to $\char93 13$. As shown above, the PSF and projection have opposite effects in that region. The model temperature of the central bin is however extremely low. The PSF correction and deprojection was done assuming that the annular temperatures are emission-weighted temperatures. This assumption is probably less and less valid with decreasing temperature and the low value we derive might be an artifact of our assumption. Furthermore the gas may be multiphase in that region (r<20 kpc) due to the interaction of the intracluster medium with the central cD galaxy (see also below).

   
6 Mass profile

6.1 Calculation of the total mass profile

The total gravitational mass distribution shown in Fig. 9 was calculated under the usual assumptions of hydrostatic equilibrium and spherical symmetry using

 \begin{displaymath}M(r) = - \frac{kT\ r}{{G}\mu {m}_{\rm p}} \left[ \frac{{\rm d... ...}{{\rm d}\ln{r}} + \frac{{\rm d}\ln{T}}{{\rm d}\ln{r}} \right] \end{displaymath} (8)

where G and $m_{\rm p}$ are the gravitational constant and proton mass, and  $\mu = 0.609$. The mass (with errors) at each radius was calculated with the Monte Carlo method described in Pratt & Arnaud (2003), which takes as input a parametric model for the gas density profile and a measured temperature profile with error bars. A random temperature at each radius of the measured temperature profile is generated assuming a Gaussian distribution with sigma equal to the $1\sigma $ error and a cubic spline interpolation (between 3 adjacent points) is used to compute the derivative. Only "physical'' temperature profiles are kept, i.e. those yielding monotically increasing total mass profiles. In total 5000 such profiles were calculated.

At large radii, the errors on the derived mass profile are dominated by the statistical errors on the temperature profile. However we have to consider possible systematical errors, specially in the central (R<100 kpc) region, where the PSF and deprojection corrections introduce noise in the derived temperature profile (see Sect. 5.5). Only data beyond  $30~{\rm kpc}$ are considered: the temperature of the central bins is highly uncertain (see Sect. 5.5.4). Furthermore, Chandra data have clearly revealed sub-structure in the central  $\theta \sim 20~{\rm kpc} = 0.2\hbox{$^\prime$ }$region. Below that radius, the hot thermal gas might interact with the radio halos, producing a non-thermal population of electrons, and therefore the hydrostatic equilibrium might be disturbed locally producing possible multiphase states for the gas at this spatial scale (see previous work on M 87: Böhringer et al. 1995; Belsole et al. 2001; and on PKS 0745-191: Chen et al. 2003).

  \begin{figure} \par\includegraphics[width=8cm,clip]{aa0856f9.eps} \end{figure} Figure 9: Integrated total mass distribution. Filled circle: the reference total mass profile obtained from the best fit BBB model for the gas density profile and the PSF-corrected deprojected model of the temperature profile (errors are $1\sigma $). Open circles: mass obtained from the deprojected temperature model profile. Triangles: mass obtained using the deprojected temperature profile derived from the spectral fit. Crosses: mass using the Chandra gas density profile.
Open with DEXTER

We first derived a reference mass profile. It was computed using our best fit BBB model for the gas density profile. For the temperature profile we used the PSF-corrected deprojected model profile. The profile derived from the spectral fit is too noisy to be used: the strong fluctuations observed are inconsistent with any underlying mass profile. It is difficult to assess the statistical errors on this model profile in an objective way. We used the errors derived from the spectral fit, which is probably a conservative approach. For bin $\char93 2$ we also add as an error the difference between the fitted temperature and the model value (the latter might be affected by the too low value derived for bin #1).

We then computed the mass profiles obtained using alternative temperature and density data, to assess the systematic uncertainties. For the gas density profile, we considered the best fit BBB model of the Chandra profile (crosses in Fig. 9). The differences between the derived mass profile and the reference profile are much smaller than the statistical uncertainties.

We then considered systematic uncertainties due to the temperature profile determination. We have shown that PSF effects in the region considered here are less important than projection effects and that pure deprojection introduces much less noise. We thus also computed the mass profile derived from the deprojected temperature profile (neglecting the PSF blurring). We used both the profile derived from the spectral fit (triangles in Fig. 9) and the deprojected model profile (open circles in Fig. 9). The latter is well within the error bars of the reference profile, but the former differs significantly (see for instance the first point). Considering that these differences are likely to be representative of the systematic uncertainties due to the PSF correction treatment, we add them quadratically to the statistical errors on the reference mass profile.

In the following, we will thus consider the reference mass profile with these errors bars.


  \begin{figure} \par\includegraphics[width=8cm,clip]{aa0856f10.eps} \end{figure} Figure 10: Modelling of the integrated total mass distribution. Filled circle: total mass profile as in Fig. 9. The errors now include systematic errors due to the PSF correction (see text). The solid line is the best fit NFW profile (c=4.18), the dotted line is the best MQGSL profile and the dashed line is the best fit King model.
Open with DEXTER

6.2 Modeling of the total mass profile

We first tried to fit the data with a King model, where the mass density profile is given by:  $\rho(r) \propto \left[1+ (r/r_{\rm s})^2\right]^{-3/2}$. This model (dashed line in Fig. 10) is inconsistent with our data, the $\chi ^{2}$ is $\chi^2 = 16.5$ for 10 d.o.f.

The total mass profile was then fitted using cusped density distributions: the Navarro et al. (1997) profile $\left(\rho(r) \propto \left[(r/r_{\rm s}) (1+ r/r_{\rm s})^2\right]^{-1}\right)$ and the Moore et al. (1999) profile $\left(\rho(r) \propto \left[(r/r_{\rm s})^{3/2} (1+ r/r_{\rm s})^{3/2}\right]^{-1}\right)$. These models have two free parameters, the central density and the scaling radius, or equivalently the total mass M200 (corresponding to a density contrast of 200, as compared to the critical density of the Universe at the cluster redshift) and the concentration parameter  $c=R_{200}/r_{\rm s}$. All useful formulae relating these quantities can be found in Pratt & Arnaud (2002).

The NFW profile provides a good fit to the data:  $\chi^2 = 9.5$ for 10 d.o.f. The best fit NFW parameters are:  $r_{\rm s}=492~\pm~71~{\rm kpc}$and  $R_{200} = 2076\pm106~{\rm kpc}$, corresponding to a concentration parameter of  $c = 4.22 \pm 0.4$ and a total mass enclosed within R200 of  $M_{200}=1.1\times 10^{15}~M_\odot$. The previous errors are quoted at 68% confidence level. This best-fit NFW model is shown overplotted on the mass profile of the cluster in Fig. 9. The upper axis is the radius in units of the derived R200. We are thus probing the dark matter shape on a scale from $\sim$0.01 to $\sim$0.5 virial radius.

The alternative MQGSL profile is rejected by our data:  $\chi^2 = 29.7/10$. It must also be noted that the deviations from the data are not only significant at low radii, where the mass estimate is most sensitive to systematic errors. There is a general deviation at large radius, where the model gives essentially a power law, while the observed profile shows a significant curvature.


  \begin{figure} \par\includegraphics[width=8cm,clip]{aa0856f11.eps} \end{figure} Figure 11: The integrated gas mass fraction as a function of the radius. The 1$\sigma $ error bars are obtained from the propagation of the errors over the total mass profile. The gas mass fraction profile computed from the best fit NFW model is plotted as a solid line.
Open with DEXTER

6.3 Gas mass fraction profile

We derived the integrated gas mass fraction profile,  $f_{\rm gas}$, from the ratio of the gas mass profile to the total mass profile. The gas mass profile is computed from the integration of the best fit BBB model for the density profile (see Sect. 4.2). The errors for the gas mass fraction are obtained from the propagation of the total mass uncertainties, the gas mass uncertainties being negligible. The resulting gas mass fraction profile is shown in Fig. 11, together with the profile derived from the NFW best fit model. There is a general increase of  $f_{\rm gas}$ with radius, although the effect is small over the [0.01-0.5] R200 range. The gradient is most pronounced in the cool core region (about $30\%$), beyond which there is only marginal evidence of a positive gradient ($\sim$$10\%$ from 0.1 to  0.5 R200).

Excluding the cool core region (e.g. r<2$^\prime$), the average value for the gas fraction is  $\bar{f}_{\rm gas}(r>2{\rm \hbox{$^\prime$ }})=0.129\pm0.008$. We interpolated the gas mass fraction value at  $r_{2500}=822~{\rm kpc}$, the radius corresponding to a density contrast of  $\delta=2500$ (2500 times the critical density of the Universe at the cluster redshift),  $f_{2500}=0.13~\pm~0.02$. This value agrees with the average value of  $0.113~\pm~0.013$ at the same overdensity derived by Allen et al. (2002b) from a sample of six massive clusters observed by Chandra. Our value is also consistent with the value derived from the analysis of A1413 (Pratt & Arnaud 2002) when scaled to the chosen cosmology of this paper:  f2500(A1413)=0.11. However, the A478 and A1413  $f_{\rm gas}$profiles have different shapes, the latter decreasing more strongly toward the center. This reflects differences in the central gas density distribution, the total mass profile of both clusters having similar concentration parameters. Such a difference is probably linked to the different thermodynamical states of A1413 and A478, the latter hosting a strong cooling core, contrary to the former.

7 Discussion and conclusion

In this paper we have analysed imaging and spatially resolved spectral data of the galaxy cluster A478 obtained with the XMM-Newton satellite. We obtained well constrained absorption, gas density and gas temperature profiles up to $\sim$0.5 virial radius.

As in previous studies, we found an excess of absorption in the direction of A478. The derived absorbing column density exceeds the 21 cm measurements by a factor of $\sim$2 in the center and the excess extends well beyond the cooling core region. This excess of absorption seen in A478 (and other cooling flow clusters) was interpreted in pre-XMM and Chandra studies (e.g. Allen et al.  1993; Fabian 1994) as the signature of intrinsic cool absorbing material, a consequence of the strong cooling flow in the cluster center. From the absorption excess extent and a detailed comparison with FIR data, we argue that the absorption excess is rather of Galactic origin. We suggest it could be the effect of a Galactic molecular/cold cloud type structure in the line of sight. The next generation of FIR space missions will help to clarify this issue with sensitive FIR mapping of the whole cluster area with a high spatial resolution.

We fitted the surface brightness profile with various parametric models of the gas density profile, taking into account the XMM-Newton PSF. The gas density profile, derived on scales of  $0.03\hbox{$^\prime$ }{-}13\hbox{$^\prime$ }$, is highly peaked towards the center and is well fitted by a quadratic sum of three $\beta$-model. The derived gas density profile is in excellent agreement both in shape and normalization with the Chandra density profile (measured up to  $5\hbox{$^\prime$ }$ of the center). This indicates that the PSF modeling we have used is basically correct and that accurate density profiles in the very center of the cluster can be derived with XMM data, in spite of the PSF blurring.

A raw temperature profile was obtained on scales of  $0.07\hbox{$^\prime$ }{-}10\hbox{$^\prime$ }$ by fitting isothermal models to spectra extracted in 13 concentric annuli. This profile shows a sharp negative gradient measured toward the center ( $r<2\hbox{$^\prime$ }$), a signature of a cooling core. Beyond that region the profile is essentially flat. We have thoroughly investigated projection and PSF effects on the temperature profile determination. The PSF effects beyond  $0.3\hbox{$^\prime$ }$ are much less important than projection effects, whereas both are important in the very center. We discuss the noise introduced by the correction of these effects and a way to overcome this problem. The derived deprojected PSF-corrected temperature profile ranges from $\sim$2 keV in the center up to an asymptotic value of $\sim$6.5 keV.

Using this temperature profile and the density profile, we have derived the total mass profile for this cluster from 0.01 up to $\sim$0.5 times the virial radius. Systematic uncertainties due to the PSF and projection correction for the temperature profile are taken into account. We have tested different models for the dark matter profile distribution against the observed mass profile. A mass distribution with a cusp in the center, as predicted from numerical simulations, is clearly preferred.

An isothermal sphere model does not provide a good fit to the data. In a second time we tested an MQGSL model and an NFW model. Those two types of models have similar shapes at large radii (they both scale like r-1.5) but differ significantly at small radii. Therefore to discriminate those two models one needs data with a high statistic quality over a wide range of radii (i.e. covering at least two decades). Our data set nearly fulfilled this requirement and we were indeed able to discriminate between the two models, the NFW model being preferred to the MQGSL model. For the NFW model, we derived a concentration parameter  $c=4.2\pm0.4$. This value is as expected from numerical simulations: $c \sim6$ (Navarro et al. 1997; Eke et al. 1998) with a typical $1\sigma $ dispersion of $\Delta(\log~(c))=0.18$ (Bullock et al. 2001). This work can be compared with the similar work on the cluster A1413 by Pratt & Arnaud (2002). In the case of A1413, if the NFW model was acceptable, the MQGSL model was slightly preferred. Although this cluster is detected out to 0.7 times the virial radius, the data are limited in the center, a shortcoming, as emphasized above, for discriminating between those two models. Moreover, data in the center only are not sufficient (see the work on A1983 by Pratt & Arnaud 2003). On the other hand, our result agrees with the analysis of A2029 by Lewis et al. (2003), which clearly favors an NFW dark matter profile. To our knowledge, this is the only other data set which covers a similar wide radial range (0.001 to 0.1 virial radius).

The key factors in fitting the mass profiles with different dark matter models, are the resolution in the center as well as the data at large radii. To date XMM-Newton is the best satellite to compute total mass profiles, especially through its capability to derive precise temperature profiles. Nevertheless, its spatial resolution limits the investigation at the very center of galaxy clusters. A direct combined analysis of XMM-Newton and Chandra data of very well relaxed clusters seems to be an ideal path to a full description of the dark matter profile in clusters. However, one has to keep in mind that this requires an excellent cross calibration between the two satellites, so that the temperature profiles derived at various scales can be combined.

Acknowledgements
The authors thank A. C. Edge, the referee, for his useful comments ans suggestions. We thank M. Sun for providing the Chandra density profile and useful discussion. E.P. and M.A. are grateful to G. W. Pratt for his help and fruitful discussions throughout this work. We thank A. Sanderson for useful discussion. E.P. acknowledges the support of CNES, the French Space Agency. This work is based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA member states and the USA (NASA). The Space Research Organization of the Netherlands (SRON) is supported financially by NWO, the Netherlands Organization for Scientific Research.

   
Appendix A: Extraction of vignetting-corrected products from merged event lists

To correct for vignetting effects we used the photon weighting method, described in Arnaud et al. (2001). An estimate of the vignetting-corrected number of counts in a given sky region Reg and in a given energy band  $E_{\rm min}-E_{\rm max}$ is the sum:

 \begin{displaymath}C = \sum_{j} w_{j} \end{displaymath} (A.1)

over all events j with sky position  $(x_{j},y_{j}) \in Reg$ and energy  $E_{j} \in [E_{\rm min}-E_{\rm max}]$. The weight coefficient wjis the ratio of effective area at the event position to the central effective area computed at the event energy. This count extraction is the same for individual or merged events lists. We computed the weight coefficients by running the task EVIGWEIGHT on each individual events list (this task can also be run on the merged events lists).

Count rate estimates are less straightforward, since the effective exposure time can strongly vary in the extraction region (from 11 ks in regions only observed with the offset pointings up to 60 ks in the overlapping region). However, the total count rate in a given region is simply the sum of the count rates in various sub-regions. The count rate can be written as

 \begin{displaymath}CR = \sum_{j} \frac{w_{j}}{t(x_{j},y_{j})} \end{displaymath} (A.2)

where  t(xj,yj) is the exposure time at the event location.

In practice we used the following convenient procedure for each camera data set:

1
- We created a mosaic exposure map of the two pointings in sky coordinates. The reference position is the same as for the merged events list. The exposure map takes into account detector regions excluded by the events selection criteria (bad pixels, CCD borders ...). We used a pixel size of  $1.1''\times1.1''$.

2
- After merging the events lists, we divided the weight coefficient of each event by the exposure time taken from this exposure map.

3
- Scientific products (spectra, images, profiles) in count rates can be readily extracted from the merged events list by binning the events weighted by these new weight coefficients. As these products are corrected for vignetting, we can then used the on-axis response for further physical analysis.

References

 
Copyright ESO 2004