A&A 423, 147-153 (2004)
DOI: 10.1051/0004-6361:20035661
R. Barnard1 - U. Kolb1 - J. P. Osborne2
1 - The Department of Physics and Astronomy, The Open University, Walton Hall, Milton Keynes MK7 6BT, UK
2 - The Department of Physics and Astronomy, The University of Leicester, Leicester LE1 7RH, UK
Received 11 November 2003 / Accepted 6 May 2004
Abstract
Stochastic variability in two out of four XMM-Newton observations of XMMU J004303+4115 along with its power spectra and X-ray luminosities suggest a low-mass X-ray binary (LMXB) with a black hole primary. However, Chandra observations resolve the object into two point sources. We use data from 35 Chandra observations to analyse the contributions of each source, and attribute the variability to CXOM31 J004303.2+411528 (known as r2-3), which varies in intensity by a factor of ![]() 100 between observations. We assume that the power density spectra of LMXBs are governed by the luminosity, and that the transition between types of power density spectra occurs at some critical luminosity in Eddington units,
100 between observations. We assume that the power density spectra of LMXBs are governed by the luminosity, and that the transition between types of power density spectra occurs at some critical luminosity in Eddington units, ![]() ,
that applies to all LMXBs. We use results from these XMM-Newton observations and past results from the available literature to estimate this transition luminosity, and find that all results are consistent with
,
that applies to all LMXBs. We use results from these XMM-Newton observations and past results from the available literature to estimate this transition luminosity, and find that all results are consistent with
![]() in the 0.3-10 keV band. CXOM31 J004303.2+411528 exhibits a low accretion rate power density spectrum at a 0.3-10 keV luminosity of
in the 0.3-10 keV band. CXOM31 J004303.2+411528 exhibits a low accretion rate power density spectrum at a 0.3-10 keV luminosity of
![]() erg s-1. Known stellar mass black holes have masses of 4-15
erg s-1. Known stellar mass black holes have masses of 4-15
![]() ;
hence our observations of CXOM31 J004303.2+411528 are consistent with
;
hence our observations of CXOM31 J004303.2+411528 are consistent with
![]() if it has a black hole primary.
if it has a black hole primary.
Key words: X-rays: general - galaxies: formation - X-rays: binaries - black hole physics - accretion, accretion disks
The Andromeda Galaxy (M 31) is an attractive and important target for X-ray astronomy, since it is the nearest spiral galaxy (760 kpc, van den Bergh 2000), and its X-ray emission is dominated by point sources. These point sources are thought to be mostly X-ray binaries, along with a few foreground objects, background active galactic nuclei (AGN), and supernova remnants (SNR). The two most recent X-ray observatories, Chandra and XMM-Newton, have finally allowed studies of variability in extra-galactic X-ray sources over time-scales of a few hundred seconds, as well as between successive observations. Such short-term time variability is often characteristic of well-studied phenomena and sometimes allows classification of the objects from X-ray observations alone, in conjunction with their X-ray spectral properties; for example, thermonuclear X-ray bursts (Lewin et al. 1995) identify an X-ray source as an X-ray binary with a neutron star primary. To date, analysis of the XMM-Newton observations of the core of M 31 has resulted in the discovery of a pulsating supersoft source with a period of 865 s (Osborne et al. 2001), the periodic dipping of the X-ray counterpart to the globular cluster Bo 158 (Trudolyubov et al. 2002), a persistently bright black hole binary (Barnard et al. 2003a, Paper I), and a Z-source (Barnard et al. 2003b, Paper II). Meanwhile Kaaret (2002) identified variability of three sources in a 47 ks Chandra HRC observation of M 31, including the black hole binary later identified in Paper I.
The XMM-Newton and Chandra missions complement each other well; Chandra provides imaging with exceptional spatial resolution, while XMM-Newton is the most sensitive imaging X-ray observatory yet flown. The current work exemplifies how XMM-Newton and Chandra results can be used together to get more detailed information than is possible from either data set alone.
XMMU J004303+4115 appears as a point source when observed with XMM-Newton, but is resolved by Chandra into two objects, 6
![]() apart. Kong et al. (2002) associate CXOM31 J004302.9+411523, the southern source, with the globular cluster Bo 146, and report transient behaviour in CXOM31 J004303.2+411528, the northern source. Following Kong et al. (2002), we designate the northern source r2-3 and the southern source r2-4. We find that in XMM-Newton observations, XMMU J004303+4115 exhibits power density spectra such as are seen in low accretion rate low-mass X-ray binaries (LMXBs), yet at 0.3-10 keV luminosities of 3-
apart. Kong et al. (2002) associate CXOM31 J004302.9+411523, the southern source, with the globular cluster Bo 146, and report transient behaviour in CXOM31 J004303.2+411528, the northern source. Following Kong et al. (2002), we designate the northern source r2-3 and the southern source r2-4. We find that in XMM-Newton observations, XMMU J004303+4115 exhibits power density spectra such as are seen in low accretion rate low-mass X-ray binaries (LMXBs), yet at 0.3-10 keV luminosities of 3-
![]() erg s-1 (Sect. 3).
erg s-1 (Sect. 3).
Van der Klis (1994, hereafter referred to as vdK94) showed that the power density spectra (PDS) of LMXBs with neutron star or black hole primaries are strikingly similar. At low accretion rates, the PDS of LMXBs have almost identical shapes (approximately broken power laws with the spectral index, ![]() ,
changing from
,
changing from ![]() 0 to
0 to ![]() 1 at frequencies higher than 0.01-1 Hz) and fractional rms amplitudes of a few times 10% (vdK94); we shall refer to these as type A PDS. At higher accretion rates, LMXBs are considerably less variable, with fractional rms amplitudes of only a few percent, and their PDS are described by power laws with
1 at frequencies higher than 0.01-1 Hz) and fractional rms amplitudes of a few times 10% (vdK94); we shall refer to these as type A PDS. At higher accretion rates, LMXBs are considerably less variable, with fractional rms amplitudes of only a few percent, and their PDS are described by power laws with
![]() -1.5 (vdK94); we will refer to these as type B PDS. Furthermore, vdK94 proposed that the transition between type A and type B PDS occurs at a critical fraction of the Eddington limit. Following vdK94, we define the critical luminosity fraction,
-1.5 (vdK94); we will refer to these as type B PDS. Furthermore, vdK94 proposed that the transition between type A and type B PDS occurs at a critical fraction of the Eddington limit. Following vdK94, we define the critical luminosity fraction, ![]() , as
, as
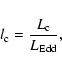 |
(1) |
In Sect. 3 we analyse longterm lightcurves of r2-3 and r2-4 from 35 Chandra observations, paying particular attention to those that were made within 30 days of one of the XMM-Newton observations. If we can associate type A PDS with either source when its luminosity, L, exceeds ![]() for a neutron star, we can establish that the primary is a black hole.
The most likely candidate for such black hole behaviour is r2-3, since most black hole binaries are transients (e.g. McClintock & Remillard 2003), and globular cluster X-ray sources mostly contain
1.4
for a neutron star, we can establish that the primary is a black hole.
The most likely candidate for such black hole behaviour is r2-3, since most black hole binaries are transients (e.g. McClintock & Remillard 2003), and globular cluster X-ray sources mostly contain
1.4 ![]() neutron stars (see Heinke et al. 2003, and references within). We present in Sect. 3 evidence that r2-3 contains a black hole primary.
neutron stars (see Heinke et al. 2003, and references within). We present in Sect. 3 evidence that r2-3 contains a black hole primary.
In Sect. 4 we first establish that r2-3 is located in M 31. We then obtain an empirical value for ![]() ,
using results from these XMM-Newton observations of globular cluster sources in M 31 and published results from analysis of a Galactic neutron star LMXB and a Galactic black hole LMXB.
We then use our value of
,
using results from these XMM-Newton observations of globular cluster sources in M 31 and published results from analysis of a Galactic neutron star LMXB and a Galactic black hole LMXB.
We then use our value of ![]() to calculate
to calculate ![]() for a neutron star with a mass of 3.1
for a neutron star with a mass of 3.1 ![]() ,
the theoretical maximum (Krishan & Kumar 1978). We assert that r2-3 exhibits a type A PDS at a luminosity that exceeds this limit and conclude that the primary in r2-3 is a black hole, consistent with its transient behaviour.
,
the theoretical maximum (Krishan & Kumar 1978). We assert that r2-3 exhibits a type A PDS at a luminosity that exceeds this limit and conclude that the primary in r2-3 is a black hole, consistent with its transient behaviour.
| Observation | Date | MJD | Exp | Filter |
| x1 | 25/06/00 (rev0100) | 51720 | 34 ks | Medium |
| x2 | 27/12/00 (rev0193) | 51906 | 13 ks | Medium |
| x3 | 29/06/01 (rev0285) | 52089 | 56 ks | Medium |
| x4 | 06/01/02 (rev0381) | 52280 | 61 ks | Thin |
Four XMM-Newton (Jansen et al. 2001) observations were made of the core of M 31; details of the observations are given in Table 1. For each observation, 0.3-10 keV lightcurves were extracted from source and background regions for each of the three EPIC instruments: one PN camera (Strüder et al. 2001) and two MOS cameras (Turner et al. 2001). The source region was circular with a radius of 20
![]() and centred on XMMU J004303+4115 while the background region was an equivalent source-free region on the same CCD and at a similar offset from the optical axis. The lightcurves were accumulated with 2.6 s binning. Background-subtracted, summed EPIC lightcurves, were then produced following the procedures laid out in Paper I. PN energy spectra from the source and background regions in the 0.3-10 keV energy band were also extracted for observations x1-x4, as described in Paper I. Strong solar flaring contaminated parts of observation x3, restricting the good data to
and centred on XMMU J004303+4115 while the background region was an equivalent source-free region on the same CCD and at a similar offset from the optical axis. The lightcurves were accumulated with 2.6 s binning. Background-subtracted, summed EPIC lightcurves, were then produced following the procedures laid out in Paper I. PN energy spectra from the source and background regions in the 0.3-10 keV energy band were also extracted for observations x1-x4, as described in Paper I. Strong solar flaring contaminated parts of observation x3, restricting the good data to ![]() 25 ks.
25 ks.
In order to assess the contributions of the two sources seen with Chandra to the properties of XMMU J004303+4115, we analysed 35 Chandra observations; 15 observations used the ACIS-I configuration, 3 used ACIS-S and 17 were made with the HRC-I. Of these, 11 observations occurred at similar times to the XMM-Newton observations. From the 35 observations, we produced long-term lightcurves for r2-3 and r2-4 in order to study the variability of these objects. In particular, we examined their contributions to the observations close to the XMM-Newton observations, to associate the variability and contributions to the X-ray luminosity with a particular source.
The date, configuration mode and exposure for each Chandra observation are listed in Table 2, avaialable at the CDS; particular attention was paid to those Chandra observations within 30 days of an XMM-Newton observation: this interval was chosen to maximise the data available on r2-3 and r2-4 at
similar epochs to x1-x4, and is not physically motivated.
Chandra lightcurves were extracted in the 0.3-7.0 keV energy band from circular extraction regions with 3
![]() radii around r2-3 and r2-4 for each observation, with 50 s binning. To do this, a binned image was created using DMCOPY; ACIS and HRC images were binned by factors
of 2 and 10 respectively. Events files were then created in the 0.3-7 keV band for r2-3 and r2-4 with DMCOPY, filtering with the relevant extraction region. Finally, lightcurves were created for each source using LIGHTCURVE.
Lightcurves from nearby, source-free regions of the same size yielded
radii around r2-3 and r2-4 for each observation, with 50 s binning. To do this, a binned image was created using DMCOPY; ACIS and HRC images were binned by factors
of 2 and 10 respectively. Events files were then created in the 0.3-7 keV band for r2-3 and r2-4 with DMCOPY, filtering with the relevant extraction region. Finally, lightcurves were created for each source using LIGHTCURVE.
Lightcurves from nearby, source-free regions of the same size yielded ![]() 1 photon per observation, hence the background contribution was negligible. Long-term lightcurves were then constructed for r2-3 and r2-4, representing each observation with a single bin. A detail of the ACIS-I image from observation c15 is presented in Fig. 1; r2-3 and r2-4 are shown, and a circle with a 20
1 photon per observation, hence the background contribution was negligible. Long-term lightcurves were then constructed for r2-3 and r2-4, representing each observation with a single bin. A detail of the ACIS-I image from observation c15 is presented in Fig. 1; r2-3 and r2-4 are shown, and a circle with a 20
![]() radius is centred between them, defining the source extraction region for the XMM-Newton observations. A 3
radius is centred between them, defining the source extraction region for the XMM-Newton observations. A 3
![]() circle is shown in the bottom left corner to indicate the size of the extraction regions used in the Chandra observations.
circle is shown in the bottom left corner to indicate the size of the extraction regions used in the Chandra observations.
X-ray spectra were extracted from ACIS-I and ACIS-S observations of r2-3 and r2-4 using PSEXTRACT, which also produced corresponding response matrices and ancillary response files. These spectra were grouped to have a minimum of 15 counts per bin, or 10 counts per bin if the total number of counts ![]() 100. No spectra were obtained from HRC-I because it is not designed for spectral work.
100. No spectra were obtained from HRC-I because it is not designed for spectral work.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0661fig2.eps}
\end{figure}](/articles/aa/full/2004/31/aa0661/Timg24.gif) |
Figure 2: Power density spectra from the 0.3-10 keV lightcurves of XMMU J004303+4115 from observations x1 (panel a)), x3 (panel b)) and x4 (panel c)). We see that there is more low-frequency power, and a steeper drop at high frequencies, in x3 and x4 than in x1. The PDS are Leahy normalised, so the Poisson noise has a power of 2. We believe the PDS of observation x1 is due to r2-4 alone (Sect. 3.3). |
Power density spectra were obtained from the 0.3-10 keV lightcurves of observations x1, x3 and x4, with (10.4 s)-1 resolution and 512 frequency bins, as described in Paper I.
The resulting PDS are presented in Fig. 2; observation x2 was too short to yield useful PDS data. We fitted the PDS with single power laws, and while the PDS of observation x1 is well fitted (![]() /d.o.f. = 7.7/9), fits to the PDS of x3 (
/d.o.f. = 7.7/9), fits to the PDS of x3 (![]() /d.o.f. = 26/9) and x4 (
/d.o.f. = 26/9) and x4 (![]() /d.o.f. = 64/9) are rejected at levels of 0.2% and
/d.o.f. = 64/9) are rejected at levels of 0.2% and ![]()
![]() % respectively.
We see that a type B PDS is observed in x1, where the combined EPIC intensity of XMMU J004303+4115 is 0.16 count s-1 in the 0.3-10 keV band and yet a type A PDS is observed in x4, where its intensity is 0.37 count s-1, i.e. over twice as bright as in x1. We also see a type A PDS in observation x3, where the intensity is 0.15 count s-1, very similar to the count rate in x1; hence we know that the lack of a broken PDS in x1 is not due to a lack of counts. Since we know that XMMU J004303+4115 is in fact composed of two X-ray sources, we can only understand these observations if the component responsible for the type A PDS is absent in x1 but present in x3 and x4.
% respectively.
We see that a type B PDS is observed in x1, where the combined EPIC intensity of XMMU J004303+4115 is 0.16 count s-1 in the 0.3-10 keV band and yet a type A PDS is observed in x4, where its intensity is 0.37 count s-1, i.e. over twice as bright as in x1. We also see a type A PDS in observation x3, where the intensity is 0.15 count s-1, very similar to the count rate in x1; hence we know that the lack of a broken PDS in x1 is not due to a lack of counts. Since we know that XMMU J004303+4115 is in fact composed of two X-ray sources, we can only understand these observations if the component responsible for the type A PDS is absent in x1 but present in x3 and x4.
| Obs. | Lb | |||
| x1 | 0.6(2) | 2.15(15) | 3.0(2) | 37/34 |
| x2 | 1.0(2) | 1.91(15) | 4.4(3) | 36/34 |
| x3 | 1.1(2) | 1.98(15) | 3.3(2) | 16/18 |
| x4 | 1.4(2) | 1.89(15) | 12.0(7) | 17/34 |
|
a An absorbed power law model was used, with line-of-sight absorption
(in units of 1021 atom cm-2) and spectral index b 0.3-10 keV luminosity/1037 erg s-1. |
We then analysed the energy spectra from the Chandra ACIS-I and ACIS-S observations. The line-of-sight absorption was not well constrained and was fixed at
![]() atom cm-2, to agree with XMM-Newton values. The spectral index of r2-3 varied over the range 1.6-2.6, while the spectral index of r2-4 ranged over 1.3-2.3. The best fit spectral index,
atom cm-2, to agree with XMM-Newton values. The spectral index of r2-3 varied over the range 1.6-2.6, while the spectral index of r2-4 ranged over 1.3-2.3. The best fit spectral index, ![]() /d.o.f. and 0.3-7 keV fluxes are provided for r2-3 and r2-4 in Table 4. There was no significant correlation between spectral index and intensity within the limits of the data, so the mean values were used in converting HRC-I intensities into ACIS-I intensities: spectral indices of
/d.o.f. and 0.3-7 keV fluxes are provided for r2-3 and r2-4 in Table 4. There was no significant correlation between spectral index and intensity within the limits of the data, so the mean values were used in converting HRC-I intensities into ACIS-I intensities: spectral indices of
![]() and
and
![]() were used for r2-3 and r2-4 respectively.
were used for r2-3 and r2-4 respectively.
The longterm lightcurve of r2-3 is quite unlike the lightcurves of classical black hole LMXBs, which are characterised by short outbursts of activity where the intensity decays exponentially over several weeks, separated by years of quiescence (McClintock & Remillard 2003). Of the Galactic black hole LMXBs, it most resembles GX 339-4 (dynamically confirmed as a black hole by Hynes et al. 2003). Zdziarski et al. (2004) present long-term lightcurves of GX 339-4 spanning ![]() 20 years from the Ginga, RXTE and CGRO satellites; around 15 outbursts were observed, varying dramatically in brightness and duration, and in the separation between outbursts. The behaviour of r2-3 (Fig. 3) is similar to that exhibited by GX 339-4 in the interval
20 years from the Ginga, RXTE and CGRO satellites; around 15 outbursts were observed, varying dramatically in brightness and duration, and in the separation between outbursts. The behaviour of r2-3 (Fig. 3) is similar to that exhibited by GX 339-4 in the interval
![]() -51 000, where GX 339-4 appears to be mostly active, with short intensity dips (Zdziarski et al. 2004).
-51 000, where GX 339-4 appears to be mostly active, with short intensity dips (Zdziarski et al. 2004).
| Observation |
|
|
|
|
||
| c1 | 2.1(2) | 3.3 | 11/18 | 1.7(2) | 2.4 | 13/14 |
| c3 | 1.4(3) | 3.9 | 16/10 | |||
| c5 | 1.9(3) | 2.5 | 16/12 | 1.5(3) | 4.1 | 20/12 |
| c7 | 2.1(4) | 2.2 | 6/9 | 1.8(3) | 2.5 | 6/11 |
| c9 | 1.7(3) | 3.4 | 15/15 | 1.5(4) | 3.4 | 12/6 |
| c12 | 1.7(2) | 3.0 | 20/11 | 2.3(4) | 0.9 | 6/7 |
| c14 | 1.7(2) | 4.0 | 11/11 | 1.5(2) | 3.0 | 10/12 |
| c15 | 1.6(2) | 4.5 | 11/16 | 1.8(2) | 3.0 | 12/11 |
| c17 | 1.6(2) | 2.0 | 11/10 | |||
| c22 | 2.2(9) | 2.0 | 4/3 | 1.9(5) | 1.8 | 3/6 |
| c23 | 2.6(7) | 0.7 | 1/3 | 1.6(2) | 4.0 | 4/11 |
| c28 | 1.8(3) | 3.8 | 8/10 | 2.2(6) | 1.9 | 10/6 |
| c29 | 1.5(3) | 4.4 | 6/9 | 1.4(2) | 3.5 | 11/11 |
| c31 | 2.1(3) | 3.0 | 11/9 | 1.3(2) | 3.7 | 13/9 |
| c34 | 1.9(3) | 2.3 | 6/7 | 2.3(4) | 2.0 | 8.5/10 |
| c35 | 2.0(4) | 2.7 | 3/7 | 1.7(3) | 3.5 | 5/7 |
|
a An absorbed power law model was used, with line-of-sight absorption b 0.3-10 keV luminosity/1037 erg s-1. |
The longterm lightcurve of r2-4, on the other hand, shows modulation on a ![]() 400 day time-scale. It is similar to the longterm RXTE ASM lightcurve of 4U 1820-30, an ultracompact neutron star LMXB in a Galactic globular cluster (Stella et al. 1987). This source exhibits brief low intensity states superposed onto cyclical variability on a
400 day time-scale. It is similar to the longterm RXTE ASM lightcurve of 4U 1820-30, an ultracompact neutron star LMXB in a Galactic globular cluster (Stella et al. 1987). This source exhibits brief low intensity states superposed onto cyclical variability on a ![]() 170 day period featuring a sharp rise and shallow decay (Simon 2003).
170 day period featuring a sharp rise and shallow decay (Simon 2003).
The ACIS-I equivalent intensities of r2-3 + r2-4 in x1-x4 and the nearby Chandra observations are presented in Fig. 4.
Table 5 lists the intensities of XMMU J004303+4115 in observations x1-x4 with the individual intensities of r2-3 and r2-4 in neighbouring Chandra observations; the fractional contribution of r2-3 to the total intensity is also given.
Observations x3 and x4 have very similar intensities to the neighbouring Chandra observations (within 0.5![]() ), so the fractional contributions of r2-3 and r2-4 to these XMM-Newton observations were assumed to be the same as in the nearest Chandra observation. However, the intensity in x1 is well below the intensities of any neighbouring Chandra observation; the intensity dropped by 67% (11
), so the fractional contributions of r2-3 and r2-4 to these XMM-Newton observations were assumed to be the same as in the nearest Chandra observation. However, the intensity in x1 is well below the intensities of any neighbouring Chandra observation; the intensity dropped by 67% (11![]() )
in 24 days then increased by 200% (12
)
in 24 days then increased by 200% (12![]() )
in 7 days.
Instead, the intensity and X-ray spectrum of x1 are consistent with that of r2-4 in c13, suggesting that r2-3 has all but disappeared, as in observations c3, c17 and c20 where the significance of detecting r2-3 is <3
)
in 7 days.
Instead, the intensity and X-ray spectrum of x1 are consistent with that of r2-4 in c13, suggesting that r2-3 has all but disappeared, as in observations c3, c17 and c20 where the significance of detecting r2-3 is <3![]() .
.
This interpretation is supported by the fact that r2-3 contributed ![]() 70% of the intensity in c11 and c12, but only
70% of the intensity in c11 and c12, but only ![]() % in c13 (Table 5), rising to
% in c13 (Table 5), rising to ![]() % in c14. The spectral index,
% in c14. The spectral index, ![]() ,
of r2-3 is
,
of r2-3 is ![]() in c12 and c14, while for r2-4,
in c12 and c14, while for r2-4,
![]() in c12 and
in c12 and ![]() in c14. In x1,
in c14. In x1,
![]() ,
which is considerably softer than in x2-x4 and consistent with that of r2-4 alone.
We cannot be sure how the two sources contribute to XMMU J004303+4115 in observation x1, but given the observed trends in observations c12-c14 the most likely explanation of the 11
,
which is considerably softer than in x2-x4 and consistent with that of r2-4 alone.
We cannot be sure how the two sources contribute to XMMU J004303+4115 in observation x1, but given the observed trends in observations c12-c14 the most likely explanation of the 11![]() drop in intensity between c12 and x1 is the fading to invisibility of r2-3.
drop in intensity between c12 and x1 is the fading to invisibility of r2-3.
![\begin{figure}
\par\includegraphics[angle=270,width=8.2cm,clip]{0661fig4.ps}
\end{figure}](/articles/aa/full/2004/31/aa0661/Timg45.gif) |
Figure 4: A comparison of XMM-Newton observations of XMMU J004303+4115 ( open squares) with neighbouring Chandra ACIS-I, ACIS-S and HRC-I observations. The XMM-Newton intensities were converted to ACIS-I count rates using PIMMS; for conversion we assumed a power law spectral model, using the best fit parameters listed in Table 3. |
| Observation | MJD |
|
|
|
|
| c11 | 51690 | 0.047(10) | 0.017(5) | 0.7(2) | |
| c12 | 51696 | 0.061(3) | 0.021(2) | 0.74(5) | |
| c13 | 51716 | 0.017(5) | 0.026(8) | 0.35(13) | |
| x1 | 51720 | 0.027(1) | |||
| c14 | 51727 | 0.044(3) | 0.037(3) | 0.55(5) | |
| c21 | 51879 | 0.010(1) | 0.048(5) | 0.17(2) | |
| c22 | 51891 | 0.015(2) | 0.021(3) | 0.42(7) | |
| x2 | 51908 | 0.034(1) | |||
| c23 | 51922 | 0.009(2) | 0.036(2) | 0.20(5) | |
| c26 | 52070 | 0.024(8) | 0.010(4) | 0.7(3) | |
| c27 | 52070 | 0.017(2) | 0.016(2) | 0.52(8) | |
| x3 | 52089 | 0.029(1) | |||
| x4 | 52280 | 0.091(1) | |||
| c31 | 52282 | 0.039(3) | 0.049(3) | 0.44(4) | |
| c32 | 52290 | 0.012(5) | 0.062(14) | 0.16(7) |
|
a Equivalent 0.3-7 keV ACIS-I intensity/count s-1. b c |
In diagnosing the nature of r2-3 we first need to be certain that it is indeed within the M 31 galaxy. We applied a column density of
![]() cm-2 and a spectral index of 1.78 to the HRC-I observations that yielded the maximum and minimum ACIS-I equivalent count rates of r2-3 and obtained a flux range of 0.012-
cm-2 and a spectral index of 1.78 to the HRC-I observations that yielded the maximum and minimum ACIS-I equivalent count rates of r2-3 and obtained a flux range of 0.012-
![]() erg cm-2 s-1 in the 0.3-10 keV band using PIMMS. This corresponds to a luminosity range of
0.08-
erg cm-2 s-1 in the 0.3-10 keV band using PIMMS. This corresponds to a luminosity range of
0.08-
![]() erg s-1 for a location in M 31. If it was local, it would be most likely to be within 1 kpc, i.e. <3 times the scale-height of the Galactic disc, since M 31 is 21.6
erg s-1 for a location in M 31. If it was local, it would be most likely to be within 1 kpc, i.e. <3 times the scale-height of the Galactic disc, since M 31 is 21.6
![]() out of the Galactic plane and 120
out of the Galactic plane and 120
![]() from the Galactic Centre. In this situation, the luminosity would be >6 orders of magnitude smaller, and hence up to 2 orders of magnitude fainter than the faintest known persistent Galactic LMXB (Wilson et al. 2003).
It would also be up to a factor of
from the Galactic Centre. In this situation, the luminosity would be >6 orders of magnitude smaller, and hence up to 2 orders of magnitude fainter than the faintest known persistent Galactic LMXB (Wilson et al. 2003).
It would also be up to a factor of ![]() 3 fainter than the faintest black hole X-ray transient in quiescence (Tomsick et al. 2003, and references within). It is likely that if r2-3 were local, it would have an optical counterpart; known absolute V magnitudes (MV) of persistent Galactic LMXBs range from -2.5 to 5.6 (van Paradijs & McClintock 1995), and the spectral types of the secondary stars in most black hole X-ray transients have been obtained in quiescence (Charles & Coe 2003), with
3 fainter than the faintest black hole X-ray transient in quiescence (Tomsick et al. 2003, and references within). It is likely that if r2-3 were local, it would have an optical counterpart; known absolute V magnitudes (MV) of persistent Galactic LMXBs range from -2.5 to 5.6 (van Paradijs & McClintock 1995), and the spectral types of the secondary stars in most black hole X-ray transients have been obtained in quiescence (Charles & Coe 2003), with
![]() -9.7. Hence, if r2-3 were local, we would expect to see an optical counterpart with
-9.7. Hence, if r2-3 were local, we would expect to see an optical counterpart with
![]() .
However, the nearest optical source in the HST catalogue of Haiman et al. (1994) is 79
.
However, the nearest optical source in the HST catalogue of Haiman et al. (1994) is 79
![]() away, with a
mv = 20.6; hence any optical counterpart to r2-3 would have to be fainter than this. Thus r2-3 is unlikely to be local.
In addition, its PDS rules out the possibility that it is a background AGN, as they exhibit spectral breaks at 10-6-10-5 Hz (Uttley et al. 2002) rather than at the
away, with a
mv = 20.6; hence any optical counterpart to r2-3 would have to be fainter than this. Thus r2-3 is unlikely to be local.
In addition, its PDS rules out the possibility that it is a background AGN, as they exhibit spectral breaks at 10-6-10-5 Hz (Uttley et al. 2002) rather than at the ![]() 0.03 Hz seen here. We therefore conclude that r2-3 is located in M 31.
0.03 Hz seen here. We therefore conclude that r2-3 is located in M 31.
By showing that we observe a type A PDS from r2-3 at a luminosity that is too high for a neutron star LMXB we can classify the primary as a black hole. To do this, we must obtain a value for ![]() ,
and assume that this applies to all LMXBs. Then we must show that r2-3 exhibits a type A PDS at a luminosity greater than
,
and assume that this applies to all LMXBs. Then we must show that r2-3 exhibits a type A PDS at a luminosity greater than ![]() for any neutron star.
for any neutron star.
In the first instance, we looked at seven X-ray sources associated with globular clusters in x4, since they are likely to contain 1.4 ![]() neutron stars. None of them exhibited type A PDS; the luminosity range was
neutron stars. None of them exhibited type A PDS; the luminosity range was ![]() 2-
2-
![]() erg s-1 (Paper I). Also, a type B PDS was exhibited by XMMU J004303+4115
in observation x1 at
erg s-1 (Paper I). Also, a type B PDS was exhibited by XMMU J004303+4115
in observation x1 at
![]() erg s-1 (which we associate with r2-4 alone, see
Sect. 3). These results suggest that
erg s-1 (which we associate with r2-4 alone, see
Sect. 3). These results suggest that ![]()
![]()
![]() erg s-1; hence
erg s-1; hence
![]() ,
assuming hydrogen accretion onto a 1.4
,
assuming hydrogen accretion onto a 1.4 ![]() neutron star.
neutron star.
| Observation |
|
|
Type |
| x1 | 0 | 3 | B |
| x3 | 1.7 | 1.6 | A |
| x4 | 5.3 | 6.7 | A |
We obtained a vital clue to ![]() from the Galactic neutron star LMXB 4U 1705-44.
Langmeier et al. (1989) analysed data from four EXOSAT observations of 4U 1705-44; they found that it exhibited a type A PDS in the faintest observation but a type B PDS in the next faintest. In their previous analysis of the observations (Langmeier et al. 1987), they obtained 1-11 keV fluxes of
from the Galactic neutron star LMXB 4U 1705-44.
Langmeier et al. (1989) analysed data from four EXOSAT observations of 4U 1705-44; they found that it exhibited a type A PDS in the faintest observation but a type B PDS in the next faintest. In their previous analysis of the observations (Langmeier et al. 1987), they obtained 1-11 keV fluxes of
![]() and
and
![]() erg cm-2 s-1 for these two observations. Hence an accurate distance to 4U 1705-44 would yield a tight constraint on
erg cm-2 s-1 for these two observations. Hence an accurate distance to 4U 1705-44 would yield a tight constraint on ![]() .
Christian & Swank (1997) estimate a distance of 11 kpc, using the most luminous X-ray burst as a standard candle; this constitutes an upper limit to the distance (see e.g. Kuulkers et al. 2003, and references within). Cornelisse et al. (2003) also estimate the distance to 4U 1705-44 using bursts, but give a distance of 8.9 kpc with an assumed uncertainty of 30%. Hence
.
Christian & Swank (1997) estimate a distance of 11 kpc, using the most luminous X-ray burst as a standard candle; this constitutes an upper limit to the distance (see e.g. Kuulkers et al. 2003, and references within). Cornelisse et al. (2003) also estimate the distance to 4U 1705-44 using bursts, but give a distance of 8.9 kpc with an assumed uncertainty of 30%. Hence
![]() .
.
Similarly, GS 2023+338 (V404 Cygni) is a Galactic black hole LMXB; the most likely mass for the primary is 12 ![]() (Shahbaz et al. 1994). It was discovered with Ginga during an outburst in 1989 (Makino 1989) and exhibited type A PDS at 2-37 keV luminosities >
(Shahbaz et al. 1994). It was discovered with Ginga during an outburst in 1989 (Makino 1989) and exhibited type A PDS at 2-37 keV luminosities >
![]() erg s-1 (Miyamoto et al. 1992; Oosterbroek et al. 1997, and references within). The X-ray spectrum for V404 Cygni was described by a power law with
erg s-1 (Miyamoto et al. 1992; Oosterbroek et al. 1997, and references within). The X-ray spectrum for V404 Cygni was described by a power law with
![]() -1.4 (Miyamoto et al. 1992), hence
-1.4 (Miyamoto et al. 1992), hence
![]() in the 0.3-10 keV band.
in the 0.3-10 keV band.
These three sets of results are all consistent with
![]() in the 0.3-10 keV band; this supports the idea of a constant
in the 0.3-10 keV band; this supports the idea of a constant ![]() proposed by vdK94.
proposed by vdK94.
Now, r2-3 appears to exhibit a type A PDS at a 0.3-10 keV luminosity of
![]() erg s-1; this is a factor of
erg s-1; this is a factor of ![]() 3 higher than
3 higher than ![]() for a 1.4
for a 1.4 ![]() neutron star. Indeed, for the maximum mass of a neutron star (i.e. 3.1
neutron star. Indeed, for the maximum mass of a neutron star (i.e. 3.1 ![]() ,
Krishan & Kumar 1978),
,
Krishan & Kumar 1978),
![]() erg s-1. Known stellar-mass black holes have masses over the range 4-15
erg s-1. Known stellar-mass black holes have masses over the range 4-15 ![]() ,
hence our results from r2-3 are consistent with
,
hence our results from r2-3 are consistent with
![]() if the primary is a black hole.
if the primary is a black hole.
Acknowledgements
The authors would like to thank the anonymous referee for suggestions that led to significant improvements to the paper. This work is supported by PPARC.
|
Obs. |
Date (obs. ID) | MJD | Mode | Exposure | Separation |
| c1 | 13/10/99 (303) | 51464 | ACIS-I | 12 ks | |
| c2 | 30/11/99 (267) | 51512 | HRC-I | 1.3 ks | |
| c3 | 11/12/99 (305) | 51523 | ACIS-I | 4.2 ks | |
| c4 | 23/12/99 (268) | 51535 | HRC-I | 5.2 ks | |
| c5 | 27/12/99 (306) | 51539 | ACIS-I | 4.2 ks | |
| c6 | 19/01/00 (269) | 51562 | HRC-I | 1.2 ks | |
| c7 | 29/01/00 (307) | 51572 | ACIS-I | 4.2 ks | |
| c8 | 13/02/00 (270) | 51587 | HRC-I | 1.5 ks | |
| c9 | 16/02/00 (308) | 51590 | ACIS-I | 4.1 ks | |
| c10 | 08/03/00 (271) | 51611 | HRC-I | 2.5 ks | |
| c11* | 26/05/00 (272) | 51690 | HRC-I | 1.2 ks | -30 days |
| c12* | 01/06/00 (309) | 51696 | ACIS-S | 5.2 ks | -24 days |
| c13* | 21/06/00 (273) | 51716 | HRC-I | 1.2 ks | -4 days |
| c14* | 02/07/00 (310) | 51727 | ACIS-S | 5.1 ks | +7 days |
| c15 | 29/07/00 (311) | 51754 | ACIS-I | 5.0 ks | |
| c16 | 18/08/00 (275) | 51774 | HRC-I | 1.2 ks | |
| c17 | 27/08/00 (312) | 51783 | ACIS-I | 4.7 ks | |
| c18 | 11/09/00 (276) | 51798 | HRC-I | 1.2 ks | |
| c19 | 12/10/00 (277) | 51829 | HRC-I | 1.2 ks | |
| c20 | 17/11/00 (278) | 51865 | HRC-I | 1.2 ks | |
| c21* | 31/11/00 (1912) | 51879 | HRC-I | 47 ks | -27 days |
| c22* | 13/12/00 (1581) | 51891 | ACIS-I | 4.5 ks | -15 days |
| c23* | 13/01/01 (1854) | 51922 | ACIS-S | 4.8 ks | +16 days |
| c24 | 01/02/01 (1569) | 51941 | HRC-I | 1.2 ks | |
| c25 | 18/02/01 (1582) | 51958 | ACIS-I | 4.4 ks | |
| c26* | 10/06/01 (1570) | 52070 | HRC-I | 1.2 ks | -19 days |
| c27* | 10/06/01 (1583) | 52070 | ACIS-I | 5.0 ks | -19 days |
| c28 | 31/08/01 (1577) | 52152 | ACIS-I | 5.0 ks | |
| c29 | 09/11/01 (1585) | 52222 | ACIS-I | 5.0 ks | |
| c30 | 19/11/01 (2904) | 52232 | HRC-I | 1.2 ks | |
| c31* | 08/01/02 (2897) | 52282 | ACIS-I | 5.0 ks | +1.5 days |
| c32* | 16/01/02 (2905) | 52290 | HRC-I | 1.1 ks | +10 days |
| c33 | 02/06/02 (2906) | 52427 | HRC-I | 1.2 ks | |
| c34 | 02/06/02 (2898) | 52427 | ACIS-I | 5.0 ks | |
| c35 | 11/08/02 (4360) | 52497 | ACIS-I | 5.0 ks |