A&A 423, 1-12 (2004)
DOI: 10.1051/0004-6361:20040220
Protostellar angular momentum evolution during gravoturbulent fragmentation
A.-K. Jappsen - R. S. Klessen
Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
Received 7 February 2004 / Accepted 26 April 2004
Abstract
Using hydrodynamic simulations we investigate the rotational
properties and angular momentum evolution of prestellar and protostellar
cores formed from gravoturbulent fragmentation of interstellar gas clouds.
We find the specific angular momentum j of molecular cloud cores in
the prestellar phase to be on average
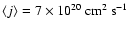 in our
models. This is comparable to the observed
values. A fraction of those cores is gravitationally unstable and goes
into collapse to build up protostars and protostellar systems, which then have
in our
models. This is comparable to the observed
values. A fraction of those cores is gravitationally unstable and goes
into collapse to build up protostars and protostellar systems, which then have
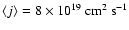 .
This is one order
of magnitude lower than their parental cores and in agreement with
observations of main-sequence binaries.
The loss of specific angular momentum during collapse is mostly due to
gravitational torques exerted by the ambient turbulent flow as well as by
mutual protostellar encounters in a dense cluster environment. Magnetic
torques are not included in our models, these would lead to even larger
angular momentum transport.
The ratio of rotational to gravitational energy
.
This is one order
of magnitude lower than their parental cores and in agreement with
observations of main-sequence binaries.
The loss of specific angular momentum during collapse is mostly due to
gravitational torques exerted by the ambient turbulent flow as well as by
mutual protostellar encounters in a dense cluster environment. Magnetic
torques are not included in our models, these would lead to even larger
angular momentum transport.
The ratio of rotational to gravitational energy  in
cloud cores that go into gravitational collapse turns out to be
similar to the observed values. We
find that
in
cloud cores that go into gravitational collapse turns out to be
similar to the observed values. We
find that  is roughly conserved during the main collapse phase. This
leads to the correlation
is roughly conserved during the main collapse phase. This
leads to the correlation
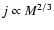 ,
between specific angular
momentum j and core mass M. Although the temporal evolution of the
angular momentum of individual protostars or protostellar systems is complex
and highly time-variable, this correlation holds well in a statistical sense
for a wide range of turbulent environmental parameters. In addition, high
turbulent Mach numbers result in the formation of more numerous protostellar
cores with, on average, lower mass. Therefore, models with larger Mach
numbers result in cores with lower specific angular momentum. We find,
however, no dependence on the spatial scale of the turbulence. Our models
predict a close correlation between the angular momentum vectors of
neighboring protostars during their initial accretion phase. Possible
observational signatures are aligned disks and parallel outflows. The latter
are indeed observed in some low-mass isolated Bok globules.
,
between specific angular
momentum j and core mass M. Although the temporal evolution of the
angular momentum of individual protostars or protostellar systems is complex
and highly time-variable, this correlation holds well in a statistical sense
for a wide range of turbulent environmental parameters. In addition, high
turbulent Mach numbers result in the formation of more numerous protostellar
cores with, on average, lower mass. Therefore, models with larger Mach
numbers result in cores with lower specific angular momentum. We find,
however, no dependence on the spatial scale of the turbulence. Our models
predict a close correlation between the angular momentum vectors of
neighboring protostars during their initial accretion phase. Possible
observational signatures are aligned disks and parallel outflows. The latter
are indeed observed in some low-mass isolated Bok globules.
Key words: stars: formation - methods: numerical - hydrodynamics - turbulence
- ISM: clouds
Angular momentum plays a pivotal role in star formation. The amount
of specific angular momentum determines whether a collapsing
protostellar core will form a single star or a binary or higher-order
multiple system.
Stars are thought to form by gravoturbulent fragmentation in
interstellar clouds. The supersonic turbulence ubiquitously observed
in molecular gas generates strong density fluctuations with gravity
taking over in the densest and most massive regions. Once gas clumps
become gravitationally unstable,
collapse sets in and the central
density increases until a protostellar object forms and grows in mass
via accretion from the
infalling envelope. Various aspects of the
relation between supersonic turbulence and star formation have been
discussed, e.g., by Hunter & Fleck (1982), Elmegreen (1993), Larson (1995),
Padoan (1995), Ballesteros-Paredes et al. (1999b,2003,1999a), Padoan & Nordlund (2002,1999),
Vázquez-Semadeni et al. (2000), Klessen et al. (2000), Heitsch et al. (2001), Klessen (2001a,b),
Gammie et al. (2003), or Vázquez-Semadeni et al. (2003). In particular see the reviews by
Larson (2003) and Mac Low & Klessen (2004).
This dynamic picture of gravoturbulent star formation challenges the
so called "standard theory'' where stars build up from the
"inside-out'' collapse of singular isothermal spheres, which are
generally assumed to result from the quasistatic contraction of
magnetically supported cloud cores due to ambipolar diffusion
(Shu 1977; Shu et al. 1987). This picture, however, has always
received strong criticism (e.g.,Whitworth & Summers 1985; Whitworth et al. 1996; Nakano 1998). In particular, it seems strongly
biased toward the formation of single stars (Whitworth et al. 1996) which is in
contradiction to the observational fact that most (if not all) stars
form as members of binary or higher-order multiple systems (see,
e.g., the reviews by Mathieu et al. 2000; Bodenheimer et al. 2000, and references therein).
Gravitational collapse in the astrophysical context always involves solving
the angular momentum problem. It results from the blatant discrepancy between
the specific angular momentum observed in low-density gas on large scales and
the amount of rotation present after collapse (Spitzer 1968; Bodenheimer 1995).
The source
of angular momentum on large scales lies in the differential rotation of the
galactic disk and, closely related to that, on intermediate to small scales it
results from the high degree of vorticity inextricably adherent to turbulent
flows.
The typical specific angular momentum j of molecular cloud material,
e.g., on scales of about 1 pc is
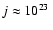 cm2 s-1, while
on scales of cloud cores, say below 0.1 pc, it is of order 1021 cm2 s-1. A
binary G star with an orbital period of 3 days
has
cm2 s-1, while
on scales of cloud cores, say below 0.1 pc, it is of order 1021 cm2 s-1. A
binary G star with an orbital period of 3 days
has
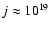 cm2 s-1, while the spin of a typical T Tauri
star is a few
cm2 s-1, while the spin of a typical T Tauri
star is a few
 cm2 s-1. Our own Sun rotates only with
cm2 s-1. Our own Sun rotates only with
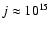 cm2 s-1. That means that during the process of star
formation most of the initial angular momentum is removed from the collapsed
object.
cm2 s-1. That means that during the process of star
formation most of the initial angular momentum is removed from the collapsed
object.
The presence of magnetic fields, in principle, provides a viable mechanism for
locally reducing the angular momentum through magnetic braking. This was
treated approximately by Ebert et al. (1960), and later calculated accurately by
Mouschovias & Paleologou (1980,1979). The criterion for effective braking is essentially that
the outgoing helical Alfvén waves from the rotating cloud have to couple to
the ambient medium over a volume that contains roughly the same mass as the
cloud itself. For the strong magnetic fields required by the standard theory
of star formation, the deceleration time can be less than the free-fall time,
leading to efficient transfer of angular momentum away from collapsing cores,
and thus, to the formation of single stars. Field strengths small enough to
allow for binary formation cannot provide support against collapse, thus pointing
toward a more dynamic picture of star formation as offered by gravoturbulent
fragmentation.
It is therefore a crucial test for any theory of star formation
whether it can produce the required angular momentum loss during
collapse while at the same time explain the high numbers of binaries
and multiple stellar systems observed (e.g., Halbwachs et al. 2003; Duquennoy & Mayor 1991). In a
semiempirical analysis of isolated binary star formation Fisher (2004)
presented the effects of turbulence in the initial state of the gas on
binary orbital parameters. These properties were in agreement with
observations if a significant loss of angular momentum was assumed. In the current investigation we focus on
models of non-magnetic, supersonically turbulent, self-gravitating
clouds and analyze the time evolution of angular momentum during
formation and subsequent collapse of protostellar cores. Our main
question is whether gravoturbulent fragmentation can solve or at least
ease the so called "angular momentum'' problem without invoking the
presence of magnetic fields.
The structure of the paper is as follows. In Sect. 2
we introduce and discuss the numerical method of calculating the
dynamical cloud evolution and the suite of models included in the
current analysis. In Sect. 3 we present results
on the angular momentum distribution of starless molecular cloud
cores. We call them prestellar cores. Some of them collapse to become
protostellar cores. In Sect. 4 we investigate
the angular momentum evolution of their central protostellar objects.
We report a statistical correlation between specific angular momentum
and mass, and analyze its dependence on the turbulent environment. The
angular momentum vectors of neighboring protostars tend to be aligned,
at least in the early accretion phase. This is discussed in
Sect. 5. Finally, in Sect. 6, we
summarize and conclude.
2 Models of dynamical cloud evolution
2.1 Numerical method
To adequately describe the angular momentum evolution during
gravoturbulent fragmentation, it is prerequisite to resolve formation
and subsequent evolution of collapsing fragments over several orders
of magnitude in density. Due to the stochastic nature of supersonic
turbulence, it is not known in advance where and when local collapse
will occur. We therefore resort to smoothed particle hydrodynamics (SPH) to solve the equations of hydrodynamics. It is a Lagrangian
method with the fluid represented by an ensemble of particles and flow
quantities obtained by local averaging (Benz 1990; Monaghan 1992). The method
is able to resolve large density contrasts as particles are free to
move and so naturally the particle concentration increases in
high-density regions. Because it is computationally prohibitive to
treat the cloud as a whole, we concentrate on subregions within the
cloud and adopt periodic boundary conditions (Klessen 1997). Once the
central region of a collapsing gas clump exceeds a density
contrast of  105, we introduce a "sink particle''
(Bate et al. 1995), which accretes gas from its surrounding and keeps
track of mass and linear and angular momentum. Replacing the high-density
cores with "sink particles'' allows us to follow the angular momentum
evolution of collapsed cores over many free-fall times.
Altogether, the performance and convergence properties of the
method are well understood and tested against analytic models and
other numerical schemes in the context of turbulent
supersonic astrophysical flows. For a
detailed discussion the reader is referred to Bate & Burkert (1997),
Mac Low et al. (1998), Lombardi et al. (1999), Klessen & Burkert (2001,2000) and
Klessen et al. (2000).
105, we introduce a "sink particle''
(Bate et al. 1995), which accretes gas from its surrounding and keeps
track of mass and linear and angular momentum. Replacing the high-density
cores with "sink particles'' allows us to follow the angular momentum
evolution of collapsed cores over many free-fall times.
Altogether, the performance and convergence properties of the
method are well understood and tested against analytic models and
other numerical schemes in the context of turbulent
supersonic astrophysical flows. For a
detailed discussion the reader is referred to Bate & Burkert (1997),
Mac Low et al. (1998), Lombardi et al. (1999), Klessen & Burkert (2001,2000) and
Klessen et al. (2000).
2.2 Models of turbulent self-gravitating clouds
The large observed linewidths in molecular clouds imply the presence
of supersonic velocity fields that carry enough energy to
counterbalance gravity on global scales (see, e.g., the review
by Williams et al. 2000). However, it is known that turbulent energy dissipates
rapidly, roughly on the free-fall timescale (Padoan & Nordlund 1999; Mac Low et al. 1998; Stone et al. 1998).
Unlike previously thought, this is independent of the presence of
magnetic fields. Magnetic fields also do not significantly alter the
efficiency of local collapse for driven turbulence (Heitsch et al. 2001). To
a first approximation, the fields are therefore taken as being
dynamically unimportant in our current models, and are not included.
We also disregard possible feedback effects from the star formation
process itself (like bipolar outflows, stellar winds, or ionizing
radiation from new-born O or B stars). Our analysis of angular
momentum evolution of protostellar cores therefore focuses on the
process of gravoturbulent fragmentation, i.e. on the interplay
between turbulence and self-gravity only.
The suite of models considered here consists of 12 numerical
simulations where turbulence is maintained with constant
root-mean-square Mach numbers in the range
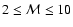 .
This roughly covers the range observed in typical Galactic molecular
clouds. We apply a non-local scheme that inserts energy in a limited
range of wavenumbers at a given rate (Mac Low 1999). We distinguish
between turbulence that carries its energy mostly on large scales, at
wavenumbers
.
This roughly covers the range observed in typical Galactic molecular
clouds. We apply a non-local scheme that inserts energy in a limited
range of wavenumbers at a given rate (Mac Low 1999). We distinguish
between turbulence that carries its energy mostly on large scales, at
wavenumbers
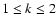 ,
on intermediate scales, i.e.
,
on intermediate scales, i.e.
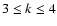 ,
and on small scales with
,
and on small scales with
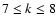 .
The corresponding
wavelengths are
.
The corresponding
wavelengths are
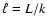 ,
where L is the total size of the
computed volume. The models are labeled mnemonically as M
,
where L is the total size of the
computed volume. The models are labeled mnemonically as M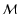 kk, with rms Mach number
kk, with rms Mach number 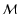 and wavenumber k.
Each of these
simulations contains 205 379 SPH particles. We also
consider a model that is globally unstable and contracts from Gaussian
initial conditions without turbulence (for details
see Klessen & Burkert 2001,2000). It is called GA
and was run with 500 000 particles. The main parameters are
summarized in Table 1.
Note that the final star formation efficiency varies between the
different models, as indicated in Col. 5 of Table 1.
This simply reflects the evolutionary stage at the time when we stop
the calculation. In some cases the accretion timescale is too long
to follow the simulation to high efficiencies.
and wavenumber k.
Each of these
simulations contains 205 379 SPH particles. We also
consider a model that is globally unstable and contracts from Gaussian
initial conditions without turbulence (for details
see Klessen & Burkert 2001,2000). It is called GA
and was run with 500 000 particles. The main parameters are
summarized in Table 1.
Note that the final star formation efficiency varies between the
different models, as indicated in Col. 5 of Table 1.
This simply reflects the evolutionary stage at the time when we stop
the calculation. In some cases the accretion timescale is too long
to follow the simulation to high efficiencies.
Table 1:
Sample parameters, name of the environment used in the text
consisting of the Mach number
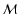 and the driving
scale k (GA denotes the model with Gaussian density), number
and the driving
scale k (GA denotes the model with Gaussian density), number
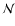 of protostellar objects (i.e. "sink particles'' in
the centers of protostellar cores) at the final stage
of the simulation, percentage of accreted mass at the final stage
of protostellar objects (i.e. "sink particles'' in
the centers of protostellar cores) at the final stage
of the simulation, percentage of accreted mass at the final stage
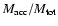 ,
parameter
,
parameter
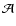 see Eq. (5), parameter
see Eq. (5), parameter
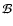 see Eq. (9).
see Eq. (9).
2.3 Physical scaling and naming convention
The models are computed in normalized units using an isothermal
equation of state. Scaled to physical units we adopt a temperature of
11.3 K corresponding to a sound speed
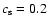 km s-1,
and we use a mean density of
km s-1,
and we use a mean density of
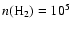 cm-3, which
is typical for star-forming molecular cloud regions (e.g. in
cm-3, which
is typical for star-forming molecular cloud regions (e.g. in
 -Ophiuchi, see Motte et al. 1998). The mean thermal Jeans mass
-Ophiuchi, see Motte et al. 1998). The mean thermal Jeans mass![[*]](/icons/foot_motif.gif) in all models is
in all models is
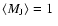
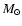 .
The turbulent models contain a
mass of 120
.
The turbulent models contain a
mass of 120 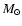 within a cube of size
within a cube of size
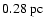 ,
and
the Gaussian model has 220
,
and
the Gaussian model has 220 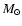 in a volume of
(0.34 pc)3. The global free-fall timescale is
in a volume of
(0.34 pc)3. The global free-fall timescale is
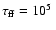 yr, and the simulations cover a density range from
yr, and the simulations cover a density range from
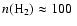 cm-3 in the lowest density regions to
cm-3 in the lowest density regions to
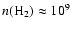 cm-3 where the central
parts of collapsing gas clumps are converted into
"sink particles''.
cm-3 where the central
parts of collapsing gas clumps are converted into
"sink particles''.
Each "sink particle'' defines a control volume with a fixed radius of
560 AU. We cannot resolve the subsequent evolution in its interior.
After 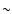 103 yr a protostar will form in the very center.
Because of angular momentum conservation most of the matter that falls
in will assemble in a protostellar disk. It is then transported inward
by viscous and possibly gravitational torques
(e.g., Papaloizou & Lin 1995; Lin & Papaloizou 1996; Bodenheimer 1995). With typical disk sizes of the order
of several hundred AU, the control volume fully encloses both star
and disk. If low angular momentum material is accreted, the disk is
stable and most of the material ends up in the central star. In this
case, the disk simply acts as a buffer and smooths eventual accretion
spikes. It will not delay or prevent the mass growth of the central
star by much. However, if material that falls into the control
volume carries large specific angular momentum, then the mass load
onto the disk is likely to be faster than the inward transport. The disk
grows large and may become gravitationally unstable and fragment.
This will lead to the formation of a binary or higher-order multiple
(Bodenheimer et al. 2000).
103 yr a protostar will form in the very center.
Because of angular momentum conservation most of the matter that falls
in will assemble in a protostellar disk. It is then transported inward
by viscous and possibly gravitational torques
(e.g., Papaloizou & Lin 1995; Lin & Papaloizou 1996; Bodenheimer 1995). With typical disk sizes of the order
of several hundred AU, the control volume fully encloses both star
and disk. If low angular momentum material is accreted, the disk is
stable and most of the material ends up in the central star. In this
case, the disk simply acts as a buffer and smooths eventual accretion
spikes. It will not delay or prevent the mass growth of the central
star by much. However, if material that falls into the control
volume carries large specific angular momentum, then the mass load
onto the disk is likely to be faster than the inward transport. The disk
grows large and may become gravitationally unstable and fragment.
This will lead to the formation of a binary or higher-order multiple
(Bodenheimer et al. 2000).
Throughout this paper, we adopt the following naming convention: in
the pre-collapse phase, we call high-density gas clumps prestellar cores or simply gas clumps. They
build up at the stagnation points of convergent flows. The flows result from
turbulent motion that establishes a complex network of interacting shocks.
The gas clumps are
identified and characterized using a three-dimensional clump-finding
algorithm as described in Appendix A of Klessen & Burkert (2000). The fluctuations in turbulent velocity fields are highly transient.
They can disperse again once the converging flow fades away. Even
clumps that are strongly dominated by gravity may get disrupted by the
passage of a new shock front. For local collapse to result in the
formation of stars, Jeans-unstable, shock-generated density
fluctuations therefore must collapse to sufficiently high densities on
time scales shorter than the typical time interval between two
successive shock passages. We include in our
analysis only Jeans-unstable gas clumps. Angular
momentum is calculated from the internal motions with respect to the
location of the density maximum. These objects correspond to the so
called starless cores observed e.g. by Goodman et al. (1993), Barranco & Goodman (1998),
Jijina et al. (1999), and others. They are thought to collapse and build up a
central protostar or protostellar system in the later stages of evolution. Once collapse has
led to the formation of an embedded protostar (in our scheme
identified by a central "sink particle'') we call the object protostellar core or also protostar. The angular momentum is
obtained as the spin accumulated by the "sink particle'' during its
accretion history. The distribution is best compared with observations
of main-sequence binaries as we expect the unresolved star-disk system
interior to the "sink particle'' to break up into a binary or
higher-order multiple.
3 Molecular cloud clumps and prestellar cores
Figure 1 shows the distribution of the specific
angular momenta of the gas clumps that were identified in the
turbulent environment M6k2 (see Table 1).
![\begin{figure}
\par\includegraphics[width=4.7cm,clip]{0220fig1.eps}
\end{figure}](/articles/aa/full/2004/31/aa0220-04/Timg55.gif) |
Figure 1:
The distribution of specific angular momenta of prestellar cores
formed in our simulations using model M6k2 (non-hatched histogram)
is compared to the distribution of specific angular momenta of
observed molecular cloud cores (hatched distributions). The
observational data were taken in a) from Table 5 in Caselli et al. (2002),
in b) from Table 2 in Goodman et al. (1993), Table 4 in Barranco & Goodman (1998) and
Table A2 in Jijina et al. (1999) and in c) from Table 7 in Pirogov et al. (2003).
We take fj to represent the percentage of the total number of
existing cores in a specific angular momentum bin. |
| Open with DEXTER |
We compare with observational values taken from Caselli et al. (2002) for
a), from Goodman et al. (1993), Barranco & Goodman (1998), Jijina et al. (1999) for b) and from Pirogov et al. (2003) for c). According to Goodman et al. (1993) the values for the
specific angular momenta are obtained by using best-fit velocity
gradients from maps of observed line-center velocities under the
assumption of solid body rotation. The cores in Goodman et al. (1993),
Barranco & Goodman (1998), Jijina et al. (1999) were mapped in the (J, K) = (1, 1) transition
of
 ,
whereas the massive cloud cores in Pirogov et al. (2003)
and the dense cloud cores in Caselli et al. (2002) were mapped in
,
whereas the massive cloud cores in Pirogov et al. (2003)
and the dense cloud cores in Caselli et al. (2002) were mapped in
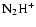 .
As found in Caselli et al. (2002) the two molecular species
trace essentially the same material, especially in starless cores.
Model clumps and observed molecular cloud clumps have comparable mass
spectra (Klessen 2001a) and similar shapes (Klessen & Burkert 2000; Ballesteros-Paredes et al. 2003).
Figure 1 demonstrates that something similar holds for the
distribution of specific angular momenta.
.
As found in Caselli et al. (2002) the two molecular species
trace essentially the same material, especially in starless cores.
Model clumps and observed molecular cloud clumps have comparable mass
spectra (Klessen 2001a) and similar shapes (Klessen & Burkert 2000; Ballesteros-Paredes et al. 2003).
Figure 1 demonstrates that something similar holds for the
distribution of specific angular momenta.
Note that, when transforming from dimensionless code units into physical
scales, the specific angular momentum depends on the mean density nand the temperature T as
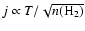 .
In
Fig. 1c, we use our standard scaling
corresponding to regions like the
.
In
Fig. 1c, we use our standard scaling
corresponding to regions like the 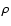 Ophiuchi main cloud (Motte et al. 1998). This is
adequate for the low-mass cores studied by Caselli et al. (2002), and in
Sect. 4 we will furthermore show that the
specific angular momenta of collapsed cores then fall into the right
range for main-sequence binaries.
Ophiuchi main cloud (Motte et al. 1998). This is
adequate for the low-mass cores studied by Caselli et al. (2002), and in
Sect. 4 we will furthermore show that the
specific angular momenta of collapsed cores then fall into the right
range for main-sequence binaries.
We find that the specific angular momenta of prestellar cores have values
between
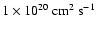 and
and
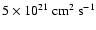 with a mean value of approximately
with a mean value of approximately
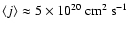 .
This is in good agreement with
the Caselli et al. (2002) sample which has
.
This is in good agreement with
the Caselli et al. (2002) sample which has
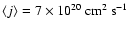 .
Their cloud cores have a mean mass of
.
Their cloud cores have a mean mass of 
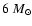 ,
comparable to the core masses in our
simulations. A Kolmogorov-Smirnov (KS) test was performed. We find
that at the
,
comparable to the core masses in our
simulations. A Kolmogorov-Smirnov (KS) test was performed. We find
that at the 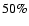 level the distributions are statistically
indistinguishable.
level the distributions are statistically
indistinguishable.
However, the cores observed by Goodman et al. (1993) and Pirogov et al. (2003) trace
lower densities and have higher mean masses of around
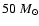 and
and
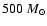 ,
respectively. In Fig. 1b
we therefore use
,
respectively. In Fig. 1b
we therefore use
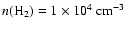 and
T=10 K leading to
and
T=10 K leading to
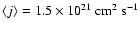 .
This matches the
observations, since Goodman et al. (1993) find
.
This matches the
observations, since Goodman et al. (1993) find
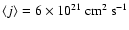 and a median value of
and a median value of
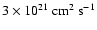 .
The massive cores mapped by
Pirogov et al. (2003) have higher velocity dispersions, higher kinetic
temperatures (
.
The massive cores mapped by
Pirogov et al. (2003) have higher velocity dispersions, higher kinetic
temperatures (
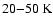 )
and densities
)
and densities
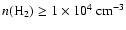 .
The resulting mean specific angular
momentum is
.
The resulting mean specific angular
momentum is
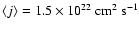 .
Again, adequate scaling in
Fig. 1a results in higher values of j in our
models and leads to better agreement with the observed distribution.
.
Again, adequate scaling in
Fig. 1a results in higher values of j in our
models and leads to better agreement with the observed distribution.
Given the simplified assumptions in our numerical models, we find remarkably good agreement with the observed specific
angular momenta in the prestellar phase. Similar findings are
reported by Gammie et al. (2003). Similar to our study, they follow the
dynamical evolution of an isothermal, self-gravitating, compressible,
turbulent ideal gas. However, they include the effects of magnetic
fields and solve the equations of motion using a grid-based method
(the well-known ZEUS code). Their approach is thus complementary to
ours. The j distribution that results from their simulations
peaks at
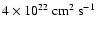 .
They fix the mean
number density at
.
They fix the mean
number density at
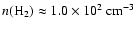 and use
and use
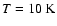 .
Using the same physical scaling
we get very similar values, i.e.
.
Using the same physical scaling
we get very similar values, i.e.
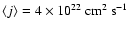 .
.
This mean value also falls in the range of specific angular momenta of cores that form in simulations by Li et al. (2004).
They also use a version of the ZEUS code (ZEUS-MP) to perform
high-resolution, three-dimensional, super-Alfvénic turbulent
simulations to investigate the role of magnetic fields in
self-gravitating core formation within turbulent molecular clouds. Adopting the
same physical scaling as in Gammie et al. (2003), the specific angular momentum of
their cores takes values between
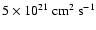 and
and
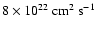 .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0220fig2.eps}
\end{figure}](/articles/aa/full/2004/31/aa0220-04/Timg78.gif) |
Figure 2:
Distribution of specific angular momenta of the protostars or
protostellar systems at different evolutionary phases of the
numerical model M6k2 as denoted by the local star formation
efficiency in percent, a)- d). We compare in e) with the
j-distribution of binaries among nearby G-dwarf stars from
Duquennoy & Mayor (1991) (for details see text) and in f) with the
distribution of specific angular momenta of binaries in the Taurus
star-forming region from Fig. 5 in Simon (1992). Again, fj represents the normalized distribution function. |
| Open with DEXTER |
4 Protostars and protostellar systems
Figure 2 shows the distribution of specific angular
momenta of collapsed cores at four different stages of mass
accretion, ranging from 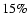 of the total available mass in the
molecular cloud accreted onto collapsed cores in
Fig. 2a to
of the total available mass in the
molecular cloud accreted onto collapsed cores in
Fig. 2a to 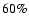 in Fig. 2d. While
the distribution narrows during the evolution, the mean specific
angular momentum remains essentially at the same value
in Fig. 2d. While
the distribution narrows during the evolution, the mean specific
angular momentum remains essentially at the same value
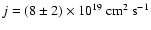 with a range from
with a range from
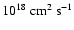 to
to
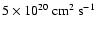 .
The specific angular momenta of the protostellar cores in the
considered model are approximately one order of magnitude smaller than
the ones of the Jeans-unstable clumps, but both distributions join
without a gap. In a statistical sense, there is a continuous transition
as loss of angular momentum occurs during contraction. The range of
specific angular momenta of the protostellar cores agrees
well with the observed values for binaries (e.g., Bodenheimer 1995).
For this reason we compare in Figs. 2a-d the model
distributions with observations of binaries among G-dwarf stars by
Duquennoy & Mayor (1991) in Fig. 2e and with observations of
young binaries in the Taurus star forming region by Simon (1992)
in Fig. 2f.
.
The specific angular momenta of the protostellar cores in the
considered model are approximately one order of magnitude smaller than
the ones of the Jeans-unstable clumps, but both distributions join
without a gap. In a statistical sense, there is a continuous transition
as loss of angular momentum occurs during contraction. The range of
specific angular momenta of the protostellar cores agrees
well with the observed values for binaries (e.g., Bodenheimer 1995).
For this reason we compare in Figs. 2a-d the model
distributions with observations of binaries among G-dwarf stars by
Duquennoy & Mayor (1991) in Fig. 2e and with observations of
young binaries in the Taurus star forming region by Simon (1992)
in Fig. 2f.
Duquennoy & Mayor (1991) derived a Gaussian-type period distribution for their
sample. Based on this distribution we calculated the distribution of
the specific angular momenta using the following equation (see
also Kroupa 1995b, Eq. (10)):
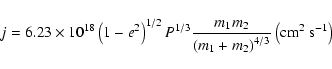 |
(1) |
where masses are in 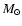 and period P is in days. We used a
primary mass m1 of
and period P is in days. We used a
primary mass m1 of
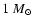 ,
a mean mass ratio
between primary and secondary
q=m2/m1=0.25 and a mean eccentricity
e=0.31.
,
a mean mass ratio
between primary and secondary
q=m2/m1=0.25 and a mean eccentricity
e=0.31.
The resulting distribution has a mean specific angular momentum of
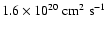 ,
which agrees well with the
values from the simulations. This also holds for
Fig. 2f which was taken from Fig. 5 in
Simon (1992). The mean specific angular momentum here has a value of
,
which agrees well with the
values from the simulations. This also holds for
Fig. 2f which was taken from Fig. 5 in
Simon (1992). The mean specific angular momentum here has a value of
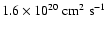 .
The agreement of the
distributions was confirmed by a
.
The agreement of the
distributions was confirmed by a 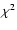 statistical test. Since
our numerical resolution is not sufficient to follow the
subfragmentation of collapsing cores into binary or higher-order
multiple systems, the time evolution of j is an important tool to
evaluate our models. We see a clear progression from the
rotational properties of gas clumps (as discussed in
Sect. 3) to those of the resulting collapsed cores.
A similar correlation is observed between cloud cores (Caselli et al. 2002)
and typical main-sequence binaries (Duquennoy & Mayor 1991). The former may be
the direct progenitors of the latter.
statistical test. Since
our numerical resolution is not sufficient to follow the
subfragmentation of collapsing cores into binary or higher-order
multiple systems, the time evolution of j is an important tool to
evaluate our models. We see a clear progression from the
rotational properties of gas clumps (as discussed in
Sect. 3) to those of the resulting collapsed cores.
A similar correlation is observed between cloud cores (Caselli et al. 2002)
and typical main-sequence binaries (Duquennoy & Mayor 1991). The former may be
the direct progenitors of the latter.
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{0220fig3.eps}
\end{figure}](/articles/aa/full/2004/31/aa0220-04/Timg87.gif) |
Figure 3:
Absolute value of specific angular momentum (solid
line) of our model M6k2 as a) a function of mass and as
b) a function of time for five different protostellar objects with
approximately equal final masses (
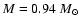 ). In a)
the x-component (dotted line), the y-component
(dashed line) and the z-component
(dashed-dotted line) of the specific angular momenta
are shown as well. For comparison the mass accretion rates onto
the protostar are indicated in b) by a dashed line (associated
y-axis on the right hand side). ). In a)
the x-component (dotted line), the y-component
(dashed line) and the z-component
(dashed-dotted line) of the specific angular momenta
are shown as well. For comparison the mass accretion rates onto
the protostar are indicated in b) by a dashed line (associated
y-axis on the right hand side). |
| Open with DEXTER |
The evolution of the specific angular momenta of individual
protostellar cores can be very complex depending on the rotational
properties of their environment. There is a strong connection to the
time evolution of the mass accretion rate.
In Fig. 3 we select five collapsed cores in model M6k2
with about the same final mass. All of them show a similar evolution
of the specific angular momentum with increasing mass
(Fig. 3a) and time (Fig. 3b). Nevertheless
there are visible differences in the details.
Initially, the specific angular momentum increases with growing mass.
However, at later stages the evolution strongly depends on the secular
properties of the surrounding flow. In cores 43, 96, and 101, for
example, j decreases again after reaching a peak value, while for
cores 17 and 47 j stays close to the maximum value. Depending on
the specific angular momentum of the accreted material, the resulting
protostellar disks are expected to evolve quite differently. For
example, preliminary 2-dimensional hydrodynamic calculations show
that core 17 and core 47 will probably develop a stable disk
(Bodenheimer 2003, private communication). The ratio of rotational to
gravitational energy for the peak value of j is
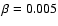 for
core 17 and
for
core 17 and
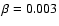 for core 43. On the other hand, core 101
will fragment into a binary star. It has a
for core 43. On the other hand, core 101
will fragment into a binary star. It has a
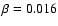 .
Also, the
disk of core 96 is highly unstable with corresponding
.
Also, the
disk of core 96 is highly unstable with corresponding
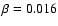 .
The evolution of core 43 has not yet been followed sufficiently long
to determine whether it will fragment to form a binary star or not.
These results show the importance of the specific angular momentum on
the evolution of the protostellar object. A high value
.
The evolution of core 43 has not yet been followed sufficiently long
to determine whether it will fragment to form a binary star or not.
These results show the importance of the specific angular momentum on
the evolution of the protostellar object. A high value
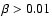 leads to fragmentation whereas
leads to fragmentation whereas
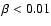 results in a stable
disk. A similar result was found by Boss (1999) for slowly
rotating, magnetic clouds.
results in a stable
disk. A similar result was found by Boss (1999) for slowly
rotating, magnetic clouds.
Figure 3b shows that the change in specific angular
momentum is closely linked to the mass accretion. At the point in time
where the mass accretion rate (dotted line) has a pronounced peak, the
change in specific angular momentum is also significant. A high mass
accretion rate can result in an increase of specific angular momentum.
But as seen for core 96 in Fig. 3b a high mass accretion
rate can also lead to a reduction of specific angular momentum.
The exact evolution of the specific angular momentum is thus closely
linked to the flow properties of the surrounding material.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0220fig4.eps}
\end{figure}](/articles/aa/full/2004/31/aa0220-04/Timg99.gif) |
Figure 4:
Absolute values of specific angular momenta (dotted lines) of all protostars (i.e. "sink particles'') from
our model M6k2 as a function of mass. The specific angular momenta
are averaged at certain mass values which are separated
by
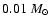 and the resulting points are indicated
by crosses. The solid line represents a fit of these
averaged specific angular momenta in the mass range between 0 and
and the resulting points are indicated
by crosses. The solid line represents a fit of these
averaged specific angular momenta in the mass range between 0 and
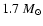 In a) we fit with a function of the
form:
In a) we fit with a function of the
form:
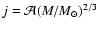 , ,
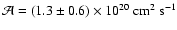 ,
and in
b) we use a square root function: ,
and in
b) we use a square root function:
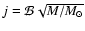 , ,
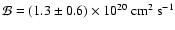 .
One standard deviation is marked by the
dashed lines. .
One standard deviation is marked by the
dashed lines. |
| Open with DEXTER |
As mentioned above we find a correlation between mass M and specific
angular momentum j in a statistical sense. The result is depicted
in Fig. 4. It shows the angular momentum evolution
as a function of mass for all 110 collapsed cores in model M6k2.
In
Fig. 4a, following Goodman et al. (1993) we adopt rigid body rotation with constant angular velocity 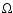 and uniform core density
and uniform core density 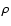 .
With these assumptions the specific angular momentum j can be written as:
.
With these assumptions the specific angular momentum j can be written as:
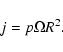 |
(2) |
For a uniform density sphere
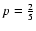 .
The mass M of a
sphere with constant density
.
The mass M of a
sphere with constant density 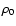 is related to the radius R via:
is related to the radius R via:
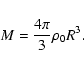 |
(3) |
From Eqs. (2) and (3) follows that j can be
expressed as:
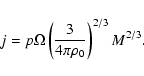 |
(4) |
Therefore we fit the average angular momentum with a function of the form:
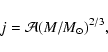 |
(5) |
where
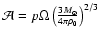 .
From Fig. 4a the constant
.
From Fig. 4a the constant
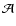 has a value of
has a value of
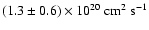 .
This fit formula can be applied to
different turbulent cloud environments, and we list the corresponding
values of
.
This fit formula can be applied to
different turbulent cloud environments, and we list the corresponding
values of
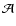 for our model suite in Table 1.
Using the fitted value and the
density
for our model suite in Table 1.
Using the fitted value and the
density
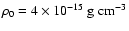 where protostellar cores are
identified, we calculate an angular
velocity
where protostellar cores are
identified, we calculate an angular
velocity
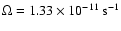 .
.
In this picture the ratio of
rotational to gravitational energy  can be written as:
can be written as:
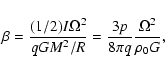 |
(6) |
where the moment of inertia is given by I = pMR2, and
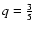 is defined such that qGM2/R represents the
gravitational potential of a uniform density sphere.
With the assumptions of constant angular velocity and uniform density it
follows that
is defined such that qGM2/R represents the
gravitational potential of a uniform density sphere.
With the assumptions of constant angular velocity and uniform density it
follows that  is also constant. With
is also constant. With 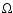 and
and 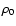 as above, we
get values
as above, we
get values
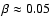 .
.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0220fig5.eps}
\end{figure}](/articles/aa/full/2004/31/aa0220-04/Timg114.gif) |
Figure 5:
Distribution of  obtained from our model M6k2 with
obtained from our model M6k2 with 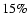 a),
a),
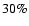 b),
b), 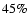 c) and
c) and 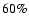 d) of the material accreted.
For the collapsed protostellar cores in our models
(solid lines) we calculate
d) of the material accreted.
For the collapsed protostellar cores in our models
(solid lines) we calculate  using Eq. (6), where we assume solid-body rotation of
a uniform density sphere and take the calculated specific angular
momentum j. For the prestellar cores (i.e. Jeans-unstable gas
clumps; see the dashed lines)
we derive
using Eq. (6), where we assume solid-body rotation of
a uniform density sphere and take the calculated specific angular
momentum j. For the prestellar cores (i.e. Jeans-unstable gas
clumps; see the dashed lines)
we derive  self-consistently from the three-dimensional density
and velocity structure, using Eq. (10). For comparison
we also indicate with dotted lines the values reported by Goodman et al. (1993, see their
Fig. 11) for observed molecular cloud cores. These were
obtained with the same assumptions,
and we use the same binning with
self-consistently from the three-dimensional density
and velocity structure, using Eq. (10). For comparison
we also indicate with dotted lines the values reported by Goodman et al. (1993, see their
Fig. 11) for observed molecular cloud cores. These were
obtained with the same assumptions,
and we use the same binning with 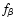 representing the fraction
of objects per
representing the fraction
of objects per
 bin.
bin. |
| Open with DEXTER |
Goodman et al. (1993) as well as Burkert & Bodenheimer (2000) derived scaling relations where  is independent of radius. Similar values for
is independent of radius. Similar values for  were also found by Goodman et al. (1993) for the
observed cloud cores. In good agreement with our calculations they
found that all values are below 0.18 with the majority under 0.05.
were also found by Goodman et al. (1993) for the
observed cloud cores. In good agreement with our calculations they
found that all values are below 0.18 with the majority under 0.05.
The fit in Fig. 4a rests on the assumption of the
collapse of an initially homogeneous sphere with constant angular
velocity. Using "sink particles'' however, which have a constant
radius, makes it necessary to examine another possibility. In
Fig. 4b we thus assume a constant radius R and a
constant  .
Choosing a constant
.
Choosing a constant  is supported by the
observations as discussed above and by our simulations as we show below. With
is supported by the
observations as discussed above and by our simulations as we show below. With  and
Eq. (6) (which still holds) it follows that the angular
velocity depends on the density as
and
Eq. (6) (which still holds) it follows that the angular
velocity depends on the density as
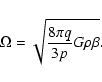 |
(7) |
Thus, the angular velocity 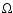 is no longer a constant. This implies for the specific angular momentum j:
is no longer a constant. This implies for the specific angular momentum j:
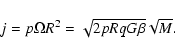 |
(8) |
Following Eq. (8) we fit our data in Fig. 4b
with a square root function:
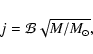 |
(9) |
where, again, the moment of inertia is given by I = pMR2, and
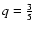 is defined such that qGM2/R represents the
gravitational potential of a uniform density sphere. With the above
density and angular velocity Eq. (6) results in
is defined such that qGM2/R represents the
gravitational potential of a uniform density sphere. With the above
density and angular velocity Eq. (6) results in
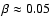 .
For the
new fit we find a scaling factor
.
For the
new fit we find a scaling factor
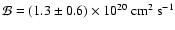 in the mass range
in the mass range
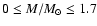 .
Again, this fit formula can be applied to
different turbulent cloud environments, and we list the corresponding
values of
.
Again, this fit formula can be applied to
different turbulent cloud environments, and we list the corresponding
values of
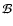 for our model suite in Table 1.
for our model suite in Table 1.
The question remains if our simulations support the assumption of a constant  .
In Fig. 5 we compare the distribution of
.
In Fig. 5 we compare the distribution of  measured by Goodman et al. (1993) with values we extract from our
model. For the prestellar cores we use the definition
measured by Goodman et al. (1993) with values we extract from our
model. For the prestellar cores we use the definition
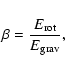 |
(10) |
and calculate rotational and potential energy,
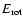 and
and
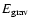 ,
consistently from the full three-dimensional gas
distribution of each gas clump. We do not adopt any assumption about
symmetry and shape of the density and velocity structure.
If we assume that each clump is spherical and has roughly constant density,
as implied for example by Eq. (6), then
,
consistently from the full three-dimensional gas
distribution of each gas clump. We do not adopt any assumption about
symmetry and shape of the density and velocity structure.
If we assume that each clump is spherical and has roughly constant density,
as implied for example by Eq. (6), then  is
overestimated by a factor of 2.7. This shows the importance of taking
the full three-dimensional clump structure into account when analyzing
the rotational properties of molecular cloud cores. Both prestellar
cores (i.e. Jeans-unstable gas clumps) and protostellar cores
in our model typically have
is
overestimated by a factor of 2.7. This shows the importance of taking
the full three-dimensional clump structure into account when analyzing
the rotational properties of molecular cloud cores. Both prestellar
cores (i.e. Jeans-unstable gas clumps) and protostellar cores
in our model typically have
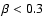 with similar
distributions. Thus,
with similar
distributions. Thus,  stays mainly in the interval [0,0.3] and in this sense it remains approximately constant during the collapse.
stays mainly in the interval [0,0.3] and in this sense it remains approximately constant during the collapse.
It should be noted in passing that we also looked at the density
structure of purely hydrodynamic turbulence, i.e. without
self-gravity. If we again perform a clump-decomposition of the density
structure and compute hypothetical  -values, we find
-values, we find
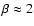 .
This is indicative of the high degree of vorticity inherent in
all turbulent flows. However, it also suggests that dense
molecular cloud cores
are strongly influenced by self-gravity. The fact that all
cores in the observational sample have
.
This is indicative of the high degree of vorticity inherent in
all turbulent flows. However, it also suggests that dense
molecular cloud cores
are strongly influenced by self-gravity. The fact that all
cores in the observational sample have
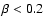 implies that
gravitational contraction is needed to achieve density contrasts high
enough for sufficiently low
implies that
gravitational contraction is needed to achieve density contrasts high
enough for sufficiently low  .
This agrees with the
picture of gravoturbulent fragmentation where molecular cloud
structure as whole is dominated by supersonic turbulence but stars can
only form in those regions where gravity overwhelms all other forms of
support.
.
This agrees with the
picture of gravoturbulent fragmentation where molecular cloud
structure as whole is dominated by supersonic turbulence but stars can
only form in those regions where gravity overwhelms all other forms of
support.
Comparing the two fits in Fig. 4 shows that our first set of
assumptions is a better representation of the data. This is especially
true during the early accretion phase where we have good statistics. It
applies to different turbulent cloud environments as well. We conclude that
- in a statistical sense - the angular momentum evolution of collapsing
cloud cores can be approximately described as contraction of initially
constant-density spheres undergoing rigid body rotation with constant angular
velocity. This is consistent with the fact that cores from gravoturbulent
fragmentation follow a Bonnor-Ebert-type radial density profile (Ballesteros-Paredes et al. 2003)
and have roughly constant density in their innermost regions. It also supports the assumptions adopted by
Goodman et al. (1993) and Burkert & Bodenheimer (2000).
![\begin{figure}
\par\includegraphics[width=16cm,clip]{0220fig6.eps}
\end{figure}](/articles/aa/full/2004/31/aa0220-04/Timg127.gif) |
Figure 6:
Average specific angular momentum of
protostellar objects in different turbulent environments as a
function of the associated Mach number. Different shapes mark
different driving scales k (circle - k=2.0,
star - k=4.0, square - k=8.0). GA stands for
the Gaussian collapse without driving (arrow pointing
downward). Different shades represent different stages of
accretion (white - 15% material accreted, gray -
30% material accreted, black - 45% material accreted).
In a) all protostars (identified as "sink particle'' in the
simulations) were used in calculating the average, in b) through d)
only objects in the denoted mass bins were considered. The error bars
show the standard deviation of
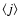 .
For more clarity the symbols
are distributed around the corresponding Mach number .
For more clarity the symbols
are distributed around the corresponding Mach number
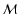 with
with
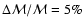 . . |
| Open with DEXTER |
When we compare the results of our complete suite of numerical models
(see Table 1) we find as a general trend that the average
angular momentum falls with increasing Mach number. This is
illustrated in Fig. 6a. However, this follows mainly
from the positive dependence of angular momentum on mass and from
a correlation between average mass of the cloud cores and Mach number.
As seen in Sect. 4.2 the specific angular momentum
increases on average as the mass of the core rises. In environments
with a low Mach number the mass growth of the cores is undisturbed
over longer periods of time and so larger masses can accumulate. This
can be inferred from Table 1, where we list both the number of
cores and the accreted mass. For higher Mach numbers more
cores form with on average less mass. Thus, the average angular
momentum is expected to decrease with increasing Mach number
(Fig. 6a).
To detect a direct dependence of the specific angular momentum on the
Mach number we select cores that belong in a certain mass bin and
average the specific angular momentum only over those cores. The
results are shown in Figs. 6b-6d. We find
that there is in general little spread of specific angular momentum
for different scales and different times in accretion history
independently of the Mach number. Low mass protostars
(Fig. 6b) are an exception, in low Mach number
environments they show especially low angular momentum in the early
accretion phase. However, within the error bars we do not find a
further dependence of j on the Mach number.
Compared to the Gaussian collapse case, turbulent driving with small
Mach numbers results in higher specific angular momenta. This is due
to input of turbulent energy that can be converted into rotational
energy if the turbulent velocities are not too high.
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{0220fig7.eps}
\end{figure}](/articles/aa/full/2004/31/aa0220-04/Timg128.gif) |
Figure 7:
The correlation of specific angular momenta of different protostellar
cores in model M6k2 with respect to their orientation as a function
of distance between the cores. As a measure for the correlation the
scalar product of different cores was taken and averaged over cores
that exhibit similar distances between each other. High positive
values denote co-aligned and high negative values denote
anti-aligned angular momenta. The three graphs a)- c) show three
different times at which 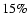 , ,
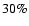 and
and 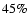 of
the available material was accreted. The error bars show the
standard deviation of the averaged correlations.
of
the available material was accreted. The error bars show the
standard deviation of the averaged correlations. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{0220fig8.eps}
\end{figure}](/articles/aa/full/2004/31/aa0220-04/Timg129.gif) |
Figure 8:
Orientation of the angular momenta (arrows) and spatial distribution of the
protostellar cores (diamonds) that formed in model M6k2. We
present the projections on the xy, xz and yz-plane. The spatial
distributions are compared for three different times at which 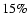 a),
a), 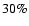 b) and
b) and 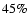 c) of the available material is
accreted. The length of the arrows scales with the specific angular
momentum of the protostellar core.
c) of the available material is
accreted. The length of the arrows scales with the specific angular
momentum of the protostellar core. |
| Open with DEXTER |
5 Orientation of angular momentum vector
We find in our simulations that neighboring protostellar cores have
similarly oriented angular momenta. In Fig. 7 the
correlation of specific angular momenta of different protostellar
cores with respect to their orientations is shown as a function of
distance. We calculate the scalar product
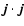 and
average over cores with similar distances.
and
average over cores with similar distances.
Figure 8a shows the spatial configuration in model M6k2
after 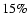 of the available material has been accreted onto the
protostellar cores. These cores form in small aggregates with
diameters below 0.07 pc.
The corresponding Fig. 7a shows
a spatial correlation of the specific angular momenta for small
distances. The correlation length is approximately 0.05 pc. Thus,
correlation length and cloud size are closely connected. This can be
understood because within one molecular cloud clump neighboring cores
accrete from the same reservoir of gas and consequently gain similar
specific angular momentum. In the early phase of accretion we
therefore expect disks and protostellar outflows of
neighboring protostars to be closely aligned.
of the available material has been accreted onto the
protostellar cores. These cores form in small aggregates with
diameters below 0.07 pc.
The corresponding Fig. 7a shows
a spatial correlation of the specific angular momenta for small
distances. The correlation length is approximately 0.05 pc. Thus,
correlation length and cloud size are closely connected. This can be
understood because within one molecular cloud clump neighboring cores
accrete from the same reservoir of gas and consequently gain similar
specific angular momentum. In the early phase of accretion we
therefore expect disks and protostellar outflows of
neighboring protostars to be closely aligned.
Indeed, several examples of parallel disks and outflows have been
reported in low-mass, isolated Bok globules by Froebrich & Scholz (2003),
Kamazaki et al. (2003), Nisini et al. (2001), and Saito et al. (1995). Alternative
explanations for the alignment of the symmetry axes of young stars
include density gradients in the prestellar phase or the presence of
strong magnetic fields. However, Duchêne & Ménard (2003) found that the disks of
T-Tauri stars driving jets or outflows are perpendicular to the
magnetic field but disks of T-Tauri stars without jet are parallel to
the field lines. This is very puzzling, showing the complexity of the
situation that will naturally arise in strongly turbulent flows.
During subsequent accretion the correlation length decreases to values
below 0.015 pc (Fig. 7b). This means that only close
systems remain correlated
(see also Fig. 8b). This has
three reasons. First, small N systems of embedded cores are likely
to dissolve quickly as close encounters lead to ejection
(e.g., Reipurth & Clarke 2001). Only close binaries are able to survive for a
long time (e.g., Kroupa 1995a,b). The correlation length
therefore decreases with time. Second, the same turbulent flow that
generated a collapsing high-density clump in the first place may also
disrupt it again before it is fully accreted. If the clump contains
several protostars they will disperse, again decreasing the
correlation. Third, the opposite may happen. Turbulence may bring in
fresh gas. The protostars are then able to continue accretion, but the
specific angular momentum of the new matter is likely to be quite
different from the original material. As protostars accrete at
different rates, we expect a spread in 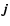 to build up and the
alignment will disappear. At later stages of the
evolution, we expect that the correlation between the specific angular
momenta of close protostellar objects has disappeared almost
completely. This is evident in Fig. 7c. Furthermore,
Fig. 8c demonstrates that most of the initial
subclustering has disappeared by then.
to build up and the
alignment will disappear. At later stages of the
evolution, we expect that the correlation between the specific angular
momenta of close protostellar objects has disappeared almost
completely. This is evident in Fig. 7c. Furthermore,
Fig. 8c demonstrates that most of the initial
subclustering has disappeared by then.
6 Summary and conclusions
We studied the rotational properties and time evolution of the
specific angular momentum of prestellar and protostellar cores formed
from gravoturbulent fragmentation in numerical models of
supersonically turbulent, self-gravitating molecular clouds. We
considered rms Mach numbers ranging from 2 to 10, and turbulence that
is driven on small, intermediate, and large scales, as well as one
model of collapse from Gaussian density fluctuations without any
turbulence. Our sample thus covers a wide range of properties observed
in Galactic star-forming regions, however, our main focus lies in
typical low- to intermediate-mass star-forming regions like
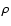 -Ophiuchi or Taurus.
-Ophiuchi or Taurus.
With the appropriate physical scaling, we find the specific angular
momentum j of prestellar cores in our models, i.e. cloud cores as
yet without central protostar, to be on average
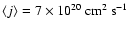 .
This agrees remarkably well with
observations of cloud cores by Caselli et al. (2002) or Goodman et al. (1993). Some
prestellar cores go into collapse to build up stars and stellar
systems. The resulting protostellar objects have on average
.
This agrees remarkably well with
observations of cloud cores by Caselli et al. (2002) or Goodman et al. (1993). Some
prestellar cores go into collapse to build up stars and stellar
systems. The resulting protostellar objects have on average
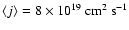 .
This is one order of
magnitude less, and falls into the range observed in G-dwarf binaries
(Duquennoy & Mayor 1991). Collapse induced by gravoturbulent fragmentation is
accompanied by a substantial loss of specific angular momentum. This
is mostly due to gravitational torque exerted by the ambient
turbulent flow and to close encounters occurring when the protostars
are embedded in dense clusters. This eases the "angular momentum
problem'' in star formation without invoking the presence of strong
magnetic fields.
.
This is one order of
magnitude less, and falls into the range observed in G-dwarf binaries
(Duquennoy & Mayor 1991). Collapse induced by gravoturbulent fragmentation is
accompanied by a substantial loss of specific angular momentum. This
is mostly due to gravitational torque exerted by the ambient
turbulent flow and to close encounters occurring when the protostars
are embedded in dense clusters. This eases the "angular momentum
problem'' in star formation without invoking the presence of strong
magnetic fields.
The time evolution of j is intimately connected to the mass
accretion history of a protostellar core. As interstellar turbulence
and mutual interaction in dense clusters are highly stochastic
processes, the mass growth of individual protostars is unpredictable
and can be very complex. In addition, a collapsing cloud core can
fragment further into a binary or higher-order multiple or evolve into
a protostar with a stable accretion disk. It is the ratio of
rotational to gravitational energy  that determines which route
the object will take. This is seen in the turbulent cloud cores
studied here as well as in simulations of isolated cores where
magnetic fields are important (e.g., Boss 1999). The
that determines which route
the object will take. This is seen in the turbulent cloud cores
studied here as well as in simulations of isolated cores where
magnetic fields are important (e.g., Boss 1999). The
 -distribution resulting from gravoturbulent cloud fragmentation
reported here agrees well with
-distribution resulting from gravoturbulent cloud fragmentation
reported here agrees well with  -values derived from
observations (Goodman et al. 1993). The average value is
-values derived from
observations (Goodman et al. 1993). The average value is
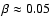 .
Note that we find
that the distribution of
.
Note that we find
that the distribution of  stays essentially the same during
collapse and accretion (see also Goodman et al. 1993; Burkert & Bodenheimer 2000).
stays essentially the same during
collapse and accretion (see also Goodman et al. 1993; Burkert & Bodenheimer 2000).
Although the accretion history and thus the evolution of the specific
angular momentum of a single protostellar object is complex, we find a
clear correlation between j and mass M. This can be interpreted
conveniently
assuming collapse of an initially uniform density sphere in solid body
rotation. Our models of gravoturbulent cloud fragmentation are best
represented by the relation
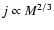 .
.
When prestellar cores form by compression as part of supersonically
turbulent flows and then go into collapse and possibly break apart
into several fragments due to the continuing perturbation by their
turbulent environment, we expect neighboring protostars to have
similarly oriented angular momentum, at least during their early
phases of accretion. Star clusters form hierarchically structured,
with several young stellar objects being embedded in the same
clump of molecular cloud material. These protostars accrete from one
common reservoir of gas and consequently gain similar specific angular
momentum. Their disks and protostellar outflows therefore will
closely align. Indeed, there are several examples of parallel disks
and outflows seen in low-mass, isolated Bok globules
(Froebrich & Scholz 2003; Nisini et al. 2001; Kamazaki et al. 2003; Saito et al. 1995). During later phases of cluster
formation, the initial substructure becomes erased by dynamical
effects and the correlation between the angular momenta of neighboring
protostars vanishes.
This is in agreement with our numerical calculations of gravoturbulent
cloud fragmentation. They show small groups of close protostellar
objects that have almost aligned specific angular momenta. As
expected, the alignment occurs during the early phase of accretion as
neighboring protostars accrete material from the same region with
similar angular momentum. During the subsequent evolution the
correlation length decreases. This is either because protostellar
aggregates disperse, or because infalling new material with different
angular momentum becomes distributed unevenly among the protostars.
Altogether, the process of gravoturbulent fragmentation, i.e. the
interplay between supersonic turbulence and self-gravity of the
interstellar gas, constitutes an attractive base for a unified theory
of star formation that is able to explain and reproduce many of the
observed features in Galactic star forming regions (Mac Low & Klessen 2004).
Our current study contributes with a detailed analysis of the angular momentum evolution
during collapse.
Acknowledgements
We thank Peter Bodenheimer and Mordecai Mac Low for
numerous stimulating discussions, and we thank our referee for
insightful comments and suggestions. A.K.J. and R.S.K. acknowledge support
by the Emmy Noether Program of the Deutsche Forschungsgemeinschaft
(grant No. KL1358/1).
- Ballesteros-Paredes,
J., Hartmann, L., & Vázquez-Semadeni, E. 1999a, ApJ, 527,
285 [NASA ADS]
- Ballesteros-Paredes,
J., Vázquez-Semadeni, E., & Scalo, J. 1999b, ApJ, 515,
286 [NASA ADS]
- Ballesteros-Paredes, J.,
Klessen, R. S., & Vázquez-Semadeni, E. 2003, ApJ,
592, 188 [NASA ADS]
- Barranco, J. A.,
& Goodman, A. A. 1998, ApJ, 504, 207 [NASA ADS] (In the text)
- Bate, M. R., &
Burkert, A. 1997, MNRAS, 288, 1060 [NASA ADS] (In the text)
- Bate, M. R.,
Bonnell, I. A., & Price, N. M. 1995, MNRAS, 277,
362 [NASA ADS] (In the text)
- Benz, W. 1990, in
Numerical Modelling of Nonlinear Stellar Pulsations Problems and
Prospects (Dordrecht: Kluwer), 269
- Bodenheimer, P. 1995,
ARA&A, 33, 199 [NASA ADS]
- Bodenheimer, P., Burkert,
A., Klein, R. I., & Boss, A. P. 2000, Protostars and
Planets IV, ed. V. Mannings, A. P. Boss, & S. S. Russell
(Tucson: Univ. of Arizona Press), 675
- Boss, A. P. 1999,
ApJ, 520, 744 [NASA ADS] (In the text)
- Burkert, A., &
Bodenheimer, P. 2000, ApJ, 543, 822 [NASA ADS] (In the text)
- Caselli, P., Benson,
P. J., Myers, P. C., & Tafalla, M. 2002, ApJ, 572,
238 [NASA ADS] (In the text)
- Duchêne, G., &
Ménard, F. 2003 [arXiv:astro-ph/0306379]
(In the text)
- Duquennoy, A., &
Mayor, M. 1991, A&A, 248, 485 [NASA ADS]
- Ebert, R., von Hoerner,
S., & Temesváry, S. 1960, Die Entstehung von Sternen
durch Kondensation diffuser Materie (Berlin: Springer-Verlag),
315
(In the text)
- Elmegreen, B. G.
1993, ApJ, 419, L29 [NASA ADS] (In the text)
- Fisher, R. T. 2004,
ApJ, 600, 769 [NASA ADS] (In the text)
- Froebrich, D., &
Scholz, A. 2003, A&A, 407, 207 [EDP Sciences] [NASA ADS] (In the text)
- Gammie, C. F., Lin,
Y., Stone, J. M., & Ostriker, E. C. 2003, ApJ, 592,
203 [NASA ADS] (In the text)
- Goodman, A. A.,
Benson, P. J., Fuller, G. A., & Myers, P. C.
1993, ApJ, 406, 528 [NASA ADS] (In the text)
- Halbwachs, J. L.,
Mayor, M., Udry, S., & Arenou, F. 2003, A&A, 397, 159 [EDP Sciences] [NASA ADS]
- Heitsch, F., Mac Low,
M.-M., & Klessen, R. S. 2001, ApJ, 547, 280 [NASA ADS] (In the text)
- Hunter, J. H., &
Fleck, R. C. 1982, ApJ, 256, 505 [NASA ADS] (In the text)
- Jijina, J., Myers,
P. C., & Adams, F. C. 1999, ApJS, 125, 161 (In the text)
- Kamazaki, T., Saito, M.,
Hirano, N., Umemoto, T., & Kawabe, R. 2003, ApJ, 584, 357 [NASA ADS] (In the text)
- Klessen, R. 1997, MNRAS,
292, 11 [NASA ADS] (In the text)
- Klessen, R. S.
2001a, ApJ, 556, 837 [NASA ADS]
- Klessen, R. S.
2001b, ApJ, 550, L77 [NASA ADS]
- Klessen, R. S.,
& Burkert, A. 2000, ApJS, 128, 287 [NASA ADS]
- Klessen, R. S.,
& Burkert, A. 2001, ApJ, 549, 386 [NASA ADS]
- Klessen, R. S.,
Heitsch, F., & Mac Low, M.-M. 2000, ApJ, 535, 887 [NASA ADS] (In the text)
- Kroupa, P. 1995a,
MNRAS, 277, 1491 [NASA ADS]
- Kroupa, P. 1995b,
MNRAS, 277, 1507 [NASA ADS] (In the text)
- Larson, R. B. 1995,
MNRAS, 272, 213 [NASA ADS] (In the text)
- Larson, R. B. 2003,
Rep. Progress Phys., 66, 1651 [NASA ADS] (In the text)
- Li, P. S., Norman,
M. L., Mac Low, M.-M., & Heitsch, F. 2004, ApJ, 605,
800 [NASA ADS] (In the text)
- Lin, D. N. C.,
& Papaloizou, J. C. B. 1996, ARA&A, 34, 703 [NASA ADS]
- Lombardi, J. C.,
Sills, A., Rasio, F. A., & Shapiro, S. L. 1999,
J. Comp. Phys., 152, 687 [NASA ADS] (In the text)
- Mac Low, M.-M. 1999, ApJ,
524, 169 [NASA ADS] (In the text)
- Mac Low, M.-M., &
Klessen, R. S. 2004, Rev. Mod. Phys., 76, 125 [NASA ADS] (In the text)
- Mac Low, M.-M., Klessen,
R. S., Burkert, A., & Smith, M. D. 1998, Phys. Rev.
Lett., 80, 2754 [NASA ADS] (In the text)
- Mathieu, R. D.,
Ghez, A. M., Jensen, E. L. N., & Simon, M. 2000,
Protostars and Planets IV, ed. V. Mannings, A. P. Boss, &
S. S. Russell (Tucson: Univ. of Arizona Press), 703
- Monaghan, J. J.
1992, ARA&A, 30, 543 [NASA ADS]
- Motte, F., André,
P., & Neri, R. 1998, A&A, 336, 150 [NASA ADS] (In the text)
- Mouschovias, T. C.,
& Paleologou, E. V. 1979, ApJ, 230, 204 [NASA ADS]
- Mouschovias, T. C.,
& Paleologou, E. V. 1980, ApJ, 237, 877 [NASA ADS]
- Nakano, T. 1998, ApJ,
494, 587 [NASA ADS]
- Nisini, B., Massi, F.,
Vitali, F., et al. 2001, A&A, 376, 553 [EDP Sciences] [NASA ADS] (In the text)
- Padoan, P. 1995, MNRAS,
277, 377 [NASA ADS] (In the text)
- Padoan, P., &
Nordlund, Å. 1999, ApJ, 526, 279 [NASA ADS]
- Padoan, P., &
Nordlund, Å. 2002, ApJ, 576, 870 [NASA ADS]
- Papaloizou,
J. C. B., & Lin, D. N. C. 1995, ARA&A,
33, 505 [NASA ADS]
- Pirogov, L., Zinchenko,
I., Caselli, P., Johansson, L. E. B., & Myers,
P. C. 2003, A&A, 405, 639 [EDP Sciences] [NASA ADS] (In the text)
- Reipurth, B., &
Clarke, C. 2001, AJ, 122, 432 [NASA ADS] (In the text)
- Saito, M., Kawabe, R.,
Ishiguro, M., et al. 1995, ApJ, 453, 384 [NASA ADS] (In the text)
- Shu, F. H. 1977,
ApJ, 214, 488 [NASA ADS]
- Shu, F. H., Adams,
F. C., & Lizano, S. 1987, ARA&A, 25, 23 [NASA ADS]
- Simon, M. 1992, in
Complementary approaches to double and multiple star research, ASP
Conf. Ser., 32, IAU Coll., 135, 41
(In the text)
- Spitzer, L. 1968, Diffuse
matter in space (New York: Interscience Publication)
- Stone, J. M.,
Ostriker, E. C., & Gammie, C. F. 1998, ApJ, 508,
L99 [NASA ADS]
- Vázquez-Semadeni,
E., Ballesteros-Paredes, J., & Klessen, R. S. 2003, ApJ,
585, L131 [NASA ADS] (In the text)
- Vázquez-Semadeni,
E., Ostriker, E. C., Passot, T., Gammie, C. F., &
Stone, J. M. 2000, Protostars and Planets IV, ed. V. Mannings,
A. P. Boss, & S. S. Russell (Tucson: Univ. of Arizona
Press), 3
(In the text)
- Whitworth, A., &
Summers, D. 1985, MNRAS, 214, 1 [NASA ADS]
- Whitworth, A. P.,
Bhattal, A. S., Francis, N., & Watkins, S. J. 1996,
MNRAS, 283, 1061 [NASA ADS]
- Williams, J. P.,
Blitz, L., & McKee, C. F. 2000, Protostars and Planets IV,
ed. V. Mannings, A. P. Boss, & S. S. Russell (Tucson:
Univ. of Arizona Press), 97
(In the text)
Copyright ESO 2004
![\begin{figure}
\par\includegraphics[width=4.7cm,clip]{0220fig1.eps}
\end{figure}](/articles/aa/full/2004/31/aa0220-04/Timg55.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0220fig2.eps}
\end{figure}](/articles/aa/full/2004/31/aa0220-04/Timg78.gif)
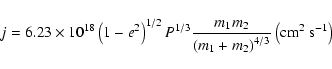
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{0220fig3.eps}
\end{figure}](/articles/aa/full/2004/31/aa0220-04/Timg87.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0220fig4.eps}
\end{figure}](/articles/aa/full/2004/31/aa0220-04/Timg99.gif)
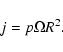
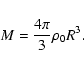
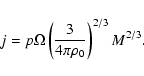
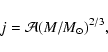
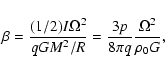
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0220fig5.eps}
\end{figure}](/articles/aa/full/2004/31/aa0220-04/Timg114.gif)
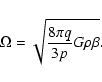
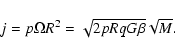
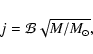
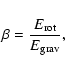
![\begin{figure}
\par\includegraphics[width=16cm,clip]{0220fig6.eps}
\end{figure}](/articles/aa/full/2004/31/aa0220-04/Timg127.gif)
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{0220fig7.eps}
\end{figure}](/articles/aa/full/2004/31/aa0220-04/Timg128.gif)
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{0220fig8.eps}
\end{figure}](/articles/aa/full/2004/31/aa0220-04/Timg129.gif)