A&A 423, 397-400 (2004)
DOI: 10.1051/0004-6361:20047100

Stark broadening of the four times ionized silicon spectral lines[*]

N. Ben Nessib1 - M. S. Dimitrijevic2,3 - S. Sahal-Bréchot4


1 - Groupe de Recherche en Physique Atomique et Astrophysique, Faculté des Sciences de Bizerte, 7021 Zarzouna, Tunisia
2 - Astronomical Observatory, Volgina 7, 11160 Belgrade, Serbia
3 - Institute Isaac Newton of Chile, Yugoslavia Branch, Yugoslavia
4 - Laboratoire d'étude du Rayonnement et de la Matière en Astrophysique, UMR CNRS 8112, Observatoire de Paris-Meudon, 92195 Meudon, France

Received 19 January 2004 / Accepted 3 May 2004

Abstract
Using a semiclassical perturbation approach, we have obtained Stark broadening parameters for 16 Si V multiplets using atomic data calculated ab initio with the SUPERSTRUCTURE code. In order to complete Stark broadening data for the most important charged perturbers in stellar atmospheres, Stark broadening parameters for proton-, He II-, and Si II-impact line widths and shifts are also presented. Results have been obtained for an electron density of 1017 cm-3 as a function of temperature. Moreover, we have performed the same calculations with oscillator strengths calculated within the Coulomb approximation. The differences, which are within the error bars of the semiclassical perturbation approach ( $\pm20{-}30\%$) confirm that the Bates & Damgaard approximation may be used to complete the atomic data set needed for the Stark broadening calculations for multicharged ions like Si V, where more reliable oscillator strength values are not available.

Key words: atomic processes - line: profiles - atomic data

1 Introduction

The semiclassical perturbation formalism (Sahal-Bréchot 1969a,b) has been used in a series of papers for large scale calculations of Stark broadening parameters for a number of spectral lines of various emitters from neutral atoms up to twelve times ionized atoms (see e.g., Dimitrijevic 1997, and references therein). The results of such calculations are of interest for a number of different problems in physics, astrophysics and plasma technology. In astrophysics, such atomic data are of interest e.g. for numerical modelling of stellar atmospheres or abundance determinations, problems correlated with nucleogenesis, mixing between atmosphere and interior, stellar structure and evolution (see e.g., Boesgaard 1988), and opacity calculations (Seaton 1988). Moreover, Stark broadening parameters are of interest for the investigation and diagnostics of laboratory and laser-produced plasmas, as well as for the theoretical studies of regularities and systematic trends.

In the case of four-times ionized atoms there exists a sufficiently complete set of the needed atomic data required for sophisticated semiclassical calculations for a number of astrophysically interesting lines. Therefore, large scale calculations have been performed with the semiclassical perturbation formalism (Sahal-Bréchot 1969a,b) for C V (Dimitrijevic & Sahal-Bréchot 1995a, 1996a), N V (Dimitrijevic & Sahal-Bréchot 1992), O V (Dimitrijevic & Sahal-Bréchot 1995b,c), P V (Dimitrijevic & Sahal-Bréchot 1995a, 1996a), S V (Dimitrijevic & Sahal-Bréchot 1997, 1998a) and V V (Dimitrijevic & Sahal-Bréchot 1998b) spectral lines. When we did not have a sufficiently complete set of reliable atomic data, the full semiclassical method could not be applied adequately, and simpler methods (Dimitrijevic & Konjevic 1980; Griem 1974, Eq. (526)) were used for the calculation of C V, O V, F V, Ne V and Al V Stark broadening parameters, including 6 multiplets of Si V (Dimitrijevic 1993a,b). Such data are of interest for the consideration of radiative transfer through subphotospheric layers (Seaton 1988), for modelling of some hot star atmospheres such as PG 1159 pre-white dwarfs with an effective temperature between 100 000 and 140 000 K (Werner & Heber 1991), as well as for fusion plasmas and laser-produced plasmas. The development of soft X-ray lasers, where Stark broadening data are needed to calculate gain values, to model radiation trapping and to consider photoresonant pumping schemes (see e.g., Fill & Schöning 1994; Griem & Moreno 1980), provided an additional interest in such results.

With the development of space-borne spectroscopy, together with the possibility of obtaining high resolution spectra for a wide wavelength range including X-rays not detectable from the Earth's surface, the interest in such results is increasing. For example the Low Energy Transmission Grating (LETG) on board the X-ray space observatory CHANDRA provides high quality spectra in the wavelength region between 5 and 140 Å, and contains a series of lines which can provide density and temperature diagnostics for relatively hot and dense stellar plasmas. An analysis of the X-ray high resolution spectrum of some stars shows spectra which may be rich in emission lines in the soft X-ray region, including Si V lines.

The aim of this paper is twofold. First we will compute Si V Stark broadening parameters within the semiclassical formalism by using oscillator strengths from the SUPERSTRUCTURE code to provide new Stark broadening data of astrophysical interest. Additionally, we perform the same calculations using the Coulomb approximation (Bates & Damgaard 1949; Oertel & Shomo 1968), in order to estimate the error introduced in the Stark broadening parameters due to uncertainties in the oscillator strengths obtained from the Coulomb approximation.

2 Theory

The energy levels of SiV are calculated using the general atomic structure code SUPERSTRUCTURE developed at the University College, London and described by Eissner et al. (1974). SUPERSTRUCTURE can calculate electric dipole (E1), electric quadrupole (E2), magnetic dipole (M1) and magnetic quadrupole (M2) transition probabilities. The wave functions are determined by diagonalization of the non-relativistic Hamiltonian using orbitals calculated in a scaled Thomas-Fermi-Dirac-Amaldi (TFDA) potential. The scaling parameters have been obtained by a self-consistent energy minimization procedure on all term energies of the eleven configurations $(1{\rm s}^{2})2{\rm s}^{2}2{\rm p}^{6}$, $2{\rm s}^{2}2{\rm p}^{5}3l$, $2{\rm s}2{\rm p}^{6}3l$ and $2{\rm s}^{2}2{\rm p}^{5}4l$ ( $l~\leq n-1$). The relativistic corrections: spin-orbit, mass, Darwin and one-body, are introduced according to the Breit-Pauli approach of Bethe & Salpeter (1957) in intermediate coupling LSJ. The main input data of this code are the charge of the ion and the configurations to be used in the model.

Stark broadening parameter calculations have been performed within the semiclassical perturbation method (Sahal-Bréchot 1969a,b). A detailed description of this formalism with all the innovations and optimizations is given in Sahal-Bréchot (1969a,b, 1974, 1991), Fleurier et al. (1977), Dimitrijevic et al. (1991), Dimitrijevic & Sahal-Bréchot (1996b), and only the basic details of calculations will be presented here. The Stark full width (W) at the intensity half maximum (FWHM) and shift (d) of an isolated spectral line, may be expressed as (Sahal-Bréchot 1969a,b)

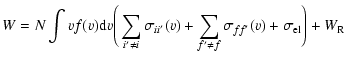    $\displaystyle W = N\int vf(v){\rm d}v \Bigg(\sum_{i'\ne i}\sigma_{ii'}(v) +\sum_{f'\ne f}\sigma_{ff'}(v) + \sigma_{{\rm el}}\Bigg) + W_{\rm R}$  
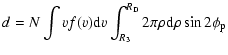    $\displaystyle d = N\int vf(v){\rm d}v\int_{R_3}^{R_{\rm D}} 2\pi \rho {\rm d}\rho \sin 2\phi_{\rm p}$ (1)

where N is the electron density, f(v) the Maxwellian velocity distribution function for electrons, $\rho $ denotes the impact parameter of the incoming electron and v is the velocity, i and f denote the initial and final atomic energy levels, and i', f' their corresponding perturber levels, while $W_{\rm R}$ gives the contribution of the Feshbach resonances (Fleurier et al. 1977). The inelastic cross section  $\sigma_{j,j'}(v)$ can be expressed by an integral over the impact parameter of the transition probability  $P_{jj'}(\rho ,v)$ as

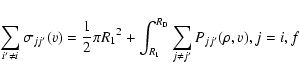\begin{displaymath}% \sum_{i'\ne i}\sigma_{jj'}(v) = {1\over 2}\pi {R_1}^2 +\int_{R_1}^{R_{\rm D}}\sum_{j \ne j'}P_{jj'}(\rho ,v), j=i,f \end{displaymath} (2)

and the elastic cross section is given by
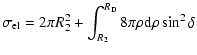    $\displaystyle \sigma_{{\rm el}} = 2\pi R_2^2 + \int_{R_2}^{R_{\rm D}}8\pi \rho {\rm d}\rho\sin^2\delta$  
    $\displaystyle \delta = \left(\phi_{\rm p}^2 + \phi_{\rm q}^2\right)^{1/2}.$ (3)

The phase shifts $\phi_{\rm p}$ and $\phi_{\rm q}$ due respectively to the polarisation potential (r-4) and to the quadrupolar potential (r-3), are given in Sect. 3 of Chapter 2 in Sahal-Bréchot (1969a). $R_{\rm D}$ is the Debye radius. All the cut-offs R1, R2, R3 are described in Sect. 1 of Chapter 3 in Sahal-Bréchot (1969b).

For electrons hyperbolic paths due to the attractive Coulomb force were used, while for perturbing ions the hyperbolic paths are different since the force is repulsive.

The formulae for the ion-impact widths and shifts are analogous to Eqs. (1)-(3), without the resonance contribution to the width. The results obtained within the semiclassical perturbation approach (Sahal-Bréchot 1969a,b) have been compared with critically selected experimental data for 13 He I multiplets (Dimitrijevic & Sahal-Bréchot 1985) and it was found that the agreement between experimental data and semiclassical calculations is within $\pm$20%, which is within the limits of predicted accuracy of the semiclassical method (Griem 1974). In addition, recent measurements of line widths for F V (Uzelac et al. 1993; Blagojevic et al. 1996), N V (Glenzer et al. 1992; Blagojevic et al. 1999) and O V (Blagojevic et al. 1999) are in excellent agreement with the corresponding semiclassical perturbation calculations (Blagojevic et al. (1996) for F V, Dimitrijevic & Sahal-Bréchot (1992) for N V and Dimitrijevic & Sahal-Bréchot (1995b,c) for O V).

3 Results and discussion

By combining the SUPERSTRUCTURE code for calculating energy levels and oscillator strengths and the code for the Stark broadening calculations we calculated Stark broadening parameters ab initio.

Using atomic energy levels obtained from the SUPERSTRUCTURE code, we have also calculated oscillator strengths using the Coulomb approximation. For higher levels, the method described by van Regemorter et al. (1979) has been used.

Electron-impact broadening widths (FWHM) and shifts for 16 Si V multiplets, have been calculated with atomic energy levels and oscillator strengths obtained using the SUPERSTRUCTURE Code. Results have also been obtained using the Bates & Damgaard method for the oscillator strengths. These data are shown in Table 1 (available only in electronic form) for a perturber density of 1017 cm-3 and temperatures from 50 000 up to 500 000 K. Additionally, in order to provide Stark broadening data for the most important ionic perturbers in stellar atmospheres, proton-, ionized helium-, and Si II-impact broadening parameters are calculated for the same perturber densities and temperatures. Again, atomic energy levels and oscillator strengths are obtained using the SUPERSTRUCTURE code, and the results are shown in Table 2 (available only in electronic form). We found results similar to those obtained using the Bates & Damgaard approximation for the set of oscillator strengths for transitions to the perturbing levels. Such temperatures are of interest for the modelling and analysis of X-ray spectra, such as the spectra obtained by CHANDRA, modelling of some hot star atmospheres (e.g. PG 1195 type), subphotospheric layers, soft X-ray lasers and laser-produced plasmas. Higher temperatures are of interest for fusion plasmas as well as for stellar interiors. We also specify a parameter C (Dimitrijevic & Sahal-Bréchot 1984), which gives an estimate for the maximum perturber density for which the line may be treated as isolated, when it is divided by the corresponding full width at half maximum. For each value given in Table 1 the collision volume (V) multiplied by the perturber density (N) is much less than one and the impact approximation is valid (Sahal-Bréchot 1969a,b). When the impact approximation is not valid, the ion broadening contribution may be estimated by using the quasistatic approach (Griem 1974; Sahal-Bréchot 1991). In the region where neither approximation is valid, a unified-type theory should be used. For example, in Barnard et al. (1974) a simple analytical formula for such a case is given. The accuracy of the results shown in Tables 1 and 2 decreases when broadening by ion interactions becomes important.

If we compare results for Stark widths obtained with oscillator strengths calculated with SUPERSTRUCTURE ($W_{\rm S}$) and by using the Bates & Damgaard approximation ( $W_{{\rm BD}}$), the average ratio of  $W_{{\rm BD}}$ and $W_{\rm S}$ is 1.09 for T = 50 000 K and 1.10 for 500 000 K. Since in Stark broadening calculations we use a set of atomic data where a particular oscillator strength value is not always critical, the result obtained confirms that the Bates & Daamgard approximation may be useful for Stark broadening calculations in the case of ions such as Si V, when more reliable data are not available. For shifts the disagreements are larger, but the shifts obtained here are typically 2-3 orders of magnitude smaller than the widths. In fact, for the widths all the important contributions have a positive sign. For the present shifts important contributions have different signs, leading to mutual cancellations. Therefore, since the usual final accuracy for the shift is about 20-30 per cent of the width value, the accuracy of the shifts determined here is bad. If we compare our present results with Stark width results obtained in Dimitrijevic (1993a) by using the modified semiempirical method (Dimitrijevic & Konjevic 1980) and with the results obtained in Dimitrijevic (1993b) by using Griem's simplified semiclassical approach (Griem 1974, Eq. (526)) we can see that the average ratio of the present widths to the simplified semiclassical ones is 1.30, and to the modified semiempirical method 1.77. As to the difference between the present work and that of Dimitrijevic (1993a,b), we have here a complete set of atomic energy levels needed for an adequate application of the semiclassical perturbation approach. One also has to take into account that these energy levels are calculated, while in Dimitrijevic (1993a,b), experimental atomic energy levels were used.

In conclusion, we see that using the SUPERSTRUCTURE code one obtains a set of energy levels and oscillators strengths, enabling an ab initio calculation of Stark broadening parameters. This is suitable especially for multicharged ions when other theoretical and experimental atomic data are scarce. This work also suggests that the set of oscillator strength values obtained with the Bates & Damgaard approximation may be useful for Stark broadening calculations when more reliable data are not available.

Acknowledgements
This work is a part of the project "Influence of collisional processes on astrophysical plasma line shapes'' (GA 1195), supported by the Ministry of Science and Environment Protection of Serbia.

References

 
Copyright ESO 2004