A&A 422, 817-830 (2004)
DOI: 10.1051/0004-6361:20040295
P. K. Fung1 - J. Kuijpers2
1 - Astronomical Institute, Utrecht University, PO Box 80000, 3508 TA Utrecht, The Netherlands
2 - Department of Astrophysics, University of Nijmegen, PO Box 9010, 6500 GL Nijmegen, The Netherlands
Received 18 February 2004 / Accepted 2 May 2004
Abstract
We have studied systematically the free-electron laser in the context of high brightness
pulsar radio emission. In this paper, we have numerically examined the case
where a transverse electromagnetic wave is distorting the motion of a
relativistic electron beam while travelling over one stellar radius
(![]()
![]() ). For different sets of parameters, coherent emission is generated by bunches of beam
electrons in the radio domain, with bandwidths of 3 GHz. Pulse power often
reached
). For different sets of parameters, coherent emission is generated by bunches of beam
electrons in the radio domain, with bandwidths of 3 GHz. Pulse power often
reached
![]() ,
which corresponds with brightness
temperature of
,
which corresponds with brightness
temperature of
![]() .
The duration of these pulses is of
the order of nanoseconds. In the context of pulsar radio emission,
our results indicate that the laser can produce elementary bursts of radiation which
build up the observed microstructures of a few tens of microseconds duration.
The process is sensitive mostly to the beam particles energy, number
density and the background magnetic field, but much less so to the
transverse wave parameters. We demonstrate
that the operation of a free-electron laser with a transverse electromagnetic wiggler in the pulsar magnetosphere occurs preferably at moderate
Lorentz factors
.
The duration of these pulses is of
the order of nanoseconds. In the context of pulsar radio emission,
our results indicate that the laser can produce elementary bursts of radiation which
build up the observed microstructures of a few tens of microseconds duration.
The process is sensitive mostly to the beam particles energy, number
density and the background magnetic field, but much less so to the
transverse wave parameters. We demonstrate
that the operation of a free-electron laser with a transverse electromagnetic wiggler in the pulsar magnetosphere occurs preferably at moderate
Lorentz factors
![]() ,
high beam density
,
high beam density
![]() where
where
![]() is the Goldreich-Julian
density at a stellar radius
is the Goldreich-Julian
density at a stellar radius ![]() ,
and finally, at large altitude
where the background
magnetic field is low
,
and finally, at large altitude
where the background
magnetic field is low
![]() .
.
Key words: masers - radiation mechanisms: non-thermal - plasmas
An important property of the pulses is their high brightness
temperature
![]() ,
given by
,
given by
![]() ,
where
,
where
![]() is the measured flux in Jansky at the
frequency
is the measured flux in Jansky at the
frequency
![]() for a pulsar at distance
for a pulsar at distance
![]() and where
and where ![]() is the radius of the emission region (in meters). For characteristic values:
is the radius of the emission region (in meters). For characteristic values:
![]() ,
,
![]() at
at
![]() ,
this implies that the brightness temperature ranges from
,
this implies that the brightness temperature ranges from
![]() to
to
![]() ,
depending on whether the radius of the emission region is
taken to be the whole pulsar (
,
depending on whether the radius of the emission region is
taken to be the whole pulsar (
![]() )
or
only the polar cap (
)
or
only the polar cap (
![]() for
for
![]() ).
If the emission process were incoherent
this would imply the presence of energetic electrons (positrons) of
individual energies
).
If the emission process were incoherent
this would imply the presence of energetic electrons (positrons) of
individual energies
![]() ,
which are difficult to achieve in view of the maximum available
voltage jump in a rotating magnetic star inside the light cylinder.
Because of this, the mechanism responsible for the radio
emission is assumed to be some form of coherent action. The emission
can then be either an antenna or a maser process.
If the radiation source is located on the open field lines above the
polar cap a maser emission process is most likely powered by a
high-energy electron-positron beam. Candidates for the emission
process are maser curvature emission (Luo & Melrose 1995), relativistic plasma
emission (Melrose & Gedalin 1999), normal and anomalous Doppler
instability (Lyutikov 1998), and linear acceleration emission (Melrose 1978).
,
which are difficult to achieve in view of the maximum available
voltage jump in a rotating magnetic star inside the light cylinder.
Because of this, the mechanism responsible for the radio
emission is assumed to be some form of coherent action. The emission
can then be either an antenna or a maser process.
If the radiation source is located on the open field lines above the
polar cap a maser emission process is most likely powered by a
high-energy electron-positron beam. Candidates for the emission
process are maser curvature emission (Luo & Melrose 1995), relativistic plasma
emission (Melrose & Gedalin 1999), normal and anomalous Doppler
instability (Lyutikov 1998), and linear acceleration emission (Melrose 1978).
Despite the efforts in the investigations over the past three decades, the mechanism responsible for the radio emission is still unknown.
The process studied here is a specific type of the free-electron
laser (FEL), a laboratory device which produces coherent radiation. In
a FEL, a beam of relativistic electrons, with velocity v, passes
through a periodic, electromagnetic field (called wiggler) and radiates at the resonance
frequency
![]() ,
where
,
where
![]() ,
and
,
and
![]() and
and
![]() are the wave frequency and
the wavenumber respectively associated with the wavelength
are the wave frequency and
the wavenumber respectively associated with the wavelength
![]() of the wiggler.
Under appropriate conditions the radiation will be enhanced by the
particles that follow, due to the bunching of the
particles. Previously mentioned linear acceleration emission
(Melrose 1978) and coherent inverse Compton scattering (Schopper et al. 2002)
are both forms of this mechanism. They differ from the case here in the
sense that, in this study, particles will undergo a small transverse
displacement, whereas in the other two cases, the distortion is along
the path of the particles. Therefore, the solution proposed here is only
applicable for the region where the background magnetic field is
sufficient small, in comparison to the magnetic field amplitude of the
wiggler, i.e. high up in the magnetosphere.
of the wiggler.
Under appropriate conditions the radiation will be enhanced by the
particles that follow, due to the bunching of the
particles. Previously mentioned linear acceleration emission
(Melrose 1978) and coherent inverse Compton scattering (Schopper et al. 2002)
are both forms of this mechanism. They differ from the case here in the
sense that, in this study, particles will undergo a small transverse
displacement, whereas in the other two cases, the distortion is along
the path of the particles. Therefore, the solution proposed here is only
applicable for the region where the background magnetic field is
sufficient small, in comparison to the magnetic field amplitude of the
wiggler, i.e. high up in the magnetosphere.
Applying the FEL concept to the pulsar, we will investigate as potential wigglers high-frequency Alfvén waves and other potential periodic structures in the pulsar magnetosphere. Such waves might be generated by a beam instability of the (remnant of the) primary beam in the ambient secondary pair plasma, or by the inhomogeneity of the pair plasma in which faster particles run into dense clumps of pairs (Asseo & Melikidze 1998; Melikidze et al. 2000; Usov 1987). The efficiency of the FEL interaction between these waves and the beam of primary/secondary particles is investigated by doing numerical simulations.
In Sect. 2 the basic concept of the free-electron laser mechanism is presented in detail before it is applied to the pulsar magnetosphere. A description of the simulation code is given is Sect. 3, and a summary of free-electron laser parameters is found in Sect. 4. In Sect. 5, we will present the results of the numerical simulations of this process under pulsar magnetosphere conditions. The conclusions and a discussion are given in Sect. 6.
Throughout the paper, SI units and Cartesian coordinates, in which ![]() is the position vector, with local magnetic field parallel to
is the position vector, with local magnetic field parallel to ![]() are used.
are used.
Note that the FEL mechanism that we treat here is an antenne process in which bunching occurs in space ("reactive'').
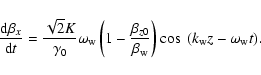 |
(3) |
This force acts on the beam in the z-direction and
drives a longitudinal current
![]() ,
where q is the
elementary charge of the beam particles, n is the number density of the
particles and
,
where q is the
elementary charge of the beam particles, n is the number density of the
particles and
![]() is the velocity which is induced by the motion
in the ponderomotive wave. As a result, like
is the velocity which is induced by the motion
in the ponderomotive wave. As a result, like
![]() ,
,
![]() is proportional to
is proportional to
![]() .
Related to
.
Related to
![]() is a density modulation according to
is a density modulation according to
![]() .
This density modulation is observed as bunching of the
particles. Note that the bunches occur at the ponderomotive
wavelength
.
This density modulation is observed as bunching of the
particles. Note that the bunches occur at the ponderomotive
wavelength
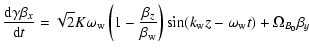 |
(9) | ||
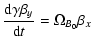 |
(10) | ||
| (11) |
Our aim is to apply the mechanism to the pulsar magnetosphere, while making as few assumptions as possible. As is common to most pulsar models, we assume that a large electric field is set up along the open field lines above the polar caps due to the fast rotation of the magnetised neutron star. This electric field pulls out and accelerates electrons, which, in the presence of a strong magnetic field, are in the lowest Landau level and thus move along the magnetic field lines. At some altitude above the pulsar surface - between a few polar cap radii and a few stellar radii - a dense plasma of electron-positron pairs is produced, either from curvature radiation of the primaries in the strong magnetic field or from their inverse Compton radiation. Very likely, the entire process is only stationary in an average sense but highly variable in space and time on small scales with inhomogeneous distributions of pair plasma intermingled with primary beams.
In our model, we investigate radiation from a mono-energetic beam of electrons in the presence of a subluminal transverse electromagnetic wiggler.
In theory, radiation of any frequency can be obtained by tuning
![]() ,
,
![]() and
and ![]() .
For radiation at frequencies
.
For radiation at frequencies
![]() in the range of 108 and
in the range of 108 and
![]() ,
and parallel wave vectors
,
and parallel wave vectors
![]() ,
the required Lorentz factors range from unity up to 107 (Fig. 1).
,
the required Lorentz factors range from unity up to 107 (Fig. 1).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0295f1.ps}
\end{figure}](/articles/aa/full/2004/30/aa0295-04/Timg128.gif) |
Figure 1:
Values for which
|
Near the stellar surface, particles move one-dimensionally along the
magnetic field lines due to extremely fast synchrotron losses in the strong magnetic field. The quantity
![]() is not invariant anymore when the timescale at which the magnetic
field changes, is small compared to one gyration period in the background
magnetic field, i.e.:
is not invariant anymore when the timescale at which the magnetic
field changes, is small compared to one gyration period in the background
magnetic field, i.e.:
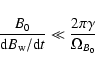 |
(12) |
Next to consider is the synchrotron loss time, which needs to be larger
than the FEL timescale when the latter process causes the pulsar radio
emission.
The synchrotron loss time
![]() ,
the time within which the particle
looses half of its initial energy
,
the time within which the particle
looses half of its initial energy
![]() ,
is defined as
,
is defined as
![]() ,
where
,
where
![]() is the
power of synchrotron radiation emitted by a charged particle moving in
a background magnetic field B0 and
is the
power of synchrotron radiation emitted by a charged particle moving in
a background magnetic field B0 and
![]() is the component of the normalised velocity perpendicular to B0. By using the upper limit for B0 (13), we find
for
is the component of the normalised velocity perpendicular to B0. By using the upper limit for B0 (13), we find
for
![]()
On timescales much smaller than
![]() ,
a change of the particle energy due to synchrotron radiation can be
neglected.
,
a change of the particle energy due to synchrotron radiation can be
neglected.
In our calculations, we used parameters such that firstly, the resonance is in the radio regime (7), secondly, the inequality (13) is satisfied so that particles can (and do) acquire transverse momentum, and finally, the synchrotron emission can be neglected (14).
This section describes how the ingredients for the FEL in the
pair plasma of a pulsar magnetosphere are represented in our numerical
simulations. The Coulomb interactions between the particles in the beam are
neglected, due to the large Lorentz factors. This is because, although the
beam particles generate an electric field radially outward Er, due to
their relativistic speeds, the generated magnetic field (in the
azimuthal direction) reduces the electric field by a factor of
![]() ,
where
,
where ![]() is the particles' speed. This results in a
reduced radial Lorentz force
is the particles' speed. This results in a
reduced radial Lorentz force
![]() .
.
Furthermore, the role of the pairplasma is mainly in providing the wiggler. Therefore, we model the presence of the wiggler by Eqs. (2) rather than generating it in a consistent way.
First, we give a brief introduction to the code. Then, the parameters for each ingredient in the case of N-particles simulations are given.
This code solves the equation of motion of each
(macro)particle in the time domain numerically. For each
macroparticle, labelled i, the differential equations
To find the radiation in the simulations, a set of differential equations for the radiated energy are solved, additional to the differential Eqs. (15). To derive this set of differential equations, we first note that there are two essential differences between a FEL in the lab and our astrophysical application: firstly, there are no reflective mirrors in the neutron star magnetosphere. For a FEL to operate under such conditions, it should be a high-gain, single-pass process. Secondly, there are no side walls bounding the FEL cavity in the magnetosphere. This is accommodated in our pulsar study by using Gaussian modes of which the field decreases in a gaussian manner to zero away from the axis.
The radiation electric field is splitted into a set of
Gaussian modes (see Appendix A):
| (18) | |||
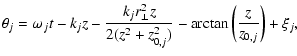 |
(19) |
Further,
![]() is the waist,
w0 is the waist at z=0, and
z0,j = (1/2)kjw02 is the
characteristic distance where the wave starts to diverge, Aj is the
amplitude of this wave at wavevector kj,
is the waist,
w0 is the waist at z=0, and
z0,j = (1/2)kjw02 is the
characteristic distance where the wave starts to diverge, Aj is the
amplitude of this wave at wavevector kj,
![]() is
the corresponding angular wavefrequency, and
is
the corresponding angular wavefrequency, and ![]() is an arbitrary phase.
is an arbitrary phase.
Note that Gaussian modes propagate initially only in one direction
and, therefore, they are suitable to describe narrow beams of pulsar
radio emission. Figure 2 shows the wavefront of a Gaussian mode
(dotted line); the solid lines are level curves at
![]() of the
maximum amplitude (left: near-field, right: far-field).
of the
maximum amplitude (left: near-field, right: far-field).
To continue the derivation of additional differential equations, we
use conservation of energy: the energy gain/loss per unit time of the ith macro-particle with
charge
Qi = Nq qi due to the interaction with the jth electric field
component is given by:
![]() ,
which is balanced by the rate of change of the electromagnetic
fields. The total power radiated
,
which is balanced by the rate of change of the electromagnetic
fields. The total power radiated
![]() is obtained from:
is obtained from:
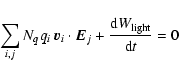 |
(21) |
Instead of calculating the change in amplitude and phase of each mode
directly, GPT rewrites the amplitudes and phases into two other independent variables mj
and nj:
A factor
![]() enters Eqs. (22) and (23) because one mode represents a frequency interval. This
gives the correct calculation of mj and nj, which is dependent on
enters Eqs. (22) and (23) because one mode represents a frequency interval. This
gives the correct calculation of mj and nj, which is dependent on
![]() ,
and ensures that the resulting spectrum, represented by Aj's,
is independent on the number of modes used.
,
and ensures that the resulting spectrum, represented by Aj's,
is independent on the number of modes used.
| Run | Input parameters | Output | Energy densities | |||||||||||
| n | K |
|
|
B0 |
|
|
|
|
|
|
|
|
||
| (
|
(m) | (T) | (GHz) | (GHz) | (
|
(
|
(106 Jm-3) | (Jm-3) | (Jm-3) | (102 Jm-3) | ||||
| 1 | 1000 | 0.23 | 10 | 50 | 0.9 | 0 | 11 | 2.42 | 9.09 | 1.02 | 1.30 | 8.15 | 0 | 8.25 |
| 2 | - | - | 5 | - | - | - | 42.8 | 9.72 | 36.6 | 1.04 | - | 2.04 | - | 34.5 |
| - | - | 10 | - | - | - | 11 | 2.42 | 9.09 | 1.02 | - | 8.15 | - | 8.25 | |
| - | - | 15 | - | - | - | 4.96 | 1.02 | 3.67 | 1.16 | - | 8.35 | - | 3.46 | |
| - | - | 20 | - | - | - | 2.84 | 0.53 | 1.61 | 0.99 | - | 32.62 | - | 1.50 | |
| 3 | - | - | - | 25 | - | - | 22.2 | 3.8 | 9.52 | 1.44 | - | 32.6 | - | 9.00 |
| - | - | - | 40 | - | - | 13.8 | 2.86 | 9.42 | 1.02 | - | 10.07 | - | 8.89 | |
| - | - | - | 50 | - | - | 11 | 2.42 | 9.09 | 1.34 | - | 8.15 | - | 8.25 | |
| - | - | - | 100 | - | - | 5.57 | 1.28 | 7.02 | 1.70 | - | 2.03 | - | 6.63 | |
| 4 | - | - | - | - | 0.2 | - | 88.5 | 14.1 | 9.59 | 0.215 | - | 94.9 | - | 9.00 |
| - | - | - | - | 0.5 | - | 55.7 | 8.12 | 9.54 | 0.37 | - | 18.2 | - | 9.00 | |
| - | - | - | - | 0.8 | - | 22.2 | 3.79 | 9.39 | 0.79 | - | 9.35 | - | 8.86 | |
| - | - | - | - | 0.9 | - | 11 | 2.42 | 9.09 | 1.02 | - | 8.15 | - | 8.25 | |
| 5 | - | - | - | - | - | 10-3 | 10.9 | 2.43 | 9.46 | 7.4 | - | - | 0.4 | 8.85 |
| - | - | - | - | - | 0.01 | 2.18 | 0.61 | 2.7 | 1.36 | - | - | 40 | 2.55 | |
| - | - | - | - | - | 0.025 | n | n | 0.455 | n | - | - |
|
|
|
| - | - | - | - | - | 0.05 | n | n |
|
n | - | - |
|
|
|
| 6 | - | 0.1 | - | - | - | - | 11.37 | 1.53 | 1.79 | 0.38 | 2.30 | - | - | 1.7 |
| - | 0.2 | - | - | - | - | 11.1 | 2.22 | 7.2 | 1.07 | 1.76 | - | - | 6.8 | |
| - | 0.3 | - | - | - | - | 10.9 | 3.01 | 16.5 | 1.73 | 1.15 | - | - | 15.5 | |
| - | 0.4 | - | - | - | - | 10.7 | 3.40 | 29.9 | 2.8 | 0.575 | - | - | 28.2 | |
| 7 | 1000 | - | - | - | - | - | 11 | 2.42 | 9.09 | 1.24 | 1.3 | - | - | 8.24 |
| 500 | - | - | - | - | - | 2.72 | 0.80 | 1.77 | 0.72 | 0.16 | - | - | 1.66 | |
| 250 | - | - | - | - | - | 0.69 | 0.16 | 0.112 | 0.23 | 0.02 | - | - | 0.10 | |
| 100 | - | - | - | - | - | 0.09 | 0.006 |
|
|
|
- | - |
|
|
The wiggler part of the electromagnetic field is assumed to have a time-independent amplitude during passage of the beam, and is not included here, for we assume that the change in the wigglers' energy is small on the considered timescales.
Summarising, the differential equations solved at
time t by GPT consist of the 2N equations:
![$\displaystyle \frac{\mbox{d}\gamma_i \mbox{\boldmath$\beta$ }_i}{\mbox{d}t} = \frac{q_i}{m_ic}[\vec{E}(\vec{x},t)+
\vec{v}_i(t) \times \vec{B}(\vec{x},t)]$](/articles/aa/full/2004/30/aa0295-04/img142.gif) |
|||
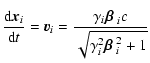 |
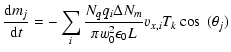 |
|||
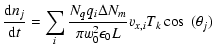 |
To retrieve the pulse in the time domain, both the electric field and the power are Fourier transformed from the frequency to the time domain, and Parseval's theorem is applied to the results to ensure a correct transformation between time and frequency domain.
Note that the results obtained with this code are independent of the number of time outputs, the number of macroparticles and the number of modes.
The wiggler is an electromagnetic disturbance propagating in the
z-direction. In the pulsar magnetosphere, the scale at which
the physical parameters change, e.g. background magnetic field, is of
the order of ![]() (
(![]()
![]() ). Therefore, the
interaction between the beam and the wiggler is simulated until the
beam particles reach this distance, so
). Therefore, the
interaction between the beam and the wiggler is simulated until the
beam particles reach this distance, so
![]() .
The parameters for the wiggler are given in
Table 1 (all labelled with "
.
The parameters for the wiggler are given in
Table 1 (all labelled with "![]() ''). The values for the
magnetic induction and angular frequency are obtained from (2) and (5).
''). The values for the
magnetic induction and angular frequency are obtained from (2) and (5).
In the first run, the wiggler's phase speed is 0.9c. The amplitude
of the magnetic induction
![]() is
is
![]() .
The wavelength
.
The wavelength
![]() is 50 metres. These values are chosen such that the
resonance is at radio frequencies, and the strength of the magnetic induction is
chosen such that the induced transverse velocity is small compared to
the initial axial velocity (
is 50 metres. These values are chosen such that the
resonance is at radio frequencies, and the strength of the magnetic induction is
chosen such that the induced transverse velocity is small compared to
the initial axial velocity (
![]() in
Eq. (4)).
in
Eq. (4)).
In the subsequent runs we investigate the effects of varying each
of these parameters as compared to the results of the first run. In run 2, the wiggler strength K is increased from five to twenty, in steps of K=5 (correspondingly the magnetic induction is increased in steps of
![]() ). In the third
run, the wavelength of the wiggler takes the values 25, 40, 50 and 100 m. In run 4, the velocity of
the wave is changed from 0.2 to 0.9.
). In the third
run, the wavelength of the wiggler takes the values 25, 40, 50 and 100 m. In run 4, the velocity of
the wave is changed from 0.2 to 0.9.
In run 5, we study the effect of a non-zero background magnetic
field. We took the most simple case is which the field in uniform (in z) and has a background magnetic field strength of
B0 = 10-3, 10-2,
![]() ,
,
![]() T.
T.
In run 6 as we change the number density n of the electron beam. In terms of the Goldreich-Julian density, the fractional density ranges from 0.1 to 0.4.
Finally, in run 7, we lower the Lorentz factor of the beam particles (the resonance frequency depends on this as
![]() ). The Lorentz factors are chosen:
). The Lorentz factors are chosen:
![]() ,
500, 250, 100.
,
500, 250, 100.
Figures 3a(Run 1) to 9c(Run 7) and
Table 1 show the end results of all runs, i.e. at
![]() .
Rather than discussing the runs
sequentially, we present the systematic trends of our computations,
using the figures as illustrations. Run 5, where a uniform
background field is included, is presented separately.
.
Rather than discussing the runs
sequentially, we present the systematic trends of our computations,
using the figures as illustrations. Run 5, where a uniform
background field is included, is presented separately.
![\begin{figure}% latex2html id marker 838\par\includegraphics[width=8.4cm,clip]...
...ntlabel {\csname p@figure\endcsname \csname thefigure\endcsnamed}
\end{figure}](/articles/aa/full/2004/30/aa0295-04/Timg222.gif) |
Figure 3d:
Run 1: time development of average Lorentz
factor (i.e. per
macro-particle) in two simulations, one with N=2 ( top) and the other
with N=200 ( bottom). The N=2 case reflects the
behaviour of particles radiating incoherently, with constant energy
loss over time as compared with the bunching case, where
there is a steep drop in energy (
|
![\begin{figure}% latex2html id marker 853\par\includegraphics[width=8cm,clip]{0...
...entlabel {\csname p@figure\endcsname \csname thefigure\endcsnamea}
\end{figure}](/articles/aa/full/2004/30/aa0295-04/Timg223.gif) |
Figure 4a:
Spectra for Run 2 plotted over
each other; we have K = 5 (solid), 10 (dotted), 15 (short-dashed) and 20 (long-dashed). The resonance frequency shifts according to Eq. (7). The bandwidth increases with increasing
|
![\begin{figure}% latex2html id marker 866\par\includegraphics[width=8cm,clip]{0...
...ntlabel {\csname p@figure\endcsname \csname thefigure\endcsnamec}
\end{figure}](/articles/aa/full/2004/30/aa0295-04/Timg226.gif) |
Figure 4c:
Run 2: (
|
An alternative illustration of the formation of bunches is found in
Fig. 3d, where the average Lorentz factor per
macro-particle
![]() is plotted. Evidently, the formation of
bunches corresponds to a steep drop of
is plotted. Evidently, the formation of
bunches corresponds to a steep drop of
![]() (e.g. Fig. 3d, the first bunch formation starts from
(e.g. Fig. 3d, the first bunch formation starts from
![]() to
to
![]() ,
and the second formation from
,
and the second formation from
![]() to
to
![]() ).
).
We notice that both the bunch duration and the beam energy loss is larger for the first bunch formation. Saturation is reached due to an increased velocity spread. Therefore, for the second bunch formation, the beam starts with a certain spread in velocity, and it reaches saturation quicker than in the initial bunching.
For the beam number density of
![]() ,
we find
a beam energy loss to radiation of
,
we find
a beam energy loss to radiation of ![]()
![]() ,
after the first time bunching. This number is only affected by n. The number of particles in each bunch scales with n, as does
,
after the first time bunching. This number is only affected by n. The number of particles in each bunch scales with n, as does
![]() (Run 6, Fig. 8c), which agrees with coherent losses.
(Run 6, Fig. 8c), which agrees with coherent losses.
As to the starting time of the first bunching, we find the following: for the same beam and different wiggler parameters (
![]() and
and
![]() ), about ten oscillations of the particles in the wave
as seen by the observer are needed before they start to bunch (Run 3, Fig. 5c and Run 4, Fig. 6c). For the same wiggler, increasing the beam density or decreasing the Lorentz factor give rise to earlier occurence of bunching (Run 6, Fig. 8c and Run 7, Fig. 9c). This suggests that the bunching sets in when the (incoherent) radiation reaches a certain level, because the ponderomotive force is dependent on the radiation field.
), about ten oscillations of the particles in the wave
as seen by the observer are needed before they start to bunch (Run 3, Fig. 5c and Run 4, Fig. 6c). For the same wiggler, increasing the beam density or decreasing the Lorentz factor give rise to earlier occurence of bunching (Run 6, Fig. 8c and Run 7, Fig. 9c). This suggests that the bunching sets in when the (incoherent) radiation reaches a certain level, because the ponderomotive force is dependent on the radiation field.
As for the wiggler strength K, it determines the maximum beam energy
loss during bunching. In Fig. 4c(Run 2) are shown (
![]() ,
t)-plots for
K = 5, 10, 15, 20. We have also run cases for
,
t)-plots for
K = 5, 10, 15, 20. We have also run cases for ![]() .
The maximum energy loss occurs when K = 1.
.
The maximum energy loss occurs when K = 1.
Note that only the maximum of the first peak satisfies
![]() .
This is not the case for the second peak in Fig. 3b, where now
.
This is not the case for the second peak in Fig. 3b, where now
![]() ,
which is less than the coherent case but much more than if it were incoherent.
,
which is less than the coherent case but much more than if it were incoherent.
![\begin{figure}% latex2html id marker 935\par\includegraphics[width=8cm,clip]{0...
...ntlabel {\csname p@figure\endcsname \csname thefigure\endcsnamec}
\end{figure}](/articles/aa/full/2004/30/aa0295-04/Timg244.gif) |
Figure 5c:
Run 3: the average Lorentz factor of the
macro-particles during
their passage in the cavity for
|
The number of temporal peaks corresponds to the number of bunching times (not the
number of bunches that is formed); e.g. in Run 1 (N=200) the beam
particles bunched twice (Fig. 3d),
and the pulse has two peaks (Fig. 3b). The maximum pulse power always occurs at the first time bunching. The following bunch formations result in less powerful pulses (though not completely incoherent). The maxima of the pulses have the same order of magnitude for most runs (Table 1), except for
![]() ,
where the coherent emission becomes less
efficient (and also for
,
where the coherent emission becomes less
efficient (and also for
![]() ,
but this is discussed in the next section). The optimum efficiency of the emission power is reached for
,
but this is discussed in the next section). The optimum efficiency of the emission power is reached for
![]() as follows from the ratio
as follows from the ratio
![]() (Table 1, Run 7: Fig. 9b)
(Table 1, Run 7: Fig. 9b)
The structure within each pulse reflects the wiggling motion of
the particles (e.g. Fig. 5b, where
![]() ).
).
The typical duration of the pulse is a few nanoseconds.
The brightness temperature
![]() is derived using
is derived using
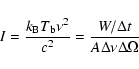 |
(24) |
![\begin{figure}% latex2html id marker 996\par\includegraphics[width=8cm,clip]{0...
...entlabel {\csname p@figure\endcsname \csname thefigure\endcsnamec}
\end{figure}](/articles/aa/full/2004/30/aa0295-04/Timg258.gif) |
Figure 6c:
Run 4: the average Lorentz factor versus the average
distance z of the
particles in simulations with changing
|
Converting the maximum power into the brightness temperature, we find
that, again, for most cases the brightness temperature is approximately
![]() (Table 1).
(Table 1).
Since only the cases where
![]() show bunching, these are discussed further.
The spectrum for this run is plotted in Fig. 7a. Only for
show bunching, these are discussed further.
The spectrum for this run is plotted in Fig. 7a. Only for
![]() ,
the characteristics of the spectrum are similar to the cases where
,
the characteristics of the spectrum are similar to the cases where
![]() .
For
.
For
![]() ,
the resonance frequency shifts to
,
the resonance frequency shifts to
![]() (as compared to the expected value of
(as compared to the expected value of
![]() ). The bandwidth is
). The bandwidth is
![]() ,
and is much smaller than before.
,
and is much smaller than before.
![\begin{figure}% latex2html id marker 1042\par\includegraphics[width=8cm,clip]{...
...entlabel {\csname p@figure\endcsname \csname thefigure\endcsnameb}
\end{figure}](/articles/aa/full/2004/30/aa0295-04/Timg271.gif) |
Figure 7b: Pulse power (logarithmic) for Run 5. The power of the radiation becomes smaller for B0 = 0.025 and 0.05 T. |
![\begin{figure}% latex2html id marker 1047\par\includegraphics[width=8cm,clip]{...
...ntlabel {\csname p@figure\endcsname \csname thefigure\endcsnamec}
\end{figure}](/articles/aa/full/2004/30/aa0295-04/Timg274.gif) |
Figure 7c:
Run 5: the average Lorentz factor versus the average
distance z of the
particles in simulations with background magnetic field
for
|
![\begin{figure}% latex2html id marker 1063\par\includegraphics[width=8cm,clip]{...
...entlabel {\csname p@figure\endcsname \csname thefigure\endcsnamea}
\end{figure}](/articles/aa/full/2004/30/aa0295-04/Timg275.gif) |
Figure 8a:
Run 6: spectrum (from top to bottom) for
|
![\begin{figure}% latex2html id marker 1072\par\includegraphics[width=8cm,clip]{...
...entlabel {\csname p@figure\endcsname \csname thefigure\endcsnameb}
\end{figure}](/articles/aa/full/2004/30/aa0295-04/Timg276.gif) |
Figure 8b:
Pulse power for Run 6 plotted for different number densities relative to
|
![\begin{figure}% latex2html id marker 1078\par\includegraphics[width=8cm,clip]{...
...entlabel {\csname p@figure\endcsname \csname thefigure\endcsnamec}
\end{figure}](/articles/aa/full/2004/30/aa0295-04/Timg278.gif) |
Figure 8c:
Run 6: from top to bottom: Average Lorentz factor per
particle, for number density of the bunch n = 0.1, 0.2,
0.3,
|
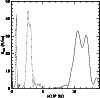 |
Figure 9a:
Run 7: spectrum for initial Lorentz factor
of the beam particles
|
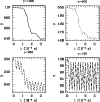 |
Figure 9c: Run 7: the average Lorentz factor versus the average distance z of the particles in simulations with changing Lorentz factor. |
We have shown that, in principle, a FEL can operate in the pulsar outer magnetosphere in the presence of a transverse wiggler. The deciding factors for particles to bunch and emission to be coherent within
![]() ,
are the following: a large beam particle density
,
are the following: a large beam particle density
![]() ,
a Lorentz factor of the beam particles
,
a Lorentz factor of the beam particles
![]() for K = 10, and a small background magnetic field
for K = 10, and a small background magnetic field
![]() .
The brightness temperature of the pulse depends sensitively on these parameters (Table 1).
.
The brightness temperature of the pulse depends sensitively on these parameters (Table 1).
The required beam particle density together with the wiggler's parameters mainly determine the timescale on which particles start to bunch. Bunching occurs after about 10 times the transit time through the wiggler (i.e. 10
![]() ,
Eq. (6)). This seem to set the level of inchorent radiation, which is then large enough for the ponderomotive force to act on the beam particles.
Then the timescale over which a bunch stays together is about one
,
Eq. (6)). This seem to set the level of inchorent radiation, which is then large enough for the ponderomotive force to act on the beam particles.
Then the timescale over which a bunch stays together is about one
![]() ,
i.e. coherent radiation only occurs during this period. Due to an increase in axial velocity spread, debunching occurs. Although particles
rebunch, the associated pulse is weaker due to the velocity
spread in the bunch. In the pulse profile, the first bunching results in one pulse. Then for larger times, particles bunch more often and the pulse acquires more peaks, which are less powerful.
,
i.e. coherent radiation only occurs during this period. Due to an increase in axial velocity spread, debunching occurs. Although particles
rebunch, the associated pulse is weaker due to the velocity
spread in the bunch. In the pulse profile, the first bunching results in one pulse. Then for larger times, particles bunch more often and the pulse acquires more peaks, which are less powerful.
The overall fractional energy losses of the beam are ![]()
![]() .
Together
with the travel time, the calculations demonstrate that when applied to the pulsar magnetosphere for
.
Together
with the travel time, the calculations demonstrate that when applied to the pulsar magnetosphere for
![]() ,
the FEL interaction can produce coherent radiation. For a dipole model, this implies
,
the FEL interaction can produce coherent radiation. For a dipole model, this implies
![]() ,
where we used
,
where we used
![]() ,
i.e. in the outer magnetosphere.
,
i.e. in the outer magnetosphere.
While the particles are bunched, most radiation is at
![]() ,
which in our runs varies from
,
which in our runs varies from
![]() to
to
![]() as in the pulsar radio emission.
The lower frequency is obtained with
as in the pulsar radio emission.
The lower frequency is obtained with
![]() .
.
The particles lose their energy most efficiently for K=1.
The measured FWHM bandwidth for the radiation ![]() ranges from
ranges from
![]() to
to
![]() ,
and is broadband
,
and is broadband
![]() .
The width of the spectrum highly depends on the number
of bunching events occurring during the simulation. After the first bunching,
the bandwidth is of the order of
.
The width of the spectrum highly depends on the number
of bunching events occurring during the simulation. After the first bunching,
the bandwidth is of the order of
![]() ;
After the second -less
effective- bunching,
;
After the second -less
effective- bunching,
![]() and so
on. Of course, the central radiation frequency agrees with radio
pulsar emission by construction. However, it is interesting that the
bandwidth is found to agree
with pulsar radio observations where average pulses and microstructures
are observed from about
and so
on. Of course, the central radiation frequency agrees with radio
pulsar emission by construction. However, it is interesting that the
bandwidth is found to agree
with pulsar radio observations where average pulses and microstructures
are observed from about
![]() to more than
to more than
![]() (average pulses: e.g. Lyne et al. (1998); D'Amico et al. (1998); Manchester et al. (1996); Lyne & Manchester (1988), microstructures: e.g. Bartel & Sieber (1978); Rickett et al. (1975)).
(average pulses: e.g. Lyne et al. (1998); D'Amico et al. (1998); Manchester et al. (1996); Lyne & Manchester (1988), microstructures: e.g. Bartel & Sieber (1978); Rickett et al. (1975)).
As for the brightness temperature
![]() ,
which is a big
obstacle for most radiation processes, we found a brightness
temperature
,
which is a big
obstacle for most radiation processes, we found a brightness
temperature
![]() at pulse maximum of
at pulse maximum of
![]() for
for
![]() and
and
![]() for a wiggler phase velocity
for a wiggler phase velocity
![]() ,
similar to the observationally derived pulsar brightness
temperatures.
,
similar to the observationally derived pulsar brightness
temperatures.
Apparently, the FEL is able to
produce the required high brightness pulse. Further, the characteristic opening angle, given by
![]() ,
is
,
is
![]() .
Again, this agrees with the observed values in pulsar radio
emission, as estimated from the microstructure duration relative to the
pulsar rotation period:
.
Again, this agrees with the observed values in pulsar radio
emission, as estimated from the microstructure duration relative to the
pulsar rotation period:
![]()
![]() for
for
![]() .
.
The radiation pulse has a duration of
![]() .
The
shortest elements of radio emission measured from pulsars are
microstructures. These are quasi-periodic structures of
.
The
shortest elements of radio emission measured from pulsars are
microstructures. These are quasi-periodic structures of ![]()
![]() ,
which are broadband and highly (linearly)
polarized (Lange et al. 1998; Rickett et al. 1975; Popov et al. 2002; Cordes & Hankins 1979).
,
which are broadband and highly (linearly)
polarized (Lange et al. 1998; Rickett et al. 1975; Popov et al. 2002; Cordes & Hankins 1979).
Since the starting time for the particles to bunch is
![]() ,
the faster the wiggler wave is, the longer it
takes for the particles to get bunched. Also, the characteristic pulse duration
,
the faster the wiggler wave is, the longer it
takes for the particles to get bunched. Also, the characteristic pulse duration
![]() increases. This is clearly shown in run 4, where we
varied the phase velocity of the electromagnetic disturbance between 0.2c and 0.9c. The computation time limitation forced us to
consider only such relatively low values for electromagnetic wigglers
in the relativistic outflow from a pulsar magnetosphere, but one can see
from the particles' behaviour in Fig. 6c,
that even more relativistic electromagnetic disturbances would lead to
longer timescales, e.g. for
increases. This is clearly shown in run 4, where we
varied the phase velocity of the electromagnetic disturbance between 0.2c and 0.9c. The computation time limitation forced us to
consider only such relatively low values for electromagnetic wigglers
in the relativistic outflow from a pulsar magnetosphere, but one can see
from the particles' behaviour in Fig. 6c,
that even more relativistic electromagnetic disturbances would lead to
longer timescales, e.g. for
![]() ,
the timescale would go up by a factor 5000, and become comparable to
the observed micropulse durations. (The same argument holds for a lower beam number density n, Fig. 8c; i.e. when
,
the timescale would go up by a factor 5000, and become comparable to
the observed micropulse durations. (The same argument holds for a lower beam number density n, Fig. 8c; i.e. when
![]() ,
bunching occur at
,
bunching occur at
![]() ).
).
Finally, we note that the coherent emission from electrons and positrons in a transverse wiggler add constructively. Therefore, the total number of electrons and positrons in a bunch, and not the charge excess, determines the emission.
In summary, the operation of a single-pass high-gain FEL with a transverse electromagnetic wiggler within the pulsar magnetosphere in the radio regime, requires a mono-energetic beam of electrons/positrons at moderate Lorentz factors in a sufficiently small background magnetic field.
We expect a FEL process to be also possible much nearer to the pulsar, where the magnetic field strength is large and the dynamics of the particles are one-dimensional, when longitudinal instead of transverse wigglers are used. This would be the domain of single-pass, high-gain Cerenkov FELs, and a next logical step to study. Strong Langmuir turbulence has been studied in this context by (Schopper et al. 2002). By using a Particle-in-Cell method, these authors show that electron scattering on Langmuir turbulence, which is excited in a self-consistent way, results in high power output of radiation.
Acknowledgements
This work has been funded under a joint research project between the Centre for Plasma Physics and Radiation Technology (CPS) and the Netherlands Research School for Astronomy (NOVA). We want to thank the anonymous referee for his/her comments. J.K. likes to thank Dr. Marnix van der Wiel and Dr. Theo Schep for stimulating interest in the project. P.K.F. likes to thank Bas van de Geer, Marieke de Loos for their support in using the code GPT and Cyrille Thomas for the description of the Gaussian modes. Also, we want to thank Kees van der Geer for setting up the simulations.
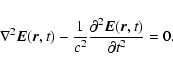 |
(A.1) |
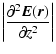 |
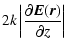 |
(A.2) | |
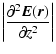 |
(A.3) |
| z0 | |
| Polar cap radius Rpc = 100 m | 24 |
| Stellar radius |
2 |
| Light cilinder Rlc = 107 m | 4
|
The general solution for each component of this equation, which is
axisymmetric, is the following:
| (A.6) | |
| (A.7) |
| Q(z) = z + q0 | (A.8) |
| P(z) = |
(A.9) |
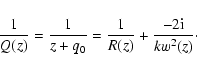 |
(A.10) |
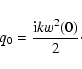 |
(A.11) |
| (A.12) | |||
| (A.13) | |||
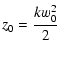 |
(A.14) | ||
| (A.15) |
| (A.16) |
| w(z) | = | 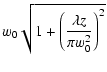 |
(A.17) |
| R(z) | = | 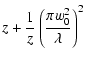 |
(A.18) |
| = | (A.19) |
The opening angle ![]() of the intensity of the mode is given by:
of the intensity of the mode is given by: