A model for the evolution of rotating binary stars is presented. The evolution of a binary system consisting of a 9
A&A 422, 981-986 (2004)
DOI: 10.1051/0004-6361:20034041
R. Q. Huang
National Astronomical Observatories/Yunnan Observatory, the Chinese Academy of Sciences, Kunmin 650011, PR China
Received 2 July 2003 / Accepted 16 March 2004
Abstract
A model for the evolution of rotating binary stars is presented.
The evolution of a binary system consisting of a 9
![]() and a 6
and a 6
![]() star is studied in the mass transfer phase Case A.
Specific attention is focused on the differences between the
evolutions with and without the effects of rotation. The results
indicate that the effects of rotation prolong the lifetime of the
primary, and causes its evolutionary track in the HR diagram to
shift towards lower luminosity. The mass and the surface helium
composition of the primary become lower and the orbital period of
the system becomes significantly longer during the later stage of
the evolution.
star is studied in the mass transfer phase Case A.
Specific attention is focused on the differences between the
evolutions with and without the effects of rotation. The results
indicate that the effects of rotation prolong the lifetime of the
primary, and causes its evolutionary track in the HR diagram to
shift towards lower luminosity. The mass and the surface helium
composition of the primary become lower and the orbital period of
the system becomes significantly longer during the later stage of
the evolution.
Key words: stars: rotation - stars: evolution
A series of observations indicate that rotational mixing exists in rotating stars (Herrero et al. 1992; Charbonnel 1994, 1995; Walborn 1976; Fransson et al. 1989). The evolution of rotating single stars has been studied by many investigations (Kippenhahn & Thomas 1970; Endal & Sofia 1976; Pinsonneaul et al. 1989; Meynet & Maeder 1997). It is important to study the evolution of rotating binary stars. To construct a model for the evolution of binary systems with the effect of rotation, we have to take into account a series of special properties occurring in the rotating binaries: (1) The Roche potential for a rotating component consists of four terms expressing the effects of gravitation, the rotation of the component, the rotation of the system and the tide, respectively. This results in the differences between the equipotential for the rotating components and for the rotating single stars. (2) Owing to the effect of tide, the rotation of the component is solid-body rotation and synchronous with the orbital motion. (3) In the case of binary systems, we have to study not only the structure and evolution of the components, but also the evolution of the system caused by the loss of mass and angular momentum via stellar winds, the transfer of mass and angular momentum between the components and the changes in the moments of inertia of the components.
In Sect. 2, we discuss the special properties occurring in
rotating binaries, and introduce a model for the binary systems
with the effects of rotation. In Sect. 3, the evolution of a
binary system consisting of a 9 ![]() and a 6
and a 6 ![]() star
is studied in the mass transfer phase
Case A, and the differences between the results for the evolutions
with and without the effects of rotation are discussed in detail.
star
is studied in the mass transfer phase
Case A, and the differences between the results for the evolutions
with and without the effects of rotation are discussed in detail.
Observations (Giuricin et al. 1984; Van Hamme &
Wilson 1990; Pan & Tan 1998) show that most
detached binary systems are synchronized systems; only a few
systems are non-synchronized. The conventional theories for the
evolution of close binaries usually assume that the synchronism of
the rotation with the orbital motion is always reached (Kippenhahn
& Weigert 1967; De Loore 1980; Huang &
Taam 1990; Vanbeveren 1991; De Greve
1993). The potential for a synchronous rotating component
in a Roche model is given by
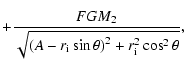 |
(1) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0041fig1.ps}
\end{figure}](/articles/aa/full/2004/30/aa0041-03/Timg13.gif) |
Figure 1: Geomety of the Roche potential. |
| Open with DEXTER | |
Introducing a quantity
q=M2/M1, the dimensionless Roche
potential can be obtained from (1) as:
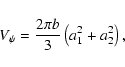 |
(3) |
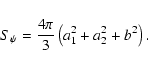 |
(4) |
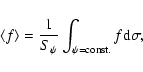 |
(5) |
We define a sphere with its volume equal to that of an
equipotential ellipsoid. The radius ![]() of the sphere is
given by
of the sphere is
given by
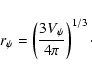 |
(6) |
Due to the effect of tide, the rotation of the component is
synchronous with the orbital motion of the system. Such
synchronous rotation exists also in the interior of the component.
Thus, the rotation of the component is solid-body rotation and
conservative. Kippenhahn & Thomas (1970) introduced a method to
simplify the two-dimensional model with conservative rotation to a
one dimensional model, and gave the structure equations as
follows:
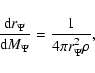 |
(7) |
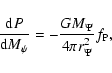 |
(8) |
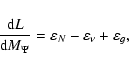 |
(9) |
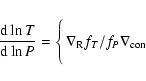 |
(10) |
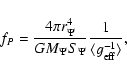 |
(11) |
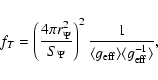 |
(12) |
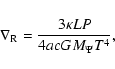 |
(13) |
According to
Eqs. (11) and (12), the key to get the values of fP and fT is to calculate the mean values
![]() and
and
![]() .
In practical calculations, the two-dimensional
model for the rotating component is simplified to a
one-dimensional model. Thus, the stratification of the component
with non-spherical equipotential is replaced by the stratification
with equivalent spheres. The calculation of the mean values of
.
In practical calculations, the two-dimensional
model for the rotating component is simplified to a
one-dimensional model. Thus, the stratification of the component
with non-spherical equipotential is replaced by the stratification
with equivalent spheres. The calculation of the mean values of
![]() and
and
![]() over the equipotential surface is divided,
therefore, into two steps: the first step is to get the
equipotential surface by giving the corresponding equivalent
sphere, the second step is to calculate the mean values of
over the equipotential surface is divided,
therefore, into two steps: the first step is to get the
equipotential surface by giving the corresponding equivalent
sphere, the second step is to calculate the mean values of
![]() and
and
![]() over the equipotential surface.
over the equipotential surface.
Assuming ![]() is the mass in the equivalent sphere of radius
is the mass in the equivalent sphere of radius ![]() ,
and the quantity
,
and the quantity
![]() ,
the
functions for the semi-axis a1,a2 and b to the
,
the
functions for the semi-axis a1,a2 and b to the ![]() of
the equipotential can be obtained from Eqs. (1), (3) and (4) as
of
the equipotential can be obtained from Eqs. (1), (3) and (4) as
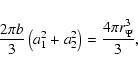 |
(14) |
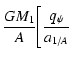 |
+ | 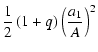 |
(15) |
![$\displaystyle +\frac 12\left( 1+q\right) \left( \frac q{1+q}-\frac{a_1%
}A\right) ^2+\frac{Fq}{1-\frac{a_1}A}\Bigg]$](/articles/aa/full/2004/30/aa0041-03/img43.gif) |
|||
![$\displaystyle =\frac{GM_1}A\left[ \frac{q_\Psi }{b/A}+\frac 12\frac{q^2}{1+q}+\frac{Fq}{\sqrt{1+\left(
\frac bA\right) ^2}}\right],$](/articles/aa/full/2004/30/aa0041-03/img44.gif) |
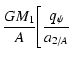 |
+ | 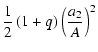 |
(16) |
![$\displaystyle +\frac 12\left( 1+q\right) \left( \frac q{1+q}+\frac{a_2}%
A\right) ^2+\frac{Fq}{1+\frac{a_2}A}\Bigg]$](/articles/aa/full/2004/30/aa0041-03/img47.gif) |
|||
![$\displaystyle =\frac{GM_1}A\left[ \frac{%
q_\Psi }{b/A}+\frac 12\frac{q^2}{1+q}+\frac{Fq}{\sqrt{1+\left(
\frac bA\right) ^2}}\right],$](/articles/aa/full/2004/30/aa0041-03/img48.gif) |
It is difficult to calculate the mean value of a quantity f over the equipotential surface directly, because the equipotential is a non-symmetric rotational ellipsoid with two semimajor axes a1and a2 (a1>a2 ). We imagine that the non-symmetric rotational ellipsoid is composed of two parts. One part is a half of a symmetric rotational ellipsoid with semimajor axis a1 and semiminor axis b (The dot-dashed curve in Fig. 2). The other part is also a half of a symmetric rotational ellipsoid with semimajor axis a2 and semiminor axis b (The dotted curve in Fig. 2). The calculation of the mean value of a quantity f over the equipotential surface can be replaced, therefore, by calculations of the mean values over the two symmetric rotational ellipsoids.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0041fig2.ps}
\end{figure}](/articles/aa/full/2004/30/aa0041-03/Timg49.gif) |
Figure 2:
Geometry of the equipotential. The solid
curve is a non-symmetric
rotational ellipsoid with two semimajor axes
|
| Open with DEXTER | |
Assuming ![]() is the mass in the equipotential, and the quantity
is the mass in the equipotential, and the quantity
![]() ,
the Roche potential of the two
symmetric rotational ellipsoids can be written from Eq. (2) as
,
the Roche potential of the two
symmetric rotational ellipsoids can be written from Eq. (2) as
| |
= | 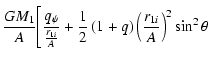 |
|
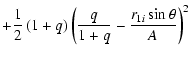 |
(17) | ||
![$\displaystyle +\frac{%
Fq}{\sqrt{\left( 1-\frac{r_{1i}\sin \theta }A\right) ^2+\frac{%
r_{1i}^2\cos ^2\theta }{A^2}}}\Bigg] ,$](/articles/aa/full/2004/30/aa0041-03/img53.gif) |
| |
= | 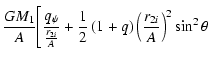 |
|
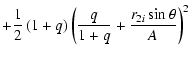 |
(18) | ||
![$\displaystyle +\frac{%
Fq}{\sqrt{\left( 1+\frac{r_{2i}\sin \theta }A\right) ^2+\frac{%
r_{12}^2\cos ^2\theta }{A^2}}}\Bigg] ,$](/articles/aa/full/2004/30/aa0041-03/img57.gif) |
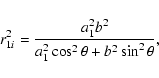 |
(19) |
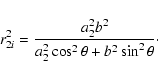 |
(20) |
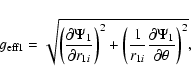 |
(21) |
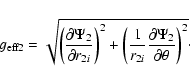 |
(22) |
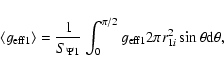 |
(23) |
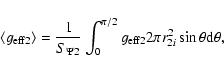 |
(24) |
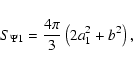 |
(25) |
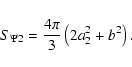 |
(26) |
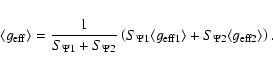 |
(27) |
The effects of meridian circulation and shear turbulence can drive
transport of the chemical elements and the angular momentum in
rotating stars. For the components with solid-body rotation there
exists no differential rotation that can drive shear turbulence.
Hence the rotational mixing in a rotating component can be driven
only by the effect of meridian circulation. Owing to the effect of
tidal motion, the calculation of the meridian circulation for the
rotating components are much more complicated than that for the
single rotating stars. Hence we use a simplified method to treat
the transport of the chemical elements as a diffusion-advection
process. Due to the fact that the transport of the chemical
compositions is caused by the effect of rotation, and the effect
of rotation of a mass layer can be expressed by the ratio of the
mean effective gravity
![]() to the gravity gi of this
layer, so the change of the composition of the element
to the gravity gi of this
layer, so the change of the composition of the element ![]() via a diffusion-advection process can be expressed as:
via a diffusion-advection process can be expressed as:
![$\displaystyle \left(
\frac\partial {\partial r}\right) _t\left[ -D_{\rm adv}\fr...
...g_i}%
-D_{\rm dif}\left( \frac{\partial X_\alpha }{\partial r}\right)
_t\right]$](/articles/aa/full/2004/30/aa0041-03/img72.gif) 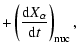 |
(28) |
At the inner and outer boundary reflecting conditions are used:
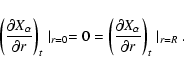 |
(29) |
Among the numerous observational and theoretical investigations on the mass loss rate via stellar winds we adopt the empirical mass loss rate law proposed by Nieuwenhuijzen & Jager (1990):
| |
= | ||
| (30) |
 |
(31) |
In the case without the effect of rotation, the components are spherically symmetric, and the condition for the mass exchange via Roche lobe overflow is when the radius of the component is equal to that of the Roche lobe. However, in the case with the effect of rotation, the components are non-symmetric rotational ellipsoids with the two semimajor axes a1 and a2 (a1>a2 ). The condition for the mass exchange through Roche lobe flow over is changed to that when the longer semimajor axis a1 of the component is equal to the critical radius of the Roche lobe.
The angular velocity of the system and the orbital separation
between the two components are variables due to the many physical
processes occurring in the binary system during evolution, such as
the loss of mass and angular momentum via stellar winds, the
exchange of mass via Roche lobe overflow, the exchange of angular
momentum between the rotation of the components and the orbital
motion of the system caused by the effect of tide, and the change
in the moments of inertia of the components. According to Huang &
Taam (1990), the changes in the angular velocity of the
system and the orbital separation between the two components can
be obtained by
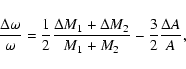 |
(32) |
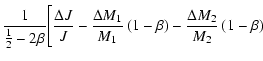 ![$\displaystyle -\frac{\Delta M_1+\Delta M_2}{M_1+M_2}\left( \beta -\frac
12\right)-\frac{\Delta I_1+\Delta I_2}{I_1+I_2}\beta\Bigg],$](/articles/aa/full/2004/30/aa0041-03/img88.gif) |
(33) |
| (34) |
| (35) |
In Eqs. (30) and (31), J is the total angular momentum of the
system, and can be written as
| (36) |
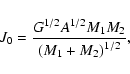 |
(37) |
The loss of angular
momentum carried away by stellar winds are given by
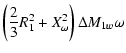 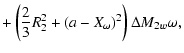 |
(38) |
The evolution of a binary system consisting of a 9
![]() and
a 6
and
a 6
![]() star is studied. Both components of the binary
system are treated simultaneously including mass transfer and the
effect of rotation. Two evolutionary sequences corresponding to
the cases with and without the effect of rotation are calculated.
The sequence denoted as STD corresponds to the evolution without
the effect of rotation, while the sequence denoted as ROT corresponds to that with the effect of rotation. The initial
chemical composition of X=0.70, Z=0.02 is adopted for the
components of the two sequences. The parameters K1 and K2 in
Eq. (28) have the values of 10-4 and 10-6. The initial
orbital separation between the two components in the two sequences
is chosen to be 20.771
star is studied. Both components of the binary
system are treated simultaneously including mass transfer and the
effect of rotation. Two evolutionary sequences corresponding to
the cases with and without the effect of rotation are calculated.
The sequence denoted as STD corresponds to the evolution without
the effect of rotation, while the sequence denoted as ROT corresponds to that with the effect of rotation. The initial
chemical composition of X=0.70, Z=0.02 is adopted for the
components of the two sequences. The parameters K1 and K2 in
Eq. (28) have the values of 10-4 and 10-6. The initial
orbital separation between the two components in the two sequences
is chosen to be 20.771
![]() so that the mass transfer via
Roche lobe occurs in Case A (during the central hydrogen-burning
phase of the primary). The effects of mass loss due to stellar
winds and convective overshooting are considered for both
sequences.
so that the mass transfer via
Roche lobe occurs in Case A (during the central hydrogen-burning
phase of the primary). The effects of mass loss due to stellar
winds and convective overshooting are considered for both
sequences.
![\begin{figure}
\par\includegraphics[angle=270,width=7.5cm,clip]{0041fig3.ps}
\end{figure}](/articles/aa/full/2004/30/aa0041-03/Timg101.gif) |
Figure 3: The evolutionary tracks of the primary in HR diagram for the two sequences. The solid curve corresponds to the track of the STD sequence, and the dotted curve corresponds to that of the ROT sequence. Points a, b, c, d and e on the tracks denote the zero age main sequence, the beginning of the mass transfer phase, the end of the central hydrogen-burning phase, the beginning of the central helium-burning phase and the end of the calculations, respectively. |
| Open with DEXTER | |
The evolutionary tracks of the primary in the HR diagram for the two sequences are illustrated in Fig. 3. The solid curve corresponds to the track of the STD sequence, and the dotted curve corresponds to that of the ROT sequence. Points a, b, c, d and e on the tracks denote the zero age main sequence, the beginning of the mass transfer phase, the end of the central hydrogen-burning phase, the beginning of the central helium-burning phase and the end of the calculations, respectively. From the difference between the solid and dotted curves in Fig. 3 one finds that the effect of rotation causes the evolutionary track of the primary to shift towards lower luminosity.
In Table 1 we list the ages, orbital periods, masses of the
primary and secondary, luminosities, effective temperatures, the
central hydrogen and helium compositions, the compositions of
hydrogen and helium on the surface and the equatorial velocity of
the primary at the critical evolutionary points of the sequences.
From the parameters at point b in Table 1 one finds that the mass
transfer phase begins at
![]() yr for the STD sequence and at
yr for the STD sequence and at
![]() yr for the ROT sequence. Thus,
the time of the beginning of mass transfer phase for the ROT sequence advances by
yr for the ROT sequence. Thus,
the time of the beginning of mass transfer phase for the ROT sequence advances by ![]() 2.4%. This can be understood by
the fact that the primary is a non-symmetric rotational ellipsoid
due to the effect of rotation, the longer semimajor axis is longer
than the equivalent radius, and the criterion for the onset of
mass transfer is that the longer semimajor axis equals to the
radius of the Roche lobe. Due to the difference between the
beginning times of mass transfer, the central hydrogen composition
of the primary at point b has a value of X(c)=0.0567 for the STD sequence instead of 0.1305 for the ROT sequence.
2.4%. This can be understood by
the fact that the primary is a non-symmetric rotational ellipsoid
due to the effect of rotation, the longer semimajor axis is longer
than the equivalent radius, and the criterion for the onset of
mass transfer is that the longer semimajor axis equals to the
radius of the Roche lobe. Due to the difference between the
beginning times of mass transfer, the central hydrogen composition
of the primary at point b has a value of X(c)=0.0567 for the STD sequence instead of 0.1305 for the ROT sequence.
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{0041fig4.ps}
\end{figure}](/articles/aa/full/2004/30/aa0041-03/Timg105.gif) |
Figure 4: The time dependent variation in the orbital period of the system. The solid and dotted curves and the points a, b, c, d, and e have the same meanings as in Fig. 3. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{0041fig5.ps}
\end{figure}](/articles/aa/full/2004/30/aa0041-03/Timg106.gif) |
Figure 5: The time dependent variation in the mass of the primary. The solid and dotted curves and the points a, b, c, d, and e have the same meanings as in Fig. 3. |
| Open with DEXTER | |
Table 1: The parameters at different evolutionary points a, b, c, d and e of the STD and ROT sequences.
In Table 1 we find that the STD sequence reaches point c at
![]() yr, while the ROT sequence reaches point c at
yr, while the ROT sequence reaches point c at
![]() yr. Thus, the ROT sequence is later by about
yr. Thus, the ROT sequence is later by about ![]() for reaching point c. Furthermore, we find in Table 1 that
the central helium-burning begins at the point d at
for reaching point c. Furthermore, we find in Table 1 that
the central helium-burning begins at the point d at
![]() yr for the STD sequence, and there is still no
central helium-burning occurring at the later poind e with the
time
yr for the STD sequence, and there is still no
central helium-burning occurring at the later poind e with the
time
![]() yr for the ROT sequence. This means
that the effect of rotation causes the primary to evolve slower.
yr for the ROT sequence. This means
that the effect of rotation causes the primary to evolve slower.
In addition, one finds in Table 1 that the surface helium composition of the primary has a value of Y=0.3307 at point c, and Y=0.9351 at point e for the STD sequence, while Y=0.3138 at point c and Y=0.8532 at point e for the ROT sequence. Thus, the effect of rotation makes the surface helium composition of the primary smaller during the later stage of the evolution.
Figures 4 and 5 illustrate the time dependent variation in the
orbital period of the system and the mass of the primary. The
solid and the dotted curves in Figs. 4 and 5 correspond to the STD and ROT sequence, respectively. Comparisons of the orbital periods
and the masses of the primary at point d between the two sequences
show that the effect of rotation causes the orbital period of the
system to increases by about ![]() ,
and the mass of the primary
to decrease by about
,
and the mass of the primary
to decrease by about ![]() .
.
Acknowledgements
This work is supported by the Chinese National Science Foundation No. 10073020P.