G. Siringo1 - E. Kreysa1 - L. A. Reichertz1,2 - K. M. Menten1
1 - Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69, 53121 Bonn, Germany
2 -
now at University of California, Department of Physics,
366 LeConte Hall, Berkeley, CA 94720, USA
Received 9 December 2003 / Accepted 1 April 2004
Abstract
A new polarimeter concept has been designed to be used together with the bolometer arrays
developed at the Max-Planck-Institut für Radioastronomie in Bonn. The new polarimeter has the unique
characteristic of being tunable over a wide range of wavelengths and of producing negligible absorption.
It has been used at the Heinrich Hertz Telescope to measure the linear polarization of several quasars
and of extended sources inside our Galaxy. Some results are presented here. We detected polarization in
the quasars 3C 279 and QSO B1633+382. In 3C 279 we also detected polarization
variability on a time scale of a week. We also produced maps of three extended sources:
the Becklin-Neugebauer/Kleinmann-Low (BNKL) complex in the Orion Molecular Cloud 1 (OMC 1),
a filamentary cloud in OMC 3, and the massive star-forming region IRAS 05358+3543.
The polarimeter has low spurious polarization and a high modulation efficiency, and the tests at the
telescope show that it is well suited to become a permanent facility.
Key words: instrumentation: polarimeters - quasars: individual: 3C 279, 1633+382 - ISM: individual objects: OMC 1, OMC 3, IRAS 05358+3543
About fifteen years ago the first steps were taken toward submillimeter polarimetry, using single-pixel bolometric
receivers. Starting with polarimetry at ![]() m (Werner et al. 1988; Novak et al. 1989) and
m (Werner et al. 1988; Novak et al. 1989) and ![]() m
(Clemens et al. 1990), between then and today the whole submillimeter range has been opened for polarimetry,
culminating (for now) with the multiwavelength 3
m
(Clemens et al. 1990), between then and today the whole submillimeter range has been opened for polarimetry,
culminating (for now) with the multiwavelength 3
![]() m imaging polarimeter of the Submillimetre Common User
Bolometer Array (SCUBA; Greaves et al. 2003) on the James Clerk Maxwell telescope.
m imaging polarimeter of the Submillimetre Common User
Bolometer Array (SCUBA; Greaves et al. 2003) on the James Clerk Maxwell telescope.
Linear polarization of submillimeter continuum radiation can be produced by optically thin synchrotron emission in extragalactic objects like radio galaxies and active galactic nuclei or by the partial magnetic alignment of elongated dust grains in interstellar molecular clouds (see Hildebrand 1988). In the latter case, the emission is almost always optically thin. Thus, the bolometer signal is proportional to the dust column density. Practically speaking, this makes dense cloud portions, in particular those associated with star-forming regions and protostellar envelopes, promising targets. In both cases magnetic morphology can be deduced from the directions of the polarization vectors, and polarimetry at millimeter and submillimeter wavelengths can trace the magnetic field in a more direct way than in the optical and radio regimes, where scattering and Faraday rotation can dominate the polarized signal. The goal of submillimeter polarimetry is therefore to map the polarization pattern of these sources with the highest possible angular resolution.
Multi-wavelength polarimetry is particularly desirable as there is a trend for decreasing polarization with increasing optical depth and, thus, decreasing wavelength (e.g. Schleuning et al. 1997). This is probably the result of collisional depolarization in the highest density environments, and thus provides a probe of these.
At submillimeter wavelengths the instabilities of the atmospheric transmission can be large, and ground based polarimetric observations are particularly challenging, as they require high accuracy and, thus, minutes to hours of integration time, because of the weakness of the polarization signal (typically a few percent of the total unpolarized flux). In the last few years great steps forward have been taken in bolometer development and technology, and today we can make use of large arrays of detectors with hundreds of elements.
Here we present a new polarimeter concept, named PolKa after the German Polarimeter für Bolometer Kameras, developed by the Bolometer Development Group of the Millimeter and Submillimeter Astronomy Group at the Max-Planck-Institut für Radioastronomie (MPIfR). The work was started with the idea of creating a versatile instrument, capable of giving good results with any of the MPIfR bolometer arrays, at multiple wavelengths, and flexible enough to be installed on any of the telescopes where MPIfR bolometer arrays are in operation (for details about MPIfR bolometer arrays see Kreysa et al. 2002).
PolKa has many characteristics in common with other polarimeters for millimeter and submillimeter wavelengths. Some of its aspects, however, are unique, such as the unusual solutions of the reflection-type half-wave plate (hereafter RHWP, see Shinnaga et al. 1999) or the continuous spinning technique. In order to extract the polarized signal from the unpolarized foreground it is common to use the modulation/demodulation technique. By means of a polarization modulator, usually a half-wave plate, the polarized component of the incoming radiation is modulated at a precise frequency. If the modulation acts only on the Q and U Stokes parameters of the radiation, the intensity of the latter will be unchanged, at least in the ideal case. Since bolometers are incoherent detectors, they are not sensitive to the phase of the wave but only to its intensity. We need to insert a linear polarizer along the optical path to translate the modulation of the Stokes parameters into a modulation of the total intensity of the transmitted wave. For more details see Siringo (2003).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aa0832f1.eps}
\end{figure}](/articles/aa/full/2004/29/aa0832/Timg9.gif) |
Figure 1: Scheme of a reflection-type half-wave plate. The incident radiation is divided into two beams with orthogonal polarization states.The two emerging rays will have a relative phase shift proportional to t. |
| Open with DEXTER | |
The RHWP consists of two main parts: a wire-grid polarizer and a mirror.
By tuning the distance t between the two parts (see Fig. 1),
it is possible to produce a phase shift between the two components of polarization, because one is reflected by the wires
and the other one by the mirror, causing a difference in path length. The phase shift is given by the simple relation
We produced two RHWPs: a small one, about 150 mm in diameter and a larger one, about 250 mm in diameter. The wire-grid
polarizers used in the RHWPs were machined in our laboratory. For the smaller one, we produced two identical wire-grids
of 146 mm clear aperture, made of Gold coated Tungsten wires with a diameter of ![]() m at a grid step of
m at a grid step of ![]() m.
For the larger version, we produced two identical wire-grids of 246 mm of clear aperture,
m.
For the larger version, we produced two identical wire-grids of 246 mm of clear aperture, ![]() m Tungsten wires and
m Tungsten wires and ![]() m
grid step. The measured mean error in the wire spacing is
m
grid step. The measured mean error in the wire spacing is ![]() m rms.
m rms.
We used two analyzers, mounted in a frame in front of the cryostat window, for easy switching between three different operating modes:
Placing a rotating HWP in the beam path will produce a modulation of the Stokes parameters, but the total intensity will remain
unchanged. To quantify this assertion, let us consider the Müller matrix for an HWP rotating at angular velocity ![]() (Collett 1993)
(Collett 1993)
At this point we introduce a fixed linear polarizer into the beam to produce an intensity modulation detectable by the bolometers.
The bolometer output is
PolKa is used in combination with receivers and amplifiers already existing on the telescope, optimized to work at the frequency
of the telescope's chopping secondary mirror (hereafter called wobbler), in most cases 2 Hz. For this reason, the amplifiers have
filters cutting off signals below 1 Hz. This will suppress 1/f noise and very slow fluctuations of the offset that is present in
the signals. In other words, the bolometer's readout is AC-coupled and the offsets are eliminated. If we apply such a filter to
Eqs. (6) and (7) we see that the information about the total intensity I of the signal
is lost because it is not modulated.
The acquired signals
![]() and
and
![]() ,
in the real case, are given by
,
in the real case, are given by
The choice of the modulation frequency is mainly based on the following two considerations.
The efficiency with which the RHWP modulates the Stokes parameters, called polarization modulation efficiency (PME) has been
measured in the laboratory. It was determined by comparing the transmission of the system with the transmission measured
when a plane mirror was used instead of the RHWP, and using a chopper wheel to modulate the radiation coming from a
polarized laboratory source at the same frequency. The laboratory source consists of an absorber (Eccosorb AN72)
at liquid Nitrogen temperature chopped by a rotating sector-wheel whose sectors are covered by an absorber at room temperature.
In front of the source is a linear polarizer that can be rotated about the optical axis to produce radiation with a well
known state of polarization (the error on the angle is about ![]() ). The measurements were carried out using
a bolometric two-channel polarimeter operating at a central wavelength of 1.2 mm. Inside a 3He/4He cryostat,
at a temperature of 300 mK, there are two bolometers and a wire-grid polarizer used as a polarization beam-splitter.
The optical beam is divided into two orthogonal beams by the cold wire-grid polarizer positioned at
). The measurements were carried out using
a bolometric two-channel polarimeter operating at a central wavelength of 1.2 mm. Inside a 3He/4He cryostat,
at a temperature of 300 mK, there are two bolometers and a wire-grid polarizer used as a polarization beam-splitter.
The optical beam is divided into two orthogonal beams by the cold wire-grid polarizer positioned at
![]() to the optical path,
such that the horizontal polarization goes straight to one bolometer while the vertical polarization is reflected onto the other one.
We found that the RHWP transmits 98% at the maxima and 1.5% at the minima, values mostly due to the distribution of the phase
shift among the large bandpass of the receiver (
to the optical path,
such that the horizontal polarization goes straight to one bolometer while the vertical polarization is reflected onto the other one.
We found that the RHWP transmits 98% at the maxima and 1.5% at the minima, values mostly due to the distribution of the phase
shift among the large bandpass of the receiver (
![]() %). The PME is 96.5% when the RHWP is used
with MPIfR systems operating at 1.2 mm and will be higher (
%). The PME is 96.5% when the RHWP is used
with MPIfR systems operating at 1.2 mm and will be higher (![]() 98%) for systems with a smaller bandpass like the HHT 19-channel
array operating at 870
98%) for systems with a smaller bandpass like the HHT 19-channel
array operating at 870 ![]() m (
m (
![]() %). For comparison, Schleuning et al. (1997) report,
for the polarimeter HERTZ, a PME of 75% at 450
%). For comparison, Schleuning et al. (1997) report,
for the polarimeter HERTZ, a PME of 75% at 450 ![]() m and 85% at 350
m and 85% at 350 ![]() m and Greaves et al. (2003) report,
for the SCUBA polarimeter, a PME of 94% and 97% at 850
m and Greaves et al. (2003) report,
for the SCUBA polarimeter, a PME of 94% and 97% at 850 ![]() m for the "photometric'' and "array'' waveplate, respectively.
m for the "photometric'' and "array'' waveplate, respectively.
PolKa was tested at the Heinrich Hertz Telescope (hereafter HHT) on Mt. Graham, Arizona, a 10 meter submillimeter telescope
equipped with a 19-channel MPIfR bolometer array operating at 870 ![]() m. In May 2001 we made a first test with a small RHWP;
a second test with a full size RHWP was made in January 2002. A typical observing session consisted of several steps.
First the usual routine scans are performed: a pointing on a strong point-like source, a focus, a second pointing, a skydip.
Then, a photometric scan is needed to detect the total flux of the source (Stokes parameter I). This is a standard photometric
procedure, chosen according to the source size: on-off for point sources, on-the-fly map for extended sources.
In both cases the wobbler modulates the signal at 2 Hz and data are acquired by the HHT's total power backend.
Right after the photometric scan, polarization scans are performed to retrieve the other two Stokes parameters Q and U.
Before the beginning of the observations the RHWP was accurately tuned to maximize the polarization modulation efficiency.
To reduce the systematic effects and for a better removal of the spurious polarization, each polarization scan was made twice,
once using the horizontal analyzer and once using the vertical one. Polarization scans were performed following two different
observing strategies: on-off, nodding the telescope on and off the source, in the case of point sources; on-the-fly maps in
case of extended sources. In both cases we do not wobble the secondary mirror and the polarization of the incoming radiation
is only modulated by the spinning RHWP. During polarization scans data are acquired by the polarization backend.
At the end of this sequence we performed another skydip and we alternated between total power data acquisition and polarization
data acquisition. The polarization backend acquired 23 signals (the bolometer signals plus reference signals used to demodulate
the data) at a sampling rate of 512 samples per second resulting in 32 samples per polarization cycle, when the RHWP rotates at 4 Hz.
Each data point, once labelled with a timestamp (synchronized by the IRIG-B signal of the telescope's GPS receiver) was stored
on a local hard disk in 2-byte-integer format. The time resolution in the data files is
m. In May 2001 we made a first test with a small RHWP;
a second test with a full size RHWP was made in January 2002. A typical observing session consisted of several steps.
First the usual routine scans are performed: a pointing on a strong point-like source, a focus, a second pointing, a skydip.
Then, a photometric scan is needed to detect the total flux of the source (Stokes parameter I). This is a standard photometric
procedure, chosen according to the source size: on-off for point sources, on-the-fly map for extended sources.
In both cases the wobbler modulates the signal at 2 Hz and data are acquired by the HHT's total power backend.
Right after the photometric scan, polarization scans are performed to retrieve the other two Stokes parameters Q and U.
Before the beginning of the observations the RHWP was accurately tuned to maximize the polarization modulation efficiency.
To reduce the systematic effects and for a better removal of the spurious polarization, each polarization scan was made twice,
once using the horizontal analyzer and once using the vertical one. Polarization scans were performed following two different
observing strategies: on-off, nodding the telescope on and off the source, in the case of point sources; on-the-fly maps in
case of extended sources. In both cases we do not wobble the secondary mirror and the polarization of the incoming radiation
is only modulated by the spinning RHWP. During polarization scans data are acquired by the polarization backend.
At the end of this sequence we performed another skydip and we alternated between total power data acquisition and polarization
data acquisition. The polarization backend acquired 23 signals (the bolometer signals plus reference signals used to demodulate
the data) at a sampling rate of 512 samples per second resulting in 32 samples per polarization cycle, when the RHWP rotates at 4 Hz.
Each data point, once labelled with a timestamp (synchronized by the IRIG-B signal of the telescope's GPS receiver) was stored
on a local hard disk in 2-byte-integer format. The time resolution in the data files is ![]() 2 ms. The mechanical angular
resolution is given by the sampling rate and by the rotation frequency: when the RHWP rotates at 4 Hz the angular distance
between two adjacent samples is
2 ms. The mechanical angular
resolution is given by the sampling rate and by the rotation frequency: when the RHWP rotates at 4 Hz the angular distance
between two adjacent samples is
![]() .
An example of the data acquisition is given in Fig. 2: the plot
shows the signals detected by the central channel
of the array on the blazar 3C 279 during two polarization on-off scans,
one performed using the horizontal analyzer
and the other performed 16 min later with the vertical analyzer. For each scan,
the data points are the mean values of the
differences between consecutive pairs of subscans on and off the source, and the
error bars represent the standard errors.
No further processing has been applied to the data. The RHWP was spinning at 3.5 Hz
modulating the Stokes parameters at 14 Hz.
We acquired 146 positions per rotation of the RHWP at an angular separation
of
.
An example of the data acquisition is given in Fig. 2: the plot
shows the signals detected by the central channel
of the array on the blazar 3C 279 during two polarization on-off scans,
one performed using the horizontal analyzer
and the other performed 16 min later with the vertical analyzer. For each scan,
the data points are the mean values of the
differences between consecutive pairs of subscans on and off the source, and the
error bars represent the standard errors.
No further processing has been applied to the data. The RHWP was spinning at 3.5 Hz
modulating the Stokes parameters at 14 Hz.
We acquired 146 positions per rotation of the RHWP at an angular separation
of ![]()
![]() .
For comparison, the polarimeter HERTZ
acquires data at 6 fixed position of the HWP at
.
For comparison, the polarimeter HERTZ
acquires data at 6 fixed position of the HWP at
![]() while modulating
at 3.1 Hz by using the wobbler (Dowell et al. 1998)
and the SCUBA polarimeter acquires data at 16 fixed positions at
while modulating
at 3.1 Hz by using the wobbler (Dowell et al. 1998)
and the SCUBA polarimeter acquires data at 16 fixed positions at
![]() while
wobbling at 7.8 Hz (Greaves et al. 2003).
while
wobbling at 7.8 Hz (Greaves et al. 2003).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aa0832f2.eps}
\end{figure}](/articles/aa/full/2004/29/aa0832/Timg50.gif) |
Figure 2:
Example of polarization data acquisition. The source is the blazar 3C 279 observed at the HHT at 870 |
| Open with DEXTER | |
Each scan in Fig. 2 is made up of 32 subscans, 16 on and 16 off the source. One subscan lasts 21 s and
consists of 75 full rotations of the RHWP and comprises 10 950 samples. One complete scan, including the time lost during nodding,
lasts about 15 min, the integration time on the source being 336 s, it comprises about 400 000 samples and requires
about 20 Mb of computer hard disk storage space in 2-byte-integer format. The plot also shows a sinusoidal fit of the detected
signals (dashed lines). The two curves are almost phaseshifted by ![]() relative to each other, as predicted by Eqs. (8)
and (9), the phase difference between the two being
relative to each other, as predicted by Eqs. (8)
and (9), the phase difference between the two being
![]() .
The deviation of
.
The deviation of ![]()
![]() (from
(from
![]() )
is due to the apparent rotation of the sky during the 16 min between the two scans caused by the HHT's altazimuthal mount.
)
is due to the apparent rotation of the sky during the 16 min between the two scans caused by the HHT's altazimuthal mount.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{aa0832f3.eps}
\end{figure}](/articles/aa/full/2004/29/aa0832/Timg55.gif) |
Figure 3: Example of polarization on-off data reduction: the configuration of the array on the sky is shown together with the measured polarization vectors of each channel. The central channel shows the detection of polarization in 3C 279 (2002 January 26, 13:17 UT). |
| Open with DEXTER | |
New software was written by the authors to reduce the data acquired in the polarization observing modes (see the beam plot in Fig. 3). The data acquired by the PolKa backend contain the information about the Q and U Stokes parameters of the source modulated by the polarimeter. This information has to be recovered by demodulation of the data. This is the same process that the photometric backend performs: the wobbler produces a modulated signal, the backend acquires the signal and simultaneously averages the differences at the same frequency. This is a demodulation process and its output is proportional to the flux of the source. This is, in general, the principle of "synchronous demodulation'', a powerful technique for detecting weak signals affected by strong noise. It is very common to use lock-in amplifiers for this type of measurements in the laboratory (Meade 1983). These special amplifiers can recover weak signals hidden in the noise if the signal is modulated at a precise frequency and if an accurate reference signal corresponding to the modulation is supplied. In our special case we take advantage of the fast acquisition made by the PolKa backend to demodulate the data via software using an algorithm called software lock-in.
Assume that we perform a polarization scan using the horizontal analyzer:
| Vi | = | (12) | |
| = | (13) |
| Si | = | (14) | |
| Ci | = | (15) |
| X | = | 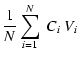 |
|
| = | ![$\displaystyle \frac{2}{N} \left[ Q \displaystyle \sum^N_{i=1} \cos^2{4 \theta_i} +
U \displaystyle \sum^N_{i=1} \cos{4 \theta_i} \sin{4 \theta_i} \right]$](/articles/aa/full/2004/29/aa0832/img71.gif) |
||
| Y | = | 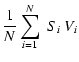 |
|
| = | ![$\displaystyle \frac{2}{N}\left[Q \displaystyle\sum^N_{i=1} \cos{4 \theta_i} \sin{4 \theta_i} +
U \displaystyle\sum^N_{i=1} \sin^2{4 \theta_i} \right].$](/articles/aa/full/2004/29/aa0832/img73.gif) |
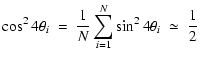 |
(16) | |
| (17) |
| (18) | |||
| (19) |
| X |
(20) |
| Y |
(21) |
The error in P is given by
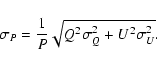 |
(23) |
![\begin{displaymath}\sigma_p = 100~\sqrt{ \left({\frac{\sigma_P }{I}}\right)^2 + \left({P~\frac{\sigma_I}{I^2}}\right)^2 }~~~\mbox{[\%]}.
\end{displaymath}](/articles/aa/full/2004/29/aa0832/img86.gif) |
(25) |
The spurious polarization was estimated by observing the planets Mars and Saturn at different positions in the sky, assuming their
emission to be unpolarized. In all the cases the spurious polarization was below 0.8%. The polarized flux was calibrated by total
power flux measurements of planets performed with the polarization backend. The polarization position angle was calibrated using a
polarized laboratory source: these calibrations are therefore absolute and independent of sky sources. The accuracy in the calibration
of the position angle is
![]() .
.
The ability to observe very low polarized fluxes is mainly limited by the combination of the following three effects:
PolKa is a polarimeter designed to be used in combination with different MPIfR bolometer arrays, at different telescope sites and at
multiple wavelengths. The sensitivity of the instrument, therefore, is strictly related to the sensitivity of the bolometers,
to the wavelength and to the efficiency of the coupling with the telescope optics. The sensitivity is also different in the two observing modes,
polarization on-off and on-the-fly maps. To estimate the sensitivity at the HHT we refer to the polarization on-off on 3C 279.
The total flux of the source, during our second telescope campaign, was
![]() Jy and we measured a polarization
degree
Jy and we measured a polarization
degree
![]() % that is a polarized flux P=879 mJy. The plot in Fig. 2 shows the spurious signals detected
in the outer channels of the array (continuous lines): after the data reduction, their residuals give a
% that is a polarized flux P=879 mJy. The plot in Fig. 2 shows the spurious signals detected
in the outer channels of the array (continuous lines): after the data reduction, their residuals give a
![]() mJy noise level.
In one polarization on-off on 3C 279 we have a
mJy noise level.
In one polarization on-off on 3C 279 we have a ![]() detection in 336 s of integration time on the source.
At the HHT, in photometric mode the noise equivalent flux density (hereafter NEFD) of the 19-channel array is 600 mJy
detection in 336 s of integration time on the source.
At the HHT, in photometric mode the noise equivalent flux density (hereafter NEFD) of the 19-channel array is 600 mJy
![]() under stable weather conditions. Given these numbers, the polarization on-off NEFD at the HHT is 1650 mJy
under stable weather conditions. Given these numbers, the polarization on-off NEFD at the HHT is 1650 mJy
![]() .
.
To estimate the integration time needed to get a signal-to-noise ratio R given the NEFD of the receiver in photometric mode,
we can use the general formula
We detected linear polarization in the two AGNs 3C 279 and QSO B1633+382.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aa0832f4.eps}
\end{figure}](/articles/aa/full/2004/29/aa0832/Timg104.gif) |
Figure 4:
Polarization position angle of 3C 279 in the 7 days of observations.
The variation is |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aa0832f5.eps}
\end{figure}](/articles/aa/full/2004/29/aa0832/Timg105.gif) |
Figure 5: Position angle of QSO B1633+382 in the 7 days of observations. There is no evidence of variability. |
| Open with DEXTER | |
The observations QSO B1633+382 of are noisier than those of 3C 279, because the source is weaker and less polarized.
The observed polarization degree, after ![]() 45 min of integration on the source, is
45 min of integration on the source, is
![]() %.
In this source there is no appreciable variation of the position angle (see Fig. 5).
The observed value is
%.
In this source there is no appreciable variation of the position angle (see Fig. 5).
The observed value is
![]() ,
in good agreement with the VLBI measurements at 5 GHz published
by Cawthorne et al. (1993).
,
in good agreement with the VLBI measurements at 5 GHz published
by Cawthorne et al. (1993).
The strong flux and the possibility of comparing our results with previous observations published by other groups made Orion OMC 1 our favorite target. We also made maps of a filament cloud in Orion OMC 3 and of the high-mass star-forming region IRAS 05358+3543.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aa0832f6.eps}
\end{figure}](/articles/aa/full/2004/29/aa0832/Timg108.gif) |
Figure 6:
Polarization degree map of Orion OMC 1 centered on IRc 2.
Polarization vectors are rotated by
|
| Open with DEXTER | |
The map shown in Fig. 6 is the result of 12 scans performed during our 2002 telescope campaign.
Each scan covers
![]() and required slightly over 30 min, resulting in a total integration time of
and required slightly over 30 min, resulting in a total integration time of ![]() 6 h.
Figure 6 shows the deduced magnetic field (polarization vectors rotated by
6 h.
Figure 6 shows the deduced magnetic field (polarization vectors rotated by
![]() ).
The information shown in the map is manifold. In the background is a total power map of OMC 1.
Superposed, polarization vectors are drawn with a resolution of 10'' per vector.
The polarization degree is proportional to the length of the vectors. In the top right corner the size of a 5% vector
is shown for reference. The position angle is indicated by the direction of the vectors. The quality of the detection
is represented by the width of the vectors (see the top right corner for a scale). The map shows only detections that
are better than
).
The information shown in the map is manifold. In the background is a total power map of OMC 1.
Superposed, polarization vectors are drawn with a resolution of 10'' per vector.
The polarization degree is proportional to the length of the vectors. In the top right corner the size of a 5% vector
is shown for reference. The position angle is indicated by the direction of the vectors. The quality of the detection
is represented by the width of the vectors (see the top right corner for a scale). The map shows only detections that
are better than ![]() .
The total power threshold in this map is fixed to 4 Jy, 2.4% of the peak. Where the total
flux is above this threshold, and no vector is drawn, no meaningful polarization signal was detected.
The maximum flux in the map is in the BN/KL area where the total power has a peak of 169 Jy/beam. In the surroundings
of the peak 1% of polarization produces a signal of about 1 Jy and a detection at
.
The total power threshold in this map is fixed to 4 Jy, 2.4% of the peak. Where the total
flux is above this threshold, and no vector is drawn, no meaningful polarization signal was detected.
The maximum flux in the map is in the BN/KL area where the total power has a peak of 169 Jy/beam. In the surroundings
of the peak 1% of polarization produces a signal of about 1 Jy and a detection at ![]() is possible. We see, however,
that the degree of polarization decreases toward areas of the map where the total flux is higher. This is a well known
depolarization effect, already observed in other dust clouds
(see, for example, Houde et al. 2002; Matthews et al. 2001).
Figure 7 shows the depolarization effect observed by PolKa in OMC 1.
The magnetic field directions in our OMC 1 map are in excellent agreement with those determined
by Coppin et al. (2000) at
is possible. We see, however,
that the degree of polarization decreases toward areas of the map where the total flux is higher. This is a well known
depolarization effect, already observed in other dust clouds
(see, for example, Houde et al. 2002; Matthews et al. 2001).
Figure 7 shows the depolarization effect observed by PolKa in OMC 1.
The magnetic field directions in our OMC 1 map are in excellent agreement with those determined
by Coppin et al. (2000) at ![]() m and by Schleuning et al. (1997) at 350 and
m and by Schleuning et al. (1997) at 350 and ![]() m,
although our polarization degrees are higher than those at 350 and
m,
although our polarization degrees are higher than those at 350 and ![]() m, as expected from the arguments mentioned in the introduction.
m, as expected from the arguments mentioned in the introduction.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aa0832f7.eps}
\end{figure}](/articles/aa/full/2004/29/aa0832/Timg114.gif) |
Figure 7:
Depolarization effect observed by PolKa in OMC 1.
Detections are better than |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aa0832f8.eps}
\end{figure}](/articles/aa/full/2004/29/aa0832/Timg115.gif) |
Figure 8: Polarization degree map of Orion OMC 3. The map is centered between the two clumps MMS3 and MMS4. The brightest clump (bottom left) is MMS6. The histogram shows the distribution of the polarization position angle relative to the position angle of the filament. |
| Open with DEXTER | |
Besides OMC 1, in the Orion A giant molecular cloud there are two other large areas of interest, OMC 2
and OMC 3, that are the consecutive parts of OMC 1 going northwards along the Integral-Shaped Filament
(Bally et al. 1987).
In the northern part of OMC 3 7 embedded cores have been identified by Chini et al. (1997), named MMS1 to MMS7. Given the results of Matthews et al. (2001) we decided to scan this area, to test the polarimeter on a dust source of known
polarization but weaker than OMC 1. Our polarization map, which is shown in Fig. 8,
is centered between the two clumps MMS3 and MMS4 (see Fig. 1 in Chini et al. 1997, for reference).
Only three scans were performed, and the total integration time is only 1.5 h, resulting in a poor signal-to-noise ratio.
The best detections in the map are at ![]()
![]() ,
but most of the vectors have signal-to-noise between 1 and
,
but most of the vectors have signal-to-noise between 1 and ![]() .
This map is presented here only to show that even if the integration time was very short, the polarization vectors show good
consistency in the detected position angle. The histogram at the top-left corner shows the distribution of the polarization
position angles of the vectors relative to the position angle of the filament between the two cores MMS1 and MMS6,
.
This map is presented here only to show that even if the integration time was very short, the polarization vectors show good
consistency in the detected position angle. The histogram at the top-left corner shows the distribution of the polarization
position angles of the vectors relative to the position angle of the filament between the two cores MMS1 and MMS6, ![]()
![]() E of N.
Our map shows, indeed, a good agreement with the results published by Matthews et al. (2001) at
E of N.
Our map shows, indeed, a good agreement with the results published by Matthews et al. (2001) at ![]() m and
by Houde et al. (2003) at
m and
by Houde et al. (2003) at ![]() m.
m.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aa0832f9.eps}
\end{figure}](/articles/aa/full/2004/29/aa0832/Timg120.gif) |
Figure 9:
The first polarization map of IRAS 05358+3543.
Polarization vectors are rotated by
|
| Open with DEXTER | |
In recent years massive outflows have been investigated in detail because they can provide information about the innermost parts of
star-forming regions. The source IRAS 05358+3543 is an extremely young and deeply embedded high-mass protostellar object.
This source is part of a recent statistical work on massive outflows by Beuther et al. (2002b). They found that low-mass correlations
of outflow and core parameters continue up to the high-mass regime, suggesting that similar star formation processes are responsible for
forming stars of all masses. However, massive star formation sites are on average more distant than well known low-mass sources, and thus
their angular sizes are smaller in spite of their larger linear sizes. This indicates that high angular resolution is needed to disentangle
real source and outflow structures. One solution is to study these sources with interferometric techniques at millimeter and submillimeter
waves. Polarization maps of the continuum emission, at the same wavelengths, can be a powerful way to obtain information about the order
of the structures in the source, and could be a valid complement to interferometric observations.
Figure 9 shows the first detection of polarization in the source IRAS 05358+3543.
We performed 8 scans on this source, collecting 4 h of integration time. The size of the map is
![]() .
At the HHT the 345 GHz flux peak of the source was
.
At the HHT the 345 GHz flux peak of the source was
![]() Jy/beam, at
Jy/beam, at
![]() from the absolute IRAS
positions given by Sridharan et al. (2002), where our map is centered. The map shows the polarization vectors rotated by
from the absolute IRAS
positions given by Sridharan et al. (2002), where our map is centered. The map shows the polarization vectors rotated by
![]() to show
the deduced magnetic field directions. All polarimetric detections in the map are better than
to show
the deduced magnetic field directions. All polarimetric detections in the map are better than ![]() .
The polarization signal is subject
to the depolarization effect going toward the most intense areas of the source, behaving in the same way as it was found to behave
in low-mass star-forming regions. On the north and south edges of the cloud, however, we can see that the strongest polarization signals
are aligned along the direction deduced by Beuther et al. (2002a) for the larger molecular outflows of the source
(see Fig. 4 in Beuther et al. 2002a). This is an interesting result that is worthy of further investigation with our polarimeter,
at different angular scales and at different wavelengths.
.
The polarization signal is subject
to the depolarization effect going toward the most intense areas of the source, behaving in the same way as it was found to behave
in low-mass star-forming regions. On the north and south edges of the cloud, however, we can see that the strongest polarization signals
are aligned along the direction deduced by Beuther et al. (2002a) for the larger molecular outflows of the source
(see Fig. 4 in Beuther et al. 2002a). This is an interesting result that is worthy of further investigation with our polarimeter,
at different angular scales and at different wavelengths.
Our polarimeter uses only metallic reflections and this gives it very low insertion losses and a high efficiency.
PolKa is tunable: by simply adjusting three screws one can switch from one operating wavelength to another. In addition, PolKa's tunability
can be used to transform the half-wave plate to a quarter-wave plate with ease and the same instrument can also be used to perform circular
polarization observations. The radiation is modulated directly by PolKa, without the need for a chopping secondary mirror. The modulation
frequency can be much higher than when using a wobbler, and the polarimeter can be used even at telescopes with a fixed secondary mirror.
Furthermore, the polarization signals are restored by digital phase-sensitive detection and not by fitting a sine wave to a noise-dominated signal,
as commonly done in other polarization experiments. The tests at the telescope showed that PolKa is able to produce high quality polarization data.
In particular, it can produce large polarization maps with high signal-to-noise in a relatively short time. PolKa as it is will be installed
on the IRAM 30 meter MRT, where the MAMBO (Max-Planck-Millimeter-Bolometer array) receiver is operating at 1.2 mm.
An improved version of PolKa will be installed on the new submillimeter telescope APEX in the Atacama desert in Chile in combination
with the new array LABOCA (Large Bolometer Camera), made of 300 bolometers operating at ![]() m.
m.
Acknowledgements
The authors would like to thank: Manfred Tonutti (Rheinisch-Westfälische Technische Hochschule, RWTH, Aachen, Germany), who suggested the way to upgrade our wire-grid machine to larger grid sizes; the Friends of the Telescope and the Astronomers on Duty at the Heinrich Hertz Telescope, for their support during our observations; Giuseppe Cimò (formerly MPIfR, now at University of Tasmania, Hobart, Australia) for his participation to the 2002 telescope campaign. We also thank the referee Jane Greaves for detailed reading of the manuscript and useful suggestions, and the language editor Jet Katgert.