G. Del Zanna 1 - K. A. Berrington 2 - H. E. Mason 1
1 -
Department of Applied Mathematics and Theoretical Physics,
University of Cambridge, Cambridge CB3 0WA, UK
2 - School of Science and Mathematics, Sheffield Hallam University, Sheffield S1 1WB, UK
Received 2 October 2003 / Accepted 7 April 2004
Abstract
This is the first in a series of papers in which we benchmark
recent atomic data available for astrophysical applications.
We review various issues related to
the completeness and accuracy of both theoretical and
experimental data.
In this paper,
the available experimental and atomic data for Fe X (n=3 configurations)
are reviewed and assessed. New collisional and radiative
data are calculated to supplement published data.
The radiative calculations are done with empirical adjustements that
take into account observed wavelengths.
Previous line identifications are also reviewed and assessed.
Our approach focuses on the brightest spectral
lines, and uses both wavelengths and line intensities to assess
the line identifications on a quantitative basis.
Although many previous line identifications are confirmed,
some are rejected (e.g. the coronal line observed at 1582.35 Å).
We confirm previously suggested identifications
(e.g. 257.262 Å, 1028.02 Å), and we present new ones,
(e.g. the lines of the 3s23p43d-3s 3p53d
transition array).
In addition, we highlight the presence of blends and
we review which spectral lines are best for density diagnostics or
for instrument calibration.
The theoretical data (line intensities and level lifetimes) are benchmarked against
well-calibrated spectroscopic observations of the solar corona and
laboratory measurements.
The agreement between theoretical and experimental data which we
achieve with our new model ion is very good.
Key words: atomic data - line: identification - Sun: corona - techniques: spectroscopic
This paper is the first in a series which aims to provide assessed sets of atomic data for the analysis of astrophysical spectra. The results will be presented on an ion by ion basis. The approach used will be similar for all ions studied. Atomic data are gathered from different sources. These data are assessed and integrated to form a model ion. Level populations and spectral line intensities are calculated and compared to experimental data (both solar and laboratory). The approach is very practical since both the intensities and wavelengths for the brightest spectral lines are compared to available observations. In this way, the identifications of the brightest spectral lines from each ion can be assessed and in addition the accuracy of the atomic data can be evaluated.
Our method assumes a steady-state collisionally-ionised optically-thin plasma, so is particularly suitable for example for direct comparisons with spectroscopic observations of stellar coronae. However, the assessment method for each ion is based on a discussion of atomic energy levels, weighted oscillator strengths (gf values), spontaneous radiative decay rates (A values), electron (proton) collisional excitation rates, and is therefore of interest for wider astrophysical applications.
In recent years, a vast amount of high-resolution spectroscopic observations in the XUV have been produced by instruments on-board the SOHO, HST-STIS, Chandra, FUSE, XMM-Newton satellites. It is therefore timely to focus on the EUV (150-900 Å), UV (900-2000 Å) and soft X (5-150 Å) wavelength ranges.
The completeness of available atomic data in the EUV is very good,
since almost all the brightest lines in the spectra have been identified.
For example, Del Zanna et al. (2001) compared SOHO Coronal Diagnostic Spectrometer (CDS) spectra of different
solar features in the 150-780 Å range
with simulated spectra calculated with the
CHIANTI![]() atomic database.
The sensitivity of the
SOHO CDS has however revealed that a host of weaker
lines are not yet identified (see for example Brooks et al. 1999).
In the UV, quite a few bright lines remain unidentified, as shown in
SOHO Solar UV Measurement of Emitted Radiation (SUMER)
spectra (see, e.g., Feldman et al. 1997, and references therein).
In the X-rays, the situation is somewhat different.
The lines from the H I and He I isoelectronic
sequences and their satellites are well known.
Most of the rest of the bright lines are produced by
Fe XVII-XXIV ions, for which good atomic data
has been lacking until recently (see Dere et al. 2001, for a
review of published atomic data).
It is of no surprise that a large number of
lines are either unidentified or have a questionable
identification (see for example the spectral line list
in Phillips et al. 1999).
atomic database.
The sensitivity of the
SOHO CDS has however revealed that a host of weaker
lines are not yet identified (see for example Brooks et al. 1999).
In the UV, quite a few bright lines remain unidentified, as shown in
SOHO Solar UV Measurement of Emitted Radiation (SUMER)
spectra (see, e.g., Feldman et al. 1997, and references therein).
In the X-rays, the situation is somewhat different.
The lines from the H I and He I isoelectronic
sequences and their satellites are well known.
Most of the rest of the bright lines are produced by
Fe XVII-XXIV ions, for which good atomic data
has been lacking until recently (see Dere et al. 2001, for a
review of published atomic data).
It is of no surprise that a large number of
lines are either unidentified or have a questionable
identification (see for example the spectral line list
in Phillips et al. 1999).
The issue of completeness of atomic data is extremely important, for two main reasons. First, even at the highest spectral resolution, many spectral lines are blended to some degree. Indeed, most of the lines useful for density diagnostics (see Mason & Monsignori Fossi 1994, for a review) are weak and therefore particularly prone to problems with blending. Second, as the number of levels in a model ion increases, so does the number of predicted spectral lines. In some wavelength ranges (mainly the X-ray range), the pseudo-continuum created by the superposition of weak lines can be comparable to the real continuum emission (as produced by e.g. free-free, free-bound transitions).
It is important to remember that a great number of current
line identifications are based on early (50's to 70's or even earlier)
observations of the solar corona in eclipses and with
rockets and satellites.
These data were supplemented by a large amount of
laboratory data.
At that time, the calculations of radiative
data were in a reasonably good state,
while the calculations of collisional excitation
data has improved dramatically over the years
(see for example Iron Project![]() and UK Rmax
and UK Rmax![]() collaborations).
collaborations).
It is now important to use the most accurate atomic calculations for each ion and to benchmark these data against the observations and laboratory measurements. The aim of this series of papers is to do this in a comprehensive way, using the method described below in Sect. 2. Our method aims to: a) build a model ion that includes the most important configurations; b) compare both calculated and observed line intensities and wavelengths in a quantitative way; c) consider all the brightest lines, spanning a broad spectral range; d) use a variety of sources of experimental data, calibrated independently from the atomic data. Special attention is paid in our method to spectral line identifications based on our semi-empirical adjustment of the energy levels, and on the calculated intensities. Hence, it is possible to assess the accuracy of the atomic calculations, identify blends, and to suggest the best diagnostic lines to be used. Some estimates of the uncertainties of the atomic data are also provided as a by-product.
In this series of papers, we do not aim to review all of the observational data (e.g. wavelength measurements and line identifications) and theoretical data that are available for each ion, since the literature is too extensive. We have selected those data which we consider to be most reliable and appropriate. A critical review of the current status of theoretical data that are available for benchmarking is presented in Sect. 3. This section also describes the standard procedures we adopt to build our ion models. Section 4 describes the experimental data that are available for the benchmark.
Much can be learnt from spectroscopic observations of the solar corona. This series of papers starts with the Fe VIII-XVI ions and focuses on the EUV range, since many new R-matrix calculations have recently been performed on these ions.
Fe X is by far the most important coronal ion, but surprisingly, many of the transitions in Fe X remain unidentified, so the energy level values are still uncertain. Given the complexity of this ion, it is of no surprise that the status of the collisional calculations was unsatisfactory until recently, when Pelan & Berrington (2001) published new R-matrix calculations for the n=3 levels. It is therefore natural to start the series with Fe X, which is discussed in Sect. 5. Conclusions and further work needed on this ion are presented in Sect. 6.
The first step is to collect and/or calculate all the collisional and radiative rates which are needed to calculate the level population for the ion, including all the relevant processes and configurations.
The second step is to calculate the level populations.
The end result is
![]() ,
the
population of level j relative to the total N(X+r)number density of the ion X+r, as a function of the electron
temperature and density.
An important part of the process is to examine the metastable levels
(see, e.g., Mason & Monsignori Fossi 1994, for a definition),
assess their effect, and make sure that all the
important rates connected with them are included.
Then, the line intensities,
,
the
population of level j relative to the total N(X+r)number density of the ion X+r, as a function of the electron
temperature and density.
An important part of the process is to examine the metastable levels
(see, e.g., Mason & Monsignori Fossi 1994, for a definition),
assess their effect, and make sure that all the
important rates connected with them are included.
Then, the line intensities,
![]() ,
proportional to
Nj Aji,
can be calculated
(Aji is the spontaneous transition probability
from the upper level j to the lower level i).
,
proportional to
Nj Aji,
can be calculated
(Aji is the spontaneous transition probability
from the upper level j to the lower level i).
The third step is to find which transitions
correspond to the brightest intensities,
and to search all the available observations
for possible identifications.
We then compare calculated and observed
![]() intensities in a comprehensive way, by using the following method.
The values
intensities in a comprehensive way, by using the following method.
The values
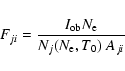 |
(1) |
The values Fji are simply the ratios of the observed
vs. the theoretical line intensities (aside from a
proportionality constant which depends on the geometry
of the source and on the units, and the factor ![]() which is introduced to scale the population, Nj,
of level j).
For allowed transitions,
which is introduced to scale the population, Nj,
of level j).
For allowed transitions,
![]() and the Fji curves are approximately constant with
and the Fji curves are approximately constant with ![]() .
If the theoretical intensities are consistent with the
observed ones, all the curves for the spectral lines
that have the same density dependence should overlap
at the value equal to the proportionality constant.
.
If the theoretical intensities are consistent with the
observed ones, all the curves for the spectral lines
that have the same density dependence should overlap
at the value equal to the proportionality constant.
Some spectral lines (e.g. those connected to metastable
levels) have Fji curves with a different
dependence from ![]() .
If agreement
between observed and theoretical intensities exist,
the Fji curves will cross at one point
(the density of the emitting plasma)
if the bulk of the emission originates from an iso-density region.
In observations of the solar corona, the observed emission
normally originates from multi-thermal and multi-density
regions along the line of sight, but the Fji curves
should still approximately cross at a point which
would be the average density of the plasma emitting
the spectral lines under consideration.
.
If agreement
between observed and theoretical intensities exist,
the Fji curves will cross at one point
(the density of the emitting plasma)
if the bulk of the emission originates from an iso-density region.
In observations of the solar corona, the observed emission
normally originates from multi-thermal and multi-density
regions along the line of sight, but the Fji curves
should still approximately cross at a point which
would be the average density of the plasma emitting
the spectral lines under consideration.
This method has already been used by Del Zanna et al. (2002) to critically revise a large amount of published work on spectral diagnostics in stellar transition regions. A plot of Fji curves has the following advantages over the individual line ratio technique (still commonly used in the literature): a) it gives a global view of all the spectral lines and can be used simultaneously for benchmarking atomic data and density diagnostics; b) it can directly confirm the accuracy of relative A-values when branching ratios are observed; c) it clearly shows which lines are obvious blends; d) it shows which combination of lines are best for density measurements; e) and at which density regimes the diagnostic lines can be used; f) it clearly shows which lines are best for calibration purposes (those that have the same behaviour with density).
We note that temperature effects can be important for some ions (e.g. those of the Be-like sequence, see Del Zanna et al. 2002, for examples), and some transitions. However, these are normally second order effects, compared to the uncertainties in the instrument calibration and in the atomic data.
If the observed plasma is multi-thermal, temperature effects can partly be taken into account by calculating each Fji curve at an effective temperature which takes into account the thermal distribution of the source, as described in Landi & Landini (1997). This method relies on the estimation of a differential emission measure. In turn, this depends on a more extended dataset of measurements, on the assumed ionization fractions, and, in the case of Fe X, on the atomic data of Fe VIII, Fe IX, Fe XI, Fe XII, all of which are currently under revision. Our method of looking at individual ions is more than adequate for our purpose. Eventually, when all the ions have been assessed, a different approach might be applicable.
The fourth step is to identify the blends whenever possible, and then to semi-empirically adjust all the energy levels using the identified transitions (normally the brightest lines). Then, and this is a crucially important step, these adjusted energy values are used to re-calculate the radiative data using the SUPERSTRUCTURE program (SS, see Eissner et al. 1974; Nussbaumer & Storey 1978) and the "term energy correction'' procedure described below in Sect. 3.2.
We then return again to the second step, in order to identify all the spectral lines (not just the strongest ones) that should be observable, and to provide a set of best wavelengths for all the lines in the model ion. We repeat the last three steps a few times while revising the line identifications and the experimental energies.
The above procedure is novel, comprehensive and non-standard. It provides a much more accurate model ion than can be provided by a completely ab-initio method, which uses only theoretical wavelengths (rather than adjusted wavelengths) and corresponding intensity ratios. Below we summarise some of the main features and difficulties in performing such an assessment method.
It is a non-trivial task to collect all the collisional and radiative rates which are needed to build a model ion. The only atomic database that freely provides a comprehensive collection of published data from different sources on energy levels, wavelengths, radiative transition probabilities and electron/proton excitation data for almost all ions of astrophysical interest is CHIANTI. In reality CHIANTI is an atomic package, in the sense that the atomic data are integrated in a suite of programs that calculate level populations, line emissivities, etc. The package is kept up-to-date, provides extensive references to the original sources, and has associated papers (Dere et al. 1997, v.1; Landi et al. 1999, v.2; Dere et al. 2001, v.3; Young et al. 2003, v.4) that describe the model ions. In a number of cases, collisional data from different sources are rescaled, interpolated and merged, and radiative data are either collected from various sources, or calculated ab initio using SUPERSTRUCTURE.
Many other good atomic databases exist, but often they: only contain data from one source; only provide a subset of all the atomic data that are needed to build an ion model (e.g. just radiative or collisional data); are not kept up-to-date; do not clearly reference the sources; refer to unpublished work.
CHIANTI contains a vast amount of atomic data gathered from a range of sources. The most reliable data available are selected and stored in a reduced/compact form. It is important to benchmark these data against solar and laboratory spectra, to confirm their accuracy. This is a time consuming and laborious process. In order to provide an assessment of the atomic data for the coronal Fe ions it is necessary review the data which are available both in CHIANTI and beyond.
In the literature, the most common reference
values used are the observed energies
![]() available from the National Institute of Science and
Technology (NIST
available from the National Institute of Science and
Technology (NIST![]() )
Atomic Spectra Database
(see Fuhr et al. 1999; but also
monographs such as Kelly 1987;
Shirai et al. 2000).
In turn, these compilations rely,
at least for the complex Fe ions,
on the original identifications and wavelength measurements
performed mostly in the 60's and 70's (or earlier), and they do not always provide
the best values.
In fact, there has been a good deal of
experimental and theoretical work since the 70's,
that has not always been included in
these compilations.
In some cases we have found energies
which are inconsistent with the observed
wavelengths.
In other cases, as for Fe X and Fe XI,
some of the energies are only known
relative to particular levels within a configuration,
but not relative to the ground level, so many line
identifications are uncertain. This information
needs to be taken into account when benchmarking atomic
data.
Many of the identifications in the past have been
based either on the variations of the wave number intervals along
isoelectronic sequences (together with gf values),
or on approximate estimates of line intensities.
In the present series, we have therefore
decided to re-assess the level energies, by reviewing
the original line identifications and derived energies,
together with the most recent studies.
)
Atomic Spectra Database
(see Fuhr et al. 1999; but also
monographs such as Kelly 1987;
Shirai et al. 2000).
In turn, these compilations rely,
at least for the complex Fe ions,
on the original identifications and wavelength measurements
performed mostly in the 60's and 70's (or earlier), and they do not always provide
the best values.
In fact, there has been a good deal of
experimental and theoretical work since the 70's,
that has not always been included in
these compilations.
In some cases we have found energies
which are inconsistent with the observed
wavelengths.
In other cases, as for Fe X and Fe XI,
some of the energies are only known
relative to particular levels within a configuration,
but not relative to the ground level, so many line
identifications are uncertain. This information
needs to be taken into account when benchmarking atomic
data.
Many of the identifications in the past have been
based either on the variations of the wave number intervals along
isoelectronic sequences (together with gf values),
or on approximate estimates of line intensities.
In the present series, we have therefore
decided to re-assess the level energies, by reviewing
the original line identifications and derived energies,
together with the most recent studies.
In the past three decades, several sophisticated atomic structure codes have been written, and a large amount of data published. However, the results often only pertain to a subset of the important configurations that produce spectral lines. The energy differences between the various calculations are often much larger than the fine-structure splittings, and this creates uncertainty in the level ordering and in turn in the line identifications. The size of the differences is particularly sensitive to which configurations have been included. Even the most comprehensive ab initio calculations are not good enough to match the observations, and the predicted wavelengths can be off by a few Å. For this reason, a large number of spectral lines remain unidentified. Within the CHIANTI package, these lines are considered to be "unobserved'', and do not normally appear in the simulated spectra, although the model ions actually predict some of them to be as bright as other "observed'' (identified) lines.
As an example, we consider the Fe X energies recently calculated by two groups. Dong et al. (1999) have performed a multi-configuration Dirac-Fock (MCDF) calculation using the well-known GRASP92 code of I. Grant for the lowest 3 configurations (31 fine-structure levels). As these authors notice, the differences with the available observed energies is up to 8000 cm-1, which results in a displacement of the strongest Fe X transition (observed at 174.53 Å) by more than 2 Å. Deb et al. (2002) have used the well-known CIV3 structure code of A. Hibbert and calculated radiative data for the lowest 4 configurations but including configuration interaction (CI) between 30 configurations (up to n=4) that involved one-, two-, and three-electron excitations with respect to the ground (a total of 1351 levels). As in the case of the Dong et al. (1999) calculation, the agreement with observations for the lower-energy states is reasonably good, while for the rest, differences are large. For the strongest Fe X transition, the difference is about 19 000 cm-1, producing a displacement of 6 Å. Such large displacements mean that the target wavefunctions are not well enough defined, hence the radiative data derived are not accurate.
In this paper we adopt the semi-empirical method, called the
Term Energy Correction (TEC) procedure
(see, e.g., Zeippen et al. 1977;
Nussbaumer & Storey 1978), applied within the
SUPERSTRUCTURE code.
Basically, empirical corrections
to the LS energies are used to modify the
non-relativistic Hamiltonian matrix, which
is then used together with the
Breit-Pauli relativistic correction
to solve the eigenvalue problem and
obtain empirically-adjusted fine-structure energies,
![]() .
Empirical corrections to the LS energies
have been applied here
whenever one fine-structure level has a known
energy.
If more than one fine-structure level for a term
within the same configuration is available, an average is used,
provided strong level mixing is not present.
If only one level within a given
configuration is known, then a single correction is applied
to the entire configuration.
Experience shows that if the right configurations are
used, the TEC within each configuration are approximately
(say within 500 cm-1) the same. The situation
improves when high-n configurations are considered.
The use of the TEC procedure improves the calculation of
the line strengths.
We note that semi-empirical adjustments within an
atomic structure code have been (and are) commonly applied
in the literature (see, e.g. the extensive work of
Bromage et al. 1977, on Fe X,XI),
but these are not the rule.
.
Empirical corrections to the LS energies
have been applied here
whenever one fine-structure level has a known
energy.
If more than one fine-structure level for a term
within the same configuration is available, an average is used,
provided strong level mixing is not present.
If only one level within a given
configuration is known, then a single correction is applied
to the entire configuration.
Experience shows that if the right configurations are
used, the TEC within each configuration are approximately
(say within 500 cm-1) the same. The situation
improves when high-n configurations are considered.
The use of the TEC procedure improves the calculation of
the line strengths.
We note that semi-empirical adjustments within an
atomic structure code have been (and are) commonly applied
in the literature (see, e.g. the extensive work of
Bromage et al. 1977, on Fe X,XI),
but these are not the rule.
The adjusted energies
![]() are then compared to the
observed energies
are then compared to the
observed energies
![]() ,
which are
defined to match the observed wavelengths
(as detailed in Table 7 and in the Appendix).
The uncertainties in the energies reflect the
estimated uncertainties in the observed wavelengths.
Ground-based measurements have been converted to vacuum
wavelengths using the standard formula for
the refractive index of air given by Edlén (1966).
,
which are
defined to match the observed wavelengths
(as detailed in Table 7 and in the Appendix).
The uncertainties in the energies reflect the
estimated uncertainties in the observed wavelengths.
Ground-based measurements have been converted to vacuum
wavelengths using the standard formula for
the refractive index of air given by Edlén (1966).
At the end of the iterative procedure, a set of
best energies
![]() is provided. These
energies are the adjusted observed energies,
whenever available, and the adjusted
is provided. These
energies are the adjusted observed energies,
whenever available, and the adjusted
![]() values
otherwise.
values
otherwise.
Ions such as Fe X are particularly complex because of the strong mixing between levels having the same J-value and parity. The mixing between fine-structure levels substantially changes depending on the configurations included in the target representation, and, more importantly, on the semi-empirical adjustments. It is therefore important to provide, as done here, information on level mixing, something that is often not provided in the literature.
The Einstein coefficients that are needed to build an ion model are the electric-dipole allowed (E1) and the "forbidden'' ones: magnetic dipole (M1), magnetic quadrupole (M2) and electric quadrupole (E2).
A first problem is one of completeness. To build an ion model, A-values for all the transitions are needed. As in the case of the energy levels and wavelengths, the NIST database only provides radiative data (often not up-to-date) for a few transitions. The number of measured A-values, based for example on laboratory measurements of level lifetimes, is increasing but still very limited, so we still have to rely on theoretical calculations. In turn, published calculations often only report a subset of all the A-values, normally just dipole allowed and some forbidden transitions.
A second problem is one of accuracy. Fortunately, atomic structure calculations, in particular for the E1 transitions, can be quite accurate and usually give consistent results with the laboratory measurements. However line strengths for forbidden transitions are less reliable and more susceptible to which configurations have been used in the calculation. The importance of including the right configurations has been emphasised by many authors (see, for example, the discussion on the Fe X case in Berrington et al. 2001).
Even if the line strengths are quite accurate, the transition rates that are published in the literature are often poor, because theoretical energies, instead of the experimental ones, are used. For E1 transitions, the rates are proportional to the cube of the energy difference, so the error is usually not too large. However, for the quadrupole E2 and M2 transitions (that have a dependence on the fifth power), the errors introduced by using theoretical energies can be significant. Again considering Fe X, for example, the A-values published by Dong et al. (1999) and Deb et al. (2002) could have been much improved if observed energies had been used. Dong et al. (1999) calculates a value of 65 s-1 for the famous Fe X 6374.6 Å forbidden transition within the ground configuration, compared to the commonly accepted value of 69 s-1, the same calculated here.
In this paper, the iterative procedure outlined above
is implemented, in order to obtain the best
energies and line strengths.
Then, the best energies
![]() are used to calculate the A-values
of E1, E2, M1, and M2 transitions in intermediate coupling
with SUPERSTRUCTURE.
are used to calculate the A-values
of E1, E2, M1, and M2 transitions in intermediate coupling
with SUPERSTRUCTURE.
As in the case of the radiative data, the number
and type of configurations included in the
scattering calculations strongly affects the results.
In the case of the data calculated in the
distorted wave (DW) approximation,
the practical approach suggested by
Flower & Nussbaumer (1974)
is adopted here.
The procedure is to rescale, for dipole-allowed transitions, the
collision strengths ![]() with the ratio of the
oscillator strengths f and the energy differences
with the ratio of the
oscillator strengths f and the energy differences ![]() :
:
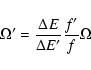 |
(2) |
A large number of R-matrix calculations have recently become available. They normally provide more accurate collision data than the DW calculations. However, if the target is not well represented, and the contributions from important resonances have been left out, the results have limited accuracy.
Despite the large number of solar observations and laboratory measurements, very few of these studies have sufficient spectral resolution, completeness and accuracy to allow reliable line identifications to be made. Indeed, very few solar observations have an accurate calibration, even though this is a fundamental requirement for any scientific analysis of spectroscopic data.
When assessing which solar observations are suitable for benchmarking atomic data, it is necessary to investigate the way in which these spectra have been calibrated. Only rarely is an independent calibration source used. Even then the ground calibration can differ from the in-flight calibration. Frequently, atomic data (assumed to be insensitive to density or temperature) are used to calibrate solar spectra. In several cases, instrument calibrations have been found to be incorrect using available atomic data. It is not straightforward to use these spectra to benchmark new atomic data. It is necessary to step back and take a more comprehensive view of available solar and laboratory spectra, to search for consistencies and inconsistencies between the atomic data and solar spectra. A re-assessment of the available calibration is sometimes required. In this series of papers, we shall study individual ions, but first it is necessary to survey the most important high- to medium-resolution spectroscopic observations relevant to our study.
Behring et al. (1972) published a line list based on a LASP rocket flight that observed the entire Sun in the 60-385 Å region with high-resolution (0.06 Å). Behring et al. (1976) have presented similar results, covering the 160-770 Å range. In both studies, the wavelengths of the lines were accurately measured, but intensities were only approximate and lines were mainly identified upon their wavelengths. We normally adopt their wavelengths, since they are still the most accurate ones that are available. Many previous studies exist (see, e.g., the review of Mason & Monsignori Fossi 1994), but they were either of lower-resolution or lower-sensitivity, or not calibrated in intensity.
Malinovsky & Heroux (1973) presented an integrated-Sun spectrum covering the 50-300 Å range with a medium resolution (0.25 Å), taken with a grazing-incidence spectrometer flown on a rocket in 1969. The spectrum was photometrically calibrated, and still, quite surprisingly, represent the best available spectrum in the EUV 150-300 Å range. These authors were among the first to confirm or reject previous identifications using line intensity estimates and not just wavelengths. The tables provided by Malinovsky & Heroux (1973) were not complete, so we have scanned their spectrum to provide additional information.
Many other line lists have been published, but are normally biased toward high-temperature lines, and are not useful for benchmarking ions such as Fe X. For example, Dere (1978) presented a list of line identifications based on all the flare observations of the NRL SO82-A instrument aboard Skylab, in the 171-630 Å range, with 0.1 Å resolution.
The ESA/NASA Solar and Heliospheric Observatory
(SOHO)
has produced a wealth of spectral data with the CDS, SUMER,
and the Ultraviolet Coronagraph Spectrometer (UVCS).
The CDS covers a wide wavelength range (150-780 Å),
with 5 detectors and nine channels
(6 in first order and 3 in second),
distributed between a Normal
Incidence (NIS) and a Grazing Incidence (GIS) Spectrometer.
SUMER is a
normal incidence spectrometer in the 500 to 1610 Å band
with high spectral resolution.
UVCS has performed off-limb (2-10 ![]() from Sun centre)
spectroscopic observations in the 940-1350 Å range.
The spectral resolution for UVCS is somewhat lower than SUMER.
from Sun centre)
spectroscopic observations in the 940-1350 Å range.
The spectral resolution for UVCS is somewhat lower than SUMER.
There has been a great deal of work
by different groups to obtain a consistent
radiometric calibration of all the instruments on-board SOHO (Pauluhn et al. 2002) to an accuracy of 30-50%.
The SUMER radiometric calibration is reported to have
a standard uncertainty of ![]() 15% (detector A, before
SOHO recovery in 1998) in the
530-1240 Å range and
15% (detector A, before
SOHO recovery in 1998) in the
530-1240 Å range and ![]() 30% at longer wavelengths.
Atomic data can be and have been used to cross-check and
improve some of the instrument calibrations.
For example, the CHIANTI atomic data were used to show that
the ground calibration of the CDS channels was
in error by factors of up to two
(cf. Del Zanna et al. 2001). The CDS instrument
calibration has been revised based on several studies,
including those using rocket flights.
It should be noted that
the in-flight calibration of the NIS-2 channel
is based on a single in-flight cross-calibration with
a coarse spectrum produced by an EGS
rocket flight launched in May 1997.
The in-flight calibration of the NIS-1 channel
also relies on a single cross-calibration study
(Thomas et al. 1999) based on the SERTS-97 flight.
The only GIS in-flight calibration
(Del Zanna et al. 2001) was obtained with the use of
CHIANTI atomic data, some of which are now under review
in this series of papers.
30% at longer wavelengths.
Atomic data can be and have been used to cross-check and
improve some of the instrument calibrations.
For example, the CHIANTI atomic data were used to show that
the ground calibration of the CDS channels was
in error by factors of up to two
(cf. Del Zanna et al. 2001). The CDS instrument
calibration has been revised based on several studies,
including those using rocket flights.
It should be noted that
the in-flight calibration of the NIS-2 channel
is based on a single in-flight cross-calibration with
a coarse spectrum produced by an EGS
rocket flight launched in May 1997.
The in-flight calibration of the NIS-1 channel
also relies on a single cross-calibration study
(Thomas et al. 1999) based on the SERTS-97 flight.
The only GIS in-flight calibration
(Del Zanna et al. 2001) was obtained with the use of
CHIANTI atomic data, some of which are now under review
in this series of papers.
The Goddard Solar Extreme Ultraviolet
Rocket Telescope and Spectrograph (SERTS)
has been flown several times since 1989,
and has produced both non overlapping spectroheliograms
and stigmatic spectra of excellent spectral resolution.
The SERTS-89 (Thomas & Neupert 1994)
covered the 170-225 Å range in second order and the
235-450 Å range in first order.
The SERTS-89 and SERTS-97 were radiometrically
calibrated on the ground against
primary standards and in theory could be used for the benchmark.
However, Young et al. (1998), when performing a detailed
benchmark of CHIANTI atomic data on the
SERTS-89 spectrum, found major
inconsistencies (by factors of 2) in the calibration
of the second order lines and of the 400-450 Å region.
These inconsistencies have been confirmed
in Del Zanna (1999), where a ![]() analysis
was performed in order to assess line blending
in the SERTS-89 spectrum.
The SERTS-97 flight only covered a narrow
wavelength region, and presents some discrepancies
both in the cross-calibration with CDS
(see Del Zanna et al. 2001),
and in the SERTS-97 line intensities themselves.
analysis
was performed in order to assess line blending
in the SERTS-89 spectrum.
The SERTS-97 flight only covered a narrow
wavelength region, and presents some discrepancies
both in the cross-calibration with CDS
(see Del Zanna et al. 2001),
and in the SERTS-97 line intensities themselves.
The SERTS-95 spectra
(Brosius et al. 1998b) covered the
171-225 Å band in second-order,
and the 235-335 Å region in first order
with excellent spectral resolution
(
![]() ,
0.05 Å respectively).
However, atomic data (CHIANTI version 1.01) were
actually used by Brosius et al. (1998a) to calibrate the
SERTS-95 spectra, and therefore the SERTS-95
data cannot easily be used here to benchmark the new atomic data.
,
0.05 Å respectively).
However, atomic data (CHIANTI version 1.01) were
actually used by Brosius et al. (1998a) to calibrate the
SERTS-95 spectra, and therefore the SERTS-95
data cannot easily be used here to benchmark the new atomic data.
In summary, very few medium- or high-resolution radiometrically-calibrated EUV spectra exist which are useful for benchmarking atomic data. The CDS data, although extremely valuable, cannot at the moment be reliably used to benchmark atomic data. The calibration of the SUMER instrument should also undergo rigourous checking before its spectra can be used with confidence for this purpose. The calibration problems will not necessarily improve in the future, since multilayer technology (successfully tested in the SERTS-95, 97 flights) will be used in most future missions such as SOLAR-B EIS. This technology has the advantage of offering high sensitivities, however the responsivities typically drop by one order of magnitude in just a few Å, hence a small error in the calibration can have a huge effect. Since no in-flight calibration sources will be flown, these instruments will most probably need to be calibrated using accurate atomic data. Hence, it is essential that we have confidence in the most recent atomic data for the coronal iron ions.
The visible coronal forbidden lines have been observed during total solar eclipses since 1869 (see for example Aly et al. (1962) on the 1952 eclipse and Magnant-Crifo (1973) on the 1965 eclipse). However, very few intensity measurements useful for the benchmark are available. A notable study is that of Jefferies et al. (1971), which provided calibrated intensities of all the lines observed on the ground during the 1965 eclipse in the 3000-11 000 Å range. Rockets were used to extend the wavelength range of the eclipse observations (see, e.g. Gabriel et al. 1971, for the 1970 eclipse, 850-2190 Å).
Information on the forbidden lines was further improved with the Skylab ATM NRL S082B spectrograph, which recorded a large number of lines. Sandlin et al. (1977) provided an extensive and accurate list of calibrated line intensities in the 970-2650 Å range. Further details were presented by Sandlin & Tousey (1979). Feldman & Doschek (1977) also provided a list of forbidden lines in the 1170-2650 Å range.
A large number of coronal forbidden lines have been observed with the SOHO SUMER instrument in the in the 500-1600 Å range (see, e.g., Feldman et al. 1997), and many still await identification. A few of these lines have also been observed with UVCS (see, e.g., Raymond et al. 1997).
In summary, a number of observations in the
UV is available for the benchmark of the Fe coronal ions,
while the situation needs improving in the visible and
at longer wavelengths, in particular in terms of
calibration.
We note that measurements and identifications of
coronal forbidden lines are important, since energy level
separations can be measured with high accuracy (![]() 1 cm-1).
1 cm-1).
Many tokamak and laser-produced high-resolution spectra have been published, but they mainly focus on high-temperature plasmas, more relevant to solar flare spectra. Since the pioneering work by Edlén in the 1930's (see e.g., Edlén 1937, on Fe X), there have been several other laboratory studies. A lot of work was carried out at the Culham laboratory (UK) in the 60-70s by a group of researchers (see, e.g. for Fe X in the EUV: Fawcett & Gabriel 1965; Gabriel et al. 1965; Fawcett & Gabriel 1966; Gabriel et al. 1966; Bromage et al. 1977).
More recently, papers based on beam-foil spectroscopy or electron beam ion traps have produced very useful spectral data for the identifications of lines from Fe VIII-XIV (see, e.g., Jupen et al. 1993; Träbert et al. 2003; Lepson et al. 2002, and the references therein).
The main advantage of laboratory data over solar observations is that they tend to be relatively free of blending from other elements, although significant blending between adjacent ionisation stages is still present. However, the spectral resolution is often poor, line intensities are not normally calibrated, and their interpretation can be even more complex than in the case of the solar corona.
Another important contribution of laboratory studies is the measurement of lifetimes and A values, which are now becoming available in the literature. However, these measurements are not always consistent with each other. Hence, these data can only provide a limited benchmark at the moment.
A selection of experimental data have been used to adjust observed energies, to identify lines, and to benchmark the atomic data. For the EUV, wavelengths are taken from Behring et al. (1976) and Thomas & Neupert (1994), while intensities are from Thomas & Neupert (1994) (only in first order), Malinovsky & Heroux (1973), and Datla et al. (1975). Cited uncertainties in the relative radiometric calibration are of the order of 10-20% for lines close in wavelength in the Malinovsky & Heroux (1973) spectrum, and similar values for the Thomas & Neupert (1994) data.
For the coronal forbidden lines, we have used the observations of Jefferies et al. (1971), Sandlin et al. (1977), Sandlin & Tousey (1979), Feldman & Doschek (1977), Jupen et al. (1993).
Jefferies et al. (1971) provided approximate wavelengths (in air) and calibrated intensities measured in two coronal condensations. Uncertainties in the radiometric calibration are difficult to assess. Sandlin et al. (1977) provided accurate wavelength measurements based on chromospheric primary standards and averages over a large number of positions around the solar disk. Uncertainties are often better than 0.01 Å. Sandlin et al. (1977) also provided calibrated intensities in off-limb spectra above two active regions. They estimated the relative intensities to be accurate within 30% in the 1210-1930 Å range and 50% above 1930 Å, given the large scattered continuum.
Off-limb coronal spectra of the 780-1600 Å range
(in first order) of excellent quality were taken with
the SUMER instrument during its first period of operation.
In particular, on June 25-26 1996, the entire SUMER spectral
region was recorded over a quiet Sun off-limb region.
These observations are described in detail by
Feldman et al. (1997).
These authors only provided the peak counts at the centre of the
lines, and not integrated
line intensities. We have therefore re-analysed the same dataset
in order to obtain calibrated line intensities.
The data have been processed using the standard
SolarSoft![]() SUMER software, and integrated line counts calculated
over an average spectrum obtained from a central portion of the
field of view.
We have used the exposures recorded at
22:31 and 23:02 UT on the 25th and 01:39 UT on the 26th of June 1996.
Finally, the standard SUMER radiometric calibration
has been applied to the measured counts.
SUMER software, and integrated line counts calculated
over an average spectrum obtained from a central portion of the
field of view.
We have used the exposures recorded at
22:31 and 23:02 UT on the 25th and 01:39 UT on the 26th of June 1996.
Finally, the standard SUMER radiometric calibration
has been applied to the measured counts.
All the lifetimes measurements found in the literature (Moehs et al. 2000; Moehs et al. 2001; Träbert 1996; Träbert et al. 2002; Träbert et al. 2003) have been used. They include a recent revision of the lifetime of the 2P1/2 by Träbert (2004).
In this paper, we restrict our discussion to the main n=3 spectroscopic configurations in Fe X (c1: 3s23p5, c2: 3s 3p6, c3: 3s23p43d, c4: 3s 3p53d), which produce 54 levels, and the majority of the brightest lines from the EUV to the infrared. Although many other Fe X lines have been observed in laboratory and astrophysical X-ray spectra, a discussion on the X-rays (n>3) is left to a future paper. The reason for this is that no reliable R-matrix or DW calculations are currently available, only the approximate calculations of Malinovsky et al. (1980).
Various calculations of collision strengths exist in the literature, as discussed by Pelan & Berrington (2001). The first comprehensive study of the lowest three configurations of Fe X was published by Mason (1975), using the DW approximation. Subsequently, R-matrix calculations were provided by Mohan et al. (1994) and Tayal (2001). However, both these calculations had limitations which render them unsuitable for our benchmark study. The former omitted some important resonance contributions (see Pelan & Berrington 1995) while the latter omitted the spectroscopically-important 4Fj and 2Fj metastable levels.
None of the published R-matrix calculations provide a sufficiently complete dataset, since only collisional excitations from the first two configurations were published. Neglecting collisional processes involving the metastable levels in the 3s23p43d configuration significantly affects the level population even at moderate densities. This is an important point to note for all coronal ions with metastable levels.
The method outlined in Sect. 2 was applied iteratively
a few times, using the following atomic data:
a) the R-matrix collisional data for the excitations between
the levels in the first two configurations (c1, c2)
and the levels in c3,
published in Pelan & Berrington (2001);
b) new R-matrix collisional data for the remaining excitations between all
the levels in c1, c2 and c3 (31 levels). These
data (Table 1)![]() have been
recalculated by us using the same
codes and specifications as those described in
Pelan & Berrington (2001); basically, a full
Breit-Pauli R-matrix calculation including 180 target levels
arising from the lowest 5 configurations (c1, c2, c3, c4, c5);
c) the set of best energies
have been
recalculated by us using the same
codes and specifications as those described in
Pelan & Berrington (2001); basically, a full
Breit-Pauli R-matrix calculation including 180 target levels
arising from the lowest 5 configurations (c1, c2, c3, c4, c5);
c) the set of best energies
![]() obtained from
the
assessment of the solar and laboratory spectra and from
SUPERSTRUCTURE;
d) new A and gf values for all transitions calculated with
SUPERSTRUCTURE using the best energies;
e) the Bhatia & Doschek (1995) data for the
3s 3p53d configuration, scaled using the
SUPERSTRUCTURE results.
Only excitations from the ground and the metastable
levels have been included.
Figure 1 gives an indication of
the adjustments required.
obtained from
the
assessment of the solar and laboratory spectra and from
SUPERSTRUCTURE;
d) new A and gf values for all transitions calculated with
SUPERSTRUCTURE using the best energies;
e) the Bhatia & Doschek (1995) data for the
3s 3p53d configuration, scaled using the
SUPERSTRUCTURE results.
Only excitations from the ground and the metastable
levels have been included.
Figure 1 gives an indication of
the adjustments required.
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{H0432f1.ps}
\end{figure}](/articles/aa/full/2004/29/aa0432-03/Timg28.gif) |
Figure 1: A plot of the gf values from the Bhatia & Doschek (1995) DW calculation vs. the values scaled using the SS results (gf'). Only the values for the dipole-allowed transitions to the 3s 3p53d levels included in the model ion are shown. The corrections are quite large, particularly for small gf values. |
| Odd | Even | ||
| c1 | 3s2 3p5 | c2 | 3s 3p6 |
| c4 | 3s 3p5 3d | c3 | 3s2 3p4 3d |
| c5 | 3s2 3p3 3d2 | c6 | 3s2 3p2 3d3 |
| c10 | 3s 3p3 3d3 | c7 | 3s2 3p4 4s |
| c11 | 3s2 3p4 4p | c8 | 3s 3p4 3d2 |
c13 |
3p5 3d2 | c9 | 3p6 3d |
| c14 | 3s 3p5 4s | c12 | 3s2 3p4 4d |
| c16 | 3s2 3p4 4f | c15 | 3s 3p5 4p |
Table 2 lists the set of configurations we finally adopted for our SUPERSTRUCTURE (SS) calculation, after a number of tests had been run. These tests confirmed the importance of including configurations with orbitals 3d2 and 3d3 (as discussed in Berrington et al. 2001) in order to have accurate gf values and energies.
Table 3 lists the results for the
54 levels, ordered according to the
energies
![]() of the target for the collisional calculations.
This table also lists SS level mixing information, together with
the energies
of the target for the collisional calculations.
This table also lists SS level mixing information, together with
the energies
![]() which we propose in this paper
to be the best set. For comparisons, the
which we propose in this paper
to be the best set. For comparisons, the
![]() values reported in NIST, and
the set of adjusted SS values
values reported in NIST, and
the set of adjusted SS values
![]() are also listed.
Two main points are worth noting. First, there is strong level mixing
for the majority of levels. Second, there is good agreement
between the adjusted SS energies and the observed ones.
We also note that in many cases our best energies
differ from the NIST values.
are also listed.
Two main points are worth noting. First, there is strong level mixing
for the majority of levels. Second, there is good agreement
between the adjusted SS energies and the observed ones.
We also note that in many cases our best energies
differ from the NIST values.
Table 4 presents the radiative
data (gf and A values)![]() for the brightest transitions.
The gf values compare well with those calculated by
Pelan & Berrington (2001), and most A values are in good agreement with the
values reported in the NIST database,
as shown in Table 4.
More importantly, the gf values for the 14 brightest transitions are in agreement, within a few percent,
with the values calculated by Fawcett (1991).
These values were calculated with the standard Slater parameter
optimization procedure,
based on accurate energy level identifications of Ti VI.
for the brightest transitions.
The gf values compare well with those calculated by
Pelan & Berrington (2001), and most A values are in good agreement with the
values reported in the NIST database,
as shown in Table 4.
More importantly, the gf values for the 14 brightest transitions are in agreement, within a few percent,
with the values calculated by Fawcett (1991).
These values were calculated with the standard Slater parameter
optimization procedure,
based on accurate energy level identifications of Ti VI.
The lifetimes of a few levels have been measured
and these values are compared with
our predicted values in Table 5.
Considering all the uncertainties involved, and
the scatter in the measurements,
there is good agreement.
Uncertainties in the calculated A values are
roughly estimated as 10% for allowed
transitions and 10-20% for the forbidden ones.
| i | Configuration (% purity) | Term |
|
|
|
|
| 1 | 3s2 3p5(96%) | 2P
|
0.0 |
0 | 0 | 0 |
| 2 | 3s2 3p5(96%) | 2P
|
15683.1 |
0 | +912 | -143 |
| 3 | 3s 3p6(72%) +27(c3 24%) | 2S
|
289236.0 |
-13 | +517 | -7 |
| 4 | 3s2 3p4 (3P) 3d(93%) | 4D
|
388713.5 |
4.5 | -4255 | +34 |
| 5 | 3s2 3p4 (3P) 3d(94%) | 4D
|
388708.0 |
-1 | -4371 | -116 |
| 6 | 3s2 3p4 (3P) 3d(92%) | 4D
|
390019.0 |
-31 | -4047 | +224 |
| 7 | 3s2 3p4 (3P) 3d(92%) | 4D
|
391554.0 |
-1 | -3829 | +351 |
| 8 | 3s2 3p4 (3P) 3d(92%) | 4F
|
417652.0 |
-1 | -6263 | +233 |
| 9 | 3s2 3p4 (1D) 3d(41%) +29(49%) | 2P
|
414249.0 |
- | -10983 | 0 |
| 10 | 3s2 3p4 (3P) 3d(89%) | 4F
|
422785.0 |
-10 | -5848 | +334 |
| 11 | 3s2 3p4 (3P) 3d(95%) | 4F
|
426260.0 |
-503 | -5885 | 0 |
| 12 | 3s2 3p4 (3P) 3d(86%) | 4F
|
427604.0 |
-694 | -5529 | 0 |
| 13 | 3s2 3p4 (1D) 3d(50%) +28(38%) | 2P
|
422844.0 |
-9084 | -10837 | +161 |
| 14 | 3s2 3p4 (3P) 3d(95%) | 4P
|
433526.0 |
-1274 | -6959 | 0 |
| 15 | 3s2 3p4 (1D) 3d(28%) +31(26%) +25(25%) | 2D
|
433088.0 |
-1526 | -7507 | 0 |
| 16 | 3s2 3p4 (3P) 3d(83%) | 4P
|
438168.0 |
- | -7036 | 0 |
| 17 | 3s2 3p4 (3P) 3d(21%) +30(15%) +26(11%) +19(45%) | 2D
|
440125.0 |
-1728 | -7493 | -355 |
| 18 | 3s2 3p4 (3P) 3d(50%) +21(31%) | 2F
|
440839.0 |
-1 | -6999 | -134 |
| 19 | 3s2 3p4 (1D) 3d(48%) +17(11%) +30(12%) +26(19%) | 4P
|
442760.0 |
- | -6833 | -161 |
| 20 | 3s2 3p4 (1D) 3d(92%) | 2G
|
450754.0 |
3 | -7070 | -28 |
| 21 | 3s2 3p4 (1D) 3d(62%) +18(25%) | 2G
|
451083.0 |
-1 | -6850 | -14 |
| 22 | 3s2 3p4 (3P) 3d(72%) +23(20%) | 2F
|
454036.0 |
1306 | -6312 | -126 |
| 23 | 3s2 3p4 (1D) 3d(76%) +22(17%) | 2F
|
482046.0 |
- | -7382 | -92 |
| 24 | 3s2 3p4 (1D) 3d(78%) +18(17%) | 2F
|
485982.0 |
-1 | -7287 | -48 |
| 25 | 3s2 3p4 (1S) 3d(57%) +15(35%) | 2D
|
511992.0 |
192 | -7614 | 0 |
| 26 | 3s2 3p4 (1S) 3d(49%) +17(42%) | 2D
|
516222.0 |
- | -7664 | 0 |
| 27 | 3s2 3p4 (1D) 3d(70%) +3(c2 23%) | 2S
|
541897.0 |
18 | -13264 | +34 |
| 28 | 3s2 3p4 (3P) 3d(50%) +13(39%) | 2P
|
564208.0 |
10 | -12461 | -137 |
| 29 | 3s2 3p4 (3P) 3d(43%) +9(51%) | 2P
|
569882.0 |
-103 | -12494 | -387 |
| 30 | 3s2 3p4 (3P) 3d(66%) +17(18%) +26(10%) | 2D
|
572964.0 |
10 | -14240 | -100 |
| 31 | 3s2 3p4 (3P) 3d(61%) +15(21%) | 2D
|
586254.0 |
10 | -13570 | +68 |
| 32 | 3s 3p5 (3P) 3d(82%) | 4P
|
661175.0 |
- | -49672 | 0 |
| 33 | 3s 3p5 (3P) 3d(81%) | 4P
|
663782.0 |
- | -49875 | 0 |
| 34 | 3s 3p5 (3P) 3d(81%) | 4P
|
668467.0 |
- | -50143 | 0 |
| 35 | 3s 3p5 (3P) 3d(85%) +(c5 10%) | 4F
|
694225.0 |
-2436 | -36455 | 0 |
| 36 | 3s 3p5 (3P) 3d(82%) +(c5 10%) | 4F
|
697016.0 |
-2476 | -36655 | 0 |
| 37 | 3s 3p5 (3P) 3d(82%) +(c5 10%) | 4F
|
700011.0 |
-2574 | -36665 | 0 |
| 38 | 3s 3p5 (3P) 3d(82%) +(c5 10%) | 4F
|
702749.0 |
-2681 | -36540 | 0 |
| 39 | 3s 3p5 (3P) 3d(78%) | 4D
|
726123.0 |
- | -40893 | 0 |
| 40 | 3s 3p5 (3P) 3d(77%) | 4D
|
727681.0 |
- | -41025 | 0 |
| 41 | 3s 3p5 (3P) 3d(79%) | 4D
|
727262.0 |
- | -41541 | 0 |
| 42 | 3s 3p5 (3P) 3d(78%) | 4D
|
727821.0 |
- | -41219 | 0 |
| 43 | 3s 3p5 (3P) 3d(73%) +(c5 11%) | 2F
|
737368.0 |
- | -55850 | -31 |
| 44 | 3s 3p5 (3P) 3d(49%) +46(27%) | 2D
|
741260.0 |
- | -54926 | 0 |
| 45 | 3s 3p5 (3P) 3d(72%) | 2D
|
745812.0 |
- | -53573 | 0 |
| 46 | 3s 3p5 (3P) 3d(49%) +44(27%) | 2F
|
749382.0 |
- | -52559 | 0 |
| 47 | 3s 3p5 (1P) 3d(41%) +54(24%) +(c5 24%) | 2P
|
760037.0 |
- | -67068 | 0 |
| 48 | 3s 3p5 (1P) 3d(38%) +53(19%) +(c5 22%) | 2P
|
767867.0 |
- | -67057 | 0 |
| 49 | 3s 3p5 (1P) 3d(57%) +(c5 12%) | 2F
|
789807.0 |
- | -81159 | 0 |
| 50 | 3s 3p5 (1P) 3d(55%) +(c5 13%) | 2F
|
793645.0 |
- | -78575 | 0 |
| 51 | 3s 3p5 (1P) 3d(41%) +(c5 14%) | 2D
|
818347.0 |
- | -81018 | 0 |
| 52 | 3s 3p5 (1P) 3d(36%) +(c5 12%) +(c5 12%) | 2D
|
819974.0 |
- | -80209 | 0 |
| 53 | 3s 3p5 (3P) 3d(54%) +(c5 18%) | 2P
|
865405.0 |
- | -108711 | 0 |
| 54 | 3s 3p5 (3P) 3d(53%) +(c5 22%) | 2P
|
864829.0 |
- | -110431 | 0 |
| i-j | Int | Int | gf | Aji | Aji | T | Terms |
|
|
|
|
|
NIST | NIST | ||||||
| 1-30 | 1.0 | 0.60 | 5.01 |
|
|
E1 | c1 2P
|
174.531 |
174.534 |
| 1-28 | 0.55 | 0.34 | 2.83 |
|
- | E1 | c1 2P
|
177.240 |
- |
| 1-27 | 0.22 | 0.17 | 1.29 |
|
|
E1 | c1 2P
|
184.537 |
184.543 |
| 1-5 | 0.14 |
|
- | 47. | 74. | M2 | c1 2P
|
257.263 |
257.262 |
| 2-27 |
|
|
0.40 |
|
|
E1 | c1 2P
|
190.037 |
190.043 |
| 2-29 |
|
0.12 | 1.12 |
|
- | E1 | c1 2P
|
180.441 |
- |
| 2-31 |
|
0.33 | 3.17 |
|
|
E1 | c1 2P
|
175.263 |
175.266 |
| 1-4 |
|
|
|
|
- | E1 | c1 2P
|
257.259 |
- |
| 1-19 |
|
|
|
|
- | E1 | c1 2P
|
225.856 |
- |
| 1-17 |
|
|
|
|
- | E1 | c1 2P
|
227.208 |
- |
| 1-22 |
|
|
|
|
|
E1 | c1 2P
|
220.247 |
(220.1) |
| 1-29 |
|
|
0.33 |
|
- | E1 | c1 2P
|
175.475 |
- |
| 2-28 |
|
|
|
|
- | E1 | c1 2P
|
182.307 |
- |
| 1-11 |
|
|
|
|
|
E1 | c1 2P
|
234.599 |
234.322 |
| 1-23 |
|
|
|
|
|
E1 | c1 2P
|
207.449 |
(207.6) |
| 1-18 |
|
|
- | 27. | - | M2 | c1 2P
|
226.840 |
- |
| 1-13 |
|
|
|
|
- | E1 | c1 2P
|
236.494 |
- |
| 2-12 |
|
|
|
|
- | E1 | c1 2P
|
242.765 |
- |
| 1-6 |
|
|
|
|
- | E1 | c1 2P
|
256.398 |
- |
| 2-9 |
|
|
|
|
- | E1 | c1 2P
|
250.900 |
- |
| 1-15 |
|
|
|
|
- | E1 | c1 2P
|
230.900 |
- |
| 1-26 |
|
|
|
|
- | E1 | c1 2P
|
193.715 |
- |
| 1-14 |
|
|
|
|
- | E1 | c1 2P
|
230.667 |
- |
| 2-16 |
|
|
|
|
- | E1 | c1 2P
|
236.695 |
- |
| 1-25 |
|
|
|
|
|
E1 | c1 2P
|
195.316 |
195.389 |
| 2-15 |
|
|
|
|
- | E1 | c1 2P
|
238.743 |
- |
1-3 |
|
|
0.12 |
|
|
E1 | c1 2P
|
345.738 |
345.723 |
| 2-3 |
|
|
|
|
|
E1 | c1 2P
|
365.560 |
365.543 |
| 18-43 |
|
|
0.18 |
|
- | E1 | c3 2F
|
337.235 |
- |
| 21-43 |
|
|
|
|
- | E1 | c3 2G
|
349.302 |
- |
| 13-44 |
|
|
|
|
- | E1 | c3 2P
|
314.055 |
- |
| 22-44 |
|
|
|
|
- | E1 | c3 2F
|
348.160 |
- |
| 5-35 |
|
|
0.45 |
|
- | E1 | c3 4D
|
327.314 |
- |
| 1-2 | 0.88 |
|
- | 69. | 69. | M1 | c1 2P
|
6376.3 |
6374.51 |
| 5-8 |
|
|
- | 12. | 12. | M1 | c3 4D
|
3454.9 |
3454.0 |
| 5-18 |
|
|
- | 25. | - | M1 | c3 4D
|
1918.2 |
- |
| 8-20 |
|
|
- | 57. | 55. | M1 | c3 4F
|
3021.0 |
3020.5 |
| 5-24 |
|
|
- | 67. | 65. | M1 | c3 4D
|
1028.0 |
1028.02 |
| 5-10 |
|
|
- | 8.8 | 8.5 | M1 | c3 4D
|
2934.5 |
2932.9 |
| 8-24 |
|
|
- | 74. | 70. | M1 | c3 4F
|
1463.5 |
1463.49 |
| 5-21 |
|
|
- | 19. | 20. | M1 | c3 4D
|
1603.2 |
1603.21 |
| 4-24 |
|
|
- | 18. | 18. | M1 | c3 4D
|
1028.1 |
1028.02 |
| 4-21 |
|
|
- | 9.2 | 8.9 | M1 | c3 4D
|
1603.3 |
1603.21 |
| 10-21 |
|
|
- | 18. | 14. | M1 | c3 4F
|
3533.8 |
3533.9 |
| 8-18 |
|
|
- | 9.9 | - | M1 | c3 4F
|
4312.8 |
- |
| 4-18 |
|
|
- | 4.3 | - | M1 | c3 4D
|
1918.4 |
- |
| 5-20 |
|
|
- | 4.9 | 4.0 | M1 | c3 4D
|
1611.7 |
1611.81 |
| 10-18 |
|
|
- | 6.9 | - | M1 | c3 4F
|
5538.9 |
- |
| i | Upper level | Measured (ms) | Calc. |
| 2 | 3s23p5 2P
|
13.64
|
14.5 |
| 3 | 3s 3p6 2S
|
2.7
|
|
| 8 | 3s23p4 (3P) 3d 4F
|
110
|
89.2 |
| 10 | 3s23p4 (3P) 3d 4F
|
58
|
75.3 |
| 18 | 3s23p4 (3P) 3d 2F
|
16
|
12.4 |
| 20 | 3s2 3p4 (1D) 3d 2G
|
17.8
|
13.7 |
| 24 | 3s23p4 (1D) 3d 2F
|
4.6
|
4.8 |
Note that our calculation imply a
lifetime of 0.21 ns for the 3s 3p6 2S1/2 level,
in better agreement with the measurement of
![]() ns by
Träbert (1996), compared to the 0.18 ns value
reported by Shirai et al. (2000).
The R-matrix results of Pelan & Berrington (2001) give 0.24 ns, in even better
agreement with the laboratory data.
ns by
Träbert (1996), compared to the 0.18 ns value
reported by Shirai et al. (2000).
The R-matrix results of Pelan & Berrington (2001) give 0.24 ns, in even better
agreement with the laboratory data.
It is interesting to point out that
Träbert (2004) used new measurements
to obtain an estimate of the lifetime associated with the
ground forbidden line (
![]() ms). The new results revise
the previous measurement (
ms). The new results revise
the previous measurement (
![]() ms) from Moehs et al. (2001),
and are in excellent agreement with the theoretical value (14.5 ms).
ms) from Moehs et al. (2001),
and are in excellent agreement with the theoretical value (14.5 ms).
The quantities useful
for radiometric calibration are not the
absolute A values, but the branching ratios.
For the 3s23p5
2P
3/2,1/2-3s 3p6 2S1/2 doublet,
Träbert (1996) reports a branching ratio of
![]() ,
which compares very well with the value 2.26 calculated with SUPERSTRUCTURE.
,
which compares very well with the value 2.26 calculated with SUPERSTRUCTURE.
![\begin{figure}
\par\includegraphics[angle=90,width=8.4cm,clip]{H0432f2a.ps}\par\vspace*{3mm}
\includegraphics[angle=90,width=8.4cm,clip]{H0432f2b.ps}
\end{figure}](/articles/aa/full/2004/29/aa0432-03/Timg183.gif) |
Figure 2: The fractional level populations of the ground and the metastable levels using the present model, with all excitations included ( top), and with only excitations from the first 3 levels included ( bottom). Note the large differences in the metastable level populations, which in turn also affect the entire level balance of the ion (see also Table 6). |
| i | A | B | BD | PB | |
| 1 | 0.67 | 0.46 | 0.72 | 0.62 | |
| 2 | 0.19 | 0.13 | 0.14 | 0.17 | M |
| 8 |
|
0.19 |
|
|
M |
| 5 |
|
0.10 |
|
|
M |
| 10 |
|
|
|
|
M |
| 18 |
|
|
|
|
M |
| 20 |
|
|
|
|
M |
| 21 |
|
|
|
|
M |
| 24 |
|
|
|
|
M |
| 4 |
|
|
|
|
|
| 6 |
|
|
|
|
|
| 22 |
|
|
|
|
|
| 19 |
|
|
|
|
|
| 17 |
|
|
|
|
|
| 15 |
|
|
|
|
|
| 13 |
|
|
|
|
|
3 |
|
|
|
|
|
| 43 |
|
|
|||
| 44 |
|
|
|||
| 30 |
|
|
|
|
|
| 28 |
|
|
|
|
|
| 45 |
|
|
|||
| 31 |
|
|
|
|
|
27 |
|
|
|
|
|
| 29 |
|
|
|
|
A detailed discussion of the main spectral identifications for each of the levels is essential in our procedure. This is in turn dependent on the level populations and line intensity calculations.
The ion level balance has been calculated using the collisional and radiative data described above. Additionally, proton excitations and photo-excitations can be important processes for the forbidden transitions taking place between levels within the same configuration. For the proton rates, the data calculated by Bely & Faucher (1970) as included in CHIANTI v.4 have been used here. For the photo-excitation, a simple 6000 K blackbody radiation field and spherical symmetry have been assumed, as described in Young et al. (2003). However, the addition of these two processes only slightly affects the Fe X level balance, for the observations considered here.
What is extremely important is the inclusion of all
the excitations and de-excitations from all the levels,
in particular from the metastable levels. Even at the
relatively low densities characteristic of the quiet solar corona,
these levels have a significant fraction of the ion
populations.
Figure 2
shows the populations of the most spectroscopically-important levels,
calculated with (top) and without (bottom) the inclusion of all collisional
excitations within the 3s23p43d configuration (see also Table 6).
The effect of including collisional processes connected with the
metastable levels is clearly shown. This affects the entire level balance.
For example, at a density of
![]() cm-3 level 3 has its population underestimated by 50%, if
only excitations from the
first 3 levels are included in the calculation.
This would lead to the underestimation of the intensity of the
bright doublet 3s23p5 2P
3/2,1/2-3s 3p62S1/2, observed at 345.7, 365.5 Å.
cm-3 level 3 has its population underestimated by 50%, if
only excitations from the
first 3 levels are included in the calculation.
This would lead to the underestimation of the intensity of the
bright doublet 3s23p5 2P
3/2,1/2-3s 3p62S1/2, observed at 345.7, 365.5 Å.
As noted by Pelan & Berrington (2001),
the most notable feature of the new R-matrix
calculations is a redistribution of the level
populations, because of the resonances.
Table 6 compares our level populations
with those calculated by Bhatia & Doschek (1995) and
Pelan & Berrington (2001) at a density of 1010 cm-3.
The differences between the various results
are due not only to the different
collisions strengths included in the models, but also
to the different A values.
For example, for the 1-3 transition,
![]() ,
according to Bhatia & Doschek (1995), Pelan & Berrington (2001),
and our calculations, while for the
1-30 transition we have
,
according to Bhatia & Doschek (1995), Pelan & Berrington (2001),
and our calculations, while for the
1-30 transition we have
![]() respectively.
The population of level 3
(3s 3p6 2S1/2) is
respectively.
The population of level 3
(3s 3p6 2S1/2) is ![]() 30% lower
compared to the value calculated by Bhatia & Doschek (1995),
however the relative intensity of e.g. the
1-3 line (345.738 Å) with respect to the brightest 1-30
(174.531 Å) one is
30% lower
compared to the value calculated by Bhatia & Doschek (1995),
however the relative intensity of e.g. the
1-3 line (345.738 Å) with respect to the brightest 1-30
(174.531 Å) one is ![]() 50% higher compared to
the Bhatia & Doschek (1995) calculation.
50% higher compared to
the Bhatia & Doschek (1995) calculation.
For Fe X all the identifications in the past have been based either on studies of the variations of the wave number intervals along isoelectronic sequences (sometimes with very approximate intensity estimates), or on intensity estimates alone. For almost all lines, no direct comparisons have been made with observed intensities. We note that previous methods have allowed the identification of many of the brightest lines in Fe X. On the other hand, weaker lines are more difficult to identify for the complex Fe ions, because of their level separations and mixing effects.
It is virtually impossible to list in detail all the line identifications proposed, discussed, or rejected in the literature. However, in what follows we have tried to list the most notable studies (including the first ones) for the configurations included here. More details are given in the Appendix. A summary is given in Table 7. This table lists not only the identifications that we propose, but also those proposed in the literature, including ones that we either reject or that we cannot confirm on the basis of the available experimental data. Previous identifications which are either consistent or inconsistent with ours are also listed. Some of the lines are self-blended or blended with transitions from other ions, the most common ones are indicated in the Table. However note that blending depends on the instrument resolution and on the plasma source (e.g. quiet Sun, active region etc.).
As illustrated by Swings (1943), Edlén (1942), upon suggestion from Grotrian (1939), identified the famous bright red coronal forbidden line at 6374.6 Å as the Fe X transition 2P3/2-2P1/2 within the ground configuration.
Transitions within the 3s23p43d configuration also produce some bright forbidden lines. Edlén (1969), on the basis of wavelength correspondences, suggested 5 possible identifications, of which none turned out to be correct.
Mason & Nussbaumer (1977) performed a detailed calculation of level populations and line intensities. This allowed a number of new identifications to be proposed on firmer ground. Mason & Nussbaumer (1977) proposed the identifications of the 1918.3, 3454.2 Å lines, and suggested possible identifications for the 1428.7, 1603.3, 3533.6, 4311.8 Å lines. Smitt (1977) confirmed the identifications of Mason & Nussbaumer (1977), further identifying other transitions and suggesting a few more that should have been observed. Edlen & Smitt (1978) made very approximate intensity calculations to confirm and extend the identifications presented in Smitt (1977).
The results of our model ion are compared with the
observations of the 3s23p5 and 3s23p4 3d forbidden lines,
in Figs. 3-5.
Considering
all the uncertainties in the observations, we can
confirm (see Table 7) all the identifications proposed by
Mason & Nussbaumer (1977). Also, we confirm most of the identifications
proposed by the other authors,
with the notable exception of the 1582.35 Å
line that is obviously not due to the
10-24 transition, as previously suggested
(see, e.g., Smitt 1977; Edlen & Smitt 1978;
Sandlin & Tousey 1979).
Doubts about this identifications have been
expressed by Bhatia & Doschek (1995), but
no direct comparisons with observations were provided.
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{H0432f3.ps}
\end{figure}](/articles/aa/full/2004/29/aa0432-03/Timg250.gif) |
Figure 3:
The Fji curves relative to a
coronal condensation observed from the ground
at 1.02 |
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{H0432f4.ps}
\end{figure}](/articles/aa/full/2004/29/aa0432-03/Timg251.gif) |
Figure 4:
The Fji curves relative to the
Skylab ATM observations 40
|
We note that all the above studies provided only the relative energies for some of the levels within the 3s23p43d configuration and not their position with respect to the ground level. As described in detail in the Appendix, the energies of the 3s23p4 3d levels ultimately depend on the position of the levels 4, 5(4D 5/2, 7/2). In fact, all the observed forbidden lines decay directly (e.g. the 5-8 3454.9 Å line) or indirectly (e.g. the 8-24 1463.5 Å one) into levels 4 or 5.
In turn, level 5 (4D7/2) is metastable, and can only decay to the ground via the M2 transition 1-5. This line is the fourth strongest line in the EUV spectrum of Fe X, and would easily have been identified if it were not for the fact that it falls in a region (250-270 Å) which is crowded with lines that all have dubious identifications. Level 4 (4D5/2) decays via the 1-4 E1 transition, which is also relatively strong and not identified with certainty. In fact, the energies of all the 4Dj levels have only been proposed in the literature but not confirmed. Smitt (1977) was the first to tentatively assign an energy of 388 708 cm-1 to both levels 4 and 5. The energies of the higher levels were assigned by Edlen & Smitt (1978) and subsequent authors (see NIST listings) by assuming the Smitt (1977) suggestion to be correct.
Levels 4 and 5 are predicted to be close, but not coincident. Deb et al. (2002) predict the 4D 5/2, 7/2 levels to be separated (although inverted) by 21 cm-1, while our SS results predict a splitting of approximately 70 cm-1. Fortunately, we found good observational evidence on the splitting of this term in Sandlin & Tousey (1979) (see Table 7). The authors report a strong component at 1603.21 Å (the 5-21 line) and a weaker one at 1603.35 Å (the 4-21 line), which result in an energy difference of 5 cm-1. We adopt this value here. Similarly, Sandlin & Tousey (1979) report an asymmetry in the red wing of the 1918.25 Å line, consistent with the splitting and intensities of the 5-18 and 4-18 transitions.
The 5-24 transition is predicted to be the
fourth strongest forbidden line (see Table 4),
and should be easily observable at approximately 1028 Å, as already
noted by Smitt (1977).
Its wavelength is well-constrained by the
observed 5-8 (3454.9 Å) and 8-24 (1463.5 Å) transitions.
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{H0432f5.ps}
\end{figure}](/articles/aa/full/2004/29/aa0432-03/Timg252.gif) |
Figure 5:
The Fji curves relative to the
Skylab ATM observations reported by Feldman & Doschek (1977).
Note that the ordinate of the plot spans three orders
of magnitude. These results confirm those presented in
Fig. 4 (the error bar indicates a |
| i-j | Rel. I |
|
Same ID | Diff. ID | |
|
1-31 |
|
170.575 |
? 170.58 (FG) | FG, B, BD | |
1-30 |
1.0 | 174.531 |
174.531 |
G, FG, MH, B, BD | |
2-31 |
|
175.263 |
175.263 |
G, FG, MH, B, BD | |
| 1-29 |
|
175.475 |
175.475 |
FG, MH, B, BD | |
1-28 |
0.55 | 177.240 |
177.239 |
G, FG, MH, B, BD | |
2-29 |
|
180.441 |
? 180.401 |
FG, B, BD | |
2-28 |
|
182.307 |
182.308 |
FG, MH, B, BD | |
1-27 |
0.22 | 184.537 |
184.536 |
FG, MH, B, BD | |
2-27 |
|
190.037 |
190.038 |
FG, B, BD | MH |
1-26 |
|
193.715 |
? 193.715 |
J(193.715) | BD(188.927) |
1-25 |
|
195.316 |
? 195.399 (B) | B | |
| 2-25 |
|
201.487 |
? 201.556 (B) | B | |
1-23 |
|
207.449 |
? 207.449 |
J(207.444) | B?(209.776), BD(204.145) |
1-22 |
|
220.247 |
? 220.247 |
J | B?(220.882), BD |
1-19 |
|
225.856 |
? 225.856 |
J(225.16) BD(222.96) | |
1-17 |
|
227.208 |
? 227.208 |
B(226.31), BD(226.32) | |
1-14 |
|
230.667 |
? 230.127 |
B(229.99), J(229.969) | |
1-15 |
|
230.900 |
? | B(230.089), BD | |
1-11 |
|
234.599 |
? 234.356 |
S, B, J(234.353), BD | |
1-13 |
|
236.494 |
? 236.494 |
J(233.53 bl O V), BD(231.52) | |
1-6 |
|
256.398 |
? 256.38 |
S, B, J(256.405 bl), BD | |
| 1-5 | 0.14 | 257.263 |
257.262 |
||
| 1-4 |
|
257.259 |
'' | S, B, J(257.257), BD | |
5-35 |
|
327.314 |
? 327.8 (BR) | S(324.726), BD | |
18-43 |
|
337.235 |
337.238 (TN) | BD(296.194) | |
1-3 |
|
345.738 |
345.739 |
F, BD | |
21-43 |
|
349.302 |
? bl Mg VI,Fe XI 349.162 (TN) | BD(288.063) | |
2-3 |
|
365.560 |
365.54 |
F(365.57) | |
5-24 |
|
1028.02 |
1028.02 (FE) | BD, FE | |
| 4-24 |
|
1028.08 |
'' | BD | |
| 8-24 |
|
1463.49 |
1463.49 |
?M, S, ES, BD | |
10-24 |
|
1582.35 |
? | S,ES(1582.56), ?BD | |
5-21 |
|
1603.21 |
1603.21 |
M, S, ES, BD | |
| 4-21 |
|
1603.35 |
1603.35 |
||
5-20 |
|
1611.71 |
1611.70 |
S, ES, BD | |
5-18 |
|
1918.24 |
1918.25 (SBT,ST) | M, S, ES, BD | |
| 4-18 |
|
1918.45 |
'' | S, ES, BD | |
5-10 |
|
2934.5 |
? | BD(2933.756) | E(3124) |
8-20 |
|
3021.0 |
? 3020.1 (MC) | S, ES, BD | |
| 5-8 |
|
3454.9 |
3454.2 (JE) | M, S, ES, BD | E(3800.8) |
10-21 |
|
3533.8 |
3533.6 (JE) | M, S, ES | E(3338.5) |
| 10-20 |
|
3575.4 |
3577.1 (JE) | S, ES | |
8-18 |
|
4312.8 |
4311.8 (JE) | M, S, ES | |
10-18 |
|
5538.9 |
5539.1 (JE) | S, ES | |
1-2 |
0.88 | 6376.3 |
6374.6 (JE) | E42, M, S, ES, BD |
Indeed there is a strong line reported
by Feldman et al. (1997) and observed at 1028.02 Å in the
SUMER spectra (see Fig. 6, top).
It is listed as the Fe X 5-24
transition, probably based on the suggestion of Smitt (1977).
It turns out that the 4-24 transition should have an intensity
of about 0.3 of the 5-24 one, and so the line
observed at 1028.02 Å is actually a blend of
both 5-24 and 4-24 transitions, since no other nearby
lines are present.
The agreement between the 1028.02 Å
and the 1463.5 Å line is only satisfactory, considering
the brightness of these lines and the quoted uncertainties in the
SUMER calibration.
The coronal line observed at 1042.5 Å, tentatively identified by
Feldman et al. (1997) with the Fe X 6-24 transition
is obviously due to an unidentified line.
![\begin{figure}
\par\includegraphics[width=5.4cm,clip]{H0432f6a.ps}\par\vspace*{2mm}
\includegraphics[angle=90,width=8.1cm,clip]{H0432f6b.ps}
\end{figure}](/articles/aa/full/2004/29/aa0432-03/Timg255.gif) |
Figure 6:
Top: average off-limb SUMER spectrum showing the bright
1028.02 and 1463.5 Å Fe X forbidden lines.
Bottom:
the relative Fji curves (calculated at log T[K] = 6.0).
The agreement between the 1028.02 Å
(here identified as a blend of the 5-24 and 4-24 transitions)
and the 1463.5 Å line is satisfactory
(the error bar indicates a |
A great aid in the identification of the
4Dj levels comes from the
beam-foil spectroscopy. For example, Jupen et al. (1993)
presented an Fe IX-XI spectrum in the 200-270 Å range
measured 18 ns after the excitation took place.
After 18 ns, all the levels with short lifetimes have decayed.
The 4D7/2 level has such a long lifetime that
the 1-4 line is the dominant
transition (as suggested by Jupen et al. 1993).
Unfortunately, however, the beam-foil spectra
had a ![]() 1-2 Å resolution, and could only provide
an approximate position for this transition (
1-2 Å resolution, and could only provide
an approximate position for this transition (![]() 257 Å).
We note that Smitt (1977) suggested a value of 257.263 Å.
257 Å).
We note that Smitt (1977) suggested a value of 257.263 Å.
In conclusion, having established a consistency between the brightest
transitions connected to the 3s23p43d levels,
we are still left with at least five candidates for the strong
EUV 1-5 transition in the high-resolution solar spectra of
Behring et al. (1976). Note that the 1-5 transition
must be blended with the 1-4 one.
The blend could correspond to the relatively bright lines observed at
256.686 Å (blended with a S XIII line);
256.925 Å; 257.262 Å;
257.392 Å (normally identified as an Fe XIV line
but probably blended with an unidentified line);
257.547 Å (possibly due to Fe XI).
We note that with medium-resolution (![]() 0.3 Å) spectroscopy
as in the Malinovsky & Heroux (1973) spectrum,
the latter three spectral lines are blended.
0.3 Å) spectroscopy
as in the Malinovsky & Heroux (1973) spectrum,
the latter three spectral lines are blended.
Thomas & Neupert (1994) and Young et al. (1998), used the SERTS-89 spectrum to suggest that the 257.262 Å line is the blend of the 2P3/2-4D 5/2, 7/2 transitions, while Brosius et al. (1998b) observed this line with SERTS-95 at 257.246 Å, but identified it as due to a blend of Fe X and Si IX.
We have used the Thomas & Neupert (1994) intensities
and the present model to
confirm, on a quantitative basis, the identification of
the important 2P3/2-4D
5/2, 7/2
blend with the 257.262 Å line, as shown in
Fig. 9.
The Fji curves indicate log ![]() = 9.5 cm-3,
in excellent agreement with results
from other ions which will be reported in further papers in this series.
Note that Young et al. (1998) obtained a lower density,
log
= 9.5 cm-3,
in excellent agreement with results
from other ions which will be reported in further papers in this series.
Note that Young et al. (1998) obtained a lower density,
log ![]() = 9.0 cm-3, using the available CHIANTI model.
= 9.0 cm-3, using the available CHIANTI model.
The transition array 3s23p5-3s23p43d
produces the brightest Fe X lines, visible in the
150-300 Å range.
Gabriel et al. (1965) and Gabriel et al. (1966)
first identified three of the lines
for this transition array.
A further six lines were identified by Fawcett & Gabriel (1966),
while other weaker lines were later
proposed by Bromage et al. (1977) and by Jupen et al. (1993).
![\begin{figure}
\par\includegraphics[angle=90,width=8.6cm,clip]{H0432f7.ps}
\end{figure}](/articles/aa/full/2004/29/aa0432-03/Timg256.gif) |
Figure 7:
The Fji curves relative to the full-Sun spectrum of
Malinovsky & Heroux (1973).
As indicated in the figure,
the intensities of the 257.26 and 182.3 Å lines have
been rescaled (by factors of 0.4 and 0.08)
taking into account known blends.
The agreement between our present model and the
Malinovsky & Heroux (1973) data is excellent
(the error bar indicates a |
![\begin{figure}
\par\includegraphics[angle=90,width=8.4cm,clip]{H0432f8a.ps}\vspace*{3mm}
\includegraphics[angle=90,width=8.4cm,clip]{H0432f8b.ps}
\end{figure}](/articles/aa/full/2004/29/aa0432-03/Timg257.gif) |
Figure 8:
The Fji curves relative to the theta-pinch laboratory
spectra of Datla et al. (1975), first ( top) and second ( bottom) case.
The estimated electron density and temperature
at the time of peak intensity of the discharge were
|
The brightest Fe X lines are found at
174.534, 177.242, 184.543, 190.0 Å. Figure 7
shows an excellent agreement between our present model and the
Malinovsky & Heroux (1973) data.
The notable features of Fig. 7 are:
a) an excellent agreement for the
bright 174.534, 177.242, 184.543 Å lines;
b) as noted by previous authors, the 2-31 transition (175.26 Å),
is an excellent density diagnostic for the quiet solar corona.
Its intensity suggests a log ![]() = 8.8 cm-3, in excellent
agreement with the electron densities derived from other ions;
c) the blend of the 1-5 and 1-4 transitions (257.26 Å)
is a good density diagnostic for active regions
(for log
= 8.8 cm-3, in excellent
agreement with the electron densities derived from other ions;
c) the blend of the 1-5 and 1-4 transitions (257.26 Å)
is a good density diagnostic for active regions
(for log ![]() > 9 cm-3).
We have included this blend in Fig. 7,
by measuring the line intensity
from the Malinovsky & Heroux (1973) spectrum (it was not
listed by the authors), and by assuming that
the Fe X blend contributes by 40%
to this very strong line;
d) the bright 184.54, 190.04 Å lines
form a branching ratio, and could therefore be useful
for instrument calibration;
e) the 190.04 Å line (labelled 8 in Fig. 7)
is however problematic. In medium-resolution spectra,
the bright 190.04 Å line is not due to Fe X, as often
reported. The calibrated theta-pinch laboratory
spectra of Datla et al. (1975)
also shows the same type of blending (labelled 3 in Fig. 8),
which should therefore be ascribed to another iron ion.
Indeed Behring et al. (1976) reported a strong nearby
(189.940 Å) line, probably due to Fe XI;
f) the 2-28 line (182.308 Å) is very weak and blended
in medium-resolution spectra with the Fe XI 182.167 Å line (see, e.g., Behring et al. 1976).
According to theory, the contribution
of the 2-28 Fe X transition to the
observed line should only be 8%, as Fig. 7
shows.
> 9 cm-3).
We have included this blend in Fig. 7,
by measuring the line intensity
from the Malinovsky & Heroux (1973) spectrum (it was not
listed by the authors), and by assuming that
the Fe X blend contributes by 40%
to this very strong line;
d) the bright 184.54, 190.04 Å lines
form a branching ratio, and could therefore be useful
for instrument calibration;
e) the 190.04 Å line (labelled 8 in Fig. 7)
is however problematic. In medium-resolution spectra,
the bright 190.04 Å line is not due to Fe X, as often
reported. The calibrated theta-pinch laboratory
spectra of Datla et al. (1975)
also shows the same type of blending (labelled 3 in Fig. 8),
which should therefore be ascribed to another iron ion.
Indeed Behring et al. (1976) reported a strong nearby
(189.940 Å) line, probably due to Fe XI;
f) the 2-28 line (182.308 Å) is very weak and blended
in medium-resolution spectra with the Fe XI 182.167 Å line (see, e.g., Behring et al. 1976).
According to theory, the contribution
of the 2-28 Fe X transition to the
observed line should only be 8%, as Fig. 7
shows.
The other Fe X transitions from the 3s23p43d levels are much weaker (see Table 4) and most fall in the 220-240 Å wavelength range. This region remain relatively unexplored since there is no radiometrically-calibrated high-resolution solar spectrum in this range. We have measured the intensities of these lines from the Malinovsky & Heroux (1973) medium-resolution spectrum, and found that all the observed lines are 3-5 times brighter than our calculated intensities. Therefore, all these lines appear to be blended in medium-resolution spectra, and their identification should only be considered tentative. Many conflicting identifications have been proposed in the past (some are listed in Table 7). Some new identifications are tentatively proposed here. Other previous identifications cannot be confirmed.
The 3s 3p6 configuration produces the two bright lines observed at 345.7, 365.5 Å first identified by Fawcett (1971). These lines form a branching ratio, and are therefore an excellent way of constraining an instrument calibration between those wavelengths. Care must be used, however, since the 365.543 Å line is strongly blended with a bright Ne V line in solar on-disc observations even at high-resolution (see, Young et al. 1998; Del Zanna et al. 2001).
As already mentioned, the new ion model predicts
ratios between the
1-2, 1-3 doublet and any other allowed line from the
3s23p43d configuration that are ![]() 50%
different compared to the Bhatia & Doschek (1995) calculation.
Any of these ratios are useful to calibrate spectra in the
170-360 Å range.
Indeed, these lines were used by
Del Zanna et al. (2001) to derive the relative calibration
between the NIS-1 (308-380 Å) and
GIS-1 (150-210 Å) channels.
It is therefore important to benchmark the collision
strengths for the 3s 3p6 and 3s23p43d configurations.
50%
different compared to the Bhatia & Doschek (1995) calculation.
Any of these ratios are useful to calibrate spectra in the
170-360 Å range.
Indeed, these lines were used by
Del Zanna et al. (2001) to derive the relative calibration
between the NIS-1 (308-380 Å) and
GIS-1 (150-210 Å) channels.
It is therefore important to benchmark the collision
strengths for the 3s 3p6 and 3s23p43d configurations.
There is virtually no independently-calibrated medium-resolution solar spectrum spanning the entire 150-400 Å range that could be used to measure the relative intensities between lines originating from the 3s 3p6 and 3s23p43d configurations. The laboratory data of Datla et al. (1975) indicate that the new collision strengths are in good agreement with the observations (cf. Fig. 8).
The transition array 3s23p43d-3s 3p53d produces weak lines. Smitt (1977) was the first to propose the identification of some lines for this transition array, but no details on the laboratory spectra were provided. NIST reports values for the 4FJ (35-38) levels, based on the identifications proposed by Smitt (1977). Other laboratory observations of these lines have not been found in the literature. We shall see that the Smitt (1977) identifications of this transition array are rejected here.
The brightest line
should be due to the 5-35 transition, at 324.7 Å according to Smitt (1977).
The second brightest would then be the
8-35 at 358.4 Å, followed by 4-36 (321.8 Å)
and 5-34 (355.5 Å).
All these identifications were rejected by
Brooks et al. (1999) using SOHO/CDS-NIS
observations.
![\begin{figure}
\par\includegraphics[angle=90,width=7.2cm,clip]{H0432f9a.ps}\vspace*{3mm}
\includegraphics[angle=90,width=8.4cm,clip]{H0432f9b.ps}
\end{figure}](/articles/aa/full/2004/29/aa0432-03/Timg258.gif) |
Figure 9:
Top: a solar CDS off-limb spectrum (Del Zanna 1999) with the newly identified 18-43
line at 337.27 Å.
The 21-43 line in these off-limb spectra is blended with an
Fe XI line.
Bottom: Fji curves relative to the SERTS-89 calibrated data
of an on-disk active region average spectrum (Thomas & Neupert 1994).
The lines 1, 2, 4 (observed at 257.257, 345.735, 337.238 Å)
are in excellent agreement (the error bar indicates a |
We have also used various CDS-NIS observations (Del Zanna 1999) to check these identifications (Fig. 9). We agree with the conclusions of Brooks et al. (1999) and reject these identifications, since the calculated intensity values are much smaller (by an order of magnitude) than the observed ones, well outside the current uncertainties in the CDS-NIS calibration. We tentatively identify the 5-35 line with the extremely weak unidentified line observed at 327.8 Å by Brooks et al. (1999).
What is surprising is that the line we
predict as the third brightest
Fe X line in the 300-400 Å wavelength range
(the 18-43 transition) has never been identified.
We identify it as the previously unidentified
line observed in CDS spectra at 337.27 Å
(see Fig. 9).
This line, being relatively bright, is reported
in most published solar spectra.
The identification of this and other lines of the
transition array is confirmed by the intensities
obtained with the CDS calibration presented in
Del Zanna et al. (2001). However, the intensity
values are not presented here since the CDS calibration
still needs further refinement.
Instead we use the
calibrated SERTS-89 data of Thomas & Neupert (1994).
Thomas & Neupert (1994) identify this line,
observed at
337.238 Å, with an Ar VIII transition.
However, according to the Ar VIII atomic model present in
CHIANTI v.4, this line should have an intensity 1/10 of a self-blend of three Ar VIII transitions
at ![]() 260.3 Å. Thomas & Neupert (1994) do not
report any lines at 260.3 Å in their
spectrum, hence the 337.238 Å line cannot be due to
Ar VIII. A similar argument applies to
the nearby 338.181 Å line, also identified as due to Ar VIII.
260.3 Å. Thomas & Neupert (1994) do not
report any lines at 260.3 Å in their
spectrum, hence the 337.238 Å line cannot be due to
Ar VIII. A similar argument applies to
the nearby 338.181 Å line, also identified as due to Ar VIII.
Instead, the observed intensity of the 337.238 Å agrees very well with the theoretical intensity of the 18-43 line as shown in Fig. 9. The other lines produced by the 2FJ levels are much weaker and are probably blended with other stronger transitions from other ions. For example, the 21-43 is probably blended with Mg VI and Fe XI lines observed at 349.162 Å.
Note that the energies of the 3s 3p53d levels were obtained by applying a single correction to the entire configuration. Therefore, the wavelengths of the lines originating from these levels could be further be refined, if for example laboratory data were available.
In this paper, which is the first in a series, we have reviewed some of the main issues related to line identifications and the calculation of level energies, collision strengths and A values. The most important data relevant for Fe X (n=3 configurations) have been reviewed.
We have described an iterative method that we have used to empirically adjust the radiative calculations by taking into account observed wavelengths. This method is particularly important for complex ions with strong level mixing such as Fe X. It considerably aids the spectral line identifications.
A benchmark of Fe X atomic data against well-calibrated observations has been performed. On the theoretical side, we have shown the importance of building a complete ion model to predict line intensities for comparison with observations. In particular, for complex ions with many metastable levels such as Fe X, it is essential to include all the populating and de-populating processes connected to these levels when calculating the level balance. New collisional and radiative data calculations are presented and used here to supplement published data. On the experimental side, only few data are complete or accurate enough to allow a proper benchmark of the atomic data to be performed. We have reviewed the most important spectroscopic observations of the solar corona and laboratory sources that are available and we have used to assess the atomic data of our Fe X model.
All previous line identifications have been reviewed and assessed, by comparing the results of our model with experimental data. The assessment takes into account both wavelength coincidences and line intensities. This is done, for the first time, in a comprehensive way and only focusing on the brightest spectral lines. The method adopted allowed us to confirm most previous identifications but also to reject some, and to suggest new ones.
The most notable rejections are the coronal line at 1582.35 Å, which cannot be due to Fe X, and the previous identifications of all the lines of the 3s2 3p4 3d-3s 3p5 3d transition array. We also reject the tentative identification by Feldman et al. (1997) of the weak 1042.5 Å line with the Fe X 6-24 transition.
We confirm the previously suggested identification of the 257.257 Å line with the Fe X 1-5, 1-4 self-blend, and revise the identification of the 1028.02 Å line, which is also a self-blend (of the 5-24, 4-24 transitions). The most notable new identification is the brightest line of the 3s2 3p4 3d-3s 3p5 3d transition array.
The assessment also indicated the presence of many blends often not reported in the literature. For the cases free of blends, the agreement between theoretical and experimental line intensities is good. The relative intensities of the lines of the transition array 3s2 3p5-3s2 3p4 3d are in excellent agreement with theory, thus giving confidence in the collision strengths for these levels. We also have indications that the relative excitations of these levels and the 3p6 one are accurate. The few laboratory measurements of metastable level lifetimes are also in good agreement with our calculations. All the above confirms the accuracy of our new atomic data and model ion.
We have pointed out which are the best lines to use for density diagnostics and instrument calibration purposes. In the EUV, the best density diagnostic lines are the 175.26, 175.48 and 257.26 Å lines (in conjunction with any of the other lines), while the rest of the lines (when not blended) could be used for instrument calibration. The two branching ratios 184.54, 190.04 Å and 345.7, 365.5 Å corresponding to bright lines would be excellent for instrument calibration, but are sometimes complicated by blending.
Further work is needed to confirm the identifications of the weaker transitions. In addition, the collision strengths for the 3s 3p5 3d configuration should be re-calculated with better wavefunctions. Finally, it is important to calculate collision strengths for the n=4,5 levels, which produce a host of spectral lines that have been observed in the X-ray wavelength range.
Acknowledgements
Support from PPARC is acknowledged.
We thank P. J. Storey for providing an updated version of SUPERSTRUCTURE. Also, P. R. Young and B. C. Fawcett for useful comments on the manuscript.
In this section, we provide provide further details on the level energies and line identifications listed in Tables 3, 4, 7. Note that level energies and line identifications are considered confirmed only when both theoretical wavelengths and line intensities match experimental data. Transitions that are obviously blended with lines from other ions cannot be identified/benchmarked with certainty, and have a question mark in Table 7. Note that, due to the lack of radiometrically-calibrated high-resolution quiet-Sun spectra (where Fe X lines are best observed) in the 200-250 Å range, we are unable to confirm the identifications of many transitions.
The splitting of the ground 2P term is well known because of the famous red coronal line, observed at 6374 Å. The position of level 3, the 3s 3p6 2S1/2e (mixed with level 27), is also well known because of the strong 1-3 transition measured by Behring et al. (1976). Note that the 2-3 transition is blended in solar spectra, however its wavelength is confirmed by the laboratory measurement of Fawcett (1971), who was the first to identify the 3s 3p6 level.
Levels 4, 5 were already discussed in Sect. 5.3.1. The 1-5 line is very bright, and the only line that matches its intensity is the line observed at 257.262 Å. This identification constraints the energies of many other levels in the configuration.
The other two 4D levels, 6,7, are not important spectroscopically. The 1-6 E1 line is weak and is blended with a Si X line in solar spectra, hence its wavelength and intensity cannot be properly assessed. In laboratory spectra, the line has also been reported by Jupen et al. (1993) as blended.
The lowest of the 4F terms, level 8 (4F9/2), is a metastable level and decays mainly to level 5 (4D7/2) via the second-brightest forbidden line observed at 3454.2 Å. This in turn constraints the energies of the other fine-structure 4FJ levels. Level 9 is strongly mixed and still unidentified, but is not spectroscopically important. Level 10 (4F7/2) should produce a strong line around 2934 Å, bf not reported in the literature, probably because it falls in a spectral region not often observed. The 4F5/2e (level 11) mainly decays via a weak E1 transition to the ground, probably blended with an He II 234.356 Å line in solar spectra (Jupen et al. (1993) identifies the line with a line observed in the laboratory at 234.353 Å).
Levels 12-16 are not spectroscopically important in the sense that they only produce weak lines. Various identifications have been proposed by previous authors, but we are unable to confirm them.
Levels 17 and 19 (J=5/2, even parity) are strongly mixed, also with other levels of the same configuration. They should produce realtively weak but measurable spectral lines. Level 17 is tentatively identified with the 1-17 line observed at 227.208 Å in solar spectra (and reported as Fe XV), but could also be associated with the 226.998 Å line (blend with Si IX). Bromage et al. (1977) predicted the line to be at 226.45 Å but identified it with a laboratory line observed at 226.31 Å. Level 19 is tentatively identified with the 1-19 line observed at 225.856 Å in solar spectra. Jupen et al. (1993) instead identified this transition with a line observed at 225.163 Å in the laboratory. Bromage et al. (1977) predicted the line to be at 225.29 Å.
Level 18, (2F7/2e) is metastable and decays via the strong M1 5-18 transition observed at 1918.25 Å. The weaker 8-18 line has also been observed, at 4312 Å. The interesting fact about level 18 is that the 1-18 M2 transitions is weak but should be measurable in high-resolution spectra. If its wavelength can be measured accurately, it could in turn confirm the energy of level 5 and hence of most of the 3s2 3p4 3d levels (relative to the ground).
Levels 20, 21 (2G 9/2, 7/2) are both metastable. The first decays mainly via the strong forbidden line 8-20, but also via the 5-20 transition. Note that the wavelength of the 5-20 transition has been accurately measured (1611.7 Å) by various authors (Sandlin et al. 1977; Feldman & Doschek 1977). The wavelength of the 8-20 transition should therefore fall at 3021.0 Å in vacuum, since the 5-8 transition is well known (the bright 3454.2 Å line, corresponding to a vacuum wavelength of 3454.9 Å). Jefferies et al. (1971) originally measured the line at 3021.3 Å, while Magnant-Crifo (1973) revised the measurement providing a value of 3020.1 Å. Level 21 produces the 10-21 line observed at 3533.6 Å and the 4-21, 5-21 lines, accurately measured by Sandlin & Tousey (1979).
Level 22 (2F5/2e) should produce an observable 1-22 line around 220 Å, a region with many unidentified lines. In agreement with Jupen et al. (1993), this level is tentatively identified according to the line observed at 220.247 Å. It is interesting to note that Bromage et al. (1977) predicted the 1-22 line at 220.12 Å but tentatively identified it with a line observed at 220.882 Å.
Level 23 also has an uncertain identification. Most probably, the 1-23 transition (weaker than the 1-22) is the line observed at 207.449 Å. Bromage et al. (1977) predicted the line at 207.58 Å and tentatively identified it with a line observed at 209.776 Å. Jupen et al. (1993) identifies it with a laboratory line observed at 207.444 Å, in agreement with our suggestion.
Level 24 (2F7/2) is metastable and not strongly mixed. The decay to level 8 is via the forbidden line observed at 1463.49 Å.
Level 25 decays to the ground with very weak lines, possibly the same identified by Bromage et al. (1977). Level 26 is tentatively identified with a weak line observed at 193.715 Å, also observed in the laboratory by Jupen et al. (1993) at the same wavelength.
Levels 27-31 produce the strongest lines in the Fe X spectrum, and their energies are accurately known. Surprisingly, as in many other cases, the values reported by NIST do not agree with the published literature (see Table 3; here we adopt the accurate wavelengths of Behring et al. 1976). Level 29 decays to the ground via two very weak transitions, both of which are blended. Hence, the wavelengths of the 1-29 and 2-29 transitions are difficult to assess. The 2-29 blends a much stronger (by a factor of 10) Fe XI transitions, while the 1-29 is probably blended with a weak Fe IX line. Hence, the theoretical intensities of these two lines can only be benchmarked once also the Fe IX and Fe XI have been assessed. A further complication is that the 1-29 line is blended with the 2-31 in medium-resolution spectra. Note that also the 2-28 (182.308 Å) in medium-resolution spectra is blended with a Fe XI line observed at 182.167 Å, as well as the 2-27 190.038 Å, with two lines observed at 189.733 and 189.940 Å.
The 3s 3p5 3d levels have some mixing, as indicated in Table 3, in particular with the 3s2 3p3 3d2 (c5) levels. Aside from a few lines already discussed, most of the 3s 3p5 3d levels produce very weak lines. The energy of all the levels was obtained by applying a single correction (-17 200 cm-1) to the entire configuration. Hence, the wavelengths of the lines originating from these levels can further be refined if accurate laboratory measurements will be available.