A&A 422, 563-572 (2004)
DOI: 10.1051/0004-6361:20040195

Me 1-1: A PN containing a cool star

Z.-X. Shen1 - X.-W. Liu1 - I. J. Danziger2


1 - Department of Astronomy, Peking University, Beijing 100871, PR China
2 - Osservatorio Astronomico di Trieste, via GB Tiepolo 11, 1-34131 Trieste, Italy

Received 4 February 2004 / Accepted 5 March 2004

Abstract
We report the detection of a cool stellar component at the center of the planetary nebula (PN) Me 1-1 and present optical spectra of the system. From measurements of nebular emission lines, we have derived electron temperature, density and chemical composition. Heavy elemental abundances deduced from collisionally excited lines (CELs) are compared with those derived from optical recombination lines (ORLs). The electron temperature and density deduced from the nebular analysis were used to calculate the nebular continuum emission, which was then subtracted from the observed spectrum in order to obtain the spectrum of the cool stellar component apparent in the observed spectrum. We calculate Band V magnitudes of the cool companion and obtain a color index of B-V=1.20. By comparing the spectrum of the cool star with standard spectra in Pickles's 1998 Stellar Flux Library, we find that the cool component has the spectral type of a K3-4 bright giant. Our analysis suggests that Me 1-1 is probably a yellow symbiotic system.

Key words: ISM: planetary nebulae: individual: Me 1-1 - stars: binaries: symbiotic

1 Introduction

The connection between planetary nebulae (PNe) and symbiotic stars has been discussed since the 1950s (Deutsch 1956). In recent years, many symbiotics have been found to have nebulae and some previously classified PNe have been shown to contain symbiotic binaries (e.g. Corradi et al. 1999, 2000, and references therein). Symbiotic stars are a special class of stellar object defined by Merrill (1944). Their spectra show absorption features of a cool giant and the presence of a hot stellar continuum along with bright emission lines such as He II and [O III], similar to the spectrum of a planetary nebula. Such composite spectra of symbiotic stars are best explained by binaries consisting of a cool giant and a hot compact source. Nebulae associated with symbiotic stars are not genuine PNe because they represent the donation of the companion cool giant, accreted and ionized by the hot compact star, rather than ejected by the hot ionization source itself. As we shall show in this paper, Me 1-1, a previously known planetary nebula, shows a composite spectrum characteristic of a symbiotic system.

Me 1-1 (PN G052.5-02.9) was discovered by Merrill et al. (1942) at Mount Wilson on photographs obtained with an objective prism, on which they detected ${\rm H}\alpha$ emission from Me 1-1. The optical angular diameter of Me 1-1 reported in the literature ranges from 8-12 arcsec (Fracman 1962; Henize 1964; Cahn & Kaler 1971; Acker et al. 1991). At radio wavelengths, Zijlstra et al. (1989) derived a diameter of 4.7 arcsec. Narrow-band images of Me 1-1 in [O  III] $\lambda$5007, H$\alpha $ and in [N  II] $\lambda$6584 have been published by Manchado et al. (1996). The images show that Me 1-1 closely resembles a three-seed peanut, with a spatial extent of approximately  $1.4 \times 3.4$ arcsec and a major axis at Position angle (PA$)\sim 352$ deg. Faint emission is seen out to radial distances of about 3 and 6 arcsec along the minor- and major-axis, respectively. The two outlying knots clearly show ionization stratification - the distance of peak emission to nebular center is the smallest in [O  III], followed by H$\alpha $ and then by [N  II], i.e. following the sequence of decreasing ionization potentials.

Me 1-1 has a 1.4 GHz radio free-free continuum flux density of 36 mJy (Condon & Kaplan 1998) and a 5 GHz flux of 43 mJy (Cahn et al. 1992). It is located within a few degrees of the Galactic plane where stars are crowded along the sight line. The radial velocity of Me 1-1 relative to the Local Standard of Rest is $11.7~{\rm km~s^{-1}}$ (Maciel 1984). The nebula has been studied spectroscopically by Aller (1951), Kaler et al. (1976) and Aller & Keyes (1987) and its chemical composition has been analyzed by Kaler & Keyes (1978), Aller & Keyes (1987) and Henry (1990). Although it is not obvious that Me 1-1 has a bipolar morphology, based on the elemental abundance criteria of Peimbert (1978), i.e. ${\rm He/H}\geq0.125$ and ${\rm log(N/O)}\geq -0.3$, Maciel & Dutra (1992) classified Me 1-1 as a Type I PN.

Table 1: Observational journal.

Tylenda et al. (1991) found a peculiar color index for Me 1-1 and suspected a cool stellar component in this PN. Here we present new spectroscopic observations of Me 1-1 taken with the ESO 1.52 m telescope. We find that the nebula has a composite optical spectrum remarkably similar to those of yellow symbiotic stars, which are rare symbiotic systems containing a cool stellar component of spectral types F, G, K or early R and show enhancements of s-process elements as in barium stars (Schmid 1994; Smith et al. 1996, 1997; Pereira & Proto de Mello 1997; Smith et al. 2001). Our spectra reveal the presence of a possible K3-4 bright giant (luminosity class  II) embedded at the center of Me 1-1. The B and V magnitudes of this cool stellar component are derived. Emission and absorption features detected in our spectra of Me 1-1 are compared with those seen in symbiotic stars.

In Sect. 2 of this paper, we describe the observations and data reduction procedures and present the observed emission line fluxes. Dust extinction towards Me 1-1 is discussed in Sect. 3. A plasma diagnostic analysis of nebular emission lines and the resultant elemental abundances derived respectively from CELs and from ORLs are presented in Sect. 4. The spectrum of the cool stellar component is analyzed in Sect. 5, which is followed by a brief discussion on the nature of the system in Sect. 6.

  \begin{figure} \par\includegraphics[width=14cm,clip]{0195fig1.ps} \end{figure} Figure 1: Optical spectrum of Me 1-1 from 3520-7420 Å. Note that H$\alpha $, [O III]  $\lambda 5007$ and [N II]  $\lambda 6584$ were saturated in this spectrum. Interstellar extinction has not been corrected for in this plot.
Open with DEXTER

2 Observation and data reduction

The observations were mainly carried out in July 1995 using the ESO 1.52 m telescope equipped with a Boller & Chivens (B&C) spectrograph. An observational journal is given in Table 1, where Col. 1 gives the UT time at the start of the exposure. Column 2 lists the spectral wavelength range. Columns 3-6 give, respectively, slit width in arcseconds, slit PA in degrees, spectral resolution in terms of FWHM (Full Width at Half Maximum) in angstroms and exposure time in seconds. The spectra were recorded on a Ford $2048\times 2048$ CCD of  $15~\mu{\rm m}$ pixel size.

All spectra except one in Table 1 were obtained with a 2 arcsec wide entrance slit. In order to obtain total ${\rm H}\beta$ flux from the entire nebula, an additional spectrum was taken with an 8 arcsec wide slit. The B&C spectrograph had a useful slit length of about 3.5 arcmin and was oriented in the east-west direction ( $\rm PA=90^\circ$), nearly perpendicular to the nebular major axis.

Table 2: Observed relative line fluxes, on a scale where H$\beta =100$.

The spectra were reduced by standard procedures using the ESO MIDAS software package. After bias subtraction, flat fielding and cosmic-ray removal, the spectra were wavelength calibrated using exposures of a helium-argon calibration lamp. The absolute flux was obtained via wide slit observations of the standard star Feige 110 (Walsh 1993).

From the spectrum taken with an 8-arcsec wide slit, we obtained an ${\rm H}\beta$ flux of $\log F({\rm H}\beta) = -11.50~ {\rm erg~cm^{-2}~s^{-1}}$. The value is slightly smaller than the value of -11.39 tabulated in Cahn et al. (1992). Given the unfortunate orientation of the slit, i.e. almost perpendicular to the nebular major axis, it is possible that we may have missed parts of the flux even with an 8 arcsec wide slit. On the other hand, a careful examination of the ${\rm H}\alpha$ image published in the IAC PN atlas makes it difficult to understand how we would have lost 25% of the flux. Since Me 1-1 is now likely a close binary system (see below), it is possible that the difference between the total H$\beta$ flux measured by us and that tabulated in Cahn et al. (1992), originally from the measurement of O'Dell (1963) may be real, caused by orbital motion or other variations. Our measurement was obtained under photometric conditions. Our measured total H$\beta$ flux, when combined with the free-free radio flux density, yields an extinction coefficient consistent with those derived from ratios of H I and He II lines (cf. Sect. 3). Based on these considerations, we shall adopt a total H$\beta$ flux of $\log F({\rm H}\beta) = -11.50~ {\rm erg~cm^{-2}~s^{-1}}$ in our analyses in the following sections. A plot showing the optical spectrum of Me 1-1 from 3520-7420 Å is given in Fig. 1.

Strong and isolated emission lines were integrated over the line profile to obtain their fluxes, while lines partially blended together were measured by Gaussian line profile fitting. The detected emission lines and their measured fluxes are given in Table 2, normalized such that ${\rm H}\beta =100$. The fluxes of the He II  $\lambda1640$ and C III] $\lambda\lambda1907,1909$ lines were obtained from an IUE spectrum retrieved from the data archive in Vilspa. The IUE (International Ultraviolet Explorer) spectrum was obtained with the large entrance aperture, an oval of  $10\hbox{$^{\prime\prime}$ }\times24\hbox{$^{\prime\prime}$ }$, large enough to cover the entire ionized nebula. The fluxes of the two UV lines were normalized to  ${\rm H}\beta =100$ using a total H$\beta$ flux of $\log F({\rm H}\beta) = -11.50~ {\rm erg~cm^{-2}~s^{-1}}$. In Table 2, Cols. 1-3 give, respectively, observed wavelengths and observed and dereddened line fluxes. Dereddened line fluxes were calculated from the observed ones using  $I(\lambda)=10^{c f(\lambda)} F(\lambda)$, where  $f(\lambda)$ is the standard Galactic extinction law for a total-to-selective extinction ratio of R=3.1(Howarth 1983) and c is logarithmic extinction at  ${\rm H}\beta$(cf. Sect. 3). Columns 4-10 are, respectively, ionic identification, laboratory wavelength (air, except for IUE lines), multiplet number, lower and upper spectral terms of the transition, and statistical weights of the lower and upper levels.

   
3 Extinction

Using the standard Galactic reddening law given by Howarth (1983), and adopting an electron temperature ($T_{\rm e}$) of  $10~000~{\rm K}$ and an electron density of $\log N_{\rm e} = 4$ cm-3, we calculate the logarithmic extinction at H$\beta$, $c=\log [I({\rm H}\beta)/F({\rm H}\beta)]$, from the observed ratios of H$\alpha $/H$\beta$ and He II  $\lambda1640$/He II $\lambda4686$, using the fluxes presented in Table 2. The results are presented in Table 3, where we also give the value derived from the ratios of the observed total H$\beta$ flux, $F({\rm H}\beta)$, to the free-free radio flux density at 5 GHz, $S(5~{\rm GHz})=0.044~{\rm Jy}$ (Zijlstra et al. 1989) and at 1.4 GHz, $S(1.4~{\rm GHz})=0.036~{\rm Jy}$ (Condon & Kaplan 1998). The extinction derived from the ratio of H$\beta$to the 5 GHz radio flux density agrees well with those derived from the H I and He II line ratios, while the value obtained from the ratio of H$\beta$ to the 1.4 GHz radio flux density is significantly smaller. Pottasch & Zijlstra (1994) remeasured the 5 GHz flux density and obtained practically the same value as Zijlstra et al. (1989). Thus the flux at 5 GHz should be quite certain. The brightness temperature calculated from the 5 GHz flux is significantly lower than $T_{\rm e}$. In addition, the ratio of the fluxes at 6 cm and 3.6 cm (Pottasch & Zijlstra 1994) agrees well with the optically thin case. All these suggest that the nebula is optically thin at 5 GHz or higher frequencies. On the other hand, it is difficult to rule out that the nebula is optically thick at 1.4 GHz, even though the nebular density we obtain (cf. Sect. 4.1) seems to be too low to indicate a large optical depth. It is possible that the measurement uncertainty at 1.4 GHz is actually larger than the 10% as claimed by Condon & Kaplan (1994) for this particular object. The H I and He II line ratios yield an average value of  $c({\rm H}\beta) = 0.666$, which is used to deredden our UV and optical fluxes.

4 Nebular emission line spectrum

In this section, we present a standard plasma diagnostic analysis of emission lines detected in the spectrum of Me 1-1. The spectrum of the cool stellar component will be discussed in the next section.

   
4.1 Plasma diagnostics

In the optical spectrum of Me 1-1, a number of collisionally excited lines (CELs), useful for nebular plasma diagnostics and abundance determinations, are observed. Electron temperatures and densities can be derived from various CEL diagnostic ratios by solving level populations for a multilevel ($\geq$5) atomic model. From the ratios of the [O III]  $(\lambda4959+\lambda5007)/\lambda4363$ and [N II]  $(\lambda6548+\lambda6584)/\lambda5754$, we obtain $T_{\rm e} = 10~500~{\rm K}$ and $12~100~{\rm K}$, respectively. The [N  II] auroral line $\lambda$5754 can be contaminated by recombination excitation (Rubin 1986; Liu et al. 2000). After correcting for the predicted contribution by recombination to the measured flux of  $\lambda5754$ using the formula given by Liu et al., we obtain $T_{\rm e} = 11~750~{\rm K}$. The average value of this corrected [N  II] temperature and the [O  III] temperature, i.e. $T_{\rm e} = 11~100~{\rm K}$, will be used for ionic abundance determinations. The doublet ratios [S II] $\lambda6731/\lambda6716$, [Cl III] $\lambda5537/ \lambda5517$ and [Ar IV] $\lambda4740/\lambda4711$ yield electron densities of  $\log N_{\rm e} = 3.85$, 3.26 and 3.93  ${\rm cm^{-3}}$, respectively. The mean value, $\log N_{\rm e} = 3.68~{\rm cm^{-3}}$, will be adopted.

4.2 Nebular abundance analysis

In this subsection, we present elemental abundances for Me 1-1, derived from observed emission line intensities relative to H$\beta$. In our calculations, a $T_{\rm e}=11~100$ K and $\log N_{\rm e} =3.68$ cm-3 are assumed for all the ionic species (cf. Sect. 4.1).

4.2.1 Ionic abundances of heavy elements from CELs

Ionic abundances of heavy elements were derived from CELs using the formula,

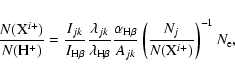\begin{displaymath}\frac{N({\rm X}^{i+})}{N({\rm H}^+)} = \frac{I_{jk}}{I_{{\rm ... ...k}} \left({\frac{N_j}{N({\rm X}^{i+})}}\right)^{-1}N_{\rm e}, \end{displaymath} (1)

where $I_{jk}/I_{{\rm H}\beta}$ is the intensity ratio of a collisionally excited line  $\lambda_{ij}$ emitted by ion  ${\rm X}^{i+}$ to H$\beta$, $\alpha_{{\rm H}\beta}$ is the effective recombination coefficient of  ${\rm H}\beta$, Ajk is the Einstein spontaneous transition probability of the ionic line, $N_j/ N({\rm X}^{i+})$ is the fractional population of the ion in its upper level j from which the ionic line  $\lambda_{jk}$ arises. $N_j/ N({\rm X}^{i+})$ is sensitive to the adopted $T_{\rm e}$ and $N_{\rm e}$; $\alpha_{{\rm H}\beta}$ is taken from Storey & Hummer (1995). Ionic abundances thus derived are given in Table 4.

4.2.2 Ionic abundances derived from ORLs

He  I and He  II lines observable in the optical are produced by recombination processes, as are H  I lines. We have also detected several optical recombination lines (ORLs) from ionized C, N and O. From the observed intensity of an ORL relative to H$\beta$, the ionic abundance of the recombining ion relative to H+ can be derived from,

 \begin{displaymath}\frac{N({\rm X}^{i+})}{N({\rm H}^+)}=\frac{I_{jk}}{I_{{\rm H... ...da_{{\rm H}\beta}} \frac{\alpha_{{\rm H}\beta}}{\alpha_{jk}}, \end{displaymath} (2)

where $\alpha_{jk}$ is the effective recombination coefficient of an ORL emitted by ion  ${\rm X}^{+i-1}$ following recombinations of ion  ${\rm X}^{i+}$with electrons. The ionic abundances derived from ORLs depend only weakly on $T_{\rm e}$, ${\rm X}^{i+}/{\rm H}^+\propto T_{\rm e}^\alpha$, where  $\vert\alpha\vert\la 1$ and are essentially independent of $N_{\rm e}$ under low nebular density conditions. Thus small uncertainties in the estimates of $T_{\rm e}$ and $N_{\rm e}$ will hardly affect the derived abundances. The resultant ORL ionic abundances are presented in Table 5.

Table 3: Extinction.

Table 4: Ionic abundances derived from CELs.

Table 5: Ionic abundances from ORLs.

The He2+/H+ abundance ratios estimated from the $\lambda\lambda$4471,5876 and 6678 lines were averaged with weights of 1:3:1, roughly proportional to the intrinsic intensity ratios of the three lines. Case A recombination was assumed for the triplet lines $\lambda$4471 and $\lambda$5876, while Case B recombination was assumed for the singlet line $\lambda$6678. Smits (1996) carried out a calculation for the effective recombination coefficients of He I lines. Contributions of collisional excitation from both the He I 2s 3S and 2s 1S metastable levels by electron impacts to the observed line fluxes were studied by Sawey & Berrington (1993). Combining the recombination coefficient data of Smits (1996) and the collision strengths of Sawey & Berrington (1993), Benjamin et al. (1999) improved the emission rate coefficients for He I lines. Here, we have adopted the analytic fits of He I line emission rate coefficients given by Benjamin et al. (1999) in determining the He+/H+ abundance ratios. The ionic abundance ratios derived from the two triplet lines, $\lambda$4471 and $\lambda$5876 agree with each other reasonably well, but are about 10% higher than the value derived from the singlet line $\lambda$6678. It is unclear if this is caused by underlying absorption from the cool stellar component. The He2+/H+ abundance ratio was calculated from the He II $\lambda$4686 line only, using the effective recombination coefficient given by Storey & Hummer (1995).

The C2+/H+ abundance ratio was estimated from the 3d 2D-4f 2F $\lambda$4267 doublet using the effective recombination coefficients of Davey, Storey & Kisielius (2000), including contributions from both radiative and dielectronic recombination. The effective recombination coefficient of the C II $\lambda$4267 multiplet is essentially case-independent. In our calculation, Case B was assumed.

The N2+/H+ abundance ratio was derived from N II ORLs of the 3d-4f configuration. Case B recombination was assumed. The recent detailed calculations of the effective recombination coefficients of N II lines, including radiative and dielectronic recombination, by Kisielius & Storey (2002) do not include 3d-4f transitions for which LS-coupling fails. Here we have adopted the effective recombination coefficients calculated by Escalante & Victor (1990).

The O2+/H+ abundance ratio was derived from O II ORLs from the 3s-3p and 3p-3d configurations. Effective recombination coefficients are from Storey (1994) for 3s-3p transitions (assuming LS-coupling) and Liu et al. (1995) for 3p-3d transitions (assuming intermediate coupling). Case B was assumed for quartets. All the multiplets used to derive O2+/H+ ratios listed in Table 5 are case-insensitive except for V 19. The O2+/H+ abundance ratio derived from V 19 is about an order of magnitude higher than values deduced from other multiplets. The discrepancy would be even higher if Case A were assumed. It is possible that the observed $\lambda$4156 line flux is dominated by a contribution from some other unknown feature. The ionic abundance derived from V 19 was therefore discarded when calculating the average O2+/H+ ionic abundance ratio.

Table 6: Nebular elemental abundances, in units where $\log N({\rm H})=12.0$.

4.2.3 Comparison of abundances from ORLs and CELs

It is a long-standing problem in nebular abundance studies that heavy element abundances derived from ORLs are systematically higher than those derived from CELs. Peimbert et al. (1993) used O II recombination lines to calculate the O2+/H+ values of the Orion Nebula and M 17 and found that they are about a factor of 2 higher than those derived from [O III] forbidden lines. They attributed this discrepancy to the presence of spatial temperature fluctuations. Further detailed comparison between ionic abundances of heavy elements derived from ORLs on one hand and from CELs on the other have been carried out for a number of bright PNe, including NGC 7009 (Liu et al. 1995; Luo et al. 2001), NGC 6153 (Liu et al. 2000), M 1-42 and M 2-36 (Liu et al. 2001). These careful multi-waveband studies, utilizing data from the UV to far IR, show that infrared fine-structure lines, which are temperature-insensitive, given their very low excitation energies ($\la$1000 K), yield low ionic abundances similar to those derived from optical/UV CELs. Consequently it is clear that $T_{\rm e}$ fluctuations alone may not be sufficient to explain the large discrepancies between the ORL and CEL abundances. Based on the detailed analyses of several PNe, Liu (2002) concluded that the very large discrepancies (over a factor of ten) between the ORL and CEL abundances observed in PNe are most likely caused by the presence of extremely cold H-deficient inclusions embedded in normal nebular material.

For Me 1-1, C2+/H+ and O2+/H+ ratios have been derived using both ORLs and CELs. In both cases, the resultant ORL abundances are found to be higher than the corresponding values derived from CELs, by a factor of 4 and 3, respectively. It is possible that such moderate discrepancies can be explained by $T_{\rm e}$ fluctuations (Peimbert 1967), $N_{\rm e}$ variations (Rubin 1989; Viegas & Clegg 1994), chemical inhomogeneities (Liu et al. 2000) or the combined effects of all.

4.2.4 Total elemental abundances

The total elemental abundances derived from nebular emission lines for Me 1-1, using both CELs and ORLs are presented in Table 6 and compared to results in the literature. In Table 6, Cols. 2 and 3 give the ionization correction factors (ICFs) for CEL and ORL abundances, respectively. The total elemental abundances, after the ICF corrections, are presented in Cols. 4 and 5. Columns 6 and 7 give the elemental abundances obtained previously by Henry (1990) and by Aller & Keyes (1987, hereafter AK). Columns 8 and 9 give the average abundances of Galactic PNe (Kingsburgh & Barlow 1994) and the solar photospheric abundances (Grevesse & Sauval 1998), respectively. Except for He, the above nebular abundances studies were all based on CEL analyses only.

For oxygen, the ionic concentration in O3+ should be negligible given the small amount of doubly ionized helium in Me 1-1. Thus the total elemental abundance of oxygen is simply the sum of ionic concentrations in O+ and O2+, both have been measured using CELs. For the ORL analysis, the O+ abundance is not available and we have assumed that the O2+/O ratio is the same as given by the CEL analysis.

The total elemental abundances of nitrogen, carbon, neon, argon and sulfur for CELs were calculated using the ICF formulae given by Kingsburgh & Barlow (1994). The total ORL abundances of carbon and nitrogen are also estimated based on the assumption that the fractions of the unobserved ionic species for the ORL abundances are the same as those found from the CEL analyses.

The ICF correction for nitrogen CEL abundance is particularly large, given that only the singly ionized species was detected. As a result there could be a large error in the N/H abundance ratio derived from CELs. Our N/H ratio is higher than what Henry (1990) obtained, but agrees well with the value of AK (1987). In all these analyses, a similar ICF formula was used for N/H derived from ${\rm N}^{+}/{\rm H}^{+}$, i.e.,

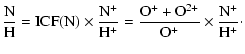$\displaystyle \frac{{\rm N}}{{\rm H}}={{\rm ICF}({\rm N})}\times{\frac{{\rm N}^... ...c{{\rm O}^++{\rm O}^{2+}}{{\rm O}^{+}}}\times{\frac{{\rm N}^+}{{\rm H}^+}}\cdot$     (3)

Given that the ionic abundance of  ${\rm O}^{+}$ is much smaller than that of  ${\rm O}^{++}$, a small difference in the estimate of the ${\rm O}^{+}/{\rm H}^{+}$ ratio will lead to a large difference in ICF(N) for the CEL analysis, and consequently the resultant N/H ratio. Any errors in the ${\rm N}^{+}/{\rm H}^{+}$ ratio will also propagate into the final N/H element ratio.

The ${\rm Ne}^{3+}$ abundance derived from [Ne IV]  $\lambda\lambda4724, 4725$ is abnormally high, given that the ionization potential of Ne III is 63.45 eV, higher than 54.4 eV of He II. We thus expect that there should be a negligible amount of  ${\rm Ne}^{3+}$ in Me 1-1. The [Ne IV]  $\lambda\lambda4724, 4725$ feature was only marginally detected in our spectrum, and was not reported by AK. It is possible that the feature seen in our spectrum is spurious or contaminated by some unidentified lines. As a result, the total neon abundance given in Table 6 is calculated from the ${\rm Ne}^{2+}/{\rm H}^{+}$ ionic abundance ratio only, adopting an ICF based on the work of Kingsburgh & Barlow (1994).

AK obtained a much higher argon abundance than ours. In their theoretical photoionization model of Me 1-1, while the [Ar III]  $\lambda7135$ was well fitted, the [Ar IV]  $\lambda4740$ was predicted to be too strong compared to observations. It is possible that the abundance of argon has been overestimated in their analysis.


  \begin{figure} \par\includegraphics[width=14cm,clip]{0195fig2.ps} \end{figure} Figure 2: Comparison of the spectrum of the cool stellar component and those of a standard K3-4 II star.
Open with DEXTER

5 The cool stellar component

Table 7: Photometry of the cool stellar component.

Using the nebular $T_{\rm e}$ and $N_{\rm e}$ derived in Sect. 4.1, we calculated the contribution of nebular continuum emission to the observed spectrum. After correcting for the interstellar extinction, the predicted nebular continuum spectrum, which contributes less than 2 per cent of the observed continuum level at 4400 Å and less than 1 per cent at 5500 Å, was subtracted from the observed low dispersion spectrum. The residual continuum spectrum peaks near 6000 Å, characteristic of a cool star, and drops rapidly towards shorter wavelengths, suggesting that the hot radiative source which ionizes the nebula has negligible continuum flux in the optical region. After manual removal of nebular emission lines, we integrated the residual spectrum over the response functions of the standard Band V photometric bands to obtain the dereddened magnitudes of the cool star in B and V bands. Repeating the process for a reddened theoretical nebular continuum spectrum and the observed low dispersion spectrum before reddening correction, we obtained the observed B and V magnitudes of the cool component. The results are tabulated in Table 7. All these measurements were made using the spectrum taken with a 2 $^{\prime\prime}$ slit width (under a seeing condition of  $1\hbox{$^{\prime\prime}$ }{-}1\hbox{$.\!\!^{\prime\prime}$ }5$) and 300 s integration time. Only a 30 s integration time exposure was obtained using a wider 8 $^{\prime\prime}$ slit. From this 8 $^{\prime\prime}$ wide slit spectrum, we derived an observed V magnitude of 13.33. The spectrum was however too noisy to make a useful measurement of the B magnitude. It seems thus our 2 $^{\prime\prime}$ wide slit may have lost about 15% of the light from the cool stellar component. Given the higher S/N ratio of the narrow slit observation, we will adopt an intrinsic color index of  (B-V)0 = 1.20 for the embedded cool stellar component. The B and V magnitudes determined by Tylenda et al. (1991) for the cool stellar component of Me 1-1 are 15.57 and 14.12, respectively. Their values are significantly larger than ours and are conceivably caused by poor observing conditions or calibration errors in their observations.

Table 7 shows that the cool stellar component in Me 1-1 has an intrinsic color index B - V = 1.20, suggesting that it is a late type star with spectral type from G5 to M0. We compared the dereddened spectrum of the cool star with those of spectral standards taken from the Stellar Flux Library of Pickles (1998) and found that the spectral energy distribution of the continuum is close to a K3-K4 bright giant. Figure 2 compares the dereddened spectrum of the cool stellar component and that of a K3-4 II star. Both are normalized to the continuum flux at 5556 Å. Apart from the spectral energy distribution, the strengths of absorption features G-band and Ca I  $\lambda4226$, seem to be close to those of a mid-K type star. Due to the existence of crowded emission lines, we were unable to make further detailed spectral classification of this cool component. If the star is type K3-K4  II, then given that the absolute magnitude of a K5  II is -2.2 (Zombeck 1990; The absolute magnitude of a K0  II star is -2.1), we estimate that the distance to Me 1-1 is 7.59 kpc, which is consistent with the value of 8.66 kpc derived by Kingsburgh & English (1992) based on the O II and S II electron densities. Another method to estimate the distance of Me 1-1 is from the rotation curve of the Milky Way (Fich et al. 1989). Given a Local Stardard of Rest velocity of $11.7~{\rm km~s^{-1}}$ for Me 1-1 (Maciel 1984), we find a distance of approximately 9.5 kpc.

In the spectrum of the cool stellar component of Me 1-1, many metal and molecular absorption lines have been observed. We have identified Fe I $\lambda$4045, $\lambda$4198, $\lambda$4271, $\lambda$4324, $\lambda$4383, Ca I $\lambda$4226 and the CN absorption feature at 4216 Å, and a CH absorption feature at 4300 Å in the high dispersion spectrum. In the low dispersion spectrum, a set of Fe I lines, Mg I $\lambda$5183, Mg II $\lambda$5207 and the TiO absorption band at 6200 Å, are also present. In the spectrum of Me 1-1, we see very strong absorption of the Na I D1, D2 lines. These absorption features are however most likely dominated by absorption by the interstellar medium along the line of sight.

6 Discussion

Me 1-1 falls in the Galactic plane ( $l=52^{\circ}$.54, $b=-02^{\circ}$.96). Although the stellar field is crowded along the sight line, given that our slit is only 2 $^{\prime\prime}$ wide and the cool stellar component appears right at the centre of the nebula, we believe that it is unlikely that the cool stellar component observed in the spectrum of Me 1-1 is simply a coincidence of a field star falling along the line of sight.

The presence of a cool K3-4 bright giant in Me 1-1 suggests that Me 1-1 is probably a yellow symbiotic system. Symbiotic stars are systems with a composite spectrum showing features of (Belczynski et al. 2000):

1.
Absorption features of a late-type giant, in practice, (among others) TiO, H2O, CO, CN and VO absorption bands, as well as Ca I, Ca II, Fe I, Fe II, and Na I absorption lines.
2.
Strong emission lines of H I and He I and either
- emission lines of ions with an ionization potential of at least 35 eV (e.g. [O III]); or
- a continuum of an A- or F-type star with additional shell absorption lines from H I, He I, and singly-ionized metals. The latter corresponds to the appearance of a symbiotic star in outburst.
3.
The $\lambda$6825 Raman scattering emission feature, even if no feature of a cool star (e.g. TiO bands) is found.
In Me 1-1, we have detected strong emission lines of H I, He I and He II as well as [O III], [Ne III] and other forbidden lines, satisfying the second requirement for a symbiotic system. We have identified the cool stellar component of Me 1-1 as a late type star. The metal and molecular absorption lines discussed above fulfill the first requirement for a symbiotic system. A marginal unresolved feature is detected at $\lambda$6825 with a FWHM of 14.75 Å, which we tentatively identify as the feature produced by the Raman scattering of the [O VI] $\lambda$1032 resonance line by neutral hydrogen.

Strong links between PNe with certain types of asymmetry (especially bipolar PNe) and symbiotic systems have been suggested by Schwarz & Monteiro (2004, and references therein). It is assumed that bipolar PNe are likely formed from binaries and share many properties with symbiotic nebulae. Me 1-1 is however not a typical bipolar nebula; it looks more like a three-seed peanut. Yet it possibly evolved from a bipolar PN (see the simulation of PNe with binary cores, Gawryszczak et al. 2002).

Given that Me 1-1 has many properties in common with symbiotic stars, it's natural for us to suspect that it has experienced similar evolutionary episodes as occur in symbiotic stars. The study of symbiotic stars has connected them to barium stars, which are binaries with element overabundances of carbon and s-process elements attributed to mass transfer (McClure et al. 1980). The similarities of orbital elements between symbiotic stars and Ba stars (as well as CH stars and Tc-poor S stars) make it natural to expect similar enrichment evidence in symbiotic stars as in barium stars. However, no such element overabundances have been found in symbiotic systems except for yellow symbiotics. The few yellow symbiotic stars discovered so far have proven to be either carbon-rich or enhanced in s-process elements or both (Schmid & Nussbaumer 1993; Schmid 1994; Smith et al. 1996, 1997; Pereira & Proto de Mello 1997; Pereira et al. 1998; Smith et al. 2001). This suggests a mass transfer episode in symbiotic stars in the past, when the now degenerate component is still a TP-AGB (thermally pulsating asymptotic giant-branch) star. Material that has undergone nuclear processing in the helium burning shell is transfered from the TP-AGB star to its companion.

Given the strong link between barium stars and yellow symbiotics, we attempted to find a chemical peculiarity in Me 1-1. The absorption at 6495 Å is remarkably strong in Me 1-1, which is attributed to a blend of absorption by Ba II, Ca I and Fe I. This strong absorption feature might suggest the possible overabundance of the s-process element Ba in Me 1-1. However we failed to detect significant absorption of Ba II at 4554 Å, 5854 Å and 6142 Å and it is the 4554 Å line that normally identifies this class of star. Because of the low resolution of our spectra, it is difficult to estimate the contribution of Ca I and Fe I to the strong absorption blend at  $\lambda6495$. Higher resolution spectra of the cool stellar component are needed for a detailed analysis of its heavy element abundance. Since Me 1-1 is likely a binary system, accurate monitoring of its radial velocity may prove to be fruitful.

Several PNe have been known to contain close binary central stars, e.g., A 41, NGC 2346, A35 (Bond 1995). Bond et al. (2003) reported the discovery of a young Ba star WeBo 1 in a ringlike PN and interpreted this to have resulted from mass transfer in a binary system of almost equal mass. Both WeBo 1 and Me 1-1 are assumed to be binaries of a cool stellar component and a hot ionization source surrounded by a nebula. If Me 1-1 is proven to be barium-rich, it is likely that Me 1-1 shares a similar formation and evolutionary development as for WeBo 1. Further studies of these systems will no doubt lead to a better understanding of possible evolutionary connection between symbiotic stars, barium stars and PNe, mass transfer and element abundance enhancement in close binary systems and the origin of X-ray emission detected in symbiotic systems.

Although Me 1-1 shares many properties in common with symbiotic stars, it has some differences. First of all, the nebular density deduced for Me 1-1, about  $10^4~{\rm cm^{-3}}$, is much lower than found in a typical symbiotic nebula, which is normally in the range of 106 to  $10^9~{\rm cm^{-3}}$. On the other hand, optical density-diagnostic lines such as the [S II], [Cl III] and [Ar IV] doublets all have a critical density much lower than  $10^6~{\rm cm}^{-3}$, thus their emission will be strongly suppressed in dense clumps of densities in excess of  $10^6~{\rm cm}^{-3}$. These lines are therefore incapable of revealing a dense symbiotic nebula even if it exists in Me 1-1. For example, from a detailed analysis of high critical-density [Fe  III] forbidden lines, Zhang & Liu (2002) demonstrated that there was a dense emission core with ${\rm log}~N_{\rm e} \sim 3\times 10^6$ cm-3 embedded at the centre of the extreme bipolar PN Mz 3. Yet a traditional plasma diagnostic analysis utilizing the [S II], [Cl III] and [Ar IV] doublet ratios yielded a very low $N_{\rm e}$ of approximately $5\times 10^3$ cm-3. Clearly emission of these diagnostic lines is dominated by the surrounding diffuse nebula. A similar result has been found in the peculiar bulge PN M 2-24 (Zhang & Liu 2003). Thus the possibility of a dense symbiotic nebula embedded in the low-$N_{\rm e}$ionized region of Me 1-1 cannot be completely ruled out. Secondly, from the ${\rm H}\beta$ flux and distance to Me 1-1, we estimate a total mass of 0.2 $M_\odot$ for the ionized gas in Me 1-1 (cf. Eq. (4.37) in Kwok 1999), which is much higher than for a typical symbiotic nebula and is difficult to have been produced from a wind of the K giant. However, again this mass refers to the diffuse nebula, rather than the hypothetical symbiotic star that may possibly be embedded in Me 1-1.

Acknowledgements
We are grateful to Y. Zhang and Y. Liu for their help with the preparation of this paper. We thank Dr. R. Tylenda for useful comments on the possible nature of Me 1-1. The work is partly supported by Beijing Astrophysics Center (BAC).

References

 
Copyright ESO 2004