A&A 422, 665-673 (2004)
DOI: 10.1051/0004-6361:20047056

On the irradiated stellar atmospheres in close binary systems: Improvements and uncertainties

A. Claret

Instituto de Astrofísica de Andalucía, CSIC, Apartado 3004, 18080 Granada, Spain

Received 12 January 2003 / Accepted 30 March 2004

Abstract
The irradiation of cool stellar atmospheres is reanalyzed using a modified version of the UMA (Uppsala Model Atmosphere) code which incorporates two improvements concerning 1) the spacial resolution (18 $\mu$ points instead of only 6 adopted previously) and 2) adopting modern atmosphere models to simulate hot companions. The implementation of a better spacial resolution is shown to be essential to describe with accuracy the center to limb variation of the specific intensities. It is also shown that only by adopting such a resolution (or a higher one) it is possible to detected and quantify the limb-brightening with confidence.

As in the case of standard (non-irradiated) plane-parallel models, the Least-Squares method applied to the series expansion for the specific intensity introduced by Claret (2000) is shown to be the best procedure to derive the limb-darkening coefficients for illuminated atmospheres producing very small scattering and conserving the flux accurately.

Since UMA does not work for wavelengths shorter than 1500 Å, the introduction of hot models to simulate the external fluxes introduces severe uncertainties in the model of irradiation. These uncertainties were ignored in previous works using the same code and similar conditions of irradiation. Other limitations of the model of irradiation, such as the suitability of applying the spherical symmetry instead of the plane-parallel approximation, are also discussed.

Key words: stars: atmospheres - stars: binaries: eclipsing

1 Introduction

The mutual irradiation of stars in close binary systems has been investigated since the first decades of the last century. From the observational point of view, Dugan (1908) and Stebbins (1911) were the first to report on the phenomenon, known generically as the reflection effect. On the other hand, Eddington (1926) and Milne (1926) initiated the theoretical study by showing that the albedo is unitary for an envelope in radiative equilibrium. Chandrasekhar, in a series of papers (1945, 1947, 1950), also investigated the physical conditions of an illuminated atmosphere and derived an exact solution in the approximation of a grey atmosphere. Geometrical improvements were introduced by Russel (1949) and Kopal (1954) to take into account the finite size of the binary components. The use of elaborated stellar atmosphere codes to investigate the limb-darkening coefficient (LDC) in irradiated atmospheres is relatively recent. Contrary to some authors' affirmation that only UMA was used to investigate the reflection effect, Buerger (1972) implemented the contribution of an external radiation field to the resulting intensities and fluxes in the ATLAS code. Rucinski (1969) found that the albedo for stars with deep convective envelopes is about 0.5 while Claret (2001), using a new numerical method which combines interior, envelope, and atmosphere models, computed the bolometric albedo as a function of the external flux, the geometry and the evolutionary status of the irradiated stars. Kirbiyik (1982) showed that the circulation currents caused by the irradiation may even penetrate into the non-irradiated hemisphere.

Concerning the limb-darkening of irradiated atmospheres, Buerger (1972) analyzed the effects of irradiation on the specific intensity distribution using an early version of the ATLAS code but, unfortunately, no quantitative results were given. Interesting papers have been published by Peraiah (1982, 1983a,b) and Peraiah & Rao (1983a,b). Although their atmosphere models were not sophisticated, they concluded that the limb-darkening for irradiated atmosphere models with spherical symmetry is different from that using the plane-parallel approximation. Giménez & Claret (1989) and Claret & Giménez (1990) used a modified version of the UMA code (Nordlund & Vaz 1990; see also Gustafsson et al. 1975) to investigate the changes in the limb-darkening of an illuminated atmosphere caused by irradiation. The authors found that, for the adopted input physics, the intensity distribution tends to be uniform under the effects of irradiation. Later, Claret & Giménez (1992) modified the code to study the albedo, the increase of the effective temperature and the change of the position of an irradiated star in the HR Diagram due to an extra radiation field. Alencar & Vaz (1999) investigated the influence of irradiation on the limb-darkening using a similar version of the same code by adopting the Flux Conservation Method to compute the LDCs, but taking into account only six emergence points.

In the present paper, we try to improve the treatment of the intensity distribution of an irradiated atmosphere concerning limb-darkening. In particular, we introduce a non-linear law which is able to describe with accuracy the intensity distribution and that simultaneously leads to the flux conservation with high accuracy (see Claret 2000). In Sect. 2 we summarize some aspects of the physics of the irradiation. Section 3 is dedicated to a preliminary comparison between the two usual methods to obtain the LDC: the Least-Squares (LSM) and the the flux conservation (FCM) method. The discussion of the results and the limitations of the present model of irradiation are presented in Sects. 4 and 5.

2 Physics of the irradiation: Changes in the atmosphere code

The implementation of irradiation in stellar atmosphere codes has been discussed in some of the papers quoted in the Introduction, so here we only review its basic aspects. A modification at the upper boundary condition is needed to consider the presence of an infalling radiation field: the intensity at the optical depth $\tau$ = 0 will depend on the nature of the external flux as well as on the angle of irradiation. As a boundary condition, the bottom of both hemispheres - the standard and the irradiated one - should present the same physical conditions since they represent the same star. Trial models, taking into account the external fluxes, are generated and their pressure-temperature relationships are then compared to those of the non-irradiated model. The correct irradiated model is obtained when the boundary condition is fulfilled. This is done by iteration. With the present version of the UMA code we can simulate the irradiation of a cool atmosphere by a cool or moderately hot companion.

The relation between the bolometric albedo A, the effective temperature of the model without irradiation $T_{\rm eff}$ and the effective temperature of the irradiated model Th is

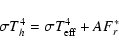\begin{displaymath}\sigma T_h^4 = \sigma T_{\rm eff}^4 + A F_r^* \end{displaymath} (1)

where Fr* is the radial external flux which depends on the effective temperature of the irradiating star T*, on the apparent radius r, and on the cosine of the incidence angle $\nu$, that is, $F_r^* = \sigma$ T*4 r2$\nu$. The simulation of irradiation is performed in 4 discrete directions: $\nu$ = 0.07, 0.33, 0.67, 0.93. This means that after irradiation, four independent models are necessary to describe the resulting perturbed atmosphere.

In a previous paper (Claret & Giménez 1990) as well as in the paper by Alencar & Vaz (1999), only six points of the emergence angle $\mu$ were used which is, of course, a very important limitation. In the present work we will show that the inclusion of extra $\mu$ points is essential to draw more definitive conclusions. One expects that the behavior of a perturbed atmosphere be more complex than that of a standard one and therefore, a more accurate sampling of the disk is needed.

A second modification with respect to the mentioned above papers is the introduction of new atmosphere models to simulate hot irradiating stars. Until now the models by Kurucz (1979) were adopted. Here we adopt the updated ones provided by the same author (Kurucz 1993). The Kurucz models are computed for a more extensive set of wavelengths than in UMA. As commented in Claret & Giménez (1992), the interpolation in the ATLAS fluxes to be used by the UMA code as source stars may introduce some loss of flux in both extremes of the spectrum, but mainly in the ultraviolet where the UMA set does not have many points (i.e. $\lambda_{\min}$(UMA) = 1533 Å, while $\lambda_{\min}$(ATLAS) = 91 Å). In this way, systematic errors are introduced in the effective temperatures T* of the irradiating star if those models are used to simulate irradiating stars. An additional complication arises from the imbalance of energy in that spectral region. The repercussion of these limitations and modifications will be analyzed in the next sections.

3 A preliminary comparison between the least-squares and flux conservation methods

Recently Claret (2000) introduced an approximation for the LDC of LTE atmospheres for ATLAS (Kurucz 2000) and PHOENIX models (Allard & Hauschildt 1995; Allard et al. 1997; Hauschildt et al. 1997a,b). Both codes use the plane-parallel approximation. The LDC law is written as a series:

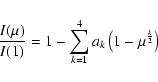\begin{displaymath}{I(\mu)\over{I(1)}} = 1 - \sum_{k=1}^{4} {a_k} \left(1 - \mu^{k\over{2}}\right) \end{displaymath} (2)

where I(1) is the specific intensity at the center of the disk, $\mu$ = $\cos(\gamma)$, and $\gamma$ is the angle between the line of sight and the emergent flux. Before the introduction of Eq. (2), the most commonly adopted approximations were:

Linear

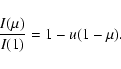\begin{displaymath}{I(\mu)\over{ I(1)}} = 1 - u(1 - \mu). \end{displaymath} (3)

Quadratic

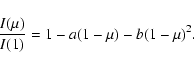\begin{displaymath}{I(\mu)\over{I(1)}} = 1 - a(1 - \mu) - b(1 - \mu)^2. \end{displaymath} (4)

Square root

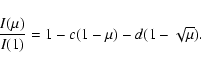\begin{displaymath}{I(\mu)\over{I(1)}} = 1 - c(1 - \mu) - d(1 - \sqrt{\mu}). \end{displaymath} (5)

Logarithmic

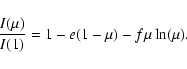\begin{displaymath}{I(\mu)\over{I(1)}} = 1 - e(1 - \mu) - f\mu\ln(\mu). \end{displaymath} (6)

The fact that we now have four coefficients instead one or two does not imply a large cost of CPU time and they can be easily implemented in the codes of light curve synthesis or in other fields where LDCs are needed. The improvements due to Eq. (2) are not only linked to the increase of the polynomial degree: we performed numerical experiments to test other combinations and Eq. (2) turned out to be the best one.

A good limb-darkening law must be able to reproduce very accurately the intensity distribution across the stellar disk and must lead to flux conservation. In this way, a compromise between an accurate description of the intensities and the flux calculation is required. Such requirements are only possible through the Least-Squares Method by using an adequate law. The LDC law must be really adequate. If very simple laws are used, the fluxes resulting from the LSM are not conserved within acceptable numerical uncertainties. Opposite to this, the LDC as derived from the FCM, once obtained, cannot be adjusted to improve the corresponding $\sigma$s.

Equation (2) presents several advantages with respect to others approximations:

1.
as mentioned by Díaz-Cordovés (1990), the square root approximation is marginally more appropriate for hot stars while the quadratic approximation is better for colder ones. By adopting Eq. (2), a single law is able to predict the intensity distribution for the whole HR Diagram simultaneously;
2.
it is capable of reproducing very accurately the intensity distribution with very small associated $\sigma$s;
3.
the flux, as computed using such a law, is conserved within a very small tolerance (see below);
4.
such a law is applicable with success to different filters or monochromatic and bolometric calculations;
5.
it is also applicable to different chemical compositions, log g and microturbulent velocities;

6.
it was applied with success even for spherically symmetric atmosphere models (Claret & Hauschildt 2003).
While the LSM-Eq. (2) prescription implies that the flux is conserved within a very small tolerance, the FCM apparently solves the flux conservation problem by definition. Of course, the flux must be preserved but not at the expense of information of how the specific intensities are distributed over the disk, particularly near the limb. The accuracy of the flux calculation depends on the adopted integration method, on the position and number of points of the emergent intensities and on other numerical details. Examples of such accuracy limitations are discussed by Wade & Rucinski (1985) who used the FCM. These authors reported differences as large as 2 per cent or more between their fluxes (integrating the Kurucz intensities) and those provided directly by the Kurucz (1979) models. Even using self-consistent calculations, the accuracy of the flux calculation is limited too. To quantify this, extensive calculations of the fluxes were performed for several values of log gand log  $T_{\rm eff}$. These computations were carried out adopting the complete solar abundance grid by Kurucz (2000). Varying the position and the number of points of the emergence angle, it was verified that the numerical accuracy of the actual flux depends on this. Typical differences are of the order of a few per cent. Such numerical limitations are often much larger than the differences we have found between the actual fluxes and those resulting from the combination LSM-Eq. (2) applied to irradiated atmospheres (18 $\mu$points). As the calculation of the LDC following the FCM recipe depends on flux calculations, it will also be affected by such numerical tolerances, in addition to the problems which will be pointed out in the next paragraph. Therefore, the requirement of flux conservation should be considered within the above limitations. Of course, the differences between both fluxes, say, the actual one and that computed by adopting the limb-darkening law, must be as small as possible.

The main problems inherent to any limb-darkening law that adopts the FCM are:

1.
It is known that the linear approximation is not adequate to describe the specific intensities (see for example Díaz-Cordovés et al. 1995; Claret 1998). Therefore, bi-parametric laws are often introduced. When the FCM is applied to these laws an extra condition, besides the flux conservation, is needed. This extra condition is arbitrary. Moreover, there is an additional arbitrariness since each FCM user imposes his own condition, that is, the corresponding LDC is not a one-valued function. The grade of arbitrariness will increase if more terms are introduced in the limb-darkening law.
2.
The intensity distribution is not well represented and the associated scattering is high. This characteristic is more pronounced near the border of the stellar disk which is obviously very important in eclipsing binary investigations. The use of the LDC, as derived from the FCM, may introduce severe errors in the calculation of the light variations during the eclipses.
3.
It does not give a priori the best law (linear or non-linear) since for all of them the flux is conserved. The users of the FCM must use the $\sigma$ criterion, or a similar one, in order to select the best approximation. Note that such users do not use the cited criterion when they compare quantitatively their $\sigma$s with those obtained through LSM.
4.
No direct information on how the intensities are distributed over the stellar disk is really used to derive the LDC. This is done only through integrations.

5.
As mentioned before, the concept of flux conservation should be taken with care given the influence of the numerical conditions of the integration ${\int I(\mu)\mu {\rm d}\mu}$. It is interesting to note that Alencar & Vaz (1999), who adopted the FCM as their basic tool, only use four points to compute the flux (the points $\mu$ = 0.5 and $\mu$ = 1.0 have zero weight).
As commented above, the limb-darkening law as expressed by Eq. (2) has been already tested in several situations for non-irradiated models. It works very well for different effective temperatures, local gravities, metallicities and microturbulent velocities. The global results are very good for any passband as well as for monochromatic calculations and the $\sigma$s are around 1000 times smaller than those associated with the FCM formalism (Claret 2000, 2003). Since the LSM-Eq. (2) combination shows such a versatility, we decided to apply it to the case of irradiated models as well.

4 Discussion

Before dealing directly with irradiated models, we have checked the modifications we have introduced in the code to increase the number of the emergent angles. We performed calculations for several models adopting 18 $\mu$ points (without irradiation) and after comparison with other atmosphere models concluded that the agreement between the respective models was acceptable, and perfectly within the expected differences due to the different input physics and numerical methods used in the respective codes.

We performed bolometric, monochromatic and passband ( ${\it u v b y U B V R I J H K}$) calculations of LDCs for some irradiated models. The models were selected in such a way that cold (3500 K) and moderately cold models (6500 K) are irradiated by moderately cold (7000 K) and moderately hot source stars (15 000 K). The simulations were carried out adopting some combinations of the above values. However, there are two implicit limitations to the present theoretical model of irradiation. The first one is related to the way the external flux is introduced in the atmosphere equations. The functions $u_{k,j} = {1\over 2}\left[I(\tau_k,\mu_j) + I(\tau_k,-\mu_j)\right]$ and $v_{k,j} = {1\over 2} \left[I(\tau_k,\mu_j) - I(\tau_k,-\mu_j)\right]$are expanded in Taylor series to obtain $I(0,\mu_j)$. This approximation limits the magnitude of the external bolometric flux.

But there is another constraint to the application of the present model of irradiation which is related mainly to the ultraviolet flux of the irradiating star. The ratio of the ultraviolet fluxes depends strongly on the ratio ( $T^*/T_{\rm eff})^4$. As UMA is specifically developed for cool stars, one must use other codes to simulate a hot irradiating star, as for example those derived from ATLAS. This not only affects the effective temperature of the irradiating star as discussed previously but also the ultraviolet imbalance since the shorter wavelength in UMA is 1533 Å. Even if we adopt a UMA model for the irradiating star to avoid this imbalance, an additional imbalance remains since the incident energy with wavelengths shorter than 1533 Å  is not taken into account. Therefore, the resulting specific intensities in the ultraviolet are less reliable than those corresponding to other spectral regions. In addition, in some cases, the monochromatic ultraviolet flux of the irradiating stars can be a few orders of magnitude larger than that of the irradiated star. This means that not only the bolometric flux ratios must be used as a check of the applicability of the perturbed equations but also the monochromatic ones.

The specific intensity for a generic band a is given by

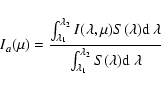\begin{displaymath}I_{a}(\mu) = {\int_{\lambda_1}^{\lambda_2} { I(\lambda,\mu) S... ...ver\int_{\lambda_1}^{\lambda_2} { S(\lambda) {\rm d}~\lambda}} \end{displaymath} (7)

where I($\lambda$,$\mu$) is the monochromatic specific intensity and S($\lambda$) is the response function which considers the terrestrial atmospheric transmission, filter transmission curves, detector sensitivity and reflection from the aluminum coated mirror. It is important to ensure that the sensitivity of the detector is adequate for each passband. Old detectors tend to be problematic, mainly for the largest and smallest effective wavelengths (for example, Alencar & Vaz 1999 used the 1P21 curve). More details on the calculation of such integrals and the response function can be found in our previous papers. The monochromatic and bolometric calculations follow their classical definition. The set of wavelengths used in the UMA code is composed of 368 wavelengths between 1533 and 124 323 Å.

4.1 Limb-darkening or limb-brightening?

Until now, works on irradiated atmospheres adopting the UMA code considered only 6 $\mu$ points with $\mu_5 = 0.33$ and $\mu_6 = 0.07$, that is, the limb was not well covered (in some modern codes the minimum value of $\mu$ is between 0.005-0.001). This is one of the reasons why reliable evidence of limb-brightening in Claret & Giménez (1990) was not detected and it was only reported as a tendency of the intensity distribution of an irradiated atmosphere to become uniform. The irradiated atmospheres presented in Figs. 3-6 by Claret & Giménez (1990) are still limb-darkened, although an increase of the specific intensity near the limb can easily be seen. The limbs of those irradiated models are brighter than those of non-irradiated ones with the same net flux, but the same also happens to the other parts of the disk which leads to a more uniform intensity distribution. Brueger (1972) found a similar effect (see his Fig. 3). On the other hand, limb-brightening is a phenomenon that appears even in standard atmosphere models (in the sense that no infalling radiation is present). Wade & Rucinski (1985) and Claret (2000) detected it for some models generated with ATLAS (and also with PHOENIX) but this is probably caused by temperature inversions which are not realistic.

To detect real limb-brightening in irradiated atmospheres a good sampling of the stellar disk is necessary. The limb in particular must be well covered. Let us investigate how the number and position of the emergence angles affect the intensity distribution. Figure 1 shows the intensity distribution for irradiated models with $T_{\rm eff} = 5300$ K, log g = 3.5, T* = 12 000 K, log g* = 4.0, $\nu = 0.67$ for r = 0.10, 0.20, 0.30 (filter b). The continuous line indicates the new actual intensities computed at 18 $\mu$ points while the asterisks indicate the 6 $\mu$points adopted previously. The inclusion of the 12 extra points is determinant to decide whether there is a darkening or brightening towards the limb. As we have mentioned in the last paragraph, the previous low $\mu$ resolution explains why such a phenomenon was not detected in the Claret & Giménez (1990) paper for similar conditions of irradiation. This reveals that the analysis of the intensity distribution based on a few $\mu$ points - whatever the numerical method to derive them - should be taken with extreme caution. Some results by Alencar & Vaz (1999), who used only 6 $\mu$ points, are interpreted as limb-brightening; see for example the model for rh=0.26 in their Fig. 3. The limb-brightening they detected in this case is more due to the bad FCM fitting (specially for the smaller $\mu$s) than to the location of the points themselves. This tendency is one of the consequences of the failure of the FCM predictions particularly for regions near the border of the disk, as already noted by Claret (2000) (Fig. 6, first frame; see also Fig. 3 of the present work). Therefore, there is an additional criticism for the use of the FCM: in some cases it predicts limb-brightening where it does not exist while in other cases it fails to detect limb-brightening when it is present. We will see in the next Section how this method introduces systematic and severe errors in the matching of the intensities of an irradiated atmosphere.


  \begin{figure} \par\includegraphics[height=8cm,width=7cm,clip]{0056fig1.eps} \end{figure} Figure 1: The effect of irradiation on the specific intensity distribution for models with log g = 3.5, $T_{\rm eff} = 5300$ K irradiated by a model with T* = 11 568 K, log g* = 4.0 as a function of the apparent radius r. Note that the if only six points are used (asterisks), limb-brightening is no longer detected. Filter b.
Open with DEXTER

4.2 LSM ${\times }$ FCM: Irradiated models

Although the versions of the code used in the previous papers are similar to the present version, there are a few basic differences. First, the irradiating models are not updated since the fluxes given by Kurucz (1979) were adopted. We introduce more recent models by Kurucz for the irradiating sources to homogenize the sample of the external radiation fields. Alencar & Vaz (1999) do not mention the systematic errors introduced in the effective temperature if an ATLAS model is used to simulate the irradiating star, nor do they mention the imbalance of energy in the ultraviolet. As we have seen in the last section, another important and serious limitation is that the calculations presented by these authors (as well as those presented in our previous papers on irradiation) were performed using only 6 $\mu$ points over the disk.

The capability of the numerical methods to derive the LDC and of the implementation of our modifications can be checked by inspecting the properties of some irradiated models. With these models, it will be possible to test under which conditions real limb-brightening appears and how the LDCs computed following the LSM and FCM prescriptions describe the intensity distribution. The characteristics of such models are given in Table 1.

Table 1: Irradiated model parameters.


  \begin{figure} \par\includegraphics[height=10cm,width=8.8cm,clip]{0056fig2.eps} \end{figure} Figure 2: Monochromatic specific intensities for some irradiated models. The full lines represent the actual intensities while the asterisks denote the fitting obtained using the LSM-Eq. (2) prescription. The FCM calculations were carried out adopting the logarithmic approach (crosses). The irradiation parameters are indicated in the figure.
Open with DEXTER


  \begin{figure} \par\includegraphics[height=10cm,width=8.8cm,clip]{0056fig3.eps} \end{figure} Figure 3: The relative difference $\Delta I\over {I}$ = $[I({\rm model}) - I({\rm fitting})] \over {I({\rm model})}$ near the border of the disk as a function of the logarithm of the wavelength. The dashed line denotes the results obtained using Eq. (2) and adopting the LSM. The continuous line represents the FCM results for the logarithmic specific intensity approximation.
Open with DEXTER

In order to evaluate the goodness of the matches, we introduce the merit function

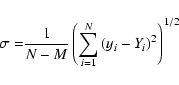\begin{displaymath}{\sigma=} {1\over{N-M}}\left(\sum_{i=1}^{N} \left( {y_i - Y_i}\right)^2\right)^{1/2} \end{displaymath} (8)

where yi is the model intensity at point i, Yi is the fitted function at the same point, N is the number of points, and M is the number of coefficients to be adjusted. For the FCM, we adopt the quadratic and logarithmic specific intensity approximations. As we have found for non-irradiated models (Claret 2000, 2003) the quality of the LSM-Eq. (2) matches are always superior compared to those resulting from the FCM fits. In some spectral ranges the $\sigma$s corresponding to the LSM-Eq. (2) are about 100-1000 times smaller than those obtained from the FCM. Of course, one could argue that such a comparison was made in unequal conditions since the LDCs computed by the FCM are obtained using only two parameters. We therefore also carried out some tests under equal conditions, that is, adopting two parameters. It turns out that the bi-parametric approximation using the LSM gives better matches than the FCM results whatever the adopted LDC law (quadratic, root square or logarithmic). However, the Eq. (2)-LSM performance is always superior for any of the quoted cases. Of course, the disagreement between the actual intensities and those fitted using the FCM is even worse if only six $\mu$ points are used. Figure 2 illustrates the situation in more detail. In that figure, the behavior of an irradiated model (see the two panels to identify the conditions of irradiation) are shown for two wavelengths, 1533 and 4707 Å. As we remarked before, the specific intensities at shorter wavelengths resulting from the FCM with a logarithmic LDC law (crosses) are not entirely reliable (note that the limb is almost 6 times brighter than the center of the disk). The LSM-Eq. (2) prescription (asterisks) on the other hand is capable of reproducing them very well even when dealing with such perturbed intensities. The situation is very similar for longer wavelengths (see second panel).

The function $\sigma$, as defined in Eq. (8), is a kind of average of the differences between the models and the fits over the entire stellar disk. The behavior of the intensity distribution near the border of the disk is crucial to compute the light variations when the stellar disk is scanned during eclipses. Therefore, it is also interesting to study how the LSM and FCM results compare near the limb. In Fig. 3 we show the relative differences in the intensities obtained using the LSM-Eq. (2) prescription and those following from the FCM (logarithmic case) as a function of the wavelength. Again, the quality of the LSM fitting is superior to the case of the FCM whatever the adopted LDC law approximation. For the LSM fitting the relative differences of the intensity near the border of the disk are almost zero. On the contrary, for the FCM, the differences are large, especially at shorter $\lambda$s.


  \begin{figure} \par\includegraphics[height=13.3cm,width=11.8cm,clip]{0056fig4.eps} \end{figure} Figure 4: The specific intensity distribution for irradiated models in the case of filter b. The conditions of irradiation are indicated inside each frame. Continuous lines denote the actual intensities, while asterisks and crosses represent the Eq. (2)-LSM and FCM (logarithmic) matches, respectively.
Open with DEXTER

Let us now examine the behavior of the passband intensities of the irradiated models. Figure 4 displays how the intensities are distributed over the disk for the conditions of irradiation indicated in the figure. The vertical bars indicate the position of the $\mu$ points used by Alencar & Vaz (1999). Again, if only 6 points are used, important information on the intensity distribution is lost, especially when $\mu$ < 0.4. Furthermore, it should be pointed out that even if we consider 18 $\mu$ points, the FCM will not give a good fitting, as indicated by the crosses.

As a final check of the LSM-Eq. (2) prescription, we plot in Figs. 5 and 6 the monochromatic and passband ratios between the actual flux and the flux computed using our new limb-darkening law (F'/F). By inspecting both figures we can conclude that the flux obtained using our new approximation is conserved to a high degree of accuracy, as required. This is a consequence of the goodness-of-the-fitting and is not imposed a priori. In the ultraviolet, the irradiated models are very perturbed and less reliable, so that the fitting at those points is less good (about 0.5 percent of deviation). Even so, the new law is able to derive the flux with an acceptable accuracy. Note that in Fig. 5, for a fixed irradiation condition but for increasing  $T_{\rm eff}$ the deviations decrease, partly due to the smaller ultraviolet ratio and partly due to the decrease of the relative importance of the ultraviolet loss. The largest scatter is found only at the 9-10 first wavelengths (asterisks in Fig. 5); for larger $\lambda$s, abs[F'-F] is smaller than 0.001. In this way, the two imposed constraints are fulfilled for any limb-darkening law: the intensity distribution is accurately described over the entire disk and simultaneously, the resulting flux is conserved within a small tolerance limit.

5 Model limitations and future perspectives

The new LDC law we have introduced is able to match the intensity distribution of the irradiated models much better than those that make use of the FCM. We have found that the ratio between the actual fluxes and those computed with this new law is very close to 1, which indicates a very good accuracy. Although the global results seem to be very reliable, some cautionary remarks should be made. The general model of irradiation presents some limitations that are not considered by other authors. For example, the set of wavelengths in the UMA code is very limited with respect to modern models not only concerning the number of $\lambda$ points, but also concerning the inferior and superior limits of $\lambda$ and the distribution of the points. As we have seen, one of the consequences of these limitations is that if we use more modern models to simulate the infalling radiation, the flux is not correctly taken into account due to the loss of information at shorter wavelengths. There is, however, an important additional problem: as the $\lambda_{\min}$ for UMA is 1533 Å, the code is not able to balance correctly the infalling radiation in this spectral region. It is true that if we use an UMA model as the source star, the problem of the wavelength set no longer raised, but the loss of information in the far ultraviolet still remains. Even if the radial relative flux F*r is small, the ratio of the monochromatic fluxes may be very high in the ultraviolet. We emphasize this point since the satellite observations in the ultraviolet are important to determine stellar parameters in close binary systems for which the irradiation effect is notorious. All this puts severe limits on the results obtained for shorter wavelengths.


  \begin{figure} \par\includegraphics[height=10cm,width=8.8cm,clip]{0056fig5.eps} \end{figure} Figure 5: The monochromatic F'/F test for irradiated models.
Open with DEXTER


  \begin{figure} \par\includegraphics[height=10cm,width=8.8cm,clip]{0056fig6.eps} \end{figure} Figure 6: The passband F'/F test for some irradiated models.
Open with DEXTER

Another significant improvement which can be introduced are wider and more recent opacities tables since UMA calculations are limited to a narrow range of effective temperatures.

A third point is the probable presence of circulation currents. Their presence and how much they can penetrate into the "dark" hemisphere may change the intensity distribution as well as other atmospheric parameters.

A final question is whether the intensities near the stellar limb are reliable. The effects of sphericity should be investigated as well. Preliminary results by Peraiah & Rao (1983) suggest that some changes in the intensity distribution may occur when spherical symmetry is used instead of the plane-parallel approximation when an external flux is considered. Results based on modern models that apply spherical symmetry indeed indicate that the profile of the intensities is very different from that derived from the plane-parallel approach: the fall of the intensities near the limb are steeper in the case of spherical geometry (Orosz & Hauschildt 2000; Claret & Hauschildt 2003).

An estimate of the importance of some of the above limitations on the LDC of irradiated atmospheres is currently under investigation. Also, we are preparing an extensive grid of irradiated models for reliable orbital parameters which will be published elsewhere.

Acknowledgements
I am grateful to B. Willems and J. Orosz, who helped to improve the paper. The Spanish DGYCIT (PB98-0499) is gratefully acknowledged for its support during the development of this work.

References

 
Copyright ESO 2004