A&A 422, 591-602 (2004)
DOI: 10.1051/0004-6361:20047001
Dust-to-gas ratios in the Kepler supernova remnant
M. Contini1,2
1 - Instituto de Astronomia, Geofísica e Ciências
Atmosféricas - USP, Brazil
2 -
School of Physics and Astronomy, Tel Aviv University, Tel Aviv
69978, Israel
Received 2 January 2004 / Accepted 31 March 2004
Abstract
A new method to evaluate the dust-to-gas ratios in the Kepler SNR
is presented. Dust emission in the infrared and bremsstrahlung
are calculated consistently, considering that dust grains are collisionally
heated by the gas throughout the front and downstream of both the expanding and the reverse shocks.
The calculated continuum SED is constrained by the observational data.
The dust-to-gas ratios are determined by the ratio of the dust emission bump and
bremsstrahlung in the infrared.
The shell-like morphological similarity of X-ray and radio emission, and of
images in H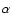 and in infrared wavelengths
confirms that both radio and X-ray emissions are created at the front of the expanding shock
and that dust and gas are coupled crossing the expanding and reverse shock fronts.
The results show that large grains with radius of
and in infrared wavelengths
confirms that both radio and X-ray emissions are created at the front of the expanding shock
and that dust and gas are coupled crossing the expanding and reverse shock fronts.
The results show that large grains with radius of  1
1 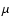 m with dust-to-gas ratios <4
m with dust-to-gas ratios <4 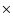 10-3 survive sputtering and are heated to a maximum temperature of 125 K
downstream of the shock expanding outwards with a velocity of about 1000
10-3 survive sputtering and are heated to a maximum temperature of 125 K
downstream of the shock expanding outwards with a velocity of about 1000
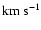 .
The high velocity shocks become radiative for dust-to-gas ratios >10-3.
Such shocks do not appear in the NE region, indicating that dust grains
are not homogeneously distributed throughout the remnant.
Smaller grains with radius of about 0.2
.
The high velocity shocks become radiative for dust-to-gas ratios >10-3.
Such shocks do not appear in the NE region, indicating that dust grains
are not homogeneously distributed throughout the remnant.
Smaller grains with radius of about 0.2 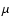 m and dust-to-gas ratios
of
m and dust-to-gas ratios
of  4
4 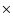 10-4 are heated to a maximum temperature of
10-4 are heated to a maximum temperature of  50 K
downstream of the reverse shock corresponding to velocities of about 50
50 K
downstream of the reverse shock corresponding to velocities of about 50
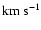 .
A maximum dust mass <0.16
.
A maximum dust mass <0.16 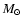 is calculated.
is calculated.
Key words: ISM: supernova remnants - X-rays: stars - shock waves - ISM: individual objects: Kepler SNR
Since the first identification by Baade (1943)
the remnant of the Kepler supernova (SN) which exploded in 1604,
has been observed in the different wavelength ranges.
Van den Bergh & Kemper (1977) studied
brightness variations and proper motions of the filaments in the supernova remnant (SNR).
Spectrophotometry data
in the spectral range 3700-10 500 Å of the bright western knots
were presented by Dennefeld (1982).
Observations in the optical range for single bright knots
were obtained by Leibowitz & Danziger (1983) and by Blair et al. (1991).
Data in the X-ray (e.g. Hughes 1999) and in the radio (e.g. DeLaney et al. 2002) ranges were also recently presented.
Morgan et al. (2003) provided SCUBA data of the continuum in the far infrared (450 and 850 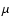 m), so the information about the infrared (IR) emission is rather complete.
m), so the information about the infrared (IR) emission is rather complete.
The main results obtained from the interpretation of the line spectra (Blair et al. 1991)
are, in particular, that the emitting gas has high densities (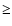 1000
1000
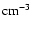 ), that the N/H relative abundance is
), that the N/H relative abundance is  3.5 times higher than solar, and that H
3.5 times higher than solar, and that H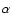 line profiles display both broad and narrow components. A distance of 5 kpc was consistently determined.
line profiles display both broad and narrow components. A distance of 5 kpc was consistently determined.
The origin of the Kepler SNR emitting features is explained by
the interaction of the high velocity ejecta with the ambient
medium (Decourchelle & Pretre 1999) and is very similar to that
found for other SNRs, e.g. Cassiopeia A (Chevalier & Oishi 2003), namely,
"that the observed shock wave positions and expansions can be interpreted in a model of supernova
interaction with a freely expanding stellar wind''. The collision with ambient matter leads to the formation of two shock fronts: a shock propagating outwards throughout the circumstellar/interstellar medium and one
propagating in reverse throughout the ejecta in the direction opposite
to the propagation of the blast wave. The gas in
the knotty regions of Kepler SNR is ionized and heated to relatively high
temperatures (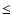 3
3  107 K) downstream of the shock which
expands with velocities of 1000-1500
107 K) downstream of the shock which
expands with velocities of 1000-1500
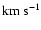 .
The reverse shock, on the other hand,
propagating with velocities of
.
The reverse shock, on the other hand,
propagating with velocities of  50
50
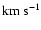 in the opposite direction,
leads to lower gas temperatures. The velocities are reduced by the density gradient of the ejected matter. The circumstellar origin of the optical emitting gas suggested that Kepler's SN was actually of Type Ib (Bandiera 1987).
in the opposite direction,
leads to lower gas temperatures. The velocities are reduced by the density gradient of the ejected matter. The circumstellar origin of the optical emitting gas suggested that Kepler's SN was actually of Type Ib (Bandiera 1987).
Very recently Morgan et al. (2003) addressed the problem of
dust in the Kepler SNR in terms of its total mass and its origin from a massive star.
They claim that dust formation in SNe is an important process, but dust
in SNRs has been detected in small quantities.
In this work we will use the method adopted by e.g. Contini & Contini (2003)
to calculate the dust-to-gas ratios in the starburst regions of luminous
infrared galaxies and by Contini et al. (2004) for Seyfert galaxies.
Namely, dust-to-gas ratios are calculated by modeling
the spectral energy distribution (SED) of the continuum in the optical-IR
frequency range.
At the shock front edge of the emitting nebulae, the gas is collisionally heated
to relatively high temperatures which depend on the shock velocity.
Dust and gas are coupled crossing the shock front,
mutually heating and cooling by collisions
(Dwek & Arendt 1992; Viegas & Contini 1994; Contini et al. 2004).
The temperature of the grains depends on the temperature of the gas and,
therefore, the maximum temperature of dust depends on the shock velocity (Contini et al. 2004). The observational data constrain the model which better explains both
the bremsstrahlung and reradiation by dust. Particularly,
the ratio between the dust radiation flux in the IR and bremsstrahlung
depends on the dust-to-gas ratio.
However, the modeling of the continuum SED must be cross-checked by the
modeling of the line spectra, which is strongly constraining.
In this paper I would like to find out the physical conditions in
the different regions of Kepler SNR, as well as the dust-to-gas ratios,
by consistent model calculations, which take into account the results of previous investigations.
The SUMA code (Viegas & Contini 1994; Contini & Viegas 2001, and references therein), which is adapted to the calculation of gas and dust spectra emitted downstream of a shock front, is adopted.
The general models are presented in Sect. 2. The models specifically calculated
for the Kepler SNR appear in Sect. 3.1. The comparison of the spectra with the data is discussed
in Sect. 3.2 and cross-checked by the fit of the continuum SED in Sect. 3.3.
Discussion and concluding remarks follow in Sect. 4.
The models result from numerical simulations with
the code SUMA that requires the following input parameters:
the shock velocity,  ,
the pre- shock density, n0,
the pre-shock magnetic field, B0,
the chemical composition of the gas, and a dust-to-gas ratio d/g by number.
The initial radius of the grains
,
the pre- shock density, n0,
the pre-shock magnetic field, B0,
the chemical composition of the gas, and a dust-to-gas ratio d/g by number.
The initial radius of the grains
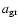 is also required.
The geometrical thickness of the cloud, D, is
an input parameter in the case of matter-bound models.
A plane-parallel symmetry is adopted with the calculations starting
at the shocked edge.
To perform the calculations a cloud is divided into a
number of slabs (up to 300) within which the
physical conditions are considered homogeneous.
The geometrical thickness of
the slabs is automatically calculated by SUMA
according to the gradient of the temperature downstream, in order to calculate
as smoothly as possible the distribution of the physical conditions throughout the
cloud. The first slabs in the
immediate post shock region show the maximum temperature which
depends on
is also required.
The geometrical thickness of the cloud, D, is
an input parameter in the case of matter-bound models.
A plane-parallel symmetry is adopted with the calculations starting
at the shocked edge.
To perform the calculations a cloud is divided into a
number of slabs (up to 300) within which the
physical conditions are considered homogeneous.
The geometrical thickness of
the slabs is automatically calculated by SUMA
according to the gradient of the temperature downstream, in order to calculate
as smoothly as possible the distribution of the physical conditions throughout the
cloud. The first slabs in the
immediate post shock region show the maximum temperature which
depends on  .
These slabs can be relatively large because
recombination coefficients are lower the higher the temperature.
The geometrical thickness of the slab closest to the shock front
is therefore determined by the model.
.
These slabs can be relatively large because
recombination coefficients are lower the higher the temperature.
The geometrical thickness of the slab closest to the shock front
is therefore determined by the model.
The spectra emitted from gas downstream of the shock front are calculated resolving a large number of equations, starting with those (e.g. Cox 1972)
for the conservation of mass, momentum, and energy, which lead to the
compression equation. Once the physical conditions are determined in a given slab,
the ionization equations for all the elements are resolved.
Then, the cooling rate is calculated from the energy losses by free-free,
free-bound, and line emission, as well as by collisional
heating of dust grains (Dwek & Arendt 1992).
The distributions of the electron temperature and of the electron
density downstream are thus obtained,
as well as the stratification of the different ions for the different elements.
The structure of the gas downstream is determined by the shock.
Near the shock front edge, the gas is collisionally heated
to relatively high temperatures (T 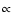
 2) which determine
the maximum of bremsstrahlung at higher frequencies.
Notice that both free-free and free-bound processes
are included in the calculation of the continuum.
2) which determine
the maximum of bremsstrahlung at higher frequencies.
Notice that both free-free and free-bound processes
are included in the calculation of the continuum.
Due to dust collisional heating by gas, the maximum
temperature of dust depends on the shock velocity, which therefore
determines the frequency of the reradiation peak in the infrared. An
analytical relation between the wavelength of the maximum intensity of
dust reradiation in the IR spectrum and shock velocity is given by
Draine (1981).
The grains are also heated by radiation. However, the only
radiation source in SNR is diffuse secondary radiation from the
hot slabs of gas, collisionally heated by the shock.
Diffuse radiation ionization rates prevail on collision rates only when
the gas temperature has dropped to T 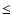 104 K.
Radiation heating of grains, which is consistently calculated
by SUMA, leads to low temperatures of the grains, <16 K
in high velocity clouds and <30 K in low velocity clouds.
104 K.
Radiation heating of grains, which is consistently calculated
by SUMA, leads to low temperatures of the grains, <16 K
in high velocity clouds and <30 K in low velocity clouds.
In models accounting for the shock, sputtering
changes the initial grain-size distribution, creating
a deficiency of small grains compared to their pre-shock
abundances (Dwek et al. 1996).
The grain size distribution depends on the shock velocity
and on the density of the medium.
The sputtering rate increases when the dust is in motion.
The present calculations account for the sputtering in the different zones
downstream of the shock front, so, starting with an initial pre-shock size,
the distribution of the grain sizes along the cloud is automatically derived by SUMA.
Generally, three populations of grains are adopted to fit
the average interstellar extinction curve: large grains of silicate
with radius
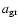
 0.01-1.0
0.01-1.0 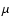 m, small graphite particles (
m, small graphite particles (
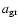 < 0.05
< 0.05 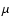 m),
and policyclic aromatic hydrocarbons (PAH) which correspond to single molecules of 25 carbon atoms
and clusters of 10-20 molecules. Small graphite particles
and PAH are underabundant with respect to the interstellar medium by
factors of 10 or more (Siebenmorgen et al. 1999).
Moreover, they are rapidly destroyed by sputtering across the shock front
(Contini & Contini 2003; Contini et al. 2004). So, only silicate grains are considered.
m),
and policyclic aromatic hydrocarbons (PAH) which correspond to single molecules of 25 carbon atoms
and clusters of 10-20 molecules. Small graphite particles
and PAH are underabundant with respect to the interstellar medium by
factors of 10 or more (Siebenmorgen et al. 1999).
Moreover, they are rapidly destroyed by sputtering across the shock front
(Contini & Contini 2003; Contini et al. 2004). So, only silicate grains are considered.
Depending on the temperature distribution in the cloud, bremsstrahlung may
contribute to the infrared continuum
(see, for instance, Contini & Viegas-Aldrovandi 1990, Fig. 2c).
The intensity of dust IR emission relative to bremsstrahlung depends on the dust-to-gas ratio.
Usually the dust contribution dominates in the far infrared range but in the near-IR, both processes may contribute to the continuum (see Sect. 3.3).
Finally, very seldom the line and continuum spectra of the galaxies can be reproduced by
single-cloud models; on the other hand, multi-cloud models are
generally required to explain the multiwavelength spectrum
and are obtained as a weighted average of the single-cloud models.
Multi-cloud models lead to IR bumps wider than black body curves.
The modeling of a spectrum consisting of only a few lines deserves
a further comment. In fact, it is worthwhile to consider it
only when such a spectrum belongs to a series of spectra observed in
neighbouring regions, for a certain object.
In this case, the input parameters
which are not likely to change in neighbouring regions,
e.g. relative abundances and the pre-shock magnetic field,
are determined from the spectra rich in number of lines,
while the shock velocity is roughly deduced from the line FWHM.
If the lines whose ratio depends on the density of the emitting gas are not observed, the pre-shock density can be roughly obtained from the modeling of neighbouring regions.
On the other hand, the geometrical thickness of the cloud
may change in different regions because it depends on fragmentation.
Sometimes, different combinations of the input parameters lead to
very similar results for one or two of the most significant line ratios.
So the final choice of the model is determined by consistency
on a large scale. In conclusion, spectra showing only a few lines provide rough information
about the conditions of the emitting gas.
A first choice of  comes from the FWHM of the observed line profiles
and, generally, from the intensity ratio of lines from different ionization levels.
The range of n0 is suggested by the [SII] 6717/6730 line ratios.
Notice, however, that the density of the line-emitting gas downstream
is higher than n0 by a factor
comes from the FWHM of the observed line profiles
and, generally, from the intensity ratio of lines from different ionization levels.
The range of n0 is suggested by the [SII] 6717/6730 line ratios.
Notice, however, that the density of the line-emitting gas downstream
is higher than n0 by a factor 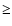 10 due to compression.
10 due to compression.
In matter-bound models the geometrical thickness of the nebula
is roughly determined by the intensity of low-level and neutral lines.
The magnetic field and the density are linked through the compression equation
(Cox 1972) which is calculated in each slab of
the gas downstream, leading to the density profile.
The range of B0 is suggested by the results obtained for the other supernova
remnants (Cygnus Loop, Cassiopeia A, etc.) and for the interstellar medium,
B0 = 10-6-10-5 Gauss
(Contini et al. 1980; Contini & Shaviv 1982; Contini 1987).
The choice of the pre-shock magnetic field in modeling is also constrained by the best agreement of all the calculated line ratios with the observational data.
Table 1:
The models selected from the grid.
![\begin{figure}
\par\includegraphics[height=8.3cm,width=8.5cm,clip]{0001fg1a.ps}\...
...e*{5mm}
\includegraphics[height=8.3cm,width=8.3cm,clip]{0001fg1b.ps}\end{figure}](/articles/aa/full/2004/29/aa0001-04/Timg16.gif) |
Figure 1:
The distribution of the electron temperature (solid line), of the dust temperature
(dotted line), and of the electron density (dashed line)
downstream ( top panels) and of the fractional abundances of some significant ions downstream
( bottom panels) for model m3 (left diagram) and model m9 (right diagram).
H+1/H: solid line; N+1/N: short-dashed line: S+1/S: long-dashed line;
O+2/O: dotted line. |
| Open with DEXTER |
The models discussed here have been obtained assuming
as a first choice cosmic chemical abundances for He, C, N, O, Ne,
Mg, Si, S, Ar, and Fe (Allen 1973). The elements which reveal depletion from the gaseous phase by trapping into grains are carbon, silicon, magnesium, iron, etc.
Most of their lines are prominent in the UV and in the infrared spectra,
while the observed lines are actually in the optical- near infrared.
Moreover, sulphur can be trapped into CS diatomic molecules.
The dust-to-gas ratios are constrained by the SED of the continuum in the IR range.
It is found that only large grains (
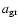
 1
1 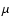 m) survive sputtering in high
velocity shocks. The sizes of grains adopted for low velocity shocks are
constrained by the data at long wavelengths (Contini et al. 2004, Fig. 7, left
panel) and
m) survive sputtering in high
velocity shocks. The sizes of grains adopted for low velocity shocks are
constrained by the data at long wavelengths (Contini et al. 2004, Fig. 7, left
panel) and
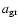 = 0.2
= 0.2 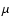 m is obtained by comparison with SCUBA data. The contributions of dust emission from all the slabs downstream are summed up and lead to the IR bump.
m is obtained by comparison with SCUBA data. The contributions of dust emission from all the slabs downstream are summed up and lead to the IR bump.
The FWHM of the observed H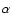 line profile suggests that two kinds of shocked clouds contribute to the spectra from each observed region, those with high (
line profile suggests that two kinds of shocked clouds contribute to the spectra from each observed region, those with high (
 1000
1000
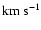 )
and those with low velocities (
)
and those with low velocities (
 50
50
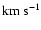 ).
The pre-shock densities must be high enough to obtain [SII]6713/[SII] 6730 < 1 downstream.
Considering the adiabatic jump at the shock front and that compression downstream increases with the shock velocity, low velocity clouds must be characterized by high pre-shock densities, while high velocity clouds which propagate outwards and have reached the outskirts of the
SNR have
lower densities. This will lead to non-radiative shocks characterized by very long recombination times of the gas downstream. Recombination coefficients are low at high temperatures, and if
the densities are also too low to speed up the cooling process, the temperatures within the cloud will never drop below T= 105 K, and the optical (and UV) lines will not be emitted. In other words, these models are matter-bound. On the other hand, X-rays which correspond to bremsstrahlung from high temperature gas are actually observed, revealing the presence of these clouds.
).
The pre-shock densities must be high enough to obtain [SII]6713/[SII] 6730 < 1 downstream.
Considering the adiabatic jump at the shock front and that compression downstream increases with the shock velocity, low velocity clouds must be characterized by high pre-shock densities, while high velocity clouds which propagate outwards and have reached the outskirts of the
SNR have
lower densities. This will lead to non-radiative shocks characterized by very long recombination times of the gas downstream. Recombination coefficients are low at high temperatures, and if
the densities are also too low to speed up the cooling process, the temperatures within the cloud will never drop below T= 105 K, and the optical (and UV) lines will not be emitted. In other words, these models are matter-bound. On the other hand, X-rays which correspond to bremsstrahlung from high temperature gas are actually observed, revealing the presence of these clouds.
If we adopt dust-to-gas ratios as those predicted for Kepler's SNR by other authors (e.g. Morgan 2003) and confirm them by cross-checking the results of the present paper (Sect. 4),
the energy losses by collisional heating of grains prevail downstream of high velocity
clouds, even characterized by a low density, leading to cooling times much
shorter than the age of the remnant (400 yr). This is an important issue in view of the choice of the models. In particular, d/g should be higher by at least a factor of 3 than normal values (10-14 by number) and the grain radius large enough (
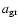
 1
1 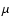 m) to survive sputtering.
m) to survive sputtering.
Due to fragmentation which follows from turbulence in shock dominated regimes, many different
emitting nebulae (clouds) coexist in each region, so to model the corresponding observed spectrum different single-cloud models must be summed up adopting relative weights.
Notice that the structure of the observed regions is very complex,
and a perfect fit to the observed spectra by some typical models is senseless.
So in the following we will try to explain only the most significant line ratios.
In Table 1 we present the single-cloud models selected from a large grid
covering all the possible physical conditions which are consistent
with the Kepler SNR events. Each of the models leads
to the rough fit of some of the observed line ratios. We reduced the number of models to
a minimum of prototypes, because modeling provides only an approximate picture.
The ranges of the input parameters were chosen considering the physical conditions which are directly suggested by the observations, and by a first modeling of some significant line ratios
([OIII] 4959+5007, [OII] 3727+3729, [OI] 6300+6364, [NII] 6548+6583, and [SII] 6717 and 6730), considering that, finally, only multi-cloud models will be compared with the data.
Table 2:
Comparison of calculated with observed line ratios (H = 1)
from the whole remnant.
= 1)
from the whole remnant.
The first three rows of Table 1 show the model input parameters.
Then, the calculated line ratios to H = 1 are given, followed by the H
= 1 are given, followed by the H absolute flux in the last row. B0 = 10-5 Gauss is adopted for all the models. The models in Table 1 are ordered by increasing shock velocities.
absolute flux in the last row. B0 = 10-5 Gauss is adopted for all the models. The models in Table 1 are ordered by increasing shock velocities.
The selected models (Table 1) show three different types characterized by
1) low velocity shocks with 
 50
50
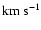 and n0
and n0 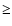 3000
3000
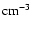 (m1-m4);
2) intermediate shocks (
(m1-m4);
2) intermediate shocks ( = 300, 400
= 300, 400
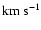 )
which propagate outwards and are decelerated by
impinging on high density debris of previously ejected matter (m5 and m6); and 3) high velocity shocks with
)
which propagate outwards and are decelerated by
impinging on high density debris of previously ejected matter (m5 and m6); and 3) high velocity shocks with 
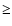 700
700
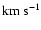 ,
n0 < 100
,
n0 < 100
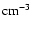 ,
and d/g > 3
,
and d/g > 3 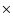 10-14 (m7-m9).
10-14 (m7-m9).
The observed FWHMs suggest that shocks with 
 50
50
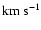 must be accounted for (m1, m2, m3, m4). The corresponding pre-shock densities are >1000
must be accounted for (m1, m2, m3, m4). The corresponding pre-shock densities are >1000
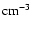 in order to obtain
[SII] 6717/6730 < 1 downstream. The spectra show rather high [OII]/H
in order to obtain
[SII] 6717/6730 < 1 downstream. The spectra show rather high [OII]/H and very low [OIII]/H
and very low [OIII]/H .
Interestingly, the [NII]6583+6548/H
.
Interestingly, the [NII]6583+6548/H line ratios are relatively high, similar to the observed ones, even adopting cosmic N/H. On the other hand, [SII] 6717/H
line ratios are relatively high, similar to the observed ones, even adopting cosmic N/H. On the other hand, [SII] 6717/H and [SII] 6730/H
and [SII] 6730/H are very low.
Notice that high [NII]/[SII] line ratios are characteristic of the observed spectra (Tables 2-6).
Actually, the first ionization potential of nitrogen is higher than that of hydrogen, while the first ionization potential of sulphur is lower. So the [NII] and [SII] lines are emitted from gas in different physical conditions. Figure 1 (left diagram) shows that the physical conditions
rapidly change downstream within small distances.
are very low.
Notice that high [NII]/[SII] line ratios are characteristic of the observed spectra (Tables 2-6).
Actually, the first ionization potential of nitrogen is higher than that of hydrogen, while the first ionization potential of sulphur is lower. So the [NII] and [SII] lines are emitted from gas in different physical conditions. Figure 1 (left diagram) shows that the physical conditions
rapidly change downstream within small distances.
The observed large FWHMs lead to models with 
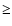 700
700
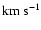 and relative low n0 = 30-60
and relative low n0 = 30-60
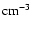 (m7, m8). These models show [OIII]/H
(m7, m8). These models show [OIII]/H ,
[OII] 3727+3729/H
,
[OII] 3727+3729/H ,
[NII]/H
,
[NII]/H ,
and [SII]/H
,
and [SII]/H higher than those calculated by models with
higher than those calculated by models with  = 300-400
= 300-400
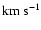 and n0 = 300
and n0 = 300
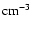 (m5, m6), but show lower [OII] 7320+7330/H
(m5, m6), but show lower [OII] 7320+7330/H .
.
Model m9 shows peculiar line ratios, because a high  leads to a strong compression of the intermediate-level line (e.g. [OIII]) emitting region, and to a large zone of gas with
leads to a strong compression of the intermediate-level line (e.g. [OIII]) emitting region, and to a large zone of gas with 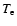 < 104 K (Fig. 1, right) which corresponds to strong low level lines ([OI], [OII], [NII], [SII], etc.). Model m10 was added in Table 1 after discussing the SED of the continuum (Sect. 3.3).
< 104 K (Fig. 1, right) which corresponds to strong low level lines ([OI], [OII], [NII], [SII], etc.). Model m10 was added in Table 1 after discussing the SED of the continuum (Sect. 3.3).
The distributions of the electron temperature, the electron density, and the fractional abundance
of the most significant ions versus the distance from the shock front (in cm) are presented in Fig. 1, for models m3 and m9. Model m3 (left diagram) represents the nebula downstream of the reverse shock which is characterized by low  and high n0, while model m9 (right diagram) represents the nebula downstream of the shock propagating outwards. Therefore, the shock front is shown on opposite edges in the two diagrams.
and high n0, while model m9 (right diagram) represents the nebula downstream of the shock propagating outwards. Therefore, the shock front is shown on opposite edges in the two diagrams.
The emitting clouds are radiation bound. The ionized region is rather narrow ( 1013 cm)
in the low velocity model m3 (Fig. 1, left panel). On the other hand, model m9 shows a high temperature zone of
1013 cm)
in the low velocity model m3 (Fig. 1, left panel). On the other hand, model m9 shows a high temperature zone of  1017 cm (Fig. 1, right panel) which is reasonable compared to the SNR diameter (3.8 pc), calculated adopting a Kepler SNR distance to Earth of 5 kpc
(Blair et al. 1991). The high dust-to-gas ratio (9
1017 cm (Fig. 1, right panel) which is reasonable compared to the SNR diameter (3.8 pc), calculated adopting a Kepler SNR distance to Earth of 5 kpc
(Blair et al. 1991). The high dust-to-gas ratio (9  10-14) corresponding to model m9 leads to a cooling time <60 yr in the downstream region.
10-14) corresponding to model m9 leads to a cooling time <60 yr in the downstream region.
The data used for modeling the line spectra come from the following observations.
Spectrophotometry data covering the spectral range 3700-10 500 Å of the bright western knots were obtained during 1979-1980 with the Boller and Chivens spectrograph attached to the ESO 3.6 telescope and were presented by Dennefeld (1982). Observations in the optical range for single bright knots in different positions and the integrated spectrum obtained in the
Anglo-Australian 3.9 m Telescope come from Leibowitz & Danziger (1983).
Blair et al. (1991) presented optical CCD/interference filter imaginery and
long-slit CCD spectrophotometry of the Kepler SNR obtained by the 2.5 m DuPont
telescope at Las Campanas Observatory. Although the data of
Blair et al.(1991) cover a relatively reduced wavelength range, the series of
single spectra observed in more than 20 regions provides the tools for modeling the SNR extended area.
The mean reddening E(B-V) to Kepler's SNR is 0.9 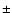 0.1 (Blair et al. 1991), lower than
E(B-V)=1.1 given by Leibowitz & Danziger.
0.1 (Blair et al. 1991), lower than
E(B-V)=1.1 given by Leibowitz & Danziger.
The comparison between calculated and observed (reddening corrected) line ratios
to H = 1 is presented in Tables 2-6. The spectra were observed by Dennefeld (1982), Leibowitz & Danziger (1983), and
Blair et al. (1991). When the H
= 1 is presented in Tables 2-6. The spectra were observed by Dennefeld (1982), Leibowitz & Danziger (1983), and
Blair et al. (1991). When the H line is not observed we adopt H
line is not observed we adopt H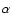 /H
/H = 3. The weights of the corresponding single-cloud models and the conversion factors (see Sect. 3.3) appear at the bottom of the tables.
= 3. The weights of the corresponding single-cloud models and the conversion factors (see Sect. 3.3) appear at the bottom of the tables.
We will aim at fits such that the discrepancies between the calculated line ratios and the observed ones are less than a factor of 2, which accounts for observational errors and modeling approximation (atomic coefficients, etc.). However, the agreement is not always satisfying for all the lines.
To have a better fit we should consider a larger number of single-cloud models (see, for instance, region D55 in Table 5). Recall that we are interested mainly in the calculation of the dust-to-gas ratios, therefore in some regions which show spectra less constrained by the poor number of lines the fit is not sufficient, leading to discrepancies beyond a factor of 2.
The two observed spectra shown in Table 2 which correspond to integrated data by
Dennefeld (1982) and Leibowitz & Danziger (1983) are similar enough. The two multi-cloud models which best explain them correspond to different weights of the single-cloud models. In Table 3 the models are compared with observations in the different regions in the western side of the remnant by Leibowitz & Danziger (1983, Plate 3).
The spectra observed by Blair et al. (1991) in the different regions are generally satisfactorily explained by modeling (Tables 4-6). At the top of the tables the observed emission regions and their rough location (D'Odorico et al. 1986) in the SNR are indicated.
The data corresponding to regions D41,45 (Blair et al. 1991) are not considered, because
the spectrum is very poor in number of lines. Actually, it is the only position showing
very low densities ([SII] 6717/6730 > 1) in the emitting gas.
Blair et al.
claim that "this emission is not simply a superposition of a non-radiative
and typical (for the Kepler SNR) radiative filament''.
The detection of [NII] 6583+ with a FWHM of  40
40
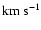 (Sollerman et al. 2003, Table 1) from a Balmer dominated region (e.g. D49, D50) is explained by the reverse shock,
which should be summed up adopting a very small weight compared with that of the high velocity model (>1000
(Sollerman et al. 2003, Table 1) from a Balmer dominated region (e.g. D49, D50) is explained by the reverse shock,
which should be summed up adopting a very small weight compared with that of the high velocity model (>1000
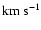 ).
Sollerman et al. (2003) claim that the [NII] emission from D49 and D50 cannot be produced in a cooling zone in Balmer - dominated knots. So the remaining possibility is that it is produced ahead of the Balmer-dominated shock, due to Alfven wave activity in a cosmic ray
precursor. Table 1 shows that models calculated with low
).
Sollerman et al. (2003) claim that the [NII] emission from D49 and D50 cannot be produced in a cooling zone in Balmer - dominated knots. So the remaining possibility is that it is produced ahead of the Balmer-dominated shock, due to Alfven wave activity in a cosmic ray
precursor. Table 1 shows that models calculated with low  show very high [NII]/H
show very high [NII]/H line ratios relative to [SII]/H
line ratios relative to [SII]/H ,
therefore the only narrow lines observable in D49 and D50 are those of [NII], and perhaps of [OII], which unfortunately were
not included in the spectra.
Blair et al. (1991) notice that D47 and D48 with a peak at 6584 ([NII]), represent a transition filament implying a minimum shock velocity of 815
,
therefore the only narrow lines observable in D49 and D50 are those of [NII], and perhaps of [OII], which unfortunately were
not included in the spectra.
Blair et al. (1991) notice that D47 and D48 with a peak at 6584 ([NII]), represent a transition filament implying a minimum shock velocity of 815
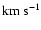 .
.
Two spectra, D56 and P2D1 (P2, diff1) in Table 5, are explained by single-cloud models, m5 and m6, respectively. However, the modeling is less constrained by the small number of observed lines.
Summarizing, the present modeling confirms that, in agreement with previous modeling, a N/H relative abundance higher than solar should be adopted, however, by a factor <2, which is lower than the factor of  3.5 suggested by
Blair et al. (1991) This leads to N/H < 1.8
3.5 suggested by
Blair et al. (1991) This leads to N/H < 1.8  10-4. Notice that models in group 1), corresponding to the slow shock, and model m9
show rather high [NII] 6583+/H
10-4. Notice that models in group 1), corresponding to the slow shock, and model m9
show rather high [NII] 6583+/H ratios (>5). So in the multi-cloud models which best fit the spectra, the higher the relative weight of these models, the closer to 1 are the ratios of calculated to observed [NII]/H
ratios (>5). So in the multi-cloud models which best fit the spectra, the higher the relative weight of these models, the closer to 1 are the ratios of calculated to observed [NII]/H .
In contrast, Fe lines are overpredicted by the models, indicating that Fe could be depleted from the gaseous phase.
.
In contrast, Fe lines are overpredicted by the models, indicating that Fe could be depleted from the gaseous phase.
Tables 2 and 3 show that models with intermediate velocities (group 2) have generally low relative weights. They give some contribution to the Leibowitz & Danziger spectra (Table 3), and even less to
Blair et al. (1991) (Tables 4-6). The weights of the high velocity clouds (group 3) in the Leibowitz & Danziger and
Blair et al. (1991) spectra are low relative to those of the low velocity clouds (group 1) particularly for D9, D38,40, D63,64, SWD9, D9,10, and D25.
High velocity models do not contribute to the spectra observed in some of the NE regions (D55, D56, D61, P2D1). Particularly, radiative high velocity shocks are not found in these regions.
This indicates that the conditions in the outer region of the Kepler SNR are not homogeneous,
showing different densities, dust-to-gas ratios, and grain sizes.
On the other hand, high  clouds are present in regions D3, D18, and D27.
The line profiles of [NII] 6548, [NII] 6583, and of H
clouds are present in regions D3, D18, and D27.
The line profiles of [NII] 6548, [NII] 6583, and of H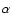 calculated by model MB3 for
region D3 (Table 4) are presented in Fig. 2. The line profiles of [NII] and H
calculated by model MB3 for
region D3 (Table 4) are presented in Fig. 2. The line profiles of [NII] and H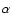 (Fig. 2),
show relative fluxes in agreement with Blair et al. (1991, Fig. 3). However, the calculated FWHMs are smaller, because the contribution of the high velocity gas which leads to the best agreement of the calculated with the observed line spectra, appears as a socket in the profiles.
In fact, the absolute fluxes of the H
(Fig. 2),
show relative fluxes in agreement with Blair et al. (1991, Fig. 3). However, the calculated FWHMs are smaller, because the contribution of the high velocity gas which leads to the best agreement of the calculated with the observed line spectra, appears as a socket in the profiles.
In fact, the absolute fluxes of the H lines (which appear in Table 1, last row as H
lines (which appear in Table 1, last row as H
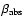 )
and of the [NII] lines ([NII]/H
)
and of the [NII] lines ([NII]/H
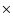 H
H
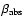 )
are low for high
)
are low for high  models.
models.
Table 3:
Comparison of calculated with observed line ratios (H = 1).
= 1).
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{0001fg2.ps}\end{figure}](/articles/aa/full/2004/29/aa0001-04/Timg20.gif) |
Figure 2:
[NII] 6548, [NII] 6583, and H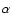 line profiles (solid lines) calculated by model MB3
for region D3 observed by Blair et al. (1991). Dotted lines correspond to model m1, short-dashed line to m3. The fluxes are calculated at the emitting nebula. line profiles (solid lines) calculated by model MB3
for region D3 observed by Blair et al. (1991). Dotted lines correspond to model m1, short-dashed line to m3. The fluxes are calculated at the emitting nebula. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{0001fg3.ps}\end{figure}](/articles/aa/full/2004/29/aa0001-04/Timg21.gif) |
Figure 3:
Comparison of single-cloud models with observational data (black squares).
m3: solid lines; m6: long-dashed lines; m7: dotted lines; m9: short-dashed lines; m10: dash-dotted lines. |
| Open with DEXTER |
Table 4:
Comparison of calculated with observed line ratios (H = 1).
= 1).
Table 5:
Comparison of calculated with observed line ratios (H = 1).
= 1).
Table 6:
Comparison of calculated with observed line ratios (H = 1).
= 1).
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{0001fg4.ps}\end{figure}](/articles/aa/full/2004/29/aa0001-04/Timg24.gif) |
Figure 4:
Consistent modeling of the Kepler SNR continuum SED by the summed model (thick solid line: bremsstrahlung; thin solid line: synchrotron radiation; dashed line: IR emission) and model m10 (dotted lines). The observational data are represented by black squares. The data point at 5400 Å from Leibowitz & Danziger (1983) is represented by an open square. The asterisks refer to Douvion et al. (2001a). |
| Open with DEXTER |
The data in the X-ray come from Becker et al. (1980), Tuhoy et al. (1979),
in the radio from DeLaney et al. (2002) and in the IR from Arendt (1989),
Saken et al. (1992), and Braun (1997). Very recently the SCUBA data at 450
and 800 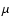 m by JCM telescope on Mauna Kea were presented by Morgan et al.
(2003).
m by JCM telescope on Mauna Kea were presented by Morgan et al.
(2003).
The data sets in the radio and IR ranges are quite complete and allow a detailed modeling of gas and dust emissions (Figs. 3 and 4). However, data in the optical-UV range are lacking. As a first check, we will constrain the models by the X-ray data, although they are upper limit.
The modeling of the continuum SED must be consistent with that of the line spectra.
The SED shows different contributions to the flux in the different frequency ranges.
The gas which is heated in the immediate post shock region to relatively high temperatures,
cools down downstream. The cooling-rates depend strongly on the gas density, on the relative
abundances of the most coolant elements, and on the dust-to-gas ratio. Diffuse radiation from the hot gas keeps the gas ionized and heated to T 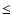 104 K in a relatively large zone downstream. The bremsstrahlung emitted from gas at different temperatures, densities, etc.,
covers a large range of frequencies, from radio to X-ray.
104 K in a relatively large zone downstream. The bremsstrahlung emitted from gas at different temperatures, densities, etc.,
covers a large range of frequencies, from radio to X-ray.
The optical-UV radiation flux is emitted from gas at T = 104-105 K, while the soft X-ray
domain shows the bremsstrahlung from high temperature gas.
The IR bump corresponds to reradiation by dust. Mutual heating of dust and gas throughout the shock front and downstream leads to a maximum dust temperature which depends on the gas maximum temperatures which is determined by  .
Therefore the frequency corresponding to the peak of dust reradiation generally depends on
.
Therefore the frequency corresponding to the peak of dust reradiation generally depends on  (see Contini et al. 2004).
The intensity of the IR flux depends, however, mainly on d/g.
The IR bump defined by the observations must be disentangled into the different components
corresponding to the different single-cloud models which are used to explain the line spectra.
(see Contini et al. 2004).
The intensity of the IR flux depends, however, mainly on d/g.
The IR bump defined by the observations must be disentangled into the different components
corresponding to the different single-cloud models which are used to explain the line spectra.
The modeling procedure starts by fitting the bremsstrahlung which indicates the range of the shock velocity, consistently with the frequency peak in the IR. Then, the IR bump is shifted along the Y-axis by changing the dust-to-gas ratio (Contini et al. 2004), in order to obtain the best fit to the data.
In the radio range of the continuum SED of SNRs, synchrotron radiation generated by the
Fermi mechanism at the shock front generally dominates on bremsstrahlung. Recall that the character of optical and X-ray magnetobremsstrahlung (synchrotron radiation) resembles that of
the radio counterpart, but to produce radiation at optical and X-ray frequencies the electrons must possess considerably higher energies than for radiation in the radio range, or the
strength of the magnetic field must be higher (Ginzburg & Syrovatskii 1965).
So the synchrotron radiation is cut off at 1013 Hz in Fig. 4 as an upper limit.
The SEDs of some significant models are presented in Fig. 3. The curves are shifted vertically on the Y-axis representing the flux, to fit as much as possible the data.
Model m3 is selected as representative of low velocity shocks (group 1), model m6 of intermediate shocks (group 2), model m7 of high velocity shocks (group 3), and model m9 is selected because it is characterized by a high  ,
a low n0, and a high d/g. We have added in Fig. 3
the continuum SED of model m10 corresponding to
,
a low n0, and a high d/g. We have added in Fig. 3
the continuum SED of model m10 corresponding to  = 1000
= 1000
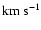 ,
n0 = 100
,
n0 = 100
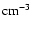 ,
d/g = 5
,
d/g = 5  10-15,
10-15,
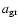 = 1
= 1 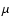 m, and D=2
m, and D=2 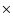 1016 cm, which is matter-bound. In fact, the gas downstream contains only the high temperature region, so the cooling time within this region is less than 2 yr. The corresponding radiation-bound model with D= 1018 cm (model m10 in Table 1) would lead to cooling times of
1016 cm, which is matter-bound. In fact, the gas downstream contains only the high temperature region, so the cooling time within this region is less than 2 yr. The corresponding radiation-bound model with D= 1018 cm (model m10 in Table 1) would lead to cooling times of  400 yr, i.e. of the order of the remnant age, because d/g is low. Model m10 shows that non-radiative shocks can contribute strongly to the soft X-rays and to IR radiation. However, in regions dominated by grains small enough to be completely destroyed by sputtering this type of models contributes only to the bremsstrahlung.
400 yr, i.e. of the order of the remnant age, because d/g is low. Model m10 shows that non-radiative shocks can contribute strongly to the soft X-rays and to IR radiation. However, in regions dominated by grains small enough to be completely destroyed by sputtering this type of models contributes only to the bremsstrahlung.
The fluxes of models m7 and m9 displayed in Fig. 3 have been multiplied by a factor of 4 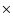 10-11 to fit the data. Those of models m3 and m6 have been multiplied by factors of 8.1
10-11 to fit the data. Those of models m3 and m6 have been multiplied by factors of 8.1 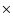 10-9 and 4
10-9 and 4 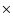 10-9, respectively, and the
flux of model m10 by a factor of 1.6
10-9, respectively, and the
flux of model m10 by a factor of 1.6 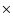 10-10.
Recall that models are calculated at the nebula while the data are observed on Earth.
Therefore, conversion factors which account for the distances
of the observed regions from the remnant center and of the remnant to Earth
must be considered. The modeling of the line spectra shows (Sect. 3.2) that the
observed regions are explained by multi-cloud models, so
in this first analysis of single-cloud models only the ratios of these factors are significant
because they show the ratio of the flux intensities of different models.
10-10.
Recall that models are calculated at the nebula while the data are observed on Earth.
Therefore, conversion factors which account for the distances
of the observed regions from the remnant center and of the remnant to Earth
must be considered. The modeling of the line spectra shows (Sect. 3.2) that the
observed regions are explained by multi-cloud models, so
in this first analysis of single-cloud models only the ratios of these factors are significant
because they show the ratio of the flux intensities of different models.
Figure 3 shows that the IR flux calculated by model m3 peaks at lower frequency than
model m6 because  is lower. The high post shock temperature corresponding to model m9 with
is lower. The high post shock temperature corresponding to model m9 with  = 1000
= 1000
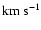 rapidly decreases by the strong cooling rate due to the high d/g, so the peak in the IR, as well as the bremsstrahlung peak, are shifted to lower frequencies.
The bremsstrahlung of model m3 corresponding to low
rapidly decreases by the strong cooling rate due to the high d/g, so the peak in the IR, as well as the bremsstrahlung peak, are shifted to lower frequencies.
The bremsstrahlung of model m3 corresponding to low  is not constrained by the soft X-ray upper limits, therefore the dust-to-gas ratio cannot be confirmed. Recall that in both m3 and m6
d/g = 10-14 by number (corresponding to 4
is not constrained by the soft X-ray upper limits, therefore the dust-to-gas ratio cannot be confirmed. Recall that in both m3 and m6
d/g = 10-14 by number (corresponding to 4 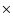 10-4 by mass for silicates) is adopted. Figure 3 shows that the calculated IR bumps fit most of the IR data well enough to confirm that the corresponding clouds contribute to the SED of Kepler's SNR.
10-4 by mass for silicates) is adopted. Figure 3 shows that the calculated IR bumps fit most of the IR data well enough to confirm that the corresponding clouds contribute to the SED of Kepler's SNR.
However, the observational data correspond to the whole SNR. So as a second step in modeling
the continuum SED we compare the data with a model which accounts for all of the
most luminous regions observed by Blair et al. (1991) (D3, D9, D18, D34,35, D38,40, D9,10, D25, D27).
Therefore, first, the continuum corresponding to the multi-cloud model which explains
the line spectrum is calculated for each observed region. Then, the results are summed adopting conversion factors (CF) which are the same for the continuum and line spectrum from each region.
The CF are, therefore, calculated from the observed H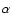 fluxes given by
Blair et al. (1991) in the different regions and included in Tables 4-6, and from the calculated H
fluxes given by
Blair et al. (1991) in the different regions and included in Tables 4-6, and from the calculated H fluxes, which are given in Table 1 for the different models. H
fluxes, which are given in Table 1 for the different models. H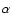 /H
/H = 3 is adopted.
The calculated CF for each region appear at the bottom of Tables 4-6. Multiplying these CF by the continua emitted from each region and summing, the total continuum SED is approximatively calculated for the Kepler SNR and can be compared with the data.
= 3 is adopted.
The calculated CF for each region appear at the bottom of Tables 4-6. Multiplying these CF by the continua emitted from each region and summing, the total continuum SED is approximatively calculated for the Kepler SNR and can be compared with the data.
In Fig. 4 the bremsstrahlung is indicated by a solid line, and dust emission by a dashed line. We have separated the dust emission curve from the bremsstrahlung to better understand their roles. Model m10, represented by dotted lines, has not been included in the sum.
ISOCAM observations presented by Douvion et al. (2001) in different regions of the SNR cover the range between 6.5 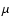 m and 16
m and 16 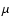 m. We have summed the fluxes from the different regions
corresponding to 12
m. We have summed the fluxes from the different regions
corresponding to 12 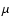 m and 16
m and 16 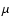 m and they are shown in Fig. 4 for comparison.
m and they are shown in Fig. 4 for comparison.
To further check whether the calculated total bremsstrahlung in the optical range is consistent with the observations, the continuum flux at 5400 Å has been roughly deduced from the spectrum observed by Leibowitz & Danziger (1983, Fig. 3) and is indicated as an open square in Fig. 4.
The constraint of the continuum SED is acceptable and confirms that the dust-to-gas
ratios adopted in single-cloud models are reliable. Nevertheless, Fig. 4 shows that the two IR data points at 60 and 100 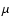 m are overpredicted by the models. A better fit could be obtained considering the observation error and/or by reducing the weight of models m7-m8 and/or by reducing the d/g ratio of these models. A lower d/g leads to large cooling times downstream of models m7 and m8, so that the model parameters should be rearranged destroying the good fit the line spectra. A lower weight, too, leads to changes in some multi-cloud line spectra.
Indeed, the fits of the observed continuum and of the line spectra could be improved separately.
However, model results for continuum and line spectra are cross-checked, leading to the best modeling of both.
m are overpredicted by the models. A better fit could be obtained considering the observation error and/or by reducing the weight of models m7-m8 and/or by reducing the d/g ratio of these models. A lower d/g leads to large cooling times downstream of models m7 and m8, so that the model parameters should be rearranged destroying the good fit the line spectra. A lower weight, too, leads to changes in some multi-cloud line spectra.
Indeed, the fits of the observed continuum and of the line spectra could be improved separately.
However, model results for continuum and line spectra are cross-checked, leading to the best modeling of both.
The synchrotron radiation calculated in the radio range is represented by a thin solid line in Fig. 4.
DeLaney et al. (2002) find a mean value of the spectral index of -0.71 for synchrotron radiation in the radio range, which generally originates from turbulence and magnetic field enhancement at the shock fronts in SNR. The present modeling shown in Fig. 4, adopting the Fermi mechanism at the shock front (Bell 1978) leads to a spectral index of -0.75, which explains the data satisfactorily. Moreover, the difference in structure between the flat and steep spectra of radio emission is explained by
DeLaney et al. (2002) by a partial decoupling of the forward and reverse shock. Although we find that both types of shock act in nearly all the observed regions,
it is difficult to predict how much they have progressed in opposite directions at the time of observations.
Summarizing, it is found by modeling that dust-to-gas ratios are 4 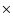 10-4 by mass
in clouds corresponding to low velocity shocks and even lower in intermediate velocity clouds.
On the other hand, d/g are relatively high in clouds corresponding to high velocity shocks,
by factors of 4, 6 , and 9 for
10-4 by mass
in clouds corresponding to low velocity shocks and even lower in intermediate velocity clouds.
On the other hand, d/g are relatively high in clouds corresponding to high velocity shocks,
by factors of 4, 6 , and 9 for  of 700, 800, and 1000
of 700, 800, and 1000
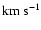 ,
respectively.
,
respectively.
In this work the calculation of dust emission is carried out consistently with emission from
gas for both line and continuum spectra, leading to the evaluation of the dust-to-gas ratios
in the Kepler SNR. A successful application of this method (Contini et al. 2004) was presented
for luminous IR galaxies (Contini & Contini 2003) and for AGN (e.g. Contini & Viegas 2000).
The two component emission observed in the FWHM of the H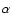 line profiles
corresponding to velocities of
line profiles
corresponding to velocities of  50
50
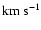 and
and  1000
1000
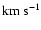 is confirmed by modeling.
They correspond to the reverse and the expanding shocks, respectively, and are explained
by the supernova interaction with a stellar wind.
is confirmed by modeling.
They correspond to the reverse and the expanding shocks, respectively, and are explained
by the supernova interaction with a stellar wind.
A grid of single-cloud models is calculated. The models cover the set of physical conditions
in the emitting gas that are revealed by the line ratios and by the FWHM of the line profiles. Multi-cloud models which account for the reverse and expanding shocks in each region are adopted to fit the observed line spectra and to calculate the corresponding continuum SED.
The total continuum which results from summing the contributions of the most luminous
regions, is compared with the observed continuum SED. Dust emission in the IR is consistently calculated. The ratio between dust emission and bremsstrahlung in the IR range
depends on the dust-to-gas ratios adopted in the models.
Relatively high dust-to gas ratios are found by modeling the IR bump in models corresponding
to high velocity shocks. The high d/g ratios in the clouds speed up the cooling rate downstream, leading to radiative shocks even in a relatively low density gas.
It is found that radiative high velocity shocks are absent in the NE region of the remnant,
suggesting that d/g is low and/or the grains are small enough to be destroyed by sputtering.
This result may indicate that dust is not homogeneously distributed throughout the remnant.
Moreover, the morphological structure of the Kepler SNR in the different wavelengths
can be explained by model results. In fact, the X-ray emission has the same shell-like morphology and is qualitatively similar to the radio emission
(Blair et al. 1991; DeLaney et al. 2002),
confirming that both radio and X-ray radiation are created at the shock front of the expanding
shock. Indeed, the high temperatures (>107 K) of the gas in the immediate
post-shock region downstream correspond to the X-ray emission.
The H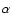 and IR images are similar (Blair et al. 1991) and are similar to the X-ray image.
Particularly, the striking similarity between the H
and IR images are similar (Blair et al. 1991) and are similar to the X-ray image.
Particularly, the striking similarity between the H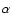 and IR images suggests that the 12
and IR images suggests that the 12 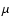 m thermal dust emission and the optical emission have the same origin
(DeLaney et al. 2002) confirming that dust grains are collisionally heated by the gas across the shock fronts and downstream. The regions of dissimilarity could be explained by the
inhomogeneous distribution of dust grains.
m thermal dust emission and the optical emission have the same origin
(DeLaney et al. 2002) confirming that dust grains are collisionally heated by the gas across the shock fronts and downstream. The regions of dissimilarity could be explained by the
inhomogeneous distribution of dust grains.
Notice that the modeling of the Kepler SNR through the line and continuum spectrum analysis
in the different regions has been presented in the previous sections with the aim of calculating the dust-to-gas ratios. Actually, this work has been inspired by Morgan et al. (2003) who claim that dust formation in supernovae is required to be an important process relative to the age of the Universe.
Morgan et al. calculate that the maximum dust mass swept up by the SNR is  10-3
10-3 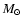 ,
assuming a maximum density n = 0.1
,
assuming a maximum density n = 0.1
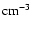 and a gas to dust ratio of 160.
However, adopting a higher n (100
and a gas to dust ratio of 160.
However, adopting a higher n (100
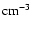 )
the dust mass swept up is
)
the dust mass swept up is  1
1 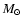 .
Douvion et al. (2001) claim that by using dust grains of "astronomical silicates''
both mid-IR ISOCAM and IRAS data can be fitted by a single grain temperature of 107 K,
while previous models required two dust components: a hot dust of 140 K and a
cold one of 54 K (Saken et al. 1992). The total mass calculated by them is 10-4
.
Douvion et al. (2001) claim that by using dust grains of "astronomical silicates''
both mid-IR ISOCAM and IRAS data can be fitted by a single grain temperature of 107 K,
while previous models required two dust components: a hot dust of 140 K and a
cold one of 54 K (Saken et al. 1992). The total mass calculated by them is 10-4 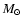 .
.
The model presented in this work shows that two main types of dust lead to a good fit of
the IR bump consistently with the bremsstrahlung. Large grains with
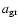 = 1
= 1 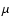 m with d/g < 4
m with d/g < 4  10-3 survive sputtering downstream of the expanding shock and are collisionally heated to a maximum temperature of 125 K. Smaller grains (
10-3 survive sputtering downstream of the expanding shock and are collisionally heated to a maximum temperature of 125 K. Smaller grains (
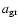 = 0.2
= 0.2 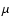 m) downstream of the reverse shock (Fig. 1) with dust-to-gas ratios of
m) downstream of the reverse shock (Fig. 1) with dust-to-gas ratios of  4
4 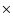 10-4 are heated to a maximum temperature of
10-4 are heated to a maximum temperature of  50 K.
50 K.
Adopting an SNR diameter of 3.8 pc, a pre-shock density  50
50
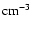 by the average of models m7, m8, m9 (Table 1) (Sect. 3.3), we obtain a swept up gas mass of 40
by the average of models m7, m8, m9 (Table 1) (Sect. 3.3), we obtain a swept up gas mass of 40 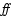
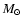 and a maximum dust mass of 0.16
and a maximum dust mass of 0.16 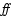
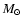 ,
where
,
where
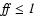 is the filling factor.
is the filling factor.
Such relatively high pre-shock densities in single clouds are justified by
the relatively young age of the Kepler SNR. In older SNR (e.g. the Cygnus Loop), n0 is less than 10
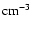 (Contini et al. 1980). Moreover, the clumpy aspect of the remnant suggests that average densities on large scales are not realistic and that
(Contini et al. 1980). Moreover, the clumpy aspect of the remnant suggests that average densities on large scales are not realistic and that 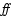 should be
should be  0.1.
0.1.
Comparing with other SNR, Douvion et al. (2001a) found that a dust mass of 10-4 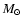 results from the warm component (140 K as for Kepler SNR) and of 4
results from the warm component (140 K as for Kepler SNR) and of 4 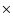 10-3
10-3 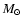 for the cold component (55 K) of Tycho. They claim that the Crab nebula IR emission is dominated by synchrotron radiation and no dust is detected. In Cassiopeia A the dust is made of more components, e.g. quartz and aluminum oxide, besides silicates which have a mass of 7.8
for the cold component (55 K) of Tycho. They claim that the Crab nebula IR emission is dominated by synchrotron radiation and no dust is detected. In Cassiopeia A the dust is made of more components, e.g. quartz and aluminum oxide, besides silicates which have a mass of 7.8 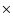 10-9
10-9 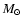 (Douvion et al. 2001b).
(Douvion et al. 2001b).
Acknowledgements
I am very grateful to an anonymous referee whose precious comments helped to improve the paper,
and to Elia Leibowitz for fruitful discussions.
- Allen, C. W. 1973,
Astrophysical Quantities (London: Athlon)
(In the text)
- Arendt, R. G. 1989, ApJS,
70, 189 [NASA ADS] (In the text)
- Baade, W. 1943, ApJ, 97,
119 [NASA ADS] [CrossRef] (In the text)
- Bandiera, R. 1987, ApJ,
319, 885 [NASA ADS] [CrossRef] (In the text)
- Bell, A. R. 1978, MNRAS,
182, 443 [NASA ADS] (In the text)
- Becker, R. H., Boldt, E.
A., Holt, S. S., Serlemitsos, P. J., & White, N. E. 1980, ApJ,
237, L77 [NASA ADS] [CrossRef] (In the text)
- Blair, W. P., Long, K.
S., & Vancura, O. 1991, ApJ, 366, 484 [NASA ADS] [CrossRef] (In the text)
- Broun, R. 1987, A&A,
171, 233 [NASA ADS]
- Chevalier, R., &
Oishi, J. 2003 [arXiv:astro-ph/0306376]
(In the text)
- Contini, M. 1987,
A&A, 183, 53 [NASA ADS] (In the text)
- Contini, M., &
Contini, T. 2003, MNRAS, 342, 299 [NASA ADS] [CrossRef] (In the text)
- Contini, M., &
Shaviv, G. 1982, Ap&SS, 85, 203 [NASA ADS] (In the text)
- Contini, M., Shaviv, G.,
& Kozlovsky, B. Z. 1980, A&A, 92, 203 [NASA ADS] (In the text)
- Contini, M., &
Viegas-Aldrovandi, S. M. 1990, ApJ, 350, 125 [NASA ADS] [CrossRef] (In the text)
- Contini, M., &
Viegas, S. M. 2000, 535, 721
(In the text)
- Contini, M., &
Viegas, S. M. 2001, ApJS, 132, 211 [NASA ADS] [CrossRef] (In the text)
- Contini, M., Viegas, S.
M., & Prieto, M. A. 2004, MNRAS, 348, 1065 [NASA ADS] [CrossRef] (In the text)
- Cox, D. P. 1972, ApJ,
178, 143 [NASA ADS] [CrossRef] (In the text)
- Decourchelle, A., &
Petre, R. 1999, AN, 320, 203 [NASA ADS] (In the text)
- DeLaney, T., Koralesky,
B., & Rudnick, L. 2002, ApJ, 580, 914 [NASA ADS] [CrossRef] (In the text)
- Dennefeld, M. 1982,
A&A, 112, 215 [NASA ADS] (In the text)
- D'Odorico, S., Bandiera,
R., Danziger, J., & Focardi, P. 1986, AJ, 91, 1382 [NASA ADS] [CrossRef] (In the text)
- Douvion, T., Lagage, P.
O., Cesarsky, C. J., & Dwek, E. 2001a, A&A, 373, 281 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Douvion, T., Lagage, P.
O., & Pantin, E. 2001b, A&A, 369, 598 [NASA ADS] (In the text)
- Draine, B. T. 1981, QpJ,
245, 880 (In the text)
- Dwek, E., & Arendt,
G. 1992, ARA&A, 30, 11 [NASA ADS] (In the text)
- Dwek, E., Foster, S. M.,
& Vankura, O. 1996, ApJ, 457, 244 [NASA ADS] [CrossRef] (In the text)
- Ginsburg, V. L., &
Syrovatskii, S. I. 1965, ARA&A, 3, 297 [NASA ADS] (In the text)
- Hughes, P. 1999, ApJ,
527, 298 [NASA ADS] [CrossRef] (In the text)
- Leibowitz, E. M., &
Danziger, I. J. 1983, MNRAS, 204, 273 [NASA ADS] (In the text)
- Morgan, H. L., Dunne, L.,
Eales, S. A., Ivison, R. J., & Edmunds, M. G. 2003
[arXiv:astro-ph/0309233]
(In the text)
- Saken, J. M., Fesen, R.
A., & Shull, J. M. 1992, ApJS, 81, 715 [NASA ADS] [CrossRef] (In the text)
- Sollerman, I., Ghavaniam,
P., Lundqvist, P., & Smith, R. C. 2003, A&A, 407, 257 [NASA ADS]
- Tuohy, I. R., Nugent, J.
J., Garmire, G. P., & Clark, D. H. 1979, Nature, 279, 139 [NASA ADS] (In the text)
- Van den Bergh, S., &
Kemper, K. W. 1977, ApJ, 218, 617 [NASA ADS] [CrossRef] (In the text)
- Viegas, S. M., &
Contini, M. 1994, ApJ, 428, 113 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2004
![\begin{figure}
\par\includegraphics[height=8.3cm,width=8.5cm,clip]{0001fg1a.ps}\...
...e*{5mm}
\includegraphics[height=8.3cm,width=8.3cm,clip]{0001fg1b.ps}\end{figure}](/articles/aa/full/2004/29/aa0001-04/Timg16.gif)
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{0001fg2.ps}\end{figure}](/articles/aa/full/2004/29/aa0001-04/Timg20.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{0001fg3.ps}\end{figure}](/articles/aa/full/2004/29/aa0001-04/Timg21.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{0001fg4.ps}\end{figure}](/articles/aa/full/2004/29/aa0001-04/Timg24.gif)