A&A 422, 253-265 (2004)
DOI: 10.1051/0004-6361:20035901
Improvement of the CORS method for Cepheids radii determination based on Strömgren photometry
A. Ruoppo
1,2 -
V. Ripepi
1 -
M. Marconi
1 -
G. Russo
2
1 - INAF - Osservatorio Astronomico di Capodimonte, via Moiariello 16, 80131 Napoli, Italy
2 -
Dipartimento di scienze fisiche università di Napoli Federico II, Complesso Monte S.Angelo, 80126 Napoli, Italy
Received 18 December 2003 / Accepted 16 April 2004
Abstract
In this paper we present a modified version of the CORS
method based on a new calibration of the Surface Brightness
function in the Strömgren photometric system. The method has
been tested by means of synthetic light and radial velocity curves
derived from nonlinear pulsation models. Detailed simulations have been
performed to take into account the quality of real observed curves
as well as possible shifts between photometric and radial velocity data.
The method has been then applied to a sample of Galactic Cepheids
with Strömgren photometry and radial velocity data to derive the
radii and a new PR relation. As a result we find
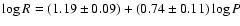 (rms = 0.07).
The comparison between our result and previous estimates
in the literature is satisfactory.
Better results are expected from the adoption of improved
model atmosphere grids.
(rms = 0.07).
The comparison between our result and previous estimates
in the literature is satisfactory.
Better results are expected from the adoption of improved
model atmosphere grids.
Key words: stars: distances -
stars: fundamental parameters -
Cepheids
Classical Cepheids are the cornerstone of the extragalactic distance scale.
Thanks to their characteristic Period-Luminosity (PL) and
Period-Luminosity-Color (PLC) relations they are traditionally
used to derive the distances to Local Group galaxies,
and (with the advent of space observations) to external galaxies distant up
to about 25 Mpc (targets of a Hubble Space Telescope Key Project, see Freedman et al. 1997, 2001). As primary indicators they are used to calibrate
a number of secondary distance indicators (see e.g., Freedman et al. 2001)
reaching the region of the so called Hubble flow where
the Hubble law can be applied and an estimate of the Hubble
constant can be derived.
Moreover, the comparison between Cepheid physical parameters
(stellar mass, luminosity, chemical composition)
based on evolutionary and pulsation models supplies
the unique opportunity to pin point the occurrence
of deceptive systematic errors (Bono et al. 2001a; Moskalik 2000) on the
Cepheid distance scale.
In particular radius determinations are important to constrain
both the intrinsic luminosity, through the application of the
Stefan-Boltzmann law, provided that an effective temperature calibration
is available, and the stellar mass, by adopting a Period-Mass-Radius
relation (e.g., Bono et al. 2001).
Many investigations have been devoted during the last decade to the
derivation of accurate Period-Radius (PR) relations for Classical Cepheids
both from the empirical (see e.g., Laney & Stobie 1995; Gieren et al. 1998; Ripepi et al. 1997) and the
theoretical (Bono et al. 1998; Marconi et al. 2003) point of view.
Empirical Cepheid radii are generally derived either by means of
the Baade Wesselink (BW) method (Moffet & Barnes 1987; Ripepi et al. 1997;
Gieren et al. 1998, just to list a few examples) both in the classical
form and in subsequent modified versions, or with interferometric coupled with trigonometric parallaxes
techniques (Nordgren et al. 2000; Lane et al. 2002).
The latter method is more direct and less model dependent but up to now
it has been applied only to a limited number of stars.
On the other hand, the different versions of the BW technique can be
applied to relatively large Cepheid samples but require
both accurate photometric and radial velocity data.
A powerful modification of the BW technique is the so called CORS method (Caccin et al. 1981), which has the advantage of taking into
account the whole light curve rather than selecting phase points
at the same color (as in the classical BW implementation), but relies on
the adoption of an accurate Surface Brightness (SB) calibration.
Originally Sollazzo et al. (1981) adopted the empirical SB photometric
calibration in the Walraven system provided by Pel (1978). More recently
Ripepi et al. (1997) modified the method, by adopting the empirical calibration
of the reduced surface
brightness FV as a function of (V-R) provided by
Barnes et al. (1976).
This modified version of the CORS method was tested, for different colors
selections, through the
application to synthetic light and radial velocity curves based
on nonlinear convective pulsation models (Ripepi et al. 2000).
The recent release of new Cepheid data in the Strömgren
photometric system (Arellano-Ferro et al. 1998), and the known sensitivity
of intermediate band colors to stellar physical parameters
(e.g. gravity and effective temperature) suggested us to
investigate the possibility of extending the CORS method to the
Strömgren filters.
To this purpose we have derived, in this system, a SB calibration based
on model atmosphere tabulations. In this paper we present a modified
version of the CORS method based on this new calibration and the
application to a sample of Galactic Cepheids.
The organization of the paper is the following: in Sect. 2 we summarize
the assumptions and the philosophy of the traditional CORS method;
in Sect. 3 we introduce the modified CORS method based on the new
SB calibration; in Sect. 4 we test the new method by means of pulsation
models; in Sect. 5 we apply the method to a sample of Galactic Cepheids
and present the comparison with the literature; in Sect. 6 our
final results concerning the PR relation for Galactic Cepheids are shown
and the theoretical fit of observed light and radial velocity variations
for Cepheid Y Oph is used as an additional check. Some final remarks
close the paper.
In this section we briefly outline the assumptions and the main features of the
CORS method in order to
better understand what follows.
The CORS method (Caccin et al. 1981) starts from the definition of the surface brightness:
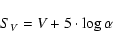 |
(1) |
where 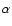 is the angular diameter of the star.
For a variable star, Eq. (1) is valid for the whole
pulsational cycle, so that
differentiating it with respect to the phase (
is the angular diameter of the star.
For a variable star, Eq. (1) is valid for the whole
pulsational cycle, so that
differentiating it with respect to the phase ( ),
multiplying by a color index (Cij) and integrating
over the whole cycle, one obtains:
),
multiplying by a color index (Cij) and integrating
over the whole cycle, one obtains:
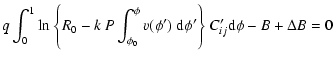 |
|
|
(2) |
where
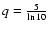
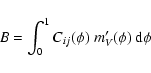 |
(3) |
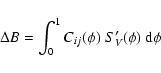 |
(4) |
where P is the period, v the radial velocity and k is the
radial velocity projection factor which relates radial to pulsation
velocity
(
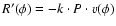 ). The typical value for kis 1.36 (see discussion
in Ripepi et al. 1997).
). The typical value for kis 1.36 (see discussion
in Ripepi et al. 1997).
From Eq. (2) we can evaluate the radius R0at an arbitrary phase 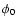 (usually
taken at the minimum of the radial velocity curve), whereas
the mean radius is obtained by integrating twice the radial velocity curve.
(usually
taken at the minimum of the radial velocity curve), whereas
the mean radius is obtained by integrating twice the radial velocity curve.
The B term can be easily calculated from observed light
and color curves. On the contrary, the  term, which
includes the Surface Brightness, is not directly observable.
By neglecting it in Eq. (2),
we obtain the pure Baade-Wesselink method (see Caccin et al. 1981).
However, Sollazzo et al. (1981) and Ripepi et al. (1997,
hereinafter RBMR)
demonstrated that the inclusion of
term, which
includes the Surface Brightness, is not directly observable.
By neglecting it in Eq. (2),
we obtain the pure Baade-Wesselink method (see Caccin et al. 1981).
However, Sollazzo et al. (1981) and Ripepi et al. (1997,
hereinafter RBMR)
demonstrated that the inclusion of  improves the accuracy
of radius estimates, provided that SV is evaluated
at each pulsation phase.
improves the accuracy
of radius estimates, provided that SV is evaluated
at each pulsation phase.
As outlined in the previous section, the inclusion of  improves the accuracy of radius estimates. In this section we present a new
good approximation for this term.
improves the accuracy of radius estimates. In this section we present a new
good approximation for this term.
As discussed by Onnembo et al. (1985), if the quasi-static approximation (QSA)![[*]](/icons/foot_motif.gif) is assumed for
Cepheid atmospheres, any photometric quantity can be expressed
as a function of effective temperature and gravity (
is assumed for
Cepheid atmospheres, any photometric quantity can be expressed
as a function of effective temperature and gravity (
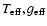 );
Then we can write:
);
Then we can write:
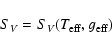 |
(5) |
and
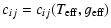 |
|
|
(6) |
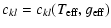 |
|
|
|
where SV is the surface brightness in the visual band,
and
cij = (mi -mj),
ckl = (mk -ml) are two arbitrary colors.
If the last two equations are invertible, i.e
the Jacobian
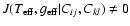 ,
then we can invert Eqs. (6), obtaining:
,
then we can invert Eqs. (6), obtaining:
and hence
We point out that Eqs. (6) do not admit a general
solution over the whole parameter space, given that the same colors
can be obtained for different pairs of
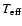 and
and
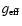 .
This notwithstanding it is possible to find a local solution,
that is a solution valid only in the parameter space defined
by Cepheids.
.
This notwithstanding it is possible to find a local solution,
that is a solution valid only in the parameter space defined
by Cepheids.
A potentially advantageous choice for the colors cij, ckl could be
represented by the Strömgren reddening free indexes [m1] and [c1]
defined as follows (Crawford & Mandwewala 1976):
|
[m1] = m1 + 0.33 (b-y)
|
(9) |
|
[c1] = c1 - 0.16 (b-y)
|
(10) |
where the coefficients 0.33 and -0.16 are suitable for F supergiant stars (Gray 1991).
In this context, an interesting possibility to derive Eqs. (7), consists in using grids of theoretical colors,
calculated by means of model atmospheres,
to obtain
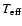 and
and
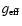 as a function of [m1] and [c1].
as a function of [m1] and [c1].
To verify this possibility, we have adopted the grids of
theoretical colors by Castelli et al.
(1997a,b, hereinafter C97a,b).
The theoretical grid (constant
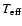 and
and 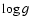 )
in the [m1], [c1] plane is shown in Fig. 1. This figure
suggests that for
)
in the [m1], [c1] plane is shown in Fig. 1. This figure
suggests that for
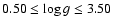 and
and
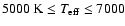 K there
is a one-to-one correspondence between a point in the [m1], [c1] plane
and the corresponding
K there
is a one-to-one correspondence between a point in the [m1], [c1] plane
and the corresponding
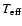 and
and 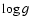 values.
Thus, in principle, in this color range it is possible to
invert Eqs. (6) and, in turn, to derive an expression for
Eq. (8).
values.
Thus, in principle, in this color range it is possible to
invert Eqs. (6) and, in turn, to derive an expression for
Eq. (8).
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0901fig1.ps}
\end{figure}](/articles/aa/full/2004/28/aa0901/Timg48.gif) |
Figure 1:
A grid of lines at constant
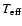 and constant
and constant 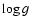 in the theoretical [m1], [c1] plane.
in the theoretical [m1], [c1] plane. |
| Open with DEXTER |
Before proceeding, it is important to verify if the location of
theoretical grids in the
[m1],[c1] plane is consistent with the one
occupied by real Cepheid data.
To this aim, we have overplotted in Fig. 1
the color-color
[m1],[c1] loop for all the stars in our sample
(see Sect. 5.1). Figure 2 shows the resulting comparison
for three stars (FF Aql, FN Aql, U Aql) of our sample,
characterized by short and intermediate periods. The figure shows that
the color-color loops for the selected stars are completely included
in the theoretical grids. The same test has been
performed for the three stars W Sgr, WZ Sgr, SV Vul,
which have longer periods. As showed by Fig. 3, in this case
the color-color loops for the selected Cepheids
lies outside (at low gravity and low effective temperature) of the region covered by theoretical grids. This unexpected
result has to be taken into account when applying our method
to such long period stars.
An explanation for this model limitation is beyond the scopes of present
paper but it is an important issue worth to be addressed in a future work.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0901fig2.ps}
\end{figure}](/articles/aa/full/2004/28/aa0901/Timg49.gif) |
Figure 2:
Theoretical grids in the
[m1],[c1] plane, compared with
the empirical loops of three stars with period shorter than 10 d. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0901fig3.ps}
\par\end{figure}](/articles/aa/full/2004/28/aa0901/Timg50.gif) |
Figure 3:
The same as in Fig. 2 but for three Cepheids with period longer than 15 d. |
| Open with DEXTER |
As shown in the previous section, the first step in the construction of a new, based on Strömgren photometry, version of the CORS method, is the formulation of SV in the form of
Eq. (8). To this aim, we have first to find relations in the form of
Eqs. (7) starting from theoretical grids.
This has been achieved by means of a 4th degree polynomial fit
to the theoretical grid (least square fit). The results of the
polynomial approximations are reported in Appendix A,
and showed in Figs. 4 and 5 for
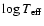 and
and
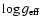 respectively. The rms of the fits are: 0.0018 dex for
respectively. The rms of the fits are: 0.0018 dex for
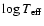 and 0.1 for
and 0.1 for
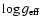 .
.
On the basis of the calculated relations we are now in the position to
estimate the surface brightness from the
expression:
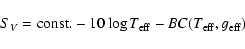 |
(11) |
where BC is the Bolometric Correction, derived as a function of effective temperature and gravity (
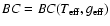 ). This function can be easily obtained
using again a 4th degree polynomial fit
to the theoretical grids. The resulting equation is also reported in
Appendix A and shown in Fig. 6. Note that the rms is only 0.003 mag.
). This function can be easily obtained
using again a 4th degree polynomial fit
to the theoretical grids. The resulting equation is also reported in
Appendix A and shown in Fig. 6. Note that the rms is only 0.003 mag.
The procedure outlined above allowed us to achieve our goal, i.e. to derive
an analytic, although approximated, expression of
SV = SV ([m1], [c1]),
and, in turn, to calculate the  term, which allows us to apply the
CORS method, in its more general formulation, for data in the Strömgren photometric system.
term, which allows us to apply the
CORS method, in its more general formulation, for data in the Strömgren photometric system.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{0901fig4.ps}
\par\end{figure}](/articles/aa/full/2004/28/aa0901/Timg55.gif) |
Figure 4:
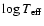 as a function of
[m1], [c1] obtained by a
4th degree polynomial fit of theoretical data (crosses) by C97a,b.
as a function of
[m1], [c1] obtained by a
4th degree polynomial fit of theoretical data (crosses) by C97a,b. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=270,width=6.8cm,clip]{0901fig6.ps}
\end{figure}](/articles/aa/full/2004/28/aa0901/Timg58.gif) |
Figure 6:
BC as a function of
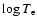 , , 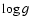 obtained by a
4 th degree polynomial fit of theoretical data (crosses) by C97a,b.
obtained by a
4 th degree polynomial fit of theoretical data (crosses) by C97a,b. |
| Open with DEXTER |
To verify the accuracy of the new approximation,
we have applied the CORS method (with the new SV calibration)
to synthetic light, color and radial velocity curves predicted
by Cepheid full amplitude, nonlinear, convective models.
The advantages of testing the method by means of pulsation model curves, rather than
empirical data, are the following:
- 1.
- for pulsation models, bolometric light curves are transformed into
the observational bands using the same model atmosphere tabulations (C97a,b) we have used to derive the surface
brightness calibration;
- 2.
- pulsation models provide a set of equally well sampled curves covering
wide period and effective temperature ranges;
- 3.
- for pulsation models the radius and intrinsic luminosity information
are available.
In the following we describe in detail how the models have been used
to test the method.
To test both the accuracy and the consistency of the new CORS method we have adopted the pulsation observables predicted by hydrodynamical
models of classical Cepheids. A detailed discussion on the physical
assumptions adopted to calculate these models can be found in
Bono et al. (1999, BMS99; 2002).
Among the different sequences of nonlinear models computed by BMS99 we have
selected canonical models![[*]](/icons/foot_motif.gif) at solar chemical composition (
Y=0.28, Z=0.02) and stellar masses
ranging from 5 to 9
at solar chemical composition (
Y=0.28, Z=0.02) and stellar masses
ranging from 5 to 9 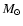 .
At fixed stellar mass, we generally
chose three models which are located in the middle of the
instability strip as well as close to the blue and the red edge.
The period of selected models roughly ranges from 3.5 to 62 days.
The input parameters (
.
At fixed stellar mass, we generally
chose three models which are located in the middle of the
instability strip as well as close to the blue and the red edge.
The period of selected models roughly ranges from 3.5 to 62 days.
The input parameters (
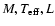 ), the computed radius and the
pulsational period are summarized in Table 1.
), the computed radius and the
pulsational period are summarized in Table 1.
Table 1:
Physical properties of the selected Cepheid models.
Theoretical observables have been transformed into the observational
plane by adopting the bolometric corrections (BC) and the
color-temperature relations by C97a,b.
We assumed
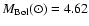 mag and adopted atmosphere models
computed by neglecting the core overshooting
and for a fixed value of the microturbolence velocity
mag and adopted atmosphere models
computed by neglecting the core overshooting
and for a fixed value of the microturbolence velocity
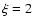 km s-1.
km s-1.
For each pulsation model we have derived the V light curve, three color curves, namely in (b-y), [m1] and [c1] and the radial velocity curve.
Figure 7 shows these curves for models with
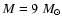 ,
,
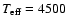 K, and
K, and
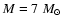 ,
,
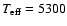 K.
K.
![\begin{figure}
\par\includegraphics[clip,width=6cm,clip]{0901fig7.ps}
\end{figure}](/articles/aa/full/2004/28/aa0901/Timg67.gif) |
Figure 7:
Variations along a full pulsation cycle of magnitude, color and radial velocity for models with
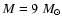 and
and
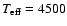 K ( left) and K ( left) and
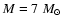 and
and
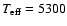 K ( right). K ( right). |
| Open with DEXTER |
As a first test, we have applied the method
to "perfect'' light, color and radial velocity curves, i.e.
the curves directly obtained from the models which, of course, do not
show random errors. This
test allows us to verify whether or not our calibration of the surface brightness
is intrinsically correct. If this is the case we do not expect
a large discrepancy between the calculated radii and the "true''
(theoretical) ones.
To perform this comparison
we have evaluated the radius of each model in the two
different approximations:
- without the
 term (Baade-Wesselink approximation);
term (Baade-Wesselink approximation);
- with the
 estimated as described in Sect. 3.
estimated as described in Sect. 3.
The results of this test are summarized in the first four columns of Table 2. We note that, the application to models with long period is justified by the fact that the bolometric light curves of pulsation models have been transformed into the observational bands by using the same model atmospheres by C97a,b. Therefore, at variance with the observed long period Cepheids, the model color-color loops are always consistent with C97a,b's grids.
Table 2:
Radii estimated with the two different approximations ,
i.e with and without the  term (respectively Cols. 2, 3), using model predictions (Col. 4), and from modified synthetic curves in the case of good (Col. 5) and fair (Col. 6) data respectively.
term (respectively Cols. 2, 3), using model predictions (Col. 4), and from modified synthetic curves in the case of good (Col. 5) and fair (Col. 6) data respectively.
The same result is also shown in Fig. 8, which suggests
that our calibration of the surface brightness
is intrinsically correct with the discrepancy between
"computed'' and "theoretical'' Cepheid radii being around 1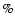 .
We also note that the inclusion of the
.
We also note that the inclusion of the  term only slightly improves the agreement with predicted radii, producing a small reduction of the scatter around the mean (see labelled values in Fig. 8).
term only slightly improves the agreement with predicted radii, producing a small reduction of the scatter around the mean (see labelled values in Fig. 8).
![\begin{figure}
\par\includegraphics[clip,width=3.5cm]{0901fig8.ps}
\end{figure}](/articles/aa/full/2004/28/aa0901/Timg76.gif) |
Figure 8:
Ratio between "computed'' and "theoretical'' radii as a
function of the logarithmic period. The bottom panel displays the radius
evaluation based on the revised CORS method, while the top one
the radius evaluations based on the pure BW method. |
| Open with DEXTER |
Once verified that the new calibration of the surface brightness is
intrinsically correct, we are in the position to estimate the
statistical error
in the radius determination due to uncertainties in the measurements, i.e.
to test the sensitivity of our technique to the accuracy of
observed light, color and radial velocity curves.
To this aim, we have transformed the synthetic curves for models in Table 1 by adopting the following steps:
- 1.
- we have reduced the number of
phase points to the typical value for observations, i.e.
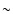 30-35;
30-35;
- 2.
- we have extracted phases randomly;
- 3.
- we have added Gaussian errors, considering the cases:
a) good data (
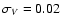 mag,
mag,
![$\sigma_{[m_1]}=0.04$](/articles/aa/full/2004/28/aa0901/img79.gif) mag,
mag,
![$\sigma_{[c_1]}=0.04$](/articles/aa/full/2004/28/aa0901/img80.gif) mag,
mag,
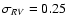 km-1, number of phase points = 35);
km-1, number of phase points = 35);
b) fair data (
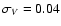 mag,
mag,
![$\sigma_{[m_1]}=0.08$](/articles/aa/full/2004/28/aa0901/img83.gif) mag,
mag,
![$\sigma_{[c_1]}=0.08$](/articles/aa/full/2004/28/aa0901/img84.gif) mag,
mag,
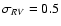 km-1, number of points = 30).
km-1, number of points = 30).
As an example, Fig. 9
shows the synthetic light, color and radial velocity curves obtained
for model Mod. 4 (see Table 1). Left panels show the pure model curves,
whereas middle and right panels
show the modified curves in the two cases a) and b) respectively.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0901fig9.ps}
\end{figure}](/articles/aa/full/2004/28/aa0901/Timg88.gif) |
Figure 9:
Light, color and radial velocity curves for the model (Mod. 4) with
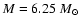 and
and
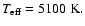 The left panels show the pure model
curves; the middle and right ones the modified curves in the
case of good and fair data respectively.
The left panels show the pure model
curves; the middle and right ones the modified curves in the
case of good and fair data respectively. |
| Open with DEXTER |
We then applied the new CORS method to the whole set of modified
synthetic curves. The resulting radii are reported in the last two columns of
Table 2, whereas in Fig. 10 we plot
the ratio between "computed'' and "theoretical'' radii as a function
of the logarithmic period. In particular, top and bottom panels
show the CORS solutions
without and with  respectively for the cases a) (left) and b) (right).
Figure 10 seems to show that including the
respectively for the cases a) (left) and b) (right).
Figure 10 seems to show that including the  term does
not improve much the results, on the contrary, the scatter in case a) worsens.
However, this disagreeable occurrence is only apparent. In fact, by excluding
"Mod. 8'' and "Mod. 10'' that show a very peculiar
morphology (a sharp bump) of the [c1] color curve
(see figure Fig. 7 for "Mod. 10''), which makes difficult the fit
and the
term does
not improve much the results, on the contrary, the scatter in case a) worsens.
However, this disagreeable occurrence is only apparent. In fact, by excluding
"Mod. 8'' and "Mod. 10'' that show a very peculiar
morphology (a sharp bump) of the [c1] color curve
(see figure Fig. 7 for "Mod. 10''), which makes difficult the fit
and the  calculation, the average uncertainties on the
radius estimation fall to
calculation, the average uncertainties on the
radius estimation fall to 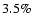 and
and 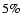 in cases a) and b) respectively (including the
in cases a) and b) respectively (including the  term).
term).
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0901fi10.ps}
\end{figure}](/articles/aa/full/2004/28/aa0901/Timg91.gif) |
Figure 10:
Ratio between "computed'' and "theoretical'' radii
as a function of the logarithmic period. In the left panels a) the radius is computed using modified curves that simulate good quality, adopting either the revised CORS method ( bottom) or the pure BW one ( top). In the right panels b) similar plots are shown for radii computed from modified curves that simulate fair quality data. |
| Open with DEXTER |
These numbers represent a useful lower limit for the error
associated with radius determination obtained by the CORS version developed
in this paper.
Another possible source of uncertainty in the radius determination
is the misalignment between light or color curves, and the radial velocity one.
In fact, the photometric and radial velocity data are rarely collected
simultaneously.
This occurrence could introduce a shift in phase
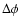 between the two different data set.
To verify the importance of this shift on the radius determination
we have introduced an artificial phase shift in the synthetic radial velocity curves with respect to the photometric
ones.
between the two different data set.
To verify the importance of this shift on the radius determination
we have introduced an artificial phase shift in the synthetic radial velocity curves with respect to the photometric
ones.
![\begin{figure}
\par\includegraphics[clip,width=5.5cm,clip]{0901fi11.ps}
\end{figure}](/articles/aa/full/2004/28/aa0901/Timg93.gif) |
Figure 11:
Ratio between the "computed'' and "theoretical''
radii as a function of the shift
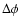 for the model
(mod. 2) with M= 5
for the model
(mod. 2) with M= 5 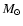 , ,
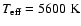 . . |
| Open with DEXTER |
The result of such a test is shown in Fig. 11, where the
ratio between "computed'' and "theoretical'' radii is plotted
as a function of the phase shift
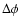 for the model Mod. 2.
The "computed'' radius is larger than the "theoretical'' one
for
for the model Mod. 2.
The "computed'' radius is larger than the "theoretical'' one
for
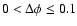 ,
whereas it becomes smaller beyond 0.1 with the effect increasing with the phase shift.
Eventually, our program does not converge for
,
whereas it becomes smaller beyond 0.1 with the effect increasing with the phase shift.
Eventually, our program does not converge for
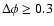 .
However, such large phase shifts are never reached when we deal
with actual data. In fact, when the temporal
distance between photometric and radial velocity data is rather long (
.
However, such large phase shifts are never reached when we deal
with actual data. In fact, when the temporal
distance between photometric and radial velocity data is rather long (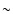 1000 cycles ), for a typical Cepheid with period
1000 cycles ), for a typical Cepheid with period
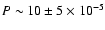 d, the resulting phase shift
is
d, the resulting phase shift
is
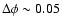 .
As shown in Fig. 11, this value
of
.
As shown in Fig. 11, this value
of
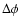 is sufficient to generate a systematic error
on the derived radius of about 17
is sufficient to generate a systematic error
on the derived radius of about 17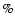 .
This occurrence confirms quantitatively the need to use photometric
and radial velocity data as close as possible in time, or otherwise to correct this shift.
.
This occurrence confirms quantitatively the need to use photometric
and radial velocity data as close as possible in time, or otherwise to correct this shift.
Having tested the capabilities of the new version of the CORS method
(see previous section), we are ready to
apply it to actual data. In the following we discuss the application to a sample of 52 Galactic Cepheids.
We searched the literature for an homogeneous sample of Galactic Cepheids with photometric data in the Strömgren system and we selected the 31 pulsators
analysed by Arellano Ferro et al. (1998) (AFGR hereafter) supplemented by data
for other 21 objects from the papers by Feltz & McNamara (1980) (FM hereafter) and Eggen (1985, 1996) (Eg hereafter).
Concerning radial velocity data, several large and homogeneous datasets
are available in the literature. In particular,
we have used the catalogues from: Evans (1980) (E hereafter),
Gieren (1981) (G hereafter), Barnes et al. (1987, 1988), (BMS hereafter),
Coulson et al. (1985) (CCG hereafter), Wilson et al. (1989) (WCB hereafter),
Metzger et al. (1993) (MCMS hereafter), Bersier et al. (1994) (BBMD hereafter), Gorynya et al. (1998) (GSSRGA hereafter),
Kiss (1998) (K hereafter) and
Imbert (1999) (I hereafter).
In general we considered only Cepheids with good photometric and radial
velocity curves,
i.e. more than 15 phase points and reasonable precision.
When measurements by different authors are available for the same stars we have chosen data which have: 1) the largest phase points number and
the best precision; 2) the lowest temporal separation with respect to the photometric
data. When we have distant data sets, that is differences between radial velocity and photometric curves larger than  1000 cycles (6 stars, see Table 3), we correct the misalignment between this two curves by using different epochs.
1000 cycles (6 stars, see Table 3), we correct the misalignment between this two curves by using different epochs.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0901fi12.ps}
\end{figure}](/articles/aa/full/2004/28/aa0901/Timg98.gif) |
Figure 12:
Comparison of radii obtained in this work (
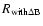 , ,
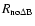 )
with those derived by other authors (Arellano Ferro & Rosenzweing (2000) )
with those derived by other authors (Arellano Ferro & Rosenzweing (2000)
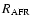 ;
Ripepi et al. (1997) ;
Ripepi et al. (1997)
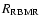 ;
Moffett & Barnes (1987) ;
Moffett & Barnes (1987)
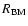 ). ). |
| Open with DEXTER |
In few cases we have merged data from different authors,
in order to obtain more sampled radial velocity curves
(see Table 3).
Our final selected dataset is summarized in Table 3.
Table 3:
The selected Cepheid sample.
Some Cepheids in our sample need to be
discussed individually:
- for the stars TT Aql, X Cyg, T Mon, RU Sct, Y Sct, WZ Sgr and SV Vul,
we can calculate the radius only in the classical Baade-Wesselink approximation
(without the
 term), because for these stars the loop in the [m1], [c1] plane does not lie completely within
the theoretical grids by C97a,b (see paragraph 3.1);
term), because for these stars the loop in the [m1], [c1] plane does not lie completely within
the theoretical grids by C97a,b (see paragraph 3.1);
- we have excluded from our sample the Cepheids GI Car, SU Cas, Y Lac,
SZ Tau, X Vul for the poor data quality;
- stars DT Cyg, FF Aql, BG Cru and V440 Per are first overtone pulsators
(Antonello et al. 1990);
- stars TU Cas, V367 Sct and BQ Ser are double mode Cepheids (Pardo & Poretti 1997, and references therein);
- stars U Aql, FF Aql, V 496 Aql,
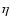 Aql, RX Aur, SU Cas,
Aql, RX Aur, SU Cas, 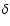 Cep, GI Car, SU Cyg, VZ Cyg,
Cep, GI Car, SU Cyg, VZ Cyg, 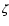 Gem, X Lac, Y Lac, Z Lac, BG Lac, T Mon, Y Oph, BF Oph, AW Per, Y Sct, S Sge, W Sgr, Y Sgr, WZ Sgr, AP Sgr, V 350 Sgr, SZ Tau, T Vul, U Vul and SV Vul are members of binary systems. Note that this list is the result of a detailed analysis of Szabados's selection (Szabados 2003, and references therein).
Gem, X Lac, Y Lac, Z Lac, BG Lac, T Mon, Y Oph, BF Oph, AW Per, Y Sct, S Sge, W Sgr, Y Sgr, WZ Sgr, AP Sgr, V 350 Sgr, SZ Tau, T Vul, U Vul and SV Vul are members of binary systems. Note that this list is the result of a detailed analysis of Szabados's selection (Szabados 2003, and references therein).
In Table 4 we report the radius obtained for all the Cepheids in our sample
and, for comparison purposes, we report the literature results renormalized to
our projection factor k.
In particular, from left to right we report for each Cepheid: the name; the period;
the CORS radii obtained without and with the  term
(
term
(
 and
and
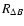 );
the radii obtained by Arellano Ferro & Rosenzweing (2000)
);
the radii obtained by Arellano Ferro & Rosenzweing (2000)
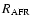 ,
Laney & Stobie (1995)
,
Laney & Stobie (1995)
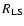 or Gieren et al. (1998)
or Gieren et al. (1998)
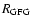 ,
Ripepi et al. (1997)
,
Ripepi et al. (1997)
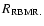 and Moffett & Barnes (1987)
and Moffett & Barnes (1987)
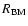 .
.
In Fig. 12 we have compared our results with those of authors reported in Table 4. As a result we find that our radii are on average
larger than the radii obtained by Arellano Ferro & Rosenzweing (2000) and
Moffett & Barnes (1987), while they are slightly smaller than Ripepi et al. (1997) ones
(see labels in Fig. 12).
The scatter in this comparisons is rather large (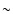 30%); this occurrence could
be due to: 1) the inclusion of binary stars in the comparison (different methods
use different colours and then binarity could affect differentially
the various determinations); 2) the use of optical colors.
Verifying hypothesis 1) by comparing only the non-binary stars
does not make sense because of the small number of "bona fide'' single stars
in our sample.
30%); this occurrence could
be due to: 1) the inclusion of binary stars in the comparison (different methods
use different colours and then binarity could affect differentially
the various determinations); 2) the use of optical colors.
Verifying hypothesis 1) by comparing only the non-binary stars
does not make sense because of the small number of "bona fide'' single stars
in our sample.
Concerning point 2), as well known in the literature (Laney & Stobie 1995;
Gieren et al. 1997), radii
obtained from NIR data are more precise than the ones obtained by using optical colors.
Unfortunately, most works with radii determinations from NIR data deal
with southern Cepheids and we have very few stars in common
(see Col. 7 of Table 4
for the comparison).
Table 4:
Radii derived with the current CORS method compared with
previous determinations (see text).
Recently it has become possible to derive accurate stellar radii from the
angular diameters measured with interferometric
techniques (see Nordgren et al. 2000 and Lane et al. 2002) combined with Hypparcos parallaxes. The comparison with these measurements represents a useful
test for our results.
In Table 5 we compare with our results the radii obtained by Nordgren et al. (2000)
and Lane et al. (2002), with the quoted interferometric techniques, for the stars in
common with our sample, namely 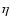 Aql,
Aql, 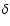 Cep and
Cep and 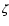 Gem. In particular,
from left to right, we report: the name of the star;
the radius (RI) obtained by means of interferometric techniques (
Gem. In particular,
from left to right, we report: the name of the star;
the radius (RI) obtained by means of interferometric techniques (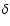 Cep
from Nordgren et al. 2000 and
Cep
from Nordgren et al. 2000 and 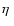 Aql and
Aql and 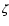 Gem from
Lane et al. 2002); our radius in the two different approximations,
without (
Gem from
Lane et al. 2002); our radius in the two different approximations,
without (
 )
and with (
)
and with (
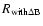 )
the
)
the  term respectively. The interferometric radii, reported in Table 5, are corrected for the different k projection factors. So we obtain the radii
term respectively. The interferometric radii, reported in Table 5, are corrected for the different k projection factors. So we obtain the radii
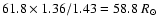 ,
,
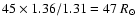 and
and
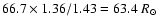 for
for 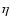 Aql,
Aql, 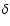 Cep and
Cep and 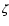 Gem, respectively.
We notice that the agreement between our results and the interferometric ones is very
good for
Gem, respectively.
We notice that the agreement between our results and the interferometric ones is very
good for 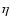 Aql and
Aql and 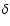 Cep, whereas some discrepancy is found for
Cep, whereas some discrepancy is found for 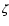 Gem. However, by
assuming a typical error of
Gem. However, by
assuming a typical error of 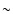
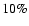 (see discussion in Sect. 7) on the radii found, we conclude that our
results are globally consistent with the interferometric ones.
(see discussion in Sect. 7) on the radii found, we conclude that our
results are globally consistent with the interferometric ones.
Table 5:
Comparison with radii measured with interferometric techniques (see text for details).
After having tested the method and the consistency of our results with
previous determinations in the literature, we are in the position
to derive a PR relation based on the new derived radii.
The PR relations for all the stars in our sample for which the
program reached the convergence are shown in Fig. 13, where
the the top and bottom panels illustrate the case without and
with  respectively.
A least square fit to the data (solid lines in Fig. 13)
leads to the following Period-Radius relations in the case
without the
respectively.
A least square fit to the data (solid lines in Fig. 13)
leads to the following Period-Radius relations in the case
without the  term (Eq. (12)) and
with the
term (Eq. (12)) and
with the  term (Eq. (13)):
term (Eq. (13)):
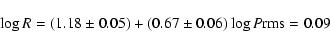 |
(12) |
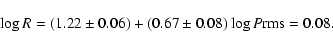 |
(13) |
An inspection of the figure suggests that the presence
of first overtone pulsators (filled triangles) could affect the
derived PR relations because, at fixed period, they are brighter
and, in turn, have larger radii than fundamental pulsators.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0901fi13.ps}
\par\end{figure}](/articles/aa/full/2004/28/aa0901/Timg116.gif) |
Figure 13:
Top: Period-Radius relation obtained in the case without
 ;
Bottom: as before, but with ;
Bottom: as before, but with  .
Open circle: Binary stars; Triangles: first overtone pulsators;
Crosses: stars with loop in the [m1], [c1] plane not
completely within the theoretical grids (see Sect. 3). .
Open circle: Binary stars; Triangles: first overtone pulsators;
Crosses: stars with loop in the [m1], [c1] plane not
completely within the theoretical grids (see Sect. 3). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0901fi14.ps}
\par\end{figure}](/articles/aa/full/2004/28/aa0901/Timg117.gif) |
Figure 14:
The same of Fig. 13 but excluding first overtone and binary stars. |
| Open with DEXTER |
Similarly, also Cepheids belonging to binary systems could
affect the radius determination. Therefore, we decided to exclude
from our relations the first overtone pulsators and the stars flagged as "B'' and "O''![[*]](/icons/foot_motif.gif) in Table 4, whereas we left in our
sample the Cepheids flagged as "B:'', "b'' and "V'' (i.e. uncertain
spectroscopic binaries and separated visual binaries respectively,
see Szabados 2003).
As a result of this selection procedure,
we are left with 20 and 16 Cepheids in the cases without and with
in Table 4, whereas we left in our
sample the Cepheids flagged as "B:'', "b'' and "V'' (i.e. uncertain
spectroscopic binaries and separated visual binaries respectively,
see Szabados 2003).
As a result of this selection procedure,
we are left with 20 and 16 Cepheids in the cases without and with  respectively. We therefore calculated new Period-Radius
relations with the following
results (see Fig. 14):
respectively. We therefore calculated new Period-Radius
relations with the following
results (see Fig. 14):
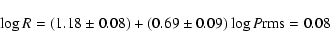 |
(14) |
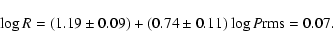 |
(15) |
A comparison between Eqs. (12), (13) and Eqs. (14), (15) shows that the net result of our
selection criterion mainly consists in increasing the slope of
the PR relation, going in the direction to improve the agreement with the literature, and, in particular with the NIR results by
Laney & Stobie (1995) and Gieren et al. (1998)
(see Table 6 for a comparison between present results and other relations in the literature). Yet, we have to note that the errors
of the derived coefficients are rather large. This is caused by:
1) the small number of Cepheids left after the selection process (in particular the number of binary stars in our sample is very large);
2) the lack of long period Cepheids in the case with  ,
as
a result of problems with synthetic model atmosphere grids (see Sect. 3.1).
We remark, however, that including or not the
,
as
a result of problems with synthetic model atmosphere grids (see Sect. 3.1).
We remark, however, that including or not the  term
in the CORS determination makes some difference, in the sense that, apart from
a few Cepheids in the low period range, the scatter in the PR relation
is slightly reduced (see Fig. 14) when the
term
in the CORS determination makes some difference, in the sense that, apart from
a few Cepheids in the low period range, the scatter in the PR relation
is slightly reduced (see Fig. 14) when the  term is included. This result seems to suggest that the modification to the CORS method presented in this
paper is well suited also when applied to real stars (not merely to synthetic
light curves).
term is included. This result seems to suggest that the modification to the CORS method presented in this
paper is well suited also when applied to real stars (not merely to synthetic
light curves).
Table 6:
Comparison between the PR (
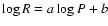 )
coefficients
obtained in this paper and the ones based on selected works in literature.
In particular, from left to right, we report the slope,
the zero point, the source and the method adopted for deriving the PR.
)
coefficients
obtained in this paper and the ones based on selected works in literature.
In particular, from left to right, we report the slope,
the zero point, the source and the method adopted for deriving the PR.
Finally, we notice that our results concerning the radii and the PR relations
could be, in principle, combined with an effective temperature
calibration to derive the intrinsic stellar luminosity,
through the Stefan-Boltzmann law, and in turn distance to studied
Cepheids. This possibility will be investigated in a forthcoming paper.
In the following section we will apply an alternative method to derive the
luminosity and distance by means of the comparison of empirical light and
radial velocity curves with the predictions of the nonlinear convective
pulsation models discussed above.
Before going to the conclusions of this paper, we note that
it has recently been suggested that nonlinear pulsation models
provide a direct tool to evaluate the intrinsic stellar properties
of pulsating stars through the comparison of observed and predicted
variations of relevant parameters along a pulsation cycle (see Wood et al. 1997; Bono et al. 2000, 2002).
This kind of analysis also provides an additional test for our radius
determination technique by means of the comparison with the radius of
the model which is able to simultaneously reproduce the period, the
amplitude and the morphology of light and radial velocity curves.
We plan to apply this method to a sample of Galactic Cepheids with
accurate photometric data and available radial velocity information.
In this paper we present a first application to the Cepheid Y Oph.
The observed properties of this star are summarized in
Table 7.
Table 7:
Top: observed properties of Y Oph; Bottom: physical parameters of the best fit model.
Starting from the observed radial velocity and light curve,
we try to reproduce their morphology and amplitude,
by computing pulsation models along isoperiodic (with period
equal to the observed one) sequences with varying pulsation
mass and effective temperature and assuming, for each mass,
a canonical mass-luminosity relation.
The best fit model resulting from these computations is shown
in Fig. 15 (solid line). The corresponding stellar
parameters are reported in Table 7 and show that
the agreement with the radius determined in this paper is good.
![\begin{figure}
\par\includegraphics[clip,width=7.2cm]{0901fi15.ps}
\end{figure}](/articles/aa/full/2004/28/aa0901/Timg124.gif) |
Figure 15:
Top panel: empirical light curve (dots)
for the star Y Oph, compared with the best fit model (solid
lines, see text for details). Bottom panel: the same but
for the radial velocity curve. |
| Open with DEXTER |
The other important information provided by the fit is the
stellar absolute magnitude
MV=-3.996 mag, which allows
us to estimate a distance of about 423 pc, consistent with
the independent evaluation by Gieren et al. (1993), thus
supporting the predictive capability of pulsation models.
Table A.1:
Coefficients for the polynomial fits described in the Appendix.
We have presented a modified version of the CORS
method based on a new calibration of the Surface Brightness
function in the Strömgren photometric system.
In particular we have been able to derive a calibration of SV as a function of the Strömgren reddening free
indexes [m1] and [c1] by adopting grids of
theoretical colors. This procedure revealed the unexpected occurrence
that the quoted theoretical grids are not able to fully
include the location of actual long period (
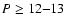 days)
Cepheids loops in the [m1],[c1] plane. This
problem could only be overcome by adopting next generation,
hopefully improved, model atmosphere grids.
Nevertheless, the modified CORS method presented here
has been tested by means of synthetic light and radial velocity
curves derived from nonlinear pulsation models and simulations have been
performed to take into account the quality of real observed curves
as well as possible time shifts between photometric and radial velocity data.
The results of such tests can be summarized as follows:
days)
Cepheids loops in the [m1],[c1] plane. This
problem could only be overcome by adopting next generation,
hopefully improved, model atmosphere grids.
Nevertheless, the modified CORS method presented here
has been tested by means of synthetic light and radial velocity
curves derived from nonlinear pulsation models and simulations have been
performed to take into account the quality of real observed curves
as well as possible time shifts between photometric and radial velocity data.
The results of such tests can be summarized as follows:
-
- a)
- The present method appears capable
to derive the radius of a Cepheid with an
average precision of around 3.5% and 5% in the case of good and fair
observational data respectively (see Sect. 4.3).
- b)
- The error associated with a phase shift between photometric and
radial velocity data could be as large as
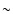 17% in the extreme
case of
17% in the extreme
case of
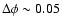 .
In a more common case of
.
In a more common case of
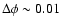 the relative error is still rather large, namely
the relative error is still rather large, namely 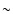 5%. If we add to the error budget the uncertainty on the
value of the projection factor k
(
5%. If we add to the error budget the uncertainty on the
value of the projection factor k
(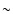
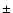 2% for
2% for
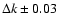 ), neglecting other
possible contributions (see Bono et al. 1994 and references therein for a detailed discussion), we
can conclude that estimating
the radius of a Cepheid by means of the Baade-Wesselink method
(at least in the present formulation) with an accuracy better than 10% is extremely difficult to be achieved.
), neglecting other
possible contributions (see Bono et al. 1994 and references therein for a detailed discussion), we
can conclude that estimating
the radius of a Cepheid by means of the Baade-Wesselink method
(at least in the present formulation) with an accuracy better than 10% is extremely difficult to be achieved.
The method has been then applied to a sample of Galactic Cepheids
with Strömgren photometry and radial velocity data to derive the
radii and a new PR relation. As a result we obtained the following
PR relation:
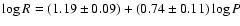 (rms = 0.07).
This relation, even if not very accurate (mainly due to
the unexpected presence of a large fraction of binary stars in our
Cepheid sample), nevertheless is in satisfactory agreement
with previous findings in the literature.
(rms = 0.07).
This relation, even if not very accurate (mainly due to
the unexpected presence of a large fraction of binary stars in our
Cepheid sample), nevertheless is in satisfactory agreement
with previous findings in the literature.
Acknowledgements
We wish to thank our anonymous referee for several pertinent suggestions
that improved the content and the readability of the paper.
This work made use of the "McMaster Cepheid Photometry
and Radial Velocity Data Archive'' maintained by Doug Welch, and of
SIMBAD database, maintained at the CDS-Strasbourg. This work was partially supported by MIUR/Cofin 2002, under the
project "Stellar Populations in Local Group Galaxies'' (Monica Tosi
coordinator).
The 4th degree polynomial fit to effective temperature, effective gravity, and bolometric corrections mentioned in Sect. 3.1.1 are the following:
the coefficients ai, bi, ci of the previous relations are listened in Table A.1 and the other symbols have their usual meaning. Note the rms of the previous relations are 0.0018 dex, 0.1 dex and 0.003 mag respectively.
-
Antonello, E., Poretti, E., & Reduzzi, L. 1990, A&A, 236,
138 [NASA ADS] (In the text)
- Arellano
Ferro, A., Rojo Arellano, E., Gonzàlez-Bedolla, S., &
Rosenzweig, P. 1998, ApJ, 117, 167 [NASA ADS] [CrossRef] (AFGR)
(In the text)
- Arellano
Ferro, A., & Rosenzweing, P. 2000, MNRAS, 315, 296 [NASA ADS] [CrossRef] (AFR)
(In the text)
- Baade, W. 1926,
Astron. Nachr., 228, 359 [NASA ADS]
- Barnes, T. G.,
Evans, D. S., & Parson, S. B. 1976, MNRAS, 174, 489 [NASA ADS] (In the text)
- Barnes, T. G.,
Moffet, T. J., & Slovak, M. H. 1987, ApJS, 65, 307 [NASA ADS] [CrossRef] (BMS)
(In the text)
- Barnes, T. G.,
Moffet, T. J., & Slovak, M. H. 1988, ApJS, 66, 43 [NASA ADS] [CrossRef] (BMS)
(In the text)
- Bersier, D.,
Burki, G., Mayor, M., & Duquennoy, A. 1994, A&AS, 108, 25 [NASA ADS]
(BBMD)
(In the text)
- Bono, G., Caputo,
F., & Marconi, M. 1998, ApJ, 497, L43 [NASA ADS] [CrossRef] (BCM)
(In the text)
- Bono, G., Caputo,
F., & Stellingwerf, R. F. 1994, ApJ, 432, L51 [NASA ADS] [CrossRef] (In the text)
- Bono, G.,
Castellani, C., & Marconi, M. 2000, ApJ, 532, L129 [NASA ADS] [CrossRef] (In the text)
- Bono, G.,
Marconi, M., & Stellingwerf, R. F. 1999a, ApJS, 122, 167 [NASA ADS] [CrossRef]
(BMS99)
- Bono, G., Gieren,
W. P., Marconi, M., & Fouqué, P., Caputo, F. 2001, ApJ,
563, 319 [NASA ADS] [CrossRef] (In the text)
- Bono, G.,
Castellani, V., & Marconi, M. 2002, ApJ, 565, L83 [NASA ADS] [CrossRef] (In the text)
- Caccin, R., Onnembo,
A., Russo, G., & Sollazzo, C. 1981, A&A, 97, 104 [NASA ADS]
-
Castellani, V., Chieffi, A., & Straniero, O. 1992, ApJS, 78,
517 [NASA ADS] [CrossRef]
- Castelli,
F., Gratton, R. G., & Kurucz, R. L. 1997a, A&A, 318, 841 [NASA ADS]
(C97a)
(In the text)
- Castelli,
F., Gratton, R. G., & Kurucz, R. L. 1997b, A&A, 324, 432 [NASA ADS]
(C97b)
- Coulson, I.
M., Caldwell, A. R., & Gieren, W. P. 1985, ApJS, 57, 595 [NASA ADS] [CrossRef]
(CCG)
(In the text)
- Crawford,
D. L., & Mandwewala, N. 1976, PASP, 88, 917 [NASA ADS] [CrossRef] (In the text)
- Eggen, O. J.
1985, AJ, 90, 1297 [NASA ADS] [CrossRef] (Eg)
(In the text)
- Eggen, O. J.
1996, AJ, 111, 1313 [NASA ADS] [CrossRef] (Eg)
(In the text)
- Evans, L. T.
1980, SAAO Circulars 1, 257 (E)
(In the text)
- Feltz, K. A.,
& McNamara, D. H. 1980, ASP, 92, 609 [NASA ADS] (FM)
(In the text)
- Freedman,
W. L., Madore, B. F., & Kennicutt, R. C. 1997, in The
Extragalactic Distance Scale, ed. M. Livio, M. Donahue, & N.
Panagia (Cambridge: Cambridge Univ. Press), 171
(In the text)
- Freedman,
W. L., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553,
47F [NASA ADS] (In the text)
- Gieren, W. P.
1981, ApJS, 46, 287 [NASA ADS] [CrossRef] (G)
(In the text)
- Gieren, P. W.,
Barnes III, T. G., & Moffett, T. J. 1993, ApJ, 418, 135 [NASA ADS] [CrossRef] (In the text)
- Gieren, P. W.,
Fouqué, P., & Gómez, M. 1997, ApJ, 488, 74 [NASA ADS] [CrossRef] (In the text)
- Gieren, P. W.,
Fouqué, P., & Gómez, M. 1998, ApJ, 496, 17 [NASA ADS] (GFG)
(In the text)
- Gorynya, N.
A., Samus, N. N., SachKov, M. E., et al. 1998, Astron. Lett., 24,
6 [NASA ADS], 815 (GSSRGA)
(In the text)
- Gray, R. O. 1991,
A&A, 252, 237 [NASA ADS] (In the text)
- Imbert, M.
1999, A&AS, 140, 791 [NASA ADS] (I)
(In the text)
- Kiss, L. L. 1998,
MNRAS, 297, 825 [NASA ADS] [CrossRef] (K)
(In the text)
- Lane, B. F.,
Creech-Eakman, M. J., & Nordgren, T. E. 2002, ApJ, 124,
541 [NASA ADS] (In the text)
- Laney, C. D.,
& Stobie, R. S. 1995, MNRAS, 274, 337 [NASA ADS] (LS)
(In the text)
- Marconi, M.,
Caputo, F., Di Criscienzo, M., & Castellani, M. 2003, ApJ, 596,
299 [NASA ADS] [CrossRef] (In the text)
- Metzger, M.
R., Caldwell, J. A. R., McCarthy, J. K., & Schechter, P. L.
1993, ApJS, 76, 803 [NASA ADS] (MCMS)
(In the text)
- Moffett, T.
J., & Barnes, T. J., III 1987, ApJ, 323, 280 [NASA ADS] [CrossRef] (In the text)
- Moskalik,
P. 2000, in The Impact of Large-Scale Surveys on Pulsating Star
Research, ed. L. Szabados, & D. W. Kurtz, IAU Coll., 176, ASP,
233
(In the text)
- Onnembo, A.,
Buonaura, B., Caccin, B., Russo, G., & Sollazzo, C. 1985,
A&A, 152, 349 [NASA ADS] (In the text)
- Nordgren,
T. E., Armstrong, J. T., German, M. E., et al. 2000, ApJ, 543,
972 [NASA ADS] [CrossRef] (In the text)
- Pardo, I., &
Poretti, E. 1997, A&A, 324, 121 [NASA ADS] (In the text)
- Pel, J. W. 1978,
A&A, 62, 75 [NASA ADS] (In the text)
- Ripepi, V.,
Barone, F., Milano, F., & Russo, G. 1997, A&A, 318, 797 [NASA ADS]
(RBMR)
(In the text)
- Ripepi, V.,
Russo, G., Bono, G., & Marconi, M. 2000, A&A, 354, 77 [NASA ADS] (In the text)
- Rojo Arellano, E.,
& Arellano Ferro, A. 1994, RMxAA, 29, 148 [NASA ADS] (RAAF)
- Sollazzo, C., Russo, G., Onnembo, A.,
& Caccin, B. 1981, A&A, 152, 3490 [NASA ADS]
- Szabados,
L. 2003, INf. Bull. Var. Stars, 5394
(In the text)
- Wilson, T. D.,
Carter, M. W., Barnes, T. G., Van Citters, G. W., & Moffett, T.
J. 1989, ApJS, 69, 951 [NASA ADS] [CrossRef] (WCB)
(In the text)
- Wood, P. R.,
Arnold, A., & Sebo, K. M. 1997, ApJ, 485, L25 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2004
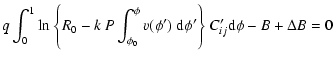
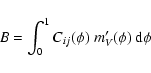
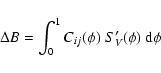
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0901fig1.ps}
\end{figure}](/articles/aa/full/2004/28/aa0901/Timg48.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0901fig2.ps}
\end{figure}](/articles/aa/full/2004/28/aa0901/Timg49.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0901fig3.ps}
\par\end{figure}](/articles/aa/full/2004/28/aa0901/Timg50.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=6.8cm,clip]{0901fig6.ps}
\end{figure}](/articles/aa/full/2004/28/aa0901/Timg58.gif)
![\begin{figure}
\par\includegraphics[clip,width=6cm,clip]{0901fig7.ps}
\end{figure}](/articles/aa/full/2004/28/aa0901/Timg67.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0901fig9.ps}
\end{figure}](/articles/aa/full/2004/28/aa0901/Timg88.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0901fi10.ps}
\end{figure}](/articles/aa/full/2004/28/aa0901/Timg91.gif)
![\begin{figure}
\par\includegraphics[clip,width=5.5cm,clip]{0901fi11.ps}
\end{figure}](/articles/aa/full/2004/28/aa0901/Timg93.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0901fi12.ps}
\end{figure}](/articles/aa/full/2004/28/aa0901/Timg98.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0901fi13.ps}
\par\end{figure}](/articles/aa/full/2004/28/aa0901/Timg116.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0901fi14.ps}
\par\end{figure}](/articles/aa/full/2004/28/aa0901/Timg117.gif)
![\begin{figure}
\par\includegraphics[clip,width=7.2cm]{0901fi15.ps}
\end{figure}](/articles/aa/full/2004/28/aa0901/Timg124.gif)