A&A 422, 351-355 (2004)
DOI: 10.1051/0004-6361:20040299

Flare-generated acoustic oscillations in solar and stellar coronal loops

D. Tsiklauri 1 - V. M. Nakariakov 2 - T. D. Arber 2 - M. J. Aschwanden 3


1 - Joule Physics Laboratory and Institute for Materials Research, School of Computing, Science & Engineering, University of Salford, Salford, M5 4WT, UK
2 - Physics Department, University of Warwick, Coventry, CV4 7AL, UK
3 - Lockheed Martin, Advanced Technology Center Solar & Astrophysics Laboratory, Dept. L9-41, Bldg. 252 3251 Hanover Street, Palo Alto, CA 94304, USA

Received 18 February 2004 / Accepted 23 April 2004

Abstract
Long period longitudinal oscillations of a flaring coronal loop are studied numerically. In the recent work of Nakariakov et al. (2004) it has been shown that the time dependence of density and velocity in a flaring loop contain pronounced quasi-harmonic oscillations associated with the 2nd harmonic of a standing slow magnetoacoustic wave. In this work we investigate the physical nature of these oscillations in greater detail, namely, their spectrum (using the periodogram technique) and how heat positioning affects mode excitation. We found that excitation of such oscillations is practically independent of the location of the heat deposition in the loop. Because of the change of the background temperature and density, the phase shift between the density and velocity perturbations is not exactly a quarter of the period; it varies along the loop and is time dependent, especially in the case of one footpoint (asymmetric) heating.

Key words: Sun: flares - Sun: oscillations - Sun: corona - stars: flare - stars: oscillations - stars: coronae

1 Introduction

Magnetohydrodynamic (MHD) coronal seismology is one of the main reasons for studying waves in the solar corona. Such studies also are important in connection with coronal heating and solar wind acceleration problems. Observational evidence of coronal waves and oscillations in EUV are numerous (e.g., Ofman et al. 1999; Ofman & Wang 2002). Radio band observations also demonstrate various kinds of oscillations (e.g., the quasi-periodic pulsations, or QPP, see Aschwanden 1987, for a review), usually with periods from a few seconds to tens of seconds. Decimeter and microwave observations show much longer periodicities, often in association with a flare. For example, Wang & Xie (2000) observed QPP with the periods of about 50 s at 1.42 and 2 GHz (in association with an M 4.4 X-ray flare). Similar periodicities have been observed in the X-ray band (e.g., Terekhov et al. 2002; McKenzie & Mullan 1997) and in the white-light emission associated with the stellar flaring loops (Mathioudakis et al. 2003). A possible interpretation of these medium period QPPs may be in terms of kink or torsional modes (Zaitsev & Stepanov 1989).

In our previous, preliminary study (Nakariakov et al. 2004), we outlined an alternative, simpler, thus more attractive mechanism for the generation of long-period QPPs. That model used a symmetric heating function (heat deposition was strictly at the apex). This left the outstanding questions: A) is the generation of the 2nd harmonic a consequence of the fact that the heating function was symmetric? B) Would the generation of these oscillations occur if we break symmetry? C) What is the spectrum of these oscillations? Is it consistent with a 2nd spatial harmonic? The present work attempts to answer these important outstanding questions.

The paper is organized as follows: in Sect. 2 we present the numerical results, with Sect. 2.1 dedicated to the case of apex (symmetric) heating which completes the work started in Nakariakov et al. (2004), and Sect. 2.2 summarizing our findings in the case of single footpoint (asymmetric) heating. We close with conclusions in Sect. 3.

2 Numerical results

The model that we use to describe plasma dynamics in a coronal loop is outlined in Tsiklauri et al. (2004); Nakariakov et al. (2004). Here we just add that, when numerically solving the 1D radiative hydrodynamic equations (infinite magnetic field approximation), and using a 1D version of the Lagrangian Re-map code (Arber et al. 2001) with the radiative loss limiters, the radiative loss function was specified as in Tsiklauri et al. (2004) which essentially is the Rosner et al. (1978) law extended to a wider temperature range (Priest 1982; Peres et al. 1982).

We have used the same heating function as in Tsiklauri et al. (2004). The choice of the temporal part of the heating function is such that at all times there is a small background heating present (either at footpoints or the loop apex) which ensures that in the absence of flare heating (when $\alpha$, which determines the flare heating amplitude, is zero) the average loop temperature stays at 1 MK. For easy comparison between the apex and footpoint heating cases we fix $Q_{\rm p}$, flare heating amplitude, at a different value in each case (which ensures that with the flare heating on when $\alpha=1$the average loop temperature peaks at about the observed value of 30 MK in both cases).

In all the numerical runs presented here $1/(2 \sigma_{\rm s}^2)$was fixed at 0.01 Mm-2, which gives a heat deposition length scale, $\sigma_{\rm s}=7$ Mm. This is a typical value determined from the observations (Aschwanden et al.  2002). The flare peak time was fixed in all numerical simulations at 2200 s. The duration of the flare, $\sigma_t$, was fixed at 333 s. The time step of data visualization was chosen to be 0.5 s. The CFL limited time-step used in the simulations was 0.034 s.

2.1 Case of apex (symmetric) heating

In this section we complete the analysis started in Nakariakov et al. (2004), namely for the same numerical run we study the spectrum of oscillations at different spatial points.

As was pointed out in Nakariakov et al. (2004), the most interesting fact is that we see clear quasi-periodic oscillations, especially in the second stage (peak of the flare) for the time interval t=2500-2800 s (cf. Fig. 1 in Nakariakov et al. 2004). Such oscillations are frequently seen during the solar flares observed in X-rays, 8-20 keV, (e.g., Terekhov et al. 2002) as well as stellar flares observed in white-light (e.g., Mathioudakis et al. 2003).

Before discussing the physical nature of these oscillations, it is worth recalling for completeness the simple 1D analytic theory of standing sound waves. For 1D, linearized, hydrodynamic equations with constant unperturbed (zero order) background variables, the solutions for density, $\rho$, and velocity, Vx, can be easily written as

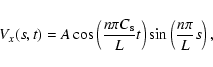\begin{displaymath}V_x(s,t)=A \cos \left( {{n \pi C_{\rm s}}\over{L}} t\right) \sin \left( {{n \pi}\over{L}} s\right), \end{displaymath} (1)


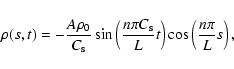\begin{displaymath}\rho(s,t)=-{{A \rho_0}\over{C_{\rm s}}} \sin \left( {{n \pi C... ... s}}\over{L}} t\right) \cos \left( {{n \pi}\over{L}} s\right), \end{displaymath} (2)

where $C_{\rm s}$ is the speed of sound, A is wave amplitude, L is loop length, n=1,2,3,... is the harmonic number, and s is the distance along the loop. Note the (relative) phase shift between Vx and $\rho$is  $\Delta P/ P=-(\pi/2)/(2 \pi)=-1/4$, where P is the standing wave period, while this ratio is zero for a propagating wave. Also, Eqs. (3) and (4) from Nakariakov et al. (2004) are missing a factor of 2, while our Eqs. (1) and (2) correct this previous omission.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms0299f1.eps} \end{figure} Figure 1: Case of apex (symmetric) heating: periodogram (spectrum) of the velocity and density oscillatory component times series outputted in the following three points: loop apex (solid curve), 1/4 (dash-dotted curve) and 1/6 (dashed curve) of the effective loop length (48 Mm), i.e. at s=0,-12,-16 Mm.
Open with DEXTER

In Fig. 1 we present a periodogram (which here we use interchangeably with the (power) spectrum, although strictly speaking the power spectrum is a theoretical quantity defined as an integral over continuous time, and of which the periodogram is simply an estimate based on a finite amount of discrete data) of the velocity and density time series outputted at the three points: loop apex, 1/4 and 1/6 of the effective loop length (48 Mm), i.e. at s=0,-12,-16 Mm (cf. Scargle 1982, and his Eq. (10) in particular). The first two points are chosen to test whether the simple analytic solution for 1D standing sound waves (see below) is relevant in this case. The third point (1/6) was chosen arbitrarily (any spatial point along the loop where density and velocity of the standing waves does not have a node would be equally acceptable). As expected for a 2nd spatial harmonic of a standing sound wave in the velocity periodogram there are two clearly defined peaks and the largest peak corresponds to 1/4 of the effective loop length, while the smaller peak corresponds to 1/6. Note that at the loop apex the periodogram gives 0 (solid line is too close to zero to be seen in the plot). The density periodogram shows the opposite behaviour to that of the velocity with the largest peak corresponding to the loop apex, while 1/6 of the effective loop length corresponds to a smaller peak, and 1/4 is close to zero. The locations of the peaks are at about 0.0155 Hz i.e. the period of the oscillation is 64 s. The period of a 2nd spatial harmonic of a standing sound wave should be

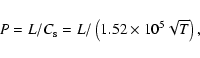\begin{displaymath}P=L/C_{\rm s}=L/\left(1.52 \times 10^5 \sqrt{T}\right), \end{displaymath} (3)

where T is plasma temperature measured in MK, while L is in meters. If we substitute an effective loop length L=48 Mm (see Fig. 2 in Nakariakov et al. 2004) and an average temperature of 25 MK (see top panel in Fig. 1 in Nakariakov et al. 2004, in the range of 2500-2800 s - the quasi periodic oscillations time interval we study) we obtain 63 s, which is close to the result of our numerical simulation. Such a close coincidence is surprising bearing in mind that the theory does not take into account variation of background density and velocity over time, while we see from Fig. 1 in Nakariakov et al. (2004) that even within a short interval of a flare, i.e. 2500-2800 s, all physical quantities vary significantly with time. To close our investigation of the physical nature of the oscillations we study the phase shift between the velocity and density oscillations and compare our simulation results with analytic theory. In Fig. 2 we plot time series, outputted at $\pm $6 and $\pm $18 Mm, of the plasma number density in units of 1011 cm-3and velocity, normalized to 400 km s-1. These points were selected so that one symmetric (with respect to the apex) pair ($\pm $6 Mm) is close to the apex, while another pair ($\pm $18 Mm) is closer to the footpoints. We choose these pairs because we wanted to compare how the phase shift is affected by spatial location. One would expect stronger upflows close to footpoints (due to chromospheric evaporation), which in turn alters the phase shift. Note that phase shift between the density and velocity is different (see below) for standing and propagating (with flows) acoustic waves). We gather from the graph that: (A) clear quasi-periodic oscillations are present; (B) they are shifted with respect to each other in time; (C) near the apex ($\pm $6 Mm) the phase shift is close to that predicted by 1D analytic theory; (D) close to the footpoints ($\pm $18 Mm) the phase shift is somewhat different from the one predicted by 1D analytic theory. In the last case the discrepancy can be attributed to the presence of flows near the footpoints. The main reason for the overall deviation is due to the fact that analytic theory does not take into account variations of background density and velocity in time and that density gradients in the transition region are not providing perfect reflecting boundary conditions for the formation of standing sound waves.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms0299f2.eps} \end{figure} Figure 2: Case of apex (symmetric) heating: oscillatory components of time series outputted at $\pm $6 Mm and $\pm $18 Mm in the time interval of 2500-2800 s. The solid curve shows plasma number density in units of 1011 cm-3. The dashed curve shows velocity normalized to 400 km s-1.
Open with DEXTER

Another interesting result is that even with the wide variation of the parameter space of the flare, its duration, peak average temperature, etc., we always obtained a dominant 2nd spatial harmonic of a standing sound wave with some small admixture of 4th and sometimes 6th harmonics. Our initial guess was that this is due to the symmetric excitation of these oscillations (recall that we use apex heat deposition). In order to investigate the issue of excitation further we decided to break the symmetry and put the heating source at one footpoint, hoping to see excitation of odd harmonics 1st, 3rd, etc.

2.2 Case of single footpoint (asymmetric) heating


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms0299f3.eps} \end{figure} Figure 3: Case of single footpoint (asymmetric) heating: average temperature, temperature at apex, and number density at the apex as functions of time.
Open with DEXTER

For single footpoint heating we fix s0= 30 Mm in Eq. (1) in Nakariakov et al. (2004), i.e. (spatial) peak of the heating is chosen to be at the bottom of the transition region (top of chromosphere). Initially we run a code without flare heating, i.e. we put $\alpha=0$ (in this manner we turn off flare heating). E0=0.02 erg cm-3 s-1 was chosen such that in the steady (non-flaring) case the average loop temperature stays at about 1 MK. Then, we run the code with flare heating, i.e. we put $\alpha=1$, and fix $Q_{\rm p}$ at  $1 \times 10^4$, so that it yields a peak average temperature of about 30 MK. The results are presented in Fig. 3. During the flare the apex temperature peaks at 38.38 MK while the number density at the apex peaks at  $3.11 \times 10^{11}$ cm-3. In this case, as opposed to the case of symmetric (apex) heating, the velocity dynamics is quite different. Since the symmetry of heating is broken there is a non-zero net flow through the apex at all times. However, as in the symmetric heating case, we again see quasi-periodic oscillations superimposed on the dynamics of all physical quantities (cf. time interval of  t=2400-2700 in Fig. 3).

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms0299f4.eps} \end{figure} Figure 4: Time-distance plots of the velocity and density oscillatory components in the time interval of 2400-2700 s for the case of single footpoint (asymmetric) heating.
Open with DEXTER

In Fig. 4 we present time-distance plots of velocity and density for the time interval  2400-2700 s, where the quasi-periodic oscillations are most clearly seen. Here we again subtracted the slowly varying background (with respect to oscillation period). The picture is quite different from the case of apex (symmetric) heating (compare it with Fig. 2 in Nakariakov et al. 2004). This is because now the node in the velocity (at the apex) moves back and forth periodically along the apex, and at later times (t>2550 s) stronger flows are now present. However, the physical nature of the oscillations remains mainly the same. i.e. a 2nd spatial harmonic of a sound wave, but now with an oscillating node at the apex.

To investigate this further we plot in Fig. 5 a periodogram (spectrum) of the velocity and density oscillatory component time series outputted at the following three points: loop apex, 1/6 and 1/4 of the effective loop length. We gather from the graph that the periodogram (spectrum) is more complex than in the case of apex (symmetric) heating. In the velocity periodogram at the apex there is a peak with a frequency higher than that of 2nd spatial harmonic of a standing sound wave. This is the frequency with which the node of the velocity oscillates (see discussion in the previous paragraph). It has nothing to do with the standing mode, but is dictated by the excitation conditions of the loop which acts as a dynamic resonator. Let us analyze now how this periodogram compares with 1D analytic theory. The peak in the periodogram corresponding to 1/6 of the effective loop length (dashed line) corresponds to a frequency of about 0.017 Hz, i.e. the period of oscillation is 59 s. Again, the period of a 2nd spatial harmonic of a standing sound wave should be calculated from Eq. (3). If we substitute the effective loop length L=48 Mm (see Fig. 4) and an average temperature of 26 MK (see top panel in Fig. 3 in the range of 2400-2700 s) we obtain 62 s, which is close to the result of our numerical simulation (59 s).

Next, we studied the phase shift between velocity and density oscillations, and compare our simulation results with the 1D analytic theory. In Fig. 6 we produce a plot similar to Fig. 2, but for the case of asymmetric heating. The deviation, which is greater than in the case of apex (symmetric) heating, can again be attributed to the over-simplification of the 1D analytic theory, which does not take into account time variation of the background physical quantities and imperfection of the reflecting boundary conditions (see above). More importantly, in the asymmetric case strong flows are present throughout the flare simulation time. Thus, if linear time dependence is assumed, which is relevant within the short interval 2400-2700 s of the flare, then Eqs. (1) and (2) would be modified such that phase shifts would vary secularly in time. This is similar to that seen in Fig. 6.

Yet another interesting observation comes from the following argument: in a steady 1D case analytic theory predicts that the phase shift between the density and velocity should be (A) zero for for a propagating acoustic wave and (B) quarter of a period for the standing acoustic wave. Since in the asymmetric case strong flows are present, we see less phase shift between the velocity and density in Fig. 6 as one would expect.

Thus, the results of the present study provide further, and more definitive proof than in Nakariakov et al. (2004) that these oscillations are indeed the 2nd spatial harmonic of a standing sound wave. However, the present work also reveals that in the case of single footpoint (asymmetric) heating the physical nature of the oscillations is more complex, as the node in the velocity oscillates along the apex and net flows are present.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms0299f5.eps} \vspace*{4mm} \end{figure} Figure 5: As is Fig. 1 but for the case of single footpoint (asymmetric) heating. Time interval here is 2400-2700 s.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms0299f6.eps} \end{figure} Figure 6: As in Fig. 2, but for the case of single footpoint (asymmetric) heating. Time interval here is 2400-2700 s.
Open with DEXTER

3 Conclusions

Initially we used a 1D radiative hydrodynamics loop model which incorporates the effects of gravitational stratification, heat conduction, radiative losses, added external heat input, presence of helium, hydrodynamic non-linearity, and bulk Braginskii viscosity to simulate flares (Tsiklauri et al. 2004). As a byproduct of that study, in practically all the numerical runs quasi-periodic oscillations in all physical quantities were detected (Nakariakov et al. 2004). Such oscillations are frequently seen during the solar flares observed in X-rays, 8-20 keV (e.g., Terekhov et al. 2002) as well as stellar flares observed in white-light (e.g., Mathioudakis et al. 2003). Our present analysis shows that quasi-periodic oscillations seen in our numerical simulations bear many similar features compared to observational datasets. In this work we tried to answer important outstanding questions (cf. Introduction section) that arose from the previous analysis (Nakariakov et al. 2004).

In summary the present study (and Nakariakov et al. 2004) established the following features:

The novelty of this study is that by studying the spectrum and phase shift of these oscillations we provide more definite proof that these oscillations are indeed the 2nd harmonic of a standing sound wave, and that the single footpoint (asymmetric) heatpositioning still produces 2nd spatial harmonics, although it is more complex than the apex (symmetric) heating as the node in the velocity oscillates along the apex and net flows are also present.

Acknowledgements
This research was supported in part by PPARC, UK. Numerical calculations of this work were performed using the PPARC funded MHD Cluster at St Andrews and Astro-Sun cluster at Warwick. D.T. would like to thank the referee, Dr. Mihalis Mathioudakis, for useful comments. D.T. kindly acknowledges support from Nuffield Foundation through an award to newly appointed lecturers in science, engineering and mathematics (NUF-NAL 04).


References

 
Copyright ESO 2004