A&A 422, 1-9 (2004)
DOI: 10.1051/0004-6361:20040256
Thermal balance in decaying 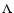 cosmologies
cosmologies
D. Puy
Geneva Observatory, University of Geneva,
Chemin des Maillettes 51, 1290 Sauverny, Switzerland
Received 12 February 2004 / Accepted 26 February 2004
Abstract
We consider cosmological models in which the vacuum decay energy is channeled
exclusively into radiation. We investigate the thermal evolution of the Universe with a variable cosmological term
which varies as a function of the scale factor a as
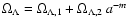 .
Using constraints given by the temperature measurements of the cosmic microwave background, at redshifts
between z=0 and z=4, we find that
.
Using constraints given by the temperature measurements of the cosmic microwave background, at redshifts
between z=0 and z=4, we find that
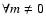
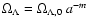 models
are clearly ruled out. The influence on the thermal decoupling between matter and radiation is also discussed.
models
are clearly ruled out. The influence on the thermal decoupling between matter and radiation is also discussed.
Key words: cosmology: theory - cosmic microwave background
Publications of the analysis of type Ia supernovae redshift data
by the High-Z Supernova Search team (Riess et al. 1998) and the Supernova
Cosmology Prospect (Perlmutter et al. 1999) have provided a strong indication that
the Universe is accelerating. However, the mechanism responsible for this acceleration
is still unknown.
A cosmic fluid called dark energy has been suggested by numerous authors
to explain this accelerating phase. A first interpretation of
this dark energy is a cosmological constant arising from vacuum energy,
see Weinberg (1989), Sahni & Starobinsky (2000).
Other possibilities describing the form of dark energy were proposed such as a
dynamical scalar field called quintessence (Caldwell 1998), an exotic
perfect fluid called Chaplygin gas (Kamenshchik et al. 2001), a Cardassian
Universe where the Friedmann Robertson Walker equation is modified
(Freese & Lewis 2002), tachyon matter (Frolov et al. 2002), four-Fermion
interaction (Inagaki et al. 2003), or the Born-Infeld quantum condensate
(Elizalde et al. 2003). A further approach arises from our
lack of understanding of gravitational physics to explain
the observed cosmic acceleration, leading to the "braneworld"
theory (Dvali et al. 2000) or a modification of the Einstein-Hilbert action
(Meng & Wang 2003).
The cosmological constant has been repeatedly studied since
Einstein (1917) first introduced it to obtain a static
cosmological solution, see Straumann (1999). The important problem
of the cosmological constant consists of explaining
the observed small value, which appears to be 120 orders of
magnitude smaller than one would expect based on contributions from
zero-point quantum fields, see Weinberg (1989). A method of
resolving this dilemna is to define a variable cosmological
term. However, energy conservation would require any decrease in the energy
density of the vacuum to be balanced by a corresponding increase elsewhere.
In this context, Ratra & Peebles (1998) and Peebles & Ratra (2003)
suggested that the Universe is permeated by a homogeneous scalar field, coupled
weakly to matter, that rolls continuously down a potential gradient
toward some minimum. Its potential energy would be converted to kinetic energy of the
scalar field.
Another possibility is a decaying vacuum that convert
its energy directly into radiation, see Özer & Taha (1986), Freese et al. (1987) and Gasperini
(1987).
The possibility that a decaying vacuum produces matter is ruled out because the annihilation
matter anti-matter (decay process does not violate baryon number) would produce
a 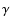 -ray background in excess of observed levels (see Freese et al. 1987).
-ray background in excess of observed levels (see Freese et al. 1987).
The consequences of decaying 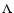 cosmologies have been investigated in different contexts such
as spontaneous symmetry breaking (Kazanas 1980), influence on the evolution of matter
density perturbations (Silveira & Waga 1994), on the age of the Universe (Matyjasek 1995),
the statistical properties of gravitational lenses (Bloomfield-Torres & Waga 1996), or more generally
on the evolution of the scale factor with several possibilities of the functional form of
cosmologies have been investigated in different contexts such
as spontaneous symmetry breaking (Kazanas 1980), influence on the evolution of matter
density perturbations (Silveira & Waga 1994), on the age of the Universe (Matyjasek 1995),
the statistical properties of gravitational lenses (Bloomfield-Torres & Waga 1996), or more generally
on the evolution of the scale factor with several possibilities of the functional form of
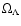 ,
see
Overduin & Cooperstock (1998).
,
see
Overduin & Cooperstock (1998).
Kimura et al. (2001) then Hashimoto et al. (2003) investigated the thermal evolution of the Universe with
a phenomenological decaying cosmological term. Kimura
et al. (2001) found that the radiation temperature predicted from the variable
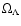 models is lowered
significantly compared with the constant
models is lowered
significantly compared with the constant
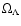 .
Hashimoto et al. (2003) pointed out that molecular
formation is shifted to earlier epochs by
.
Hashimoto et al. (2003) pointed out that molecular
formation is shifted to earlier epochs by
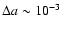 compared to the case in the standard big bang cosmology
(i.e.
compared to the case in the standard big bang cosmology
(i.e.
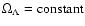 ). We consider the same appproach. However, prospects for constraining the cosmology by the
extragalactic
microwave background temperature become possible due to the feasibility of measuring this background temperature at
redshifts between z=0 and z=4. Here we use these measurements to constrain the effects of a decaying cosmological term on
the evolution of cosmic microwave radiation (CMBR) temperature.
). We consider the same appproach. However, prospects for constraining the cosmology by the
extragalactic
microwave background temperature become possible due to the feasibility of measuring this background temperature at
redshifts between z=0 and z=4. Here we use these measurements to constrain the effects of a decaying cosmological term on
the evolution of cosmic microwave radiation (CMBR) temperature.
The remainder of this paper is organized as follows: cosmological equations are presented in Sect. 2, in Sect. 3 we
introduce the present cosmological parameters and our choice of parameters. In Sect. 4 we investigate the evolution of radiation
temperature in which the cosmological term
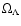 varies. In Sect. 5 we discuss the observational constraints, then
in Sect. 6 we analyse the consequences of decaying
varies. In Sect. 5 we discuss the observational constraints, then
in Sect. 6 we analyse the consequences of decaying 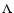 cosmologies (constrained by observations) on the thermal decoupling between
matter and radiation. Our conclusions are summarized in Sect. 7.
cosmologies (constrained by observations) on the thermal decoupling between
matter and radiation. Our conclusions are summarized in Sect. 7.
Assuming the cosmological principle, it follows directly from the observed near-isotropy of the CMBR that the Universe is
approximately isotropic and homogeneous. Thus with these usual assumptions, the Einstein field equations (in standard
notation):
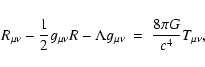 |
(1) |
associated with the Friedmann-Lemaître-Robertson-Walker metric
![\begin{displaymath}{\rm d}s^2 ~ = ~ c^2 {\rm d}t^2 -a(t)^2 \Bigr[ \frac{{\rm d}r...
...}^2\theta + r^2 {\rm sin}^2\theta ~
{\rm d}^2\varphi^2 \Bigr]
\end{displaymath}](/articles/aa/full/2004/28/aa0256-04/img21.gif) |
(2) |
lead to the Friedmann-Lemaître equations:
| |
|
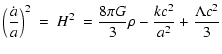 |
(3) |
| |
|
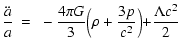 |
(4) |
where G is the gravitational constant, c the speed of light and a the scale factor.
H is the Hubble parameter and k the curvature constant.
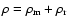 is the energy density associated with the pressure p, where
is the energy density associated with the pressure p, where
 is the matter energy
density and
is the matter energy
density and
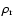 the radiation energy density. These equations, normalised to the critical density
the radiation energy density. These equations, normalised to the critical density
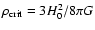 ,
become:
,
become:
| |
|
![$\displaystyle \Bigr( \frac{\dot{a}}{a} \Bigr)^2 ~ = ~
H^2 ~ = ~
H_0^2 \Bigr[ \O...
...{\rm r} + \Omega_{\rm m} + \frac{\Omega_{\rm K,0}}{a^2} + \Omega_\Lambda \Bigl]$](/articles/aa/full/2004/28/aa0256-04/img28.gif) |
(5) |
| |
|
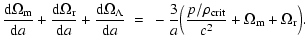 |
(6) |
The curvature
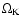 and cosmological
and cosmological
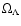 density parameter is defined by
density parameter is defined by![[*]](/icons/foot_motif.gif) :
:
| |
|
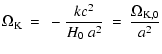 |
(7) |
| |
|
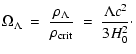 |
(8) |
The conservation of matter leads to the scale dependence:
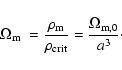 |
(9) |
At the present epoch all density parameters,
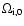 ,
are correlated through the Friedmann-Lemaître condition:
,
are correlated through the Friedmann-Lemaître condition:
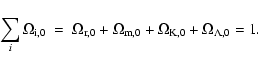 |
(10) |
From the equation of state:
| |
|
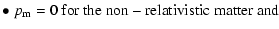 |
|
| |
|
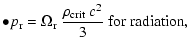 |
(11) |
and from Eq. (6) we get the evolution of radiation density parameter:
 |
(12) |
In the case
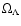 = constant, we deduce easily the standard evolution
= constant, we deduce easily the standard evolution
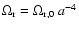 .
Excellent progress has been made recently toward the measurement of the Hubble constant with the
Hubble Space Telescope. Combined with current estimates, the results favor the following value (see Freedman 2000):
.
Excellent progress has been made recently toward the measurement of the Hubble constant with the
Hubble Space Telescope. Combined with current estimates, the results favor the following value (see Freedman 2000):
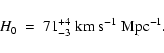 |
(13) |
The Far Infrared Absolute Spectrometer, (e.g. FIRAS), on board the
COBE satellite (see Mather et al. 1999) has precisely measured the present radiation
temperature in the frequency range 2-20 cm-1:
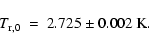 |
(14) |
The anisotropies of the CMBR contain information about basic cosmological parameters.
De Bernardis et al. (2000) with the balloon-borne observations of millimetric
extragalactic radiation and geophysics (e.g. BOOMERANG), and Bennett et al. (2003)
with the Wilkinson microwave anisotropy probe (e.g. WMAP satellite) found evidence for a
Euclidian geometry of the Universe:
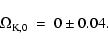 |
(15) |
The high absolute luminosity of type Ia supernovae (used
as calibrated standard candles) suggests that these objects can be seen out to
large distances, making them ideal candidates for measuring and
constraining cosmological parameters. The results obtained by both
Riess et al. (1998) and Perlmutter et al. (1999)
present direct evidence for a non-zero
cosmological constant. These two experiments converge to
a value for the present cosmological density parameter:
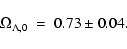 |
(16) |
In our context we choose the central value at z=0 such as:
H0=71 km s-1 Mpc-1,
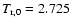 K,
K,
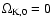 and
and
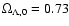 .
.
Numerous cosmological models with the common property of having a
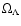 parameter decreasing with time were proposed. Of special interest for us is the
dependence of
parameter decreasing with time were proposed. Of special interest for us is the
dependence of
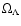 on the scale factor, suggested by Gasparini (1987), Chen & Wu (1990), Ozer (1999) and
Waga (1993). Here we consider the variable-
on the scale factor, suggested by Gasparini (1987), Chen & Wu (1990), Ozer (1999) and
Waga (1993). Here we consider the variable-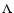 term
term
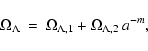 |
(17) |
where
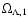 ,
,
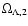 and m are
constants. Thus the present cosmological density parameter is given by:
and m are
constants. Thus the present cosmological density parameter is given by:
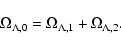 |
(18) |
In this context we get the evolution of the radiation density parameter (see Eq. (12)):
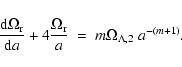 |
(19) |
With the initial condition
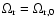 at a=a0=1, the superposition principle of solutions for
ordinary linear differential equations easily leads to the following solution:
at a=a0=1, the superposition principle of solutions for
ordinary linear differential equations easily leads to the following solution:
![\begin{displaymath}\Omega_{\rm r} = \Bigr[ \Omega_{\rm r,0} + \Omega_{{\rm r},\Lambda} \Bigl] ~ (1+z)^4 .
\end{displaymath}](/articles/aa/full/2004/28/aa0256-04/img52.gif) |
(20) |
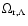 is the
is the 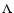 -decay contribution to the photon background:
-decay contribution to the photon background:
where we introduce the redshift z
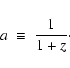 |
(23) |
Freese et al. (1987), Overduin et al. (1993) and Matyjasek (1995) pointed out that the
extra photons produced by a vacuum decay are distributed with a Planckian spectrum due to
thermalization by double Compton and bremsstrahlung processes at very early times![[*]](/icons/foot_motif.gif) ,
then keep the Planckian spectrum. Thus the radiation density parameter can be expressed by
,
then keep the Planckian spectrum. Thus the radiation density parameter can be expressed by
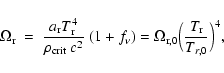 |
(24) |
where 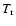 is the temperature of radiation,
is the temperature of radiation,
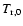 the present CMBR temperature and
the present CMBR temperature and 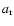 the radiation density constant.
the radiation density constant.
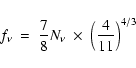 |
(25) |
is the neutrino contribution for 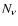 massless, non-degenerate neutrino types
massless, non-degenerate neutrino types![[*]](/icons/foot_motif.gif) . Finally we get the following evolution equation:
. Finally we get the following evolution equation:
![\begin{displaymath}T_{\rm r} = ~ T_{\rm r,0} (1+z) ~ \Bigr[ 1+ \frac{\Omega_{{\rm r},\Lambda}}{\Omega_{\rm r,0}} \Bigl]^{1/4} \cdot
\end{displaymath}](/articles/aa/full/2004/28/aa0256-04/img67.gif) |
(26) |
Notice that in the standard case where m=0 (i.e.
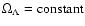 )
we have
)
we have
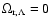 ,
and find the standard evolution
,
and find the standard evolution
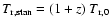 .
.
The analysis of the sign of
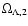 leads to the following evolution:
leads to the following evolution:
Kimura et al. (2001) analysed the thermal evolution of the Universe and showed that the radiation temperature predicted by models
with a decaying cosmological term can be lowered significantly compared to the standard model (i.e. m=0). Here, we calculate the evolution of the
radiation temperature with different decaying cosmological terms. In Table 1 we provide our group of
parameters (the K-runs are relative to Kimura's runs).
Figure 1 compares the CMBR temperature evolution with the standard evolution. Despite that
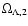 is very low, the
difference to the standard case is clear. A larger difference is found for the D1-model where
is very low, the
difference to the standard case is clear. A larger difference is found for the D1-model where
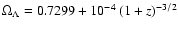 .
.
Table 1:
Model parameters of runs, H0 is in km s-1 Mpc-1.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0256fig1.eps}\end{figure}](/articles/aa/full/2004/28/aa0256-04/Timg75.gif) |
Figure 1:
Evolution of the radiation temperature for different decaying 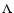 -cosmologies. -cosmologies. |
| Open with DEXTER |
It is remarquable that several current observations ruled out all cosmological models in which the cosmic microwave background
spectrum is non-Planckian at z=0. However those data are not able to constrain models with a purely blackbody spectrum but with
a different
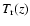 dependence than in the standard model.
dependence than in the standard model.
The CMBR populates excited levels of atomic and molecular species when the energy separations involved are not too different from
the CMBR peak frequency. Thus the first measurement of the local CMBR temperature was made with fine structure lines in the cyanogen
molecule.
Bahcall & Wolf (1968) first suggested that this method could be extended to high redshift, where the
background radiation
temperature is larger, using atomic fine-structure transitions in absorbing clouds toward high-redshift quasars.
Transitions of neutral carbon and C+ are particularly well suited for this. Thus it is (in theory) possible
to estimate the CMBR temperature from this method. However the fine-structure fine levels can be populated by several processes,
mainly collisions with hydrogen atoms and electrons, and pumping due to the local ultraviolet radiation and to the CMBR. The different
contributions can be estimated once the temperature and the particle density are known (see discussions in Levshakov et al.
1999 on the measurability of kinetic temperature from absorption-line spectra). Generally an upper limit on
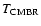 is obtained by assuming
that the CMBR is the only excitation process at work. The measurements have been attempted several times, but have been generally limited
by the resolution and signal-to-noise available in reasonable exposure times.
is obtained by assuming
that the CMBR is the only excitation process at work. The measurements have been attempted several times, but have been generally limited
by the resolution and signal-to-noise available in reasonable exposure times.
Songaila et al. (1994) reported the detection of absorption
from the first fine-structure level of neutral carbon atoms in a
cloud towards the quasar Q1331+170. The population ratio yields a temperature of
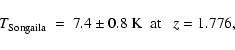 |
(29) |
assuming that no other significant sources of excitation are present.
We take this range for the CMBR temperature, even though these values could be
considered to be an upper limit.
Ge et al. (1997) presented detections of absorption from
the ground state and excited states
of C in the damped Ly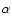 system of the quasar QSO 0013-004. From the population ratio of the
excited state to the ground state, they derive an estimate for the CMBR
temperature:
system of the quasar QSO 0013-004. From the population ratio of the
excited state to the ground state, they derive an estimate for the CMBR
temperature:
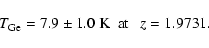 |
(30) |
Srianand et al. (2000) detected the absorption lines from the first and
second fine-structure levels of neutral carbon atoms in an
isolated cloud of gas towards the quasar
PKS1232+0815; they found
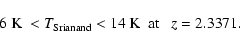 |
(31) |
From the analysis of the C+ fine-structure
population ratio in the damped Ly system towards the quasar
Q0337-3819, Molaro et al. (2002) derive
an upper bound on the CMBR temperature
system towards the quasar
Q0337-3819, Molaro et al. (2002) derive
an upper bound on the CMBR temperature
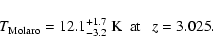 |
(32) |
The possibility of determining the CMBR temperature from
measurements of the Sunyaev-Zel'dovich (SZ) effect in the galaxy
cluster has been suggested by the group of Melchiorri, see Fabbri et al. (1978). The
steep frequency dependence of the change, due to the SZ effect,
and the weak dependence of the ratios of intensity changes measured at
two frequencies allow the estimation of the CMBR
temperature at the redshift of the cluster. Recently Battistelli et al. (2003) deduced the CMBR temperature
using data of the Coma cluster and Abell 2163 over four bands at radio and microwave frequencies with the millimeter and infrared Testa Grigia
observatory (e.g. MITO). They found the following radiation temperature:
Thus we have six observables of the radiation temperature at different redshifts. Figure 2 compares the evolution of radiation
temperature of our preceeding models with the observational value of the CMBR temperature.
Figure 2a gives the measurements of CMBR temperature at redshifts between z=0 and z=4, the
lower panel gives the measurements, with the SZ effect, between the redshifts z=0 and z=0.25. We see that in some models,
for example the D1-model and D2-model, radiation temperature is not included in the domain of observational estimates. Thus it is
necessary to adjust the parameters to reconcile the decaying- model with the observations.
model with the observations.
![\begin{figure}
\par\includegraphics[width=11.8cm,clip]{0256fig2.eps}\end{figure}](/articles/aa/full/2004/28/aa0256-04/Timg87.gif) |
Figure 2:
Evolution of the radiation temperature for different decaying 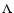 -cosmologies; a) shows the evolution between
1+z=1 and 1+z=5, b) is relative to the range 1+z=1 and 1+z=1.25. Current measurements of some extragalactic cosmic
microwave background temperatures are labeled as follows: (1) -cosmologies; a) shows the evolution between
1+z=1 and 1+z=5, b) is relative to the range 1+z=1 and 1+z=1.25. Current measurements of some extragalactic cosmic
microwave background temperatures are labeled as follows: (1)
 ,
(2) ,
(2)
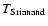 ,
(3) ,
(3)
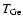 ,
(4) ,
(4)
 ,
(5) ,
(5)
 ,
(6) ,
(6)
 . . |
| Open with DEXTER |
The six preceeding observational measurements
impose a range of validity, at the observation redshift
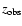 ,
on the radiation temperature:
,
on the radiation temperature:
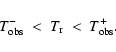 |
(35) |
We introduce the
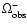 and
and
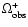 quantities:
quantities:
Thus, for each observable we have
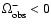 and
and
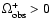 .
From Eqs. (26) and (35)
we get the following condition between
.
From Eqs. (26) and (35)
we get the following condition between
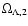 and m:
and m:
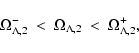 |
(38) |
where the bounds
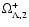 and
and
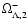 are such as
are such as
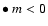 :
:
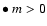 and
and 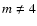 :
:
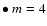 :
:
Figures 3 and 4 show the bounds on
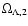 deduced from the six observational constraints. The
left panels give
deduced from the six observational constraints. The
left panels give
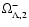 ,
the right panels indicate
,
the right panels indicate
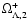 .
The shaded region marks the non-allowed parameters
(
.
The shaded region marks the non-allowed parameters
(
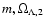 ).
).
The Melchiorri measurements with the Coma cluster at z=0.0231 (see Figs. 4c and 4d) are the most restrictive.
In Fig. 5 we summarize the allowed parameters regions. We get the following constraint:
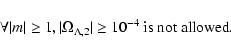 |
(42) |
Moreover cosmological parameters such as
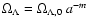 with
with 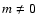 are clearly ruled out.
are clearly ruled out.
![\begin{figure}
\par\includegraphics[width=13.6cm,clip]{0256fig3.eps}\end{figure}](/articles/aa/full/2004/28/aa0256-04/Timg116.gif) |
Figure 3:
Bounds on
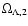 given by the observations. a) and b) corresponds to Songaila observations, c) and d) to
Ge observations, e) and f) to Srianand observations. The left panels give the limit on
given by the observations. a) and b) corresponds to Songaila observations, c) and d) to
Ge observations, e) and f) to Srianand observations. The left panels give the limit on
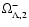 when the right panels are
relative to
when the right panels are
relative to
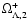 .
Cross-hatching indicates the non-allowed regions. The vertical axis corresponds to .
Cross-hatching indicates the non-allowed regions. The vertical axis corresponds to
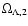 and the horizontal axis to m.
and the horizontal axis to m. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=13.6cm,clip]{0256fig4.eps}\end{figure}](/articles/aa/full/2004/28/aa0256-04/Timg117.gif) |
Figure 4:
Bounds on
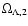 given by the observations. a) and b) correspond to Molaro observations, c) and d) to
Melchiorri1 observations, e) and f) to Melchiorri2 observations. The left panels give the limit on
given by the observations. a) and b) correspond to Molaro observations, c) and d) to
Melchiorri1 observations, e) and f) to Melchiorri2 observations. The left panels give the limit on
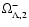 ,
the right
panels are relative to ,
the right
panels are relative to
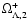 .
Cross-hatching indicates non-allowed regions. The vertical axis corresponds to .
Cross-hatching indicates non-allowed regions. The vertical axis corresponds to
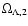 and the horizontal axis to m.
and the horizontal axis to m. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=12.1cm,clip]{0256fig5.eps}\end{figure}](/articles/aa/full/2004/28/aa0256-04/Timg118.gif) |
Figure 5:
Total bounds on
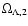 given by the observations. The left panel gives the limit on
given by the observations. The left panel gives the limit on
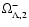 and the right panels is relative to
and the right panels is relative to
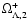 .
The black area represents the excluded regions. The vertical axis corresponds
to .
The black area represents the excluded regions. The vertical axis corresponds
to
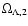 and the horizontal axis to m.
and the horizontal axis to m. |
| Open with DEXTER |
The thermal history of the early Universe depends on the tight coupling between radiation and matter resulting from Thomson scattering.
The evolution of the gas temperature 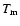 is governed by the equation (see Kompaneets 1957; Peebles 1968):
is governed by the equation (see Kompaneets 1957; Peebles 1968):
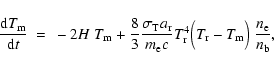 |
(43) |
where
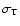 is the Thomson cross section and
is the Thomson cross section and 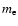 the mass of the electron.
the mass of the electron. 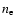 and
and 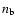 are
the numerical density, i.e. number of particles per cm-3, for electrons and for baryons. We neglect the energy transfer via the molecular
transitions and the enthalpies of reaction (see Puy et al. 1993; Pfenniger & Puy 2003).
are
the numerical density, i.e. number of particles per cm-3, for electrons and for baryons. We neglect the energy transfer via the molecular
transitions and the enthalpies of reaction (see Puy et al. 1993; Pfenniger & Puy 2003).
The matter temperature depends on the fraction of electrons![[*]](/icons/foot_motif.gif) . We use the reaction network developped by Galli & Palla (1998) and couple this primordial kinetic
with the hydrodynamic equations (see Puy & Signore 2002) .
. We use the reaction network developped by Galli & Palla (1998) and couple this primordial kinetic
with the hydrodynamic equations (see Puy & Signore 2002) .
The evolution of the numerical density of baryons is given by
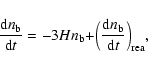 |
(44) |
where
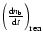 describes the contribution of the reactions (see Pfenniger & Puy
2003). All of these equations depend on the Hubble
parameter defined by:
describes the contribution of the reactions (see Pfenniger & Puy
2003). All of these equations depend on the Hubble
parameter defined by:
![$\displaystyle H^2 = H_0^2 \Bigr[
\Bigr(\Omega_{\rm r,0} + \Omega_{\rm r,\Lambda...
...ga_{\rm m,0} (1+z)^3 +
\Omega_{\Lambda,1} + \Omega_{\Lambda,2} (1+z)^m \Bigl] ,$](/articles/aa/full/2004/28/aa0256-04/img127.gif) |
|
|
(45) |
where the redshift is expressed by
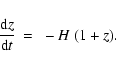 |
(46) |
The numerical integration is a typical initial value problem for stiff differential equations (see Hindmarsh & Petzold 1995). We start
our integration at redshift
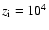 which corresponds to the age of the Universe
which corresponds to the age of the Universe 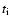 :
:
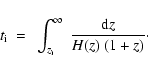 |
(47) |
We have developed seven runs (see Table 2) plus one run (RUN-A) illustrating (m,
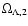 )
parameters of
non-allowed regions
(see Fig. 5 and condition 42). For each run, through a careful spline approach, we have compared
the temperatures with the ones of the standard
case (i.e.
)
parameters of
non-allowed regions
(see Fig. 5 and condition 42). For each run, through a careful spline approach, we have compared
the temperatures with the ones of the standard
case (i.e.
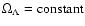 ).
).
Figure 6 shows the ratio of temperatures between a 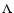 -run and the standard case (i.e. m=0).
The difference is negligible for RUN-1, RUN-2 and RUN-3 and a few 10% for the rest (except the large difference for RUN-A).
-run and the standard case (i.e. m=0).
The difference is negligible for RUN-1, RUN-2 and RUN-3 and a few 10% for the rest (except the large difference for RUN-A).
Table 2:
Model parameters of runs and initials temperature and time; 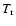 is in K and
is in K and 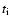 is in years.
is in years.
![\begin{figure}
\par\includegraphics[width=11.4cm,clip]{0256fig6.eps}\end{figure}](/articles/aa/full/2004/28/aa0256-04/Timg133.gif) |
Figure 6:
Ratio of temperatures between a 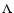 -run and the standard case -run and the standard case
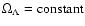 .
Bold curves represent the ratio of
radiation temperatures, dotted curves is the ratio of matter temperatures. .
Bold curves represent the ratio of
radiation temperatures, dotted curves is the ratio of matter temperatures. |
| Open with DEXTER |
These differences can affect the recombination mechanisms and the thermal decoupling between matter and radiation. We define the redshift
of recombination
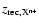 ,
the epoch where the abundances
,
the epoch where the abundances
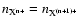 .
We introduce the decoupling
redshift
.
We introduce the decoupling
redshift
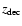 below which the ratio
below which the ratio
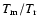 is lower than 0.99.
is lower than 0.99.
Table 3 summarizes the different redshifts of recombination and decoupling. He2+ recombination is
in the range of redshift z=5365 and z=6320 with the extreme case z=8695 (RUN-A), He+ recombination is between z=2291 and z=2696
(z=3701 for the RUN-A), D+ and H+ recombination is between z=1255 and z=1477 (z=2024 for the RUN-A). We find that the redshift
of decoupling is in the range of redshift z=633 and z=811 (z=1258 for the RUN-A).
Table 3:
Redshifts of recombination and thermal decoupling for the different runs.
Changes in recombination and decoupling could affect the formation of the primordial molecules in the post-recombination Universe.
Recently Hashimoto et al. (2003) investigated the primordial chemistry and formation of the first objects in a
model with a decaying cosmological term. They found that molecular formation is significantly shifted to an earlier epoch by
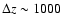 compared to the standard case. Nevertheless, in our analysis, the decaying cosmological term
compared to the standard case. Nevertheless, in our analysis, the decaying cosmological term
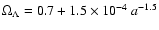 ,
considered by Hashimoto et al. (2003), is ruled out, see Fig. 5.
,
considered by Hashimoto et al. (2003), is ruled out, see Fig. 5.
In this work, we have quantitatively shown that the allowed values of
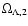 and m are very low. Thus to give a
thermal interpretation of the cosmological constant through a decaying vacuum scenario seems to have stringent limits as determined by the recent
analysis of the CMBR temperature at different redshifts.
and m are very low. Thus to give a
thermal interpretation of the cosmological constant through a decaying vacuum scenario seems to have stringent limits as determined by the recent
analysis of the CMBR temperature at different redshifts.
Measurements from the analysis of the carbon fine-structure population ratio are particularly difficult because of numerous
sources of excitation. For example, fluorescence and dust emission are possible in the population of the excited levels.
As Songaila et al. (1994) mentioned, it would be gratifying to find an appropriate C absorber at higher
redshift to improve existing, much less sensitive, limits from C+.
The multi-frequency measurements through the SZ effect are the most promising. Precise values of
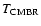 ,
with a significantly larger number
of targets (i.e. clusters), could be obtained by this method. In this context several projects are planned, such as the upgraded MITO (see
Lamagna et al. 2002) or the next balloon-borne telescope to measure the cosmic microwave radiation
(or OLIMPO experiment, see Masi et al. 2003), and could lead to interesting constraints on
,
with a significantly larger number
of targets (i.e. clusters), could be obtained by this method. In this context several projects are planned, such as the upgraded MITO (see
Lamagna et al. 2002) or the next balloon-borne telescope to measure the cosmic microwave radiation
(or OLIMPO experiment, see Masi et al. 2003), and could lead to interesting constraints on
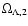 .
.
Acknowledgements
This work was supported by the Swiss National Science Foundation and the University of Geneva.
The author acknowledges Daniel Pfenniger, Monique Signore, Norbert Straumann and
Patrick Vonlanthen for fruitful discussions on 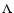 -cosmologies,
Francesco Melchiorri and Paolo Molaro for communications on CMBR temperature
measurements. Special thanks to Agnese Blasina-Puy.
-cosmologies,
Francesco Melchiorri and Paolo Molaro for communications on CMBR temperature
measurements. Special thanks to Agnese Blasina-Puy.
- Bahcall, J., & Wolf,
R. 1968, ApJ, 152, 701 [NASA ADS] [CrossRef] (In the text)
- Barger, V., Kneller, J.,
Lee, H., Marfatia, D., & Steigmann, G. 2003, Phys. Lett. B,
566, 8 [NASA ADS] [CrossRef]
- Battistelli, E., de
Petris, M., Lamagna, L., et al. 2003, Mem. S. A. It. 74, 316
(In the text)
- Bennett, C., Halpern, M.,
Hinshaw, G., et al. 2003, ApJS Lett., 148, 1 [NASA ADS] (In the text)
- Bloomfield Torres, L.,
& Waga, I. 1996, MNRAS, 279, 712 [NASA ADS] (In the text)
- Caldwell, R., Dave, R.,
& Steinhardt, P. 1998, Phys. Rev. Lett., 80, 1582 [NASA ADS] [CrossRef] (In the text)
- Chen, W., & Wu, Y.
1990. Phys. Rev. D, 41, 695
(In the text)
- de Bernardis, P., Ade, P.
A. R., Bock, J. J., et al. 2000, Nature, 404, 955 [NASA ADS] [CrossRef] (In the text)
- Danese, L., & de
Zotti, G. 1977, Riv. Nuovo Cimento, 7, 277 [NASA ADS]
- Dvali, G., Gabadze, G.,
& Porrati, M. 2000, Phys. Lett. B, 485
(In the text)
- Einstein, A. 1917,
Sitzungber. Preuss. Akad. Wiss. Phys. Math. Kl., 142, 177 [NASA ADS] (In the text)
- Elizalde, E., Lidsey, J.,
Nojiri, S., & Odintsov, S. 2003, Phys. Lett. B, 574, 1 [NASA ADS] [CrossRef] [MathSciNet] (In the text)
- Fabbri, R., Melchiorri,
F., & Natale, V. 1978, Ap&SS, 59, 223 [NASA ADS] (In the text)
- Freedman, W. 2000, Phys.
Rep., 333, 13 [NASA ADS] (In the text)
- Freese, K., Adams, F. C.,
Frieman, J. A., Mottola, E., et al. 1987, Nucl. Phys. B, 287,
797 [NASA ADS] [CrossRef] (In the text)
- Freese, K., & Lewis,
M. 2002, Phys. Lett. B, 540, 1 [NASA ADS] [CrossRef] [MathSciNet] (In the text)
- Frolov, A., Kofman, L.,
& Starobinsky, A. 2002, Phys. Lett. B, 545, 8 [NASA ADS] [CrossRef] (In the text)
- Galli, D., & Palla,
F. 1998, A&A, 335, 403 [NASA ADS] (In the text)
- Gasperini, M. 1987, Phys.
Lett. B, 194, 347 [NASA ADS] [CrossRef] (In the text)
- Ge, J., Bechtold, J., &
Black, J. 1997, ApJ, 474, 67 [NASA ADS] [CrossRef] (In the text)
- Hashimoto, M., Kamikawa,
T., & Arai, K. 2003, ApJ, 598, 13 [NASA ADS] [CrossRef] (In the text)
- Hindmarsh, A., &
Petzold, L. 1995, Comput. Phys., 9, 34 [NASA ADS] [CrossRef] (In the text)
- Inagaki, T., Meng, X.,
& Murata, T. 2003 [arXiv:hep-th/0306010]
(In the text)
- Kamenshchik, A.,
Moschella, U., & Pasquier, V. 2001, Phys. Lett. B, 511,
265 [NASA ADS] [CrossRef] (In the text)
- Kazanas, D. 1980, ApJ,
241, L59 [NASA ADS] [CrossRef] (In the text)
- Kimura, K., Hashimoto,
K., Sakoda, K., & Arai, K. 2001, ApJ, 561, L19 [NASA ADS] [CrossRef] (In the text)
- Kompaneets, A. 1957, Sov.
Phys. JETP, 4, 430 [NASA ADS] [MathSciNet] (In the text)
- Lamagna, L., de Petris,
M., Melchiorri, F., et al. 2002, in Experimental Cosmology at
Millimetre Wavelengths, ed. M. de Petris, & M. Gervasi, AIP
Conf. Proc., 616, 92
(In the text)
- Levshakov, S., Takahara,
F., & Agafonova, I. 1999 ApJ, 517, 609
(In the text)
- Mangano, G., Miele, G.,
Pastor, S., & Peloso, M. 2002, Phys. Lett. B, 534, 8 [NASA ADS] [CrossRef] [MathSciNet]
- Masi, S., Ade, P., de
Bernardis, P., et al. 2003, Mem. S. A. It., 74, 96 [NASA ADS] (In the text)
- Mather, J., et al. 1999,
ApJ, 512, 51 [NASA ADS] [CrossRef] (In the text)
- Matyjasek, J. 1995, Phys.
Rev. D, 51, 4154 [NASA ADS] [CrossRef] (In the text)
- Molaro, P., Levshakov, S.
A., Dessauges-Zavadsky, M., & D'Odorico, S. 2002, A&A, 381,
L64 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Meng, X., & Wang, P.
2003 [arXiv:astro-ph/0308284]
(In the text)
- Overduin, J., Wesson, P.,
& Bowyer, S. 1993, ApJ, 404, 1 [NASA ADS] (In the text)
- Overduin, J., &
Cooperstock, F. 1998, Phys. Rev. D, 58, 043506 [NASA ADS] [CrossRef] (In the text)
- Özer, M., &
Taha, M. 1986, Phys. Lett. B, 171, 363 [NASA ADS] [CrossRef] (In the text)
- Özer, M. 1999, ApJ,
520, 45 [NASA ADS] (In the text)
- Peebles, P. J. E. 1968,
ApJ, 153, 1 [NASA ADS] [CrossRef] (In the text)
- Peebles, P. J. E., &
Ratra, B. 2003, Rev. Mod. Phys., 75, 559 [NASA ADS] [CrossRef] [MathSciNet] (In the text)
- Perlmutter, S., Aldering,
G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] (In the text)
- Pfenniger, D., & Puy,
D. 2003, A&A, 398, 447 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Puy, D., Alecian, G., Le
Bourlot, J., Leorat, J., & Pineau Des Forets, G. 1993, A&A,
267, 337 [NASA ADS] (In the text)
- Puy, D., & Signore,
M. 2002, New Ast. Rev., 46, 709 [NASA ADS] (In the text)
- Ratra, B., & Peebles,
P. J. E. 1988, Phys. Rev. D, 37, 3406 [NASA ADS] [CrossRef] (In the text)
- Riess, A., Filippenko, A.
V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] (In the text)
- Sahni, V., &
Starobinsky, A. 2000. Int. J. Mod. Phys. D, 9, 373
(In the text)
- Silveira, V., & Waga,
I. 1994, Phys. Rev. D, 50, 4890 [NASA ADS] [CrossRef] (In the text)
- Songaila, A., Cowie, L.
L., Vogt, S., et al. 1994, Nature, 371, 43 [NASA ADS] [CrossRef] (In the text)
- Srianand, R., Petitjean,
P., & Ledoux, C. 2000, Nature, 408, 931 [NASA ADS] [CrossRef] (In the text)
- Straumann, N. 1999, Eur.
J. Phys., 419, 427 [NASA ADS] (In the text)
- Waga, I. 1993, ApJ, 414,
436 [NASA ADS] [CrossRef] (In the text)
- Weinberg, S. 1989, Rev.
Mod. Phys., 61, 1 [NASA ADS] [CrossRef] [MathSciNet] (In the text)
Copyright ESO 2004
![]() .
Using constraints given by the temperature measurements of the cosmic microwave background, at redshifts
between z=0 and z=4, we find that
.
Using constraints given by the temperature measurements of the cosmic microwave background, at redshifts
between z=0 and z=4, we find that
![]()
![]() models
are clearly ruled out. The influence on the thermal decoupling between matter and radiation is also discussed.
models
are clearly ruled out. The influence on the thermal decoupling between matter and radiation is also discussed.
![]() -ray background in excess of observed levels (see Freese et al. 1987).
-ray background in excess of observed levels (see Freese et al. 1987).
![]() cosmologies have been investigated in different contexts such
as spontaneous symmetry breaking (Kazanas 1980), influence on the evolution of matter
density perturbations (Silveira & Waga 1994), on the age of the Universe (Matyjasek 1995),
the statistical properties of gravitational lenses (Bloomfield-Torres & Waga 1996), or more generally
on the evolution of the scale factor with several possibilities of the functional form of
cosmologies have been investigated in different contexts such
as spontaneous symmetry breaking (Kazanas 1980), influence on the evolution of matter
density perturbations (Silveira & Waga 1994), on the age of the Universe (Matyjasek 1995),
the statistical properties of gravitational lenses (Bloomfield-Torres & Waga 1996), or more generally
on the evolution of the scale factor with several possibilities of the functional form of
![]() ,
see
Overduin & Cooperstock (1998).
,
see
Overduin & Cooperstock (1998).
![]() models is lowered
significantly compared with the constant
models is lowered
significantly compared with the constant
![]() .
Hashimoto et al. (2003) pointed out that molecular
formation is shifted to earlier epochs by
.
Hashimoto et al. (2003) pointed out that molecular
formation is shifted to earlier epochs by
![]() compared to the case in the standard big bang cosmology
(i.e.
compared to the case in the standard big bang cosmology
(i.e.
![]() ). We consider the same appproach. However, prospects for constraining the cosmology by the
extragalactic
microwave background temperature become possible due to the feasibility of measuring this background temperature at
redshifts between z=0 and z=4. Here we use these measurements to constrain the effects of a decaying cosmological term on
the evolution of cosmic microwave radiation (CMBR) temperature.
). We consider the same appproach. However, prospects for constraining the cosmology by the
extragalactic
microwave background temperature become possible due to the feasibility of measuring this background temperature at
redshifts between z=0 and z=4. Here we use these measurements to constrain the effects of a decaying cosmological term on
the evolution of cosmic microwave radiation (CMBR) temperature.
![]() varies. In Sect. 5 we discuss the observational constraints, then
in Sect. 6 we analyse the consequences of decaying
varies. In Sect. 5 we discuss the observational constraints, then
in Sect. 6 we analyse the consequences of decaying ![]() cosmologies (constrained by observations) on the thermal decoupling between
matter and radiation. Our conclusions are summarized in Sect. 7.
cosmologies (constrained by observations) on the thermal decoupling between
matter and radiation. Our conclusions are summarized in Sect. 7.
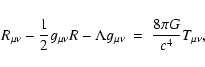
![\begin{displaymath}{\rm d}s^2 ~ = ~ c^2 {\rm d}t^2 -a(t)^2 \Bigr[ \frac{{\rm d}r...
...}^2\theta + r^2 {\rm sin}^2\theta ~
{\rm d}^2\varphi^2 \Bigr]
\end{displaymath}](/articles/aa/full/2004/28/aa0256-04/img21.gif)
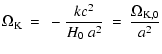
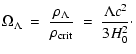
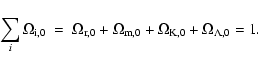
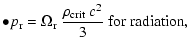
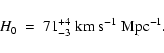
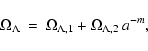
![\begin{displaymath}\Omega_{\rm r} = \Bigr[ \Omega_{\rm r,0} + \Omega_{{\rm r},\Lambda} \Bigl] ~ (1+z)^4 .
\end{displaymath}](/articles/aa/full/2004/28/aa0256-04/img52.gif)
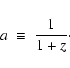
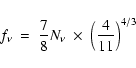
![]() leads to the following evolution:
leads to the following evolution:
![]() is very low, the
difference to the standard case is clear. A larger difference is found for the D1-model where
is very low, the
difference to the standard case is clear. A larger difference is found for the D1-model where
![]() .
.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0256fig1.eps}\end{figure}](/articles/aa/full/2004/28/aa0256-04/Timg75.gif)
![]() dependence than in the standard model.
dependence than in the standard model.
![]() is obtained by assuming
that the CMBR is the only excitation process at work. The measurements have been attempted several times, but have been generally limited
by the resolution and signal-to-noise available in reasonable exposure times.
is obtained by assuming
that the CMBR is the only excitation process at work. The measurements have been attempted several times, but have been generally limited
by the resolution and signal-to-noise available in reasonable exposure times.
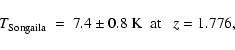
![]() system of the quasar QSO 0013-004. From the population ratio of the
excited state to the ground state, they derive an estimate for the CMBR
temperature:
system of the quasar QSO 0013-004. From the population ratio of the
excited state to the ground state, they derive an estimate for the CMBR
temperature:
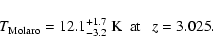
![]() model with the observations.
model with the observations.
![\begin{figure}
\par\includegraphics[width=11.8cm,clip]{0256fig2.eps}\end{figure}](/articles/aa/full/2004/28/aa0256-04/Timg87.gif)
![]() ,
on the radiation temperature:
,
on the radiation temperature:
![$\displaystyle \Omega_{\rm r,0} \Bigr[\Bigr( \frac{T_{\rm obs}^-}{T_{\rm r,0}(1+z_{\rm obs})} \Bigl)^4 -1 \Bigl]$](/articles/aa/full/2004/28/aa0256-04/img93.gif)
![$\displaystyle \Omega_{\rm r,0} \left[\Bigr( \frac{T_{\rm obs}^+}{T_{\rm r,0}(1+z_{\rm obs})} \Bigl)^4 -1 \right] .$](/articles/aa/full/2004/28/aa0256-04/img95.gif)
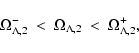
![$\displaystyle \frac{4-m}{m ~ \Bigr[ (1+z_{\rm obs})^{m-4} -1 \Bigl]} ~ \Omega_{\rm obs}^- <0$](/articles/aa/full/2004/28/aa0256-04/img103.gif)
![$\displaystyle \frac{4-m}{m ~ \Bigr[ (1+z_{\rm obs})^{m-4} -1 \Bigl]} ~ \Omega_{\rm obs}^+ >0;$](/articles/aa/full/2004/28/aa0256-04/img105.gif)
![$\displaystyle \frac{4-m}{m ~ \Bigr[ (1+z_{\rm obs})^{m-4} -1 \Bigl]} ~ \Omega_{\rm obs}^+ <0$](/articles/aa/full/2004/28/aa0256-04/img108.gif)
![$\displaystyle \frac{4-m}{m ~ \Bigr[ (1+z_{\rm obs})^{m-4} -1 \Bigl]} ~ \Omega_{\rm obs}^- >0;$](/articles/aa/full/2004/28/aa0256-04/img109.gif)
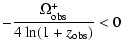
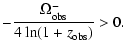
![\begin{figure}
\par\includegraphics[width=13.6cm,clip]{0256fig3.eps}\end{figure}](/articles/aa/full/2004/28/aa0256-04/Timg116.gif)
![\begin{figure}
\par\includegraphics[width=13.6cm,clip]{0256fig4.eps}\end{figure}](/articles/aa/full/2004/28/aa0256-04/Timg117.gif)
![\begin{figure}
\par\includegraphics[width=12.1cm,clip]{0256fig5.eps}\end{figure}](/articles/aa/full/2004/28/aa0256-04/Timg118.gif)
![]() . We use the reaction network developped by Galli & Palla (1998) and couple this primordial kinetic
with the hydrodynamic equations (see Puy & Signore 2002) .
. We use the reaction network developped by Galli & Palla (1998) and couple this primordial kinetic
with the hydrodynamic equations (see Puy & Signore 2002) .
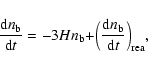
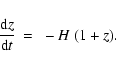
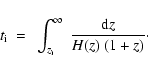
![]() -run and the standard case (i.e. m=0).
The difference is negligible for RUN-1, RUN-2 and RUN-3 and a few 10% for the rest (except the large difference for RUN-A).
-run and the standard case (i.e. m=0).
The difference is negligible for RUN-1, RUN-2 and RUN-3 and a few 10% for the rest (except the large difference for RUN-A).
![]() is in K and
is in K and ![]() is in years.
is in years.![\begin{figure}
\par\includegraphics[width=11.4cm,clip]{0256fig6.eps}\end{figure}](/articles/aa/full/2004/28/aa0256-04/Timg133.gif)
![]() ,
the epoch where the abundances
,
the epoch where the abundances
![]() .
We introduce the decoupling
redshift
.
We introduce the decoupling
redshift
![]() below which the ratio
below which the ratio
![]() is lower than 0.99.
is lower than 0.99.
![]() compared to the standard case. Nevertheless, in our analysis, the decaying cosmological term
compared to the standard case. Nevertheless, in our analysis, the decaying cosmological term
![]() ,
considered by Hashimoto et al. (2003), is ruled out, see Fig. 5.
,
considered by Hashimoto et al. (2003), is ruled out, see Fig. 5.
![]() ,
with a significantly larger number
of targets (i.e. clusters), could be obtained by this method. In this context several projects are planned, such as the upgraded MITO (see
Lamagna et al. 2002) or the next balloon-borne telescope to measure the cosmic microwave radiation
(or OLIMPO experiment, see Masi et al. 2003), and could lead to interesting constraints on
,
with a significantly larger number
of targets (i.e. clusters), could be obtained by this method. In this context several projects are planned, such as the upgraded MITO (see
Lamagna et al. 2002) or the next balloon-borne telescope to measure the cosmic microwave radiation
(or OLIMPO experiment, see Masi et al. 2003), and could lead to interesting constraints on
![]() .
.
-cosmologies, Francesco Melchiorri and Paolo Molaro for communications on CMBR temperature measurements. Special thanks to Agnese Blasina-Puy.