A&A 422, 55-64 (2004)
DOI: 10.1051/0004-6361:20047071
Periodic bursts of star formation in irregular galaxies
F. I. Pelupessy - P. P. van der Werf - V. Icke
Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
Received 14 January 2004 / Accepted 24 March 2004
Abstract
We present N-body/SPH simulations of the evolution of an isolated dwarf
galaxy including a detailed model for the ISM, star formation and stellar
feedback. Depending on the strength of the feedback, the modelled dwarf galaxy
shows periodic or quasi-periodic bursts of star formation of moderate
strength. The period of the variation is related to the dynamical timescale,
of the order of 1.5 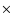 108 yr. We show that the results of these simulations
are in good agreement with recent detailed observations of dwarf irregulars (dIrr) and
that the peculiar kinematic and morphological properties of these objects,
as revealed by high resolution HI studies, are fully reproduced. We discuss these
results in the context of recent surveys of dwarf galaxies and point out that if
the star formation pattern of our model galaxy is typical of dwarf irregulars this
could explain the scatter of observed properties of dwarf galaxies. Specifically,
we show that the time-sampled distribution of the ratio between the instanteneous
star formation rate (SFR) and the mean SFR is similar to the
distribution in observed samples of dwarf galaxies.
108 yr. We show that the results of these simulations
are in good agreement with recent detailed observations of dwarf irregulars (dIrr) and
that the peculiar kinematic and morphological properties of these objects,
as revealed by high resolution HI studies, are fully reproduced. We discuss these
results in the context of recent surveys of dwarf galaxies and point out that if
the star formation pattern of our model galaxy is typical of dwarf irregulars this
could explain the scatter of observed properties of dwarf galaxies. Specifically,
we show that the time-sampled distribution of the ratio between the instanteneous
star formation rate (SFR) and the mean SFR is similar to the
distribution in observed samples of dwarf galaxies.
Key words: methods: numerical - methods: N-body simulations - galaxies: dwarf - Galaxy: evolution - galaxies: ISM - galaxies: irregular
The nature of the processes regulating star formation in irregular galaxies is
poorly understood. While there is at least some understanding of
star formation in regular spiral galaxies, this is less so for irregulars. For
spiral galaxies the guiding observation that the star formation rate (SFR) is
related to the gas surface density by the Schmidt law has given rise to a number
of competing theories that reproduce the general features of star formation in large spiral
galaxies (Elmegreen 2002; Dopita & Ryder 1994). These systems seem to be
regulated by large-scale gravitational instabilities. Star formation in irregular
galaxies has proven to be more difficult to understand. Irregulars have a widely varying
SFR, spanning 4 orders of magnitude for the normalized SFR/area (Hunter 1997),
possibly due to the fact that gas thermodynamics, governed by varying heating and cooling
processes, plays the decisive role (Elmegreen 2002). But why do some irregulars
have very high SFRs relative to their mass, while others hardly show any activity? Are
there any intrinsic properties of the galaxies that can explain this disparity between
SFRs or do all dwarf galaxies exhibit episodes of high star formation?
In recent years a number of studies have highlighted these questions by
investigating samples of dwarf galaxies and comparing their properties as derived
from photometry, HI and H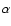 observations. Van Zee (2000, 2001)
investigated a sample of isolated dwarf galaxies and found no strong correlation
between star formation and independent physical parameters. Hunter et al. (1998)
tested different regulating processes, amongst which disk instabilities, thermal and shear
regulated star formation, but found that none could explain patterns of star formation.
Stil (1999) investigated the relation between star formation and HI gas kinematics.
observations. Van Zee (2000, 2001)
investigated a sample of isolated dwarf galaxies and found no strong correlation
between star formation and independent physical parameters. Hunter et al. (1998)
tested different regulating processes, amongst which disk instabilities, thermal and shear
regulated star formation, but found that none could explain patterns of star formation.
Stil (1999) investigated the relation between star formation and HI gas kinematics.
On the other hand, detailed studies of a number of nearby dwarf galaxies have fully revealed
the complex structure of the ISM in these systems. High resolution aperture synthesis
mapping (e.g., Kim et al. 1998; Wilcots & Miller 1998; Puche et al. 1992; Walter & Brinks 2001) of their HI has shown the
interstellar medium (ISM) of these dwarfs to have a frothy structure, with holes of varying
sizes, shells and filaments, even extending far beyond the optical radius. From velocity dispersion studies (Young et al. 1997) the presence of cold and warm neutral components predicted by the two phase model for the ISM (Field 1965) has been deduced. Comparison with
H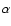 and UV observations shows that the dense walls of these holes are the sites
of star formation (Walter et al. 2001), and suggest "chains'' of
successive star forming sites (Stewart et al. 2000). The cause of the holes in
the HI distribution seems to be the energy input from ionizing radiation, stellar winds
and supernovae, although Rhode et al. (1999) and Efremov et al. (1998)
discuss other possible scenarios.
and UV observations shows that the dense walls of these holes are the sites
of star formation (Walter et al. 2001), and suggest "chains'' of
successive star forming sites (Stewart et al. 2000). The cause of the holes in
the HI distribution seems to be the energy input from ionizing radiation, stellar winds
and supernovae, although Rhode et al. (1999) and Efremov et al. (1998)
discuss other possible scenarios.
Together these two types of observations have painted a picture of the complex interaction
between star formation and the ISM of these systems that is challenging to capture
theoretically. Some early attempts have been made to understand star formation qualitatively
by the application of stochastic self-propagating star formation (SSPSF) models to dwarf
galaxies (Gerola & Seiden 1980; Comins 1983). While they probably
capture some general characteristics of star formation, they are phenomenological and do not
include the underlying physics of the ISM.
Efforts to investigate the influence of star formation on the ISM of dwarf galaxies have
mainly concentrated on the effects of large (central) bursts and on questions concerning
the ejection of gas and the distribution of metals (e.g., Mac-Low & Ferrara 1999;
Mori et al. 1997). Recently there also have been some simulations adressing
the question of survival of small galaxies (Mori et al. 2002). Generally these
simulations have not tried to set up a self consistent model for the ISM and star formation,
but prescribed a certain SFR.
The importance of a good model for the ISM and feedback has been recognized by a number of authors.
Andersen & Burkert (2000) formulated an extensive model for the ISM in terms of a phenomenological model for the interstellar clouds. Their model showed self regulation of the SFR and they found moderate fluctuations in SFR. Berczik & Hensler (2003) incorporated such a cloud model into a chemodynamical galaxy evolution code. Semelin & Combes (2002) formulated a model with similar characteristics, representing clouds by sticky particles, but did not apply these to dwarf galaxies. Springel & Hernquist (2003) formulated a subgrid model for the multiphase interstellar medium, producing a quiescent self-regulating ISM. However, relatively little effort has been directed towards resolving the normal evolution of irregular dwarfs and providing the connection with detailed studies of single systems
and extensive unbiased samples. Nevertheless dwarf galaxies are good test systems for exploring star formation in galaxies: they are dynamically simple systems in the sense that they do not exhibit spiral density waves or shear. Furthermore their small size means that simulations can follow the various physical processes at finer linear and density scales. As the small scale physics of star formation and feedback presumably do not differ between normal and dwarf galaxies, we can use results obtained from these simulations and apply the same methods to larger systems. Here we present results of a simulation of the evolution of a normal dwarf irregular galaxy including a detailed model for the ISM, star formation and feedback. The distinguishing characteristics of this work are that the model for the ISM we employ does not explicitly postulate the presence of a two phase medium, rather it forms it as a result of the physics of the model. Furthermore we take special care in formulating a star formation model that is solely based on the Jeans instability, and we formulate a feedback scheme that gives us unambiguous control over the
strength of the feedback. We will discuss the results of the simulation both in relation to
detailed observations of comparable single systems, as well as in the context
of recent surveys of dwarf galaxies.
We employ an N-body/SPH code for the evolution of a general astrophysical fluid on galactic
scales, extended from TreeSPH (Hernquist & Katz 1989), to simulate the evolution
of an isolated dwarf galaxy. We use the conservative SPH formulation of Springel & Hernquist
(2002). Main features of our code are: a realistic model for the ISM solving for
the ionization and thermal balance for the neutral and ionized components of the ISM, star
formation based on a gravitational instability model for clouds, and a new method of
including feedback for SPH. We will summarize the features of the code with an emphasis on
the aspects most relevant for the present work.
Table 1:
Overview of the processes included in the ISM model used. For H and He ionization equilibrium is explicitly calculated, for other elements collisional ionization equilibrium (CIE) is assumed. Both the heating and cooling strongly depend on the ionization fraction 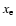 .
Exact expressions adopted for the various processes can be found in:
1) Wolfire et al. (1995); 2) Raga et al. (1997);
3) Verner & Ferland (1996); 4) Silva & Viegas (2001).
.
Exact expressions adopted for the various processes can be found in:
1) Wolfire et al. (1995); 2) Raga et al. (1997);
3) Verner & Ferland (1996); 4) Silva & Viegas (2001).
Our model for the ISM is, although simplified, qualitatively similar to the model for the
Cold Neutral Medium (CNM) and Warm Neutral medium (WNM) of Wolfire et al. (1995, 2003). We consider a gas with arbitrary but fixed chemical abundances Xi, scaled to the target metallicity from the solar abundances of Grevesse & Sauval (1998).
We solve for the ionization and thermal evolution of the gas. The various processes included are
given in Table 1. A similar model to that employed here
was used by Gerritsen & Icke (1997) and Bottema (2003) for galaxy simulations. The main differences are the following: we use more accurate cooling, that is calculated in accordance with the chemical composition, we have included a solver for the ionization balance, and we use the full photoelectric heating efficiency as given in Wolfire et al. (1995). Gerritsen & Icke (1997) found that the structure of the resulting ISM depended strongly on the ionization fraction they assumed, as this strongly influences the cooling. We do not have to assume an ionization fraction, as we calculate it (on the other hand, we do assume a cosmic ray ionization rate that is poorly constrained). Our use of the full heating efficiency means that FUV heating will become less efficient for high radiation fields, due to grain charging. In our model supernova (SN) heating is more important in regulating star formation than it was for Gerritsen & Icke (1997).
A concise overview of the ISM model is given in Fig. 1. The plots in this figure show that as density varies, the equilibrium state of the gas changes from a high temperature/high ionization state (
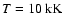 ,
,
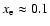 )
at low densities, to a low temperature/low ionization state (
)
at low densities, to a low temperature/low ionization state (
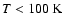 ,
,
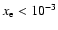 )
at high densities. In between is a density domain where the negative slope of the P-n relation indicates that the gas is unstable to isobaric pressure variations, the classic thermal
instability (Field 1965). The shape of these curves and hence the exact densities of the thermal instability vary locally throughout the simulation according to the conditions of UV and supernova heating. The gas in the simulation may be out of equilibrium, although the timescales for reaching equilibrium are generally short, <
)
at high densities. In between is a density domain where the negative slope of the P-n relation indicates that the gas is unstable to isobaric pressure variations, the classic thermal
instability (Field 1965). The shape of these curves and hence the exact densities of the thermal instability vary locally throughout the simulation according to the conditions of UV and supernova heating. The gas in the simulation may be out of equilibrium, although the timescales for reaching equilibrium are generally short, <
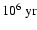 .
In principle the cooling properties of the gas depend on the local chemical composition.
In practice, only small metallicity gradients are observed in dwarfs (Pagel & Edmunds 1981), so we take constant metallicity (
.
In principle the cooling properties of the gas depend on the local chemical composition.
In practice, only small metallicity gradients are observed in dwarfs (Pagel & Edmunds 1981), so we take constant metallicity (
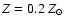 ). Potentially more serious is the fact that we assume a constant cosmic ray ionization rate
). Potentially more serious is the fact that we assume a constant cosmic ray ionization rate 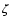 throughout the galaxy. The low energy (
throughout the galaxy. The low energy (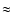
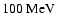 )
cosmic rays that are important for heating and ionization of the ISM, have relatively short mean free paths (<10 pc) so probably
)
cosmic rays that are important for heating and ionization of the ISM, have relatively short mean free paths (<10 pc) so probably 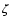 will vary substantially across a galaxy. However, the exact sources, let alone production
rates, of these low energy cosmic rays are not well known. Hence a satisfying model for the distribution of cosmic rays is difficult to formulate. We take a "standard'' value of
will vary substantially across a galaxy. However, the exact sources, let alone production
rates, of these low energy cosmic rays are not well known. Hence a satisfying model for the distribution of cosmic rays is difficult to formulate. We take a "standard'' value of 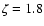
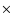
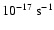 .
For this value cosmic ray heating only becomes important in the outer parts of the galaxy (it may be substantially too low, see McCall et al. 2003).
.
For this value cosmic ray heating only becomes important in the outer parts of the galaxy (it may be substantially too low, see McCall et al. 2003).
The FUV luminosities of the stellar particles, which are needed to calculate the local FUV field used in the photoelectric heating, are derived from Bruzual & Charlot (1993,
and updated) population synthesis models for a Salpeter IMF with cutoffs at 0.1 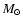 and 100
and 100 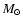 .
In the present work we do not account for dust extinction of UV light.
.
In the present work we do not account for dust extinction of UV light.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{figures/0071fig1.eps}\end{figure}](/articles/aa/full/2004/28/aa0071-04/Timg25.gif) |
Figure 1:
Overview of the ISM model: equilibrium plots of a) temperature T,
b) electron fraction xe and c) pressure P as a function of density n for two different values of the UV field G0, drawn line: G0=1, dotted: G0=10 ( 1.6 1.6 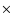
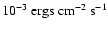 ). ). |
| Open with DEXTER |
We use the star formation recipe of Gerritsen & Icke (1997). A region is
considered unstable to star formation if the local Jeans mass 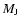 is smaller than
the mass of a typical molecular cloud
is smaller than
the mass of a typical molecular cloud
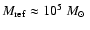 .
The rate of star
formation is set to scale with the local free fall time:
.
The rate of star
formation is set to scale with the local free fall time:
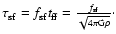 The delay factor
The delay factor
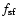 is uncertain, but from observations a value
is uncertain, but from observations a value
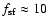 seems reasonable (Zuckerman & Palmer 1974). Once a gas particle is determined to
be forming stars, a fraction
seems reasonable (Zuckerman & Palmer 1974). Once a gas particle is determined to
be forming stars, a fraction
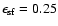 of the mass is converted to stars. This sets a minimum to the star formation efficiency (a neighbourhood of gas particles of about 64 particles that has become capable of star formation will thus form at least a fraction
0.25/64=0.004 of stars). The actual efficiency of star formation is determined by the number of stars needed to quench star formation locally by the UV and SN heating and is determined by the cooling properties of the gas and the energy input from the stars.
of the mass is converted to stars. This sets a minimum to the star formation efficiency (a neighbourhood of gas particles of about 64 particles that has become capable of star formation will thus form at least a fraction
0.25/64=0.004 of stars). The actual efficiency of star formation is determined by the number of stars needed to quench star formation locally by the UV and SN heating and is determined by the cooling properties of the gas and the energy input from the stars.
The recipe is certainly not unique, we have based our choice on the following considerations:
it is simple and based on presence of substructure and the driving role of gas self gravity,
and it reproduces the Schmidt law without actually imposing it (Gerritsen & Icke 1997).
An additional advantage is the fact that the Jeans mass criterion for star formation also
prevents the simulation from violating the resolution requirements for self gravitating
SPH (Bate & Burkert 1997; Whitworth 1998). It does assume substructure
to be present (actually its assumption is more restrictive still, namely that substructure is
mainly at
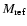 sized clouds, but this is not overly important). For this type of
simulation one is always restricted by the limited ability to follow the starforming
process, so we are forced to adopt a phenomenological description at some level.
Another concern that could be adressed is that the SF according to this recipe is independent
of metallicity, other than that induced by the metallicity dependence of the cooling.
Furthermore, we assume the stellar IMF to be universal.
sized clouds, but this is not overly important). For this type of
simulation one is always restricted by the limited ability to follow the starforming
process, so we are forced to adopt a phenomenological description at some level.
Another concern that could be adressed is that the SF according to this recipe is independent
of metallicity, other than that induced by the metallicity dependence of the cooling.
Furthermore, we assume the stellar IMF to be universal.
The inclusion of feedback in SPH simulations is complicated by the so-called overcooling
problem (Katz 1992). A number of methods has been devised to overcome this, based on the
return of energy as either thermal (Thacker & Couchman 2000; Gerritsen 1997) or kinetic (Navarro & White 1993; Springel & Hernquist 2003). None has been entirely satisfactory as the former requires the artificial suppression of cooling, while the latter suffers from too strong effects for feedback, unless an unrealistically low SN efficiency is adopted or the affected particles are decoupled from the gasdynamics. Here, we employ a new method. It is based on the creation at the location of young stellar clusters of a zero mass SPH particle. Its contribution to gas forces on neighbouring gas
particles is determined by taking the formal zero mass limit with constant particle energy
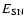 of the usual SPH equations of motion (see Pelupessy et al. 2004, for more details). The amount of feedback (the energy
of the usual SPH equations of motion (see Pelupessy et al. 2004, for more details). The amount of feedback (the energy
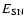 given to the zero mass SPH particle) is an important and uncertain parameter; we estimate it by multiplying the number of type II supernovae per mass of stars formed,
given to the zero mass SPH particle) is an important and uncertain parameter; we estimate it by multiplying the number of type II supernovae per mass of stars formed,
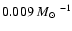 ,
with the effective energy per supernova,
,
with the effective energy per supernova,
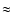
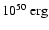 ,
thus assuming that
,
thus assuming that 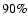 of the energy is radiated away, a value which comes from more detailed simulations of the effect of supernova and stellar winds on the ISM (Silich et al. 1996), and is also used in other simulations of galaxy evolution (e.g., Semelin & Combes 2002; Springel & Hernquist 2002; Buonomo et al. 2000). This energy is then gradually added to the supernova particle over a period of
of the energy is radiated away, a value which comes from more detailed simulations of the effect of supernova and stellar winds on the ISM (Silich et al. 1996), and is also used in other simulations of galaxy evolution (e.g., Semelin & Combes 2002; Springel & Hernquist 2002; Buonomo et al. 2000). This energy is then gradually added to the supernova particle over a period of
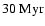 ,
the lifetime of SN progenitors, after which it ceases to exist. This model for the mechanical energy input from stellar clusters resembles the one adopted by Oey & Clarke (1997), who have shown that it is fully consistent with the differential size distribution of superbubbles in a.o. the SMC and Holmberg II. We do not
include the effect of SN Ia, which are mainly important for the chemical enrichment.
,
the lifetime of SN progenitors, after which it ceases to exist. This model for the mechanical energy input from stellar clusters resembles the one adopted by Oey & Clarke (1997), who have shown that it is fully consistent with the differential size distribution of superbubbles in a.o. the SMC and Holmberg II. We do not
include the effect of SN Ia, which are mainly important for the chemical enrichment.
Here we will restrict ourselves to following the evolution of an isolated dwarf galaxy in an
attempt to understand the interplay between star formation and the ISM. These processes play a role for dwarf galaxies in general, and indeed in all places were star formation is happening. It is important to keep in mind, however, that dwarf galaxy evolution is easily influenced by external factors such as infall of gas, collisions, and recently receiving much attention, ram pressure stripping by the inter galactic medium and tidal stripping by galactic potentials (see e.g., Marcolini et al. 2003; Mori & Burkert 2000; Mayer et al. 2001; Pasetto et al. 2003, for recent work on these). Nevertheless the isolated case remains very relevant as it allows a straightforward comparison with suitably selected samples of observed galaxies which exist in the literature (e.g., van Zee 2001), unaffected by the uncertainties of additional external influences. The understanding of the complex processes of star
formation and feedback gained from the isolated case can then be aplied to more general evolution scenarios.
We thus set up a model dwarf galaxy resembling current dIrrs. Although these exhibit a wide range of morphologies, they are very similar in their averaged radial profiles to scaled down versions of
ordinary disk galaxies. Hence we take for the initial condition a three component model for a
small disc galaxy, consisting of a gas disk, a stellar disk and a dark halo, modelled loosely
on the properties of DDO 47 and similar dIrrs. The gas disk we construct with a radial surface
density profile,
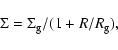 |
(1) |
with central density
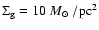 and radial scale
and radial scale
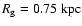 ,
truncated at 6 kpc. It is somewhat involved, due to the thickness of the gas disk, to solve its vertical structure exactly. Hence, before we start the simulation proper, we set up the galaxy with an quadratically rising gas scaleheight and we it run isothermally (
,
truncated at 6 kpc. It is somewhat involved, due to the thickness of the gas disk, to solve its vertical structure exactly. Hence, before we start the simulation proper, we set up the galaxy with an quadratically rising gas scaleheight and we it run isothermally (
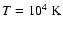 )
and without star formation and feedback for some time until it settles in equilibrium. This results in a scaleheight set by hydrostatic equilibrium of
)
and without star formation and feedback for some time until it settles in equilibrium. This results in a scaleheight set by hydrostatic equilibrium of
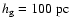 at the center to
at the center to
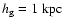 at
at
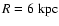 .
An exponential stellar disk,
.
An exponential stellar disk,
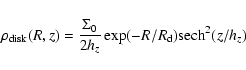 |
(2) |
with central surface density
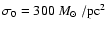 ,
,
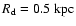 and
vertical scale height
and
vertical scale height
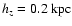 ,
is constructed as in Kuijken & Dubinski (1995). The total mass of the gas is
,
is constructed as in Kuijken & Dubinski (1995). The total mass of the gas is
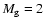
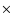
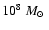 and the total mass of the stellar disk is
and the total mass of the stellar disk is
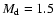
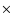
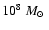 .
Both the gas disk and stellar disk are represented by N=105 particles. The ages of the initial population of stars are distributed according to a constant SFR of 0.007
.
Both the gas disk and stellar disk are represented by N=105 particles. The ages of the initial population of stars are distributed according to a constant SFR of 0.007
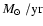 .
.
Dwarf galaxies are amongst the most dark matter dominated objects, exhibiting dark to luminous matter ratios of 10-100. Their rotation curves are best fit by flat central density cores (Flores & Primack 1994; Burkert 1995). Therefore we take a halo profile
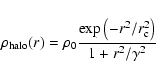 |
(3) |
with core radius
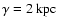 ,
cutoff radius
,
cutoff radius
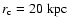 and central density
and central density
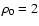
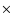
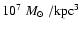 ,
for a total mass of
,
for a total mass of
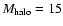
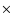
 and a peak rotation velocity of about 50 km s-1. The profile (3) is very similar to the Burkert (1995) profile for dwarf galaxies, differing in its asymptotic behavior for
and a peak rotation velocity of about 50 km s-1. The profile (3) is very similar to the Burkert (1995) profile for dwarf galaxies, differing in its asymptotic behavior for
 .
This will only give significant deviations well outside
the region of interest for our simulations. We represent the dark halo by a static potential.
This is deemed sufficient for the dynamical modelling presented here, as we evolve the galaxy in
isolation and the perturbations in the gaseous and stellar disk are expected to have only minor
impact on the halo structure. Furthermore, discreteness noise of a particle halo can induce bars
to form, and excite spiral structure or bending modes in the stellar and gaseous disk (Kuijken
& Dubinski 1995; Hernquist 1993).
.
This will only give significant deviations well outside
the region of interest for our simulations. We represent the dark halo by a static potential.
This is deemed sufficient for the dynamical modelling presented here, as we evolve the galaxy in
isolation and the perturbations in the gaseous and stellar disk are expected to have only minor
impact on the halo structure. Furthermore, discreteness noise of a particle halo can induce bars
to form, and excite spiral structure or bending modes in the stellar and gaseous disk (Kuijken
& Dubinski 1995; Hernquist 1993).
![\begin{figure}
\par\includegraphics[width=14.4cm,clip]{figures/0071fig2.ps} \end{figure}](/articles/aa/full/2004/28/aa0071-04/Timg63.gif) |
Figure 2:
Simulated dwarf galaxy after 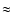 1 Gyr. Shown are
UBV composite pictures overplotted with HI density contours at different times. Last frame shows
the central regions at 1 Gyr. Shown are
UBV composite pictures overplotted with HI density contours at different times. Last frame shows
the central regions at
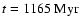 .
HI contour
levels are at .
HI contour
levels are at
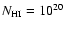 ,
2.1 ,
2.1 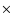 1020, 3.6
1020, 3.6 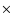 1020
and 2
1020
and 2 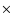
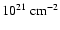 .
(This figure is available in color in electronic form.) .
(This figure is available in color in electronic form.) |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=16.2cm,clip]{figures/0071fig3.eps} \end{figure}](/articles/aa/full/2004/28/aa0071-04/Timg64.gif) |
Figure 3:
HI surface density & velocity dispersion map in quiescent phase ( left, taken
at 1165 Myr) and in burst phase ( right, at 1211 Myr). |
| Open with DEXTER |
In Fig. 2 a range of snapshots of the simulated dwarf galaxy is shown, taken
after about 1 Gyr of evolution and spaced about 50 million years apart. UBV composite
images are plotted with HI contours overplotted. If we look at the contours and maps of HI
of the upper panels of Fig. 3 we see that the HI distribution of the galaxy is
dominated by holes of varying sizes. Dense shells of HI combine to form big HI clouds, which
correspond to the sites of intense star formation. Sometimes structures resembling spiral arms
form, but generally there are no spiral density waves in gas or stars, and, due to the low
shear, a flocculent spiral structure also does not develop. As the cold clouds
move about in the galaxy they are in turn destroyed by mechanical feedback from the stars
to perpetuate the cycle of star formation, cloud destruction and formation. Clearly the
ISM of the galaxy is in a very dynamical state. This can only be fully appreciated
while looking at the time sequence of the complete simulation. The ISM of
dwarf irregulars is continuously stirred and material from different radii is mixed
through the action of supernovae and stellar winds. While this may have been expected
beforehand from energy considerations, it is nonetheless an important and often
overlooked fact. As such it should not be surprising that irregulars often show
very little radial metallicity gradients (apart from the fact that metals may be lost from
hot outflows). Note that the presence of the hydrodynamics of the ISM is a fundamental
difference between classical SSPSF and phenomological models and our full dynamical
simulations.
If we look at the UBV images we see that the appearance of the galaxy varies with time.
Episodes of strong star formation (e.g. at 1024 Myr) are followed by quiescent phases (1071 and 1118 Myr). During star formation bursts the galaxy is dominated by a few
very active star formation sites, during quiet times the galaxy fades and seems relatively
featureless. If we compare the stellar and HI distribution of Fig. 2 to observed
systems, it is striking how similar these are. For example Holmberg II and NGC 4214, which have
been studied in great detail (Puche et al. 1992; Walter & Brinks 2001),
show an HI distribution with a similar number of holes of similar sizes. Also the extent of
structure in the gas outside the optical disk is reproduced in the simulations. Large regions of
star formation are associated with the highest contours of HI (corresponding to a column density
of about N=2 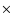
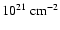 ), which is also found in comparisons of optical and HI morphology for observed systems.
), which is also found in comparisons of optical and HI morphology for observed systems.
As we have a complete representation of the neutral phases of the ISM we can also compare our
simulation with the HI kinematics of observed systems. In Fig. 3 we have
plotted maps of the HI density and the (line of sight) velocity dispersion of the gas.
The gas typically has random velocities of the order of 3-10 km s-1, with regions of higher
(up to 20 km s-1) velocity dispersion associated with expanding bubbles, in good agreement with observations (Stil 1999; Young et al. 1997).
![\begin{figure}
\par\includegraphics[width=16.7cm,clip]{figures/0071fig4.ps} \end{figure}](/articles/aa/full/2004/28/aa0071-04/Timg65.gif) |
Figure 4:
Star Formation History of a simulated dwarf galaxy. Upper panel: density plot of
the azimutally averaged star formation rate. Lower panel: total star formation rate. The
dotted line indicates the SFR for a run with 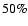 reduced feedback strength.
reduced feedback strength. |
| Open with DEXTER |
The evolution of the SFR is shown in Fig. 4. It shows a gray scale plot of
the temporal evolution of the (azimuthally averaged) star formation density and below
it the resulting total SFR. We see that after an initial transient period the galaxy
settles in a mode of periodically varying star formation, with a minimum SFR of about
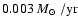 while the peak SFR is about a factor of 10 higher. Also plotted are the results for a run with reduced feedback strength. In this case variations are smaller in amplitude,
and quasi-periodic. Even lower feedback strengths would probably quench the variations
completely, but in that case morphology and kinematics of the gas would no longer match
observed systems. In the upper panel of Fig. 4 we see the pattern of propagating star formation. The azimuthally averaged density plot may give the false impression that star formation is happening in inward and outward moving rings; however visual inspection shows that it moves around in patches and partial rings: if some region starts to form stars, nearby dense regions will be triggered to form stars, often moving the star formation in a particular direction along a dense filament or bridge. Furthermore we see that periodic bursts happen only relatively close to the centre of the galaxy, whereas in the outer parts stars form at a more or less constant low rate. This behaviour is expected (see Ehlerová & Palous 2002) because star formation can only be triggered in the expanding shells around the holes induced by feedback if the column density is high enough,
while the peak SFR is about a factor of 10 higher. Also plotted are the results for a run with reduced feedback strength. In this case variations are smaller in amplitude,
and quasi-periodic. Even lower feedback strengths would probably quench the variations
completely, but in that case morphology and kinematics of the gas would no longer match
observed systems. In the upper panel of Fig. 4 we see the pattern of propagating star formation. The azimuthally averaged density plot may give the false impression that star formation is happening in inward and outward moving rings; however visual inspection shows that it moves around in patches and partial rings: if some region starts to form stars, nearby dense regions will be triggered to form stars, often moving the star formation in a particular direction along a dense filament or bridge. Furthermore we see that periodic bursts happen only relatively close to the centre of the galaxy, whereas in the outer parts stars form at a more or less constant low rate. This behaviour is expected (see Ehlerová & Palous 2002) because star formation can only be triggered in the expanding shells around the holes induced by feedback if the column density is high enough,
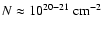 .
So we see that the galaxy has three different SF regimes: an outer region where the gas density is generally
not high enough for the CNM to form (beyond the so called thermal cut off, see Elmegreen &
Parravano 1994; Gerritsen & Icke 1997) so SF will be strongly
supressed there; a region at intermediate radii where the gas density is high enough to be thermally unstable, and where star formation proceeds at a steady pace; and a central region that is both thermally unstable and unstable to shell instabilities, where the dominant mode of SF is triggered star formation. Figure 5 shows a plot of the resulting radial dependence of the star forming density, clearly visible are the three different regions with different star forming behaviour. The bursting region is confined within 1.5 kpc, while star formation extends further out, stopping abrubtly at
.
So we see that the galaxy has three different SF regimes: an outer region where the gas density is generally
not high enough for the CNM to form (beyond the so called thermal cut off, see Elmegreen &
Parravano 1994; Gerritsen & Icke 1997) so SF will be strongly
supressed there; a region at intermediate radii where the gas density is high enough to be thermally unstable, and where star formation proceeds at a steady pace; and a central region that is both thermally unstable and unstable to shell instabilities, where the dominant mode of SF is triggered star formation. Figure 5 shows a plot of the resulting radial dependence of the star forming density, clearly visible are the three different regions with different star forming behaviour. The bursting region is confined within 1.5 kpc, while star formation extends further out, stopping abrubtly at 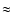
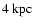 ,
well short of the edge of the gasdisk. Interestingly, De Blok & Walter (2003) found evidence for similar low level star formation outside the optical disk of NGC 6822.
,
well short of the edge of the gasdisk. Interestingly, De Blok & Walter (2003) found evidence for similar low level star formation outside the optical disk of NGC 6822.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{figures/0071fig5.ps} \end{figure}](/articles/aa/full/2004/28/aa0071-04/Timg69.gif) |
Figure 5:
Radial profile of the mean star formation density (drawn line, dotted lines are
exponentials with scalelengths of 0.25 and 1. kpc). |
| Open with DEXTER |
The cyclical pattern of star formation raises a number of further questions: what is
the driver of these variations? What determines the period and amplitude of the oscillation?
Why is star formation apparently synchronized over the whole galaxy? While some previous
models of galaxies have shown variations of the star formation rate, these were either
connected to an imposed time scale (the duration of supernova feedback,
Wada & Norman 2001) or due to random scatter of a probabilistic model (Gerola
et al. 1980). Significant quasi random variations in SF rate were found by
Carraro et al. (2001) to happen during formation of dwarf ellipticals (dEs), in
their case caused by local depletion of the starforming gas reservoir, happening on
timescales of 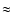 108-9 yr. Similar variations driven mainly by internal proccesses were
found by Pasetto et al. (2003) even for dIrrs subjected to tidal stirring.
In our case the timescale of the variations is related to a physical time scale: the period of
the oscillation is about 165 Myr, which is slightly larger than double the dynamical time scale
of the darkhalo, (
108-9 yr. Similar variations driven mainly by internal proccesses were
found by Pasetto et al. (2003) even for dIrrs subjected to tidal stirring.
In our case the timescale of the variations is related to a physical time scale: the period of
the oscillation is about 165 Myr, which is slightly larger than double the dynamical time scale
of the darkhalo, (
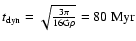 ). This suggests that supernova feedback provides the kick for the oscillation, expelling gas and increasing the velocity dispersion and thus inflating the gas disk, after which the gas falls back for the next cycle on a dynamical time scale. The period is thus determined by the density of the halo (the main
mass component of dwarf galaxies), while the amplitude is related to the strength of the
supernova feedback. Note that this would not be sufficient to account for the regularity of
the variations: in general one would expect that gas from different parts of the gas disk
would experience kicks of different strength, and would fall back on different time scales,
giving rise to a more chaotic pattern of star formation. However dwarf galaxies
are in solid body rotation and thus their potential corresponds to a harmonic oscillator, which
means that material flung out of the disc falls back in the same time, irrespective of
location and speed, synchronizing the SFR over the whole galaxy. This effect certainly adds
to the phenomenon shown in Fig. 4, namely that the overall star formation cycle looks
remarkably regular.
). This suggests that supernova feedback provides the kick for the oscillation, expelling gas and increasing the velocity dispersion and thus inflating the gas disk, after which the gas falls back for the next cycle on a dynamical time scale. The period is thus determined by the density of the halo (the main
mass component of dwarf galaxies), while the amplitude is related to the strength of the
supernova feedback. Note that this would not be sufficient to account for the regularity of
the variations: in general one would expect that gas from different parts of the gas disk
would experience kicks of different strength, and would fall back on different time scales,
giving rise to a more chaotic pattern of star formation. However dwarf galaxies
are in solid body rotation and thus their potential corresponds to a harmonic oscillator, which
means that material flung out of the disc falls back in the same time, irrespective of
location and speed, synchronizing the SFR over the whole galaxy. This effect certainly adds
to the phenomenon shown in Fig. 4, namely that the overall star formation cycle looks
remarkably regular.
When we compare the star formation in our model and observed SFR (for example in
Van Zee 2001) we see that the agreement is quite good: our values fall well
within the range of observed rates of
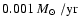 to
to
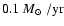 ,
although
admittedly the star formation rate in our model does depend fairly strongly on poorly
constrained quantities such as the shape of the IMF, the amount of energy released in SN and stellar winds, and the various parameters regulating star formation. It is
however encouraging that we can use reasonable values for the parameters and get SFR
that are close to observed rates.
,
although
admittedly the star formation rate in our model does depend fairly strongly on poorly
constrained quantities such as the shape of the IMF, the amount of energy released in SN and stellar winds, and the various parameters regulating star formation. It is
however encouraging that we can use reasonable values for the parameters and get SFR
that are close to observed rates.
In our model the star formation rate is seen to vary over time. This is difficult to verify in
real dwarf galaxies. One would have to derive accurate SFH over hundreds of Myr for galaxies, and
variations of within a factor 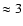 of the mean as observed in our
model would not be too conspicous in the data. For most dwarf galaxies the long term star
formation histories determined from global colours indicate an approximately constant SFR.
Detailed examinations of nearby resolved dwarfs do show evidence of variations
in the SFR (Dohm-Palmer et al. 1998, 2002) of the correct order of magnitude. Strong additional evidence for variations in the SFR is the observed scatter in the ratio of current star formation to past star formation: the Scalo b parameter. If the variations in our model were generic for isolated dwarf galaxies, this would explain the observed distribution of b. To see this we have plotted in Fig. 6 the histograms of
of the mean as observed in our
model would not be too conspicous in the data. For most dwarf galaxies the long term star
formation histories determined from global colours indicate an approximately constant SFR.
Detailed examinations of nearby resolved dwarfs do show evidence of variations
in the SFR (Dohm-Palmer et al. 1998, 2002) of the correct order of magnitude. Strong additional evidence for variations in the SFR is the observed scatter in the ratio of current star formation to past star formation: the Scalo b parameter. If the variations in our model were generic for isolated dwarf galaxies, this would explain the observed distribution of b. To see this we have plotted in Fig. 6 the histograms of
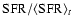 for our simulation together with the distribution of b for a sample of isolated dwarf galaxies as derived by Van Zee (2001). Clearly these two are qualitatively the same. There are two main differences: (1) the distribution of our model extends to higher and lower ratios and (2) the galaxy sample contains galaxies with b>4, which are extreme bursting systems. The first difference would be remedied by decreasing the strength of feedback. We also have plotted the results
for a run with
for our simulation together with the distribution of b for a sample of isolated dwarf galaxies as derived by Van Zee (2001). Clearly these two are qualitatively the same. There are two main differences: (1) the distribution of our model extends to higher and lower ratios and (2) the galaxy sample contains galaxies with b>4, which are extreme bursting systems. The first difference would be remedied by decreasing the strength of feedback. We also have plotted the results
for a run with 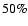 less feedback. In this case the amplitude of variations is somewhat too small (although both are in good agreement with the observed distribution given the uncertainties inherent in deriving it, see discussion in Van Zee 2001). For the second point we should mention
that our simulation really only samples a limited number of cycles; the bursts may be rarer
events that have not (yet) happened in the simulation. Of course it also possible that high powered
bursts are due to outside influences, such as interactions or infalling gas clouds, ingredients of
galaxy evolution not present in our model.
less feedback. In this case the amplitude of variations is somewhat too small (although both are in good agreement with the observed distribution given the uncertainties inherent in deriving it, see discussion in Van Zee 2001). For the second point we should mention
that our simulation really only samples a limited number of cycles; the bursts may be rarer
events that have not (yet) happened in the simulation. Of course it also possible that high powered
bursts are due to outside influences, such as interactions or infalling gas clouds, ingredients of
galaxy evolution not present in our model.
The distribution of b is a highly degenerate indicator of the SF history, and we are aware
that the above comparison presupposes a number of properties for the population of dwarf
galaxies: the assumption that the dwarf galaxies form a homogeneous population; variations
in SFR are assumed to be of similar strength and shape,
independent of galaxy properties (although the b distribution is independent of the period);
and that the variations in SFR are periodic. Nevertheless we think that this is the simplest
explanation for the observed scatter and that our model captures a number of essential features
of the variations in star formation given the characteristic shape of the observed b distribution, namely: moderate bursting, long periods of low SF, and the "peakiness'' of the
SF enhancements. It is also difficult to see what would induce non-periodic variations in
isolated galaxies, especially since no properties independent of the SFR that correlate
with the SFR (Van Zee 2001) have been found.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{figures/0071fig6.ps} \end{figure}](/articles/aa/full/2004/28/aa0071-04/Timg75.gif) |
Figure 6:
distribution of
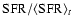 for a sample of isolated dwarfs
(squares with error bars), a simulation with full feedback (drawn line) and a simulation with
for a sample of isolated dwarfs
(squares with error bars), a simulation with full feedback (drawn line) and a simulation with 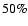 feedback (dotted line). Data is taken from Van Zee (2001).
feedback (dotted line). Data is taken from Van Zee (2001). |
| Open with DEXTER |
The model we employed to calculate the evolution of a single dwarf galaxy is quite extensive and
complicated and necessarily contains a number of free parameters, some of which we tried to constrain using observational data or theory (as in the case of the supernova energy), yet some
remain only constrained by physical intuition. Therefore, it is worthwhile to
summarize again the features of observed dwarf systems successfully reproduced by the model: 1) the
morphology and kinematics of the HI distribution; 2) the two phase structure of the ISM; 2) the spatial pattern of star formation; 3) the star formation rate; 4) consistency with the observed distribution of Scalo b parameter. These provide strong and independent checks of our modelling approach as they result from the intricate interplay of the model for the ISM we employed, the scheme for star formation and the method of returning mechanical energy to the ISM. These successes give some confidence that the model captures the essentials of dwarf galaxy evolution and to its predictive power.
Comparing our model with recent simulations of dwarf galaxy evolution (e.g., Berzcik et al. 2003; Mayer et al. 2001; Andersen & Burkert 2000; Pasetto et al. 2003; Mori et al. 1997, 1999; Carraro et al. 2001) we see that our work differs from previous work in two crucial aspects: 1) the modelling of the physics of the neutral ISM; 2) the treatment
of supernova feedback. We follow the evolution of the WNM and CNM of the ISM explicitly, this process being the upper part of a cascade leading down to star formation. Star formation in our model happens in cold (
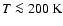 )
and dense (
)
and dense (
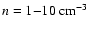 )
gas. These are realistic sites for star formation as we know that molecular clouds are embedded in neutral envelopes. The further stages of star formation, molecular cloud formation and collapse, are not included as they require prohibitive resolution and the inclusion of additional physics. These processes are only implicit
in our star formation recipe, but at least our methods follows collapsing gas to the point that it has experienced a transition to a cold, dense state from which it may be trusted to form stars with rates and efficiencies that are constrained by observations. Some authors have tried to bypass this problem by formulating a phenomenological ISM model in terms of "sticky'' particles representing molecular clouds (Andersen & Burkert 2000),
sometimes in addition to a smooth SPH component representing the WNM (Semelin & Combes 2002; Berczik et al. 2003). They also succesfully reproduce a selfregulated ISM, including some effects, like evaporation of molecular clouds that are probably not well represented in our model. In these models stars form from the cloud particles, imposing a Schmidt law, not, as in our model, from the consideration of the the instabilities in the ISM. Furthermore, our model has a consistent representation of the ISM linking phases by physical processes, rather than prescriptions.
)
gas. These are realistic sites for star formation as we know that molecular clouds are embedded in neutral envelopes. The further stages of star formation, molecular cloud formation and collapse, are not included as they require prohibitive resolution and the inclusion of additional physics. These processes are only implicit
in our star formation recipe, but at least our methods follows collapsing gas to the point that it has experienced a transition to a cold, dense state from which it may be trusted to form stars with rates and efficiencies that are constrained by observations. Some authors have tried to bypass this problem by formulating a phenomenological ISM model in terms of "sticky'' particles representing molecular clouds (Andersen & Burkert 2000),
sometimes in addition to a smooth SPH component representing the WNM (Semelin & Combes 2002; Berczik et al. 2003). They also succesfully reproduce a selfregulated ISM, including some effects, like evaporation of molecular clouds that are probably not well represented in our model. In these models stars form from the cloud particles, imposing a Schmidt law, not, as in our model, from the consideration of the the instabilities in the ISM. Furthermore, our model has a consistent representation of the ISM linking phases by physical processes, rather than prescriptions.
Simulations of dwarf galaxy evolution that include supernova feedback have typically included this as a local heating term. This method for implementing supernova feedback is not effective in forming the structures associated with stellar feedback and simulations using it do not show any effect of SN feedback. This is a well understood numerical artefact and some authors have devised methods to prevent the radiative loss of mechanical energy that is the root of the problem (Springel & Hernquist 2003; Thacker & Couchman 2000; Gerritsen & Icke 1997;
the problem is also not exclusive to SPH type codes see e.g., Fragile et al. 2003). They have not applied their methods to the evolution of dIrrs so a direct comparison is not yet possible. However, the notion that the energy input from stellar winds and SN of young stellar clusters is crucial for the understanding the structure and kinematics of the ISM of dIrrs is borne out by our simulations: if feedback is not included, the ISM stays in a smooth disk with very low random motions (2-3 km s-1). The self propagating mode of
star formation is absent in that case. The dwarf galaxy will only poorly resemble a real dIrr.
Chemical enrichment is not yet included in our code. We can estimate the importance of a
changing chemical composition for our simulation. The total amount of metals Mz produced during the simulation is
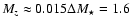
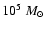 .
This will raise
the metallicity of the galaxy, under the assumption that the metals will be well mixed, with at most
.
This will raise
the metallicity of the galaxy, under the assumption that the metals will be well mixed, with at most 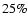 ,
which is not entirely insignificant, although to first approximation the thermal evolution is independent of metallicity as both the cooling and UV heating scale with Z. Note also that metals may be lost from the galaxy in galactic winds. It does mean that we should include chemical enrichment to follow the evolution for longer timescales and especially if we want to investigate extremely metal-poor galaxies. In principle the inclusion of chemical enrichment will also add further constrains when comparing with observations, very important to asses the long term evolution of the model. Both these points, however, do not alter the conclusion for simulations as presented here.
,
which is not entirely insignificant, although to first approximation the thermal evolution is independent of metallicity as both the cooling and UV heating scale with Z. Note also that metals may be lost from the galaxy in galactic winds. It does mean that we should include chemical enrichment to follow the evolution for longer timescales and especially if we want to investigate extremely metal-poor galaxies. In principle the inclusion of chemical enrichment will also add further constrains when comparing with observations, very important to asses the long term evolution of the model. Both these points, however, do not alter the conclusion for simulations as presented here.
The methods we use can be applied more generally. Questions that we plan to address are
for example the following:
- In view of the recent realization that there is a deficit of observed small galaxies as
compared to predictions of
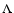 CDM models of galaxy formation
(Klypin et al. 1999) it is interesting to consider what happens for galaxies of
progressively smaller mass. We are in the process of running a grid of models exploring
this question, but some effects may be clear from the preceding: for smaller galaxies,
variations will be on longer time scales (scaling as
CDM models of galaxy formation
(Klypin et al. 1999) it is interesting to consider what happens for galaxies of
progressively smaller mass. We are in the process of running a grid of models exploring
this question, but some effects may be clear from the preceding: for smaller galaxies,
variations will be on longer time scales (scaling as
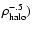 and
greater in amplitude (because the feedback becomes relatively stronger as the escape velocity
decreases). Ultimately halos will be too small to retain their ISM, leaving them bare.
The mass ranges for which this happens, the influence of other galactic parameters and the
timescales on which these processes take place will be of interest to validate cosmological
and galaxy formation models.
and
greater in amplitude (because the feedback becomes relatively stronger as the escape velocity
decreases). Ultimately halos will be too small to retain their ISM, leaving them bare.
The mass ranges for which this happens, the influence of other galactic parameters and the
timescales on which these processes take place will be of interest to validate cosmological
and galaxy formation models.
- We also plan to investigate a possible relation between dwarf irregulars and dwarf ellipticals. Although recent simulations (Mayer et al. 2001; Pasetto et al. 2003) have shown for satellite galaxies that a transition from dIrr to dE or dwarf Spheroidal (dSph) is plausible as a result of the action of tidal fields, it has not been conclusively determined whether a transition from dIrr to dE is to be expected in general. Various groups have put forward arguments in favour (Davies & Phillipps 1988) and against (Bothun et al. 1986; Marlowe et al. 1999) such a descendancy for the dE. Although the results presented here do not immediately illuminate this question, we think that additional simulations of the sort presented here, testing a wider range of galactic properties and
following the evolution for longer time scales may answer whether this is a viable
scenario and whether we can put the various classes of small galaxies into an unified
evolutionary framework.
In summary, our model suggests that it is possible that a large part of the current dIrr population is in a quasi-periodic burst mode of star formation. The scatter in observed
properties in this picture is mainly due to the fact that galaxies are observed at different phases
of their evolution. The main difference between our model and classical SSPSF models is that
in our models variations are due to the interplay of stellar feedback and gas dynamics, the galaxy
being periodically stirred by bursts of star formation after which a quiescent period occurs during
which gas falls back to the disk. In classical SSPSF models the variations are due to the
fact that star formation is described by a correlated stochastic process and the small size of the
galaxies, which induces large statistical variations. Our model predicts that the amplitude
of the variations depends on the strength of the feedback and that the period depends on the
dynamical time scale.
Acknowledgements
The authors want to thank Jeroen Gerritsen and Roelof Bottema for providing
software and analysis tools. F.I.P. wants to thank Padelis Papadopoulos for contributing to
this paper by lending his time to many discussions on dwarf galaxies.
This work was sponsored by the stichting Nationale Computerfaciliteiten
(National Computing Facilities Foundation) for the use of supercomputer
facilities, with financial support from the Nederlandse Organisatie voor
Wetenschappelijk Onderzoek (Netherlands Organisation for Scientific Research,
NWO). F.I.P. was supported by a grant from NWO.
- Andersen, R.-P., &
Burkert, A. 2000, ApJ, 531, 296 [NASA ADS] [CrossRef] (In the text)
- Bate, M. R., &
Burkert, A. 1997, MNRAS, 288, 1060 [NASA ADS] (In the text)
- Berczik, P., Hensler,
G., Theis, C., & Spurzem, R. 2003, Ap&SS, 284, 865 [NASA ADS] (In the text)
- Bothun, G. D.,
Mould, J. R., Caldwell, N., & MacGillivray, H. T.
1986, AJ, 92, 1007 [NASA ADS] [CrossRef] (In the text)
- Bottema, R. 2003, MNRAS, 344,
358 [NASA ADS] [CrossRef] (In the text)
- Bruzual, A. G., &
Charlot, S. 1993, ApJ, 405, 538 [NASA ADS] [CrossRef] (In the text)
- Buonomo, F., Carraro,
G., Chiosi, C., & Lia, C. 2000, MNRAS, 312, 371 [NASA ADS] [CrossRef] (In the text)
- Burkert, A. 1995, ApJ, 447,
L25 [NASA ADS] (In the text)
- Carraro, G., Chiosi,
C., Girardi, L., & Lia, C. 2001, MNRAS, 327, 69 [NASA ADS] [CrossRef] (In the text)
- Comins, N. F. 1983, ApJ,
266, 543 [NASA ADS] [CrossRef] (In the text)
- Davies, J. I., &
Phillipps, S. 1988, MNRAS, 233, 553 [NASA ADS] (In the text)
- de Blok,
W. J. G., & Walter, F. 2003, MNRAS, 341, L39 [NASA ADS] (In the text)
- Dohm-Palmer, R. C.,
Skillman, E. D., Gallagher, J., et al. 1998, AJ, 116,
1227 [NASA ADS] [CrossRef] (In the text)
- Dohm-Palmer, R. C.,
Skillman, E. D., Mateo, M., et al. 2002, AJ, 123,
813 [NASA ADS] [CrossRef] (In the text)
- Dopita, M. A., &
Ryder, S. D. 1994, ApJ, 430, 163 [NASA ADS] [CrossRef] (In the text)
- Efremov, Y. N.,
Elmegreen, B. G., & Hodge, P. W. 1998, ApJ, 501,
L163 [NASA ADS] [CrossRef] (In the text)
- Ehlerová, S., &
Palous, J. 2002, MNRAS, 330, 1022 [NASA ADS] [CrossRef] (In the text)
- Elmegreen, B. G. 2002,
ApJ, 577, 206 [NASA ADS] [CrossRef] (In the text)
- Elmegreen, B. G.,
& Parravano, A. 1994, ApJ, 435, L121 [NASA ADS] [CrossRef] (In the text)
- Field, G. B. 1965, ApJ,
142, 531 [NASA ADS] [CrossRef] (In the text)
- Flores, R. A., &
Primack, J. R. 1994, ApJ, 427, L1 [NASA ADS] [CrossRef] (In the text)
- Fragile, P. C.,
Murray, S. D., Anninos, P., & Lin, D. N. C.
2003, ApJ, 590, 778 [NASA ADS] [CrossRef] (In the text)
- Gerola, H., Seiden,
P. E., & Schulman, L. S. 1980, ApJ, 242, 517 [NASA ADS] [CrossRef] (In the text)
- Gerritsen,
J. P. E. 1997, Ph.D. Thesis, Groningen
(In the text)
- Gerritsen,
J. P. E., & Icke, V. 1997, A&A, 325, 972 [NASA ADS] (In the text)
- Grevesse, N., & Sauval,
A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] (In the text)
- Hernquist, L. 1993, ApJS, 86,
389 [NASA ADS] [CrossRef] (In the text)
- Hernquist, L., & Katz,
N. 1989, ApJS, 70, 419 [NASA ADS] [CrossRef] (In the text)
- Hunter, D. 1997, PASP, 109,
937 [NASA ADS] [CrossRef] (In the text)
- Hunter, D. A.,
Elmegreen, B. G., & Baker, A. L. 1998, ApJ, 493,
595 [NASA ADS] [CrossRef] (In the text)
- Katz, N. 1992, ApJ, 391,
502 [NASA ADS] [CrossRef] (In the text)
- Kim, S.,
Staveley-Smith, L., Dopita, M. A., et al. 1998, ApJ, 503,
674 [NASA ADS] [CrossRef] (In the text)
- Klypin, A., Kravtsov,
A. V., Valenzuela, O., & Prada, F. 1999, ApJ, 522, 82 [NASA ADS] [CrossRef] (In the text)
- Kuijken, K., &
Dubinski, J. 1995, MNRAS, 277, 1341 [NASA ADS] (In the text)
- Mac Low, M., & Ferrara,
A. 1999, ApJ, 513, 142 [NASA ADS] [CrossRef] (In the text)
- Marcolini, A., Brighenti,
F., & D'Ercole, A. 2003, MNRAS, 345, 1329 [NASA ADS] [CrossRef] (In the text)
- Marlowe, A. T.,
Meurer, G. R., & Heckman, T. M. 1999, ApJ, 522,
183 [NASA ADS] [CrossRef] (In the text)
- Mayer, L., Governato, F.,
Colpi, M., et al. 2001, ApJ, 559, 754 [NASA ADS] [CrossRef] (In the text)
- McCall, B. J.,
Huneycutt, A. J., Saykally, R. J., et al. 2003,
Nature, 422, 500 [NASA ADS] [CrossRef] (In the text)
- Mori, M., & Burkert, A.
2000, ApJ, 538, 559 [NASA ADS] [CrossRef] (In the text)
- Mori, M., Ferrara, A.,
& Madau, P. 2002, ApJ, 571, 40 [NASA ADS] [CrossRef] (In the text)
- Mori, M., Yoshii, Y.,
& Nomoto, K. 1999, ApJ, 511, 585 [NASA ADS] [CrossRef] (In the text)
- Mori, M., Yoshii, Y.,
Tsujimoto, T., & Nomoto, K. 1997, ApJ, 478, L21 [NASA ADS] [CrossRef] (In the text)
- Navarro, J. F., &
White, S. D. M. 1993, MNRAS, 265, 271 [NASA ADS] (In the text)
- Oey, M. S., &
Clarke, C. J. 1997, MNRAS, 289, 570 [NASA ADS] (In the text)
- Pagel, B. E. J.,
& Edmunds, M. G. 1981, ARA&A, 19, 77 [NASA ADS] (In the text)
- Pasetto, S., Chiosi, C.,
& Carraro, G. 2003, A&A, 405, 931 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Pelupessy, F. I.,
van der Werf, P. P., & Icke, V. 2004,
in preparation
(In the text)
- Puche, D., Westpfahl,
D., Brinks, E., & Roy, J. 1992, AJ, 103, 1841 [NASA ADS] [CrossRef] (In the text)
- Raga, A. C.,
Mellema, G., & Lundqvist, P. 1997, ApJS, 109, 517 [NASA ADS] [CrossRef] (In the text)
- Rhode, K. L.,
Salzer, J. J., Westpfahl, D. J., & Radice, L. A.
1999, AJ, 118, 323 [NASA ADS] [CrossRef] (In the text)
- Semelin, B., & Combes,
F. 2002, A&A, 388, 826 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Silich, S. A.,
Franco, J., Palous, J., & Tenorio-Tagle, G. 1996, ApJ, 468,
722 [NASA ADS] [CrossRef] (In the text)
- Silva, A. I., &
Viegas, S. M. 2001, Computer Physics Communications, 136,
319 [NASA ADS] [CrossRef] (In the text)
- Springel, V., &
Hernquist, L. 2002, MNRAS, 333, 649 [NASA ADS] [CrossRef] (In the text)
- Springel, V., &
Hernquist, L. 2003, MNRAS, 339, 289 [NASA ADS] [CrossRef] (In the text)
- Stewart, S. G.,
Fanelli, M. N., Byrd, G. G., et al. 2000, ApJ, 529,
201 [NASA ADS] [CrossRef] (In the text)
- Stil, J. M. 1999,
Ph.D. Thesis, Leiden
(In the text)
- Thacker, R. J., &
Couchman, H. M. P. 2000, ApJ, 545, 728 [NASA ADS] [CrossRef] (In the text)
- van Zee, L. 2000, AJ, 119,
2757 [NASA ADS] [CrossRef] (In the text)
- van Zee, L. 2001, AJ, 121,
2003 [NASA ADS] [CrossRef] (In the text)
- Verner, D. A., &
Ferland, G. J. 1996, ApJS, 103, 467 [NASA ADS] [CrossRef] (In the text)
- Wada, K., & Norman,
C. A. 2001, ApJ, 547, 172 [NASA ADS] [CrossRef] (In the text)
- Walter, F., & Brinks,
E. 2001, AJ, 121, 3026 [NASA ADS] [CrossRef] (In the text)
- Walter, F., Taylor,
C. L., Hüttemeister, S., Scoville, N., & McIntyre, V.
2001, AJ, 121, 727 [NASA ADS] [CrossRef] (In the text)
- Whitworth, A. P. 1998,
MNRAS, 296, 442 [NASA ADS] [CrossRef] (In the text)
- Wilcots, E. M., &
Miller, B. W. 1998, AJ, 116, 2363 [NASA ADS] [CrossRef] (In the text)
- Wolfire, M. G.,
Hollenbach, D., McKee, C. F., Tielens,
A. G. G. M., & Bakes, E. L. O. 1995,
ApJ, 443, 152 [NASA ADS] [CrossRef] (In the text)
- Wolfire, M. G.,
McKee, C. F., Hollenbach, D., & Tielens,
A. G. G. M. 2003, ApJ, 587, 278 [NASA ADS] [CrossRef] (In the text)
- Young, L. M., &
Lo, K. Y. 1997, ApJ, 490, 710 [NASA ADS] [CrossRef] (In the text)
- Zuckerman, B., & Evans,
N. J. 1974, ApJ, 192, L149 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2004
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{figures/0071fig1.eps}\end{figure}](/articles/aa/full/2004/28/aa0071-04/Timg25.gif)
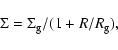
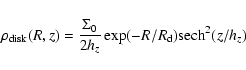
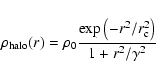
![\begin{figure}
\par\includegraphics[width=14.4cm,clip]{figures/0071fig2.ps} \end{figure}](/articles/aa/full/2004/28/aa0071-04/Timg63.gif)
![\begin{figure}
\par\includegraphics[width=16.2cm,clip]{figures/0071fig3.eps} \end{figure}](/articles/aa/full/2004/28/aa0071-04/Timg64.gif)
![\begin{figure}
\par\includegraphics[width=16.7cm,clip]{figures/0071fig4.ps} \end{figure}](/articles/aa/full/2004/28/aa0071-04/Timg65.gif)
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{figures/0071fig5.ps} \end{figure}](/articles/aa/full/2004/28/aa0071-04/Timg69.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{figures/0071fig6.ps} \end{figure}](/articles/aa/full/2004/28/aa0071-04/Timg75.gif)