A&A 421, 969-976 (2004)
DOI: 10.1051/0004-6361:20035957

A possible age-metallicity relation in the Galactic thick disk?[*]

T. Bensby - S. Feltzing - I. Lundström

Lund Observatory, Box 43, 221 00 Lund, Sweden

Received 30 December 2003 / Accepted 21 March 2004

Abstract
A sample of 229 nearby thick disk stars has been used to investigate the existence of an age-metallicity relation (AMR) in the Galactic thick disk. The results indicate that that there is indeed an age-metallicity relation present in the thick disk. By dividing the stellar sample into sub-groups, separated by 0.1 dex in metallicity, we show that the median age decreases by about 5-7 Gyr when going from [Fe/H]  $\approx -0.8$ to [Fe/H]  $\approx -0.1$. Combining our results with our newly published $\alpha $-element trends for a local sample of thick disk stars that show signatures from supernovae type Ia (SN Ia), we draw the conclusion that the time-scale for the peak of the SN Ia rate is of the order of 3-4 Gyr in the thick disk. The tentative evidence for a thick disk AMR that we present here also has implications for the thick disk formation scenario; star-formation must have been an ongoing process for several billion years. This appears to strengthen the hypothesis that the thick disk originated from a merger event with a companion galaxy that puffed up a pre-existing thin disk.

Key words: stars: Hertzsprung-Russell (HR) and C-M diagrams - stars: kinematics - Galaxy: disk - Galaxy: kinematics and dynamics - Galaxy: solar neighbourhood - Galaxy: formation

1 Introduction

Chemical evolution of stellar populations is an important part of any model of galaxy formation and evolution. Many studies have shown how we are able to further refine and constrain models of Galactic chemical evolution by combining kinematics and elemental abundances of local dwarf stars (e.g., Chiappini et al. 2003; Matteucci 2001; Edvardsson et al. 1993; Feltzing & Gustafsson 1998; Feltzing et al. 2003a; Bensby et al. 2003; Reddy et al. 2003). As evidenced by the cited articles our understanding of chemical evolution is mainly driven by the studies in the solar neighbourhood but have far reaching impact for our interpretation of integrated light from other galaxies (e.g., Matteucci 2001).

However, it is not only the elemental abundances and kinematics of the stars that are of importance to further improve the models of galaxy formation and evolution but also the ages of the stars (see e.g. Edvardsson et al. 1993; Raiteri et al. 1996; Pilyugin & Edmunds 1996; Berczik 1999).

Many studies have found there to be a clear relation between the ages and the metallicities of the solar neighbourhood disk stars (Twarog 1980a,b; Rocha-Pinto et al. 2000; Meusinger et al. 1991). In contrast to this Edvardsson et al. (1993) found no particular evidence for an age-metallicity relation in the Galactic disk in the solar neighbourhood and Feltzing et al. (2001) confirmed this. Feltzing et al. (2001) also showed how dangerous selection effects could be and how an artificial age-metallicity relation can be created (see their Figs. 13 and 14).

Gilmore & Reid (1983) showed that our galaxy is host to two kinematically distinct disk structures. The "new'' disk was dubbed the thick disk and was found to have a mean metallicity around -0.6 dex (Wyse & Gilmore 1995) and a scale-height of 800-1300 pc (e.g., Reylé & Robin 2001; Chen 1997) while the thin disk has a mean metallicity of around -0.1 dex and a scale height of 100-300 pc (e.g., Gilmore & Reid 1983; Robin et al. 1996). Recent studies have shown that stars selected to belong to either the thin or the thick disk show different trends for the elemental abundances (e.g., Fuhrmann 1998; Feltzing et al. 2003a; Bensby et al. 2003, 2004; Reddy et al. 2003; Prochaska et al. 2000; Mashonkina & Gehren 2001).

The question then arises: could it be that the lack of a relation between ages and metallicities for stars in the solar neighbourhood is in fact a population effect? That is, are we looking at a mixture of stars from (at least) two populations that have different chemical enrichment histories?

It thus appears natural to, yet again, revisit the question of an age-metallicity relation in the solar neighbourhood. In the study presented here we will address the question of a relation between ages and metallicities for stars that are kinematically selected to resemble the thick disk closely.

The paper is organized as follows: in Sect. 2 we describe the stellar sample and the kinematical selection criteria and investigate if there are potential biases present in the sample. In Sect. 3 we describe the choice of $\alpha $-enhancement used in the isochrones when deriving the stellar ages. In Sect. 4 we derive ages from stellar isochrone fitting and find that there is a possible age-metallicity relation present in the thick disk. In Sect. 6 we discuss the implications this tentative age-metallicity relation has on the star-formation history of the thick disk, on the time-scale of SN Ia rate in the thick disk, and on our understanding of the origin and evolution of the thick disk. Finally, in Sect. 7 we give a short summary.

   
2 Stellar sample

The stellar sample has been selected on purely kinematical grounds (see also Bensby et al. 2003; Bensby et al. submitted). We have assumed that the Galactic space velocities ( $U_{\rm LSR}$, $V_{\rm LSR}$, and  $W_{\rm LSR}$) for the stellar populations in the solar neighbourhood all can be described by Gaussian distributions. For each star (with its specific combination of  $U_{\rm LSR}$, $V_{\rm LSR}$, and  $W_{\rm LSR}$) it is then possible to calculate the probabilities that it belongs to either the thin disk (D), thick disk (${\it TD}$), or the halo (H). These can then be used to, for each star, calculate the "relative probabilities" ${\it TD}/D$ and ${\it TD}/H$. When doing this, the fraction (normalization) of the three components in the solar neighbourhood must be taken into account. The final relationship is (see Bensby et al. 2003):

 \begin{displaymath}P = X \cdot k \cdot \exp\left( -\frac{U^{2}_{\rm LSR}}{2~\si... ...ma_{V}^{2}} -\frac{W^{2}_{\rm LSR}}{2~\sigma_{W}^{2}}\right), \end{displaymath} (1)

where

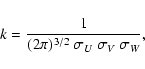\begin{displaymath}k = \frac{1}{(2\pi)^{3/2}~\sigma_{U} ~\sigma_{V} ~\sigma_{W}}, \end{displaymath} (2)

normalizes the expression, $\sigma _{W}$, $\sigma _{V}$, $\sigma _{W}$ are the characteristic velocity dispersions, $V_{\rm asym}$is the asymmetric drift and X is the observed fraction of stars in the solar neighbourhood for each population. The values for the velocity dispersions and the asymmetric drifts are taken from Bensby et al. (2003) and the values for the normalizations in the solar neighbourhood from Bensby et al. (submitted) (see also discussion below). All values are given in Table 1.

Table 1: Characteristic velocity dispersions ( $\sigma _{U}$, $\sigma _{V}$, and $\sigma _{W}$) in the thin disk, thick disk, and stellar halo, used in Eq. (1). X is the observed fraction of stars for the populations in the solar neighbourhood and  $V_{\rm asym}$ is the asymmetric drift (values taken from Bensby et al. 2003 and Bensby et al. submitted).

A ${\it TD}/D$ ratio of 10 means that the star is ten times more likely to be a thick disk star than a thin disk star. For our previous studies of elemental abundances in the thick and thin disks we selected stars with  ${\it TD}/D>10$ as thick disk stars and ${\it TD}/D<0.1$ as thin disk stars. In Bensby et al. (2003) we also analyzed spectra of a few stars with  ${\it TD}/D$ between 10 and 2 and it turns out that these stars show the typical thick disk trends for the elemental abundances that the stars with  ${\it TD}/D>10$ showed. Thus it appears likely that we could use a somewhat lower  ${\it TD}/D$ than 10 to increase our sample of thick disk stars without compromising the results, but see discussion in Sect. 5.

The most uncertain parameter in the calculation of the ${\it TD}/D$ ratios is the normalization of the number density of thick disk stars in the solar neighbourhood. Different authors quote different values: 2% was found by Gilmore & Reid (1983) and Chen (1997), $\sim$6% was found by Robin et al. (1996) and Buser et al. (1999) and $\sim$15% by Chen et al. (2001) and Soubiran et al. (2003). As there is no simple way to determine which is the correct value we inspected colour-magnitude diagrams (CMD) of the thin and thick disks, respectively, derived using different normalizations for the solar neighbourhood thick disk contribution (see Bensby et al. submitted). From this inspection it is clear that a very low normalization (2%) must be ruled out since then the thin disk CMD showed a population that was identical in age and turn-off properties to that of the thick disk CMD. The other values of the normalization are, however, not as easily distinguished. As a compromise we will use a normalization of 10% and a  ${\it TD}/D>2$ and  ${\it TD}/H>1$ as our selection criteria for thick disk stars. The other parameters, such as the velocity dispersions, of course also influence the ${\it TD}/D$ ratios. They are however better known.

That the resulting samples are well defined regardless of the normalization can be understood through the following argument. All stars with ${\it TD}/D\ga 2$, using a 10% normalization, will for all normalizations lower than 10% still have ${\it TD}/D>1$. This means that if we select stars with ${\it TD}/D\ga 2$ (10% normalization) as our thick disk stars they would also be selected as thick disk stars using any of the normalizations listed in the literature. In the same way stars with ${\it TD}/D\la 0.6$ (10% normalization) would always be selected as thin disk irrespective of the value of the thick disk normalization.

  \begin{figure} \par\hspace{6mm}\includegraphics[width=6.9cm,clip]{0957F1.eps}\par\vspace*{2mm} \includegraphics[width=7.5cm,clip]{0957F2.eps} \end{figure} Figure 1: Boxplots showing the distribution in (B-V), $M_{\rm V}$, $U_{\rm LSR}$, $V_{\rm LSR}$, and $W_{\rm LSR}$ for the full thick disk sample (295 stars, white boxes) and the thick disk sample with uvby photometry (229 stars, gray boxes). In the boxplots the central vertical line represents the median value. The lower and upper quartiles are represented by the outer edges of the boxes, i.e. the box encloses 50% of the sample. The notches (waists) indicate the 95% confidence intervals for the median value. The whiskers extend to the farthest data point that lies within 1.5 times the inter-quartile distance. Those stars that do not fall within the reach of the whiskers are regarded as outliers and are marked by solid circles. A common rule is that samples for which the boxplot notch intervals do not overlap are likely to be different in their distributions.
Open with DEXTER

We will restrict the selection of the stellar sample to a certain area in the $(B-V){-}M_{\rm V}$ plane. The limits have been marked in Fig. 3 by the dotted lines. This area has been selected on the grounds that we do not want to include stars for which age determinations are nearly impossible, which is the case for the lower part of the main sequence where the isochrones are very crowded (i.e. $M_{\rm V}>6$). We also exclude stars that lie on the giant branch, since the metallicity calibrations are not valid for such stars (see Feltzing et al. 2001). In this region the colour of the stellar isochrones are also uncertain (see e.g. Yi et al. 2001, their Fig. 2). We have also excluded stars that fall outside the following boundaries: (B-V)<0, (B-V)>1 and $M_{\rm V}<0$(see Fig. 3).

Selecting all stars in the Hipparcos catalogue that have relative errors in their parallaxes less than 25% (and not flagged as binaries or probable binaries) and that have radial velocities published in the compilation by Barbier-Brossat et al. (1994) we get a sample of $\sim$12 600 stars. Adding our thick disk criteria ( ${\it TD}/D>2$and  ${\it TD}/H>1$) and the restrictions in (B-V) and $M_{\rm V}$ given above, we get a sample of 295 stars that are likely to belong to the Galactic thick disk.

Estimates of [Fe/H] for the stars can be derived using calibrations of Strömgren photometry (compare Feltzing et al. 2001). However, not all the stars in the Hipparcos catalogue have published Strömgren photometry. 229 out of the 295 thick disk stars have Strömgren photometry from the compilation by Hauck & Mermilliod (1998).


  \begin{figure} \par\includegraphics[width=7.7cm,clip]{0957F3.eps} \end{figure} Figure 2: The [Mg/Fe] trend for a sample of thick disk stars from Bensby et al. (2003) (circles) and Bensby et al. (submitted) (triangles). The stars were selected according to the same kinematical criteria as discussed in Sect. 2. The solid line indicates the degree of $\alpha $-enhancement that we have used at different [Fe/H] (see Table 2).
Open with DEXTER

We use the metallicities calculated for the catalogue used in Feltzing & Holmberg (2000) and Feltzing et al. (2001). In Fig. 1 we compare the distributions of (B-V) and $M_{\rm V}$ and the distributions of the space velocities for the full thick disk sample (295 stars) and the thick disk sub-sample that has metallicities (229 stars).

At a quick glance, the distributions of the MV, (B-V) and the  $U_{\rm LSR}$, $V_{\rm LSR}$, $W_{\rm LSR}$ velocities do not seem to be appreciably affected when the stars without Strömgren photometry are rejected. We verify this by performing two-sample Kolmogorov-Smirnov (KS) tests. The probability that the distributions are identical is 99.4% for MV, 89.7% for (B-V) and >99.9% for all three velocities. This means that for all but (B-V) the distributions are essentially the same. For (B-V) we have inspected the CMDs before and after adding the Strömgren photometry. This inspection showed that there is no appreciable deterioration in the sampling of red, old stars. This makes us comfortable in believing that we do not introduce any of the biases discussed in Feltzing et al. (2001).

In summary we do not introduce any bias to our thick disk sample by only selecting those stars with published Strömgren photometry.

   
3 Abundances of $\alpha $-elements in the stars

Stars more metal-poor than the Sun have long been known to show enhanced levels of $\alpha $-elements (see e.g. Edvardsson et al. 1993). In Bensby et al. (2003) and Bensby et al. (submitted) we use the same kinematic definitions of thick disk stars as we do here and we derive stellar abundances for a large number of thin and thick disk stars spanning a range of metallicities. In Fig. 2 we show the resulting [Mg/Fe] vs. [Fe/H] trend for the thick disk stars in those two papers.

As can be seen from Fig. 2 the enhancement of [Mg/Fe] varies with [Fe/H] for the thick disk. At $\rm [Fe/H] = -0.4$ the enhancement is $\sim$0.3 dex while at [Fe/H] = 0 it has decreased to almost solar values. The thick disk stars in Mashonkina et al. (2003) show the same degree of Mg enhancement, i.e. [Mg/Fe]  $\approx 0.3$-0.4 for metallicities below [Fe/H] =-0.4. (Note that the $\alpha $-element abundance often is defined as the average of the Mg, Si, Ca, and Ti abundances, while in Fig. 2 we show Mg).

It is important to know how enhanced the stars are in the $\alpha $-elements as $\alpha $-enhancement has a strong effect on stellar evolutionary tracks, and hence on the stellar isochrones that we want to use to determine the ages. A set of isochrones with an $\alpha $-enhancement of [$\alpha $/Fe] = 0.3 is compared to a set of solar-scaled isochrones in Fig. 3. The effect of taking $\alpha $-enhancement into account is that ages will be lower than otherwise.


  \begin{figure} \par\includegraphics[width=7.7cm,clip]{0957F4.eps} \end{figure} Figure 3: Example of how $\alpha $-enhancement changes the stellar isochrones. The plotted isochrones are the Y2-isochrones from Kim et al. (2002) and Yi et al. (2001) and have ages, [Fe/H], and $\alpha $-enhancements as indicated. The area enclosed by the dotted lines are the restrictions in (B-V) and MV discussed in Sect. 2.
Open with DEXTER

In the determination of stellar ages from isochrones with different [Fe/H] we will use $\alpha $-enhancements that are in concordance with the the trend that has been outlined in Fig. 2 and is also listed in Table 2. The Yonsei-Yale (Y2) set of isochrones (Yi et al. 2001; Kim et al. 2002) provides a versatile tool since they not only have published calculated sets of isochrones but also an interpolator that enables the user to calculate a set of isochrones with a specific [Fe/H] and [$\alpha $/Fe].

   
4 Age-metallicity relation in the thick disk

Table 2: Median ages and spreads for the sub-samples. The first column gives the central metallicity, and the second column the $\alpha $-enhancement. Columns 3-6 give the following for the samples selected with ${\it TD}/D>2$: the number of stars in the sub-sample, the lower quartile for the age distribution, the median age, and the upper quartile for the age distribution. Columns 7-10 give the same information but for the samples selected with ${\it TD}/D>10$.

Figure 4 shows three CMDs for stars with thick disk kinematics and [Fe/H] derived from Strömgren photometry. Each CMD is centered at a different metallicity; [Fe/H] = -0.7, -0.4, and -0.1, respectively. Stellar isochrones with relevant metallicities and $\alpha $-enhancements (see Sect. 3) are also plotted.

A visual inspection of these CMDs directly shows that the turn-off for the CMD centered at -0.1 dex is significantly younger than the turn-off in the CMD centered at -0.7 dex (see Figs. 4a and 4c, respectively).

We now proceed to quantify this visual impression. The stars are divided into 10 sub-samples according to their metallicities. Each sub-sample has a central metallicity and all stars $\pm$0.15 dex around this value are included in the sub-sample. The central metallicity changes by 0.1 dex between each sub-sample. In this way we create a sliding metallicity binning for the age determinations, i.e. the sub-samples are not independent.

Ages for each sub-sample were simply estimated in the following way:

The results are collected in Table 2. The individual stellar ages are good estimates of the stars age given the set of isochrones. More sophisticated methods to derive stellar ages from isochrones exist (compare e.g. Ng & Bertelli 1998; Feltzing et al. 2001; Pont & Eyer 2004; Rosenkilde Jørgensen et al., in preparation), However, the age estimates we make are virtually identical to those from the more sophisticated methods (e.g., Rosenkilde Jørgensen who uses a method akin to Pont & Eyer 2004). Errors on derived ages are different, though (Rosenkilde Jørgensen, private communication).


  \begin{figure} \par\mbox{\includegraphics[width=5.84cm,clip]{0957F5.eps} \includ... ...clip]{0957F6.eps} \includegraphics[width=5.2cm,clip]{0957F7.eps} }\end{figure} Figure 4: CMDs for the thick disk which show how the age distribution increases to older ages as we move to lower [Fe/H]. The isochrones are as indicated. We show ages from 20 to 1 Gyr with a step of 1 Gyr. The isochrones for 5, 10, 15, and 20 Gyrs are indicated by solid lines.
Open with DEXTER

The age estimates together with the central metallicities for each bin can now be plotted together in an age-metallicity diagram (see Fig. 5). We see here clearly that the central ages keep decreasing as the metallicity increases.

We believe that the change in age with [Fe/H] is significant as we are using a set of isochrones and a sample of stars that have had their parameters determined in the same way. Thus we should not expect systematic errors between bins. Furthermore the decline is up to 5 billion years from the most metal-poor to the most metal-rich bin. Such a large, and systematic, change would be hard to achieve through an erroneous analysis.


  \begin{figure} \par\includegraphics[width=7.7cm,clip]{0957F8.eps} \end{figure} Figure 5: Age-metallicity diagram for the age estimates and central metallicities listed in Table 2 for the samples selected with ${\it TD}/D>2$. We use boxplots to illustrate the age distributions within each sub-sample. For a description of box plots see caption of Fig. 1.
Open with DEXTER

   
5 Thin disk - thick disk confusion?


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{0957F9.eps} \end{figure} Figure 6: Histograms showing the distributions of the ${\it TD}/D$ ratios in three different metallicity ranges for all stars having  ${\it TD}/D>2$ (same stars as in Fig. 4).
Open with DEXTER

In Fig. 5 we see a strong decrease in the mean age for the highest metallicities. Given that the thin disk dominates more and more as we go to higher metallicities the question arises: are we simply adding more and more of the younger thin disk stars into our sample?

There is in fact some hint in our data that we are picking up thin disk stars in our most metal-rich bins. Figure 6 shows the distributions of  ${\it TD}/D$ for the three CMDs in Fig. 4. As can be seen we detect more and more stars with low ${\it TD}/D$ ratios as we go to higher metallicities. The stars with ${\it TD}/D<10$ could be intervening thin disk stars.

Ideally, if the metallicity distribution functions for the two disks were well known we could weight the probabilities we use to select the stars accordingly.

The metallicity distributions of the thin and thick disks peak at different metallicities (Wyse & Gilmore 1995). The thick disk appears to peak in the interval $\rm -0.7 < [Fe/H] < -0.5$and the thin disk around -0.2 dex. However, the two distributions are not well constrained. The distribution for the thick disk truncates at $\rm [Fe/H]\approx -0.2$ in Wyse & Gilmore (1995). We find that due to the shortcomings in our knowledge about the metallicity distribution functions of the two disk populations it is not possible to use them to further deconvolve the two populations.


  \begin{figure} \par\mbox{ \includegraphics[width=5.84cm,clip]{0957F10.eps} \incl... ...ip]{0957F11.eps} \includegraphics[width=5.2cm,clip]{0957F12.eps} }\end{figure} Figure 7: Same as Fig. 4 but using ${\it TD}/D>10$.
Open with DEXTER

We will here try to address the issue of intervening thin disk stars in a different way. In Fig. 7 we show the same CMDs as in Fig. 4 but with a stronger constraint on ${\it TD}/D$, i.e. ${\it TD}/D>10$, and compare Fig. 6. In this figure we see the same trend (albeit with fewer stars) as in the original CMDs, strengthening our earlier conclusion that there is an AMR present in the thick disk. In Fig. 8 we show the resulting AMR constructed in the same way as in Fig. 5. Note, however, in this new case we have as a furher precaution excluded all stars with MV>5.4to make sure that we have as accurate ages as possible. Furthermore, very few stars are on the sub-giant branch, where the evolutionary timescale is short and hence age determinations can be erroneous (see Pont & Eyer 2004). As a further extreme test we have inspected the CMDs where all stars with $V_{\rm LSR}>-50$ km s-1have been excluded. These CMDs clearly show that the stars centered on $\rm [Fe/H] = -0.4$ form on average a younger population that the stars centered around $\rm [Fe/H]=-0.7$.

Thus we again find an AMR to be present in the thick disk.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{0957F13.eps} \end{figure} Figure 8: Same as Fig. 5 but using ${\it TD}/D>10$.
Open with DEXTER

   
6 Discussion

From a spectroscopist's point of view there is now mounting evidence that the stars that today have kinematics that we associate with the thick disk show elemental abundance trends that are distinct from those seen in stars on solar-type orbits (thin disk). A recent review can be found in Nissen (2003). Our own results have been published in Feltzing et al (2003a,b) and Bensby et al. (2003, 2004), see also Fig. 9. These observations appear to point to some homogeneity in the chemical enrichment process that proceeded the formation of the stars that we today associate with the thick disk.

Our new result, that there is a possible age-metallicity relation in the thick disk, adds a further dimension. The results indicate that star formation continued up to 5 billion years in the population we identify as the thick disk.

The observational properties and a standard interpretation for the chemical evolution of the thick disk is the following: the abundance trends for the thick disk are well-defined and show large $\alpha $-enhancements at a constant value for metallicities below [Fe/H] $\approx$ -0.4. This is normally interpreted as that the star formation was intense and that massive stars were the main contributors to the chemical enrichment. At higher [Fe/H] the $\alpha $-enhancement starts to decline toward solar values. This is typical for what happens when long-lived low-mass stars start to contribute to the chemical enrichment through the explosion of SN Ia. The SN Ia mainly produce iron peak elements and none or only little of the $\alpha $-elements which results in a lowering of the [$\alpha $/Fe] ratio (compare e.g. Fig. 8.6 in Pagel 1997).

The time at which the decline starts is not only a function of the lifetime of SN Ia but also of the SN Ia rate. The exact model, and hence lifetime for SN Ia, is still debated. The two most probable scenarios are a double or a single degenerate system consisting of either two white dwarfs or a white dwarf and a red giant. In the latter case the life time is set by the main sequence lifetime of the star that becomes the red giant, while in the first case the lifetime for the system prior to becoming supernova is set by the time it takes the two white dwarfs to spiral in and coalesce, and hence it depends on the initial separation and could be longer than the Hubble time. For a recent, in-depth discussion of these issues see Livio (2001). Furthermore, the population synthesis of the SN Ia progenitors does, in general, not agree too well with the observed frequencies of possible progenitor systems (see Livio 2001, and references therein). This means that any interpretation of our $\alpha $-abundance trends in terms of a minimum timescale for the star formation period in the thick disk will be rather complex (see also Fig. 5.7 in Matteucci 2001).

However, our investigation of the relation between ages, metallicities, and elemental abundances for stars with typical thick disk kinematics points to a conclusion that the SN Ia rate peaked after a few ($\sim$3-4) billion years. We also note that the observed abundance trends are tight (compare the oxygen trends in Fig. 9) which should indicate that the gas must have been rather well mixed throughout. This seems to indicate that the gas that the thick disk stars formed out of must have been confined to a reasonably "small" physical volume for the mixing to work efficiently.


  \begin{figure} \par\includegraphics[width=8cm,clip]{0957F14.eps} \end{figure} Figure 9: Abundance trends for oxygen in the thin and thick disks (Bensby et al. 2004). Thin and thick disk stars are marked by open and filled symbols, respectively. Triangles are data points that have been gathered from Nissen et al. (2002).
Open with DEXTER

Simulations of galaxy formation indicate that we should expect all or a large part of our galaxy to have been assembled from smaller parts (e.g., Murali et al. 2002). The question then arises - did these smaller building blocks form stars before they merged into today's thick disk? If they did and if they were of different sizes, as one may imagine, then they would each form their own unique set of elemental abundance trends which would depend on the initial mass function and the star formation rate in each individual building block. Then clearly we would not see any homogeneous elemental abundance trends as has been found by several authors (Fuhrmann 1998; Mashonkina & Gehren 2001; Prochaska et al. 2000; Feltzing et al. 2003a). Of course, if these building blocks were collected before they formed stars it might be possible to find abundance trends in today's thick disk. Another, and perhaps more likely possibility, is that what we today observe as a thick disk originally was a thin disk that, after having produced its stars, was puffed up (see e.g. Robin et al. 1996; Quinn et al. 1993). Such a scenario would allow the gas to be more well mixed at the time of star formation and abundance trends would be possible.

Another possible scenario is a close encounter between the Milky Way and another galaxy. This scenario has been modelled by Kroupa (2002) who shows that such an event would result in a kinematical heating of a pre-existing gaseous disk and an increased star formation in this gas.

   
7 Summary

Using a sample of 229 kinematically-selected thick disk stars we have been able to probe the existence of an age-metallicity relation in Galactic thick disk. Ages have been determined in a consistent way, using isochrones with the appropriate levels of $\alpha $-enhancement at different metallicities as indicated by recent studies that use detailed abundance analysis. Although the stellar sample is rather small we believe it to be free from severe biases that could affect the results. From the investigation we are able to draw three main conclusions:

1.
There is an age-metallicity relation present in the Galactic thick disk, indicating that it has had an ongoing star formation for a time-period of up to 5 Gyr (this is model-dependent).
2.
The thick disk age-metallicity relation in combination with the abundance trends for $\alpha $-elements in the thick disk, that show signatures of SN Ia, indicate that the time-scale for the peak of the SN Ia rate in the thick disk is of the order of 3-4 Gyr.
3.
The quite long star formation period in the thick disk strengthens the hypothesis that the thick disk formed as a result of an ancient merger event between the Milky Way and a companion galaxy.
Studies of the thick disk using nearby stars will always be subject to uncertainties due to the overlapping velocity and metallicity distributions of the thin and thick disk. At distances well above  $Z\approx1.5$ kpc from the Galactic plane the thick disk is the dominant stellar population. Determining accurate metallicities and $\alpha $-abundances for a larger sample of dwarf stars at high Z would therefore enable accurate age determinations that would verify the existence (or non-existence) of the thick disk AMR deduced from nearby stars.

Acknowledgements
We would like to thank Poul Erik Nissen and the anonymous referee for valuable comments on the first version of the paper.

References


Copyright ESO 2004