A&A 421, 783-795 (2004)
DOI: 10.1051/0004-6361:20035778

The cellular burning regime in type Ia supernova explosions

II. Flame propagation into vortical fuel

F. K. Röpke1 - W. Hillebrandt2 - J. C. Niemeyer3


1 - Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741 Garching, Germany
2 - Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741 Garching, Germany
3 - Universität Würzburg, Am Hubland, 97074 Würzburg, Germany

Received 1 December 2003 / Accepted 8 April 2004

Abstract
We investigate the interaction of thermonuclear flames in Type Ia supernova explosions with vortical flows by means of numerical simulations. In our study, we focus on small scales, where the flame propagation is no longer dominated by the turbulent cascade originating from large-scale effects. Here, the flame propagation proceeds in the cellular burning regime, resulting from a balance between the Landau-Darrieus instability and its nonlinear stabilization. The interaction of a cellularly stabilized flame front with a vortical fuel flow is explored applying a variety of fuel densities and strengths of the velocity fluctuations. We find that the vortical flow can break up the cellular flame structure if it is sufficiently strong. In this case the flame structure adapts to the imprinted flow field. The transition from the cellularly stabilized front to the flame structure dominated by vortices of the flow proceeds in a smooth way. The implications of the results of our simulations for Type Ia Supernova explosion models are discussed.

Key words: stars: supernovae: general - hydrodynamics - instabilities - turbulence

   
1 Introduction

In the canonical astrophysical model Type Ia supernovae (SNe Ia in the following) are associated with thermonuclear explosions of white dwarf (WD) stars (Hoyle & Fowler 1960). These WDs are composed of carbon and oxygen. Due to the high temperature sensitivity of the activation energy of carbon and oxygen burning, the reaction is confined to a very narrow region and propagates as a combustion wave. This defines a thermonuclear flame. The theoretical understanding of flame propagation in WDs provides the key to SN Ia explosion models with the effective flame velocity being the most important parameter. What are the phenomena that mediate the combustion wave? The answer to that question is given by the hydrodynamics of combustion. Conservation laws across the flame admit two fundamental modes of flame propagation: the detonation, in which the flame propagates due to shock waves, and the deflagration, which is based on microphysical transport phenomena such as heat conduction and species diffusion.

Flame propagation in the detonation mode is certainly the easiest to model. Here the flame propagation velocity with respect to the unburnt material is larger than the corresponding sound speed. Therefore the WD star has no time to expand prior to the incineration in this detonation model of SN Ia explosions and all the material is consumed at high densities resulting in ashes consisting solely of iron-peak elements (Arnett 1969). However, this is in conflict with observational spectra, which show strong indication of intermediate mass elements.

Consequently, the star has to expand considerably before it is processed by the thermonuclear flame. This is possible if flame propagation starts out in the deflagration mode, since here the microphysical transport processes lead to a subsonic flame velocity. In the present study, we refer to that deflagration model of SNe Ia. Moreover, underlying to our model is the so-called single-degenerate scenario, where the progenitor is a binary system with the WD accreting matter from the non-degenerate companion until it reaches the Chandrasekhar mass. At this point, thermonuclear reaction ignites near the center of the WD and propagates outward as a deflagration flame. For a review of SN Ia explosion models we refer to Hillebrandt & Niemeyer (2000).

In the framework of the deflagration model, recent large-scale SN Ia explosion models have been quite successful (Gamezo et al. 2003; Reinecke et al. 2002). Nevertheless, the determination of the flame propagation speed is much harder in this case. A planar deflagration flame would be far too slow to cause powerful SN Ia explosions, but these models predict an acceleration of the deflagration flame due to interaction with turbulence. The resulting energy release is sufficient to unbind the WD star. Following the reasoning by Niemeyer & Woosley (1997), the turbulent motions are evoked by large-scale instabilities - such as the Rayleigh-Taylor (buoyancy) instability and the Kelvin-Helmholtz (shear) instability - and decay to smaller scales forming a turbulent eddy cascade (Richardson 1922). Eddies of that cascade wrinkle the flame and increase its surface. This corresponds to an acceleration of the effective flame propagation speed. However, the vast range of spatial scales relevant to the problem of SN Ia explosions (from the radius of the star down to the width of a typical flame it covers about 11 orders of magnitude) restricts these models to the simulation of effects on the largest scales only. This makes it impossible to directly determine the turbulent flame propagation velocity in the simulations and therefore assumptions on the physics on unresolved small scales must be made. The fundamental idea here is that flame propagation is dominated by the turbulent cascade that is driven solely from large-scale instabilities and that no other effects contribute to the generation of turbulence.

However, due to the scaling law of the turbulent cascade, which predicts the turbulent velocity fluctuations to monotonically decrease with smaller scale, there exists a certain length scale below which the flame burns faster through the corresponding eddies than these can deform it. For chemical flames, this scale is identified with the Gibson scale (Peters 1986) and we will use this term in the context of thermonuclear combustion, too. Below the Gibson scale the flame propagates in a "frozen turbulence field'' and is no longer affected by the eddy cascade. Large scale models assume stable flame propagation here. Although some theoretical concepts support this idea, no hydrodynamical simulations provided convincing proofs yet.

In order to fill that gap in SN Ia models we performed numerical studies of flame propagation around the Gibson scale. The basic physical effects that determine flame propagation here are the hydrodynamical Landau-Darrieus instability (Darrieus 1938; Landau 1944) and the counteracting nonlinear stabilization of the flame (Zel'dovich 1966). The balance of the two effects gives rise to a stable cellular flame structure characterizing the cellular burning regime. The goals of our investigations were to determine whether or not the cellular burning regime exists for thermonuclear flames in WD matter and to test how robust the anticipated cellular stabilization is under varying conditions. On the one hand, these studies examine a fundamental assumption of present SN Ia explosion models and on the other hand they are intended to explore the possibility of new physical effects that may have to be included into these. In particular, the question of the robustness of the cellular stabilization of the flame is closely connected to the so-called delayed detonation models of SN Ia explosions. In these models, the flame starts out as a deflagration wave, but later turns into a supersonic detonation. Empirical one-dimensional SN Ia models support this idea, since those lead to quite realistic spectra if a deflagration-to-detonation transition (DDT) is imposed artificially at low fuel densities (Iwamoto et al. 1999; Höflich & Khokhlov 1996). Although DDTs are frequently observed in terrestrial combustion, a mechanism that could account for such a transition under conditions of SN Ia explosions could not be identified so far (Niemeyer 1999). However, one possibility is a breakdown of the flame stabilization and a subsequent generation of turbulence on small scales by the flame itself, that would result in an additional acceleration of the flame. This active turbulent combustion (ATC) mechanism has been proposed by Niemeyer & Woosley (1997) on the basis of a work by Kerstein (1996). Niemeyer & Woosley (1997) suggest that the cellular flame stabilization could break down at the Gibson scale leading to ATC. One motivation for our study is to examine this idea. Note, that we use the term "active turbulent combustion'' in the sense it was originally suggested by Niemeyer & Woosley (1997), who speculated on the interaction of turbulent motions with the cellular flame pattern around the Gibson scale in context of burning in the flamelet regime. Effects of turbulence on the internal flame structure - i.e. the transition to the so-called distributed burning regime - are expected on much smaller scales and in later stages of the SN Ia explosion. These will not be addressed here.

The present paper is the third in a series of publications on the investigation of the cellular burning regime in Type Ia supernova explosions. After the introduction of the numerical methods to study this regime together with providing some examples of application (Röpke et al. 2003), the implementation was used to study flame propagation into quiescent fuel (Röpke et al. 2004). The results obtained there (to be summarized in the next section) raised the question of the interaction of a cellular flame with turbulent flows. This topic is also motivated from the supernova model. Around the Gibson scale one can still expect turbulent velocity fluctuations of the order of the laminar burning speed of the flame originating from the turbulent cascade. Additionally, pre-ignition convection in the WD may result in relic turbulent motions of considerable strength. Höflich & Stein (2002) claim surprisingly high values of convective velocities.

A brief description of the physical effects underlying the cellular burning regime and of the numerical methods applied to model it will be provided in the next section. In Sect. 3 the results of our numerical simulations will be presented and discussed. Finally, we will draw conclusions emphasizing the implications of our results for SN Ia models.

2 The cellular burning regime and its numerical simulation

Since our study aims at the flame evolution around the Gibson scale, which is expected to be well-separated from the scale of the flame width for fuel densities above $10^7~{\rm g}~{\rm cm}^{-3}$, we will treat the flame in the discontinuity approximation in the following. That is, we describe the flame as a simple discontinuity between fuel and ashes and ignore its internal structure. Note that this picture does not account for the microphysical transport phenomena and therefore the laminar burning speed of the flame (i.e. the velocity of a planar deflagration flame) is not intrinsically given in this model.

The Gibson scale is determined by this laminar burning speed $s_{\rm l}$, by the velocity fluctuations at the integral scale of turbulence, and by the scaling law of the eddy cascade. Timmes & Woosley (1992) determined the laminar burning velocity by means of one-dimensional simulations fully resolving the internal structure of the flame, and we apply the fitting formula given there to obtain the value for a particular composition and density of the fuel. As has been mentioned by Röpke et al. (2004), this formula is afflicted with some uncertainties, which introduce a considerable ambiguity to the exact value of the Gibson scale. Following the approach of Röpke et al. (2004), we will arrange our simulations at length scales around  $10^4~{\rm cm}$ as a crude estimate of the Gibson length, since our goal is to qualitatively explore the possible effects here rather than to perform highly precise measurements.

Below the Gibson scale, flame propagation is determined by the competition between the Landau-Darrieus (LD) instability and its nonlinear stabilization. However, it is well-known (Khokhlov 1995; Bychkov & Liberman 1995) that strong gravitational fields can inhibit a stabilization and lead instead to an unstabilized Rayleigh-Taylor-like nonlinear flame evolution. The reason why the effect of gravity can safely ignored in our model is that it aims on scales around the Gibson length. In order to develop a Rayleigh-Taylor instability, flame propagation must be sufficiently slow. Otherwise it would wash out velocity fluctuations stemming from Rayleigh-Taylor effects. This sets the minimum length at which gravity effects will be important (Timmes & Woosley 1992). Velocity fluctuations induced by the nonlinear stage of the Rayleigh-Taylor instability scale with the square root of the length scale (Davies & Taylor 1950). The Gibson scale, on the other hand, results from the comparison of the laminar burning velocity with turbulent motion in the eddy cascade which are proportional to the cubic root of the length scale assuming Kolmogorov scaling. Therefore it is always smaller than the lowest scale at which gravity has to be taken into account. Because the exact value of the Gibson scale in SNe Ia is uncertain, the particular choice of length scales in our simulations is somewhat arbitrary and may differ from those in a realistic SN Ia environments. Nevertheless, the qualitative results will apply to SNe Ia on scales close to the Gibson scale, whatever this scale turns out to be.

The LD instability is of pure hydrodynamical origin and results from the density contrast across the flame front in combination with mass flux conservation. This leads to a refraction of the stream lines at the flame causing a flow field that enhances initial perturbations of the planar flame shape. The fact that the LD instability acts on thermonuclear flames under conditions of SN Ia explosions has been proven by means of a full hydrodynamical simulation by Niemeyer & Hillebrandt (1995). The refined numerical model that was described by Röpke et al. (2003) allowed us to investigate this instability in detail. We simulated the propagation of a sinusoidally perturbed flame front into quiescent fuel. The initial linear regime of flame evolution was shown to be indeed determined by the LD instability. The flow field accounting for this effect was apparent in our simulations (Röpke et al. 2004). Moreover, the growth rate of the amplitude of the perturbation was found to be consistent with the dispersion relation that Landau (1944) derived by means of a linear stability analysis (Röpke et al. 2003).

The nonlinear stabilization of the flame is a geometrical effect. Zel'dovich (1966) explained the mechanism by following the propagation of a perturbed flame by means of Huygens' principle of geometrical optics (see also Fig. 1 in Röpke et al. 2003). Once the perturbation has grown to a critical size, former recesses of the flame front develop into cusps between bulges of the front. It can easily be shown that the propagation velocity  $v_{{\rm cusp}}$ of such a cusp exceeds the laminar burning velocity $s_{\rm l}$ of the other parts of the flame by

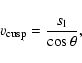\begin{displaymath}% v_{{\rm cusp}}= \frac{s_{\rm l}}{\cos \theta}, \end{displaymath} (1)

where $\theta$ denotes the inclination angle of the bulges adjacent to the cusp. This effect balances further growth of the perturbation due to the LD instability and causes a cellular shape of the flame front. Therefore the regime of flame propagation at scales where it is dominated by the interplay between the LD instability and its nonlinear stabilization will be termed cellular burning regime in the following.

The nonlinear stage of flame evolution could not be reached by early attempts of hydrodynamical simulations of flame propagation (Niemeyer & Hillebrandt 1995). However, applying a semi-analytical description of flame evolution, Blinnikov & Sasorov (1996) explored effects of the cellular burning regime in the context of SN Ia explosions and also Bychkov & Liberman (1995) discussed the cellular flame stabilization. With help of the numerical implementation that was described by Röpke et al. (2003) on the basis of the work by Reinecke et al. (1999), it was possible to prove by means of a hydrodynamical simulation, that cellular stabilization holds for thermonuclear flames in SN Ia explosions (Röpke et al. 2003,2004). In connection with flame interaction with vortical flows, which will be studied in the following, the most important results of the investigation of the cellular stabilization of the flame propagating into quiescent fuel were the following:

These results will be helpful in the interpretation of the simulations of flame propagation in vortical flows. The possibility of a weaker cellular stabilization at low fuel densities is a further motivation to test the interaction of the flame with physical noise, represented by a vortical flow field.

We will only briefly outline the numerical implementation here and refer to Röpke et al. (2003) and Reinecke et al. (1999) for detailed discussions. The description of the flame in the discontinuity approximation allows us to separate the flame propagation from the hydrodynamics in a first step. The hydrodynamics part of the numerical implementation thus reduces to the solution of the reactive Euler equations, which is performed applying a finite-volume approach. In particular we employ the piecewise parabolic method (PPM) suggested by Colella & Woodward (1984) in the P ROMETHEUS implementation by Fryxell et al. (1989). Flame propagation is modeled using the level-set method (e.g., Sussman et al. 1994; Osher & Sethian 1988; Reinecke et al. 1999; Smiljanovski et al. 1997). For the correct reproduction of hydrodynamical effects, such as the LD instability, a precise coupling between flame and flow turned out to be essential (Röpke et al. 2003). This is provided by applying the in-cell reconstruction/flux-splitting technique introduced by Smiljanovski et al. (1997).

   
3 Flame interaction with a vortical flow

In the following we will present the results from simulations of the interaction of cellular flames with vortical flows. After discussing the simulation setup we will make some general remarks on what can be expected in the simulations. This will be followed by a survey of flame evolution depending on the strength of the vortices for an exemplary case at a fixed fuel density. Finally, we will capture the simulation results for various fuel densities in a quantitative way.


  \begin{figure} \par\includegraphics[width=8cm,clip]{0778fig1.eps} \end{figure} Figure 1: Vortical flow field as applied in the simulations (here for the case $\rho = 7.5$ $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$, $v' = 2.0 s_{\rm l}$). The frame of reference is comoving with the vortices. The snapshot is taken at  $t = 2.97~{\rm ms}$.
Open with DEXTER

   
3.1 Simulation setup

The basic setup of our simulations was similar to that used to describe flame propagation into quiescent fuel (Röpke et al. 2003,2004). The flame was initialized in a computational domain with periodic boundary conditions transverse to the direction of flame propagation. In order to capture the full flame front in cases of strong deformation, we changed from a quadratic domain to a rectangle of 300 $\times $ 200 computational cells. The cell width was set to $\Delta x = \Delta y = 50~{\rm cm}$. Several experiments with initially planar flames yielded drastic responses of the flame shape when the vortices encountered it. This can be attributed to the high sensitivity of planar flames to perturbations. Consequently, in order to make the results of different simulations comparable and to enable a quantification of the flame evolution, the flame was perturbed initially in a sinusoidal way with eight periods fitting into the domain. This initial perturbation grows due to the LD instability and stabilizes in a cellular pattern, before the injected vortices reach the flame front. In this way it was possible to study the interaction of a stabilized flame with a vortical flow field preventing the incoming flow from unpredictably deforming the flame shape at the first encounter.

The numerical investigation of flame interaction with turbulence is generally an intricate issue. In principle, the straight forward way to go would be to produce an isotropic turbulence field by external forcing and to set up a flame in this field. This approach is, however, too expensive for the purpose of the parameter study we are aiming at. For this reason we simply modified the inflow boundary condition in order to inject a vortical flow field instead of quiescent fuel. The flow field is not stirred and turbulence is not actively produced inside the computational domain by external forcing. As a consequence turbulence injected here partly decays before reaching the flame front - an effect which we have to take into account in the measurement of characteristic quantities.

Table 1: Setup values for the simulations of the flame evolution.

As suggested by Helenbrook & Law (1999), we applied an oscillating inflow boundary condition on the right hand side of the computational domain, which generates a vortical velocity field approaching the flame. The velocity at the boundary now reads:

  
    $\displaystyle v_x = s_{\rm l} \left\{ -1 + v' \sin 2 k_y \pi y \cos 2 k_x \pi (x - t s_{\rm l})\right\}$ (2)
    $\displaystyle v_y = s_{\rm l}~ v' \cos 2 k_y \pi y \sin 2 k_x \pi (x - t s_{\rm l}).$ (3)

The parameter v' characterizes the strength of the imprinted velocity fluctuations and kx and ky denote the wavenumbers of the oscillation.
  \begin{figure} \par\includegraphics[width=7.45cm,clip]{0778fig2.eps} \end{figure} Figure 2: Profile of the y-component of the vortical flow field parallel to the x-axis in our simulations a) $\rho = 7.5$ $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$ at $t = 2.72~{\rm ms}$; b) $\rho =5$ $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$ at $t = 3.20~{\rm ms}$; both with $v' = 2.0 s_{\rm l}$. The dotted line indicates the flame position.
Open with DEXTER

This produces what is termed "square vortices'' by Helenbrook & Law (1999). A similar flow field is applied by Vladimirova et al. (2003) who name it "cellular flow'' and also Zhu & Ronney (1994) use a flow with cellular vortices to study flame propagation in it. The particular flow has the advantage of being very simple - ideally containing only one Fourier mode. This helps to make the effects visible more clearly and simplifies the interpretation. Figure 1 illustrates the vortical flow applied in our simulations. It shows an example at a density of $\rho = 7.5$ $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$. In Fig. 2a the y-component of the velocity is plotted against the x-coordinate for the same simulation. Obviously, the velocity fluctuation is damped while propagating from the inflow boundary into the computational domain. The damping is even stronger for lower densities. Figure 2b shows a plot for $\rho =5$ $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$.

In order to be able to follow the long-term flame evolution, the simulations are carried out in a frame of reference comoving with the flame. For a planar flame this could be achieved by applying an inflow condition on the right hand side of the domain, where fuel enters at the laminar burning velocity, and an outflow condition on the opposite side of the domain. Since flame wrinkling and subsequent surface enhancement due to the LD instability and interaction with turbulent eddies will accelerate the flame, additional measures have to be taken in order to keep the flame centered in the domain. In the simulations presented by Röpke et al. (2003,2004) the grid was simply shifted according to the flame motion relative to $s_{\rm l}$. However, this approach is not consistent with the oscillating boundary condition. Therefore we modified Eq. (2) to

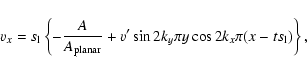\begin{displaymath}% v_x = s_{\rm l} \left\{ -\frac{A}{A_{{\rm planar}}} + v' \sin 2 k_y \pi y \cos 2 k_x \pi (x - t s_{\rm l})\right\}, \end{displaymath} (4)

where A denotes the actual flame surface (measured in each time step) and  $A_{{\rm planar}}$ stands for the surface of the corresponding planar flame, which is equivalent to the width of the domain in our case. This ensures that the velocity with which the fuel enters the domain adapts to the current effective flame propagation speed (cf. Eq. (6) in Sect. 3.4) and the position of the flame relative to the grid is kept approximately fixed.

We performed a number of simulations with different fuel densities. The fuel was assumed to consist of pure carbon. For convenience of the reader, a compilation of the setup values is given in Table 1. The laminar burning velocities $s_{\rm l}$ are determined according to the formula given by Timmes & Woosley (1992); marked "TW'' in the table.


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{0778fig3.eps} \end{figure} Figure 3: a) Flame propagation into quiescent fuel at a density of 5 $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$ and interaction with a vortical fuel field for velocity fluctuations at the right boundary of b) $v'/s_{\rm l} = 0.7$, c) $v'/s_{\rm l} = 2.0$, and d) $v'/s_{\rm l} = 2.5$. Each contour represents a time step of 3.2 $\times $ $10^{-3}~{\rm s}$.
Open with DEXTER

3.2 What can be expected?

Before we present the results of our numerical study we discuss what we actually are looking for in the simulations. That is, we somehow have to define how to discriminate between stable flame propagation and a breakdown of the stabilization. Why is this a question of definition? From the conjecture of active turbulent combustion it may appear that a breakdown of the stabilization must be obvious from a rapid and unlimited growth of the flame propagation velocity. However, this cannot be expected to occur in a numerical simulation where the growth of the flame surface due to ATC would be limited by discretization and resolution. Hence, the maximum effect that can be anticipated is a rapid increase in flame surface and burning velocity and a saturation at some higher value. A second possibility is that with increasing strength the vortical flow starts to dominate the flame evolution.

On the other hand, how can we guarantee flame stabilization? Owing to the high computational costs it will not be possible to follow the flame propagation for an arbitrarily long time. However, in case of stabilization we can actually make use of the knowledge of the flame pattern that is to be expected in case of stability in our specific simulation setup. From the preceding studies of flame propagation into quiescent fuel (Röpke et al. 2003,2004) it is known that the flame finally stabilizes in a single domain-filling cusp-like structure for our setup. This structure may be superimposed by a smaller-scale cellular pattern in sufficiently resolved simulations. A similar result can be anticipated for interaction with weak imprinted vortices.

Thus we may expect two extremal behaviors of the flame. In one case the flame stabilizes and the incoming perturbation fails to break up the cellular pattern. The cells of the stabilized small wavelength pattern caused by the initial perturbation of the flame front will then merge forming the single domain-filling cusp which then propagates stably. Alternatively, if the intensity of the incoming vortices is high enough to destroy the stabilization, no single domain-filling cusp will finally emerge. In this second case the flame should rather show a transient pattern.


  \begin{figure} \par\includegraphics[width=8.6cm,clip]{0778fig4.eps} \end{figure} Figure 4: Flame interaction with a vortical fuel field at a density of 5 $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$ for velocity fluctuations at the right boundary of $v'/s_{\rm l} = 3.0$. Resolution: 600 $\times $ 400 cells. Each contour represents a time step of 2.52 $\times $ $10^{-3}~{\rm s}$.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=17.1cm,clip]{0778fig5.eps} \end{figure} Figure 5: Flame evolution for a fuel density of 5 $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$ and a velocity fluctuation of $v'/s_{\rm l} = 2.5$ at the right boundary. Snapshots taken at time steps a) t=4.0 $\times $ $10^{-3}~{\rm s}$, b) t=8.0 $\times $ $10^{-3}~{\rm s}$, c) t=3.2 $\times $ $10^{-2}~{\rm s}$, and d) t=4.8 $\times $ $10^{-2}~{\rm s}$. The vorticity $\zeta $ (cf. Eq. (5)) is color-coded and the flame position is indicated by solid white curves.
Open with DEXTER

   
3.3 General features

As an example, we consider the case of a fuel density amounting to 5 $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$ (cf. Table 1). Figure 3 gives an overview over the flame evolution in interaction with vortical fuel flows of different strengths. The values $v'/s_{\rm l} = 0.7$, $v'/s_{\rm l} = 2.0$, and $v'/s_{\rm l} = 2.5$ indicate the amplitudes of velocity fluctuations imposed at the right boundary of the domain. Note, however, that they do not necessarily represent the values experienced by the flame front for reasons given in Sect. 3.1.

Figure 3a provides the comparison with flame propagation into quiescent fuel for the chosen setup. In this simulation v'was set to zero. It resembles the features of the simulations presented by Röpke et al. (2003,2004). Due to the LD instability, the initial perturbation grows and the flame shape evolves into a cellular pattern in the nonlinear regime. The subsequent contours show the "merging'' of the short-wavelength cells imprinted by the initial condition resulting in the formation of larger cells. This behavior was observed in a simulation of the long-term flame evolution in quiescent fuel (Röpke et al. 2004). There a cusp-like structure that was centered in the domain finally emerged as the steady state structure. The tendency to form a domain-filling cell is also apparent in Fig. 3a. However, following the evolution until the steady-state is reached is very expensive and shall not be tried here. This is certainly a drawback in the current study, but it was chosen as a compromise in order to be able to explore a larger parameter space with given computational resources.

Contrary to the flame evolution in Fig. 3a, the case of $v'/s_{\rm l} = 2.5$ (Fig. 3d) clearly shows the disruption of the initial cellular pattern by interaction of the flame with vortices. Also, the formation of a single domain-filling cell is suppressed by the interaction. The overall flame shape evolution in this case can be interpreted as an adaptation to the imprinted vortical flow structure. This is emphasized by Fig. 5. It provides a more detailed visualization of the interaction between the flame shape and the vortical flow, which is characterized by the color-coded logarithm of the absolute value of the vorticity $\zeta $ of the flow field,

 \begin{displaymath}\zeta = \frac{\partial v_y}{\partial x} - \frac{\partial v_x}{\partial y}, \end{displaymath} (5)

pointing out the vortices imprinted on the fuel flow.

The transition in the flame evolution between the extreme cases depicted in Figs. 3a and 3d does, however, not proceed abruptly, but rather in a smooth transition. Figures 3b,c present two examples of intermediate behaviors at $v'/s_{\rm l} = 0.7$ and $v'/s_{\rm l} = 2.0$, the first of which is again illustrated by snapshots in Fig. 6. In this case, still a tendency to form a long-wavelength cellular structure is visible. Here the mechanism of the advection of small perturbations toward the cusp (Zel'dovich et al. 1980; Röpke et al. 2003,2004) dominates over the effects of the vortical flow on the flame shape.


  \begin{figure} \par\includegraphics[width=17.1cm,clip]{0778fig6.eps} \end{figure} Figure 6: Flame evolution for a fuel density of 5 $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$ and a velocity fluctuation of $v'/s_{\rm l} = 0.7$ at the right boundary. Snapshots taken at time steps a) t=8.0 $\times $ $10^{-3}~{\rm s}$, b) t=2.4 $\times $ $10^{-2}~{\rm s}$, c) t=3.2 $\times $ $10^{-2}~{\rm s}$, and d) t=4.8 $\times $ $10^{-2}~{\rm s}$. The vorticity $\zeta $ (cf. Eq. (5)) is color-coded and the flame position is indicated by solid white curves.
Open with DEXTER

Simulations similar to the aforementioned were also performed in some cases with higher resolution of the numerical grid in order to test whether or not insufficient resolution prevents small scale flame structures from developing. However, no significant difference to the flame evolution depicted in Figs. 3a-d could be noticed. An example with double resolution is given in Fig. 4. Note that here the intention is not to provide a resolution study in the strict sense. The development of the particular realization of the cellular pattern as a transient phenomenon is determined by small perturbations (including numerical noise) which cannot be reproduced in different setups. However, the important point is that the flame in both resolutions finally adapts its shape to the vortices in the incoming fuel and no features develop below the scale of these vortices, which could have been overlooked in lower resolution. This agrees with Helenbrook & Law (1999), who found in their simulations of chemical flames that the wavelength of perturbations that develop in the interaction with a vortical flow is determined by the scale of the vortices and not by a critical wavelength (introduced by a curvature-dependent burning speed of the flame front according to Markstein 1951).

   
3.4 A parameter study

In order to quantify the flame evolution as qualitatively described in the preceding section, we conducted a parameter study. It aimed at the determination of flame behavior as a function of the strength of the vortices in the incoming flow and in dependence on the fuel density.

As discussed by Röpke et al. (2004), the simulation of flame stabilization at around 1.0 $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$ requires unaffordable high numerical resolutions and furthermore our thin flame approximation is certainly not a realistic description of thermonuclear burning in SNe Ia at these low densities. On the other hand, it can be observed, that at higher fuel densities (around $10^8~{\rm g}~{\rm cm}^{-3}$) the sensitivity of the initial flame to small-wavelength perturbations increases. This causes difficulties in producing a stable flame configuration prior to the incoming vortices encountering the flame front. However, in connection with a possible DDT we are mainly interested in the late stages of the SN Ia explosions (see Sect. 1). Therefore we restricted the study to four fuel densities: $\rho_u = 1.25$ $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$, $\rho_u = 2.5$ $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$, $\rho_u = 5$ $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$, and $\rho_u = 7.5$ $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$ (cf. Table 1).

Plots similar to Fig. 3 corresponding to simulations with different fuel densities are given by Röpke (2003). The flame evolution in these simulations can be summarized as follows: at lower fuel densities the effect of the incoming vortices on the flame structure is generally more drastic. For $\rho_u = 2.5$ $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$ the tendency of the formation of the domain-filling structure is still visible in the case of propagation into quiescent fuel. This is not the case for $\rho_u = 1.25$ $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$for reasons discussed by Röpke et al. (2004). However, with increasing strengths of the imprinted velocity fluctuations, the flame still gradually adapts to the flow for both fuel densities. At $\rho_u = 7.5$ $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$ the flame evolution is similar to that at $\rho_u = 5$ $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$. Only in case of propagation into quiescent fuel an initial destabilization with respect to small wavelength perturbations (cf. Röpke et al. 2004) alters the evolution for a transition period, before the flame finally stabilizes in a domain-filling single-cell structure.

In a quantitative evaluation of our parameter study regarding the flame evolution for different fuel densities we will now address (i) the dependency of the effective flame propagation velocity on the strength of the imprinted velocity fluctuations and (ii) the amplification of the velocity fluctuation by the flame front.

For the exemplary case of $\rho_u = 5$ $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$we discuss the measurement of the necessary quantities in our simulations.

The effective propagation velocity $v_{{\rm eff}}$ of the flame is determined via the flame surface:

 \begin{displaymath}% \frac{v_{{\rm eff}}}{s_{\rm l}} = \frac{A_{{\rm surf}}}{A_{{\rm planar}}}\cdot \end{displaymath} (6)

Underlying to that relation is the assumption of a constant, geometry independent burning velocity $s_{\rm l}$ of the flame. This assumption has been discussed in the context of the present flame model by Röpke et al. (2003). The measured flame surface area as a function of time is plotted in Figs. 7a and 7b for the simulations with $v'/s_{\rm l} = 0.7$ and $v'/s_{\rm l} = 2.5$, respectively. Here adaptation of the flame structure to the strong vortical fuel flow is obvious. After the imprinted velocity fluctuations reach the flame at $t\sim 150 \tau_{\Delta x}$, its surface becomes dominated by the vortices and changes with the frequency of these. This is reflected by the high-frequency fluctuations of A in Fig. 7b. In addition to fluctuations on a small time scale, the interaction with the vortical flow field introduces considerable long term fluctuations. These are, of course, expected in the initial phase when the flame begins to react to the incoming vortices. But even at much later times the flame surface area does not reach a steady state.

The standard deviation of the velocity field is obtained separately in the fuel upstream of the front and in the ashes downstream of it in order to determine the amplification of the velocity fluctuations across the flame front. In Fig. 8 the quantities are plotted against time for our exemplary case. As mentioned above, the strength of the vortices produced at the inflow boundary is not a reliable measure of what the flame actually experiences, since the velocity fluctuations get damped quickly when propagating toward the flame and bending of the flame front may lead to different velocity fluctuations at different locations on the flame. Moreover, the dependence of the damping on the fuel density hampers the comparability of simulations with this parameter varying. Therefore we determine the standard deviations of the velocity fields, $\sigma(v_u)$ and  $\sigma(v_b)$, within a certain belt around the flame front. This belt was scaled in a way that the time for flame crossing over its width remained the same for all fuel densities.

All quantities measured in our simulations fluctuate considerably with time. Hence we averaged them over a time ranging from 480  $\tau _{\Delta x}$ to 720  $\tau _{\Delta x}$ ( $\tau _{\Delta x}$ denotes the crossing time of the corresponding laminar flame over one grid cell).

In Fig. 9 the temporal mean value of flame surface area  $A_{{\rm surf}}$ (normalized to the surface area of the corresponding planar flame front  $A_{{\rm planar}}$) is plotted against the temporal mean of standard deviation of the velocity in the fuel region (normalized to the laminar burning velocity of the flame). The increase of the flame speed with stronger incoming velocity fluctuations is evident here. However, there is quite a large scatter in the data. This has two reasons. First, we certainly did not follow the flame evolution long enough to undoubtly reach the steady state of the flame shape - which should ideally be the clearly distinct single domain-filling cusp-like structure in case of weak incoming vortices. To follow the flame propagation up to this stage would be much too expensive for a parameter study. Second, some peculiar features of the flame shape may develop as a result of small perturbations (e.g. due to numerical noise). In particular, this may cause substantial deviations if it affects the long-wavelength structure of the flame and is primarily responsible for the scatter of the results in case of strong incoming velocity fluctuations. This scatter could very likely be cured by taking the mean over longer time intervals.


  \begin{figure} \par\includegraphics[width=7.1cm,clip]{0778fig7.eps} \end{figure} Figure 7: Flame surface area as function of time (normalized to the crossing time of the laminar flame over one grid cell  $\tau _{\Delta x}$) for a) $v'/s_{\rm l}$ = 0.7 and b) $v'/s_{\rm l} = 2.5$.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=13.45cm,clip]{0778fig8.eps} \end{figure} Figure 8: a), b) Standard deviation of the velocity field ahead of the front as function of time, and c), d) ratio of the standard deviations of the velocity fields beyond and ahead of the flame as function time. The left and right columns of plots correspond to $v'/s_{\rm l}$ = 0.7 and $v'/s_{\rm l} = 2.5$, respectively.
Open with DEXTER

Damköhler (1940) proposed a linear dependence of the effective flame propagation velocity on the turbulence intensity for turbulent combustion in what is today called the flamelet regime (Peters 1986). Our results are consistent with a linear growth law. Corresponding fits to the data are included in Fig. 9 and values for the parameter a according to the fitting formula

 \begin{displaymath}% \frac{\langle A_{{\rm surf}}\rangle}{A_{{\rm planar}}} = 1.0 + a ~ \frac{\langle\sigma(v_u)\rangle}{s_{\rm l}} \end{displaymath} (7)

are given in Table 2. It is evident from Fig. 9 that interaction of the flame in the cellular regime with turbulent velocity fluctuation can lead to a substantial acceleration of the flame propagation velocity. Unfortunately, it is not possible to infer a clear trend of the slope depending on the fuel density from this parameter study.

In order to estimate the amplification of the velocity fluctuations across the flame for different densities, we compared the strength of velocity fluctuations downstream of the flame with the strength of the imprinted vortices in the fuel. As already shown for the case of flame propagation into quiescent fuel (Röpke et al. 2004), the flame produces vorticity in the ashes. Here, the question is addressed whether vorticity present in the fuel will be amplified in the flame.

The result of the study for a variety of fuel densities is plotted in Fig. 10. In this plot, trends show up much more clearly than in Fig. 9. However, some scatter is still present in the data. As can be seen from snapshots of the evolution of the flame front (an example is depicted in Fig. 5c), the merging of cusps can eventually produce transient "bursts'' in the vorticity downstream of the flame. This is particularly prominent in case of changes in the long-wavelength flame structure, but not necessarily connected to it. From Fig. 8d, where this "burst'' in velocity fluctuation appears as a spike in the profile, it can be concluded that the duration of those events is very short. Hence their contribution to the temporal mean is small (whereas the long-wavelength flame structure and thus the flame surface change slowly). Consequently, the scatter in plot 10 is much smaller than in plot 9.

The data plotted in Fig. 10 can be fit rather well by a linear relation between the ratio $\langle\sigma (v_b)/ \sigma(v_u)\rangle$ and the incoming turbulence intensity, i.e.

 \begin{displaymath}% \langle\sigma(v_b)\rangle = b + c \langle\sigma(v_u)\rangle. \end{displaymath} (8)

Table 2 provides the fit parameters. In contrast to Fig. 9, the plot in Fig. 10 reveals a clear trend for the fuel density. The slope c increases with lower $\rho_u$. This is what would be expected taking into account the increased production of specific volume across the flame with lower $\rho_u$. In Fig. 11 the factor c is plotted against the corresponding density ratio $\mu $, accentuating the trend. Of course, a functional dependence cannot be inferred from this small sample of data. It is interesting to note that for $\rho_u \approx 1.25$ $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$ the slope c becomes greater than unity, indicating a slight amplification of velocity fluctuation in this case.

The above interpretation of this result requires some caution, since the cellular stabilization of the flame has been shown to be weaker with lower fuel density. However, this seems to be a numerical rather than a physical effect, since the cusps become more stable with higher resolution. Thus, at the given resolution of our parameter study, the flame evolution shows peculiar behavior at a fuel density of 1.25 $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$ and below. Here, cusps may loose stability distorting the flame shape, which then responds with accelerated propagation of the perturbed part for a short period, after that the flame stabilizes again. The interaction with the vortical flow outweighs this effect in our simulations, but the simulation at these density may be less reliable. However, we do not observe such a flame evolution at the higher fuel densities included in this parameter study. Thus, the dependency on the fuel density is likely to be (at least partially) of physical origin.


  \begin{figure} \par\includegraphics[width=8.15cm,clip]{0778fig9.eps} \end{figure} Figure 9: Dependence of the flame surface area on the strength of the imprinted velocity fluctuations.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.1cm,clip]{0778fig10.eps} \end{figure} Figure 10: Relation between velocity fluctuations upstream and downstream of the flame front.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.2cm,clip]{0778fig11.eps} \end{figure} Figure 11: Ratio of the velocities upstream and downstream of the flame front as a function of the density contrast $\mu $ over it.
Open with DEXTER

4 Conclusions

In the presented simulations we performed the first attempt to investigate the interaction of cellular flames with turbulent velocity fluctuations in the context of SN Ia explosions. The results can be summarized as follows:

1.
In case of the interaction of the flame with weak vortices in the fuel flow, the flame exhibits an evolution similar to that observed in case of flame propagation into quiescent fuel. In the setup chosen for our simulations the flame front showed a tendency to align in a single domain-filling cellular structure.

Table 2: Fit parameters according to fitting formulas (7) and (8) with corresponding asymptotic standard errors.

Interaction with the incoming vortices leads to a superposition of this fundamental structure with a cellular pattern of shorter wavelength. Similar to the simulations presented by Röpke et al. (2003), where a cellular superposition of the basic flame structure was observed in case of wide computational domains, this does not lead to a destabilization of the domain-filling cell. In accord with theoretical predictions (Zel'dovich et al. 1980) the small superimposed perturbations are advected toward the cusp where they disappear. The flow field accounting for this effect was studied by Röpke et al. (2004).
2.
If the cellularly stabilized flame interacts with vortices of sufficient strength, then the initial cellular pattern will break up in the sense that the initial shape is lost and the flame adapts to the incoming vortical flow. The tendency of the flame to form a single-cell structure is suppressed by this effect. However, we do not observe a sharp transition but rather a gradual change in the flame behavior.
3.
Our numerical simulations suggest that the flame smoothly adapts to the incoming vortical flow with increasing turbulence intensity. No drastic effects were observed. Although we measured an amplification of the strength of the velocity fluctuation across the flame for $\rho_u = 1.25$ $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$, we could not observe a deviation from a linear scaling between the flame surface area (and thus the effective flame propagation speed) and the strength of the imprinted velocity fluctuations.
We draw the conclusion that the results of our study are consistent with flame propagation in the flamelet regime of turbulent combustion, at least at fuel densities above $\rho_u \approx 1.25$ $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$. Thus, our study corroborates the assumption of flame stability at unresolved scales in large-scale SN Ia explosion models. This is an important contribution that our small-scale model makes to the credibility of those simulations. The slight amplification of the turbulent velocity fluctuations across the flame at $\rho_u = 1.25$ $\times $ $10^7~{\rm g}~{\rm cm}^{-3}$ (and possibly even more pronounced below that value) may have no significant impact on the current SN Ia models, since the flame width at those densities will become non-negligible (cf. the data given by Timmes & Woosley 1992). Then the burning is expected to enter the distributed regime of turbulent combustion, whose simulation requires completely different numerical methods. In the context of SN Ia explosions, an approach to study this regime was discussed by Lisewski et al. (2000).

Although the increase in effective flame propagation resulting from the cellular regime is negligible compared to the increase in flame speed at larger scales where the flame is affected by the turbulent cascade, it may be significant in the early stages of the explosion. In the current large-scale models (e.g., Reinecke et al. 2002), the flame is assumed to propagate with its laminar flame velocity before the rising Rayleigh-Taylor bubbles establish the turbulent cascade. This may cause a problem with the nucleosynthetic yields from the SN Ia explosion (Reinecke 2001). Since the laminar flame speed is very low, the WD expands slowly in the beginning of the explosion and thus the combustion products remain at rather high densities for a considerable time. This effect causes a neutronization of the material by electron capture and an overproduction of neutron-rich heavy nuclei (Nomoto & Kondo 1991; Brachwitz et al. 2000), eventually even leading to a collapse of the star. Taking into account the velocity increase resulting from the cellular regime, this problem could be extenuated. As has been shown in this study, this may be in particular the case if strong velocity fluctuations left over from the pre-ignition convection interact with the flame. However, the strength of turbulence resulting from pre-ignition effects is not well-determined yet. Höflich & Stein (2002) claim values as high as $\sim$ $10^7~{\rm cm}~{\rm s}^{-1}$. The impact of the cellular burning regime on the nucleosynthesis yields of the SN Ia explosion models will be investigated in a forthcoming study.

Even though we can probably not completely rule out the possibility of active turbulent combustion, we found no convincing hint for such an effect in our numerical investigations. Our simulations indicate that effects resulting from the cellular regime of flame propagation are unlikely to trigger a presumed deflagration-to-detonation transition. Hence, the search for active turbulent combustion and deflagration-to-detonation transition should focus on the distributed burning regime.

Acknowledgements
This work was supported in part by the European Research Training Network "The Physics of Type Ia Supernova Explosions'' under contract HPRN-CT-2002-00303 and by the DFG Priority Research Program "Analysis and Numerics for Conservation Laws'' under contract HI 534/3. A pleasant atmosphere to prepare this publication was provided at the workshop "Thermonuclear Supernovae and Cosmology'' at the ECT*, Trento, Italy. We would like to thank M. Reinecke, S. Blinnikov, and W. Schmidt for stimulating discussions. The numerical simulations were performed on an IBM Regatta system at the computer center of the Max Planck Society in Garching.

References


Copyright ESO 2004