A&A 421, 1101-1111 (2004)
DOI: 10.1051/0004-6361:20035762
On the possible interconversion between pairs of deuterated
isotopomers of methanol, its ion, and its protonated ion in star-forming regions
Y. Osamura1 - H. Roberts2 - E. Herbst3
1 - Department of Chemistry, Rikkyo University, 3-34-1
Nishi-ikebukuro, Tokyo 171-8501, Japan
2 - Department of Physics,
The Ohio State University, Columbus, OH 43210, USA
3 - Departments of Physics, Chemistry, and Astronomy, The Ohio State
University,
Columbus, OH 43210, USA
Received 28 November 2003 / Accepted 7 April 2004
Abstract
Deuterated isotopomers of methanol have been detected both
in hot cores and in the protostellar source IRAS 16293-2422. It is
currently thought that these species are formed on cold grain
surfaces in a previous era by the hydrogenation and deuteration of CO
via reactions with atomic H and D. Methanol and its singly, doubly,
and multi-deuterated isotopomers then evaporate or are sputtered
into the gas as star formation occurs. In studying the
post-evaporative gas-phase chemistry of these isotopomers, it is
important to know if pairs of isotopomers with D atoms in different
places (e.g. CH3OD and CH2DOH) can be interconverted or
whether they can be viewed as separate entities with depletion
mechanisms that are independent of each other. Here we show that it
is difficult to exchange protons and deuterons on the two different
parts of the methanol backbone. It is then possible that CH3OD
can be destroyed on a much faster time scale than CH2DOH, an explanation
that may partially explain the relatively low abundance of the former in
IRAS 16293-2422.
Key words: astrochemistry - molecular processes - ISM: abundances - ISM:
molecules - ISM: individual: IRAS 16293-2422
The study of deuterated isotopomers is telling us much about the
physical and chemical conditions in an assortment of environments of
the interstellar medium (Millar 2003; Roberts & Millar 2000a,b; Bacmann et al. 2003). Although much of the
deuterium fractionation occurs in the gas-phase under cold
conditions, the detection of high abundances of D2CO and
assorted deuterated isotopomers of methanol in star-forming regions
(Cecarelli et al. 2002; Parise et al. 2002, 2003, 2004) is
particularly challenging to modelers. The explanation for the
methanol isotopomers can only be attempted using surface chemistry
(Charnley et al. 1997): in a previous colder era, CO produced in the gas
accretes onto the mantles of dust particles, where it is converted
into formaldehyde, methanol, and their deuterated isotopomers by
reactions with H and D atoms landing on the grains and diffusing
rapidly over their surfaces. Once these assorted species are
produced, they are thought to remain on grain surfaces until the
onset of star formation, when simple evaporation due to rising
temperatures or sputtering due to high-velocity winds results in the
desorption of the species.
In formulating a detailed theory of the
post-evaporative gas-phase abundances of the deuterated isotopomers of
methanol, it is necessary to consider what happens to these species
once they are in the gas. It is important to realize that all but the fully deuterated
one can be divided into pairs, in which a deuteron exists on either
the C-end or the O-end of the molecule; viz.,
CH3OD-CH2DOH, CH2DOD-CHD2OH, and
CHD2OD-CD3OH. The depletion of all of these species occurs
by ion-molecule reactions, which lead to protonation,
charge exchange, and other products. Once the
isotopomers are protonated or ionized,
it is possible that, with enough internal energy, a pair of D and H
atoms can rearrange between the C- and O-ends efficiently so that
the two ions should really be considered one rather floppy system.
Even if this rearrangement does not occur during the lifetime of the
protonated ions, it might occur during their dissociative
recombination with electrons. And following dissociative
recombination, it might occur between the regenerated neutral
methanol isotopomers if they are sufficiently energized.
Rearrangement by any of the above mechanisms can erase potential
differences in the rates of depletion of the isotopomeric neutral pairs.
On the other hand, if interconversion does not occur
appreciably, the depletion of the two isotopomers should be distinct,
and it would be possible for one to have a much faster depletion rate
than the other.
In this paper, we report detailed quantum
chemical calculations on the internal rearrangements possible in
energized normal methanol, ionized methanol, and protonated methanol,
during the dissociative recombination of protonated methanol, the
reactions of protonated and ionized methanol with hydrogen atoms, and
even during the reaction between neutral methanol and hydrogen
atoms. In all of these cases, we find that exchange between protons
(or protons and deuterons) from the two ends of the molecular
structure is unlikely to occur efficiently. Thus, we can, for
example, think of the singly deuterated isotopomers CH3OD and
CH2DOH as quite distinct species with possibly different
depletion mechanisms and time scales. Such an argument,
first proposed by Charnley et al. (1997), can be used to
explain the low abundance of the former compared with the
latter in the protostellar source IRAS 16293-2422. In this argument,
protonation of CH3OD leads to its destruction at a more rapid rate
than protonation of CH2DOH because
CH2DOH2+ reforms CH2DOH upon dissociative recombination,
whereas dissociative recombination of CH3ODH+ leads to
both CH3OD and CH3OH.
In our
calculations, we will confine ourselves to the exchange of protons
between the C- and the O-ends of methanol-related molecules. It is
not necessary to specifically follow deuterons since the reaction
pathways for H-H and H-D exchange are the same, according to the
Born-Oppenheimer approximation. Thus, if we conclude that a
proton cannot go from one end of methanol to the other, or that
simultaneous transfer of two protons between the C- and O-ends is
impossible, the same holds true for motions involving a proton and a
deuteron. We will consider two types of processes: (i) motion of
one proton (known as an H-shift), and (ii) simultaneous exchange of
two protons (known as synchronous H-H exchange). Note that two
consecutive H-shift motions are needed to effect an exchange that
is not synchronous.
The remainder of the paper is organized in
the following manner. Following a brief discussion of quantum
chemical methods in Sect. 2, we consider the possibility of
proton-proton exchanges in energized methanol, its ion, and its
protonated form in Sect. 3. In Sect. 4, we consider the
possibility of exchange during chemical reactions. Finally, in
Sect. 5, we employ what has been learned in new detailed models of
IRAS 16293-2422 and the Orion Compact Ridge and compare our results with
observations of the deuterated isotopomers of methanol and selected other species.
We have applied the hybrid density functional B3LYP method with a
6-311G(d, p) basis set to calculate the potential energy surfaces for
the exchange of protons between the C- and O-ends of methanol, its
ion, and its protonated form. We have also
calculated potential surfaces relevant to the dissociative
recombination of CH3OH2+ and the formation of assorted
neutral fragments, as well as energy barriers (corresponding to
so-called transition state structures) for the reactions of hydrogen
atoms with (i) neutral methanol and (ii) protonated methanol.
In addition, the potential surfaces for the reactions between protons
and methanol have been looked at. All
computations were carried out with the Gaussian 98 program suite
(Frisch et al. 1998). The structures on the potential energy
surfaces were confirmed to be energy minima or transition states
(saddle points) by a vibrational analysis. In order to refine the
relative energies along the assorted potential energy surfaces, we
utilized the CCSD(T) method with the augmented
correlation-consistent polarized-valence triple-zeta basis set
(aug-cc-pVTZ) of Dunning (1989) at the geometries obtained with the
B3LYP method. The relative energies presented in this paper are
corrected by zero-point vibrational energies obtained with the B3LYP
method without scaling.
The energies are expressed in units of kcal mol-1, where 1 kcal mol
-1 = 503 K.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0762fig1.eps}
\end{figure}](/articles/aa/full/2004/27/aa0762/Timg2.gif) |
Figure 1:
Optimized structures of transition states for the synchronous
hydrogen-exchange reaction in methanol (H-H exchange TS) and in
protonated methanol (H-H exchange TSH+) obtained with the B3LYP method. Bond distances are in Å and bond angles are in degrees.
The relative transition state energies
with the CCSD(T) method are +148.6 kcal mol-1 for TS and
+148.9 kcal mol-1 for TSH+. |
| Open with DEXTER |
We start by discussing the possibility that protons
from the C- and O-ends of neutral, ionized,
and protonated methanol can exchange spontaneously. This is most
likely to occur following a chemical reaction in which the
methanol-like species possess internal energy. If two hydrogen
atoms on the C-atom and O-atom, respectively, can exchange,
H-D exchange is possible between the singly
deuterated pairs CH3OD - CH2DOH, CH3OD+ -
CH2DOH+, and CH3OHD+ - CH2DOH2+, and
their multiply deuterated analogs. Note that the deuterated pairs of
isomers do have slightly different zero-point energies, but this will
only affect a dynamic equilibrium, not prohibit it from occurring.
These energy differences are not large; we calculate for example that
CH3OD is more stable than CH2DOH by about 50 K.
Figure 1 shows transition state structures for neutral and
protonated methanol for the case of synchronous H-H exchange. The
calculated energies of these transition state structures compared
with methanol and protonated methanol are 148.6 kcal mol-1 and
148.9 kcal mol-1, respectively, at our highest level of calculation.
These
very large values mean that isomerization does not occur via this
mechanism unless the species are very internally excited. Unlike the
protonated ion, the methanol ion does not show a true transition
state for synchronous H-H exchange, so the process does not occur at
any energy.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0762fig2.eps}
\end{figure}](/articles/aa/full/2004/27/aa0762/Timg3.gif) |
Figure 2:
The upper panels show the optimized structures of methanol,
its hydrogen-shift
transition state, and the isomer CH2OH2, while the lower
panels show the structures of the methanol ion, its hydrogen-shift
transition state, and the isomer CH2OH2+. Bond distances are in Å and bond angles are in degrees. The numbers
outside of and in
parentheses are the relative energies in kcal mol-1 obtained with
the CCSD(T) and B3LYP methods. |
| Open with DEXTER |
Figure 2 shows transition state structures
and energies for a simple proton shift from the C-end to the O-end, or its reverse,
in methanol and its ion. In this case, the full exchange
would also require motion of another proton in the opposite direction
over the same transition state. The transition state energies are
not as large as for the simultaneous H-H transfer but they are still
sufficiently large so that spontaneous isomerization does not happen
under thermal interstellar conditions. But we must also consider
isomerization following chemical reactions in which the products
possess large amounts of internal energy which can only be radiated
away.
The protonated ion does not possess a transition state for
the single H-shift mechanism, so, as is the case for the normal ion attempting to
undergo synchronous H-H exchange, the process of a single H-shift or consecutive
H-shifts does not occur for protonated methanol.
The most
likely reaction sequence leading to excited neutral methanol involves
protonation followed by dissociative recombination to reform
methanol:
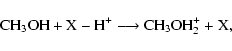 |
(1) |
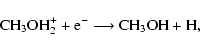 |
(2) |
where X-H+ represents a protonating ion, and protonation occurs
on the O-end. The exothermicity of the dissociative
recombination reaction, discussed more fully in Sect. 4, is
calculated to be 134.6 kcal mol-1, and a significant amount of
that energy is likely to be present initially in the methanol
product. Among the different unimolecular reactions that can
spontaneously occur from energized methanol is the exchange of
the C- and O-protons. Since the barrier for synchronous H-H transfer (see Fig. 1) exceeds the maximum internal energy that methanol can possess, the exchange
via two
consecutive H-shifts is the only possibility. For this mechanism, the two transition states, each at an energy of 82.4 kcal mol-1, lie considerably below 134.6 kcal mol-1. Of course,
not all of the 134.6 kcal mol-1 will go into internal energy of
methanol product, since there is also translational energy between
the methanol and the H atom. In addition, only vibrational energy is efficient at promoting isomerization; rotational energy has a much more subtle effect (Herbst et al. 2000).
There have been very few theoretical and experimental studies of the vibrational energy distribution of neutral products of dissociative recombination reactions. Bates (1993) developed a classical theory with several mechanisms, including the so-called "impulse'' and "relic'' processes. Tomasehvsky et al. (1998) developed a quantum mechanical treatment, and applied it to the case of the CO product of HCO+ + e-, which had been studied experimentally in its
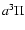 state by Adams and co-workers (Adams & Babcock 1994; Butler et al. 1997).
More limited experimental studies of the vibrational distribution
of OH product from an assortment of dissociative recombination reactions were reported by Herd et al. (1990). The general picture from all of these studies is that for a diatomic product, the vibrational distribution peaks at or near the ground state, and gradually declines as the vibrational quantum number increases. In most cases, the majority of the energy on average seems to be in modes other than vibration, most probably translation. The extension to a polyatomic neutral product such as methanol, with many modes of vibration, is uncertain, but it is likely that product translational energy must be large since dissociative recombination cannot occur unless the products rapidly leave the vicinity of configuration space in which the parent product neutral is formed. Thus, although the vibrational distribution of energized methanol emerging as a product of dissociative recombination is uncertain, it is most likely that only a small fraction of the product molecules will possess enough vibrational energy to undergo isomerization, since in this instance the threshold for isomerization requires over 60 percent of the exothermicity of the dissociative recombination reaction.
state by Adams and co-workers (Adams & Babcock 1994; Butler et al. 1997).
More limited experimental studies of the vibrational distribution
of OH product from an assortment of dissociative recombination reactions were reported by Herd et al. (1990). The general picture from all of these studies is that for a diatomic product, the vibrational distribution peaks at or near the ground state, and gradually declines as the vibrational quantum number increases. In most cases, the majority of the energy on average seems to be in modes other than vibration, most probably translation. The extension to a polyatomic neutral product such as methanol, with many modes of vibration, is uncertain, but it is likely that product translational energy must be large since dissociative recombination cannot occur unless the products rapidly leave the vicinity of configuration space in which the parent product neutral is formed. Thus, although the vibrational distribution of energized methanol emerging as a product of dissociative recombination is uncertain, it is most likely that only a small fraction of the product molecules will possess enough vibrational energy to undergo isomerization, since in this instance the threshold for isomerization requires over 60 percent of the exothermicity of the dissociative recombination reaction.
To estimate the actual unimolecular rate
of isomerization of methanol via two H-shifts as a function of vibrational energy, we can use RRKM
theory (Smith 1980; Holbrook et al. 1996). Let us first consider a single H-shift from
methanol to its isomer CH2OH2.
In the RRKM approach, the isomerization rate
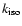 is given by
the expression
is given by
the expression
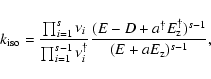 |
(3) |
where the 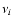 are the vibrational frequencies, D is the transition state energy
(82.4 kcal mol-1), E is the total vibrational internal energy,
are the vibrational frequencies, D is the transition state energy
(82.4 kcal mol-1), E is the total vibrational internal energy, 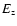 is the zero-point energy, s
= 12 is the number of vibrational degrees of freedom, and a is an empirical factor between zero and unity. Parameters with the
is the zero-point energy, s
= 12 is the number of vibrational degrees of freedom, and a is an empirical factor between zero and unity. Parameters with the 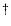 symbol refers to the transition state, while those without this symbol refer to normal methanol. The RRKM expression used here is without tunneling, and so is only valid if the total vibrational energy exceeds the transition state barrier of
82.4 kcal mol-1. Using calculated values of the vibrational frequencies, we estimate that the rate of isomerization at energies very close to the vibrational energy threshold of
82.4 kcal mol-1 (
symbol refers to the transition state, while those without this symbol refer to normal methanol. The RRKM expression used here is without tunneling, and so is only valid if the total vibrational energy exceeds the transition state barrier of
82.4 kcal mol-1. Using calculated values of the vibrational frequencies, we estimate that the rate of isomerization at energies very close to the vibrational energy threshold of
82.4 kcal mol-1 (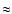 106 s-1) is still much faster than the radiative relaxation rate of vibrationally energized methanol, which occurs at a rate of 102-3 s-1 (Herbst 1982; see his Fig. 3).
Although we have only calculated the rate for a
single H-shift to form CH2OH2; a double shift is likely to
follow with an overall rate a sizable fraction of that of the single shift,
because CH2OH2 lies at
a significantly higher energy than methanol and so will likely
re-isomerize with or without a net exchange. The rate coefficient for D-H exchange via two shifts is likely to be somewhat smaller still because of mass and statistical effects, but RRKM theory still predicts it to be dominant over radiative relaxation at almost all energies above threshold. So, exchange, including that of D and H atoms, can occur if the energized methanol product possesses a sufficient amount of internal vibrational energy. This result must be viewed with some caution, since it is likely that the statistical theory overestimates the rate of isomerization given its steric complexity.
This caution, combined with the unlikelihood that a sufficient amount of vibrational energy (>82.4 kcal mol-1) is available in the first place, suggests strongly that most energized methanol molecules relax radiatively without undergoing isomeric shifts. We discuss this point further in the section below on dissociative recombination.
It is interesting to note that in an earlier paper on HNC-HCN isomerization (Herbst et al. 2000), we concluded that dissociative recombination of the parent ion HCNH+ does not lead to enough internal energy for facile interconversion of the two isomers. A different conclusion was reached, however, for HCN and HNC products of the neutral-neutral reactions
106 s-1) is still much faster than the radiative relaxation rate of vibrationally energized methanol, which occurs at a rate of 102-3 s-1 (Herbst 1982; see his Fig. 3).
Although we have only calculated the rate for a
single H-shift to form CH2OH2; a double shift is likely to
follow with an overall rate a sizable fraction of that of the single shift,
because CH2OH2 lies at
a significantly higher energy than methanol and so will likely
re-isomerize with or without a net exchange. The rate coefficient for D-H exchange via two shifts is likely to be somewhat smaller still because of mass and statistical effects, but RRKM theory still predicts it to be dominant over radiative relaxation at almost all energies above threshold. So, exchange, including that of D and H atoms, can occur if the energized methanol product possesses a sufficient amount of internal vibrational energy. This result must be viewed with some caution, since it is likely that the statistical theory overestimates the rate of isomerization given its steric complexity.
This caution, combined with the unlikelihood that a sufficient amount of vibrational energy (>82.4 kcal mol-1) is available in the first place, suggests strongly that most energized methanol molecules relax radiatively without undergoing isomeric shifts. We discuss this point further in the section below on dissociative recombination.
It is interesting to note that in an earlier paper on HNC-HCN isomerization (Herbst et al. 2000), we concluded that dissociative recombination of the parent ion HCNH+ does not lead to enough internal energy for facile interconversion of the two isomers. A different conclusion was reached, however, for HCN and HNC products of the neutral-neutral reactions
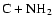 and
and
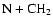 .
.
In addition to
the single-H and double-H shift isomerization, dissociation
processes that the excited methanol can undergo are listed in
Table 1.
As can be seen, dissociation of methanol into
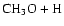 ,
,
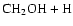 ,
,
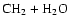 and
and
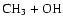 requires almost the entire
internal energy of the excited methanol so that the four processes are quite
unlikely. The one major exception is the dissociation of methanol to
form formaldehyde and molecular hydrogen, which requires only
20.4 kcal mol-1, as shown in Table 1. But this process must
occur over a very large activation energy barrier (Kline &
Penner 1982)
and, if it occurs at all, will not have the effect of
interconverting isotopomeric pairs. We have calculated the activation energy to be
100.5 kcal mol-1.
requires almost the entire
internal energy of the excited methanol so that the four processes are quite
unlikely. The one major exception is the dissociation of methanol to
form formaldehyde and molecular hydrogen, which requires only
20.4 kcal mol-1, as shown in Table 1. But this process must
occur over a very large activation energy barrier (Kline &
Penner 1982)
and, if it occurs at all, will not have the effect of
interconverting isotopomeric pairs. We have calculated the activation energy to be
100.5 kcal mol-1.
Table 1:
Possible products and required energies (kcal mol-1) for the
unimolecular dissociation of excited methanol.
For protonated methanol, excitation occurs during
formation via reaction (1). For example, the
exothermicity for the protonation reaction between methanol and
H3+ is 84 kcal mol-1, while that for the analogous reactions
involving other major protonating ions is at most half as great. Once again, all of this
energy does not go into protonated methanol; some goes into
translational energy and some goes into the neutral product, e.g., H2.
Even if protonated methanol is the recipient of all of the reaction
exothermicity, there is still nowhere near enough energy to surmount the
transition state barrier for synchronous exchange (see Fig. 1). Nor can any single H-shift occur given the saturated
nature of the species. So, we find that H-H (and by extension H-D)
exchange cannot occur between pairs of protonated isotopomers
of methanol.
For energized methanol ion, the only possible pathway to isomerization
is shown in Fig. 2. For two single-H shifts, the transition states lie at
only 25.1 kcal mol-1. Ionization of methanol via charge exchange
with protons can lead to an internal energy of as much as 64.5 kcal mol-1, according to our calculations. This amount of energy is,
once again, enough to allow an isomerization via two H-shifts. The
isomerization must compete with other unimolecular processes, most
notably the single H-shift reaction:
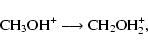 |
(4) |
which, unlike the analogous case for neutral methanol,
is exothermic by 8.1 kcal mol-1. It is likely here that single
H-shift is favored because in a dynamic equilibrium, the lower energy
isomer - CH2OH2+ - is likely to dominate. Moreover,
even if exchange of the protons occurs, the ionized methanol,
unlike protonated methanol, is not likely to reform neutral
methanol. Thus, if we start with a deuterated isotopomer such as
CH3OD and ionize it to CH3OD+, whether the ion can
partially convert to CH2DOH+ does not
mean that the new ion can lead to the production of the isomeric
pair CH2DOH. Remember that recombination of ions with electrons
is dissociative in nature.
Now let us consider what types of reactions
can help to exchange protons/deuterons. It is important to remember
here that energized species in the low density interstellar medium
will typically radiate their internal
energy before undergoing subsequent reactions, so that we need
consider only thermal reactants.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{0762fig3.eps}
\end{figure}](/articles/aa/full/2004/27/aa0762/Timg20.gif) |
Figure 3:
Transition state structures for studied reactions calculated at the
B3LYP/6-311G(d, p) level, except for TS1, which is calculated at the HF/6-311G(d, p) level. Bond distances are in Å and bond angles are in degrees. |
| Open with DEXTER |
Transition state structures for the reactions discussed in this section are to be found in
Fig. 3, although some of the transition states including the hydrogen abstraction reaction of methanol by H atoms (TS4 and TS5) have already been studied by several authors (Lendvay et al. 1997; Jodkowski et al. 1999).
The reaction between atomic H
and neutral methanol has actually been studied in the laboratory,
where a variety of different products are formed, all with moderate
activation energy barriers (see the NIST chemical kinetics database at http://kinetics.nist.gov/index.php). In Fig. 4, we show a
variety of calculated pathways for the reaction including simple exchange.
Barriers with associated transition states (TS1-TS6) are found for
all reactions. There are two transition states for H-H exchange: TS1 and TS3. TS1 lies
20.3 kcal mol-1 above the reactants while
TS3 lies 40.4 kcal mol-1 above, so that
exchange does not occur under thermal interstellar conditions via either of these pathways. Moreover, neither H-H exchange is of interest for isotopic problems because both involve exchange of one type of proton: TS1 on the O-end and TS3 on the C-end of methanol!
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0762fig4.eps}
\end{figure}](/articles/aa/full/2004/27/aa0762/Timg21.gif) |
Figure 4:
Potential energy surfaces of the reactions between CH3OH and
H atoms calculated with the CCSD(T)/aug-cc-pVTZ method. The energy of TS1
(dashed line) is calculated with CCSD(T) method at the geometry
obtained with the HF/6-311G(d, p) method. The values in parentheses are
the relative energies obtained with the B3LYP/6-311G(d, p) method. |
| Open with DEXTER |
We have also examined the possibility of a hydrogen exchange
reaction between H and protonated methanol. Figure 5
shows the schematic potential profile both for reaction and for
exchange. The energy of the transition state TS8 for hydrogen
exchange is calculated to be 48.6 kcal mol-1, so that once
again, exchange cannot take place in the interstellar medium.
Moreover, the exchange occurs fully on the oxygen end of the
molecule, and so once again is useless for exchanging protons from
different ends of the molecule. Although the energy barriers for hydrogen abstraction reactions (TS10 and TS11) are lower than that for hydrogen exchange, they are also high enough to impede reaction under interstellar conditions.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0762fig5.eps}
\end{figure}](/articles/aa/full/2004/27/aa0762/Timg22.gif) |
Figure 5:
Potential energy surfaces of the reaction between
CH3OH2+
and H atoms calculated with the CCSD(T)/aug-cc-pVTZ method. The values in
parentheses are the relative energies obtained with the B3LYP/6-311G(d, p)
method. |
| Open with DEXTER |
Finally, consider the exothermic reaction between the methanol ion and atomic hydrogen:
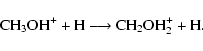 |
(5) |
If the reaction occurs by a single H-shift mechanism in which the H atom acts as a very limited chaperone, there is a significant barrier of 25.1 kcal mol-1, which is essentially the barrier for unimolecular isomerization. Another possibility is the barrierless formation of protonated methanol followed by a barrierless H atom elimination leading to the products shown. Barrierless dissociation into the fragments CH3+ + H2O may also occur. Whatever the final products, there is insufficient energy available for H-H exchange to occur over a transition state during the lifetime of the protonated methanol complex.
Figure 6 shows the schematic potential energy surfaces
for the ground electronic states of protonated methanol and its neutralized species
(CH3OH2) relevant for dissociative recombination.
As can be seen, the structure for protonated methanol
(CH3OH2+ ) is located at a very deep minimum, while
the neutralized species with the same structure does
not occur at a potential minimum although it lies considerably below the
potential minimum of the ion. In order for dissociative recombination to
occur at a rapid rate, either an excited repulsive potential surface of
CH3OH2 must intersect the ionic potential around its minimum
(the so-called "direct'' mechanism) or the ion must initially
cross over to excited Rydberg states of the neutral species,
which then cross repulsive neutral
states (the so-called "indirect'' mechanism) (Guberman 2003).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0762fig6.eps}
\end{figure}](/articles/aa/full/2004/27/aa0762/Timg24.gif) |
Figure 6:
Potential energy surfaces of CH3OH2+
( upper curve) and its neutralized species ( lower curve) calculated by using
the CCSD(T)/aug-cc-pVTZ method at the optimized geometries obtained
with the B3LYP/6-311G(d, p) method. The relative energies are shown in
kcal mol-1. The values in
parentheses are the calculated relative energies with the
B3LYP/6-311G(d, p) method. Bond distances are in Å and bond angles are in degrees. |
| Open with DEXTER |
When an electron recombines with protonated methanol, the
neutralized species is calculated to lie 106.1 kcal mol-1 below
CH3OH2+ neglecting any small kinetic energy for the incident
electron, as shown in Fig. 6. This ground neutral state is not accessed directly since it does not cross the ionic state near its minimum. Nevertheless, it and excited valence states of CH3OH2 are repulsive and can be accessed via the indirect mechanism. The
CH3OH2 species subequently slips down toward the exothermic products
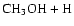 or
or
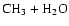 along the O-H and C-O bond
dissociation pathways, respectively. Since re-ionization ("auto-ionization'') of the parent neutral species can occur on a rapid time scale if a chemical bond is not broken even more quickly, it is obvious that a large fraction of the energy of reaction must go into the relative translational energy of the separating products. It is this necessity that limits the amount of internal vibrational energy that can accumulate in the products.
Nevertheless, since the exothermicities for these two sets of products are extremely
large, secondary bond dissociation might occur during the course of reaction. This type of dissociation is distinct from dissociation of energized methanol after reaction. Table 2
shows the energetically possible primary and secondary dissociation products of
CH3OH2+ + e-. Of the primary products, the lowest energy fragments are
CH3 + H2O. Of the secondary channels, the most
important probably involve elimination of a second hydrogen atom.
Because the energies of CH3O + 2H and CH2OH + 2H are only 32.5 and
40.6 kcal mol-1 below
the energy of CH3OH2+ + e-, and because
the neutralized
CH3OH2 moves rapidly on the repulsive surface towards O-H bond rupture,
the elimination of a
second hydrogen atom from CH3OH seems to be improbable, but
cannot be ruled out in the absence of detailed dynamical calculations
given the number of storage ring measurements
showing the preponderance of three-body channels (see, e.g.,
Semaniak et al. 1998). The formation of a hydrogen molecule from
CH3OH2+ + e- is energetically favorable, as
shown in Table 2, but this process is only possible when a
departing hydrogen atom from neutralized protonated methanol
abstracts a second hydrogen atom of methanol, which is dynamically
very unlikely. Most of the other exothermic fragments shown in Table 2 require significant rearrangements and do not appear to be
possible.
along the O-H and C-O bond
dissociation pathways, respectively. Since re-ionization ("auto-ionization'') of the parent neutral species can occur on a rapid time scale if a chemical bond is not broken even more quickly, it is obvious that a large fraction of the energy of reaction must go into the relative translational energy of the separating products. It is this necessity that limits the amount of internal vibrational energy that can accumulate in the products.
Nevertheless, since the exothermicities for these two sets of products are extremely
large, secondary bond dissociation might occur during the course of reaction. This type of dissociation is distinct from dissociation of energized methanol after reaction. Table 2
shows the energetically possible primary and secondary dissociation products of
CH3OH2+ + e-. Of the primary products, the lowest energy fragments are
CH3 + H2O. Of the secondary channels, the most
important probably involve elimination of a second hydrogen atom.
Because the energies of CH3O + 2H and CH2OH + 2H are only 32.5 and
40.6 kcal mol-1 below
the energy of CH3OH2+ + e-, and because
the neutralized
CH3OH2 moves rapidly on the repulsive surface towards O-H bond rupture,
the elimination of a
second hydrogen atom from CH3OH seems to be improbable, but
cannot be ruled out in the absence of detailed dynamical calculations
given the number of storage ring measurements
showing the preponderance of three-body channels (see, e.g.,
Semaniak et al. 1998). The formation of a hydrogen molecule from
CH3OH2+ + e- is energetically favorable, as
shown in Table 2, but this process is only possible when a
departing hydrogen atom from neutralized protonated methanol
abstracts a second hydrogen atom of methanol, which is dynamically
very unlikely. Most of the other exothermic fragments shown in Table 2 require significant rearrangements and do not appear to be
possible.
What about the possibility that H-atom exchange can occur before
CH3OH2 dissociates? Since the dissociation to methanol and H
occurs rapidly, the
chance that protons from the C- and O-ends can exchange before the
formation of products is remote given the complexity of the mechanism.
To quantify this conjecture, we can crudely use the expression in Eq. (3), making the additional assumption that the departing H atom does
not change the energetics of the exchange. The result for the rate
of exchange is so much slower than the rate of dissociation of
CH3OH2, which occurs on the time scale of a vibrational
period, that H-atom exchange cannot occur.
Finally, we can use the calculated potential surface for the protonated ion to consider exchange via the reaction between H+ and neutral methanol assuming that it proceeds via the protonated methanol complex. This complex will dissociate to charge exchange products, to CH2OH2+ + H, and to other fragments. During the time that the complex exists, there is a finite chance that exchange can take place, because the transition state for synchronous exchange, labeled "H-H exchange TSH+'' in Fig. 1, lies about 30 kcal mol-1 below the energy of reactants. Nevertheless, there is no transition state barrier to charge exchange, and products such as CH3OH+ + H and CH2OH2+ + H lie considerably below the transition state for synchronous exchange in the protonated methanol complex. So, it is most likely that H-H exchange does not occur during reaction, and that even if it does, the products will not lead directly to neutral methanol.
Table 2:
Relative energies (kcal mol-1) of the possible exothermic products of
CH3OH2+ + e- .
Observations in the well-studied protostellar source IRAS 16293-2422
show that there is significantly more CH2DOH than CH3OD,
perhaps as much as 15 times more (Parise et al. 2004), as shown in Table 3, which also contains less dramatic results for the Orion Compact Ridge (OCR). Indeed, there
appears to be more CHD2OH than CH3OD in IRAS 16293-2422, while in the Orion Compact Ridge, on the other hand, the two singly deuterated isotopomers of methanol are of similar abundance.
Table 3:
Observations.
Although it is thought that the granular synthesis of CH2DOH is
somewhat more efficient than that of CH3OD (Charnley et al. 1997;
Caselli et al. 2002; Stantcheva & Herbst 2003), a differential rate of
depletion is also needed to reproduce the large asymmetry between the
two in IRAS 16293-2422. So let us consider the relative destruction rates of
CH3OD and CH2DOH. Let us assume that protonation to form
CH3OHD+ and CH2DOH2+ occurs competitively.
Following protonation, the dissociative recombination pathways that lead back
to a methanol
structure and an atom can produce the following isotopically distinct
products:
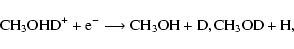 |
(6) |
and
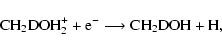 |
(7) |
where we have utilized our analysis that D-H exchange between the C- and O-ends of the methanol skeleton is inefficient during and after reaction.
Thus, we see that there is an
asymmetry built into the depletion: CH3OD can be destroyed via
the mechanism whereas CH2DOH cannot be. This asymmetry was
first recognized by Charnley et al. (1997) in their study of methanol
deuteration in the Orion Compact Ridge. Of course, the importance of
this asymmetry depends upon how large the methanol product
channel is in the dissociative recombination of protonated methanol,
and how competitive the CH3OH + D channel is compared with the
CH3OD + H channel. In other studies, it has been shown that the
removal of an H atom can be more efficient than that of a D atom
(Jensen et al. 2000).
Table 4:
Initial conditions based mainly on a grain-surface chemistry model with an accreting D/H ratio of 0.3.
We have run some new protostellar models, starting
immediately after the loss of grain mantles, to determine how
severe the abundance gradients between pairs of deuterated
isotopomers of methanol can become. A new gas-phase
model that contains multiply deuterated species and an expanded
number of chemical reactions has been used (Roberts et al. 2003).
The network does not contain processes in which D and H atoms on methanol-type isotopomers can exchange. The initial
fractional abundances of some normal species and the ratios of
deuterated isotopomers to these normal species are listed in Table 4. These
initial abundances derive from a gas-phase plus accretion model for
the cold (10 K) pre-protostellar phase, which is run until
everything that can do so is frozen onto the grains (Roberts et al. 2003).
Additional amounts of water, formaldehyde, methanol, and H2S
were added to account for surface chemistry, which is not considered
in the model of Roberts et al. (2003).
The initial fractionation ratios
utilized derive from our gas-phase plus accretion model and the grain model of Stantcheva & Herbst (2003) with a
gas-phase atomic deuterium-to-hydrogen ratio of 0.3. Initially, we assume that the
temperature of both the gas and the dust
after evaporation is 50 K, and the gas density is 106 cm-3.
Species are assumed to evaporate via thermal desorption, using
desorption energies from Hasegawa & Herbst (1993) and Aikawa et al. (1997).
Figure 7 shows the results for the ratios of the
deuterated isotopomers to normal methanol as functions of time. It
can be seen that the ratio for CH3OD declines more strongly over
the first
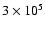 yr than does the ratio for CH2DOH.
Similarly, the ratio for CH2DOD declines more precipitously than
does the ratio for CHD2OH, while that for CHD2OD declines
more rapidly than that for CD3OH. Thus, it can be seen that
the effect discussed in the body of the paper is making its presence known in
the overall chemistry. Eventually all fractionation ratios decline
since fractionation at a temperature of 50 K is nowhere near as large
an effect as the initial ratios. Those methanol isotopomers with the deuterium in the methyl group (CH2DOH, CHD2OH, CD3OH), however, are still fractionated via the methyl ions CH2D+, CHD2+ and CD3+. The exchange reactions between these ions and HD are endothermic in the reverse direction by
yr than does the ratio for CH2DOH.
Similarly, the ratio for CH2DOD declines more precipitously than
does the ratio for CHD2OH, while that for CHD2OD declines
more rapidly than that for CD3OH. Thus, it can be seen that
the effect discussed in the body of the paper is making its presence known in
the overall chemistry. Eventually all fractionation ratios decline
since fractionation at a temperature of 50 K is nowhere near as large
an effect as the initial ratios. Those methanol isotopomers with the deuterium in the methyl group (CH2DOH, CHD2OH, CD3OH), however, are still fractionated via the methyl ions CH2D+, CHD2+ and CD3+. The exchange reactions between these ions and HD are endothermic in the reverse direction by  370 K, which means that fractionation via this route is efficient at temperatures up to
370 K, which means that fractionation via this route is efficient at temperatures up to  60 K (see e.g., Roberts & Millar 2000a).
60 K (see e.g., Roberts & Millar 2000a).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.1cm,clip]{0762fig7.ps}
\end{figure}](/articles/aa/full/2004/27/aa0762/Timg33.gif) |
Figure 7:
Fractionation ratios of deuterated methanols to normal methanol
plotted vs.
time for a protostellar source. Lines in black are for the observed species. T=50 K,
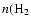 ) = 106 cm-3. ) = 106 cm-3. |
| Open with DEXTER |
When compared with the methanol observations of IRAS 16293-2422,
the model yields excellent agreement at a time of 105 yr,
with the differences between computed and observed
fractionation ratios for deuterated methanols within or very close
to the observed uncertainties. Unfortunately, this timescale is five times longer than the age of the IRAS 16293-2422 protostar, as estimated by Ceccarelli et al. (2001). How can the rate of the chemistry be speeded up under these physical conditions? Increasing the density usually decreases the timescale for the chemistry, but in the case of hot-core chemistry, the gas is initially neutral and so the abundances of the species do not change much after evaporation until the abundance of molecular ions has built up. Because increasing the density reduces the ionisation fraction, it does not speed up the chemistry significantly. The most effective way to do that is to increase the cosmic ray ionisation rate (Hatchell et al. 1998). An increase in the cosmic ray ionisation rate from
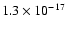 s-1 to one order of magnitude greater does indeed have the desired effect; reasonable agreement with observations now occurs after a few
s-1 to one order of magnitude greater does indeed have the desired effect; reasonable agreement with observations now occurs after a few  104 yr. Support for a high ionisation rate in IRAS 16293-2422 is also provided by the detailed chemical model of Doty et al. (2004), which, however, does not contain deuterium fractionation.
104 yr. Support for a high ionisation rate in IRAS 16293-2422 is also provided by the detailed chemical model of Doty et al. (2004), which, however, does not contain deuterium fractionation.
But IRAS 16293-2422 is a complex source with evidence for a "hot-core'' region within 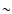 150 AU of the central object where
150 AU of the central object where
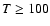 K and
K and
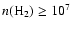 cm-3 (Ceccarelli et al. 2000; Schöier et al. 2002). Ceccarelli et al. (2001) have derived an H2CO abundance profile with two jumps: one at
cm-3 (Ceccarelli et al. 2000; Schöier et al. 2002). Ceccarelli et al. (2001) have derived an H2CO abundance profile with two jumps: one at 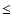 700 AU, where the dust temperature reaches 50 K, and one at
700 AU, where the dust temperature reaches 50 K, and one at 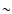 150 AU where
150 AU where
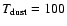 K, while Schöier et al. (2002) have calculated that the methanol abundance jumps by a factor of
K, while Schöier et al. (2002) have calculated that the methanol abundance jumps by a factor of 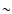 1000 in the hot core region, compared with the cooler, less dense envelope.
1000 in the hot core region, compared with the cooler, less dense envelope.
We have also, therefore, run the model at a temperature of 100 K and a density of 107 cm-3 in order to simulate conditions within the hot-core region. For times greater than a few times 104 yr, the methanol abundance in the gas-phase is calculated to be very similar to that derived by Schöier et al. (2002) in the hot-core region of IRAS 16293-2422 (
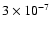 ). The fractionation results are shown in Fig. 8. At early times, there is little change in the gas-phase fractionation.
Interestingly, we now see the opposite effect to that which we would expect: at times greater than 105 yr the relative abundance of those methanol species with an OD group actually increases, and these enhanced abundances last until almost 106 yr have passed. The reason for this effect is that at temperatures above 80 K, all of the surface water evaporates during the first 105 yr, whereas at 50 K the bulk of the water remains frozen. In the model run at 100 K, therefore, protonation of H2O and HDO in the gas-phase leads to H3O+ and H2DO+, and the high initial HDO/H2O ratio (from the surface chemistry; see Table 4) leads to a high H2DO+/H3O+ ratio in the gas. This high ratio, in turn , leads to additional fractionation throughout the reaction network. Based on the quantum chemical results discussed in this paper, only the methanol isotopomers with OD groups, however, are enhanced. As can be seen in Fig. 8, the CH3OD fractionation is, obviously, much larger than that observed by Parise et al. (2003) in IRAS 16293-2422, and the predicted D2CO fractionation is lower than that observed by Ceccarelli et al. (2001) in this source. On the other hand, perhaps this model is appropriate for the Orion Compact Ridge,
where the temperature is at least 70 K, and the H2O abundance is
). The fractionation results are shown in Fig. 8. At early times, there is little change in the gas-phase fractionation.
Interestingly, we now see the opposite effect to that which we would expect: at times greater than 105 yr the relative abundance of those methanol species with an OD group actually increases, and these enhanced abundances last until almost 106 yr have passed. The reason for this effect is that at temperatures above 80 K, all of the surface water evaporates during the first 105 yr, whereas at 50 K the bulk of the water remains frozen. In the model run at 100 K, therefore, protonation of H2O and HDO in the gas-phase leads to H3O+ and H2DO+, and the high initial HDO/H2O ratio (from the surface chemistry; see Table 4) leads to a high H2DO+/H3O+ ratio in the gas. This high ratio, in turn , leads to additional fractionation throughout the reaction network. Based on the quantum chemical results discussed in this paper, only the methanol isotopomers with OD groups, however, are enhanced. As can be seen in Fig. 8, the CH3OD fractionation is, obviously, much larger than that observed by Parise et al. (2003) in IRAS 16293-2422, and the predicted D2CO fractionation is lower than that observed by Ceccarelli et al. (2001) in this source. On the other hand, perhaps this model is appropriate for the Orion Compact Ridge,
where the temperature is at least 70 K, and the H2O abundance is 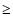 10-5 (Wright et al. 1997). Of course, a better model for the Orion Compact Ridge would have to start with lower fractionation ratios for the methanol isotopomers.
10-5 (Wright et al. 1997). Of course, a better model for the Orion Compact Ridge would have to start with lower fractionation ratios for the methanol isotopomers.
The high abundances of gaseous water and HDO in the 100 K model are clearly important
in leading to the very different result from our 50 K model.
But are they reasonable for IRAS 16293-2422? Between 1000 and 105 yr,
the H2O fractional
abundance from the model exceeds
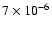 ,
whereas Ceccarelli et al. (2000) determine the fractional abundance at the centre of IRAS 16293-2422 to be 3
,
whereas Ceccarelli et al. (2000) determine the fractional abundance at the centre of IRAS 16293-2422 to be 3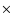 10-6. Also, searches for solid HDO have put its abundance <0.2-2% of H2O (Dartois et al. 2003; Parise et al. 2003), so we have investigated lowering both the initial abundance and fractionation of water on the grains.
In particular, we have run a model where the initial abundances of three species (water, formaldehyde, and methanol) are constrained by observations towards the centre of IRAS 16293-2422, as shown in Table 5. In addition, the initial fractionation of water has been lowered, while that of D2CO has been increased to the highest ratio observed by Ceccarelli et al. (2001) in the envelope.
10-6. Also, searches for solid HDO have put its abundance <0.2-2% of H2O (Dartois et al. 2003; Parise et al. 2003), so we have investigated lowering both the initial abundance and fractionation of water on the grains.
In particular, we have run a model where the initial abundances of three species (water, formaldehyde, and methanol) are constrained by observations towards the centre of IRAS 16293-2422, as shown in Table 5. In addition, the initial fractionation of water has been lowered, while that of D2CO has been increased to the highest ratio observed by Ceccarelli et al. (2001) in the envelope.
Table 5:
Altered initial abundances and fractionations for the "hot-core'' region of IRAS 16293-2422.
With the new initial abundances, after 104 yr, the abundances of H2O and CH3OH are very similar to those observed (
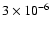 and
and
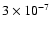 ,
respectively), while the abundance of H2CO is within a factor of two of the observation.
Results for the fractionation are shown in Fig. 9, where it can be seen that the lower initial abundances of H2O and HDO have removed the peaks in fractionation of CH3OD et al., seen in Fig. 8 at 105-106 yr. Still, the new results show the fractionation ratio for CH3OD to remain roughly constant until 106 yr. This result stems from the fact that
there is still
,
respectively), while the abundance of H2CO is within a factor of two of the observation.
Results for the fractionation are shown in Fig. 9, where it can be seen that the lower initial abundances of H2O and HDO have removed the peaks in fractionation of CH3OD et al., seen in Fig. 8 at 105-106 yr. Still, the new results show the fractionation ratio for CH3OD to remain roughly constant until 106 yr. This result stems from the fact that
there is still 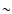 4 times more water in the gas-phase than in the first model run at 50 K. Thus, at
4 times more water in the gas-phase than in the first model run at 50 K. Thus, at
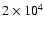 yr (the probable age of the IRAS 16293-2422 protostar) the CH2DOH, CHD2OH and CD3OH relative abundances are in agreement with the observations of Parise et al. (2003), but CH3OD is 4.5 times higher. For D2CO, despite its high initial abundance, the fractionation is still somewhat low.
yr (the probable age of the IRAS 16293-2422 protostar) the CH2DOH, CHD2OH and CD3OH relative abundances are in agreement with the observations of Parise et al. (2003), but CH3OD is 4.5 times higher. For D2CO, despite its high initial abundance, the fractionation is still somewhat low.
In fact, the timescale for the chemistry may be even shorter in the hot-core region, since, with the assumption of a free-fall velocity, the transit time for grains and molecules through the central 150 AU region is only 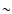 300 yr (Schöier et al. 2002). This does not give sufficient time for much processing of the material evaporated from the grains to take place, so that our predictions are essentially the initial evaporated abundances which, for the deuterated methanols, are not too different from the results at
300 yr (Schöier et al. 2002). This does not give sufficient time for much processing of the material evaporated from the grains to take place, so that our predictions are essentially the initial evaporated abundances which, for the deuterated methanols, are not too different from the results at
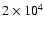 yr. On the other hand, the abundance of D2CO is much higher, and in better agreement with observation. In their recent survey of IRAS 16293, however, Cazaux et al. (2003) found significant amounts of complex O- and N-bearing species. When compared with the models of Rodgers & Charnley (2001), this finding implies that the injected material has been processed over a timescale of
yr. On the other hand, the abundance of D2CO is much higher, and in better agreement with observation. In their recent survey of IRAS 16293, however, Cazaux et al. (2003) found significant amounts of complex O- and N-bearing species. When compared with the models of Rodgers & Charnley (2001), this finding implies that the injected material has been processed over a timescale of 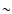
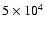 yr, although the timescale in chemical models of hot cores is sensitive to the cosmic ray ionisation rate (Hatchell et al. 1998).
yr, although the timescale in chemical models of hot cores is sensitive to the cosmic ray ionisation rate (Hatchell et al. 1998).
Given all of these complications, it is obvious that IRAS 16293-2422 is too complex a source for the relatively simple one-point models discussed here. More detailed models are clearly necessary, in which we will have to consider both the hot core and its envelope with at least a two-phase approach (see, e.g., Doty et al. 2004). Currently, we can only state that our best explanation of the observations of the deuterated isotopomers of methanol in IRAS 16293-2422 is that much of the methanol emission is coming from the region outside 150 AU.
A further test of
the importance of differential depletion rates can be made
when the spectrum of CH2DOD over a useful
frequency range is measured in the laboratory, a task currently being
pursued at Ohio State. If the model shown in Fig. 7 is
correct, the fractionation
ratio of this doubly deuterated species will be significantly less
than that of CHD2OH, but still large enough (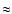 0.02) that
CH2DOD should be detectable.
0.02) that
CH2DOD should be detectable.
Acknowledgements
This research was partly supported by grants-in-aid for Scientific
Research on Priority Areas from the
Ministry of Education, Science, and Culture, Japan. Most of the quantum
chemical calculations were carried out using the computer center of the
Institute for Molecular Science, Japan.
The Astrochemistry Program at The Ohio State University is supported
by The National Science Foundation (US).
- Adams, N. G., &
Babcock, L. M. 1994, ApJ, 434, 184 [NASA ADS] [CrossRef] (In the text)
- Aikawa, Y., Umebayashi,
T., Nakano, T., & Miyama, S. M. 1997, ApJ, 486, L52 [NASA ADS] (In the text)
- Bacmann, A., Lefloch, B.,
Ceccarelli, C., et al. 2003, ApJ, 585, L55 [NASA ADS] [CrossRef] (In the text)
- Bates, D. R. 1993, MNRAS,
263, 369 [NASA ADS] (In the text)
- Butler, J. N.,
Babcock, L. M., & Adams, N. G. 1997, Mol. Phys., 91, 81 [NASA ADS] [CrossRef] (In the text)
- Caselli, P., Stantcheva,
T., Shalabiea, O., Shematovich, V. I., & Herbst, E. 2002,
P&SS, 50, 1257 [NASA ADS] (In the text)
- Cazaux, S., Tielens, A.
G. G. M., Ceccarelli, C., et al. 2003, ApJ, 593, L54 [NASA ADS] (In the text)
- Ceccarelli, C., Loinard,
L., Castets, A., Tielens, A. G. G. M., & Caux, E. 2000,
A&A, 357, L9 [NASA ADS] (In the text)
- Ceccarelli, C., Loinard,
L., Castets, A., et al. 2001, A&A, 372, 998 [EDP Sciences] [NASA ADS] (In the text)
- Ceccarelli, C., Vastel,
C., Tielens, A. G. G. M., et al. 2002, A&A, 381, L17 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Charnley, S. B., Tielens,
A. G. G. M., & Rodgers, S. D. 1997, ApJ, 482, L203 [NASA ADS] [CrossRef] (In the text)
- Dartois, E., Thi,
W.-F., Geballe, T. R., et al. 2003, A&A, 399, 1009 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Doty, S. D.,
Schöier, F. L., & van Dishoeck, E. F. 2004, A&A, 418,
1021 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Dunning, Jr. T. H. 1989,
J. Chem. Phys., 90, 1007 [NASA ADS] [CrossRef] (In the text)
- Frisch, M. J., et
al. 1998, Gaussian 98, Revision A.11 (Pittsburgh: Gaussian)
(In the text)
- Guberman, S. L. 2003,
Dissociative Recombination of Molecular Ions with Electrons
(Dordrecht: Kluwer)
(In the text)
- Hasegawa, T. I., &
Herbst, E. 1993, MNRAS, 261, 83 [NASA ADS] (In the text)
- Hatchell, J., Thompson,
M. A., Millar, T. J., & MacDonald, G. H. 1998, A&A, 338,
713 [NASA ADS] (In the text)
- Herbst, E. 1982, Chem.
Phys., 65, 185 [NASA ADS] [CrossRef] (In the text)
- Herbst, E., Terzieva,
R., & Talbi, D. 2000, MNRAS, 311, 869 [NASA ADS] [CrossRef] (In the text)
- Herd, C. R., Adams, N. G.,
& Smith, D. 1990, ApJ, 349, 388 [NASA ADS] [CrossRef] (In the text)
- Holbroook, K. A.,
Pilling, M. J., & Robertson, S. H. 1996, Unimolecular Reactions
(New York: John Wiley)
(In the text)
- Jacq, T., Walmsley, C. M.,
Mauersberger, R., et al. 1993, A&A, 271, 276 [NASA ADS]
- Jensen, M. J., Bilodeau, R.
C., Safvran, C. P., et al. 2000, ApJ, 543, 764 [NASA ADS] [CrossRef] (In the text)
- Jodkowski, J. T., Rayez,
M.-T., Rayez, J.-C., Berces, T., & Dobe, S. 1999, J. Phys.
Chem. A, 103, 3750 [NASA ADS] [CrossRef] (In the text)
- Kline, J. M., &
Penner, S. S. 1982, Proc. Int. Symp. Shock Tubes Waves, 13,
869 [NASA ADS]
- Lendvay, G., Berces,
T., & Marta, F. 1997, J. Phys. Chem. A, 101, 1588 [NASA ADS] [CrossRef] (In the text)
- Mauersberger, R., Henkel,
C., Jacq, T., & Walmsley, C. M. 1988, A&A, 194, L1 [NASA ADS]
- Millar, T. J. 2003,
Space Sci. Rev., 106, 73 [NASA ADS] [CrossRef] (In the text)
- Parise, B., Ceccarelli,
C., Tielens, A. G. G. M., et al. 2002, A&A, 393, L49 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Parise, B., Simon, T.,
Caux, E., et al. 2003, A&A, 410, 897 [EDP Sciences] [NASA ADS] [CrossRef]
- Parise, B., Castets, A.,
Herbst, E., et al. 2004, A&A, 416, 159 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Roberts, H., &
Millar, T. J. 2000a, A&A, 361, 388 [NASA ADS] (In the text)
- Roberts, H., &
Millar, T. J. 2000b, A&A, 364, 780 [NASA ADS]
- Roberts, H., Herbst, E.,
& Millar, T. J. 2003, ApJ, 591, L41 [NASA ADS] [CrossRef] (In the text)
- Rodgers, S. D., &
Charnley, S. B. 2001, ApJ, 546, 324 [NASA ADS] [CrossRef] (In the text)
- Semaniak, J., Larson, A.,
Le Padellec, A., et al. 1998, ApJ, 498, 886 [NASA ADS] [CrossRef] (In the text)
- Schöier, F. L.,
Jorgensen, J. K., van Dishoeck, E. F., & Blake, G. A. 2002,
A&A, 390, 1001 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Smith, I. W. M. 1980,
Kinetics and Dynamics of Elementary Gas Reactions (London:
Butterworth)
(In the text)
- Stantcheva, T., &
Herbst, E. 2003, MNRAS, 340, 983 [NASA ADS] [CrossRef] (In the text)
- Tomashevsky, M., Herbst,
E., & Kraemer, W. P. 1998, ApJ, 498, 728 [NASA ADS] [CrossRef] (In the text)
- Turner, B. E. 1990, ApJ,
362, L29 [NASA ADS] [CrossRef]
- van Dishoeck, E. F.,
Blake, G. A., Jansen, D. J., & Groesbeck, T. D. 1995, ApJ, 447,
760 [NASA ADS] [CrossRef]
- Wright, M. C. H.,
Plambeck, R. L., & Wilner, D. J. 1996, ApJ, 469, 216 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2004
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0762fig1.eps}
\end{figure}](/articles/aa/full/2004/27/aa0762/Timg2.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0762fig2.eps}
\end{figure}](/articles/aa/full/2004/27/aa0762/Timg3.gif)
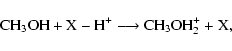
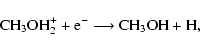
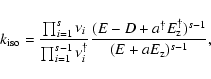
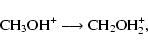
![\begin{figure}
\par\includegraphics[width=10cm,clip]{0762fig3.eps}
\end{figure}](/articles/aa/full/2004/27/aa0762/Timg20.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0762fig4.eps}
\end{figure}](/articles/aa/full/2004/27/aa0762/Timg21.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0762fig5.eps}
\end{figure}](/articles/aa/full/2004/27/aa0762/Timg22.gif)
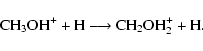
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0762fig6.eps}
\end{figure}](/articles/aa/full/2004/27/aa0762/Timg24.gif)
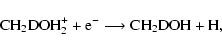
![\begin{figure}
\par\includegraphics[angle=-90,width=8.1cm,clip]{0762fig7.ps}
\end{figure}](/articles/aa/full/2004/27/aa0762/Timg33.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{0762fig8.ps}
\end{figure}](/articles/aa/full/2004/27/aa0762/Timg42.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{0762fig9.ps}
\end{figure}](/articles/aa/full/2004/27/aa0762/Timg44.gif)