A&A 421, 1031-1043 (2004)
DOI: 10.1051/0004-6361:20034156
Synoptic study of the SMC SNRs using XMM-Newton
K. J. van der Heyden1,2 - J. A. M. Bleeker1 - J. S. Kaastra1
1 - SRON National Institute for Space Research, Sorbonnelaan 2,
3584 CA Utrecht, The Netherlands
2 -
South African Astronomical Observatory, PO Box 9,
Observatory 7935, Cape Town, South Africa
Received 4 August 2003 / Accepted 11 March 2004
Abstract
We present a detailed X-ray spectral analysis of 13 supernova remnants (SNR) in
the Small Magellanic Cloud (SMC). We apply both single-temperature
non-equilibrium
ionisation models and models based on the Sedov similarity solution, where
applicable. We also present detailed X-ray images of individual SNRs, which
reveal a range of different morphological features. Eight remnants,
DEM S 32, IKT 2, HFPK 419, IKT 6, IKT 16, IKT 18 and IKT 23, are
consistent with being in their Sedov evolutionary phase. IKT 6 and IKT 23 both
have a clear shell like morphology with oxygen-rich X-ray emitting material in
the centre. We draw attention to similarities between these two remnants and the
well studied, oxygen-rich remnant IKT 22 (SNR 0102-72.3) and propose that they
are more evolved versions of IKT 22. IKT 5, DEM S 128 and IKT 25 are
evolved remnants which are in, or in the process of entering, the radiative
cooling stage. The X-ray emission from these three remnants is possibly from
the ejecta remains of type Ia SNe. Our modeling allows us to derive
estimates for physical parameters, such as densities, ages, masses and initial
explosion energies. Our results indicate that the average SMC hydrogen density
is a factor of 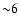 lower as compared to the Large Magellanic Cloud.
This has obvious implications for the evolution and luminosities of the SMC SNRs. We
also estimate the average SMC gas phase abundances for the elements O, Ne, Mg, Si
and Fe.
lower as compared to the Large Magellanic Cloud.
This has obvious implications for the evolution and luminosities of the SMC SNRs. We
also estimate the average SMC gas phase abundances for the elements O, Ne, Mg, Si
and Fe.
Key words: shock waves - ISM: supernova remnants - X-rays: ISM - galaxies: Magellanic
Clouds
The low interstellar absorption and relative closeness of the Large and Small
Magelanic Clouds (LMC and SMC) allows for the study of individual X-ray sources
in these
galaxies. For supernova remnants (SNRs) in particular, the low absorption makes
it possible to detect X-rays in the important 0.5-3.0 keV energy band, which
includes emission lines from highly ionised elements such as O, Ne, Mg, Si, S
and Fe. The well known distance to the SMC,
i.e. 60 kpc (Westerland 1990),
allows for good estimates of quantities such as physical size, mass, age and so on.
While the LMC SNRs have been relatively well studied, the remnants in the SMC
have
not received much attention. For example, Hughes et al. (1998)
conducted a systematic study of ASCA-SIS spectra of 7 SNRs in the LMC, while
Nishiuchi (2001) analysed 9 fainter remnants. They were able to
derive good estimates for the physical parameters of individual SNRs.
In contrast, while individual or small samples of SNRs in the SMC have
been studied (e.g. Mathewson et al. 1983, 1984;
Yokogawa et al. 2002; Hughes & Smith 1994; Nazé
et al. 2002), a detailed synoptic X-ray spectral study has not been carried
out.
This is mainly because SNRs in the SMC are fainter than their LMC counterparts.
To date a total of 16 SNRs have been identified from a number of extensive
X-ray
surveys with the instruments aboard the Einstein, ASCA and
ROSAT Observatories (e.g., Inoue et al. 1983; Wang &
Wu 1992; Haberl et al. 2000). The availability of the Chandra and XMM-Newton Observatories now provides an opportunity to study these remnants
with far greater sensitivity and spatial/spectral resolution than before.
We present XMM-Newton observations of 13 SNRs in the SMC.
Three remnants, viz. SNR 0039-73.9 (Filipovic et al. 1998),
SNR 0050-72.8 and SNR 0058-71.8 (last two both Mathewson et al. 1984),
have not yet been covered by the XMM-Newton SMC observation
fields and are
thus not included in this paper.
The major emphasis of this
work is on the spectral analysis of the CCD-resolution data obtained with the
European Photon Imaging Cameras (EPIC) (Turner et al. 2001;
Strüder
et al. 2001). In addition, we also present high resolution spectra of
IKT 22 and IKT 23 as measured by the Reflection Grating Spectrometers (RGS)
(den Herder et al. 2001).
Our data are extracted from five pointings towards the SMC. The log of the
observations are given in Table 1. The pointings, as listed in Table 1, are
centred on the remnants IKT 5, IKT 18, IKT 23 and IKT 22 respectively.
The raw EPIC data were initially processed with the XMM-Newton Science Analysis
System (SAS) version 5.4. This involved the subtraction of hot, dead, or
flickering pixels, and the removal of events due to electronic noise. The
spectra were extracted using the SAS task evselect. We used the
standard
redistribution matrices available on the VILSPA site, while the ancillary
matrices were
created
using the SAS task arfgen. Background subtraction was done by selecting
blank
sky regions within the same observation.
Mosaic images of the SMC fields were created using our own image and mosaicing
software. The image extraction programme selects the photons with
the appropriate grades and quality flags and saves the images in FITS file
format. The latter is necessary in order to use the standard SAS
eexpmap
programme
to make exposure maps for each extracted image. eexpmap produces
exposure maps normalized to the on axis exposure time, so each exposure map
was multiplied with the appropriate EPIC-pn or EPIC-MOS effective area by the
mosaicing
programme. The routines were called from a script that applied those programmes
to
each event-list and each channel range.
We also have high resolution spectra of IKT 22 and IKT 23 in addition to the
CCD-resolution spectra. RGS spectra of IKT 22 and IKT 23 were obtained with
effective exposure times of 70 and 37 ks respectively. The RGS data were
processed with SAS version 5.4.
Table 1:
XMM-Newton EPIC observation log. The abbreviations used are: EF - Extended
Full Frame , FF - Full Frame , LW - Large Window, T - Thin Filter, M - Medium Filter.
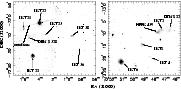 |
Figure 1:
Mosaic images of the SMC region in the 0.5-3.0 keV energy band. The
left image is the combined
observations of XMM-Newton Rev's 157, 247 and 433, while the right panel is an image
of Rev 156. Individual remnants are indicated. The out-of-time events from IKT 22 can be seen. |
| Open with DEXTER |
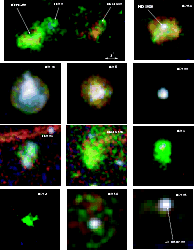 |
Figure 2:
Details of the remnants in our sample. Red, green and blue
represents the 0.5-0.7 keV, 0.7-1.0 and 1.0-3.0 keV energy bands. All the
images are on the same plate scale, as indicated in the upper left image. |
| Open with DEXTER |
In Fig. 1 we present a mosaic of our observations. The left image
is a mosaic of XMM-Newton revolutions 157, 247 and 433, while the right image shows the
southwestern part of the SMC (Rev 156). We are able to identify
13 SNRs in our field, these are indicated in Fig. 1
and listed in Table 1. All the remnants are quite soft X-ray
sources, with
the peak of their emission in the 0.5-1.0 keV band. A number of
point sources, which generally display much harder spectra than the remnants,
are also visible in
the field-of-view.
We present detailed colour coded maps of each remnant in Fig. 2.
It is clear from Fig. 2 that the remnants exhibit a range of different
morphological
features. The physical intepretation of these morphologies will be discussed in
more detail in Sect. 4.1.
The spectral analysis was performed using the SRON SPEX package (Kaastra et al. 1996), which contains the MEKAL atomic database (Mewe et al. 1995) for thermal emission. Also contained in SPEX are a
number of plasma models appropriate for SNR analysis.
We extracted spectra from the entire region of each SNR, while the background
spectra were taken from nearby blank-sky regions.
The extraction regions were constructed so as to exclude possible point
source contamination, where applicable. Broad band EPIC-pn count rates are given
are
given in Table 2. The estimated percentage point source or possible
residual point source
contamination (due to the XMM-Newton PSF) is also listed in Table 2.
The point source fluxes were estimated from the ROSAT HRI values.
The XMM-Newton fluxes were compatible with the ROSAT HRI ones.
The spectra of individual remnants are shown in Figs. 3
and 4. A typical background spectrum is also displayed in
Fig. 4. All our SNR spectra are thermal in nature and show
emission from highly ionised atoms of O, Ne, Mg, Si and Fe.
We first attempted to fit all the spectra with a single temperature
non-equilibrium ionisation (NEI) model. This assumes that the plasma has been
instantly shock-heated to a temperature 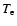 some time (t) ago. The
NEI model does not contain any dynamical model for SNR evolution. In this model
we fit the volume emission measure (
some time (t) ago. The
NEI model does not contain any dynamical model for SNR evolution. In this model
we fit the volume emission measure (
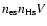 ), the electron
temperature (
), the electron
temperature (
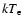 ), the ionisation parameter (
), the ionisation parameter (
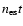 ), the
elemental abundances and the column density
), the
elemental abundances and the column density 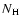 of absorbing gas along
the line of sight.
of absorbing gas along
the line of sight.
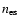 and
and
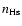 are the electron and hydrogen
density of the shocked gas, respectively and V is the volume of emitting gas.
Both IKT 21 and IKT 25 have point sources in the field which could not
be unambiguously excluded in the spectrum extraction.
Here we have added power-law components to account for the point emission.
are the electron and hydrogen
density of the shocked gas, respectively and V is the volume of emitting gas.
Both IKT 21 and IKT 25 have point sources in the field which could not
be unambiguously excluded in the spectrum extraction.
Here we have added power-law components to account for the point emission.
During the fitting procedure we initially kept the abundances fixed at the mean
SMC ISM value of 0.2 solar (Russel & Dopita 1992). We started by
allowing only the normalisations of the plasma components to vary and
subsequently we
also allowed the temperature, ionisation age, absorption and abundances (where
necessary) to vary. The spectra from EPIC-pn and EPIC-MOS were fitted simultaneously,
but sparately.
The results of the fits are given in Table 3. The abundances are
all relative to their solar values (Anders & Grevese 1989). We give
the unabsorbed luminosities in the 0.5-2.0 keV band.
We also estimated the electron density and radiating mass based on the best-fit
emission measure. Here it is provisionally assumed that the emitting gas is
confined to shells of a typical thickness R/12. The radii were estimated from
the X-ray images. The
mass estimates indicate that most of the sources are evolved remnants that
have swept-up a considerable amount of mass and should thus be emitting in
their
Sedov phases. Moreover, a number of remnants could not be adequately described
by the simple NEI model, in particular, the spectra with higher statistics
(viz., IKT 6, IKT 22, IKT 23). These spectra appear to show an ionisation and/or
temperature distribution. We thus consider a Sedov model to be the most
appropriate for fitting the data. This model is based on the
Sedov solution (Sedov 1959) which describes the self-similar expansion
of an adiabatic blast wave in a homogeneous medium.
Table 2:
Log of the SNRs in our field.
We proceed to fit the IKT 6, IKT 18, IKT 22 and IKT 23 spectra with a Sedov
model, based on unacceptable
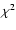 's and large swept-up mass,
obtained from the NEI model fits. IKT 6 and IKT 23 have a shell and centrally
filled morphology. We extract and fit only the shell part of the spectra of
these two remnants with a Sedov model.
The Chandra data reveal that IKT 22 has
a blastwave and reverse shock structure (Hughes et al. 2000),
however, XMM-Newton cannot resolve these two regions so we fit the spectrum extracted
from the entire remnant.
Even though IKT 22 is clearly less
evolved than IKT 6 and IKT 23 (for example), we do find that the Sedov model
provides a much better fit to the data. Hayashi (1997) also
found that Sedov model fits to the ASCA data of IKT 22 gave the most
reliable results. We also fit, based on the high mass estimates for the NEI
fits, the DEM S 32, IKT 2,
HFPK 419, and IKT 16 spectra with a Sedov model.
's and large swept-up mass,
obtained from the NEI model fits. IKT 6 and IKT 23 have a shell and centrally
filled morphology. We extract and fit only the shell part of the spectra of
these two remnants with a Sedov model.
The Chandra data reveal that IKT 22 has
a blastwave and reverse shock structure (Hughes et al. 2000),
however, XMM-Newton cannot resolve these two regions so we fit the spectrum extracted
from the entire remnant.
Even though IKT 22 is clearly less
evolved than IKT 6 and IKT 23 (for example), we do find that the Sedov model
provides a much better fit to the data. Hayashi (1997) also
found that Sedov model fits to the ASCA data of IKT 22 gave the most
reliable results. We also fit, based on the high mass estimates for the NEI
fits, the DEM S 32, IKT 2,
HFPK 419, and IKT 16 spectra with a Sedov model.
The free parameters of the Sedov model are the normalisation (
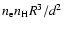 ), shock temperature (
), shock temperature (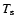 ), ionisation parameter (
), ionisation parameter (
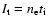 ), elemental abundances and the column density
), elemental abundances and the column density 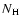 of
absorbing gas. Here
of
absorbing gas. Here 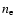 is the pre-shock electron density,
is the pre-shock electron density, 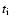 is the ionisation age of the remnant, R is the SNR shock radius and d is
the
distance to the source. The fitting procedure for the Sedov models is the same
as in the case of the NEI models. The fit results are summarised in
Table 4.
is the ionisation age of the remnant, R is the SNR shock radius and d is
the
distance to the source. The fitting procedure for the Sedov models is the same
as in the case of the NEI models. The fit results are summarised in
Table 4.
From these fits, we can estimate several physical parameters for the SNRs in
question.
If 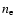 is the electron
density,
is the electron
density, 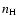 is the hydrogen density,
is the hydrogen density, 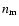 is the total
number density of protons+neutrons (including those bound up in nuclei), then,
using the elemental abundances
and assuming a fully ionised plasma we can calculate the number of electrons
per hydrogen atom
is the total
number density of protons+neutrons (including those bound up in nuclei), then,
using the elemental abundances
and assuming a fully ionised plasma we can calculate the number of electrons
per hydrogen atom
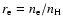 and the effective number of
protons and neutrons
(baryon mass) per hydrogen atom
and the effective number of
protons and neutrons
(baryon mass) per hydrogen atom
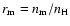 .
By adopting
the
values of the parameters mentioned above we estimate the electron density (
.
By adopting
the
values of the parameters mentioned above we estimate the electron density (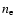 ),
the hydrogen density (
),
the hydrogen density (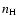 ), the Sedov dynamical age (
), the Sedov dynamical age (
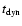 ), the effective ionisation age (
), the effective ionisation age (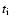 ), the total emitting
mass (M) and initial explosion energy (E0) by using:
), the total emitting
mass (M) and initial explosion energy (E0) by using:
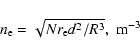 |
(1) |
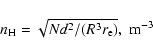 |
(2) |
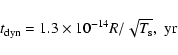 |
(3) |
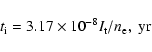 |
(4) |
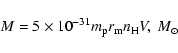 |
(5) |
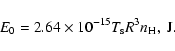 |
(6) |
Here N is the normalisation (m-5), 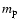 (kg) is the proton
mass, R (m) is the shock radius,
(kg) is the proton
mass, R (m) is the shock radius,
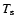 (keV) is the shock temperature,
(keV) is the shock temperature, 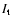 (m-3 s)
is the ionisation parameter
and
(m-3 s)
is the ionisation parameter
and
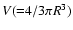 is the total volume. We do not apply a volume filling
factor to our estimates (Eqs. (1)-(6)) as it is already
implicitely contained within the Sedov model. We assume that the remnants are
spherically symmetric. The results are given in
Table 5. The mass estimates based on the NEI fits compare
well to those obtained from the Sedov model fits.
However, any deviation from symmetry (e.g. fragmentary shells) or
sphericity will, of course, affect the volume estimates which in turn influences
the estimates of derived parameters such as densities, explosion energy and mass.
The effect of an incorrect volume estimate on the derived parameters can be
estimated by applying a volume factor
is the total volume. We do not apply a volume filling
factor to our estimates (Eqs. (1)-(6)) as it is already
implicitely contained within the Sedov model. We assume that the remnants are
spherically symmetric. The results are given in
Table 5. The mass estimates based on the NEI fits compare
well to those obtained from the Sedov model fits.
However, any deviation from symmetry (e.g. fragmentary shells) or
sphericity will, of course, affect the volume estimates which in turn influences
the estimates of derived parameters such as densities, explosion energy and mass.
The effect of an incorrect volume estimate on the derived parameters can be
estimated by applying a volume factor
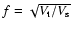 ,
where
,
where
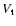 is the true emitting volume and
is the true emitting volume and 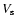 is the estimated volume
for spherical symmetry. The following corrections would then hold: (
is the estimated volume
for spherical symmetry. The following corrections would then hold: (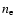 ,
,
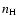 ,
,
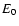 )
)
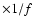 and (M,
and (M, 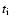 )
)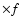 .
For
example, an ellipsoidal morphology with one axis
.
For
example, an ellipsoidal morphology with one axis 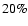 larger than the radius
of a sphere would give
larger than the radius
of a sphere would give
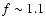 .
.
We also fit the spectra from the inner regions of IKT 6 and 23. As a model we
use one NEI component to account for emission from the central region. In
addition to this, we added the same plasma component and parameters as derived
from the fits to the outer region, only the normalisations from these
components were allowed to vary. This method accounts for any projected
fore/background shell emission. The fit results supplied in Table 3,
are very similar between the two remnants.
The best fit models generally provides good fits to the data, though a few
discrepancies exist. Uncertainties in the modeling of the data include the
calibration differences between the EPIC-pn and EPIC-MOS and incompleteness of the
atomic database. For example, the most prominent residual is the
underestimation of the spectra at
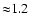 keV. This is a known problem
and is probably due to missing high excitation lines of Fe XVII-XIX in
the plasma code (see Brickhouse et al. 2000).
keV. This is a known problem
and is probably due to missing high excitation lines of Fe XVII-XIX in
the plasma code (see Brickhouse et al. 2000).
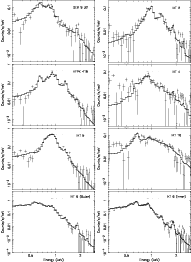 |
Figure 3:
Combined EPIC (i.e. EPIC-pn+EPIC-MOS) background-subtracted spectra of
individual SNRs. The crosses represent the data points and error bars and the
solid histogram represent the best fit models (i.e. Sedov model for all spectra
appearing in Table 4, and the single temperature NEI model for the rest). |
| Open with DEXTER |
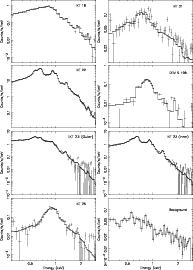 |
Figure 4:
Same as for Fig. 3. The lower right panel
represents a
typical background spectrum. |
| Open with DEXTER |
Shock waves in the shells of SNRs are thought to be collisionless because at the
low densities encountered in remnants the shock front is thinner than the mean
free path for collisions. The actual heating mechanism in collisionless shocks
is not straightforward and needless to say, not well understood. The heating
of particles at the shock-front is thought to be produced by collective
processes, such as plasma waves (for a review see for instance, Draine &
McKee 1993; Laming 2000). Since the heating is not
collisional the plasma can be regarded as a two fluid system consisting of
electrons and ions. There is no guarantee
that there will be equilibration between the electron and ion temperature. We
therefore investigated the effect of non-equipartion on our derived parameters,
as our model fits assume equilibration between electron and ion temperatures. We
fitted a sample of our brighter remnants with a Sedov model in which the
electron temperature lags the shock temperature (see Borkowski et al. 2001). We initially left both the shock and electron temperature
free, but both these values tracked each other. We then imposed fixed shock to
electron temperature ratios of 0.5 and 0.2. We found that the derived
parameters, except for the ionisation parameter and
emission measure, did not differ significantly from the electron-ion temperature
equilibration models. In fact, we obtained slightly better fits (in terms
of reduced
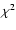 )
with the equilibration models. This could be because
most of our remnants are evolved and have already attained or are approaching
electron-ion temperature
equilibration.
)
with the equilibration models. This could be because
most of our remnants are evolved and have already attained or are approaching
electron-ion temperature
equilibration.
Table 3:
NEI model spectral fitting results. The fit errors (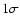 )
are
given in
brackets.
The abundances are all relative to their solar
values (Anders & Grevese 1989).
)
are
given in
brackets.
The abundances are all relative to their solar
values (Anders & Grevese 1989).
Table 4:
Sedov model spectral fitting results. The fit errors (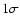 )
are
given in
brackets. The
abundances are all relative to their solar
values (Anders & Grevese 1989).
)
are
given in
brackets. The
abundances are all relative to their solar
values (Anders & Grevese 1989).
4.1 Progenitor types
IKT 6 and IKT 23 are remarkably similar remnants, both morphologically and
spectrally (Figs. 3 and 4 ). IKT 23 has a
clear shell and a centrally filled morphology. The colours in
Fig. 2 indicate that the outer region is softer than the inner
region. IKT 6 exhibits a similar morphology, although it is not as clearly
resolved. IKT 6 is located towards the edge of the detector where the effective
area and spatial resolution is lower. The other remnant in our sample with a
clear shell structure is IKT 22. This remnant is quite striking since it
is orders of magnitude more luminous than the other SNRs in the field.
The spectra extracted from the two regions (i.e. outer and inner) of IKT 6 and
IKT 23 (see Figs. 3 and 4) are distinctly
different. However, the spectra are remarkably similar between the two
remnants. The spectral fitting results given in Tables 3
and 4 also yield similar parameters for the two remnants. Although
not clearly visible in the XMM-Newton data (because of the lower spatial resolution),
the Chandra data do reveal that IKT 22 has a blastwave and reverse shock
structure (Hughes et al. 2000). The spectra from these two regions
are also distinctly different.
Table 5:
Physical parameters derived from the best fit Sedov model results.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{0156fig5.ps}}\end{figure}](/articles/aa/full/2004/27/aa0156/Timg54.gif) |
Figure 5:
RGS spectrum of IKT 22 ( top) and IKT 23 ( bottom). The most
prominent emission lines are labeled. |
| Open with DEXTER |
Table 6:
Comparison of the O, Ne and Mg complexes (error weighted mean) to the
Fe abundance values for the core-collapse and type Ia candidates
The abundance derived from the fits to the
outer regions of IKT 6 and IKT 23 are consistent with the SMC ISM abundances,
while the inner
regions reveal much higher abundance values. We propose, based on the abundance
profiles, that the inner region represents reverse shock heated ejecta material
while the outer region represents a blastwave moving through the ISM/CSM. The
fit results also show that the inner (ejecta-rich) regions are hotter (
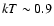 keV) than the outer regions (
keV) than the outer regions (
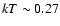 keV). This is expected from
models such as proposed by Truelove & McKee (2001), which predict
that the
blastwave in more evolved remnants eventually attains a lower velocity than the
reverse shock.
keV). This is expected from
models such as proposed by Truelove & McKee (2001), which predict
that the
blastwave in more evolved remnants eventually attains a lower velocity than the
reverse shock.
The spectra extracted from the inner regions of IKT 6 and IKT 23 are also
similar to the IKT 22 spectrum. All three remnants show enhanced O, Ne and Mg
abundances with respect to Fe. The abundance values of these elements (w.r.t.
solar) are also an order of
magnitude larger than their SMC ISM values. We also obtained RGS spectra of
IKT 22 and IKT 23. The spectra were extracted from the entire remnants. The
high-resolution RGS spectra of IKT 22 and IKT 23, displayed in
Fig. 5, again bear striking similarities and reveal prominent
emission lines of O and Ne species. The most obvious difference between the two
spectra is in the count rate. The flux in the emission lines of IKT 22 are an
order of magnitude larger than compared to IKT 23. Much of this flux difference
can be attributed to the differences in abundance values. This is because the
RGS (and EPIC) spectrum of IKT 22 is dominated by emission from ejecta-rich
material, while the IKT 23 spectrum is dominated by emission from the swept-up
ISM material, which has an average abundance of 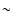 0.2 solar. Fits to the
EPIC data extracted from the entire remnant also show that the abundances for
IKT 22 are an order of magnitude larger than compared to IKT 23. A more
detailed RGS analysis of IKT 22 is provided by Rasmussen et al. (2001).
0.2 solar. Fits to the
EPIC data extracted from the entire remnant also show that the abundances for
IKT 22 are an order of magnitude larger than compared to IKT 23. A more
detailed RGS analysis of IKT 22 is provided by Rasmussen et al. (2001).
The similarities between IKT 6, IKT 22 and IKT 23 suggests that these three
remnants have common progenitors. IKT 22 is a well studied remnant that has
been classified as being the result of a core-collapse SN. IKT 6 and
IKT 23 should thus also be the remnants of core-collapse SNe. Both the
derived abundances and
masses for the inner regions of IKT 6 and IKT 23 are consistent with this
interpretation. These remnants represent very different stages of SNR
evolution. IKT 22 is a 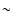 2000 yr old remnant (Blair et al. 1989)
while IKT 6 and IKT 23 are much
more evolved (14 000-20 000 yr). We propose that IKT 6 and IKT 23 are
evolved versions of IKT 22 and studying these remnants in more detail presents
a
unique opportunity to probe the evolution of oxygen-rich remnants in the SMC.
It is also interesting to note that the ejecta are still visible in remnants as
evolved as IKT 6 and IKT 23.
2000 yr old remnant (Blair et al. 1989)
while IKT 6 and IKT 23 are much
more evolved (14 000-20 000 yr). We propose that IKT 6 and IKT 23 are
evolved versions of IKT 22 and studying these remnants in more detail presents
a
unique opportunity to probe the evolution of oxygen-rich remnants in the SMC.
It is also interesting to note that the ejecta are still visible in remnants as
evolved as IKT 6 and IKT 23.
IKT 2 and HFPK 419 are located in the large emission nebulae N19. These
remnants
have rather irregular and complicated X-ray morphologies. For example, it is
not clear whether IKT 2 and HFPK 419 are indeed two separate remnants or part
of
a larger SNR. However, the spectra from these remnants
are rather different, which indicate that they might actually be two separate
objects. IKT 2 and HFPK 419 both show high metal abundances, which indicate that
much of the X-ray emission is from ejecta enriched material. Their abundance
profiles show a
similar pattern in that the Ne and Mg abundances are higher than Fe (see
Table 4).
While the Ne and Mg abundances are enhanced above the SMC mean by only
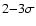 ,
the error weighted mean O, Ne and Mg abundances, as supplied in
Table 6, are enhance at the
,
the error weighted mean O, Ne and Mg abundances, as supplied in
Table 6, are enhance at the
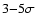 level.
Furthermore, the Si and Fe abundances are lower and in line with their SMC
values.
The enhanced Ne and Mg abundances, as compared to the Si and Fe values,
indicate a core-collapse origin (e.g. Nomoto et al. 1997; Woosley &
Weaver 1995). We thus suggest, based on their abundance profiles, that
these remnants are the results of
core-collapse SNe. This is also in agreement with their surroundings which
suggest recent, at least modest, starburst activity (Dickel et al. 2001).
Yokogawa et al. (2002) analysed ASCA and ROSAT data
of IKT 2 and also find enhanced abundances, even though their age
estimate is rather large. They suggest that IKT 2 is the result of a core
collapse SN with a progenitor mass of
level.
Furthermore, the Si and Fe abundances are lower and in line with their SMC
values.
The enhanced Ne and Mg abundances, as compared to the Si and Fe values,
indicate a core-collapse origin (e.g. Nomoto et al. 1997; Woosley &
Weaver 1995). We thus suggest, based on their abundance profiles, that
these remnants are the results of
core-collapse SNe. This is also in agreement with their surroundings which
suggest recent, at least modest, starburst activity (Dickel et al. 2001).
Yokogawa et al. (2002) analysed ASCA and ROSAT data
of IKT 2 and also find enhanced abundances, even though their age
estimate is rather large. They suggest that IKT 2 is the result of a core
collapse SN with a progenitor mass of 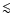 20
20 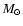 .
.
IKT 16 is one of the weaker X-ray sources in our sample. The X-ray morphology
appears consistent with the radio and H classification of it being
a shell like SNR (Mathewson et al. 1984). A harder emission spot
can be seen in the centre of the X-ray image.
This emission region was excluded spectral extraction region.
We also attempted to extract a separate
spectrum from this region, but the data is of insufficient quality to speculate
on the X-ray nature of this region. A longer exposure observation is needed to
investigate whether this source is thermal or non-thermal in nature.
classification of it being
a shell like SNR (Mathewson et al. 1984). A harder emission spot
can be seen in the centre of the X-ray image.
This emission region was excluded spectral extraction region.
We also attempted to extract a separate
spectrum from this region, but the data is of insufficient quality to speculate
on the X-ray nature of this region. A longer exposure observation is needed to
investigate whether this source is thermal or non-thermal in nature.
Also interesting is the high explosion energy (
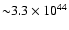 W)
and low ionisation age (
W)
and low ionisation age (
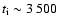 yr) associated with IKT 16. The fit
parameters are not very well constrained due to the low count rate so the
discrepancies might originate from statistical limitations. However, in their
analysis of the LMC remnants, Hughes et al. (1998) found a connection
between low ionisation age (as compared to the dynamical age) and high explosion
energy. They explain this connection as SNRs which exploded within pre-existing
low-density cavities in the ISM. The remnant expands rapidly to the cavity
wall, where it then encounters denser gas and begins to emit X-rays. This
results in a lower dynamical age and explosion energy than that inferred from
the Sedov model. A similar scenario could thus be applicable to IKT 16. If
this is the case, then IKT 16 would be the result of the core-collapse of a
massive star whose stellar wind has caused a low density circumstellar
cavity.
yr) associated with IKT 16. The fit
parameters are not very well constrained due to the low count rate so the
discrepancies might originate from statistical limitations. However, in their
analysis of the LMC remnants, Hughes et al. (1998) found a connection
between low ionisation age (as compared to the dynamical age) and high explosion
energy. They explain this connection as SNRs which exploded within pre-existing
low-density cavities in the ISM. The remnant expands rapidly to the cavity
wall, where it then encounters denser gas and begins to emit X-rays. This
results in a lower dynamical age and explosion energy than that inferred from
the Sedov model. A similar scenario could thus be applicable to IKT 16. If
this is the case, then IKT 16 would be the result of the core-collapse of a
massive star whose stellar wind has caused a low density circumstellar
cavity.
The images in Fig. 2 show that IKT 5, DEM S 128 and IKT 25 have similar diffuse X-ray morphologies with no clear shell like structure.
The emission peaks in the 0.7-1.0 keV band. This indicates that the flux of
these sources are dominated by emission from Fe-L transitions.
The X-ray sizes of IKT 5, DEM S 128 and IKT 25 are much smaller than
their optical or radio diameters (see Mathewson et al. 1983;
Mathewson
et al. 1984; Filipovic et al. 2000). The large optical
diameters imply that they are
evolved remnants. Mathewson et al. (1984) also attribute the
high S II emission detected in IKT 5 and IKT 25 to the onset of
radiative cooling due to the evolved nature of these remnants. In this scenario
IKT 5, DEM
S 128 and IKT 25 would have evolved to such a degree that the shells have
eventually become too faint or too cool to be seen in X-rays and we only see the
hotter Fe-rich ejecta remains. The morphologies and temperature structure of IKT 6
and IKT 23 also add credence to such a scenario.
We fitted the spectra of these three remnants with NEI models. Hughes &
Smith (1994) reported a point source, possibly a Be-binary system,
with a power law spectrum in
the field of IKT 25. We thus added a power-law component to the NEI model of IKT 25.
We fixed the photon index of the powerlaw to 1.5 and flux to
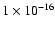 W m-2 (Hughes & Smith 1994), since we
could not constrain any power-law parameters in out data. The best fit
parameters are given in Table 3. These fits also
show enhanced Fe abundances. Although the spectra of IKT5, DEM S 128 and IKT 25
were well fitted with
an NEI model with free abundances, we could not constrain the abundances very
well due to
the limited statistics. What is obvious, though, is that the Fe abundance
values were consistently, and at least 3
W m-2 (Hughes & Smith 1994), since we
could not constrain any power-law parameters in out data. The best fit
parameters are given in Table 3. These fits also
show enhanced Fe abundances. Although the spectra of IKT5, DEM S 128 and IKT 25
were well fitted with
an NEI model with free abundances, we could not constrain the abundances very
well due to
the limited statistics. What is obvious, though, is that the Fe abundance
values were consistently, and at least 3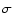 ,
above the SMC mean
metallicity.
We also tried to fix the abundances, except for Fe, to the SMC mean, but here it
is also clear that we
need an enhanced Fe abundance.
It is clear from Table 6 that the Fe abundance is
enhanced with respect to the mean O, Ne and Mg abundance values.
It has been argued (e.g., Nishiuchi et al. 2001; Hughes et al.
1995) that the excess
of emission around 1 keV, interpreted as an overabundance of Fe, may suggest
that the progenitor of the SNR origin was a type Ia SN.
The apparent excess emission around
,
above the SMC mean
metallicity.
We also tried to fix the abundances, except for Fe, to the SMC mean, but here it
is also clear that we
need an enhanced Fe abundance.
It is clear from Table 6 that the Fe abundance is
enhanced with respect to the mean O, Ne and Mg abundance values.
It has been argued (e.g., Nishiuchi et al. 2001; Hughes et al.
1995) that the excess
of emission around 1 keV, interpreted as an overabundance of Fe, may suggest
that the progenitor of the SNR origin was a type Ia SN.
The apparent excess emission around 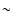 0.9 keV and the high Fe abundance in
these remnants suggests that these remnants are the result of type Ia
supernovae. A possible
interpretation is that these remnants are much more evolved versions of SNR DEM
L 71 in the LMC (Hughes et al. 2003; van der Heyden et al. 2003).
Here we see a bright ISM dominated shell with fainter
Fe-rich ejecta material in the centre.
However, higher spectral resolution is required to investigate the
elemental abundance ratios of these remnants in more detail.
It should also be noted that an association between IKT 25 and the Be-binary system
would imply that this SNR would be the remnant of a massive star rather than a
type Ia SN.
0.9 keV and the high Fe abundance in
these remnants suggests that these remnants are the result of type Ia
supernovae. A possible
interpretation is that these remnants are much more evolved versions of SNR DEM
L 71 in the LMC (Hughes et al. 2003; van der Heyden et al. 2003).
Here we see a bright ISM dominated shell with fainter
Fe-rich ejecta material in the centre.
However, higher spectral resolution is required to investigate the
elemental abundance ratios of these remnants in more detail.
It should also be noted that an association between IKT 25 and the Be-binary system
would imply that this SNR would be the remnant of a massive star rather than a
type Ia SN.
IKT 18 has a rectangular shape. The emission is diffuse with no obvious limb
brightening. The Chandra data (Nazé et al. 2002) do reveal a few
bright or dark arcs, but apart from these, the brightness is rather uniform.
The luminous blue variable (LBV) HD 5980 can also be seen in the centre of IKT 18. The spatial coincidence of IKT 18 with the peculiar binary system HD 5980
suggests an association with this system. The possible association was recently
investigated by Nazé et al. (2002). They drew attention to
similarities between IKT 18 and the Carina nebula. However, they concluded that
based on the non-thermal radio emission (Ye et al. 1991) and a high
velocity expansion (Chu & Kennicutt 1988), IKT 18 should be regarded as
a SNR with HD 5980 located behind the remnant.
The results of our NEI model fits differ from those obtained by Nazé et al. (2002)
(Mekal model fits to the Chandra
data) and Yokogawa et al. (2002) (NEI model fits to the ASCA
data) in that our column density is a factor of 2 higher and our
abundances are generally lower. However, Yokogawa et al. (2002) fixed
their abundance values to 0.2 times solar while the model used by
Nazé et al. (2002) only gives a mean metallicity. It should be noted
that the results obtained from fits to the XMM-Newton, Chandra and ASCA
data set are
generally consistent within the errors. All three spectral analyses give a total
X-ray emitting mass estimate of 100-200 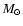 ,
which indicate that this
remnant is in the Sedov evolutionary stage. We thus proceeded to fit our data
with a Sedov model. This model gave abundances profiles which are very much in
line with the SMC ISM abundances of Russel & Dopita (1992).
The low SMC-like abundances and high mass (196
,
which indicate that this
remnant is in the Sedov evolutionary stage. We thus proceeded to fit our data
with a Sedov model. This model gave abundances profiles which are very much in
line with the SMC ISM abundances of Russel & Dopita (1992).
The low SMC-like abundances and high mass (196 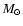 )
and age estimate
(11 000 yr) derived from our fits
are also consistent with the picture of an evolved SNR which has swept-up ISM
material. While the low abundances do not allow for a
progenitor typing, Yokogawa et al. (2002) argue that the location in
a giant H II region favours a type II origin.
More XMM-Newton data will be available in the near future, which will allow for a
more detailed assessment of the nature of this object.
)
and age estimate
(11 000 yr) derived from our fits
are also consistent with the picture of an evolved SNR which has swept-up ISM
material. While the low abundances do not allow for a
progenitor typing, Yokogawa et al. (2002) argue that the location in
a giant H II region favours a type II origin.
More XMM-Newton data will be available in the near future, which will allow for a
more detailed assessment of the nature of this object.
DEM S 32 is another remnant, as is IKT 2 and HFPK 419, in the vicinity of N19.
It has a shell-like
structure with enhanced emission towards the southwestern limb. The abundance
yields from DEM S 32 are lower than for IKT 2 and HFPK 419 and no clear
distinction in progenitor type can be infered from these yields.
The environment (N19), however, might suggest that DEM S 32 has a massive
star progenitor and is thus possibly the result of a core-collapse SN
explosion.
There is no clear X-ray emission associated with the optical emission from IKT 21.
The X-ray emission from the vicinity of the optical remnant is dominated
by the Be-pulsar binary system AX J0103-722 (Hughes & Smith 1994;
Israel et al. 2000).
We extracted our spectrum from the region containing the optical emission,
which includes the
pulsar system. Although not visible in Fig. 4, the spectrum
clearly extends above 3 keV. Our
model for IKT 21 thus consists of a NEI component for thermal emission from the
SNR and a power-law component to account for the pulsar emission. The power-law
component normalisation and photon index were initially fixed to values obtained
from Hughes & Smith (1994) and were subsequently allowed to vary.
The best fit model gives a power-law component normalisation of 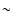
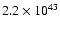 ph s-1 keV-1, a photon index of
ph s-1 keV-1, a photon index of 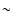 0.9 and a
luminosity of
0.9 and a
luminosity of
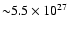 W (0.5-2.0 keV band). Our results for
the thermal emission indicate a temperature of
W (0.5-2.0 keV band). Our results for
the thermal emission indicate a temperature of
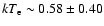 and a luminosity of
and a luminosity of 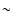
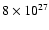 W (0.5-2.0 keV band). These results
compare well with estimates obtained by Hughes & Smith (1994). It
is not clear whether the pulsar AX J0103-722 is associated with the SNR as it is
not near the centre of the remnant. An association would mean that IKT 21 would
be the remnant of a massive-star SN (Hughes & Smith 1994).
W (0.5-2.0 keV band). These results
compare well with estimates obtained by Hughes & Smith (1994). It
is not clear whether the pulsar AX J0103-722 is associated with the SNR as it is
not near the centre of the remnant. An association would mean that IKT 21 would
be the remnant of a massive-star SN (Hughes & Smith 1994).
IKT 4 has a very similar morphology to IKT 5, DEM S 128 and IKT 25. Its X-ray
emission, which peaks in the Fe-L band, lies inside its optical emission. The
spectrum is too weak to constrain the abundance, so we cannot speculate on its
progenitor based on the spectrum. However, the morphology does argue for a type
Ia SN origin.
The abundance values for the swept-up matter dominated SNRs
(Table 4) show some spread among the remnants and also
between different elemental species. The general trend is that the larger
remnants have lower abundance values while the smaller ones have larger
values. The interpretation is that the older remnants have swept-up so much ISM
material that the abundances are approaching the ISM values. The abundance
yields from the older remnants with larger swept-up masses could thus be used
to
probe the ISM abundance distribution.
We use the abundances derived from the spectral fits to IKT 6 (outer region),
IKT 18 and IKT 23 (outer region) to determine the gas-phase abundances of the
SMC. These remnants are selected
because of their high (swept-up) masses. We average, for each
elemental species, the fitted abundances from the three remnants. In
Fig. 6 we plot the error weighted average abundances versus
elemental species. The uncertainties represent the rms-scatter among the
remnants. The derived abundances are also compared to the average SMC abundance
values presented by Russel & Dopita (1992). The work of Russel &
Dopita (1992) is based on the spectral analysis of F supergiants for
heavier elements (Z>12) and H II regions and SNRs for lower Z elements.
However, they only have 1 SMC SNR in their studies. Our average abundance
values for the low-Z elements appear slightly higher than those obtained by
Russel & Dopita (1992), but are in good agreement within the
uncertainties.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{0156fig6.ps}}\end{figure}](/articles/aa/full/2004/27/aa0156/Timg67.gif) |
Figure 6:
Average SMC abundances. The average abundance values obtained from
fits to IKT 6 IKT 18 and IKT 23 are represented by diamonds. Results from
Russel & Dopita (1992) are indicated with circles. |
| Open with DEXTER |
4.3 Physical parameters
The ionisation ages given in Table 5 are generally consistent
with the dynamical age within a factor 2, the exceptions being IKT 2 and HFPK 149. The factor of 2 difference can be easily be attributed to inaccurate
volume estimates, which could be due to any deviation from the assumed symmetry
or sphericity of the SNRs, as described in a previous section.
This would afect the electron
density and thus reduce the ionisation age estimates. The possibility of
fragmentary shells or clumping means that the initial explosion energy E0
and mass estimates should be regarded as lower and upper bounds respectively.
In the case of IKT 2 and HFPK 149 the plasma has reached ionisation
equilibrium. In this regime the ionisation parameter becomes insensitive as an
age indicator since the spectrum changes very slowly with increasing ionisation
parameter.
The mean SMC ISM hydrogen density derived from the Sedov model fits is
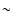
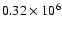 m-3. This is nearly an order of magnitude lower than
the mean density of
m-3. This is nearly an order of magnitude lower than
the mean density of 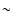
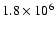 m-3 derived from Sedov fits
to a sample of LMC remnants by Hughes et al. (1998).
The lower SMC abundance and densities easily explains the lower SNR luminosities compared to their LMC counterparts, as the X-ray emission scales with the densities.
The lower abundances and densities also have implications for the dynamical
evolution of SNRs
in the SMC.
Cox (1972) predicts that the onset of radiative
cooling occurs at a time
m-3 derived from Sedov fits
to a sample of LMC remnants by Hughes et al. (1998).
The lower SMC abundance and densities easily explains the lower SNR luminosities compared to their LMC counterparts, as the X-ray emission scales with the densities.
The lower abundances and densities also have implications for the dynamical
evolution of SNRs
in the SMC.
Cox (1972) predicts that the onset of radiative
cooling occurs at a time
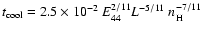 yr
where E44 is the
explosion energy in 1044 J, L is the cooling coefficient in W m3and
yr
where E44 is the
explosion energy in 1044 J, L is the cooling coefficient in W m3and 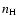 is in m-3. The radiative cooling will be governed by L and the hydrogen density, since the explosion
energies derived from the SMC and LMC samples are similar. L is a strong
function of elemental abundance. The SMC/LMC ratio of this coefficient is
is in m-3. The radiative cooling will be governed by L and the hydrogen density, since the explosion
energies derived from the SMC and LMC samples are similar. L is a strong
function of elemental abundance. The SMC/LMC ratio of this coefficient is
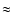 0.6, assuming average metallicity of 0.2 and 0.35 solar for the SMC and
LMC respectively. The lower hydrogen
density and metallicity means that the SMC remnants take
0.6, assuming average metallicity of 0.2 and 0.35 solar for the SMC and
LMC respectively. The lower hydrogen
density and metallicity means that the SMC remnants take 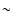 4 times longer
to reach the
radiative cooling stage, compared to the LMC remnants.
The SMC remnants should
thus be radiating X-rays for a longer time than in the LMC. This point is
illustrated by the fact that the oldest remnant in our sample is
4 times longer
to reach the
radiative cooling stage, compared to the LMC remnants.
The SMC remnants should
thus be radiating X-rays for a longer time than in the LMC. This point is
illustrated by the fact that the oldest remnant in our sample is 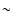 20 000 yr
while the oldest remnant in the LMC sample analysed by Hughes et al. (1998) is 10 000 yr.
20 000 yr
while the oldest remnant in the LMC sample analysed by Hughes et al. (1998) is 10 000 yr.
A number of conflicting SMC SN rate estimates have been made. For
example, Mathewson et al. (1983) gave a birth rate of one SNR per
800 yr, while Filipovic et al. (1998) gives a birth-rate of
one SNR per 350 yr. Both these estimates are higher than a rate of one in every
1100-2500 yr invoked by van den Berg
& Tammann (1991), which is derived from the star formation rate
inferred from the total H luminosity of the SMC.
luminosity of the SMC.
If we follow the arguments from the previous section (Sect. 4.3) then
we estimate that the onset of the radiative cooling stage commences at
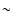 30 000 yr. Now if we consider that 16 X-ray emitting SNRs have been detected,
to date, then the SN rate in the SMC should be closer to one per
30 000 yr. Now if we consider that 16 X-ray emitting SNRs have been detected,
to date, then the SN rate in the SMC should be closer to one per 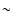 1800 yr.
This rate is in line with the rate inferred from van den Berg
& Tammann (1991). The derived rate is
also consistent with our age estimate (
1800 yr.
This rate is in line with the rate inferred from van den Berg
& Tammann (1991). The derived rate is
also consistent with our age estimate ( 2700 yr) of the youngest SMC
SNR (viz. IKT 22).
2700 yr) of the youngest SMC
SNR (viz. IKT 22).
Acknowledgements
We thank Jacco Vink for the use of and help with his image processing software
and for valuable discussions. The results presented are based on
observations obtained with XMM-Newton,
an ESA science mission with instruments and contributions directly funded by
ESA Member States and the USA (NASA). SRON is supported financially by NWO,
the Netherlands Organisation for Scientific Research.
- Anders, E., &
Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [NASA ADS] [CrossRef] (In the text)
- van den Berg, S., &
Tammann, G. 1991, ARA&A, 29, 363 [NASA ADS] (In the text)
- Blair, W. P., Raymond, J.
C., Danziger, J., & Matteucci, F. 1989, ApJ, 338, 812 [NASA ADS] [CrossRef] (In the text)
- Borkowski, K. J.,
William, J. L., & Reynolds, S. P. 2001, ApJ, 548, 820 [NASA ADS] [CrossRef] (In the text)
- Brickhouse, N.
S., Dupree, A. K., Edgar, R. J., et al. 2000, ApJ, 530, 387 [NASA ADS] [CrossRef] (In the text)
- Cappellaro, E.,
Evans, R., & Turrato, M. 1999, A&A, 351, 459 [NASA ADS]
- Chu, Y.-H, & Kennicutt,
R.C. 1988, AJ, 95, 1111 [NASA ADS] [CrossRef] (In the text)
- Cox, D. P. 1972, ApJ, 178,
159 [NASA ADS] [CrossRef] (In the text)
- Davies, R. D., Elliot,
K. H., & Meaburn, J. 1976, Roy. Astron. Soc. Mem., 81, 89 [NASA ADS]
- Dickel, J. R.,
Williams, R. M., Carter, L. M., et al. 2001, AJ, 122, 849 [NASA ADS] [CrossRef] (In the text)
- Draine, B. T., &
McKee, C. F. 1993, ARA&A, 31, 373 [NASA ADS] (In the text)
- Filipovic, M. D.,
Pietsch, W., Haynes, R. F., et al. 1998, A&ASS, 127, 119 [NASA ADS] (In the text)
- Filipovic, M.
D., Haberl, F., Pietsch, W., & Morgan, D. H. 2000, A&A,
353, 129 [NASA ADS] (In the text)
- Haberl, F., Filipovic,
M. D., Pietsch, W., & Kahabka, P. 2000, A&ASS, 142, 41 [NASA ADS] (In the text)
- Hayashi, I. 1997,
Ph.D. Thesis, Graduate School of Science, Kyoto University
(In the text)
- den Herder, J. W.,
Brinkman, A. C., Kahn, S. M., et al. 2001, A&A, 365, L7 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- van der Heyden, K.
J., Behar, E., Vink, J., et al. 2002, A&A, 392, 955 [EDP Sciences] [NASA ADS] [CrossRef]
- van der
Heyden, K. J., Bleeker, J. A. M, Kaastra, J., & Vink, J. 2003,
A&A, 406, 141 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Hughes, J. P.,
& Smith, R. C. 1994, AJ, 107, 1363 [NASA ADS] [CrossRef] (In the text)
- Hughes, J. P.,
Hayashi, I., Helfand, D. J., et al. 1995, ApJ, 444, L81 [NASA ADS] [CrossRef] (In the text)
- Hughes, J. P.,
Hayashi, I., & Koyama, K. 1998, ApJ, 505, 732 [NASA ADS] [CrossRef] (In the text)
- Hughes, J. P.,
Rakowski, C. E., & Decourchelle, A., 2000, ApJ, 543, L61 [NASA ADS] [CrossRef] (In the text)
- Hughes, J. P.,
Ghavamian P., Rakowski C. E., & Slane, P. 2003, ApJ, 582,
L95 [NASA ADS] [CrossRef] (In the text)
- Inoue, H., Koyama, K.,
& Tanaka, Y. 1983, in Supernova Remnants and Their X-ray
Emission, ed. P. Gorenstein & J. Danziger (Dordrecht: Reidel),
IAU Symp., 101, 535
(In the text)
- Israel, G. L., Campana,
S., Covino, S., et al. 2000, ApJ, 531, L131 [NASA ADS] [CrossRef] (In the text)
- Kaastra, J. S., Mewe,
R., & Nieuwenhuijzen, H. 1996, in UV and X-ray Spectroscopy of
Astrophysical and Laboratory Plasmas, ed. K. Yamashita, & T.
Watanabe (Tokyo: Univ. Ac. Press), 411
(In the text)
- Laming, J. M. 2000,
ApJS, 127, 409 [NASA ADS] [CrossRef] (In the text)
- Massey, P., Lang, C.
C., DeGioia-Eastwood, K., & Garmany, C. D. 1995, ApJ, 438,
188 [NASA ADS] [CrossRef]
- Mathewson, D.
S., Ford, V. L., Dopita, M. A., et al. 1983, ApJS, 51, 345 [NASA ADS] [CrossRef] (In the text)
- Mathewson, D.
S., Ford, V. L., Dopita, M. A., et al. 1984, ApJS, 551, 189 [NASA ADS] (In the text)
- Mewe, R., Kaastra, J. S.,
& Liedahl, D. A. 1995, Legacy 6, 16
(In the text)
- Migliazzo, J.,
Canizares, C. D., Flanagan, K., Pannuti, T., & Fredericks, A.
2002, APS Meet., 47, N17039
- Nazé, Y., Hartwell, J.
M., Stevens, I. R., et al. 2002, ApJ, 580, 225 [NASA ADS] [CrossRef] (In the text)
- Nishiuchi, M.
2001, Ph.D. Thesis, Kyoto University
(In the text)
- Nishiuchi, M.,
Yokogawa, J., Koyama, K., & Hughes J.P. 2001, PASJ, 53, 99 [NASA ADS] (In the text)
- Nomoto, K., Iwamoto,
K., Nakasato N., et al. 1997, Nucl. Phys. A, 621, 467 [NASA ADS] [CrossRef] (In the text)
- Rasmussen,
A., Behar, E., Kahn, S. M., et al. 2001, A&A, 365, L231 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Russel, S. C., &
Dopita, M. A. 1992, ApJ, 384, 509 [NASA ADS] (In the text)
- Sedov, L.I. 1959,
Similarity and Dimensionless Methods in Mechanics (New York:
Academic)
(In the text)
- Strüder, L.,
Briel, U. G., Dennerl, K., et al. 2001, 365, L18
(In the text)
- Truelove, J. K.,
& McKee, C. F. 1999, ApJS, 120, 299 [NASA ADS] [CrossRef] (In the text)
- Turner, M. J. L.,
Abbey, A., Arnaud, M., et al. 2001, 365, L27
(In the text)
- Wang, Q., & Wu, X.
1992, ApJS, 78, 391 [NASA ADS] [CrossRef] (In the text)
- Westerland, B.
E. 1990, A&ARv, 2, 29 [NASA ADS] (In the text)
- Woosley, S. E., &
Weaver, T.A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] (In the text)
- Ye, T., Turtle, A. J., &
Kennicutt, R. C. 1991, MNRAS, 249, 722 [NASA ADS] (In the text)
- Yokogawa, J.,
Imanishi, K., Koyama, K., & Nishiuchi, M., & Mizuno, N.
2002, PASJ, 54, 53 [NASA ADS] (In the text)
Copyright ESO 2004


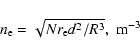
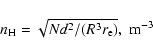
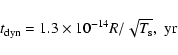
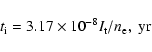
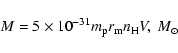
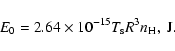


![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{0156fig5.ps}}\end{figure}](/articles/aa/full/2004/27/aa0156/Timg54.gif)
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{0156fig6.ps}}\end{figure}](/articles/aa/full/2004/27/aa0156/Timg67.gif)