A&A 421, 425-432 (2004)
DOI: 10.1051/0004-6361:20034433
G. Amosov1 - P. Schuecker2
1 - Moscow Institute of Physics and Technology, Institutski 9, 141700 Dolgoprudni, Russia
2 -
Max-Planck-Institut für extraterrestrische Physik, Giessenbachstraße, 85741 Garching, Germany
Received 2 October 2003 / Accepted 11 February 2004
Abstract
The excursion set model provides a convenient theoretical
framework to derive dark matter halo abundances. This paper
generalizes the model by introducing a more realistic merging and
collapse process. A new parameter regulates the influence of the
environment and thus the coherence (non-Markovianity) of the merging
and the collapse of individual mass shells. The model mass function
also includes the effects of an ellipsoidal collapse. Analytic
approximations of the halo mass function are derived for
scale-invariant power spectra with the slopes n=0,-1,-2. The n=-2mass function can be compared with the results obtained from the
"Hubble volume'' simulations. A significant detection of non-Markovian
effects is found for an assumed accuracy of the simulated mass
function of 10%.
Key words: galaxies: clusters: general - cosmology: theory - cosmology: dark matter
The hierarchical growth of virialized cosmic structures provides a useful physical paradigm for the understanding of the formation of galaxies and clusters of galaxies in the Universe (White & Rees 1978). The Zel'dovich (1970) theory also includes a description of partially virialized structures like filaments and walls. In both models, cosmic structures grow from initial Gaussian density fluctuations via gravitational instability, leading after merging and their (partial) virialization to mass functions which are used as powerful statistical diagnostics.
Theoretical mass functions of dark matter halos are estimated from N-body simulations with accuracies of 10-30% (e.g. Jenkins et al. 2001). More physical insights can be obtained from analytic treatments based on Press-Schechter (PS)-like arguments (Press & Schechter 1974; Bond et al. 1991, hereafter BCEK). Alternative derivations are based on, e.g., non-Gaussian statistics (Lucchin & Matarrrese 1988), or treat both fluctuations and interactions of density perturbations within one process (Cavaliere & Menci 1994), or directly consider the non-linear regime (Valageas & Schaeffer 1997). The inclusion of non-spherical dynamical approximations (Monaco 1995; Lee & Shandarin 1998) and ellipsoidal collapse models (Sheth et al. 2001, hereafter SMT, 2002) modify the assumption of a spherical collapse while preserving the simplicity of the original excursion set idea.
The excursion set model of BCEK assumes a Gaussian density field which
is smoothed at a given spatial location with a top-hat filter in
wavenumber space (sharp k-space filter) using different comoving
filter radii R. The resulting filtered density contrasts ![]() perform a highly jagged diffusion trajectory (Fig. 1) where
the mass function is derived - as a function of the standard
deviation
perform a highly jagged diffusion trajectory (Fig. 1) where
the mass function is derived - as a function of the standard
deviation ![]() of the mass density fluctuations - from the
loss rate of trajectories at the barrier
of the mass density fluctuations - from the
loss rate of trajectories at the barrier
![]() at their
lowest
at their
lowest ![]() level (highest R or mass scale). For the spherical
collapse model and for the Einstein-de Sitter Universe we have
level (highest R or mass scale). For the spherical
collapse model and for the Einstein-de Sitter Universe we have
![]() ,
weakly dependent on cosmology. The halo mass
function is thus directly related to the first passage time
distribution of the trajectories.
,
weakly dependent on cosmology. The halo mass
function is thus directly related to the first passage time
distribution of the trajectories.
There is a problem with this approach related to the assumption of a sharp k-space filter. The filter gives a quite unrealistic mass assignment scheme, with a growth of cosmic structure which depends only on the mass of a halo it has within an infinitesimally small time interval at a given cosmic epoch, and without any dependency on past or future properties of the halo (Markov assumption). Therefore, the merging events occur as completely uncorrelated, sudden, jumps in the formation history. We will replace the sharp k-space filter by a non-sharp filter. This leads to a more realistic mass assignment scheme. The corresponding growth of cosmic structure depends on the properties of the halo over a finite and future-directed time range (non-Markov assumption).
The idea to invoke non-Markovian processes is not new. A discussion of the physical consequences of the Markov assumption and why related processes could fail can be found in White (1996, 1997). BCEK pointed out the relation between the shape of a mass filter and the Markov assumption. Their discussion of non-Markovian processes is, however, mainly restricted to results obtained with Monte-Carlo experiments.
Using the traditional excursion set model as a guideline, Sect. 2 introduces a simple analytic model which describes a more uniform mass assignment scheme, and thus a more uniform spherical collapse of dark matter halos. This model is further improved in Sect. 3, by including the effects of an ellipsodial collapse similar to SMT. The combined model can be regarded as a simple though typical example of a non-Markovian process. It generalizes the traditional excursion set model in a manner such that non-Markovianity can now be gradually increased by a new filter parameter. The same filter parameter also increases the smoothness of the profile of the mass filter (see Eq. (8) in Sect. 4).
| |
Figure 1: Trajectories for the extended PS process (Markovian process, jagged curves, T=0) and for the non-Markovian process (smooth curves, T=0.23). |
| Open with DEXTER | |
The standard mirror image method is used in Sect. 5 to derive an analytic form for the halo mass function. We show why this method, which in general does not work for non-Markovian processes, can be used in our specific case. The resulting mass function has the same functional form as the standard excursion set result in terms of the variance of the mass distribution and the critical density threshold. However, non-Markovian effects change the relations between filter radius, mass and variance. These relations become a function of the power spectrum of the underlying mass distribution. After the corresponding transformations of the mass functions they also become apparent in the halo mass function itself. This is the reason why in our non-Markovian context, the profile of the mass filter and thus how much mass is swep in from the surrounding mass of a collapsing region becomes a function of the power spectrum.
How much mass the filter sweeps in for a given filter radius can be a quite complex function, especially when general power spectra are considered. We could derive approximate analytic results for scale-invariant power spectra with the slopes n=0,-1,-2. The latter case is close to the observed value and allows a comparison with the Jenkins et al. (2001) mass function obtained from the "Hubble Volume'' simulations (Sect. 6). The basic aim is to test under the given assumptions the presence of non-Markovian effects in the simulations and to determine how accurately mass functions should be measured to detect the effects. A discussion of general power spectra goes beyond the scope of our analytic treatment and is postponed to a further paper.
The Markov assumption corresponds to an oscillating filter in configuration space or a sharp filter in k-space. For the determination of the total collapsed mass of a halo, the formal weighting of each mass shell with an oscillating filter suggests the following collapse picture. The innermost mass shell located around a peak in the cosmic mass distribution (though not necessarily around a massive particle) is up-weighted in the mass budget and is thus expected to collapse, whereas the next overlaying mass shell located around the first minimum of the filter is down-weighted, the following mass shell is up-weighted again, and so on. Similarily, for the determination of merger trajectories, the sharpness of the filter in k-space leads to the addition of statistically independent fluctuation power in disjunct k-shells and thus to highly jagged trajectories with completely independent increments. Both the collapse and the merger trajectories are regard as unrealistic (Fig. 1).
BCEK showed that a smooth, non-oscillating filter can be obtained with a non-Markovian process. It is also well-known that smooth filters like a Gaussian or a standard top-hat are consistent with the uniform (coherent) collapse of all concentric mass shells. Moreover, the smoothness of the filter in k-space mixes fluctuation power located in disjunct k-shells and thus smoothes the merger trajectories. We are thus searching for diffusion processes with smooth merger trajectories. The physical significance of the corresponding mass filter is evaluated by the comparison with mass functions derived from simulations (Sect. 6).
Formally, the merger trajectories of the excursion set model are
described by the Wiener stochastic diffusion process W(t) - the
Brownian motion. We follow the general convention and work with a
pseudo time or mass resolution variable t(R) in ![]() which
will be specified later (Eq. (9)), and the filtered density
contrast
which
will be specified later (Eq. (9)), and the filtered density
contrast
![]() (see BCEK and Lacey & Coles 1993 for more
details). A non-Markovian process with the desired properties has the
increments of the density contrast
(see BCEK and Lacey & Coles 1993 for more
details). A non-Markovian process with the desired properties has the
increments of the density contrast
The theory of ellipsoidal collapse (Bond & Myers 1996, SMT) provides
a relation between the critical density contrast of an ellipsoidal
collapse
![]() and a spherical collapse
and a spherical collapse
![]() of the form
of the form
![]() .
For convenience we set
.
For convenience we set
![]() ,
yielding mathematically exact first passage time
distributions. Our approximation
,
yielding mathematically exact first passage time
distributions. Our approximation
![\begin{figure}
\par\includegraphics[height=5.55cm,width=5.65cm,clip]{0433fi2a.ps...
...0.5mm}
\includegraphics[height=5.5cm,width=5.15cm,clip]{0433fi2c.ps}\end{figure}](/articles/aa/full/2004/26/aa0433-03/Timg40.gif) |
Figure 2:
Filter profiles WT(k) as a function of comoving wavenumber k in units of
|
| Open with DEXTER | |
The smoothness (differentiability) of the sample trajectories
(Fig. 1) is a clear signature of the non-Markovianity of
the process (Eq. (4)). A general discussion of non-Markovianity
can be found in Feller (1968). As mentioned above, a non-Markovian
process can be obtained by integrating certain Markov processes. It is
well-known from diffusion theory that if one starts with the Markov
process V(t) representing particle velocities in a viscid medium,
then positions X(t) defined as
![]() form the simplest
non-Markovian process. Note that setting a complete path
form the simplest
non-Markovian process. Note that setting a complete path
![]() is not the same as setting only one position X(t)which provides the non-Markov property of X(t). In our case, the
process
is not the same as setting only one position X(t)which provides the non-Markov property of X(t). In our case, the
process ![]() can be represented as an integral over the
Ornstein-Uhlenbeck process (see Sect. 5) and is thus
non-Markovian. Moreover, the
can be represented as an integral over the
Ornstein-Uhlenbeck process (see Sect. 5) and is thus
non-Markovian. Moreover, the
![]() are Gaussian and have a
probability distribution which is similar to the probability
distribution of
are Gaussian and have a
probability distribution which is similar to the probability
distribution of
![]() .
.
The mass filter of the non-Markovian process can be derived as in Schuecker et al. (2001a) by equating the process variance (Eq. (5)) and the variance of the underlying matter
fluctuations,
A new aspect is the dependence (for T>0) of the filter on the power spectrum (Fig. 2). For standard filters, the profile does not change with P(k) and only normalization factors like the characteristic mass scale M* used to get convenient invariance properties of the halo mass function depend on P(k). In the present case the filter profile depends on P(k) and thus on the spatial correlation function. The correlation function approximates the mean shape of density peaks. Therefore, the profile of the filter roughly follows the mean profile of density peaks.
From the volume VT of the filter we can estimate the mass
![]() extracted by the filter from the mean cosmic matter
density
extracted by the filter from the mean cosmic matter
density
![]() .
The volume VT(R) is related to the Fourier
transform of Eq. (8) by
.
The volume VT(R) is related to the Fourier
transform of Eq. (8) by
For the mass function, the relation between the filter radius and mass
are needed. Therefore, Eqs. (11), (13), (15) have
to be solved for R. For n=0 we have
For n=-1 we can neglect the final exponential term in Eq. (13) which has an effect of <![]() for
for ![]() up to halo masses of
up to halo masses of
![]() .
Solving the truncated equation for
R yields
.
Solving the truncated equation for
R yields
For the case n=-2 the final exponential term in Eq. (15)
can be neglected which has an effect of <![]() for
for ![]() up to halo
masses of
up to halo
masses of
![]() .
Note that Eq. (15) without the
exponential term can also be obtained by asymptotic expansion of
Eq. (10), which is important for generalizing the present
discussion to other power spectra. Solving the truncated equation for
R yields the radius-mass relation
.
Note that Eq. (15) without the
exponential term can also be obtained by asymptotic expansion of
Eq. (10), which is important for generalizing the present
discussion to other power spectra. Solving the truncated equation for
R yields the radius-mass relation
We define the halo mass function
![]() as the number
of dark matter halos per unit volume and mass. As first shown in BCEK,
the fraction f(M) may be obtained from the first passage time
distribution function of the assumed diffusion process.
as the number
of dark matter halos per unit volume and mass. As first shown in BCEK,
the fraction f(M) may be obtained from the first passage time
distribution function of the assumed diffusion process.
![\begin{figure}
\par\includegraphics[height=5.3cm,width=5.9cm,clip]{0433fi3a.ps}\...
...{4mm}
\includegraphics[height=5.25cm,width=4.85cm,clip]{0433fi3c.ps}\end{figure}](/articles/aa/full/2004/26/aa0433-03/Timg75.gif) |
Figure 3:
Mass functions f(M) for Gaussian fluctuation fields with a power spectrum with n=0,-1,-2. Mass M in solar units: T=0, |
| Open with DEXTER | |
Let ![]() be a random variable which determines the first passage
time when
be a random variable which determines the first passage
time when
![]() achieves the critical value
achieves the critical value
![]() .
Taking into account that
.
Taking into account that
![]() ,
let us define the process
,
let us define the process
![]() obtained
by replacing the origin to
obtained
by replacing the origin to
![]() such that
such that
![]() .
Both processes are
Gaussian. Calculating the probabilities p(t) and P(t) of the
trajectories of
.
Both processes are
Gaussian. Calculating the probabilities p(t) and P(t) of the
trajectories of
![]() and
and
![]() which attain the level
which attain the level
![]() at the same moment t, we obtain
at the same moment t, we obtain
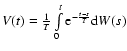 is the Ornstein-Uhlenbeck
process. Hence, increments of the processes
is the Ornstein-Uhlenbeck
process. Hence, increments of the processes
![\begin{eqnarray*}F(t)&=&P(\tau \geq t)=P(\delta (t)\leq \delta _{\rm c})-
P(\del...
...ta\sigma ^2(t)\right)^2}{2\sigma ^2(t)}\right]}{\rm d}x\right\}.
\end{eqnarray*}](/articles/aa/full/2004/26/aa0433-03/img94.gif)
The process (Eq. (4)) corresponds to a smooth filter profile and allows a simple discussion of non-Markovian effects within the excursion set model. The model includes the standard excursion set result as a limiting case, and allows non-Markovian effects to be increased gradually by the new filter parameter T.
Figure 3 shows halo mass functions f(M) for different power spectra and values of the T parameter. In all cases the non-Markovian effects described by Eq. (4) increase (decrease) the number density of high (low) mass halos. At high masses the ellipsoidality slightly decreases the number density of high mass halos and thus partially compensates non-Markovianity. At small masses both non-Markovianity and ellipsoidality decrease the number density (Fig. 4).
The result of equating the mass and the process variances in Eq. (7) is a mass filter with a profile which depends on the power spectrum of the mass distribution and thus on the mean profile
of density peaks. To show that this is a generic property of non-Markovian processes with increments determined by integrals of the form (Eq. (1)), we generalize the
![]() term in Eq. (4) by a function KT(s,t) so that Eq. (7) reads
term in Eq. (4) by a function KT(s,t) so that Eq. (7) reads
![\begin{figure}
\par\includegraphics[height=6cm,width=6.5cm,clip]{0433fig4.ps}\end{figure}](/articles/aa/full/2004/26/aa0433-03/Timg105.gif) |
Figure 4:
Mass functions f(M) for Gaussian fluctuation fields with a power spectrum with n=-2.0. Mass M in solar units. T=0, |
| Open with DEXTER | |
We further conclude that for merging and accretion processes described by the comparatively simple integration scheme (Eq. (3)), the mass filter and thus how much mass is swept in from the surrounding mass by a collapsing region must also depend on the global mass distribution, and thus on the power spectrum.
Equations (10)-(19) follow a "natural'' choice of the relation between the filter radius, used in the process of halo detection, and the halo mass as determined by the material which eventually collapses to form a virialized structure. However, other choices are also possible (BCEK) and still a matter of debate.
We further note that the application of filters to all spatial points of a density field, as proposed in all PS-like models, leads to a large scatter between filter mass and group mass. The introduction of non-Markovianity follows the same local filtering scheme and is thus not expected to significantly reduce the scatter on the halo-by-halo level.
On the statistical level, PS-like models predict mass functions, merger rates, formation times, biasing schemes etc. remarkably accurately. A comparison of the theoretical mass functions (Eq. (23)) with the results from large and high-resolution N-body simulations (e.g., Jenkins et al. 2001) should thus be more fruitful and should give more important information about the significance of non-Markovian effects.
![\begin{figure}
\par\includegraphics[height=6cm,width=6.65cm,clip]{0433fig5.ps}\end{figure}](/articles/aa/full/2004/26/aa0433-03/Timg106.gif) |
Figure 5:
Best fit mass function f(M) with T=0.23,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=4.8cm,width=5cm,clip]{0433fi6a.ps}\hs...
...ace*{2mm}
\includegraphics[height=4.8cm,width=5cm,clip]{0433fi6c.ps}\end{figure}](/articles/aa/full/2004/26/aa0433-03/Timg107.gif) |
Figure 6:
|
| Open with DEXTER | |
The Jenkins et al. (2001) mass function can be used for fluctuation fields with effective power spectrum slopes between
![]() and -1 at
and -1 at
![]() in the mass range
in the mass range
![]() .
Observations suggest a slope of about n=-2.0 (see, e.g., Schuecker et al. 2001b who found n=-1.8 on scales <
.
Observations suggest a slope of about n=-2.0 (see, e.g., Schuecker et al. 2001b who found n=-1.8 on scales <
![]() for X-ray clusters of galaxies - quite consistent with the power spectrum of galaxies, see their
Fig. 16). We thus compare with our n=-2 model.
for X-ray clusters of galaxies - quite consistent with the power spectrum of galaxies, see their
Fig. 16). We thus compare with our n=-2 model.
To be consistent with our "natural'' choice of the radius-mass
relation (Eq. (19)), the Jenkins et al. mass function
(e.g. their Eq. (9)) has to be transformed accordingly by using the
![]() relation of the non-Markovian process for n=-2. To
say it in another way, the non-Markovian effects of the process
(Eq. (3)) can only become apparent after the transformation of
relation of the non-Markovian process for n=-2. To
say it in another way, the non-Markovian effects of the process
(Eq. (3)) can only become apparent after the transformation of
![]() to f(M) because non-Markovianity changes the
radius-mass assignment scheme. Therefore, when we want to search for
non-Markovian effects we have to transform
to f(M) because non-Markovianity changes the
radius-mass assignment scheme. Therefore, when we want to search for
non-Markovian effects we have to transform
![]() of both the
theoretical and the simulated mass function and test different values
of T. For this test we multiply the prefactor
of both the
theoretical and the simulated mass function and test different values
of T. For this test we multiply the prefactor ![]() in the
normalization (Eq. (16)) by 1.234 to be consistent with the
standard
in the
normalization (Eq. (16)) by 1.234 to be consistent with the
standard ![]() normalization (obtained with the top-hat filter)
for T=0.
normalization (obtained with the top-hat filter)
for T=0.
The comparison with the Jenkins et al. (2001) mass function within the
mass range
![]() (for the lower limit see
Sect. 6.3) gives the best fit parameter values T=0.23 and
(for the lower limit see
Sect. 6.3) gives the best fit parameter values T=0.23 and
![]() with
with
![]() for three degrees of freedom
(Fig. 5). The statistical significance of the
non-Markovian effects strongly depends on the assumed error of the
Jenkins et al. mass function. For errors of 20-30%, non-Markovian
effects must be regarded as insignificant, whereas for 10% errors,
non-Markovianity is clearly detected (Fig. 6). We thus
conclude that for the most optimistic error estimates of the Jenkins
et al. mass function, its shape suggests the presence of non-Markovian
effects, i.e., effects of the environment on the coherence of the
collapse. Moreover, non-Markovian effects seem to be not very large
and cosmic mass functions with errors better than 10% are needed for
their clear detection.
for three degrees of freedom
(Fig. 5). The statistical significance of the
non-Markovian effects strongly depends on the assumed error of the
Jenkins et al. mass function. For errors of 20-30%, non-Markovian
effects must be regarded as insignificant, whereas for 10% errors,
non-Markovianity is clearly detected (Fig. 6). We thus
conclude that for the most optimistic error estimates of the Jenkins
et al. mass function, its shape suggests the presence of non-Markovian
effects, i.e., effects of the environment on the coherence of the
collapse. Moreover, non-Markovian effects seem to be not very large
and cosmic mass functions with errors better than 10% are needed for
their clear detection.
![\begin{figure}
\par\includegraphics[height=5.65cm,width=5.7cm]{0433fig7.ps}\end{figure}](/articles/aa/full/2004/26/aa0433-03/Timg118.gif) |
Figure 7:
|
| Open with DEXTER | |
It should be mentioned that we simultaneously tested in Fig. 6 for the significance of the scaling parameter aintroduced by SMT to account for a failure of the simple counting argument of the excursion set formalism (R. Sheth, private communication). The best fit has a=0.99 (Fig. 7) which means that the inclusion of non-Markovian effects does not require this correction. Therefore, the likelihood contours in Fig. 6 are only plotted in the a=1 plane.
The effects of ellipsoidality on the halo mass function are in general
much larger and are detected for all random errors ![]()
![]() with
clear significance. The best fit
with
clear significance. The best fit
![]() is lower than
is lower than
![]() obtained from simulations (see Sect. 2). In
addition, the model starts to deviate from the Jenkins et al. function
at masses smaller than
obtained from simulations (see Sect. 2). In
addition, the model starts to deviate from the Jenkins et al. function
at masses smaller than
![]() .
In order to understand
these failures of the model one should not forget that our goal to
give a full analytic treatment of the problem forces us to approximate
the ellipsoidal collapse by a linear drift. Sheth & Tormen (2002)
give a simple prescription for approximating the solution to the
general barrier in the Markov case which better fits the low-mass
range. Therefore, a useful direction for future work is to see if
their method works in our particular non-Markovian context also.
.
In order to understand
these failures of the model one should not forget that our goal to
give a full analytic treatment of the problem forces us to approximate
the ellipsoidal collapse by a linear drift. Sheth & Tormen (2002)
give a simple prescription for approximating the solution to the
general barrier in the Markov case which better fits the low-mass
range. Therefore, a useful direction for future work is to see if
their method works in our particular non-Markovian context also.
Future observed mass functions from e.g. X-ray clusters of galaxies and lensing studies have high enough precision for detailed studies of non-Markovian effects expected in the high-mass regime. On the theoretical side, further studies are in preparation to predict mass functions also for Cold Dark Matter power spectra to improve the comparison with observed and simulated mass functions.
Acknowledgements
We would like to thank Hans Böhringer, Gerard Lemson, Gabriel Pratt, Ravi Sheth, and the anonymous referee for helpful comments on the manuscript. GGA is partially supported by INTAS grant No. 00-738 and PS by DLR grant No. 50 OR 0108.
A summary is given of the equations used for the computation of the dark matter halo mass functions discussed in the main text. The meaning of the different symbols is as follows.
![]() dark matter mass function as a function of the variance
dark matter mass function as a function of the variance ![]() of the random mass field or of the diffusion process. f(M) dark matter halo mass function as a function of mass M.
of the random mass field or of the diffusion process. f(M) dark matter halo mass function as a function of mass M.
![]() critical density threshold.
critical density threshold. ![]() parameter regulating the ellipsoidality of the collapse (
parameter regulating the ellipsoidality of the collapse (![]() spherical collapse). T parameter regulating the coherence of the collapse,
i.e., the deviation from Markovianity (T=0 traditional Markovian
excursion set model). P0 amplitude of the scale-invariant power spectrum in
P(k)=P0kn with the spectral index n.
spherical collapse). T parameter regulating the coherence of the collapse,
i.e., the deviation from Markovianity (T=0 traditional Markovian
excursion set model). P0 amplitude of the scale-invariant power spectrum in
P(k)=P0kn with the spectral index n.
![]() mean cosmic matter density.
mean cosmic matter density. ![]() normalized cosmic matter
density. h Hubble constant in units of
normalized cosmic matter
density. h Hubble constant in units of
![]() .
t pseudo diffusion time or mass resolution variable. R filter radius. W(z) the principal branch of the Lambert W-function.
.
t pseudo diffusion time or mass resolution variable. R filter radius. W(z) the principal branch of the Lambert W-function.
![]() ,
,
![]() auxiliary
functions, and
auxiliary
functions, and
![]() ,
,
![]() their derivatives with respect to M.
their derivatives with respect to M.
The mass functions
![]() with the spectral indices n=0,-1,-2have the same form
with the spectral indices n=0,-1,-2have the same form
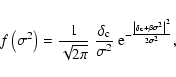 |
(A.1) |
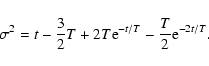 |
(A.2) |
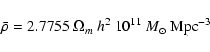 |
(A.3) |
Dark matter halo mass function:
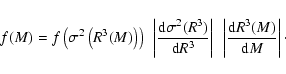 |
(A.4) |
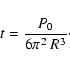 |
(A.5) |
![\begin{displaymath}%
R^3 = \frac{M}{6\pi^2\bar{\rho}+\frac{6\pi^2TM}{P_0}\left[1+W(z)\right]}\cdot
\end{displaymath}](/articles/aa/full/2004/26/aa0433-03/img132.gif) |
(A.6) |
![\begin{displaymath}%
P_0 = 3072\pi^2\left\{\sigma_8^2 + 1.98T\left[1-{\rm e}^{-\left(\sigma_8^2/T\right)^{0.363}}\right]\right\}.
\end{displaymath}](/articles/aa/full/2004/26/aa0433-03/img133.gif) |
(A.7) |
![\begin{displaymath}%
z = -\exp{\left[-\left(1+\frac{\bar{\rho}P_0}{MT}\right)\right]}
\end{displaymath}](/articles/aa/full/2004/26/aa0433-03/img134.gif) |
(A.8) |
![$\displaystyle %
\frac{{\rm d}R^3}{{\rm d}M}=\frac{1}{6\pi^2\bar{\rho}+\frac{6\p...
...(z)}\right\}}
{6\pi^2\left\{\bar{\rho}P_0+TM\left[1+W(z)\right]\right\}^2}\cdot$](/articles/aa/full/2004/26/aa0433-03/img135.gif) |
(A.9) |
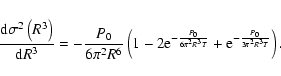 |
(A.10) |
Dark matter halo mass function:
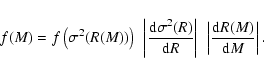 |
(A.11) |
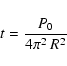 |
(A.12) |
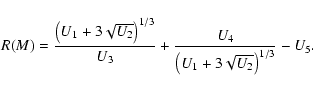 |
(A.13) |
![\begin{displaymath}%
P_0=256\pi^2\left[\sigma_8^2+1.98~T\left(1-
{\rm e}^{-\left(\frac{\sigma_8^2}{T}\right)^{0.363}}\right)\right]~{\rm Mpc}^2.
\end{displaymath}](/articles/aa/full/2004/26/aa0433-03/img55.gif) |
(A.19) |
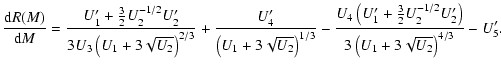 |
(A.20) |
| (A.21) | |||
| (A.22) | |||
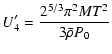 |
(A.23) | ||
| (A.24) |
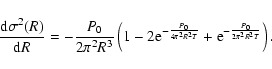 |
(A.25) |
Dark matter halo mass function:
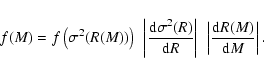 |
(A.26) |
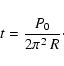 |
(A.27) |
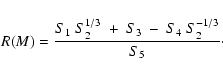 |
(A.28) |
| (A.31) | |||
| (A.32) | |||
| (A.33) |
![\begin{displaymath}%
P_0=16\pi^2\left[\sigma_8^2+1.98~T\left(1-
{\rm e}^{-\left(\frac{\sigma_8^2}{T}\right)^{0.363}}\right)\right]~{\rm Mpc}
\end{displaymath}](/articles/aa/full/2004/26/aa0433-03/img160.gif) |
(A.34) |
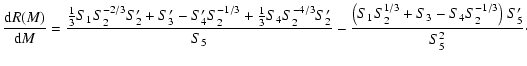 |
(A.35) |
| S2' | = | ||
| (A.36) | |||
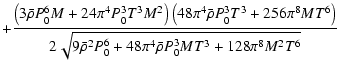 |
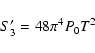 |
(A.37) |
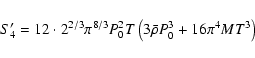 |
(A.38) |
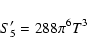 |
(A.39) |
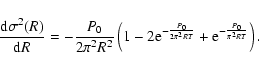 |
(A.40) |