A&A 421, 399-405 (2004)
DOI: 10.1051/0004-6361:20040244

Search for low energy $\nu $ in correlation with the 8 events observed by the EXPLORER and NAUTILUS detectors in 2001[*]

M. Aglietta1 - P. Antonioli2 - G. Bari2 - C. Castagnoli1 - W. Fulgione1,[*] - P. Galeotti1 - M. Garbini2 - P. L. Ghia1 - P. Giusti2 - F. Gomez1 - E. Kemp3 - A. S. Malguin4 - H. Menghetti2 - A. Porta1 - A. Pesci2 - I. A. Pless5 - V. G. Ryasny4 - O. G. Ryazhskaya4 - O. Saavedra1 - G. Sartorelli2 - M. Selvi2 - D. Telloni1 - C. Vigorito1 - L. Votano6 - V. F. Yakushev4 - G. T. Zatsepin4 - A. Zichichi2


1 - IFSI - CNR, Torino, University of Torino and INFN-Torino, Italy
2 - University of Bologna and INFN-Bologna, Italy
3 - University of Campinas, Campinas, Brazil
4 - Institute for Nuclear Research, Russian Academy of Sciences, Moscow, Russia
5 - Massachusetts Institute of Technology, Cambridge, USA
6 - INFN-LNF, Frascati, Italy

Received 11 February 2004 / Accepted 15 March 2004

Abstract
We report on a search for low-energy neutrino (antineutrino) bursts in correlation with the 8 time coincident events observed by the gravitational waves detectors EXPLORER and NAUTILUS (GWD) during the year 2001.
The search, conducted with the LVD detector (INFN Gran Sasso National Laboratory, Italy), has considered several neutrino reactions, corresponding to different neutrino species, and a wide range of time intervals around the (GWD) observed events. No evidence for statistically significant correlated signals in LVD has been found.
Assuming two different origins for neutrino emission, the cooling of a neutron star from a core-collapse supernova or from coalescing neutron stars and the accretion of shocked matter, and taking into account neutrino oscillations, we derive limits to the total energy emitted in neutrinos and to the amount of accreting mass, respectively.

Key words: neutrinos - gravitational waves

1 Introduction

The analysis of the data collected in coincidence by the gravitational wave bar detectors EXPLORER and NAUTILUS during the year 2001 (Astone et al. 2002) shows an excess (8 events against 2.6 expected from the background) when the two detectors are favorably oriented with respect to the Galactic Disc. Moreover, this result comes from the present day most sensitive experiments for the detection of gravitational wave bursts and a search for neutrino bursts in correlation with the 8 GWD events is, therefore, appropriate.

A few astrophysical transient sources are indeed expected to produce associated bursts of neutrinos and gravitational waves. It is well known that most of the energy ($99\%$) released in the gravitational core collapse of a massive star is carried away by neutrinos originated both from the matter accretion in the shock and from the cooling of the proto-neutron star (see for example Burrows et al. 1992). Depending on the collapse dynamics, some fraction of the total energy is emitted in GW (Thorne 1988; Muller 1997), asymmetric supernovae in our Galaxy being the best candidate sources for GW bar detectors. Two coalescing neutron stars would also constitute a source for both neutrinos and gravitational waves. From the point of view of GW emission, it is likely that the merging event would produce powerful gravitational wave bursts, and, even if the physics of the merger is not known, there are estimates that, for binary systems of large mass, coalescence waves are likely to be stronger than the inspiral ones. Some amount of the kinetic energy is converted in thermal energy so that the hot remnant would probably emit thermal neutrinos.

The search for a neutrino burst associated to the events detected by the GWD EXPLORER and NAUTILUS in 2001 has been performed with the LVD apparatus, operating in the INFN Gran Sasso National Laboratory (Italy) since 1992 with the main purpose of searching for neutrinos from gravitational stellar collapses within the whole Galaxy.

The paper is planned as follows: in Sect. 2 we briefly describe the LVD detector, and we explain the selection of the data. In Sect. 3 we present the results of the analysis: a time interval spanning from 12 h preceding each of the 8 events up to 12 h later, has been scanned, searching for any excess over the statistical fluctuation of the background. Further, a search for a $\nu $signal coincident in time with every event has been performed. We conclude in Sect. 4, where we discuss the results of the search, taking into account $\nu $ oscillations, and considering the two processes for $\nu $ emission, i.e., cooling and accretion. Since we do not find any neutrino burst candidate associated with the 8 GWD mentioned events, we derive upper limits:

2 The LVD experiment and the data selection

The Large Volume Detector (LVD) in the INFN Gran Sasso National Laboratory, Italy, consists of an array of 840 scintillator counters, 1.5 m3 each, interleaved by streamer tubes, arranged in a compact and modular geometry (see Aglietta et al. 1992, for a detailed description). The active scintillator mass is M=1000t. The experiment has been taking data, under different larger configurations, since 1992, and reached its final one during 2001.

There are two subsets of counters: the external ones ($43 \%$), operated at energy threshold ${\cal E}_{\rm h}\simeq 7$ MeV, and inner ones ($57 \%$), better shielded from rock radioactivity and operated at ${\cal E}_{\rm h}\simeq 4$ MeV. To tag the delayed $\gamma$pulse due to n-capture, all counters are equipped with an additional discrimination channel, set at a lower threshold, ${\cal E}_{\rm l}\simeq 1$ MeV.

The main purpose of the telescope is the detection of neutrinos from gravitational stellar collapses in the Galaxy. In the following we will focus on $\nu $ reactions with free protons and  $^{12}{\rm C}$ nuclei, constituting the bulk of the expected signal and having the best signature in the detector, namely:

After being subjected to a preliminary process to reject muons, the raw data are grouped in three different classes, with specific signatures to tag the different described reactions:
1.
IBD class (inverse beta decay): pulses with $E_{\rm d} \geq {\cal E}_{\rm h}$ followed by a delayed ( $\Delta t \leq 1 {\rm ms}$) low energy ( $E_{\rm d}>{\cal E}_{\rm l}$) pulse in the same counter. The efficiency in tagging the n-capture is $\epsilon=60$% for the core counters, $\epsilon=50$% for the whole detector;
2.
NC class (neutral current): pulses with 11  ${\rm MeV} \leq E_{\rm d} \leq 17.5$ MeV, the efficiency in tagging the $\gamma$ from $^{12}{\rm C}$ de-excitation being $\epsilon=55$%
3.
CC class (charged current): two pulses with $E_{\rm d} \geq {\cal E}_{\rm h}$ MeV, within $\Delta t \leq 150~ {\rm ms}$, in the same counter. The efficiency in tagging the $^{12}{\rm N}$ and $^{12}{\rm B}$ decay are $\epsilon=85$% and $\epsilon=70$%, respectively.

3 The analysis

The LVD detector is sensitive to neutrino bursts from core collapse supernovae within the whole Galaxy (Aglietta et al. 1992). The scintillator counting rate is continuously monitored: all the events are examined on-line on the basis of their time sequence. Neutrino burst candidates are identified as clusters of scintillator counter pulses with an imitation frequency less than a predefined threshold (Fulgione et al. 1996). During the year 2001, no neutrino burst candidate has been evidenced, thus allowing to conclude that no $\nu $ signal from gravitational stellar collapse in the Galaxy has been detected (Aglietta et al. 2003).

However, the absence of candidates in the LVD detector taken alone does not preclude the possibility of positive effects, when combining it with another detector, since the joint measurement allows to increase the sensitivity. The analysis in correlation with the 8 candidate events has then been conducted, in four steps described in the following.

3.1 Step 1. Check of the detector stability

First of all, the LVD detector performance at the occurrence of the 8 GW events (see the list in Astone et al. 2002) has been checked by studying the behavior of the counting rate in a 24 h interval around the time of each of them.

  \begin{figure} \par\includegraphics[height=10cm,width=8.8cm,clip]{0244fig1.eps} \end{figure} Figure 1: Distributions of the deviations of n15 (see text), with respect to $\langle n_{15}\rangle$, for events of IBD class ( top) and NC class ( middle), and n15 distribution, for CC class ( bottom). The superimposed dashed lines are the fits to zero mean and unit-width Gaussians (IBD and NC) and Poissonian (CC).
Open with DEXTER

For each event, the 24 h average of the number of counts every 15 min, $\langle n_{15}\rangle$, is evaluated: including all the 8 events, we show in Fig. 1 the distributions of the deviations of n15, with respect to $\langle n_{15}\rangle$, for events of IBD class (top) and NC class (middle); for CC class (bottom), due to the small $\langle n_{15}\rangle$, we directly show the n15 distribution. They have been fitted with zero mean and unit-width Gaussians (IBD and NC) and Poissonian (CC): they are shown superimposed in the same figures, together with the resulting reduced $\chi^2$ values. The LVD counting rate, for all the 8 events and all the data classes, is then well understood in terms of Poissonian statistics: this sets a firm base for the following steps.

3.2 Step 2. Search in a sliding window

The search for a possible $\nu $ burst has been conducted in a 24 h interval T around the occurrence of each of the 8 events. The 8 intervals have been scanned through a "sliding window'' of variable duration: more in detail, they have been divided into $N_{\delta t} = 2 \cdot \frac{T}{\delta t }-1$ intervals of different duration $\delta t$, each one starting at the middle of the previous one. The multiplicity distributions of clusters (i.e., the number of events within each $\delta t$) have then been studied for the three classes of data and for $\delta t =1,5,10,20,50,100$ s, and have been compared with the expectations from Poissonian fluctuations of the background.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{0244fig2.eps} \end{figure} Figure 2: Distributions of cluster multiplicities, for IBD class events ( top), NC class ( medium), CC class ( bottom), together with expectations from Poissonian fluctuations, in the case of GW event n.5.
Open with DEXTER

We show as an example the case of GW event n.5: the distributions of cluster multiplicity, for events of IBD class (top), NC class (middle) and CC class (bottom), in the case of the 6 different $\delta t$, can be seen in Fig. 2, together with the expectations from Poissonian fluctuations of the background, the relative reduced $\chi^2$ values ranging from 0.1 to 1.2. The agreement between data and expectations holds also in the case of the other seven events. This, together with the check of the Poissonian probabilities associated to each measured multiplicity, in each class and for each event, allows to state that there is no evidence for any detectable $\nu $ signal in correspondence of any of the considered events.

3.3 Step 3. Search in a fixed window

The search for a $\nu $ signal in coincidence with every GW event has been further conducted using a "fixed window'' centered at the time of each of them. In particular, for each data class, we compare the number of pulses ($N_{\rm d}$), recorded during time windows of different duration $\delta t$, centered on each event time, with the average number of pulses expected from background, $N_{{\rm bk}}$. The value of  $N_{{\rm bk}}$ is evaluated by using the rate in the 24 h around each event, excluding the contribution of the central portion of time to avoid the contamination due to a possible signal. Results corresponding to $\delta t = 1,5,10,20,50,100~$s, for each of the 8 events, are summarized in Tables 1, 2 for IBD and NC classes, respectively. The table relative to CC class is not shown since in all the cases $N_{\rm d}=0$, and $N_{{\rm bk}}<3\times 10^{-2}$.

Table 1: IBD class: number of events detected in coincidence with the 8 GW events, for different durations of the time window ($\delta t$), compared with the expectations from the background. The effective LVD mass, M, at the time of each event is also shown.

Table 2: NC class: number of events detected in coincidence with the 8 GW events, for different durations of the time window ($\delta t$), compared with the expectations from the background. The effective LVD mass, M, at the time of each event is also shown.

The differences between $N_{\rm d}$ and $N_{{\rm bk}}$ are within the statistical fluctuations, for all data classes and for all the events. The most significant effect is observed in correspondence of GW event n.5: 11 pulses detected against 3.4 expected, when using IBD class data and $\delta t = 100$ s. Taking into account the number of trials ( $8\times 3\times 6$), the associated chance probability is P=0.03. In order to check the consistency of such an effect with a physical one, we complete the coincidence analysis with the study of the time distribution of both high and low energy signals.

3.4 Step 4. Time distribution of pulses

We have studied the time distribution of LVD pulses around each GW event. Figure 3 shows such a distribution for each of the 8 events (and for their sum), for IBD data (full line) and NC data (dash-dotted line), (t=0 corresponds to the time of the GW event): no particular time structure is present.

Finally, for IBD class data, we have also checked the time distribution of secondary pulses (i.e., those possibly due to neutron capture) with respect to the prompt ones. The measured distribution is uniform and compatible with the one expected in the case of pure background, where delayed and prompt signals are uncorrelated and the distribution of the differences in time is flat (on the contrary, if the pulses were due to  $\bar\nu_{\rm e}$interactions with protons, the distribution of time delays should show an exponential behavior, with $\tau \sim 180~ \mu\rm s$, corresponding to the average capture time of neutrons in the LVD counters).

4 Calculation of upper limits

4.1 Upper limits on neutrino fluence

No evidence for any statistically relevant signal in LVD, in the three considered reaction channels (corresponding to different neutrino species) and over a wide range of time durations, has been found in correspondence of any of the 8 excess events detected in coincidence by NAUTILUS and EXPLORER.

In the absence of any $\nu $ signal, we calculate $90\%$ C.L. neutrino fluence upper limits at the detector without assuming particular energy spectra, i.e., on mono-energetic neutrinos at different energies:

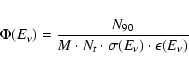\begin{displaymath}\Phi(E_{\nu})=\frac{N_{90}}{M \cdot N_t \cdot \sigma(E_{\nu}) \cdot \epsilon(E_{\nu}) } \end{displaymath} (1)

where: N90 is the $90\%$ c.l. upper limit on the number of LVD signals per GW event, obtained following Montanet et al. (1994) in the case of Poisson processes with background. The considered background value represents the total number of expected background events for all the 8 GWD events; the signal value, as well, is the total number of detected events for all the 8 GWD events. M is the detector active mass in ton (summed over the 8 events); $N_{\rm t}$ is the number of targets per ton (either protons or  $^{12}{\rm C}$ nuclei); $\varepsilon$ is the detection efficiency; $\sigma(E_{\nu})$ is the appropriate cross section. Results are shown in Table 3 for $\delta t =20~\rm s$ and $100~\rm s$.
  \begin{figure} \par\includegraphics[height=8.8cm,width=8.8cm,clip]{0244fig3.eps} \end{figure} Figure 3: Time distribution (bin = 5 s) of the detected pulses (full line for IBD class data and dash-dotted line for NC class data) around the corresponding GW event time (t=0); the bottom panel shows the distribution for the 8 events taken together.
Open with DEXTER

Table 3: Fluence upper limits ($90\%$ C.L.) for neutrinos of different energies, obtained from IBD and NC classes of events.

This model independent fluence can be used to test a specific model (characterized by $\Phi_{\rm test}(E_{\nu})$) by performing the convolution:

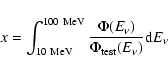\begin{displaymath}x = \int^{100 ~\rm MeV}_{10 ~\rm MeV} \frac{\Phi(E_{\nu})}{\Phi_{\rm test}(E_{\nu})} {\rm d}E_{\nu} \end{displaymath} (2)

and if the quantity x is less (greater) than 1.0, the model predicts more (fewer) events than the event limit N90, and is therefore excluded (not excluded) at the $90\%$ confidence level.

4.2 A model dependent interpretation

We can discuss the result of the search within two possible simplified scenarios for neutrino production, namely (i) thermal emission (which we will call "cooling'') and (ii) non thermal emission (which we will address as "accretion'').

We assume that the 8 events are due to a unique kind of source and that the distance to the hypothetical sources is d=10 kpc, since the 8 GWD events are consistent with a galactic origin.

Concerning neutrino oscillations (Dighe & Smirnov 2000; Takahashy et al. 2001; Aglietta et al. 2002), due to the unknown $\nu $ oscillation parameters, i.e., $\vert U_{\rm e3}\vert^2$ and the mass hierarchy, we consider four different cases:

1 -
normal mass hierarchy with adiabatic transition at the high density (H) resonance ( $\rm NH_{\rm ad}$);
2 -
normal mass hierarchy with non-adiabatic transition at the H resonance ( $\rm NH_{\rm non-ad}$);
3 -
inverted mass hierarchy with adiabatic transition at the H resonance ( $\rm IH_{\rm ad}$);
4 -
inverted mass hierarchy with non-adiabatic transition at the H resonance ( $\rm IH_{\rm non-ad}$).
More details on the effect of neutrino oscillations in the supernova neutrino signal in LVD can be found in (LVD coll. 2004).

We refer to Appendix A for details on the calculation of the number of events in each detection channel.

4.2.1 Cooling
In the simplified "cooling'' process we are considering (for example in the case of a newly formed neutron star), neutrinos of every flavor are emitted by electron-positron annihilation ( ${\rm e^- e}^+,\nu_i \bar\nu_i$, $i=e,\mu,\tau$) with thermal spectra, that is, we are assuming zero pinching. We assume exact equipartition of the total emitted energy EB among all neutrino flavors ( $E_{\nu_i}=f_{\nu_i} E_B$ with $f_{\nu_i}=1/6$) and a hierarchy of the mean temperatures of the different flavors $T_{\nu_x}>T_{\bar\nu_{\rm e}}=T_{\nu_{\rm e}}$ ( $x=\mu,\tau$). The characteristics of this emission process and the numerical values used are summarized in Table 4 and in the Appendices.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{0244fig4.eps} \end{figure} Figure 4: $90\%$ c.l. limits to the total energy emitted in neutrinos, in the cooling process, during 20 s, assuming pure Fermi-Dirac spectrum. The dashed line represents the $\rm IH_{\rm ad}$ case, while the other three cases are represented by the solid curve. The limit obtained through NC events is represented by the dash-dotted line.
Open with DEXTER

The limits obtained using IBD events - which are the most stringent (see the appendices for the calculation) - in terms of total emitted energy EB, are shown in Fig. 4 as a function of $T_{\bar \nu_{\rm e}}$, in the case of exact energy equipartition among all flavors, with $T_{\nu_x}=1.5 T_{\bar \nu_{\rm e}}$ and $\delta t = 20~$s[*]. The dashed line represents the  $\rm IH_{\rm ad}$ case, while the other three cases are not distinguishable among them and are represented by the solid curve. For the sake of completeness, we show in the same figure the limit obtained through NC events (dash-dotted line) which is independent on $\nu $ flavor.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{0244fig5.eps} \end{figure} Figure 5: $90\%$ c.l. limits to the total accretion mass, multiplied by the factor $Y_{\rm n}$, as a function of $T_{\bar \nu_{\rm e}}$. The solid line represents the limits obtained using IBD interactions in the case of NH and $\rm IH_{\rm non-ad}$, the dash-dotted one refers to limit derived through NC events.
Open with DEXTER

As an example for the case of cooling, we show in the same figure the total energy expected to be emitted in two of the most probable sources: a new-born neutron star (Keil et al. 2002, and references therein) empty box, and colliding neutron stars, full box (Ruffert & Janka 1998).

4.2.2 Accretion
During matter accretion in a neutron-rich ambient, another process appears to generate $\nu $ emission (see e.g. Loredo & Lamb 2002): ${\rm e}^{\pm}$ pairs, created in the accreting matter, are captured by protons and neutrons and the resulting $\nu $fluxes have the following characteristics: (i) only $\nu_{\rm e}$ and $\bar\nu_{\rm e}$ are emitted; (ii) the thermal energy spectrum is multiplied for a $E_{\nu}^2$ term accounting for the capture cross section energy dependence. The characteristics of this emission process and the numerical values are shown in Table 4. The obtained limits (see the appendices for the calculation) in terms of accretion mass multiplied by the neutron fraction of accreting matter, Yn, are shown in Fig. 5, as a function of $T_{\bar \nu_{\rm e}}$. The solid line represents the limits obtained using IBD interactions in the case of NH and $\rm IH_{\rm non-ad}$. Since for $\rm IH_{\rm ad}$ only a minimum part ( $\vert U_{\rm e3}\vert^2$) of the original $\bar\nu_{\rm e}$ flux will interact as $\bar\nu_{\rm e}$, we do not use the IBD events. It still remains valid the one obtained with NC events, represented by the dash-dotted line.

Table 4: Characteristics of the considered processes of $\nu $ emission and numerical values used in the limits calculation.

As an example, we show in the same figure (full box) the amount of accreted matter (multiplied by Yn=0.5) expected for coalescing neutron stars (Ruffert & Janka 2001).

5 Conclusions

We have conducted a search for low-energy antineutrino (neutrino) bursts with the LVD detector in coincidence with the 8 event excess found by the gravitational waves detectors EXPLORER and NAUTILUS during the year 2001.

We have found no evidence for any statistically relevant signal in LVD, in three different reaction channels (inverse beta decay, charged current and neutral current interactions with  $^{12}{\rm C}$) corresponding to different neutrino species, over a wide range of time durations, for any of the 8 events. Consequently, we have derived $90\%$ fluence upper limits to antineutrino and neutrino emission from an average GW event, at different energies in the range of sensitivity of the LVD detector.

We have then related the result of the search with two possible simplified models for neutrino emission, i.e., "cooling'' and "accretion'', deriving limits, on the one side, to the total energy emitted in neutrinos at the source, and, on the other, to the amount of accreting mass. Assuming a source distance d=10 kpc, possible candidates as new-born and colliding neutron stars have been excluded by this analysis. This makes even more challenging and interesting the search for a likely astrophysical source for the reported GWD events.

Acknowledgements
The authors are grateful to the director and the staff of the National Gran Sasso Laboratory for their constant and valuable support. The authors thank precious comments by Francesco Vissani.

References

  Online Material

Appendix A: Limits calculation: Inverse $\beta $ decay interactions

The number of $\bar\nu_{\rm e}$ interactions due to inverse beta decay in a detector is given by:

 \begin{displaymath}N_{\rm ev}^{\rm IBD}=M \cdot N_{\rm p} \cdot \int_{Q}^{\infty... ...\varepsilon(E_{\rm d},E_{\rm th}) {\rm d}E_{\bar{\nu}_{\rm e}} \end{displaymath} (3)

where: M is the detector active mass in ton; $N_{\rm p}=9.36\times 10^{28}$ is the number of free protons per ton; $\varepsilon_{\rm n}$ is the neutron detection efficiency; $\varepsilon(E_{\rm d},E_{\rm th})$ is the ${\rm e}^+$ detection efficiency; $E_{\rm d}=E_{\bar{\nu}_{\rm e}}-Q+2m_{\rm e}c^2$, with $Q=M_{\rm n}+m_{\rm e}-M_{\rm p}=1.8$ MeV is the positron detectable energy; $E_{\rm th}$ is the detector energy threshold; $\sigma(E_{\bar{\nu}_{\rm e}})$ is the cross section (Vogel & Beacom 1999; Strumia & Vissani 2003); $\frac{{\rm d}N_{\bar\nu_{\rm e}}}{{\rm d}E_{\bar\nu_{\rm e}}}$ is the antineutrino energy spectrum.

In the case of cooling process it is:

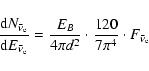\begin{displaymath}\frac{{\rm d}N_{\bar\nu_{\rm e}}}{{\rm d}E_{\bar\nu_{\rm e}}}... ...}{4\pi d^2} \cdot \frac{120}{7\pi^4} \cdot F_{\bar\nu_{\rm e}} \end{displaymath} (4)

where $d=10~\rm kpc$ is the assumed source distance; $E_{B} = \sum_{i}f_{\nu_i}E_{B}$ is the total energy emitted in neutrinos; $F_{\nu}$ is the term accounting for different $\nu $ oscillation scenarios[*]: with: $\vert U_{\rm e1}\vert^2 \approx \cos^2\theta_{12}=0.67$, $\vert U_{\rm e2}\vert^2 \approx \sin^2\theta_{12}=0.33$, $\vert U_{\rm e3}\vert^2 \geq 10^{-4}$ for the adiabatic case and $\vert U_{\rm e3}\vert^2 \leq 10^{-6}$ for the non adiabatic one (Apollonio et al. 1999; Bahcall & Pena-Garay 2003).

In the case of mass accretion process it is (Loredo & Lamb 2002):

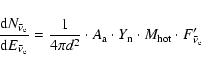\begin{displaymath}\frac{{\rm d}N_{\bar\nu_{\rm e}}}{{\rm d}E_{\bar\nu_{\rm e}}}... ...} \cdot Y_{\rm n} \cdot M_{\rm hot} \cdot F'_{\bar\nu_{\rm e}} \end{displaymath} (7)

where: $M_{\rm hot}$ is the mass of hot emitting material; $Y_{\rm n}$ is the neutron fraction; $A_{\rm a}=\frac{1+3g^2_A}{8}\frac{\sigma_{0}c}{m_{\rm n}(m_{\rm e}c^2)^2}\frac{8\pi}{(hc)^3}$, with gA=1.254, $\sigma_{0}=1.7 \times 10^{44} ~\rm cm^2$; and with respect to $F'_{\nu}$:

Appendix B: Limits calculation: Neutral current interactions

The number of interactions in the detector due to the neutral current is given by:

 \begin{displaymath}N_{ev}^{\rm NC}=M \cdot N_{\rm C} \cdot \varepsilon_{\rm C} \... ..._{\nu_i}}{{\rm d}E_{\nu_i}} \sigma(E_{\nu_i})\right] {\rm d}E~ \end{displaymath} (10)

where: $N_{\rm C}=4.24\times 10^{28}$ is the number of $^{12}{\rm C}$ nuclei per ton; $\varepsilon_C$ is the detector efficiency for 15.1 MeV gamma; $\sigma(E_{\nu})$ is the cross section (Fukugita et al. 1988).

The neutrino energy spectrum in the case of cooling process is:

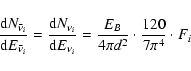\begin{displaymath}\frac{{\rm d}N_{\bar\nu_i}}{{\rm d}E_{\bar\nu_i}}=\frac{{\rm ... ...}= \frac{E_{B}}{4\pi d^2} \cdot \frac{120}{7\pi^4} \cdot F_{i} \end{displaymath} (11)

with $F_i= \frac{f_{\nu_{\rm e}}}{T_{{\nu}_{\rm e}}^4}\frac{E^2}{1+{\rm e}^{E/ T_{{\n... ...+ 2 \cdot \frac{f_{\nu_x}}{T_{{\nu}_x}^4}\frac{E^2}{1+{\rm e}^{E/ T_{{\nu}_x}}}$
while, for the mass accretion case, we considered all the events as $\bar\nu_{\rm e}s$ and we used:

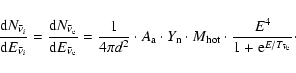\begin{displaymath}\frac{{\rm d}N_{\bar\nu_i}}{{\rm d}E_{\bar\nu_i}}=\frac{{\rm ... ...ot} \cdot \frac{E^4}{1+{\rm e}^{E/ T_{\bar \nu_{\rm e}}}}\cdot \end{displaymath} (12)


Copyright ESO 2004