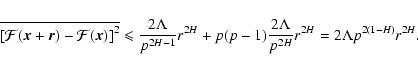A&A 421, 387-398 (2004)
DOI: 10.1051/0004-6361:20047139
Velocity centroids and the structure of interstellar turbulence
I. Analytical study![[*]](/icons/foot_motif.gif)
F. Levrier
LERMA / LRA - UMR 8112 du CNRS, École normale supérieure, 24 rue Lhomond, 75231 Paris Cedex 05, France
Received 26 January 2004 / Accepted 15 March 2004
Abstract
We present an analytical study of the statistical properties of integrated emission and velocity centroids for a slightly compressible turbulent slab model, to retrieve the underlying statistics of three-dimensional density and velocity fluctuations. Under the assumptions that the density and velocity fields are homogeneous and isotropic, we derive the expressions of the antenna temperature for an optically thin spectral line observation, and of its successive moments with respect to the line of sight velocity component, focusing on the zeroth (intensity or integrated emission I) and first (non-normalized velocity centroid C) moments. The ratio of the latter to the former is the normalized centroid C0, whose expression can be linearized for small density fluctuations. To describe the statistics of I, C and C0, we derive expansions of their autocorrelation functions in powers of density fluctuations and perform a lowest-order real-space calculation of their scaling behaviour, assuming that the density and velocity fields are fractional Brownian motions. We hence confirm, within the scope of this study, the property recently found numerically by Miville-Deschênes et al. (2003a) that the spectral index of the normalized centroid is equal to that of the full velocity field. However, it is also argued that, in order to retrieve the velocity statistics, normalization of centroids may actually not be the best way to remove the influence of density fluctuations. In this respect, we discuss the modified velocity centroids introduced by Lazarian & Esquivel (2003) as a possible alternative. In a following paper, we shall present numerical studies aimed at assessing the validity domain of these results.
Key words: ISM: structure - methods: analytical - turbulence
The proper exploitation of astronomical observations requires one to deal with several problems to accurately describe the objects and processes under study. In particular, regarding the physics of the interstellar medium (ISM), it should be stressed that spectral emission data depends on the velocity field solely via its component along the line of sight, through Doppler shifts. Furthermore, this information is necessarily integrated along the line of sight, and radiative transfer leads to expressions in which the contributions of the density and velocity fields are mixed in a complex way (Hegmann & Kegel 2000). Hence, to describe the physical conditions and processes in the ISM, one has to rely on a single number (e.g. antenna temperature) for any given direction in the plane of the sky and any given velocity along the line of sight. Although the comparison of antenna temperatures for various tracers helps, it is necessary to solve an inverse problem to have access to the three-dimensional properties of the medium, such as density and velocity, and compare them with various models, for instance to assess the roles of gravity, magnetic field or turbulence.
Indeed, it is now recognized that the different components of the ISM are subjected to turbulent motion. This has been observed in the ionized gas (Van Langevelde et al. 1992), in HII regions (O'Dell & Castaneda 1987) and in the neutral atomic phase (Miville-Deschênes et al. 2003b; Spicker & Feitzinger 1988), but molecular cloud studies are by far the most numerous (see e.g. Kleiner & Dickman 1985a; Kitamura et al. 1993; Miesch & Bally 1994). Estimates of Reynolds numbers from molecular viscosity in these clouds are of the order of 108, consistent with turbulent flows (Chandrasekhar 1949). Moreover, molecular lines in this phase exhibit suprathermal widths over a wide range of spatial scales, from a few km s-1 in small dark clouds to a few tens of km s-1 in giant complexes, while the thermal dispersion is only of about 0.3 km s-1 for molecular hydrogen at T=10 K. These linewidths scale as a power-law of the cloud's size (Larson 1981), with an exponent close to that predicted by the classical theory of turbulence (Kolmogorov 1941). Such random motions within molecular clouds may in turn account for a number of other properties of spectral lines (Baker 1976), as well as provide support against gravitational collapse, explaining the fact that the lifetime of molecular clouds is larger than their free-fall time (Scalo 1985) and that the star formation rate is therefore much smaller than predicted by gravitationally collapsing cloud models (Zuckerman & Evans 1974).
Because of this interplay between random motion and many physical processes at work in the ISM in general and in the molecular phase in particular, one needs to accurately describe these turbulent flows (see the review by Vázquez-Semadeni et al. 2000). As noted earlier, this has to be done using the antenna temperature which represents the emission from a given direction and at a given velocity, and so a number of methods were devised to derive the statistical properties of the three-dimensional fields from those of the observational data. Among these, the velocity channel analysis (VCA) of Lazarian & Pogosyan (2000) is based on an analytical derivation of the properties of channel maps with varying velocity widths. It may however prove difficult to apply to actual observations, as shown by Miville-Deschênes et al. (2003a). The modified velocity centroids (MVC) of Lazarian & Esquivel (2003) are a recent promising attempt to reduce the influence of density fluctuations in the statistical properties of centroids, although it can be argued that they are only defined through their structure function. As a final example of velocity statistics retrieval methods, principal component analysis (PCA), which works on the full position-position-velocity cubes, is meant to decompose data onto an orthogonal basis and derive properties of the velocity field at each scale, as calibrated numerically by Brunt et al. (2003). The main objective of these works is to relate the scaling behaviour observed in the two-dimensional maps to scaling laws inferred for the three-dimensional fields. For instance, Stutzki et al. (1998) showed that for optically thin media, the spectral index of the integrated emission map is the same as that of the full density field, provided that the depth probed is larger than the transverse scales considered. In a recent work, Miville-Deschênes et al. (2003a) used numerical simulations to show that the same is true for the normalized velocity centroid with respect to the three-dimensional velocity field. However, this latter result lacks theoretical support, and it is therefore the goal of this paper to present an analytical study aimed at clarifying the relationship between the velocity centroids and the velocity field, within a simple turbulent cloud model.
Given the observational data, one may derive moments of the antenna temperature profiles, each of these moments yielding a potentially informative two-dimensional map. For instance, the zeroth moment is the integrated emission, or intensity, while the first moment is the velocity centroid, which can also be normalized to the intensity (Münch 1958; Miville-Deschênes et al. 2003a; Dickman & Kleiner 1985b). For an optically thin line and uniform excitation conditions, the non-normalized centroid can be related to the cloud's total momentum, while the normalized centroid is a measure of average velocity within the medium. While density fluctuations may bias the description of the turbulent motion (Lazarian & Esquivel 2003), it is however commonly believed, and intuitively plausible, that their effects are somewhat compensated by normalization. To properly assess these, and following Dickman & Kleiner (1985b) (see also Scalo 1984; Kitamura et al. 1993; Miesch & Bally 1994), we shall use autocorrelation functions of the moment maps and relate them to correlation functions of the underlying three-dimensional fields. To this end, we first describe the model we shall use and introduce the notations and assumptions in Sect. 2. We then present a brief summary of how moments of the line profile can be related to the density and velocity fields within the medium (Sect. 3). Section 4 contains a general study of the statistical properties of intensity, normalized and non-normalized velocity centroid maps as functions of the three-dimensional density and velocity fields' statistics. The equations obtained in the lowest order are then applied to the test case of fractional Brownian motion (fBm) density and velocity fields (Sect. 5). Section 6 presents a discussion of the various results obtained with respect to earlier works. Our concluding remarks are given in Sect. 7 and details on the calculations can be found in the appendix.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{aa0139-04f1.eps}\end{figure}](/articles/aa/full/2004/26/aa0139-04/Timg6.gif) |
Figure 1:
Notations used in the paper ( left) and schematics of the turbulent slab model ( right). A lowercase boldface letter stands for a three-dimensional vector, while the corresponding uppercase represents its projection on the plane of the sky (xOy). The slab is infinite in the x and y directions and is limited to
ID=[-D/2,D/2] in the z direction. The density 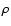 and line-of-sight velocity v distributions along a line of sight are shown on the right. The mean values
and line-of-sight velocity v distributions along a line of sight are shown on the right. The mean values 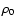 and v0 are taken over the whole slab.
and v0 are taken over the whole slab. |
| Open with DEXTER |
2 The model
Throughout the paper, boldface notations stand for vector quantities. A point in three-dimensional space is given by its position 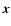 ,
which can be written as
,
which can be written as
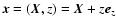 ,
where
,
where 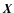 is a two-dimensional vector in the plane of the sky and z marks the line-of-sight position of the point considered,
is a two-dimensional vector in the plane of the sky and z marks the line-of-sight position of the point considered, 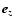 being the unit vector along the line of sight. The three-dimensional separation between points
being the unit vector along the line of sight. The three-dimensional separation between points 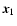 and
and 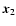 is written as
is written as
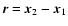 and the separation between their respective lines of sight
and the separation between their respective lines of sight 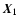 and
and 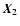 is
is
 .
In short, three-dimensional vectors are written in lowercase, while vectors in the plane of the sky are written in uppercase. These notations are illustrated in Fig. 1. It should be emphasized that we shall only consider small scales on the plane of the sky, so that all lines of sight are parallel.
.
In short, three-dimensional vectors are written in lowercase, while vectors in the plane of the sky are written in uppercase. These notations are illustrated in Fig. 1. It should be emphasized that we shall only consider small scales on the plane of the sky, so that all lines of sight are parallel.
Hereafter, our model is a slab of gas of width D, perpendicular to the line of sight, and of infinite transverse extensions![[*]](/icons/foot_motif.gif) , with z=0 conventionally placed halfway through the slab (see Fig. 1). Within the slab, the average density (that is, the average number of emitters per unit volume taken over the whole slab) is a constant noted
, with z=0 conventionally placed halfway through the slab (see Fig. 1). Within the slab, the average density (that is, the average number of emitters per unit volume taken over the whole slab) is a constant noted 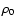 .
As for the velocity
.
As for the velocity 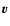 of the gas with respect to the observer, we shall write v to stand for its component along the line of sight, the mean value of which over the slab is v0. These averages (
of the gas with respect to the observer, we shall write v to stand for its component along the line of sight, the mean value of which over the slab is v0. These averages (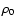 and v0) are obviously constants, independent of the line of sight. To assume the most general case, we shall take v0 to be nonzero
and v0) are obviously constants, independent of the line of sight. To assume the most general case, we shall take v0 to be nonzero![[*]](/icons/foot_motif.gif) . The gas velocity within the rest frame of the cloud is simply
. The gas velocity within the rest frame of the cloud is simply
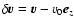 ,
assuming that there is no systematic transverse velocity. Furthermore, fluctuations of density along any given line of sight are supposed to be small compared to the average value
,
assuming that there is no systematic transverse velocity. Furthermore, fluctuations of density along any given line of sight are supposed to be small compared to the average value 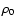 ,
in the sense that the standard deviation of the density field should be less than
,
in the sense that the standard deviation of the density field should be less than 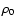 .
It is also assumed that the turbulent flow within the slab is homogeneous and isotropic. These last hypotheses are to be understood in the strong sense of Monin & Yaglom (1975): not only are the scalar field
.
It is also assumed that the turbulent flow within the slab is homogeneous and isotropic. These last hypotheses are to be understood in the strong sense of Monin & Yaglom (1975): not only are the scalar field 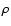 and the vector field
and the vector field
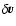 homogeneous and isotropic, but the same should apply to the four-dimensional field
homogeneous and isotropic, but the same should apply to the four-dimensional field
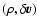 .
This will be useful in the derivation of our results in Sect. 4. Outside the slab, the density and velocity are set to zero. We further assume that the observation is done in an optically thin transition, at a frequency for which the Rayleigh-Jeans approximation is valid, that uniform excitation conditions apply within the slab, and that no background radiation is present.
.
This will be useful in the derivation of our results in Sect. 4. Outside the slab, the density and velocity are set to zero. We further assume that the observation is done in an optically thin transition, at a frequency for which the Rayleigh-Jeans approximation is valid, that uniform excitation conditions apply within the slab, and that no background radiation is present.
With these assumptions in mind, the antenna temperature
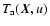 representing the emission from a given line of sight
representing the emission from a given line of sight 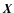 at an observed velocity u can be written as the integral (Dickman & Kleiner 1985b),
at an observed velocity u can be written as the integral (Dickman & Kleiner 1985b),
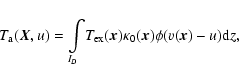 |
(1) |
where ID is the segment
[-D/2,D/2] over which the integration is performed. At each position 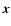 ,
,
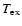 is the excitation temperature and
is the excitation temperature and 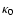 is the integrated absorption coefficient. The normalized line profile function
is the integrated absorption coefficient. The normalized line profile function 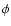 is assumed to be symmetrical about zero and independent of
is assumed to be symmetrical about zero and independent of 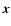 .
For instance, if one only considers thermal broadening,
.
For instance, if one only considers thermal broadening, 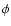 takes the form
takes the form
![\begin{displaymath}%
\phi(w)=\frac{1}{\sqrt{2\pi}\sigma_{{\rm th}}}\exp{\left[-\frac{w^2}{2\sigma_{{\rm th}}^2}\right]},
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img26.gif) |
(2) |
with
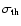 the thermal velocity dispersion. The shifted argument
the thermal velocity dispersion. The shifted argument
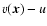 of
of 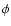 in Eq. (1) simply expresses the fact that the emission at position
in Eq. (1) simply expresses the fact that the emission at position 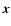 is broadened around the local line of sight velocity
is broadened around the local line of sight velocity
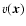 .
Assuming uniform excitation conditions,
.
Assuming uniform excitation conditions,
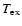 is a constant, and
is a constant, and
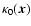 is proportional to the local gas density
is proportional to the local gas density
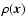 ,
so we can write
,
so we can write
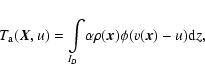 |
(3) |
where 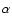 is a proportionality constant. The expression in Eq. (3) shows that, even under simplifying assumptions, the task of extracting properties of the density and velocity fields from the observational data
is a proportionality constant. The expression in Eq. (3) shows that, even under simplifying assumptions, the task of extracting properties of the density and velocity fields from the observational data
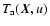 is a difficult one.
is a difficult one.
3 Velocity moments
In order to obtain information about the velocity field properties from the data sets, one may compute the various moments of the antenna temperature profiles
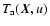 for a given line of sight
for a given line of sight 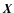 .
This is a logical step considering that knowledge of the moments of a random variable is equivalent to that of the full probability distribution. We shall therefore consider the moment maps
.
This is a logical step considering that knowledge of the moments of a random variable is equivalent to that of the full probability distribution. We shall therefore consider the moment maps
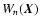 defined by
defined by
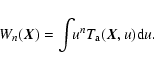 |
(4) |
The integration is done over all velocities from  to
to  ,
which poses no convergence problem since the line profile has a finite support
,
which poses no convergence problem since the line profile has a finite support![[*]](/icons/foot_motif.gif) . Using Eq. (3) to express
. Using Eq. (3) to express 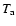 as a function of the local line profile and of the density,
as a function of the local line profile and of the density,
where we introduced the variable
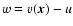 .
Developing the integrand in the innermost integral, and since the local line profile
.
Developing the integrand in the innermost integral, and since the local line profile 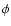 is assumed to be independent of the position
is assumed to be independent of the position 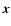 ,
we get the following expression
,
we get the following expression
where the Cnk are the binomial's coefficients and the hk are related to the moments of the normalized line profile 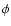 ,
,
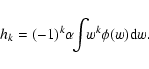 |
(7) |
It should be noted that the assumed evenness of  leads to
h2p+1=0. The first two moments are of particuler interest, since, by definition, they are the total emergent intensity I and the non-normalized velocity centroid C, respectively,
leads to
h2p+1=0. The first two moments are of particuler interest, since, by definition, they are the total emergent intensity I and the non-normalized velocity centroid C, respectively,
Here,
 is the column density at position
is the column density at position 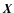 .
In the rest of this paper, we shall only consider the intensity and the velocity centroid. The use of higher order moments would theoretically give access to more information about the structures of the density and velocity fields, but, in practice, noise levels and limited spectral resolution may very well jeopardize their usefulness.
.
In the rest of this paper, we shall only consider the intensity and the velocity centroid. The use of higher order moments would theoretically give access to more information about the structures of the density and velocity fields, but, in practice, noise levels and limited spectral resolution may very well jeopardize their usefulness.
4 Statistics of intensity and centroid maps
We may use the line profile moments defined above to quantify the structure of the turbulent flow within the slab. Obviously, the zeroth moment
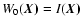 can only be used to derive statistics of the density field, as it is proportional to the column density
can only be used to derive statistics of the density field, as it is proportional to the column density
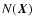 .
The first moment or non-normalized velocity centroid
.
The first moment or non-normalized velocity centroid
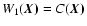 is the first appropriate quantity to study the velocity field, as can be seen from Eq. (8). However,
is the first appropriate quantity to study the velocity field, as can be seen from Eq. (8). However,
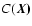 represents the integration of a momentum, rather than of a velocity proper, and it appears that density fluctuations may affect the estimation of the velocity statistics from this map. To circumvent this problem, it is common to use normalized centroids
represents the integration of a momentum, rather than of a velocity proper, and it appears that density fluctuations may affect the estimation of the velocity statistics from this map. To circumvent this problem, it is common to use normalized centroids
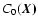 ,
which are simply defined as the ratio
,
which are simply defined as the ratio
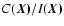 .
This is usually and empirically justified by the assumption that density fluctuations in
.
This is usually and empirically justified by the assumption that density fluctuations in
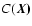 are also present in
are also present in
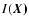 and therefore somehow vanish from
and therefore somehow vanish from
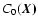 .
In the simplified case where density does not fluctuate along the line of sight, such a reasoning is obviously correct, even if transverse density fluctuations are present, and normalization then only serves as a dimensionality factor. As far as we are aware, however, no analytical study exists of the influence of longitudinal fluctuations of density on velocity centroids, even in the quite simplified model used here.
.
In the simplified case where density does not fluctuate along the line of sight, such a reasoning is obviously correct, even if transverse density fluctuations are present, and normalization then only serves as a dimensionality factor. As far as we are aware, however, no analytical study exists of the influence of longitudinal fluctuations of density on velocity centroids, even in the quite simplified model used here.
Now, in order to gain a better understanding of the underlying three-dimensional statistics of the velocity field through velocity centroids, it seems natural to consider the two-dimensional statistics of the centroid maps. Indeed, structural properties of the velocity and density fields should arise, under one form or another, in statistical measures performed on the maps
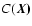 and
and
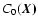 .
Of course, it is similarly reasonable to look for the influence of density structure in the statistics of the intensity map
.
Of course, it is similarly reasonable to look for the influence of density structure in the statistics of the intensity map
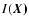 .
One such useful measure to be performed on the available two-dimensional maps is the autocorrelation function (ACF), which gives the mean degree of correlation between values of a field taken at points separated on the plane of the sky by a given vector
.
One such useful measure to be performed on the available two-dimensional maps is the autocorrelation function (ACF), which gives the mean degree of correlation between values of a field taken at points separated on the plane of the sky by a given vector 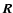 (Kleiner & Dickman 1984). More precisely, the autocorrelation function
(Kleiner & Dickman 1984). More precisely, the autocorrelation function
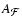 of a field
of a field
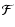 is defined by
is defined by
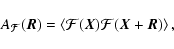 |
(9) |
where the brackets stand for a spatial average over position 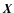 in the plane of the sky. Hereafter, we shall consider the autocorrelation functions of the intensity and of both types of centroid, respectively noted
in the plane of the sky. Hereafter, we shall consider the autocorrelation functions of the intensity and of both types of centroid, respectively noted
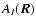 ,
,
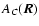 and
and
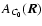 ,
and compute them as functions of statistical measures of the three-dimensional density and velocity fields. In order to do so, we first separate mean and fluctuating contributions of density and velocity in the quantities involved, with
,
and compute them as functions of statistical measures of the three-dimensional density and velocity fields. In order to do so, we first separate mean and fluctuating contributions of density and velocity in the quantities involved, with
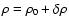 and
and
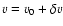 .
These expressions can be used to write the first two moment maps as
.
These expressions can be used to write the first two moment maps as
where we have introduced the following integrated fluctuation terms![[*]](/icons/foot_motif.gif)
The normalized centroid C0 is then simply written as
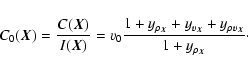 |
(12) |
This last expression can be used to clarify the usefulness of the small fluctuations hypothesis. Indeed, for a perturbative method to be applicable in the computation of the autocorrelation function of the normalized velocity centroid map, one should be able to linearize Eq. (12), and therefore we need to assume that
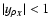 ,
so that the denominator can be expanded as a converging series,
,
so that the denominator can be expanded as a converging series,
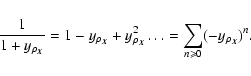 |
(13) |
Such a condition is obviously achieved if local density fluctuations themselves are small in the sense, expressed in Sect. 2, that the standard deviation of the density field
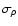 should be smaller than the average density
should be smaller than the average density 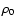 ,
since
,
since
The identification of the mean squared density fluctuations along a single line of sight with the variance
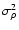 of the whole density field is based on the homogeneity hypothesis. Indeed, any line of sight should statistically represent the full field. Although the stronger assumption
of the whole density field is based on the homogeneity hypothesis. Indeed, any line of sight should statistically represent the full field. Although the stronger assumption
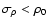 is not strictly necessary for the linearization mentioned earlier, it is useful in the expansion of the autocorrelation functions since, in this case, the hybrid integrated fluctuation term
is not strictly necessary for the linearization mentioned earlier, it is useful in the expansion of the autocorrelation functions since, in this case, the hybrid integrated fluctuation term
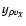 is of the same order in density as
is of the same order in density as
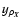 ,
,
where we used the Cauchy-Schwarz inequality and introduced the standard deviation 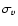 of the line-of-sight component of the velocity field
of the line-of-sight component of the velocity field![[*]](/icons/foot_motif.gif) . This allows us to develop the intensity and the velocity centroid maps, as well as their autocorrelation functions, according to the powers of
. This allows us to develop the intensity and the velocity centroid maps, as well as their autocorrelation functions, according to the powers of
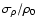 .
It should be made clear that the expansion in Eq. (13) is not necessarily true for real data, but that it is used here as a reasonable first step towards understanding the effects of realistic density fluctuations on velocity centroids.
.
It should be made clear that the expansion in Eq. (13) is not necessarily true for real data, but that it is used here as a reasonable first step towards understanding the effects of realistic density fluctuations on velocity centroids.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{aa0139-04f2.eps}\end{figure}](/articles/aa/full/2004/26/aa0139-04/Timg87.gif) |
Figure 2:
Interpretation of the average
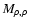 appearing in Eq. (23). The slab is viewed edge-on in the left figure, and face-on in the right. The value of
appearing in Eq. (23). The slab is viewed edge-on in the left figure, and face-on in the right. The value of
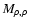 at any lag
at any lag 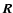 is the average of the correlation function
is the average of the correlation function
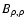 over all pairs of points whose projected separation on the plane of the sky is
over all pairs of points whose projected separation on the plane of the sky is 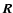 .
Three such pairs are presented on the left. .
Three such pairs are presented on the left. |
| Open with DEXTER |
Taking the autocorrelation function
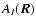 of the intensity map
of the intensity map
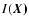 ,
and using the linearity property of averages, we have terms of order up to two in density fluctuations, namely
,
and using the linearity property of averages, we have terms of order up to two in density fluctuations, namely
![$\displaystyle %
A_I(\vec{R})= %
(\alpha\rho_0D)^2\left[1+\left<y_{\rho_{\vec{X}...
...{R}}}\right>+\left<y_{\rho_{\vec{X}}} y_{\rho_{\vec{X}+\vec{R}}}\right>\right],$](/articles/aa/full/2004/26/aa0139-04/img88.gif) |
|
|
(16) |
where we recall that the brackets stand for an average over 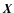 .
These are performed on quantities integrated over z, and can therefore be interpreted as averages over the whole turbulent slab. Indeed, if one considers a three-dimensional field
.
These are performed on quantities integrated over z, and can therefore be interpreted as averages over the whole turbulent slab. Indeed, if one considers a three-dimensional field
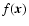 ,
its integrated map
,
its integrated map
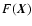 defined by
defined by
has an average
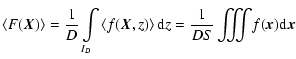 |
|
|
(17) |
over a surface S of the sky. The quantity
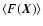 can then be seen as an average of f over the volume DS, and, assuming ergodicity, it can also be identifid with the ensemble average
can then be seen as an average of f over the volume DS, and, assuming ergodicity, it can also be identifid with the ensemble average
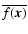 at any given position
at any given position 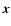 within the flow. In the present case, the term
within the flow. In the present case, the term
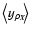 ,
which is of the first order in density fluctuations, can be written as
,
which is of the first order in density fluctuations, can be written as
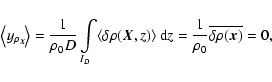 |
(18) |
since, by definition, the average of the density fluctuations over the whole volume of the slab is zero. The assumption of homogeneity allows one to write that
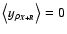 as well. As for the second order term, which reads
as well. As for the second order term, which reads
and where I2D is the square domain ID  ID, it includes an average over
ID, it includes an average over 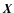 that, following the idea used above, should be replaced by an ensemble average characteristic of the turbulent flow. Indeed, one can see that
that, following the idea used above, should be replaced by an ensemble average characteristic of the turbulent flow. Indeed, one can see that
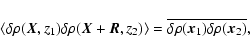 |
(20) |
with the three-dimensional vectors
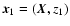 and
and
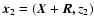 .
Introducing the autocorrelation function
.
Introducing the autocorrelation function
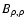 of the density fluctuations, which is defined, for any pair of points
of the density fluctuations, which is defined, for any pair of points
 within the slab, by
within the slab, by![[*]](/icons/foot_motif.gif)
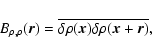 |
(21) |
we therefore can write the term under study as
or, more concisely,
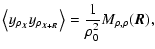 |
|
|
(22) |
where
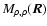 ,
which is defined by the double integral
,
which is defined by the double integral
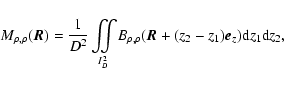 |
(23) |
is interpreted as an average of
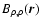 taken over all pairs of points within the slab whose three-dimensional separation
taken over all pairs of points within the slab whose three-dimensional separation 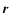 has the given vector
has the given vector 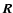 for component in the plane of the sky (see Fig. 2). Eventually, the autocorrelation function of the intensity simply reads
for component in the plane of the sky (see Fig. 2). Eventually, the autocorrelation function of the intensity simply reads
![\begin{displaymath}%
A_I(\vec{R})=(\alpha D)^2\left[\rho_0^2+M_{\rho,\rho}(\vec{R})\right].
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img114.gif) |
(24) |
This expression will be exploited later on when compared with the autocorrelation functions of velocity centroids.
The same general method applies when considering the non-normalized velocity centroid
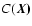 .
Its expansion, written in Eq. (10), includes terms of order zero and one in density fluctuations. Therefore, its autocorrelation function
.
Its expansion, written in Eq. (10), includes terms of order zero and one in density fluctuations. Therefore, its autocorrelation function
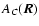 features terms of order up to two. Namely,
features terms of order up to two. Namely,
where an is a term of order n in density. The explicit forms of these coefficients are given by
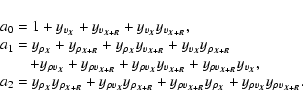 |
(26) |
The linearity of the averaging process over the plane of the sky implies then that we should consider terms of the form
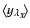 and
and
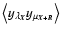 ,
where
,
where 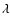 and
and 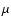 represent either
represent either 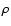 ,
v or
,
v or 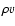 .
Due to the homogeneity hypothesis, terms of the form
.
Due to the homogeneity hypothesis, terms of the form
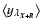 are of course equal to
are of course equal to
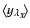 ,
and so, considering the zeroth order contribution
,
and so, considering the zeroth order contribution
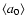 ,
we have
,
we have
with
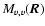 being defined similarly to
being defined similarly to
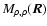 in Eq. (23),
in Eq. (23),
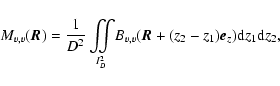 |
(28) |
and
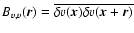 is the autocorrelation function of the fluctuations of the line-of-sight velocity component. Turning to the first order term, we have, since
is the autocorrelation function of the fluctuations of the line-of-sight velocity component. Turning to the first order term, we have, since
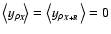 as shown in the previous section,
as shown in the previous section,
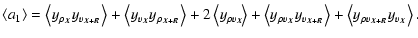 |
|
|
(29) |
Each term in this equation can be related to correlation functions of the fluctuation fields
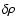 and
and 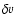 ,
beginning with
,
beginning with
introducing the mixed correlation function
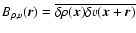 .
Considering the next term
.
Considering the next term
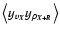 ,
the homogeneity hypothesis allows us to shift the arguments by
,
the homogeneity hypothesis allows us to shift the arguments by  so that, exchanging the integration variables,
so that, exchanging the integration variables,
Combination of both terms leads to
Now, according to Monin & Yaglom (1975), and assuming that the four-dimensional field
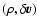 ,
made up of the density
,
made up of the density 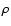 and vector velocity
and vector velocity
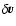 ,
is homogeneous and isotropic, the correlation function of
,
is homogeneous and isotropic, the correlation function of 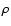 and
and
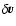 is a vector quantity, and due to isotropy should be along the separation vector
is a vector quantity, and due to isotropy should be along the separation vector 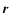 .
It should therefore be of the form
.
It should therefore be of the form
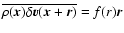 ,
so that, projecting this relation on
,
so that, projecting this relation on 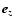 ,
we have
,
we have
using the fact that
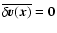 .
As a consequence, we have
.
As a consequence, we have
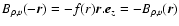 ,
so that
,
so that
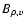 is an antisymmetric field. Of course, this is a statistical property, and does not hold when considering the specific values of velocity and density fluctuations for a given pair of points within the flow. What one can conclude is that the integrand in Eq. (32) is zero, and so
is an antisymmetric field. Of course, this is a statistical property, and does not hold when considering the specific values of velocity and density fluctuations for a given pair of points within the flow. What one can conclude is that the integrand in Eq. (32) is zero, and so
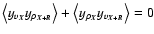 .
So is the next term
.
So is the next term
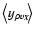 ,
since
,
since
because the antisymmetry of
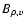 implies that
implies that
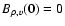 .
Similarly, the last two terms of
.
Similarly, the last two terms of
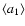 are given by
are given by
| |
|
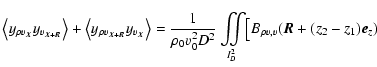 |
|
| |
|
![$\displaystyle \hspace*{3.5cm} \left. +B_{\rho v,v}(-\vec{R}+(z_1-z_2)\vec{e}_z)\right] {\rm d} z_1 {\rm d} z_2,$](/articles/aa/full/2004/26/aa0139-04/img164.gif) |
(35) |
introducing the two-point correlation function
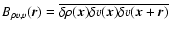 .
This last combination of terms, unlike the one considered previously, is not necessarily zero. According to Monin & Yaglom (1975), it is of the form
.
This last combination of terms, unlike the one considered previously, is not necessarily zero. According to Monin & Yaglom (1975), it is of the form
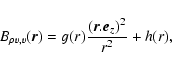 |
(36) |
where g and h are functions of the scalar separation r. This form stems from the fact that
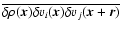 ,
where i and j stand for any of the x, y and z coordinates, is a tensor of rank 2 which we suppose to be homogeneous and isotropic. It follows that
,
where i and j stand for any of the x, y and z coordinates, is a tensor of rank 2 which we suppose to be homogeneous and isotropic. It follows that
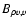 is symmetric, and so, using an averaging notation
is symmetric, and so, using an averaging notation
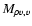 defined, similarly to the expressions of
defined, similarly to the expressions of
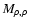 and Mv,v, by
and Mv,v, by
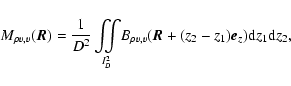 |
(37) |
we can write
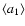 ,
contribution of the first order in density fluctuations to the autocorrelation function AC, as
,
contribution of the first order in density fluctuations to the autocorrelation function AC, as
Lastly, the second order term in density fluctuations
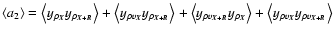 is computed in much the same way, introducing the two-point correlation functions
is computed in much the same way, introducing the two-point correlation functions
and their averages defined by
With these notations, it is straightforward to derive the expression of the second order term,
![\begin{displaymath}%
\left<a_2\right>=\frac{1}{\rho_0^2}\left[ M_{\rho,\rho}(\ve...
...o}(\vec{R})+\frac{1}{v^2_0} M_{\rho v,\rho v}(\vec{R})\right],
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img179.gif) |
(41) |
with the (s) superscript indicating the symmetric part of a given function, defined by the relation
![\begin{displaymath}%
f^{(s)}(x)=\frac{1}{2}\left[f(x)+f(-x)\right].
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img180.gif) |
(42) |
Now, still following Monin & Yaglom (1975),
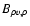 exhibits the same antisymmetry property as
exhibits the same antisymmetry property as
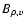 and we can conclude that the symmetric part of
and we can conclude that the symmetric part of
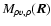 is zero, so that the autocorrelation function AC of the non-normalized velocity centroid eventually reads
is zero, so that the autocorrelation function AC of the non-normalized velocity centroid eventually reads
![$\displaystyle %
A_C(\vec{R})=(\alpha D)^2\left[\rho_0^2v_0^2+\rho_0^2M_{v,v}(\v...
...o v,v}(\vec{R}) +v_0^2M_{\rho,\rho}(\vec{R})+M_{\rho v,\rho v}(\vec{R})\right].$](/articles/aa/full/2004/26/aa0139-04/img183.gif) |
|
|
(43) |
When considering only the zeroth order in density fluctuations, one finds that the expression of
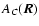 is very similar to that of
is very similar to that of
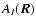 ,
with
,
with
![$A_C(\vec{R}) \simeq (\alpha D\rho_0)^2\left[v_0^2+M_{v,v}(\vec{R})\right]$](/articles/aa/full/2004/26/aa0139-04/img184.gif) .
This is not surprising, as we shall discuss in Sect. 6. Moreover, as the forthcoming comparison of the autocorrelation functions of both normalized and non-normalized velocity centroids will be performed on expressions of order up to one only, it is useful to write out the truncation of
.
This is not surprising, as we shall discuss in Sect. 6. Moreover, as the forthcoming comparison of the autocorrelation functions of both normalized and non-normalized velocity centroids will be performed on expressions of order up to one only, it is useful to write out the truncation of
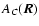 at that order, which is, given Eq. (43),
at that order, which is, given Eq. (43),
![\begin{displaymath}%
A_C(\vec{R})=(\alpha D)^2\left[\rho_0^2v_0^2+\rho_0^2M_{v,v}(\vec{R})+2\rho_0M_{\rho v,v}(\vec{R})\right].
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img185.gif) |
(44) |
There is little qualitative change to the method when dealing with the normalized centroid. Contributions of each order can be computed as easily as for the non-normalized case, with the main difference being that, given the expansion written in Eq. (13),
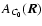 is a theoretically infinite series which reads
is a theoretically infinite series which reads
with
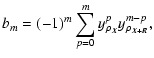 |
|
|
(45) |
the generic term
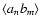 obviously being of order n+m in density fluctuations. Now, given that the highest order present in
obviously being of order n+m in density fluctuations. Now, given that the highest order present in
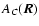 is two, it seems reasonable to consider only terms of order at most two in the expansion. However, it may also be argued that, since density fluctuations effectively contribute to the first order in the expression of
is two, it seems reasonable to consider only terms of order at most two in the expansion. However, it may also be argued that, since density fluctuations effectively contribute to the first order in the expression of
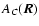 ,
assessing the effects of normalization may already be performed when limiting the expansion to that order,
,
assessing the effects of normalization may already be performed when limiting the expansion to that order,
| |
|
![$\displaystyle A_{C_0}(\vec{R})=v_0^2\left[\left<a_0b_0\right>+\left<a_0b_1\right>+\left<a_1b_0\right>\right]=v_0^2\left(S_0+S_1\right)$](/articles/aa/full/2004/26/aa0139-04/img189.gif) |
|
| |
|
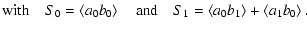 |
(46) |
Now, the zeroth order term in
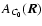 has been computed in the previous subsection,
has been computed in the previous subsection,
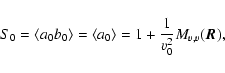 |
(47) |
so we turn to the first order term
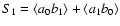 which reads, after a long but straightforward calculation,
which reads, after a long but straightforward calculation,
| S1 |
= |
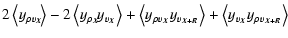 |
|
| |
|
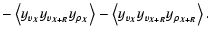 |
(48) |
The first term is zero, as shown before. So is the second term, for we have
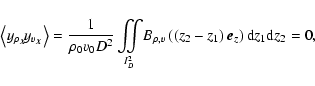 |
(49) |
since the integration domain is symmetric about z2-z1=0 and
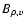 is antisymmetric. The combination of third and fourth terms has been computed in the previous subsection
is antisymmetric. The combination of third and fourth terms has been computed in the previous subsection
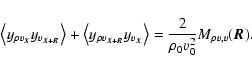 |
(50) |
The remaining terms require a more elaborate, although similar, treatment. Taking for instance the last term, we have
where the integration is performed over the cubic domain ID3=ID  ID
ID 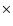 ID. Introducing the three-point correlation function
ID. Introducing the three-point correlation function
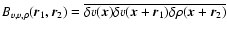 ,
this expression reads
,
this expression reads
with an averaging notation
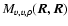 reminiscent of the ones used previously,
reminiscent of the ones used previously,
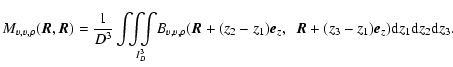 |
|
|
(53) |
Similarly, the next-to-last term can be written as
so that
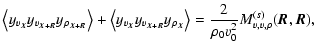 |
|
|
(54) |
with
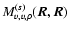 being the symmetric part of the function
being the symmetric part of the function
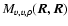 ,
,
![\begin{displaymath}%
M^{(s)}_{v,v,\rho}(\vec{R},\vec{R})=\frac{1}{2}\left[M_{v,v,\rho}(\vec{R},\vec{R})+M_{v,v,\rho}(-\vec{R},-\vec{R})\right].
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img209.gif) |
(55) |
Finally, the autocorrelation function
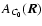 of the normalized centroid has the following expression when limited to contributions of the first order in density fluctuations,
of the normalized centroid has the following expression when limited to contributions of the first order in density fluctuations,
![\begin{displaymath}%
A_{C_0}(\vec{R})=v_0^2+M_{v,v}(\vec{R})+\frac{2}{\rho_0}\le...
...\rho v,v}(\vec{R})-M^{(s)}_{v,v,\rho}(\vec{R},\vec{R})\right].
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img210.gif) |
(56) |
It appears then that normalization of velocity centroids indeed performs a first order correction, as compared with Eq. (44), although it does not necessarily fully remove the density structure, as will be discussed in more detail in Sect. 6.
5 The case of fractional Brownian motion fields
Explicitly computing the forms of the two-dimensional statistical measures
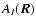 ,
,
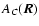 and
and
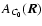 requires the knowledge of the three-dimensional correlation functions appearing as integrated terms in Eqs. (24), (44) and (56). However, it may prove impossibly difficult to build a complete and consistent set of such functions and then to analytically compute their averages. Therefore, as a first step, one should stick to the lowest order terms in the expressions of the two-dimensional autocorrelation functions,
requires the knowledge of the three-dimensional correlation functions appearing as integrated terms in Eqs. (24), (44) and (56). However, it may prove impossibly difficult to build a complete and consistent set of such functions and then to analytically compute their averages. Therefore, as a first step, one should stick to the lowest order terms in the expressions of the two-dimensional autocorrelation functions,
In this limit, one only has to compute the
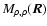 and
and
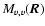 averages given density and velocity fields with known autocorrelation functions
averages given density and velocity fields with known autocorrelation functions
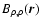 and
and
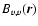 .
One possibility is to suppose that both of the three-dimensional fields are fractional Brownian motions (fBm). These are defined in the following way: if
.
One possibility is to suppose that both of the three-dimensional fields are fractional Brownian motions (fBm). These are defined in the following way: if
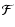 is such a field in N dimensions, it is characterized by a single-index power-law structure function,
is such a field in N dimensions, it is characterized by a single-index power-law structure function,
![\begin{displaymath}%
S_\mathcal{F}(\vec{r})=\overline{\left[\mathcal{F}(\vec{x}+...
...{F}(\vec{x})\right]^2}=2\Lambda \left(\frac{r}{D}\right)^{2H},
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img215.gif) |
(58) |
where
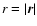 is the length of the separation vector,
is the length of the separation vector, 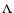 is a positive constant and H is a real number in [0,1] called the Hurst exponent. The restriction
is a positive constant and H is a real number in [0,1] called the Hurst exponent. The restriction
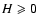 corresponds to the fact that the amplitude of fluctuations should decrease at smaller scale, while we impose
corresponds to the fact that the amplitude of fluctuations should decrease at smaller scale, while we impose
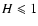 because an fBm field having a Hurst exponent H > 1 would be uniform, as shown in Appendix D. Fractional Brownian motion fields have already been used (Stutzki et al. 1998; Miville-Deschênes et al. 2003a; Brunt & Heyer 2002) to model clouds of the diffuse, non-starforming interstellar medium. In this section, we shall use them to model the three-dimensional density and velocity fields, so that, for the former,
because an fBm field having a Hurst exponent H > 1 would be uniform, as shown in Appendix D. Fractional Brownian motion fields have already been used (Stutzki et al. 1998; Miville-Deschênes et al. 2003a; Brunt & Heyer 2002) to model clouds of the diffuse, non-starforming interstellar medium. In this section, we shall use them to model the three-dimensional density and velocity fields, so that, for the former,
since the density fluctuations field is supposed to be homogeneous. Similarly, for the velocity field,
These last two equations make use of the relationship between the second order structure function
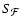 of an homogeneous field
of an homogeneous field
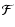 and its autocorrelation function
and its autocorrelation function
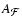 ,
which is
,
which is
![$S_\mathcal{F}(\vec{R})=2\left[A_\mathcal{F}(\vec{0})-A_\mathcal{F}(\vec{R})\right]$](/articles/aa/full/2004/26/aa0139-04/img227.gif) .
In the results of Sect. 4, we then have to inject the following relations
.
In the results of Sect. 4, we then have to inject the following relations
To compute the averages
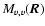 and
and
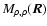 featured in the expressions of
featured in the expressions of
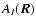 ,
,
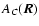 and
and
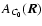 ,
we can use the calculation scheme of Chandrasekhar & Münch (1952), which is given in Appendix A, to write them as single integrals over the separation
,
we can use the calculation scheme of Chandrasekhar & Münch (1952), which is given in Appendix A, to write them as single integrals over the separation
 along the line of sight, noting that
along the line of sight, noting that
![$\Delta z \in I_{2D}=[-D,D]$](/articles/aa/full/2004/26/aa0139-04/img231.gif) .
We then have
.
We then have
In these expressions, the factor
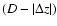 represents the weight of each separation
represents the weight of each separation 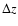 ,
that is the relative number of pairs of points taken into account whose projected separation along the line of sight is
,
that is the relative number of pairs of points taken into account whose projected separation along the line of sight is 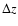 .
With the expressions above for Bv,v and
.
With the expressions above for Bv,v and
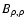 ,
it is possible, as shown in Appendix C, to write these averages under the form
,
it is possible, as shown in Appendix C, to write these averages under the form
where
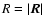 is the scalar separation on the plane of the sky, and the function K is given by
is the scalar separation on the plane of the sky, and the function K is given by
![$\displaystyle %
K(R,H)=\frac{2}{D^{2H+1}}\int_0^D\!\! \left(R^2+z^2\right)^{H} ...
...left(1+\frac{R^2}{D^2}\right)^{H+1}
-\left(\frac{R^2}{D^2}\right)^{H+1}\right].$](/articles/aa/full/2004/26/aa0139-04/img239.gif) |
|
|
(64) |
The integral in Eq. (64) cannot be explicited (Gradshteyn & Ryzhik 1980) unless H=0 or H=1, but one interesting limit to consider is that of small separations on the plane of the sky (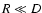 ), in which case K(R,H) can be developed in powers of R/D. As shown in Appendix C, this yields the following scaling relations for
), in which case K(R,H) can be developed in powers of R/D. As shown in Appendix C, this yields the following scaling relations for
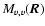
| |
|
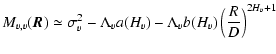 |
|
| |
|
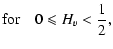 |
(65) |
| |
|
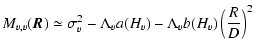 |
|
| |
|
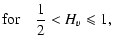 |
(66) |
| |
|
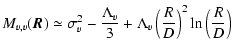 |
|
| |
|
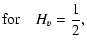 |
(67) |
where a and b are functions of Hv only. Similar relations are satisfied by
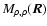 depending on the value of
depending on the value of 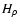 .
To the lowest order, the structure function
.
To the lowest order, the structure function
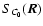 of the normalized centroid C0 therefore reads
of the normalized centroid C0 therefore reads
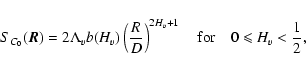 |
(68) |
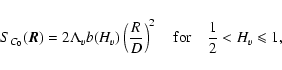 |
(69) |
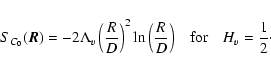 |
(70) |
According to Eq. (57), the structure function SC of the non-normalized velocity centroid has the same scaling behaviour. This is also the case for the structure function SI of the intensity, depending on the value of 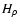 .
The consequences of such forms are presented in the next section.
.
The consequences of such forms are presented in the next section.
6 Discussion
As expected, the statistical measures on the intensity and centroid maps can be expressed in terms of the statistical properties of the underlying three-dimensional velocity and density fields. More precisely, it should come as no surprise that the autocorrelation functions
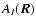 ,
,
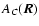 and
and
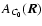 should be written as averages of correlation functions within the slab in the manner described in Fig. 2, since all pairs of points with a given separation
should be written as averages of correlation functions within the slab in the manner described in Fig. 2, since all pairs of points with a given separation 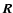 in the plane of the sky should contribute to the two-dimensional statistical measures at lag
in the plane of the sky should contribute to the two-dimensional statistical measures at lag 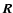 .
.
It also appears that the zeroth order term in the autocorrelation functions of the velocity centroids has the same form as the autocorrelation of the intensity map, since we then have
while
![$\displaystyle A_I(\vec{R})=(\alpha D)^2\left[\rho_0^2+M_{\rho,\rho}(\vec{R})\right].$](/articles/aa/full/2004/26/aa0139-04/img253.gif) |
|
|
(71) |
The identity of these forms was to be expected, since the zeroth order terms in the autocorrelation functions of the velocity centroids are the limits obtained when the density is uniform. In this case, the centroids simply are integrals of v, as the intensity is a simple integral of 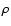 .
In the context of fBm fields, the implication of this limit is that both non-normalized and normalized velocity centroids have a fractional Brownian motion behaviour, since their structure functions are power laws, with respective Hurst exponents HC and HC0 such that
.
In the context of fBm fields, the implication of this limit is that both non-normalized and normalized velocity centroids have a fractional Brownian motion behaviour, since their structure functions are power laws, with respective Hurst exponents HC and HC0 such that
And similarly, the intensity map has a fractional Brownian motion behaviour with a Hurst exponent HI with
These results should be interpreted in the light of what is already known about the statistical properties of the integrated emission map I from studies in the Fourier domain. Indeed, in the case of optically thin lines, the power spectrum index 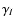 of the intensity map is the same as that of the three-dimensional density field
of the intensity map is the same as that of the three-dimensional density field
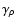 (see e.g. Goldman 2000) provided the depth probed D is larger than the transverse scales R, which is the case in the limit considered in Sect. 5. Now, spectral index
(see e.g. Goldman 2000) provided the depth probed D is larger than the transverse scales R, which is the case in the limit considered in Sect. 5. Now, spectral index 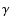 and Hurst exponent H are related by
and Hurst exponent H are related by
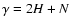 ,
with N the dimension of the space over which the field is defined. As a result, Stutzki et al. (1998) concluded that the Hurst exponent of the integrated emission map is
,
with N the dimension of the space over which the field is defined. As a result, Stutzki et al. (1998) concluded that the Hurst exponent of the integrated emission map is
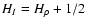 for
for
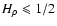 with a turnover to HI=1 for
with a turnover to HI=1 for
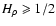 ,
since
,
since
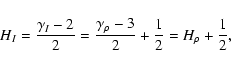 |
(74) |
using the fact that the integrated emission map is two-dimensional, while the original density field is three-dimensional. This result is precisely what we find from our analytical study performed solely in real space. Similarly, the expression for the structure function of the normalized centroid confirms the numerical findings of Miville-Deschênes et al. (2003a), who showed that the spectral index
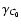 of normalized centroid maps was equal to that of the three-dimensional velocity field,
of normalized centroid maps was equal to that of the three-dimensional velocity field, 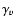 .
It should be noted that their result holds even for density fields with large fluctuations, which implies that our analytical result may be applicable to a more general class of fields. On the other hand, in the limit of negligible density fluctuations, one should find the same behaviour for the non-normalized centroid, a result Miville-Deschênes et al. (2003a) have not reported on.
.
It should be noted that their result holds even for density fields with large fluctuations, which implies that our analytical result may be applicable to a more general class of fields. On the other hand, in the limit of negligible density fluctuations, one should find the same behaviour for the non-normalized centroid, a result Miville-Deschênes et al. (2003a) have not reported on.
Returning to a study of the autocorrelation functions of velocity centroids in the first order approximation,
we see that, since
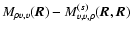 is not necessarily zero, normalization actually does not remove the first order contribution of density fluctuations. The empirical assumption that normalization somehow eliminates the influence of density fluctuations on velocity centroids may therefore not be true, although assessing the magnitude of the remaining first order contribution in the normalized centroid's autocorrelation function with respect to the non-normalized case could be difficult, as it involves computing averages of correlation functions whose forms are still unknown. This will be investigated in a forthcoming paper.
is not necessarily zero, normalization actually does not remove the first order contribution of density fluctuations. The empirical assumption that normalization somehow eliminates the influence of density fluctuations on velocity centroids may therefore not be true, although assessing the magnitude of the remaining first order contribution in the normalized centroid's autocorrelation function with respect to the non-normalized case could be difficult, as it involves computing averages of correlation functions whose forms are still unknown. This will be investigated in a forthcoming paper.
Such shortcomings of the normalized centroids as a way to retrieve the actual velocity statistics from the observational data have already been pointed out by Lazarian & Esquivel (2003), albeit in the case of simulations of highly compressible MHD turbulence. Instead, they introduced modified velocity centroids (MVC) 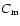 ,
defined through their second order structure function
,
defined through their second order structure function
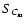 as
as
where SC and SI are the structure functions of the non-normalized velocity centroid and of the intensity, respectively. Given the relationship between the structure and autocorrelation functions, we can write the autocorrelation function
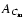 of the modified velocity centroids as
of the modified velocity centroids as
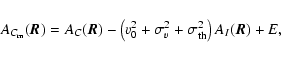 |
(76) |
E being a constant involving the values of AC and AI at zero lag.
Now, since AI contains no first-order term, it appears that modified and non-normalized velocity centroids have the same first order contribution in their autocorrelation functions. As noted earlier, however, it is not yet clear whether this contribution is actually more important than the first order term in the autocorrelation function of normalized centroids. If it is, it would tend to prove that normalization may be a better way of retrieving velocity statistics in weakly compressible flows. To make the comparison of correction schemes clearer, one can show a relationship between the autocorrelation functions of I, C and C0 as written in Eqs. (24), (43) and (56),
where
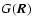 stands for the terms of order at least two in density fluctuations. Deriving the relationship between the structure functions of I, C and C0, the latter being noted SC0, we have
stands for the terms of order at least two in density fluctuations. Deriving the relationship between the structure functions of I, C and C0, the latter being noted SC0, we have
Comparing this with Eq. (75), it is clear that modified velocity centroids subtract more of the intensity structure, thus removing second order terms, while normalization performs a more complex correction, involving all orders in density fluctuations. Actual comparison of the merits of normalized and modified velocity centroids requires numerical tests, which have only been performed by Lazarian & Esquivel (2003) on highly compressible MHD turbulence. That particular case is actually not within the scope of our study, firstly because density fluctuations are large and the condition for the expansion in the normalized velocity centroid's case may not be met, and secondly because the presence of a magnetic field implies anisotropy. Both limitations render the comparison with the work of Lazarian & Esquivel (2003) a bit uncertain, although it is likely that terms of higher order in density fluctuations may become dominant. Thus, the effectiveness of modified velocity centroids, as compared to normalized centroids, in their simulations may be related to the second order correction through SI, which is more important in modified velocity centroids. In any case, further analytical and numerical work is warranted in order to establish these conclusions more firmly, especially in the weakly compressible flow regime.
7 Conclusions
An analytical study of a simple slightly compressible turbulent cloud model was presented, assuming homogeneity and isotropy of the turbulent flow. From the expressions of the antenna temperature for an optically thin spectral line and of its successive moments with respect to the line of sight velocity component, we computed the autocorrelation functions of the intensity and of both normalized and non-normalized velocity centroids, which involve averages, along the line of sight, of correlation functions of the three-dimensional density and velocity fields.
To the lowest order, the autocorrelation functions of the velocity centroids behave, with respect to the velocity field, as the autocorrelation function of the intensity with respect to the density field. This sheds light on the numerical result of Miville-Deschênes et al. (2003a), who found that, for fractional Brownian motion density and velocity fields, the spectral index of the normalized centroid is equal to that of the velocity field. We derived this result analytically, for separations across the sky much smaller than the cloud's depth, and in real space, while previous studies such as that of Goldman (2000) were performed in Fourier space. However, the result of Miville-Deschênes et al. (2003a) holds for fields outside of the validity domain for our calculation.
Comparison of the expansions of the autocorrelation functions of both types of velocity centroids shows that normalization performs a correction of the first order in density fluctuations, although its magnitude remains to be assessed, a task for which numerical simulations are probably necessary. Numerical tests should also provide us with a robust comparison between normalized velocity centroids and the modified velocity centroids of Lazarian & Esquivel (2003), which imply corrections of order two in density fluctuations. At present, this comparison has been performed only on simulations of highly compressible and magnetized turbulence, a case beyond the scope of our analytical study, and has shown that, in this particular case, modified velocity centroids provide a more reliable tool than normalized centroids.
In a forthcoming paper, we shall therefore present numerical simulations aimed at assessing the validity domain of our calculations and, beyond normalized and modified velocity centroids, pursuing the search for a better correction scheme able to retrieve the underlying velocity statistics from observational data.
Acknowledgements
I wish to acknowledge fruitful discussions with Alex Lazarian during his stay at the École normale supérieure. His suggestions, in the early stages of this work, proved very helpful. I also wish to thank Enrique Vázquez-Semadeni for his careful reading of the manuscript and insightful remarks.
- Goldman, I.
2000, ApJ, 541, 701 [NASA ADS] [CrossRef] (In the text)
- Baker, P. L. 1976,
A&A, 50, 327 [NASA ADS] (In the text)
- Brunt, C. M.,
& Heyer, M. H. 2002, ApJ, 566, 276 [NASA ADS] [CrossRef]
- Brunt, C.
M., Heyer, M. H., Vásquez-Semadeni, E., & Pichardo, B.
2003, ApJ, 595, 824 [NASA ADS] [CrossRef] (In the text)
-
Chandrasekhar, S. 1949, ApJ, 110, 329 [NASA ADS] [CrossRef] (In the text)
-
Chandrasekhar, S., & Münch, G. 1952, ApJ, 115, 103 [NASA ADS] [CrossRef] [MathSciNet] (In the text)
- Dickman, R. L.,
& Kleiner, S. C. 1985, ApJ, 295, 479 [NASA ADS] [CrossRef]
- Gradshteyn,
I. S., & Ryzhik, I. M. 1980, Tables of integrals, series and
products (Academic Press)
(In the text)
- Hegmann, M.,
& Kegel, W. H. 2000, A&A, 359, 405 [NASA ADS] (In the text)
- Kitamura, Y.,
Sunada, Y., Hayashi, M., & Hasegawa, T. 1993, ApJ, 413,
221 [NASA ADS] [CrossRef]
- Kleiner, S. C.,
& Dickman, R. L. 1984, ApJ, 286, 255 [NASA ADS] [CrossRef] (In the text)
- Kleiner, S. C.,
& Dickman, R. L. 1985, ApJ, 295, 466 [NASA ADS] [CrossRef]
- Kolmogorov, A. N. 1941, Dokl.
Akad. Nauk. SSSR, 30, 299 [NASA ADS] (In the text)
- Larson, R. B. 1981,
MNRAS, 194, 809 [NASA ADS] (In the text)
- Lazarian, A., &
Pogosyan, D. 2000, ApJ, 537, 720 [NASA ADS] [CrossRef] (In the text)
- Lazarian,
A., & Esquivel, A. 2003, ApJ, 592, L37 [NASA ADS] [CrossRef] (In the text)
- Miesch, M. S.,
& Bally, J. 1994, ApJ, 429, 645 [NASA ADS] [CrossRef]
-
Miville-Deschênes, M. A., Levrier, F., & Falgarone, E.
2003a, ApJ, 593, 831 [NASA ADS] [CrossRef] (In the text)
-
Miville-Deschênes, M. A., Joncas, G., Falgarone, E., &
Boulanger, F. 2003b, A&A, 411, 109 [EDP Sciences] [NASA ADS] [CrossRef]
- Monin, A. S., &
Yaglom, A. M. 1975, Statistical Fluid Mechanics, Vol. 2
(Cambridge, MA: MIT Press)
(In the text)
- Münch, G. 1958,
Rev. Mod. Phys., 30, 1035 [NASA ADS] [CrossRef]
- O'Dell, C. R., &
Castaneda, H. O. 1987, ApJ, 317, 686 [NASA ADS] [CrossRef] (In the text)
- Scalo, J. M. 1984,
ApJ, 277, 556 [NASA ADS] [CrossRef]
- Scalo, J. M. 1985, in
Protostars and Planets II, ed. D. C.
Black, & M. S. Matthews (Tucson: Univ. Arizona Press),
201
(In the text)
- Spicker, J.,
& Feitzinger, J. V. 1988, A&A, 191, 10 [NASA ADS]
- Stutzki, J.,
Bensch, F., Heithausen, A., Ossenkopf, V., & Zielinsky, M.
1998, A&A, 336, 697 [NASA ADS] (In the text)
- Van
Langevelde, H. J., Frail, D. A., Cordes, J. M., & Diamond,
P. J. 1992, ApJ, 396, 686 [NASA ADS] [CrossRef] (In the text)
-
Vázquez-Semadeni, E., Ostriker, E. C., Passot, T., Gammie,
C. F., & Stone, J. M. 2000, in Protostars and
Planets IV, ed. V. Mannings et al. (Tucson: Univ.
Arizona Press), 3
(In the text)
- Zuckerman,
B., & Evans, N. J., II 1974, ApJ, 192, L149 [NASA ADS] [CrossRef] (In the text)
Online Material
Appendix A: The Chandrasekhar-Münch scheme
For a function
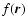 depending on the three-dimensional separation
depending on the three-dimensional separation 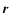 ,
double integrals of the form
,
double integrals of the form
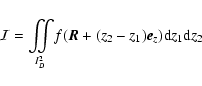 |
(A.1) |
can be transformed, taking into account the fact that the integrand only depends on the difference
 ,
because
,
because  is fixed, as shown in Chandrasekhar & Münch (1952). Making the variable change
is fixed, as shown in Chandrasekhar & Münch (1952). Making the variable change
 and z=z1,
and z=z1,
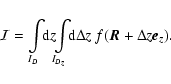 |
(A.2) |
where the notation IDz stands for the segment ID shifted by -z,
IDz=[-D/2-z,D/2-z], which we can separate in two, with a negative part,
IDz-=[-D/2-z,0], and a positive part
IDz+=[0,D/2-z].
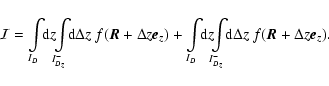 |
(A.3) |
Exchanging the order of integrations in each of these two terms, and expliciting the integral over z, we have
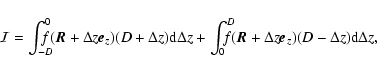 |
(A.4) |
which can be finally written as
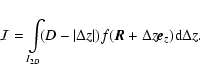 |
(A.5) |
The factor
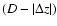 expresses the fact that for a finite slab, two given separations
expresses the fact that for a finite slab, two given separations 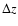 and
and 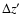 are not represented by the same number of pairs of points.
are not represented by the same number of pairs of points.
Appendix B: Autocorrelation functions of the velocity centroid maps in the case v0=0
When the mean velocity v0 is null, the method used in the main body of the paper cannot be applied without some modification. Little needs to be done, however, as velocity fluctuations can be measured with respect to the sound speed cs, which we assume to be uniform within the turbulent slab. We may then write the velocity centroid C as
![\begin{displaymath}%
C(\vec{X})=\alpha\!\!\int\limits_{I_D} \!\!\! \left(\rho_0+...
...X},z)}{\rho_0}\frac{\delta v(\vec{X},z)}{c_s}{\rm d} z\right],
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img291.gif) |
(B.1) |
which can be written in the shorthand form
![$C(\vec{X})=\alpha \rho_0 c_s D\left[y_{v_{\vec{X}}}+y_{\rho v_{\vec{X}}}\right]$](/articles/aa/full/2004/26/aa0139-04/img292.gif) .
The normalized velocity centroid then reads
.
The normalized velocity centroid then reads
![\begin{displaymath}%
C_0(\vec{X})=\frac{C(\vec{X})}{I(\vec{X})}=c_s\left[y_{v_{\...
...rho v_{\vec{X}}}\right]\left[1+y_{\rho_{\vec{X}}}\right]^{-1}.
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img293.gif) |
(B.2) |
The calculation therefore proceeds in the same way, with cs taking the place of v0 and the ai of Eq. (26) being replaced by new coefficients a'i given by
It follows that the autocorrelation function of the non-normalized centroid is, in this case,
![\begin{displaymath}%
A_C(\vec{R})=\left(\alpha D\right)^2\left[\rho_0^2M_{v,v}(\...
...rho_0M_{\rho v,v}(\vec{R})+M_{\rho v,\rho v}(\vec{R})\right],
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img295.gif) |
(B.3) |
which is precisely what is found form the general case when setting v0=0. Similarly, for the normalized centroid,
![\begin{displaymath}%
A_{C_0}(\vec{R})=M_{v,v}(\vec{R})+\frac{2}{\rho_0}\left[M_{\rho v,v}(\vec{R})-M^{(s)}_{v,v,\rho}(\vec{R},\vec{R})\right].
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img296.gif) |
(B.4) |
Appendix C: Expansion of the averaged autocorrelation function of an fBm field
We wish to compute the following expression as a function of the lag
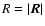 ,
in the limit
,
in the limit  ,
,
 {\rm d} z,
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img298.gif) |
(C.1) |
where  is a positive constant and
is a positive constant and
![$H \in [0,1]$](/articles/aa/full/2004/26/aa0139-04/img299.gif) is the Hurst exponent.
is the Hurst exponent.
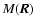 can be expressed as an integral over [0,D],
can be expressed as an integral over [0,D],
The last integral is easily shown to be equal to D2/2, and so
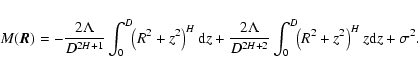 |
(C.2) |
The second of the remaining integrals can be explicited by setting
R2+z2=r2, since
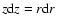 for R fixed,
for R fixed,
![\begin{displaymath}%
\int_0^D\!\! \left(R^2+z^2\right)^{H}z {\rm d} z=\int_R^{\s...
...left[\left(R^2+D^2\right)^{H+1}-\left(R^2\right)^{H+1}\right],
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img304.gif) |
(C.3) |
since
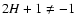 for
for
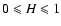 .
We therefore have
.
We therefore have
![\begin{displaymath}%
M(\vec{R})=-\frac{2\Lambda}{D^{2H+1}} \int_0^D\!\! \left(R^...
...t)^{H+1}-\left(\frac{R^2}{D^2}\right)^{H+1}\right] + \sigma^2.
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img307.gif) |
(C.4) |
For a zero separation in the plane of the sky, this expression is, explicitly,
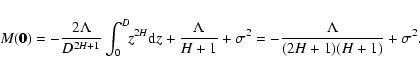 |
(C.5) |
When 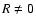 ,
the first integral in Eq. (C.4) generally cannot be written in closed form (Gradshteyn & Ryzhik 1980). Notable exceptions are for H=0 and H=1, when, respectively,
,
the first integral in Eq. (C.4) generally cannot be written in closed form (Gradshteyn & Ryzhik 1980). Notable exceptions are for H=0 and H=1, when, respectively,
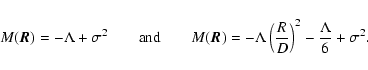 |
(C.6) |
To simplify the notations, we introduce the function K=K'-K'', defined by
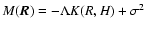 ,
with
,
with
![\begin{displaymath}%
K'(R,H)=\frac{2}{D^{2H+1}}\int_0^D\!\! \left(R^2+z^2\right)...
...2}\right)^{H+1}-\left(\frac{R^2}{D^2}\right)^{H+1}\right]\cdot
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img312.gif) |
(C.7) |
It is now interesting to consider the case of separations 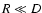 ,
which corresponds to studying the small scale structure of centroid maps. This allows to develop K(R,H) in powers of R/D. Expansion of K'' is straightforward,
,
which corresponds to studying the small scale structure of centroid maps. This allows to develop K(R,H) in powers of R/D. Expansion of K'' is straightforward,
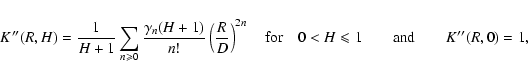 |
(C.8) |
where we introduced
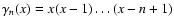 .
As for K', since we consider
.
As for K', since we consider
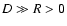 we can write it as
we can write it as
![\begin{displaymath}%
K'(R,H)=2\int_0^{D/R}\!\! \left(1+y^2\right)^{H} {\rm d} y\...
...d} y+\int_1^{D/R}\!\! \left(1+y^2\right)^{H} {\rm d} y\right].
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img316.gif) |
(C.9) |
The first integral, between 0 and 1, which we dub K0(H), cannot be explicited, but since it does not depend on R, it is unimportant with respect to the structure of the moment maps. The second integral can be transformed in order to develop the integrand through
1+y2=y2(1+y-2),
![\begin{displaymath}%
K'(R,H)=2\left(\frac{R}{D}\right)^{2H+1}\left[K_0(H)+ \sum_...
...{\gamma_k(H)}{k!} \int_1^{D/R}\!\! y^{2H-2k} {\rm d} y\right].
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img317.gif) |
(C.10) |
Computing the integrals in the equation above for 0 < H < 1 and
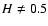 ,
we have
,
we have
![\begin{displaymath}%
K'(R,H)=2\left(\frac{R}{D}\right)^{2H+1}\left\{K_0(H)+ \sum...
...k+1}\left[\left(\frac{D}{R}\right)^{2H-2k+1}-1\right]\right\},
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img319.gif) |
(C.11) |
which, after rearranging the terms, leads to the following expression for K',
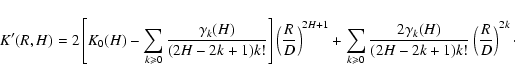 |
(C.12) |
If
0 < H < 0.5, then
1 < 2H+1 < 2 and the leading order expansion is therefore
![\begin{displaymath}%
K'(R,H)\simeq\frac{2}{2H+1} + 2\left[K_0(H)-\sum_{k \geqsla...
...\gamma_k(H)}{2H-2k+1}\right] \left(\frac{R}{D}\right)^{2H+1},
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img321.gif) |
(C.13) |
while if
0.5 < H < 1, then
2 < 2H+1 < 3 and the k=1 term of the last sum is dominant,
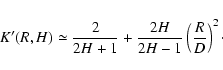 |
(C.14) |
This last expression is also valid for H=1, while obviously K'(R,0)=2. For H=0.5, the k=1 integral is
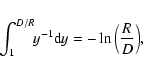 |
(C.15) |
and for 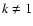 the integrals are unchanged. It follows that
the integrals are unchanged. It follows that
![\begin{displaymath}%
K'(R,0.5)=2\left(\frac{R}{D}\right)^2\left\{K_0(0.5)- \frac...
...[\left(\frac{D}{R}\right)^{2-2k}\!\!\!\!\!\!-1\right]\right\},
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img325.gif) |
(C.16) |
which gives, after rearranging the terms,
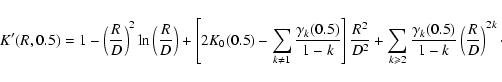 |
(C.17) |
Finally, the leading order expansion of K(R,H) for small separations 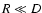 is
is
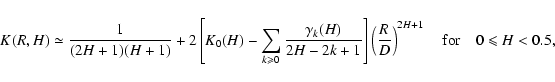 |
(C.18) |
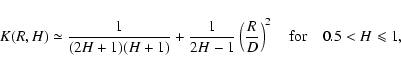 |
(C.19) |
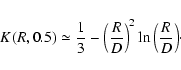 |
(C.20) |
Consequently, the expansion of
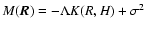 reads
reads
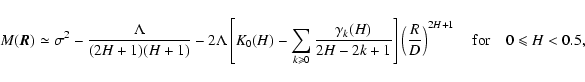 |
(C.21) |
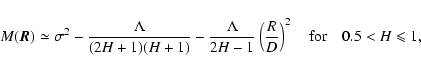 |
(C.22) |
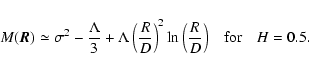 |
(C.23) |
The consequences on the statistical measures performed on the moment maps are straightforward to derive. They are given and analyzed in the main body of the paper.
Appendix D: The uniformity of fBm fields with H> 1
We consider the mean squared increment of an fBm field
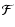 of Hurst exponent H > 1 between positions
of Hurst exponent H > 1 between positions 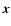 and
and
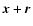 .
The separation vector
.
The separation vector 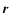 is then separated in p equal parts, so that
is then separated in p equal parts, so that
![\begin{displaymath}%
\overline{\left[\mathcal{F}(\vec{x}+\vec{r})-\mathcal{F}(\v...
...\overline{\left[\sum_{k=0}^{p-1}\Delta\mathcal{F}_k\right]^2},
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img334.gif) |
(D.1) |
where
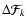 is the increment of
is the increment of
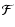 between the
between the
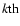 and
and
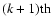 positions. Expansion of the expression above yields
positions. Expansion of the expression above yields
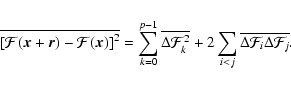 |
(D.2) |
Now,
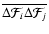 can be written as an autocorrelation product of the function
can be written as an autocorrelation product of the function
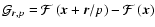 ,
,
![\begin{displaymath}%
\overline{\Delta\mathcal{F}_i\Delta\mathcal{F}_j}=\overline...
...G}_{\vec{r},p}\left(\vec{x}+\frac{j}{p}\vec{r}\right)\right]}.
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img341.gif) |
(D.3) |
Since autocorrelation functions are decreasing from their zero spacing value, we have
![\begin{displaymath}%
\overline{\Delta\mathcal{F}_i\Delta\mathcal{F}_j}\leqslant\...
...e{\left[\mathcal{G}_{\vec{r},p}\left(\vec{x}\right)\right]^2},
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img342.gif) |
(D.4) |
which allows us to give an upper limit for the mean squared increment of
 ,
,
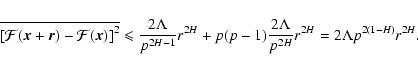 |
(D.5) |
This result being valid for any value of p, which characterizes a subdivision of the separation vector 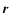 ,
we see that since H > 1, the limit
,
we see that since H > 1, the limit
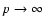 implies
implies
![$\overline{\left[\mathcal{F}(\vec{x}+\vec{r})-\mathcal{F}(\vec{x})\right]^2}=0$](/articles/aa/full/2004/26/aa0139-04/img345.gif) and therefore
and therefore
 is a uniform field.
is a uniform field.
Copyright ESO 2004
![\begin{figure}
\par\includegraphics[width=18cm,clip]{aa0139-04f1.eps}\end{figure}](/articles/aa/full/2004/26/aa0139-04/Timg6.gif)
![]() ,
which can be written as
,
which can be written as
![]() ,
where
,
where ![]() is a two-dimensional vector in the plane of the sky and z marks the line-of-sight position of the point considered,
is a two-dimensional vector in the plane of the sky and z marks the line-of-sight position of the point considered, ![]() being the unit vector along the line of sight. The three-dimensional separation between points
being the unit vector along the line of sight. The three-dimensional separation between points ![]() and
and ![]() is written as
is written as
![]() and the separation between their respective lines of sight
and the separation between their respective lines of sight ![]() and
and ![]() is
is
![]() .
In short, three-dimensional vectors are written in lowercase, while vectors in the plane of the sky are written in uppercase. These notations are illustrated in Fig. 1. It should be emphasized that we shall only consider small scales on the plane of the sky, so that all lines of sight are parallel.
.
In short, three-dimensional vectors are written in lowercase, while vectors in the plane of the sky are written in uppercase. These notations are illustrated in Fig. 1. It should be emphasized that we shall only consider small scales on the plane of the sky, so that all lines of sight are parallel.
![]() , with z=0 conventionally placed halfway through the slab (see Fig. 1). Within the slab, the average density (that is, the average number of emitters per unit volume taken over the whole slab) is a constant noted
, with z=0 conventionally placed halfway through the slab (see Fig. 1). Within the slab, the average density (that is, the average number of emitters per unit volume taken over the whole slab) is a constant noted ![]() .
As for the velocity
.
As for the velocity ![]() of the gas with respect to the observer, we shall write v to stand for its component along the line of sight, the mean value of which over the slab is v0. These averages (
of the gas with respect to the observer, we shall write v to stand for its component along the line of sight, the mean value of which over the slab is v0. These averages (![]() and v0) are obviously constants, independent of the line of sight. To assume the most general case, we shall take v0 to be nonzero
and v0) are obviously constants, independent of the line of sight. To assume the most general case, we shall take v0 to be nonzero![]() . The gas velocity within the rest frame of the cloud is simply
. The gas velocity within the rest frame of the cloud is simply
![]() ,
assuming that there is no systematic transverse velocity. Furthermore, fluctuations of density along any given line of sight are supposed to be small compared to the average value
,
assuming that there is no systematic transverse velocity. Furthermore, fluctuations of density along any given line of sight are supposed to be small compared to the average value ![]() ,
in the sense that the standard deviation of the density field should be less than
,
in the sense that the standard deviation of the density field should be less than ![]() .
It is also assumed that the turbulent flow within the slab is homogeneous and isotropic. These last hypotheses are to be understood in the strong sense of Monin & Yaglom (1975): not only are the scalar field
.
It is also assumed that the turbulent flow within the slab is homogeneous and isotropic. These last hypotheses are to be understood in the strong sense of Monin & Yaglom (1975): not only are the scalar field ![]() and the vector field
and the vector field
![]() homogeneous and isotropic, but the same should apply to the four-dimensional field
homogeneous and isotropic, but the same should apply to the four-dimensional field
![]() .
This will be useful in the derivation of our results in Sect. 4. Outside the slab, the density and velocity are set to zero. We further assume that the observation is done in an optically thin transition, at a frequency for which the Rayleigh-Jeans approximation is valid, that uniform excitation conditions apply within the slab, and that no background radiation is present.
.
This will be useful in the derivation of our results in Sect. 4. Outside the slab, the density and velocity are set to zero. We further assume that the observation is done in an optically thin transition, at a frequency for which the Rayleigh-Jeans approximation is valid, that uniform excitation conditions apply within the slab, and that no background radiation is present.
![]() representing the emission from a given line of sight
representing the emission from a given line of sight ![]() at an observed velocity u can be written as the integral (Dickman & Kleiner 1985b),
at an observed velocity u can be written as the integral (Dickman & Kleiner 1985b),
![\begin{displaymath}%
\phi(w)=\frac{1}{\sqrt{2\pi}\sigma_{{\rm th}}}\exp{\left[-\frac{w^2}{2\sigma_{{\rm th}}^2}\right]},
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img26.gif)
![]() for a given line of sight
for a given line of sight ![]() .
This is a logical step considering that knowledge of the moments of a random variable is equivalent to that of the full probability distribution. We shall therefore consider the moment maps
.
This is a logical step considering that knowledge of the moments of a random variable is equivalent to that of the full probability distribution. We shall therefore consider the moment maps
![]() defined by
defined by
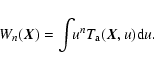
![$\displaystyle \int \!\! u^n \left[ \alpha \!\!\int\limits_{I_D} \!\!\! \rho(\vec{x})\phi(v(\vec{x})-u){\rm d} z \right] {\rm d} u$](/articles/aa/full/2004/26/aa0139-04/img40.gif)
![$\displaystyle \alpha \!\!\int\limits_{I_D} \!\!\! \rho(\vec{x}) \left[\int\limi...
...om{I_D}} \!\!\! \left(v(\vec{x})-w\right)^n \phi(w) {\rm d} w\right] {\rm d} z,$](/articles/aa/full/2004/26/aa0139-04/img41.gif)
![$\displaystyle \alpha \sum_{k=0}^n (-1)^kC_n^k \left[\int\limits_{I_D} \!\!\! \r...
... z \right]\left[\int\limits_{\phantom{I_D}} \!\!\! w^k \phi(w) {\rm d} w\right]$](/articles/aa/full/2004/26/aa0139-04/img43.gif)
![$\displaystyle \sum_{k=0}^n C_n^k h_k \left[\int\limits_{I_D} \!\!\! \rho(\vec{x})v^{n-k}(\vec{x}){\rm d} z \right],$](/articles/aa/full/2004/26/aa0139-04/img44.gif)
![]() can only be used to derive statistics of the density field, as it is proportional to the column density
can only be used to derive statistics of the density field, as it is proportional to the column density
![]() .
The first moment or non-normalized velocity centroid
.
The first moment or non-normalized velocity centroid
![]() is the first appropriate quantity to study the velocity field, as can be seen from Eq. (8). However,
is the first appropriate quantity to study the velocity field, as can be seen from Eq. (8). However,
![]() represents the integration of a momentum, rather than of a velocity proper, and it appears that density fluctuations may affect the estimation of the velocity statistics from this map. To circumvent this problem, it is common to use normalized centroids
represents the integration of a momentum, rather than of a velocity proper, and it appears that density fluctuations may affect the estimation of the velocity statistics from this map. To circumvent this problem, it is common to use normalized centroids
![]() ,
which are simply defined as the ratio
,
which are simply defined as the ratio
![]() .
This is usually and empirically justified by the assumption that density fluctuations in
.
This is usually and empirically justified by the assumption that density fluctuations in
![]() are also present in
are also present in
![]() and therefore somehow vanish from
and therefore somehow vanish from
![]() .
In the simplified case where density does not fluctuate along the line of sight, such a reasoning is obviously correct, even if transverse density fluctuations are present, and normalization then only serves as a dimensionality factor. As far as we are aware, however, no analytical study exists of the influence of longitudinal fluctuations of density on velocity centroids, even in the quite simplified model used here.
.
In the simplified case where density does not fluctuate along the line of sight, such a reasoning is obviously correct, even if transverse density fluctuations are present, and normalization then only serves as a dimensionality factor. As far as we are aware, however, no analytical study exists of the influence of longitudinal fluctuations of density on velocity centroids, even in the quite simplified model used here.
![]() and
and
![]() .
Of course, it is similarly reasonable to look for the influence of density structure in the statistics of the intensity map
.
Of course, it is similarly reasonable to look for the influence of density structure in the statistics of the intensity map
![]() .
One such useful measure to be performed on the available two-dimensional maps is the autocorrelation function (ACF), which gives the mean degree of correlation between values of a field taken at points separated on the plane of the sky by a given vector
.
One such useful measure to be performed on the available two-dimensional maps is the autocorrelation function (ACF), which gives the mean degree of correlation between values of a field taken at points separated on the plane of the sky by a given vector ![]() (Kleiner & Dickman 1984). More precisely, the autocorrelation function
(Kleiner & Dickman 1984). More precisely, the autocorrelation function
![]() of a field
of a field
![]() is defined by
is defined by
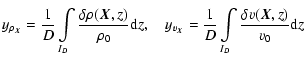
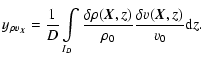
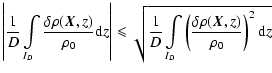
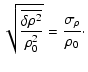
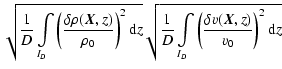
![\begin{figure}
\par\includegraphics[width=18cm,clip]{aa0139-04f2.eps}\end{figure}](/articles/aa/full/2004/26/aa0139-04/Timg87.gif)
![]() of the intensity map
of the intensity map
![]() ,
and using the linearity property of averages, we have terms of order up to two in density fluctuations, namely
,
and using the linearity property of averages, we have terms of order up to two in density fluctuations, namely
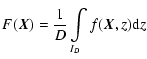
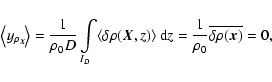
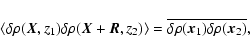
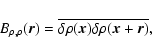
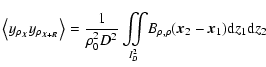
![]() .
Its expansion, written in Eq. (10), includes terms of order zero and one in density fluctuations. Therefore, its autocorrelation function
.
Its expansion, written in Eq. (10), includes terms of order zero and one in density fluctuations. Therefore, its autocorrelation function
![]() features terms of order up to two. Namely,
features terms of order up to two. Namely,
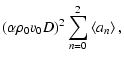
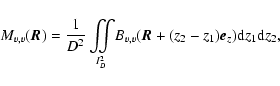
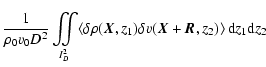
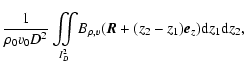
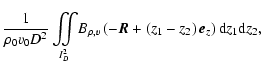
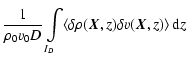
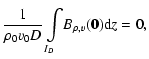
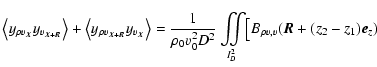
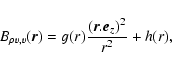
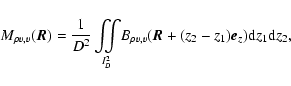
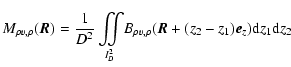

![\begin{displaymath}%
\left<a_2\right>=\frac{1}{\rho_0^2}\left[ M_{\rho,\rho}(\ve...
...o}(\vec{R})+\frac{1}{v^2_0} M_{\rho v,\rho v}(\vec{R})\right],
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img179.gif)
![\begin{displaymath}%
f^{(s)}(x)=\frac{1}{2}\left[f(x)+f(-x)\right].
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img180.gif)
![]() is a theoretically infinite series which reads
is a theoretically infinite series which reads
![$\displaystyle A_{C_0}(\vec{R})\!=\!v_0^2\left<\left[\sum_{p,q}(-1)^{p+q}y^p_{\r...
...[\sum_{n=0}^2a_n\right]\right>\!=\!v_0^2\sum_{m}\sum_{n=0}^2\left<a_nb_m\right>$](/articles/aa/full/2004/26/aa0139-04/img186.gif)
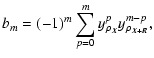
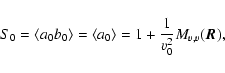
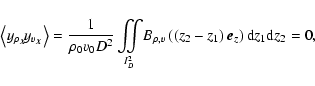
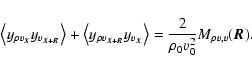
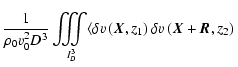
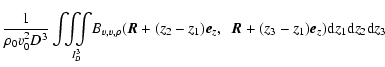
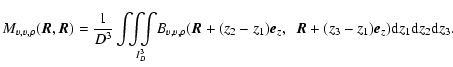
![\begin{displaymath}%
M^{(s)}_{v,v,\rho}(\vec{R},\vec{R})=\frac{1}{2}\left[M_{v,v,\rho}(\vec{R},\vec{R})+M_{v,v,\rho}(-\vec{R},-\vec{R})\right].
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img209.gif)
![]() ,
,
![]() and
and
![]() requires the knowledge of the three-dimensional correlation functions appearing as integrated terms in Eqs. (24), (44) and (56). However, it may prove impossibly difficult to build a complete and consistent set of such functions and then to analytically compute their averages. Therefore, as a first step, one should stick to the lowest order terms in the expressions of the two-dimensional autocorrelation functions,
requires the knowledge of the three-dimensional correlation functions appearing as integrated terms in Eqs. (24), (44) and (56). However, it may prove impossibly difficult to build a complete and consistent set of such functions and then to analytically compute their averages. Therefore, as a first step, one should stick to the lowest order terms in the expressions of the two-dimensional autocorrelation functions,
![$\displaystyle 2\left[\sigma_\rho^2 -B_{\rho,\rho}(\vec{r})\right]=2\Lambda_\rho \left(\frac{r}{D}\right)^{2H_\rho},$](/articles/aa/full/2004/26/aa0139-04/img222.gif)
![$\displaystyle 2\left[\sigma_v^2 -B_{v,v}(\vec{r})\right]=2\Lambda_v \left(\frac{r}{D}\right)^{2H_v}.$](/articles/aa/full/2004/26/aa0139-04/img225.gif)
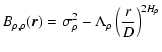
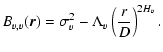
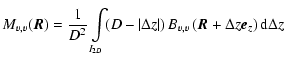
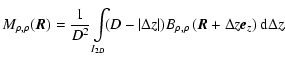
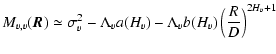
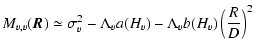
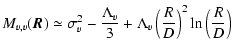
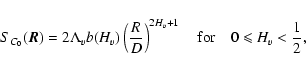
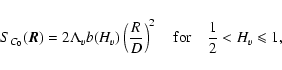
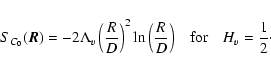
![]() ,
,
![]() and
and
![]() should be written as averages of correlation functions within the slab in the manner described in Fig. 2, since all pairs of points with a given separation
should be written as averages of correlation functions within the slab in the manner described in Fig. 2, since all pairs of points with a given separation ![]() in the plane of the sky should contribute to the two-dimensional statistical measures at lag
in the plane of the sky should contribute to the two-dimensional statistical measures at lag ![]() .
.
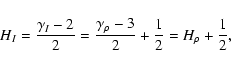
![\begin{eqnarray*}&& A_C(\vec{R})\simeq(\alpha D\rho_0)^2\left[v_0^2+M_{v,v}(\vec...
..._{\rho v,v}(\vec{R})-M^{(s)}_{v,v,\rho}(\vec{R},\vec{R})\right],
\end{eqnarray*}](/articles/aa/full/2004/26/aa0139-04/img268.gif)
![]() ,
defined through their second order structure function
,
defined through their second order structure function
![]() as
as
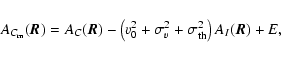
![]() depending on the three-dimensional separation
depending on the three-dimensional separation ![]() ,
double integrals of the form
,
double integrals of the form
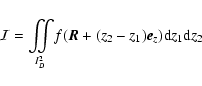
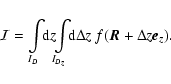
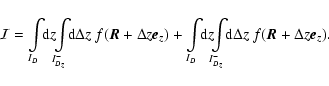
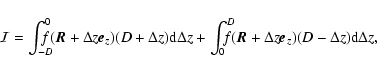
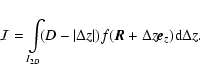
![\begin{displaymath}%
C(\vec{X})=\alpha\!\!\int\limits_{I_D} \!\!\! \left(\rho_0+...
...X},z)}{\rho_0}\frac{\delta v(\vec{X},z)}{c_s}{\rm d} z\right],
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img291.gif)
![\begin{displaymath}%
C_0(\vec{X})=\frac{C(\vec{X})}{I(\vec{X})}=c_s\left[y_{v_{\...
...rho v_{\vec{X}}}\right]\left[1+y_{\rho_{\vec{X}}}\right]^{-1}.
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img293.gif)
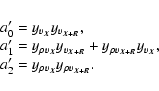
![\begin{displaymath}%
A_C(\vec{R})=\left(\alpha D\right)^2\left[\rho_0^2M_{v,v}(\...
...rho_0M_{\rho v,v}(\vec{R})+M_{\rho v,\rho v}(\vec{R})\right],
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img295.gif)
![\begin{displaymath}%
A_{C_0}(\vec{R})=M_{v,v}(\vec{R})+\frac{2}{\rho_0}\left[M_{\rho v,v}(\vec{R})-M^{(s)}_{v,v,\rho}(\vec{R},\vec{R})\right].
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img296.gif)
![]() ,
in the limit
,
in the limit ![]() ,
,
 {\rm d} z,
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img298.gif)
![\begin{displaymath}M(\vec{R})=\frac{2}{D^2}\int_0^D\left[-\Lambda \frac{\left(R^...
...-z) {\rm d} z + \sigma^2 \int_0^D\!\! (D-z) {\rm d} z \right].
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img301.gif)
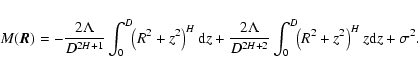
![\begin{displaymath}%
\int_0^D\!\! \left(R^2+z^2\right)^{H}z {\rm d} z=\int_R^{\s...
...left[\left(R^2+D^2\right)^{H+1}-\left(R^2\right)^{H+1}\right],
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img304.gif)
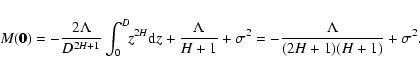
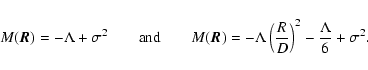
![\begin{displaymath}%
K'(R,H)=\frac{2}{D^{2H+1}}\int_0^D\!\! \left(R^2+z^2\right)...
...2}\right)^{H+1}-\left(\frac{R^2}{D^2}\right)^{H+1}\right]\cdot
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img312.gif)
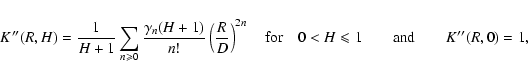
![\begin{displaymath}%
K'(R,H)=2\int_0^{D/R}\!\! \left(1+y^2\right)^{H} {\rm d} y\...
...d} y+\int_1^{D/R}\!\! \left(1+y^2\right)^{H} {\rm d} y\right].
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img316.gif)
![\begin{displaymath}%
K'(R,H)=2\left(\frac{R}{D}\right)^{2H+1}\left[K_0(H)+ \sum_...
...{\gamma_k(H)}{k!} \int_1^{D/R}\!\! y^{2H-2k} {\rm d} y\right].
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img317.gif)
![\begin{displaymath}%
K'(R,H)=2\left(\frac{R}{D}\right)^{2H+1}\left\{K_0(H)+ \sum...
...k+1}\left[\left(\frac{D}{R}\right)^{2H-2k+1}-1\right]\right\},
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img319.gif)
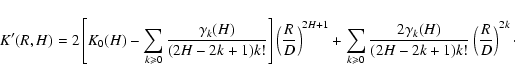
![\begin{displaymath}%
K'(R,H)\simeq\frac{2}{2H+1} + 2\left[K_0(H)-\sum_{k \geqsla...
...\gamma_k(H)}{2H-2k+1}\right] \left(\frac{R}{D}\right)^{2H+1},
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img321.gif)
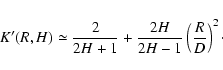
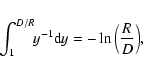
![\begin{displaymath}%
K'(R,0.5)=2\left(\frac{R}{D}\right)^2\left\{K_0(0.5)- \frac...
...[\left(\frac{D}{R}\right)^{2-2k}\!\!\!\!\!\!-1\right]\right\},
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img325.gif)
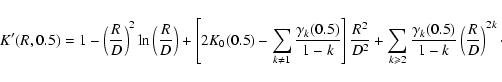
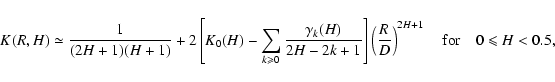
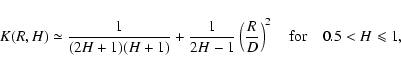
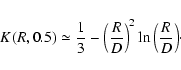
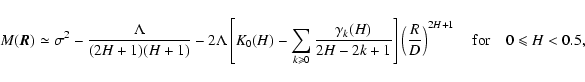
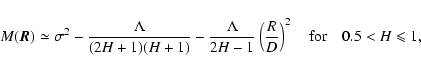
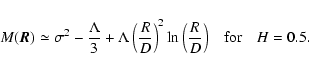
![]() of Hurst exponent H > 1 between positions
of Hurst exponent H > 1 between positions ![]() and
and
![]() .
The separation vector
.
The separation vector ![]() is then separated in p equal parts, so that
is then separated in p equal parts, so that
![\begin{displaymath}%
\overline{\left[\mathcal{F}(\vec{x}+\vec{r})-\mathcal{F}(\v...
...\overline{\left[\sum_{k=0}^{p-1}\Delta\mathcal{F}_k\right]^2},
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img334.gif)
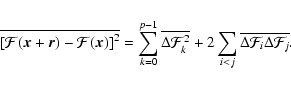
![\begin{displaymath}%
\overline{\Delta\mathcal{F}_i\Delta\mathcal{F}_j}=\overline...
...G}_{\vec{r},p}\left(\vec{x}+\frac{j}{p}\vec{r}\right)\right]}.
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img341.gif)
![\begin{displaymath}%
\overline{\Delta\mathcal{F}_i\Delta\mathcal{F}_j}\leqslant\...
...e{\left[\mathcal{G}_{\vec{r},p}\left(\vec{x}\right)\right]^2},
\end{displaymath}](/articles/aa/full/2004/26/aa0139-04/img342.gif)