A&A 421, L9-L12 (2004)
DOI: 10.1051/0004-6361:20040169

Diamagnetic effects of heliospheric Pick-up ions and magnetic fluxes in the outer heliosphere

H. J. Fahr - K. Scherer

Institut für Astrophysik und Extraterrestrische Forschung der Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany

Received 29 March 2004 / Accepted 12 May 2004

Abstract
For a long time it has been suggested that at larger solar distances the interplanetary magnetic field may not be behaving as predicted by Parker`s Archimedian spiral field model. This phenomenon, partly identified as the "magnetic flux deficit'' paradox, appears as deficits in the azimuthal magnetic field components connected with "underwound'' magnetic fields, though the pick-up ion decelerated solar wind should rather lead to excesses. Up to now no satisfactory explanation for this phenomenon has been presented. In this paper we study for the first time the diamagnetic effect of pick-up ions which systematically load the solar wind with suprathermal ions at its expansion to larger distances and diamagnetize the plasma. We shall demonstrate that such ions mainly reduce the azimuthal magnetic field component by their diamagnetic action. As we can show the field deficits can easily theoretically be explained by this effect. Also some new light is now shed on the problem of the magnetic field jump to be expected at the termination shock.

Key words: magnetic fields - plasma

1 Introduction

In the paper by Winterhalter et al. (1990) it was shown that, on the basis of PIONEER-11 magnetic field data a systematic flux deficit appears in the outer heliosphere with respect to field predictions made by the Parker model (Parker 1958). The resulting deficits amount to about 20 percent at distances of 24 AU. This phenomenon was confirmed by ongoing measurements as documented by Smith et al. (1997,2004) based on ULYSSES magnetic field measurements. However, other authors came to the conclusion, that no such deficit exists (e.g. Burlaga et al. 2002) and there might be still no sufficient observational data to decide on this phenomena. Here we argue that, on a purely theoretical basis, the flux deficit reported by (Smith et al. 1997) should be expected. The latter authors clearly revealed that the magnetic flux invariant  $\Phi_{r}=r^{2}B_{r}$ behaves normal and interestingly enough, is revealed as latitude-independent. In contrast to the azimuthal component $B_{\rm a}$ clearly violates Parker's expected field invariant  $\Phi_{\rm a}=rV_{r}B_{\rm a}=-\Omega_{\rm s}\Phi_{r} \cos\vartheta$, showing that especially at latitudes with  $\cos \vartheta\simeq1$ (i.e. near the ecliptic) an azimuthal field deficit by about 10 to 15 percent is recognizable. As these authors state, this latitudinally dependent deficit can hardly be explained by unknown latitudinal variations of the solar rotation period  $\Omega_{\rm s}=\Omega _{\rm s}(\vartheta)$, i.e. effects of differential solar rotation. Also, earlier explanations of an out-of-ecliptic transport of magnetic fields due to meridional solar wind flow components as offered by Pizzo & Goldstein (1987) or Suess et al. (1985) in view of the latitude-independent invariant $\Phi_{r}$ are obviously ruled out. Hence it still remains to explain why azimuthal field components in the outer heliosphere appear to be reduced instead of enhanced due to the pile-up in the pick-up ion decelerated solar wind when compared with the expectations from Parker`s field model. It is interesting to notice that the well-known pick-up ion effect to decelerate the solar wind at larger distances (see Fahr & Rucinski 2001; Isenberg 1997; Fahr & Rucinski 1999) inducing a magnetic field pile-up should tend to produce flux excesses rather than deficits. Here, we will restrict ourselves only to the derivation of the diamagnetic effect of pick-up ions and its possible implications.

2 The diamagnetic influence of the pick-up ions

It is well known vacuum electric and magnetic fields, $\vec{E}$ and $\vec{H}$, are converted into different fields, $\vec{D}$ and $\vec{B}$, in dielectric and magnetically susceptible media like solid, liquid or gaseous materials or plasmas. In such media not only free electric charges and currents may be present, but also "bound'' charges in form of electrically polarizable materials or in form of "bound'' electrical currents which are connected with motions of "bound'' electric charges. In a plasma for instance charged particles may be magnetically bound to gyro-orbits and thus cause microscopic electric circle currents  $\vec{j}_{\rm b}$. One can ask the question what relations may exist between $\vec{E}$ and $\vec{D}$ as well as $\vec{H}$ and $\vec{B}$ in a space plasma like the solar wind. In a fully ionized plasma the polarizability vanishes for stationary cases (i.e. for the frequency $\omega=0$) and the dielectric coefficient  $\epsilon(\omega=0)$ is equal to 1, meaning that  $\vec{D}=\epsilon(\omega=0)\vec{E}=\vec {E}$. The effective magnetic induction $\vec{B}$, measurable in a plasma background is nevertheless different from the vacuum field $\vec{H}$ since the plasma matter develops bound electric currents  $\vec{j}_{\rm b}$ connected with gyrating electric charges which by themselves produce magnetic fields.

Hence for instance at some heliocentric distance r in interplanetary space the fields $\vec{B}$ and $\vec{H}$, taking into account the effect of these bound currents  $\vec{j}_{\rm b}$, are thus connected by (see e.g. Chen 1977):

$\displaystyle \vec{B}=\vec{H}+4\pi\vec{M}$     (1)

where $\vec{H}$ is the vacuum magnetic field and $\vec {M}$ is the magnetic moment per volume due to the bound currents of the plasma particles with the relation  $\vec{j}_{\rm b}={\rm rot}\vec{M}$. The magnetic moments of electrons and ions are  $\vec{\mu}_{\rm {e}}=(j_{\rm {be}}/c)\vec{A}_{\rm {e}}$ and  $\vec{\mu}_{\rm {i}}=(j_{\rm {bi}}/c)\vec{A}_{\rm {i}}$, respectively. Though these particles gyrate in opposite directions around the field (all ions have right-handed, all electrons left-handed gyrations), the magnetic moments have the same orientation, namely in both cases opposite to the original field $\vec{H}$(i.e. resulting in all cases in a diamagnetic action upon the field). Here  $j_{\rm {be,i}}$ and  $\vec{A}_{\rm {e,i}}$ denote the bound currents and the oriented encircled areas of the gyrating electrons and ions, respectively. The magnetic moment of an individual ion (or electron) is thus given by:
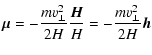$\displaystyle \vec{\mu}=-\frac{mv_{\perp}^{2}}{2H}\frac{\vec{H}}{H} = -\frac{mv_{\perp}^{2}}{2H} \vec{h}$     (2)

where $v_{\perp}$ is the ion velocity perpendicular to $\vec{H}$, and  $\vec{h} = \vec{H}/H$ is the unit vector in direction of $\vec{H}$. One can see that in the outer solar system, where normal solar wind ions and electrons have cooled down, only pick-up ions (PUI`s) with their large values of  $v_{\perp}\simeq V_{\rm s}$, where $V_{\rm s}$ is the solar wind bulk velocity, shall contribute to $\vec {M}$. Thus one can assume that $\vec {M}$ is simply given by:
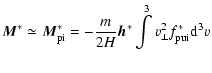$\displaystyle \vec{M}^{\ast}\simeq\vec{M}_{\rm {pi}}^{\ast}=-\frac{m} {2H}\vec{h}^{\ast}\int\limits^{3}v_{\perp}^{2}f_{\rm {pui}}^{\ast}{\rm d}^{3}v$     (3)

where  $f_{\rm {pui}}^{\ast}$ and  $\vec{H}^{\ast}$ are the local PUI distribution function and the vacuum field in the solar wind rest frame, in which the parameters are denoted by $^\ast$.

At larger solar distances the PUI distribution function due to rapid pitch-angle scattering can reasonably well be approximated by a distribution which is essentially gyrotropic and isotropic with respect to pitch angle $\vartheta$ or its cosine  $\eta=\cos\vartheta$ (see e.g. Chalov & Fahr 1998). Thus the above expression transforms to:

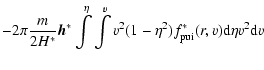                              $\displaystyle \vec{M}^{\ast}$ = $\displaystyle -2\pi\frac{m}{2H^{\ast}}\vec{h}^{\ast} \int\limits^{\eta}\int\limits^{v}v^{2}(1-\eta^{2})f_{\rm {pui}}^{\ast}(r,v){\rm d}\eta v^{2}{\rm d}v$  
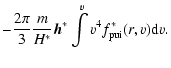  = $\displaystyle -\frac{2 \pi}{3}\frac{m}{H^{\ast}}\vec{h}^{\ast} \int\limits^{v}v^{4}f_{\rm {pui}}^{\ast}(r,v){\rm d}v.$ (4)

This expression has a strong analogy to that one representing the PUI pressure which is given by:
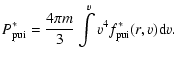$\displaystyle P_{\rm {pui}}^{\ast}=\frac{4\pi m}{3}\int\limits^{v}v^{4}f_{\rm {pui}}^{\ast}(r,v){\rm d}v.$     (5)

Therefore one finds:
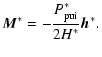$\displaystyle \vec{M}^{\ast}= -\frac{P_{\rm {pui}}^{\ast}} {2H^\ast}\vec{h}^{\ast}.$     (6)

A fairly realistic expression for  $P_{\rm {pui}}^{\ast}$ can be derived from results obtained for  $f_{\rm {pui}}^{\ast}$ by Chalov et al. (1995,1997) as solutions of a complete PUI phase-space transport equation. As was shown by Fahr & Lay (2000) these numerical results for  $f_{\rm {pui}}^{\ast}$ can fairly adequately be represented by the following analytical formula:

 
$\displaystyle f_{\rm {pui}}^{\ast}=\Pi \left( x^{-0.33}\right) w^{\beta}\exp\left[ -C(x)\left( w-w_{0}\right) ^{\kappa}\right] ,$     (7)

where $\Pi$ is a constant,  $x=r/r_{\rm {E}}$ is the radial solar distance in units of AU,  $w=\left( v/V_{\rm s}\right) ^{2}$ is the squared PUI velocity normalized with the solar wind velocity $V_{\rm s}$, and w0being a typical PUI injection value. Furthermore the quantities $\beta$, $\kappa$, and C are found as:  $\beta=-\frac{1}{6}$; $\kappa=\frac{2}{3}$; and:  C(x)=0.442 x0.2. With the above representation of  $f_{\rm {pui}}^{\ast}$ in Eq. (7) one then obtains the PUI density by:
 
$\displaystyle \rho_{\rm pui}=2\pi m \Pi x^{-0.33}\left[ \frac{3}{2}C(x)^{-2} \Gamma(2)\right] = 3 \pi m \Pi x^{-0.33} C(x)^{-2},$     (8)

and the PUI pressure by:
 
$\displaystyle P_{\rm {pui}}=\frac{2\pi}{3}\Pi x^{-0.33}\left(\frac{1}{2}m_{\rm ... ...) \left[ \frac{3}{2}C(x)^{-\frac{7}{2}} \Gamma\left(\frac{7} {2}\right)\right],$     (9)

where $\Gamma$ is the Gamma function. Equations (8) and (9) thus yield the following form for  $P_{\rm {pui}}$:
 
$\displaystyle P_{\rm {pui}}=\frac{5}{16}\sqrt[2]{\pi}C(x)^{-\frac{3}{2}}\rho_{\rm {pui}}V_{\rm s}^{2} =\alpha(x)\cdot\rho_{\rm {pui}}V_{\rm s}^{2}.$     (10)

In this expression for  $P_{\rm {pui}}(x)$ the function $\alpha$ is found as given by:  $\alpha=\alpha(x)=1.83$ x-0.3. The above formula (10) based on the results by Fahr & Lay (2000) is valid at distances of  $x\geq x_{\rm {c}}=20$where  $\alpha =\alpha_{\rm {c}}=\alpha(x_{\rm {c}})$ evaluates to  $\alpha_{\rm {c}}=0.44$.

Coming back now to the magnetic moment given by Eq. (5) one thus finds:

 
$\displaystyle \vec{M}^{\ast}=-\frac{P_{\rm {pui}}}{2H^{\ast}}\vec{h}^{\ast}= -\frac{\alpha(x)}{2H^{\ast}}\rho_{\rm {pui}}V_{\rm s}^{2}\vec{h}^{\ast}$     (11)

and the magnetic induction  $\vec{B}^{\ast}$ in the solar wind frame hence is given by:
 
                             $\displaystyle \vec{B}^{\ast}$ = $\displaystyle \vec{H}^{\ast}+4\pi\vec {M}^{\ast}=\vec{H}^{\ast}\!\cdot\!\left[ 1-\frac{\alpha(x)m} {4(H^{\ast2}/8\pi)}n_{\rm {pui}}V_{\rm s}^{2}\right]$  
  = $\displaystyle \vec{H}^{\ast}\!\cdot\!\left[ 1-\frac {\alpha(x)}{2}\frac{V_{\rm ... ...-\frac{\alpha(x)}{2} M_{\rm a}^{2} \frac{\rho_{\rm {pui}}}{\rho_{\rm s}}\right]$ (12)

where $v_{\rm a}$ denotes the Alfvén velocity and  $\rho_{\rm s}$ is the total solar wind proton mass density and $M_{\rm a}$ is the Alfvénic Mach number. As derived by Fahr (2002) or Chashei et al. (2003) the relative abundance of pick-up ions over total solar wind ions for the upwind direction is given by:
$\displaystyle \frac{\rho_{\rm {pui}}}{\rho_{\rm s}}=1-\exp(-\Lambda(\zeta-1)) = R_{\rho}$     (13)

with $\Lambda$ given by:
$\displaystyle \Lambda=n_{\rm H\infty}\sigma_{\rm ex}r_{0}=1.5\times 10^{-2}$     (14)

and  $\zeta=r/r_{0}$. Here the LISM H-atom density is introduced by its presently most favored value of  $n_{\rm H\infty}\simeq0.1$ cm-3. The charge exchange cross section is taken to be $\sigma_{\rm ex}=2\times 10^{-15}$ cm2, and the reference distance taken to be r0=20 AU. We obtain from Eq. (12):
$\displaystyle \vec{B}^{\ast}=\vec{H}^{\ast}\cdot\left[ 1 - \frac{\alpha(\zeta)}{2}M_{\rm a}^{2} R_\rho \right].$     (15)

Since fields are not measured in the solar wind rest frame, but in a spacecraft frame which is nearly identical with the heliocentric rest frame, we have to transform Eq. (16) into the heliocentric rest frame. Therefore, we use the special relativistic transformation of the fields from the solar wind rest frame to the heliocentric rest frame and, reminding that the Lorentz factor  $\gamma(V_{\rm s})\simeq1-(1/2)(V_{\rm s}/c)^{2}\simeq1$, and in the comoving frame  $ \vec {E}^{\ast} \simeq0$, we then find:

$\displaystyle \vec{H} = \gamma(V_{\rm s}) \cdot \left(\vec{H}^{\ast} - \frac{1}{c} \left[\vec{V}_{\rm s} \times \vec{E}^{\ast}\right]\right)\simeq\vec{H}^{\ast}.$     (16)

Taking now as an expectation value for the vacuum field $\vec{H}$ Parker's value for the Archimedian spiral field based on the frozen-in field condition, we find that the Alfvén Mach number behaves nearly like  $M_{\rm a}\simeq10\simeq {\rm const}$. at larger distances. Therefore, we obtain the interesting result that the Parker field in the case of the PUI-loaded diamagnetic plasma at large solar distances should be reduced approximately by:
 
$\displaystyle \vec{B} = \vec{H}\cdot\left[ 1 -\frac{\alpha(\zeta)}{2}M_{\rm a}^{2} R_\rho \right].$     (17)

As can be seen from Eqs. (14) and (15) in this approximation for $\zeta=4$, corresponding to 80 AU, the magnetic induction nearly vanishes.

The Archimedian Parker field is assumed to behave as frozen-in the solar wind flow. This is derived from the well-known frozen-in field condition:

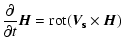$\displaystyle \frac{\partial}{\partial t}\vec{H}={\rm rot}(\vec{V_{\rm s}}\times\vec{H})$     (18)

which itself is derived from Maxwell's equation:
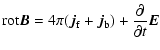$\displaystyle {\rm rot}\vec{B}=4\pi(\vec{j}_{\rm f}+\vec{j}_{\rm b})+\frac{\partial}{\partial t}\vec{E}$     (19)

with  $\vec{j}_{\rm f}$ and  $\vec{j}_{\rm b}$ denoting the free and bound electrical currents. With  ${\rm rot}\vec{M}=\vec {j}_{\rm b}$ and  $\vec{H}=\vec{B}-4\pi\vec{M}$one thus obtains the above equation in the usual Maxwellian style:
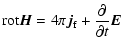$\displaystyle {\rm rot}\vec{H}=4\pi\vec{j}_{\rm f}+\frac{\partial}{\partial t}\vec{E}$     (20)

and with the generalized Ohm's law $\vec{j}_{\rm f}=\sigma(\vec{E}+\frac{1} {c}(\vec{V_{\rm s}}x\vec{H}))$ and high values of an electric conductivity one then is lead to the well known results, where in the vacuum the magnetic induction is equal to the magnetic field. In our case we write the Parker spiral field as:
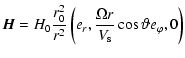$\displaystyle \vec{H} = H_{0} \frac{r_0^2}{r^2} \left(e_r,\frac{\Omega r}{V_{\rm s}} \cos \vartheta e_{\varphi}, 0\right)$     (21)

where $\Omega$ is the solar rotation frequency and H0 a reference value of the magnetic field at Earth.

Of interest in the ecliptic of the outer heliosphere is only the $\varphi$-component of the magnetic field. With the help of Eq. (17), we then find for the magnetic induction $B_\varphi$:

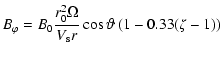$\displaystyle B_\varphi = B_{0} \frac{r_0^2 \Omega}{V_{\rm s} r} \cos \vartheta \left(1 - 0.33 (\zeta - 1)\right)$     (22)

where we have assumed that the diamagnetic effect is negligible at Earth and hence B0 = H0. Thus the Parker spiral "field'' should appear as fairly reduced at large distances, where it mainly becomes an azimuthal field. This on the basis of the above simplified approach predicts the decrease of measurable azimuthal field components with respect to the Parker expectations.

Perhaps in a more detailed consideration it also needs to be studied that pick-up ions not only represent bound currents  $\vec{j}_{\rm b}$, but they also contribute to "free'' electric currents  $\vec{j}_{\rm f}$ for the period of time, $\tau_{\eta\eta}$, before they become fully isotropized by pitch angle scattering, i.e. as long as they are slipping along the local field lines. These currents can be estimated by  $\vec{j}_{\rm f}\simeq en_{\rm H}n_{\rm s}\sigma_{\rm ex}V_{\rm s}\tau_{\eta\eta }(\vec{V}_{\rm s}-\vec{h} (\vec{V}_{\rm s}\cdot\vec{h}))$and they are mainly oriented in radial direction and thus cause a latitudinal gradient of the azimuthal field component by means of the relation:  ${\rm rot}\vec{H} = 4 \pi e n_{\rm H} n_{\rm s} \sigma_{\rm ex} V_{\rm s} \tau_{\eta\eta} \vec{V}_{\rm s}$.

3 Application to the termination shock

The Rankine-Hugoniot field relation for the MHD shock given by the Poisson bracket reads (see e.g. Diver 2001; McKenzie & Westphal 1969; Baumjohann & Treumann 1996): $\lbrack\vec{n}\times(\vec{V}_{\rm s}\times\vec{H})]=0$, where $\vec{n}$ is the unit vector of the shock normal.

For the measurable magnetic field $\vec{B}$ in a magnetized background plasma the above relation thus translates to:

$\displaystyle \left[\vec{n} \times (\vec{V}_{\rm s}\times\vec{H})\right]= \left[ \vec{n} \times (\vec{V}_{\rm s} \times (\vec{B} - 4 \pi \vec{M} )) \right]=0.$     (23)

Especially for the case of the nose region of the solar wind termination shock which represents a perpendicular shock, i.e. with  $\vec{n} \cdot\vec{B}=0$and  $\vec{n}\times\vec{V}_{\rm s}=0$, one hence derives with the above relation:

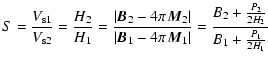$\displaystyle S = \frac{V_{{\rm s1}}}{V_{{\rm s2}}}=\frac{H_{2}}{H_{1}} = \frac... ...\vec{M}_1\right\vert} = \frac{B_2 + \frac{P_2}{2 H_2}}{B_1 + \frac{P_1}{2 H_1}}$     (24)

where S is the compression ratio and  $H = \vert\vec{B} - 4\pi \vec{M}\vert = B + p/2H$ (collinear vectors). Pre- and post-shock quantities are denoted by the indices 1 and 2, respectively. With some algebraic manipulations, we get from Eq. (25):
 
$\displaystyle S = \frac{\frac{B_2} {B_1} + \frac{P_2}{2 H_2 B_1}}{\frac{H_1}{B_... ..._2}{H_1} \frac{P_2}{2 H_2^2} \left(1 - \frac{P_1}{2 H_1^2} \right)^{-1} \right)$     (25)

where we have made use of Eqs. (11) and (17). Solving for the magnetic compression ratio  RB = B2/B1 yields:
 
$\displaystyle R_B = \frac{B_2}{B_1} = \frac{S}{1 - \frac{P_1}{2 H_1^2}} \left(1 - \frac{P_2}{2 H_2^2}\right)\cdot$     (26)

>From the magneto-hydrodynamic Rankine-Hugoniot shock relations (see e.g. Diver 2001) one obtains:

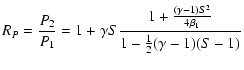$\displaystyle R_P = \frac{P_2}{P_1} = 1 + \gamma S \frac{1 + \frac{(\gamma - 1) S^2}{4 \beta_1}}{1 - \frac{1}{2} (\gamma -1) (S - 1)}$     (27)

with the ratio $\beta_{1}$ of the speed of sound to the Alfvén speed, i.e. $\beta_1 = c_1^2 / v_{A_{1}}^2 = 8 \pi \gamma P_1 / H^2_1 = M_{A_{1}}^2/M_{\rm s_{1}}^2$. With Eqs. (30) and (31) one finally finds
 
$\displaystyle R_B = \frac{S}{1 - \frac{\beta_1}{8 \pi \gamma} } \left(1 - \frac{\beta_1}{8 \pi \gamma} \frac{R_p}{S^{2}}\right)\cdot$     (28)

The functional dependence for the ratio RB/S is shown in Fig. 1 for five different values of  $M_{{\rm A}_{1}}/M_{{\rm s}_{1}}$. It can be seen that the compression ratio S can be smaller or larger than the magnetic compression ratio RB, while in the non-diamagnetic case they are identical. Furthermore, for very large compression ratios S the standard magnetohydrodynamic Rankine-Hugoniot relations are no longer valid, since $R_{\rm b}$ depends on  $R_{\rm p} \rightarrow \infty$ for  $S \rightarrow 4$, leading to negative values of  $R_{\rm b}/S$.

Nevertheless, we can state here that without the knowledge of the Alfvén Mach number  $M_{{\rm A}_{1}}$ and the plasma Mach number  $M_{{\rm s}_{1}}$ the magnetic compression ratio RB cannot be fixed and not be connected with the standard compression ratio S.


  \begin{figure} \par\includegraphics[width=7cm,clip]{Gc293_f1.eps} \end{figure} Figure 1: The ratio RB/S as function of the standard compression ratio S. The labels at the curves are the ratio of the Alfvén Mach number to the plasma Mach number  $m = M_{{\rm A}_{1}}/M_{{\rm s}_{1}}$.
Open with DEXTER

4 Conclusion and discussion

We have shown, that the diamagnetic effect of PUIs has to be taken into account, because it reduces dramatically the magnetic induction in the solar wind with increasing distances. In order to get an analytic expression, we had to make some moderate simplifications to the problem. Therefore, we derived only upper limits of the diamagnetic effect, but we clearly have shown, that the decrease in the magnetic induction $\vec{B}$ due to the diamagnetism of the pickup ion plasma has to be taken into account.

Furthermore we have shown, that the magnetic compression ratio RB and the standard compression ratio S are related in a complicated way and cannot be determined from each other without the knowledge of the sound speed and Alfvén speed at the shock.

Similar complications should also arise at cometary shocks, however, here the pick-up ion diamagnetism is harder to estimate since the resulting distribution functions are not well known.

Acknowledgements
The authors are grateful for financial support granted to them by the Deutsche Forschungsgemeinschaft in the frame of the project "Heliotrigger'' (Fa 97/28-1).

References


Copyright ESO 2004